Additive Manufacturing of Smart Composite Structures Based on Flexinol Wires
Abstract
1. Introduction
- -
- pseudo-elasticity phenomenon;
- -
- unidirectional shape memory effect;
- -
- bi-directional shape memory effect.
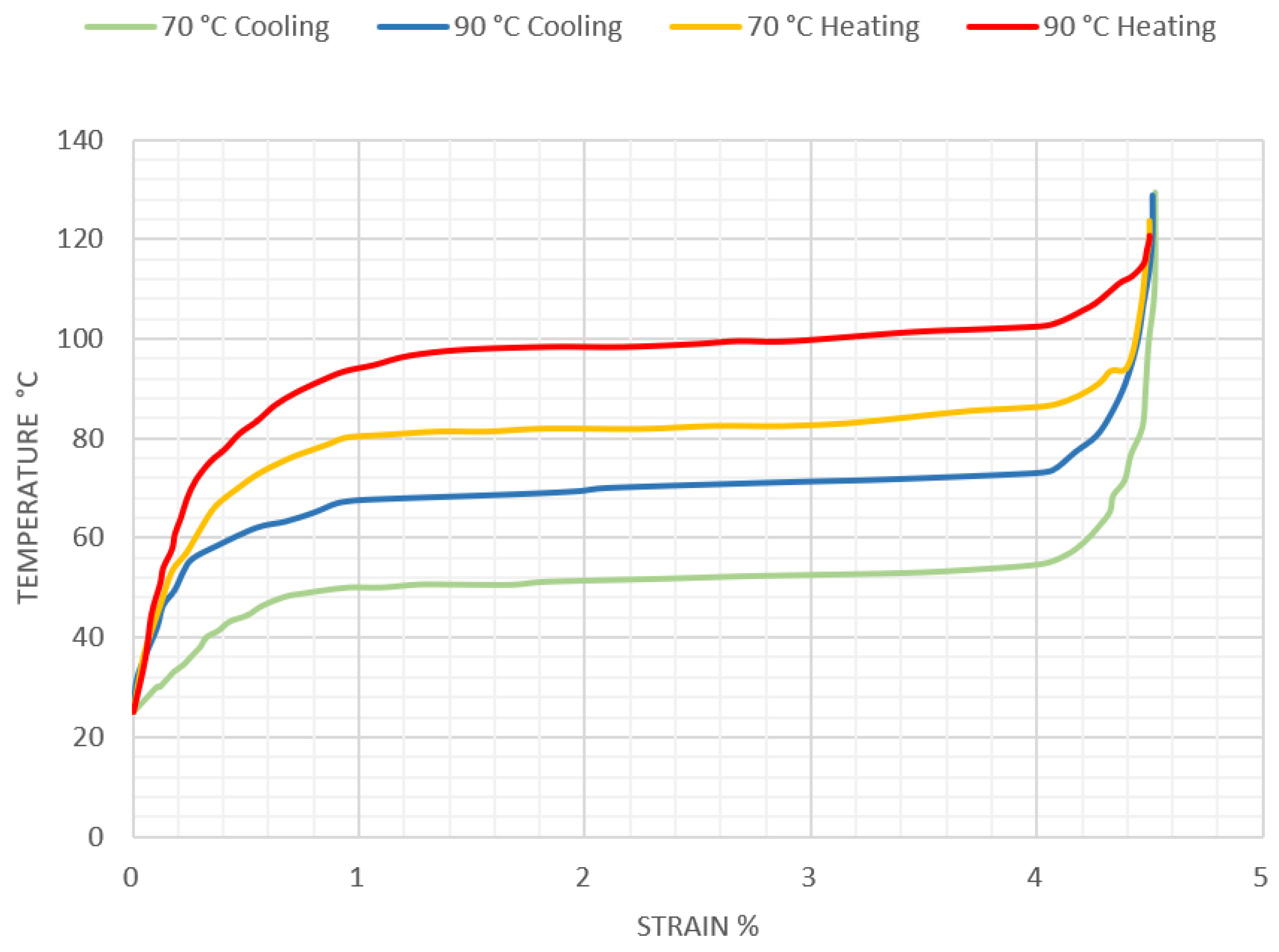
2. Materials
3. Method
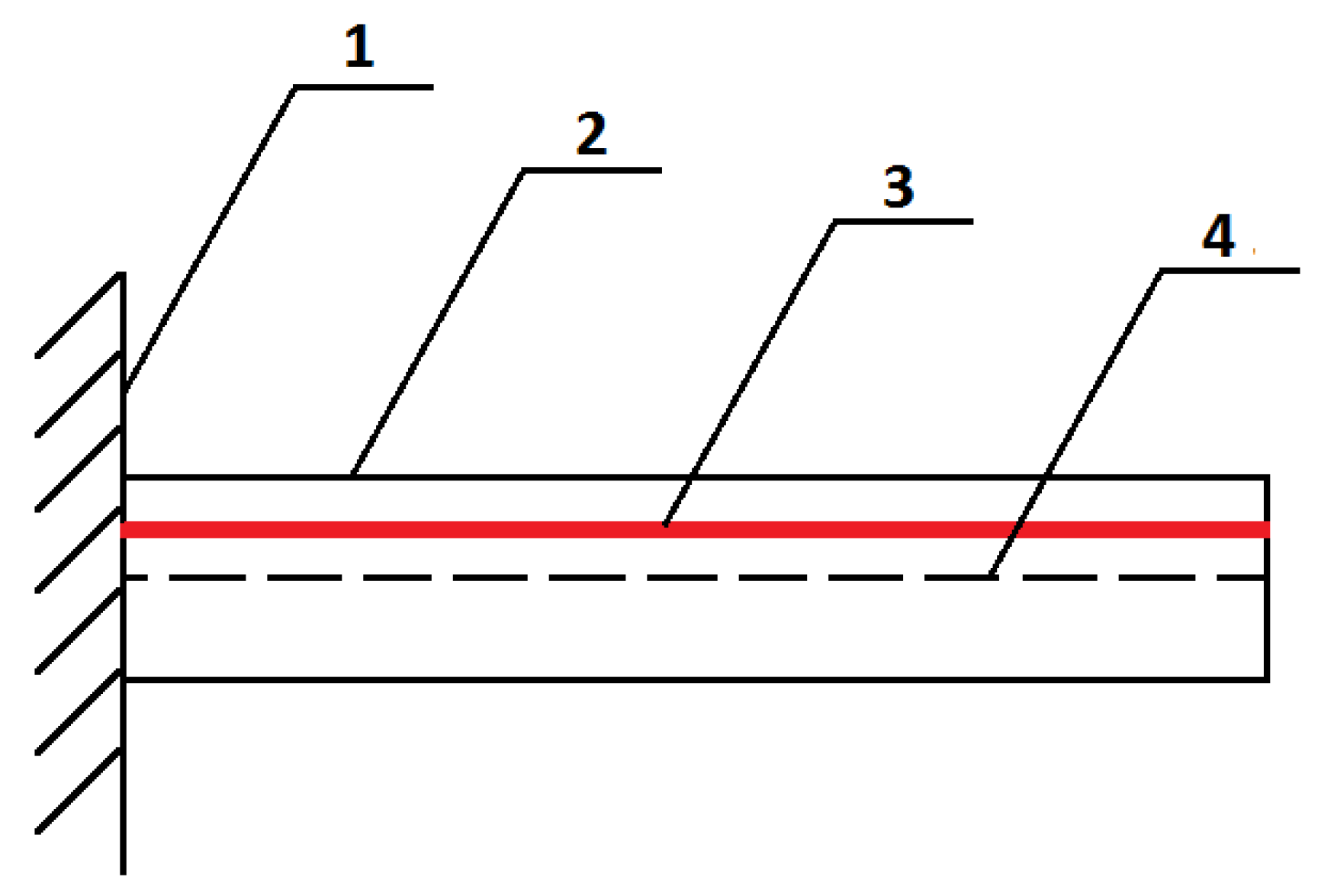
3.1. Analytical Model
3.2. Numerical Model
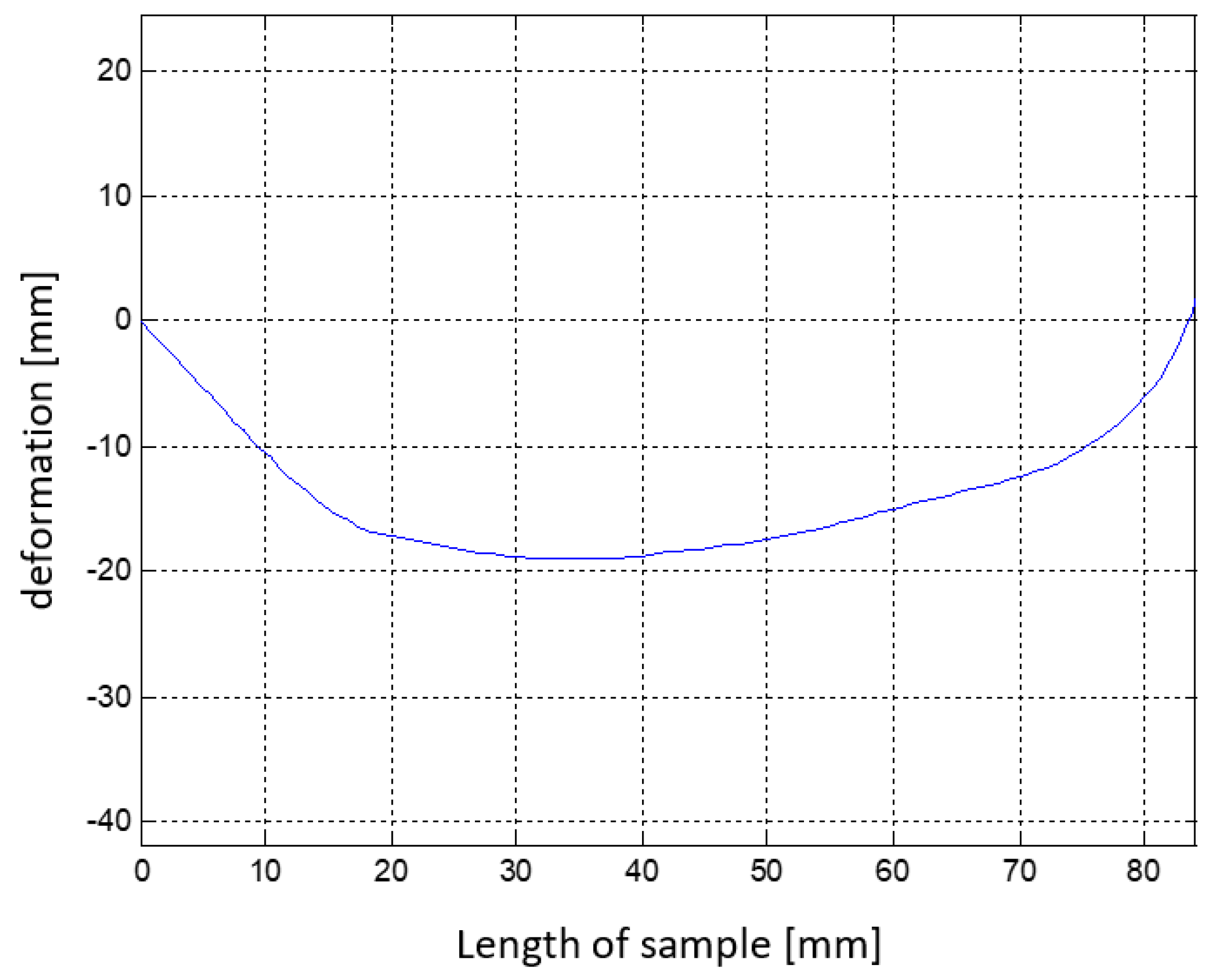
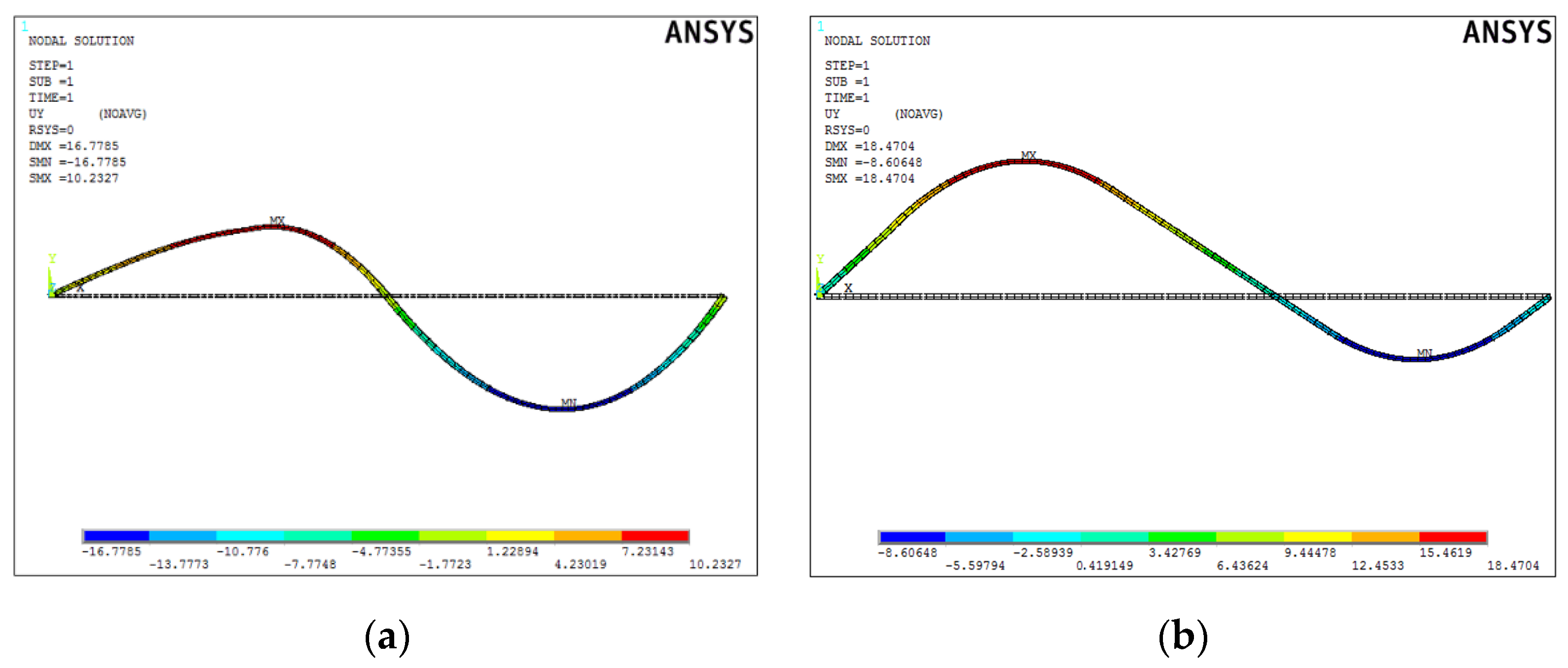
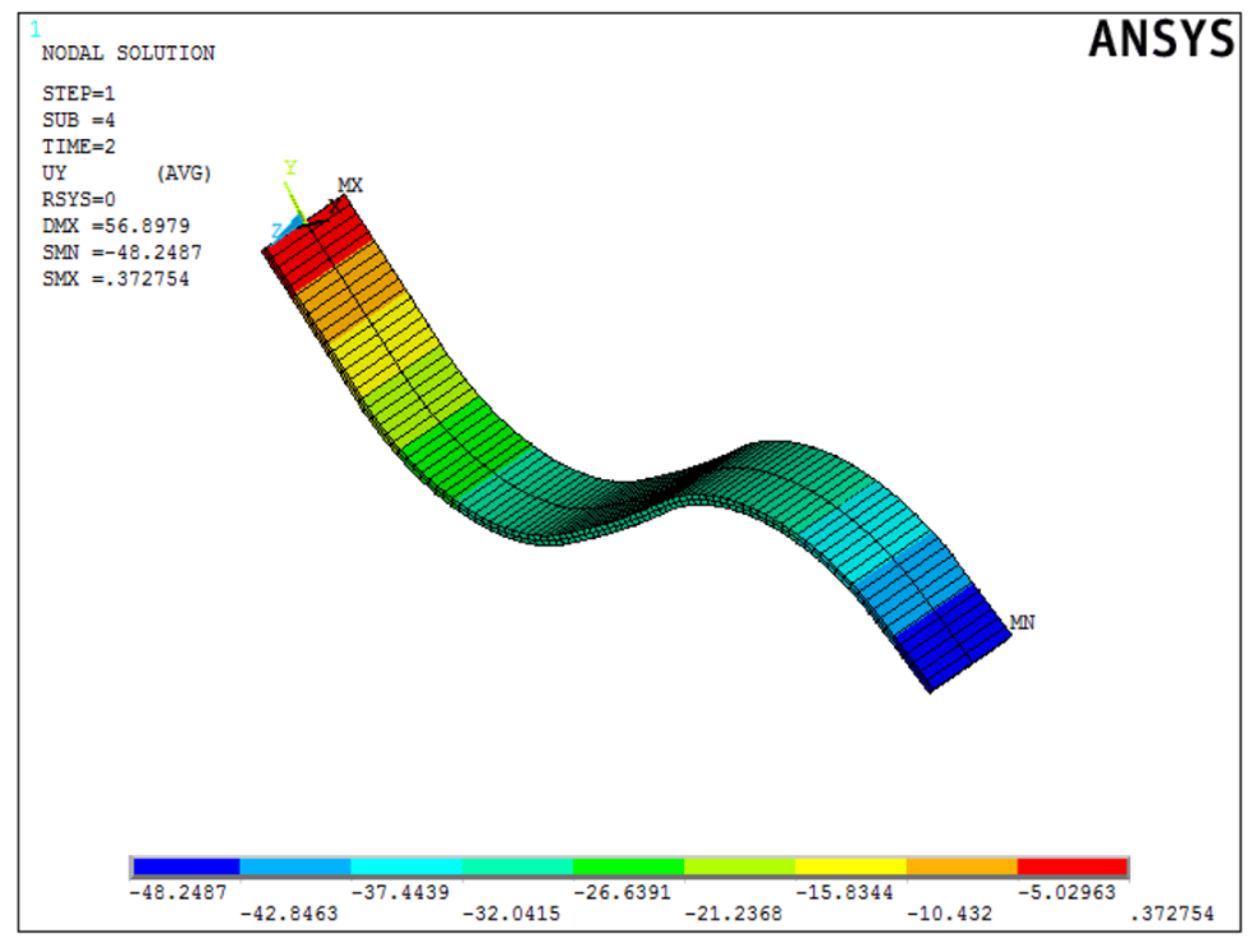
4. Results
4.1. Sensitivity Analysis
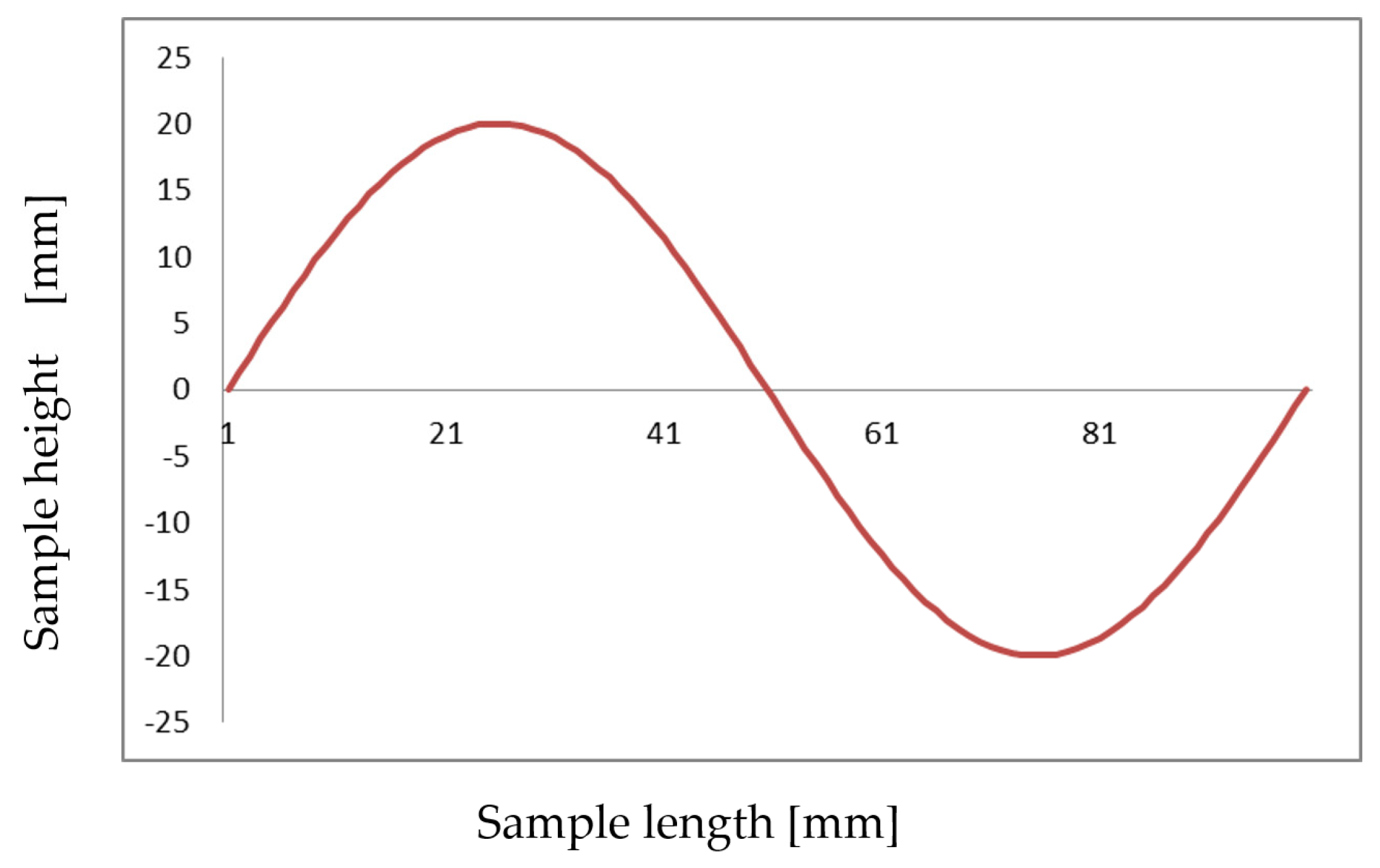
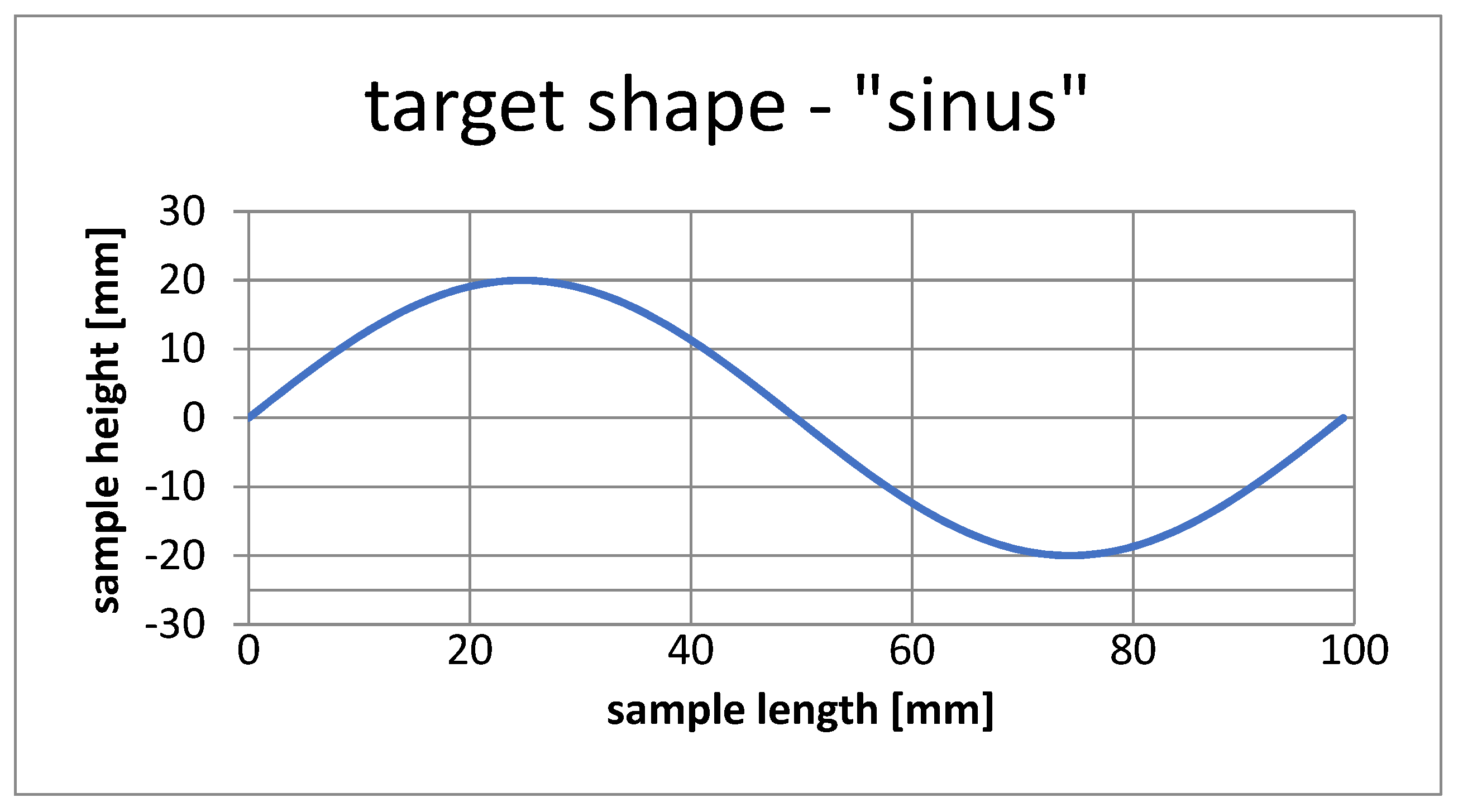
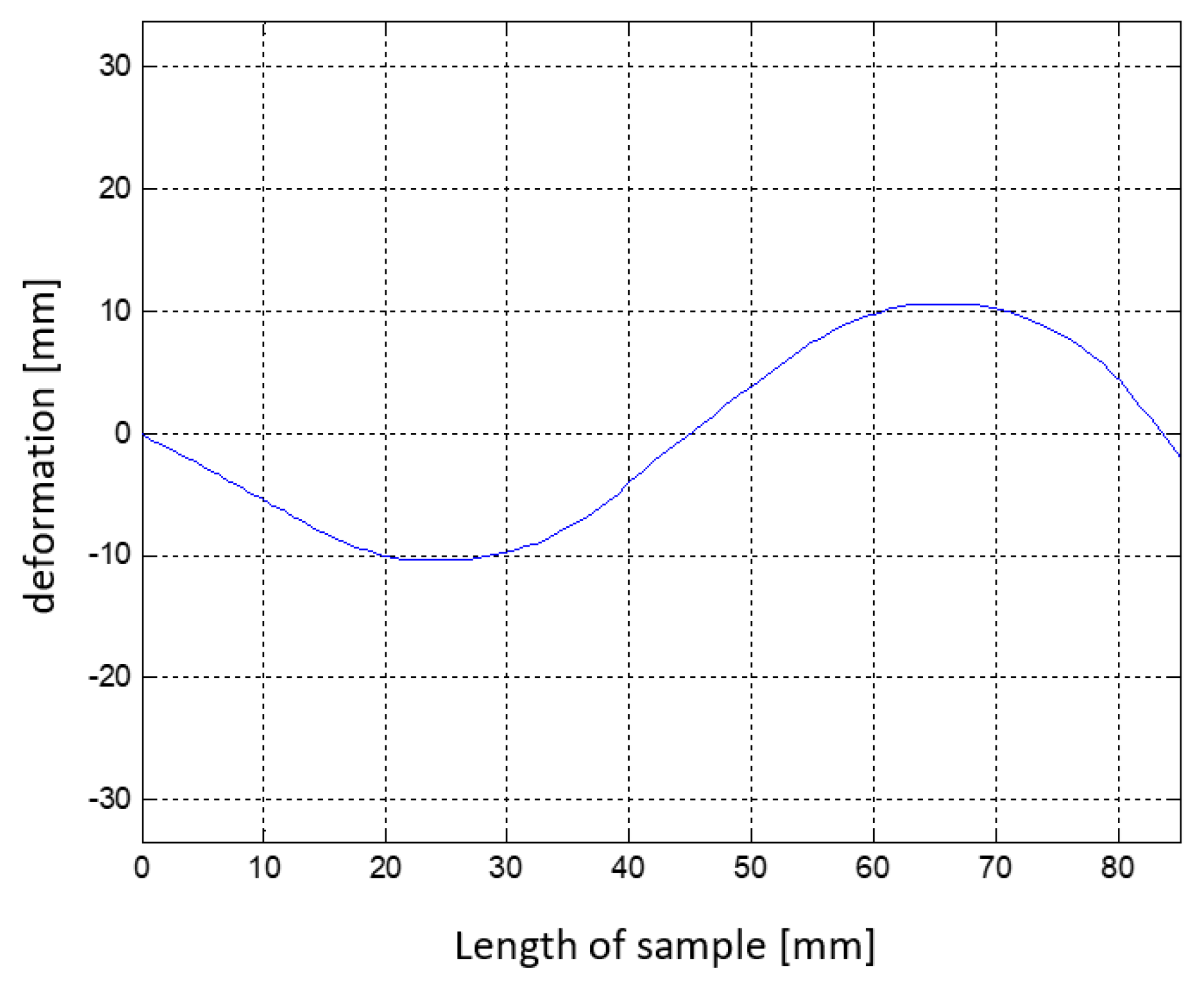
4.2. Shape Pattern ‘Sinus’ Simulation
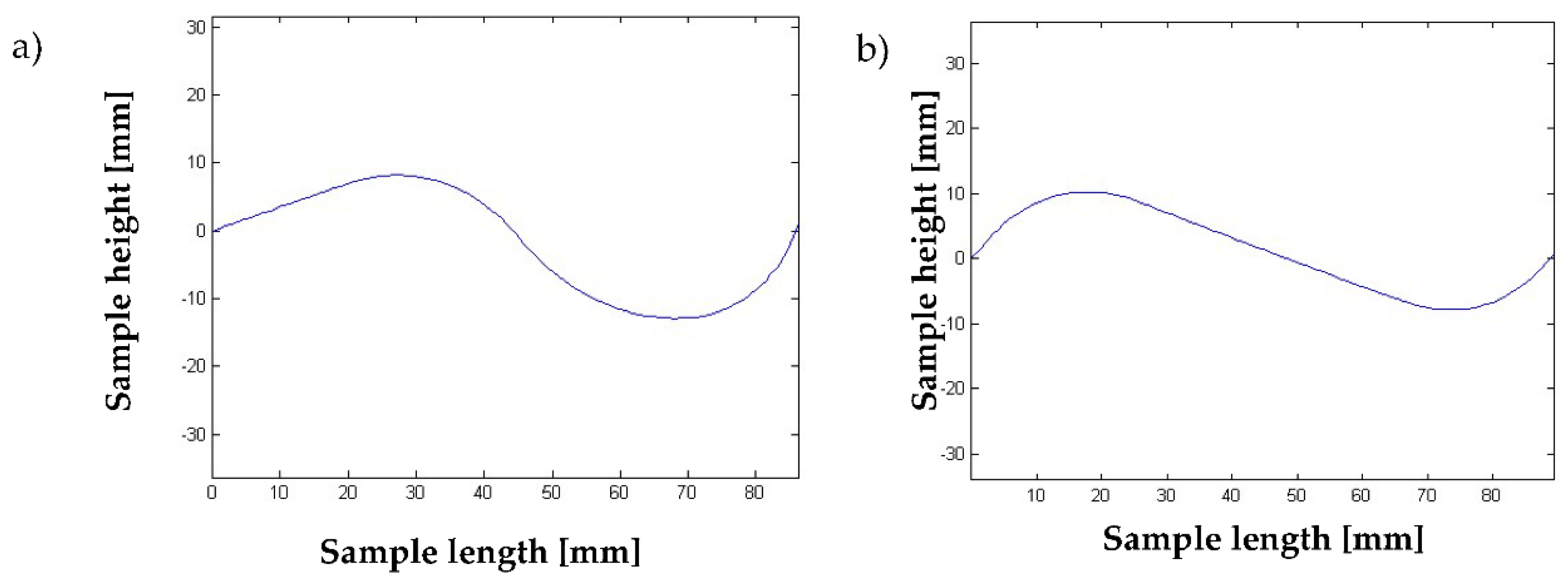
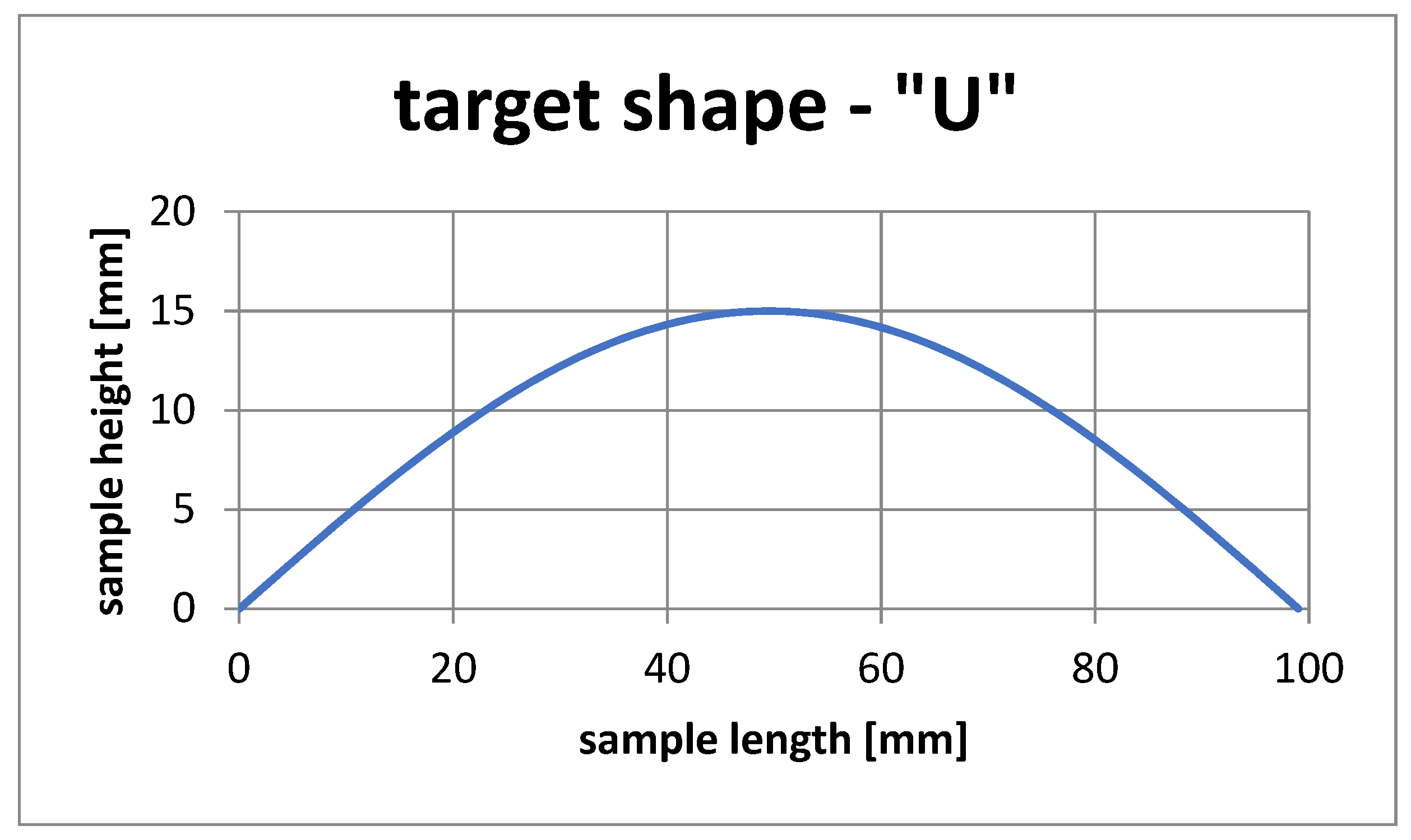
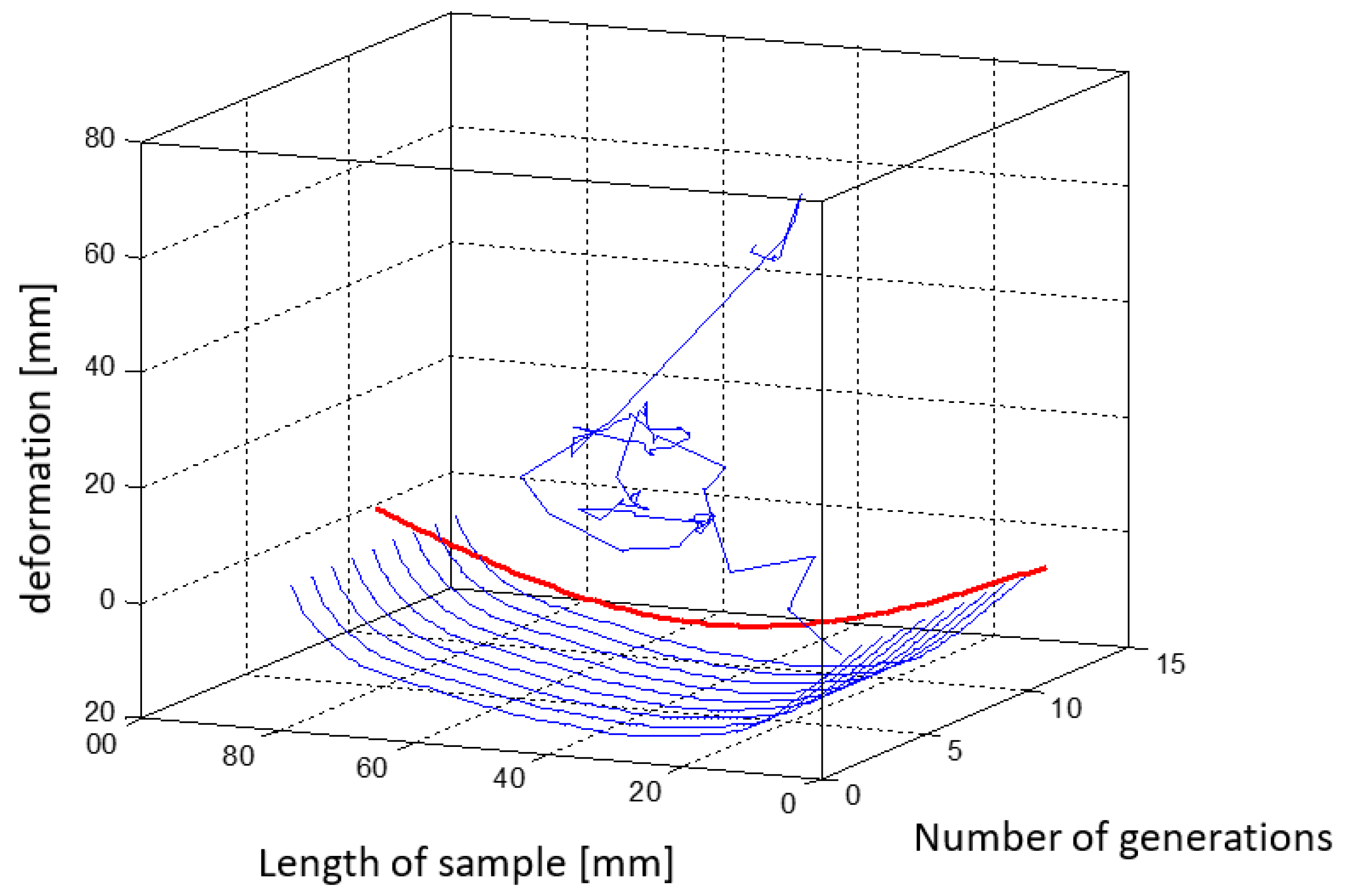
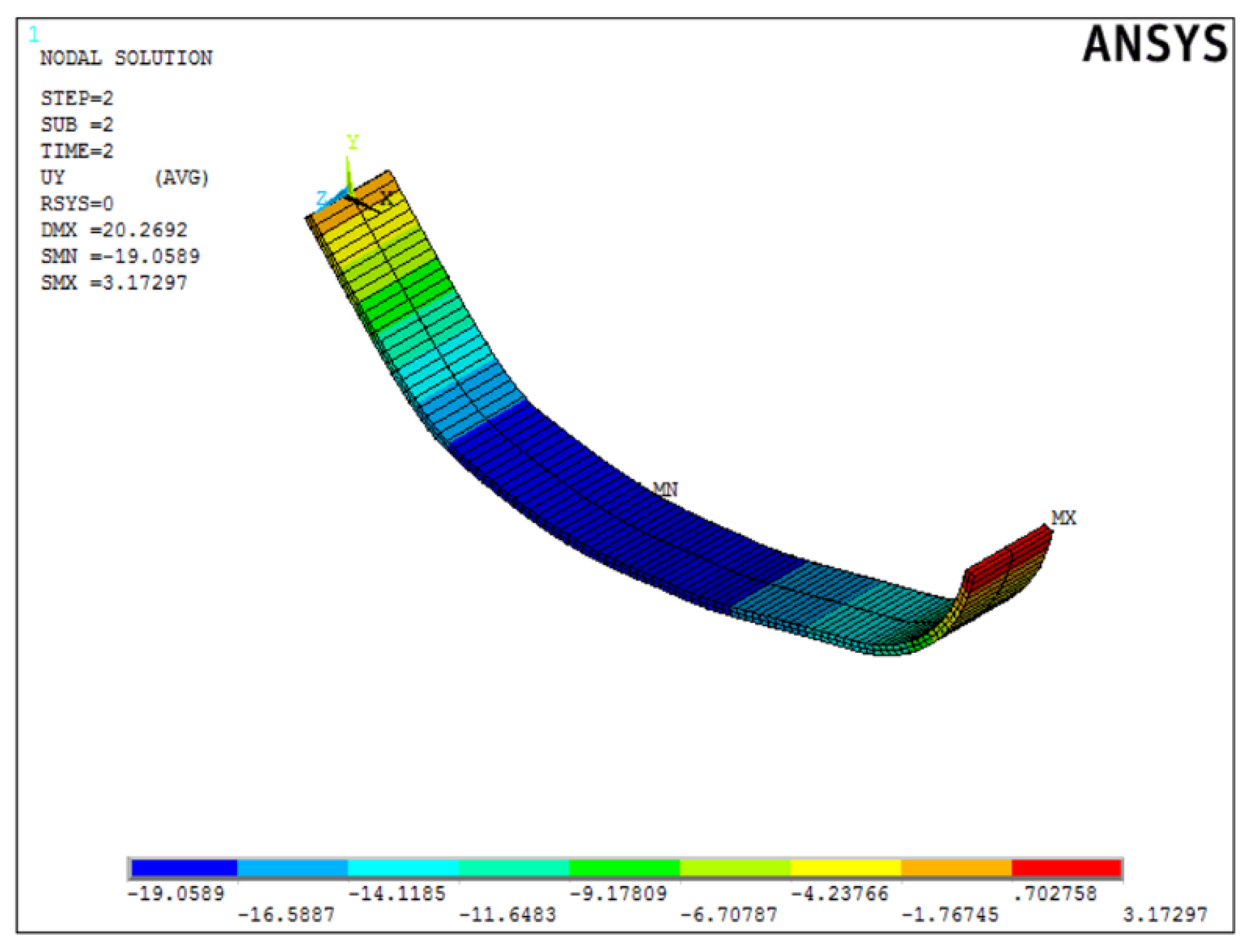
4.3. Shape Pattern ‘U’ Simulation
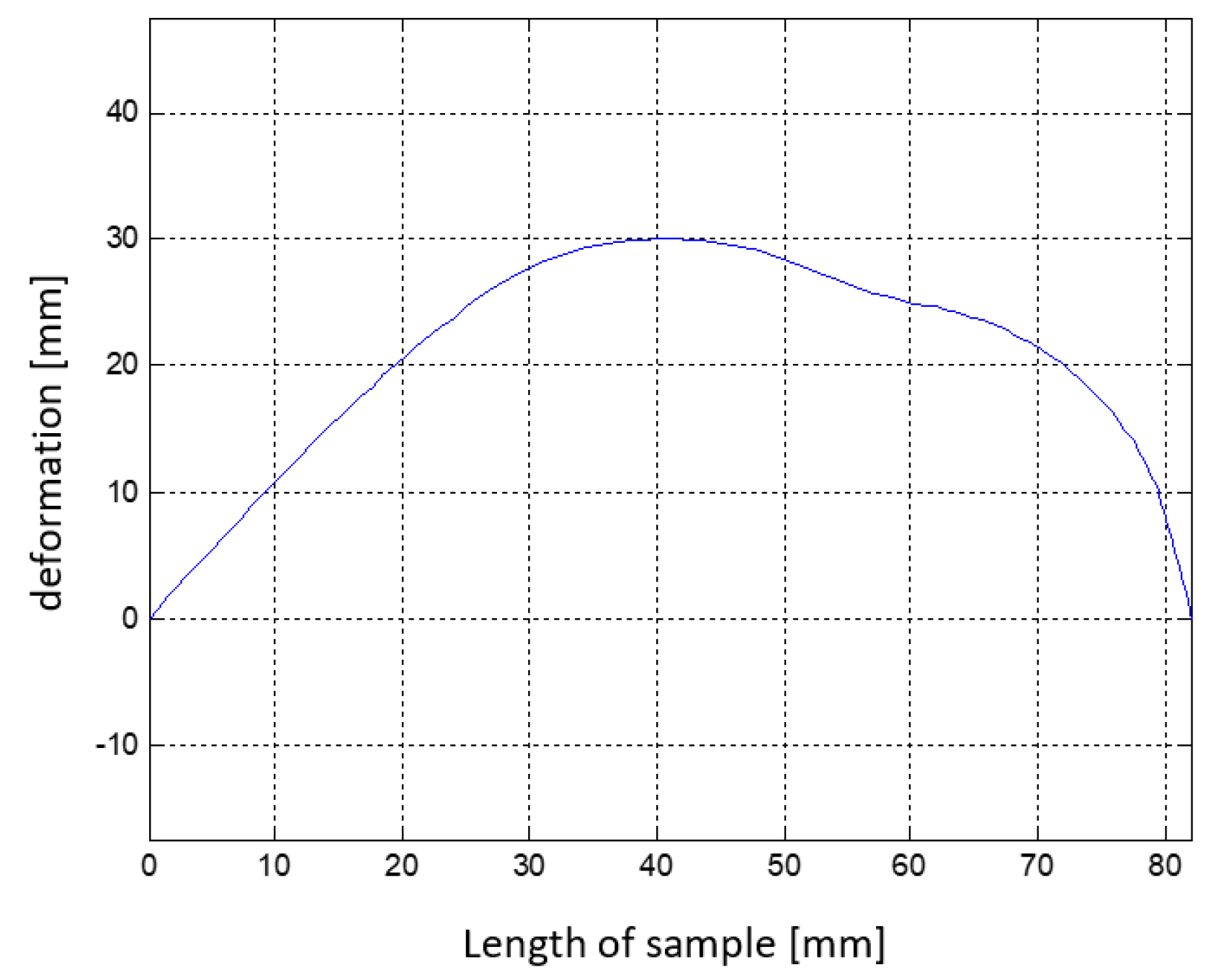
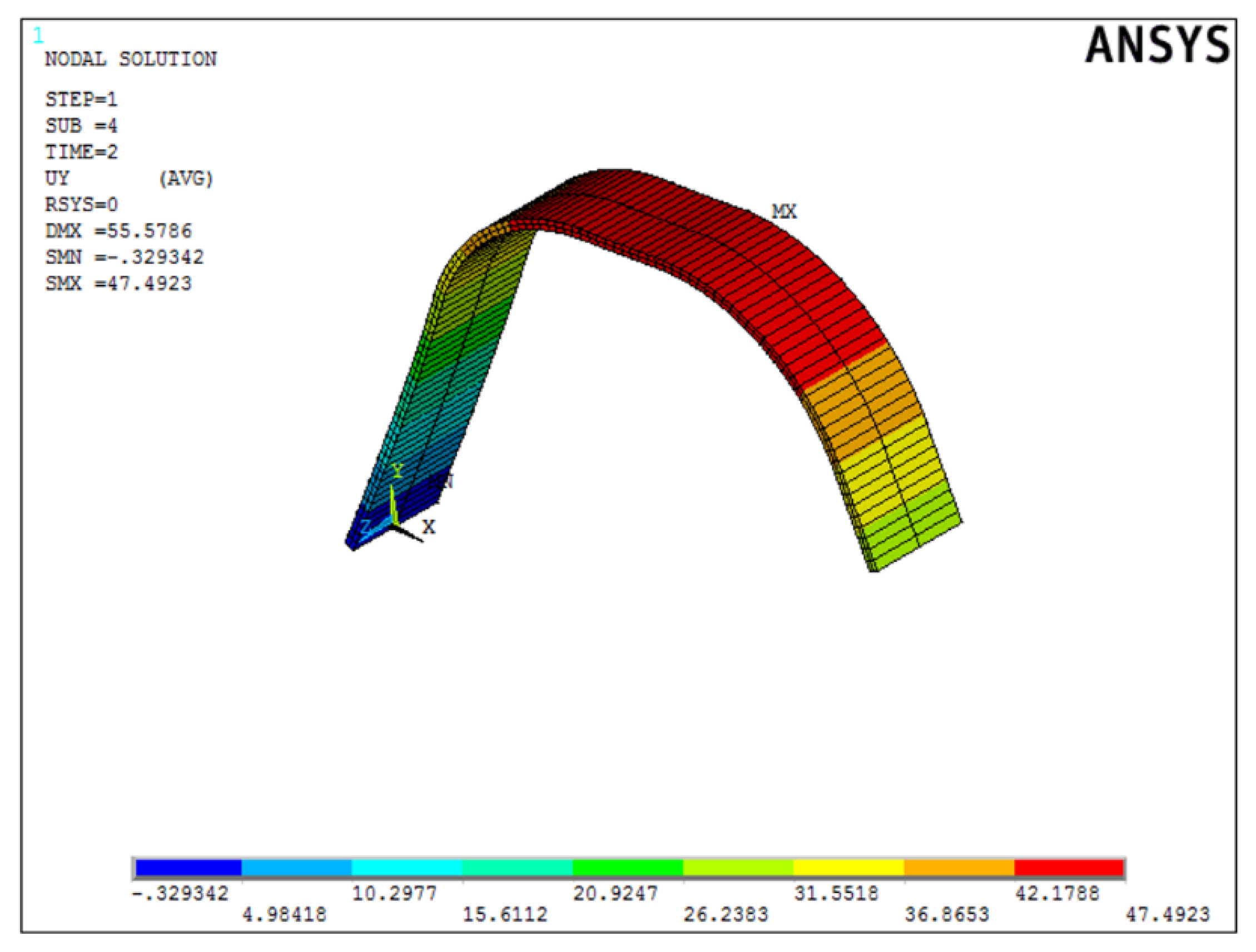
4.4. Shape Pattern “Trapezium” Simulation
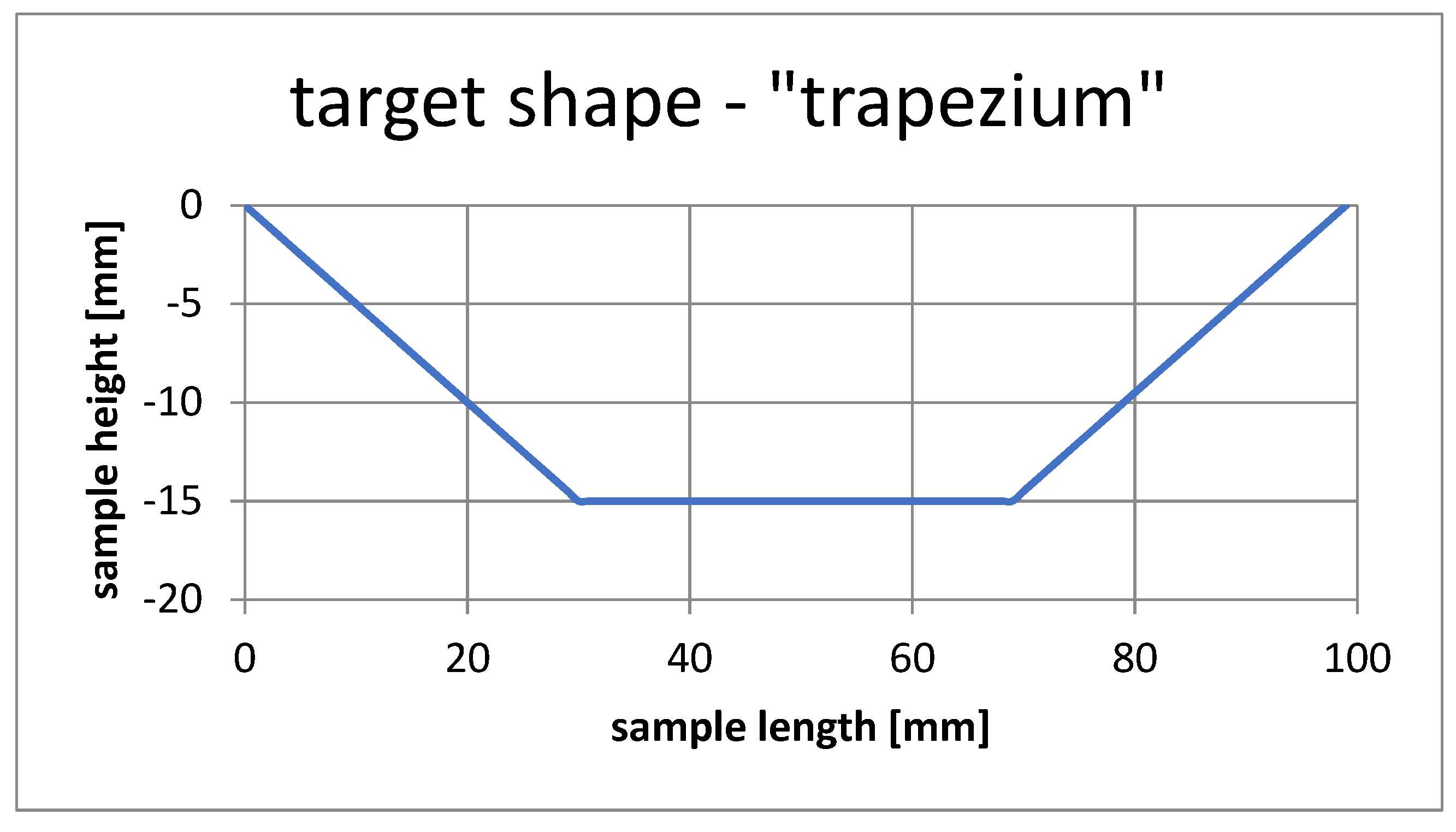

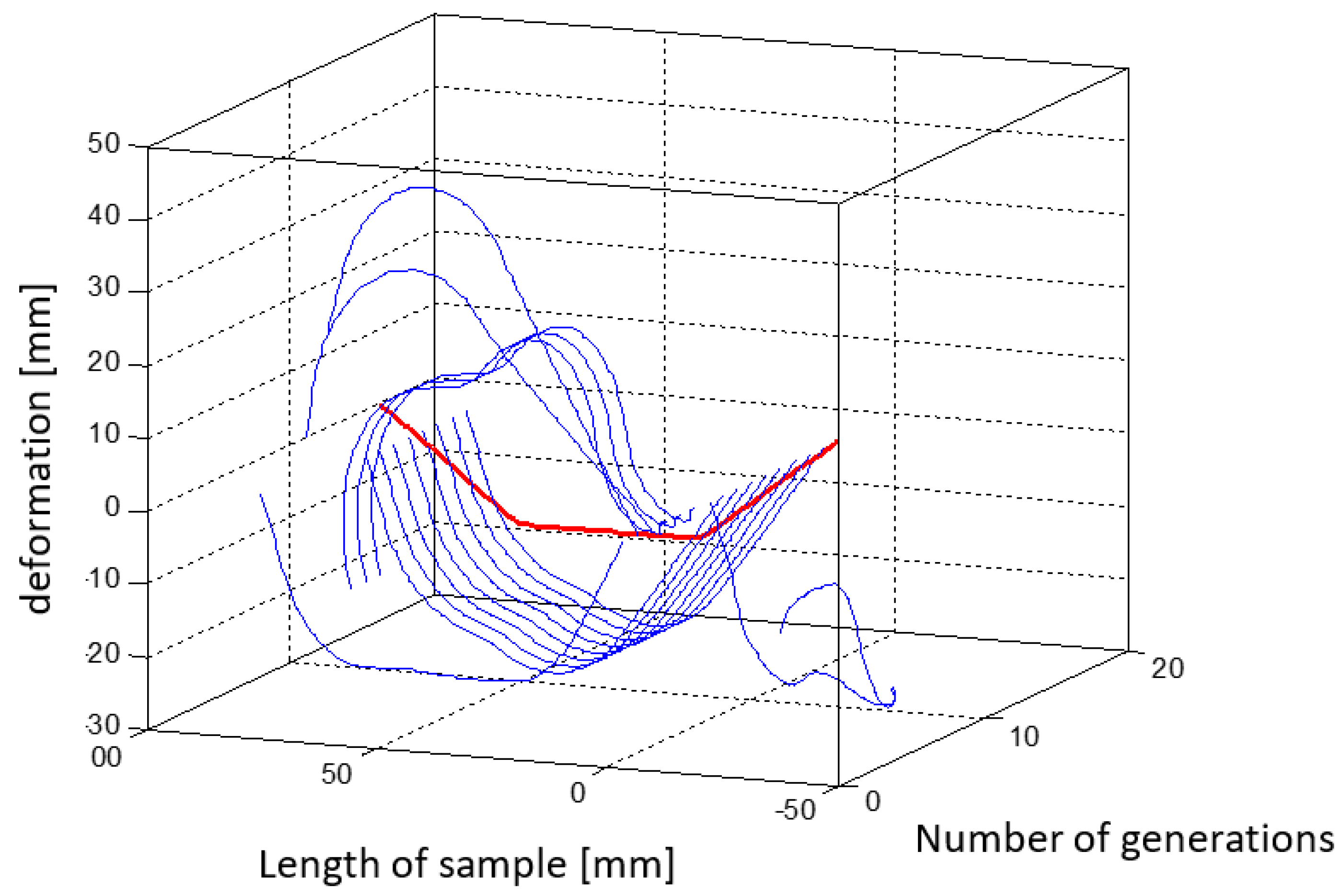
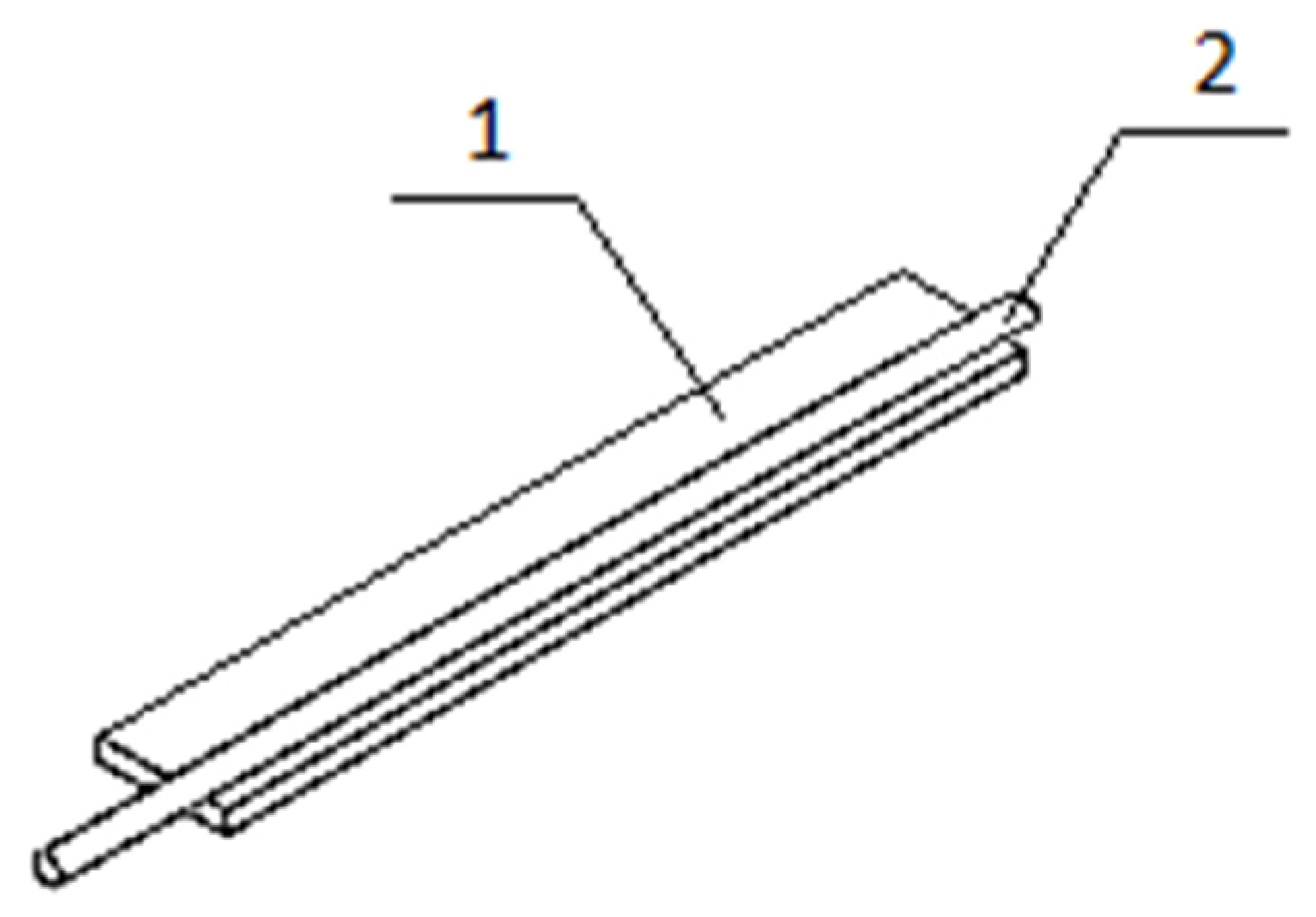
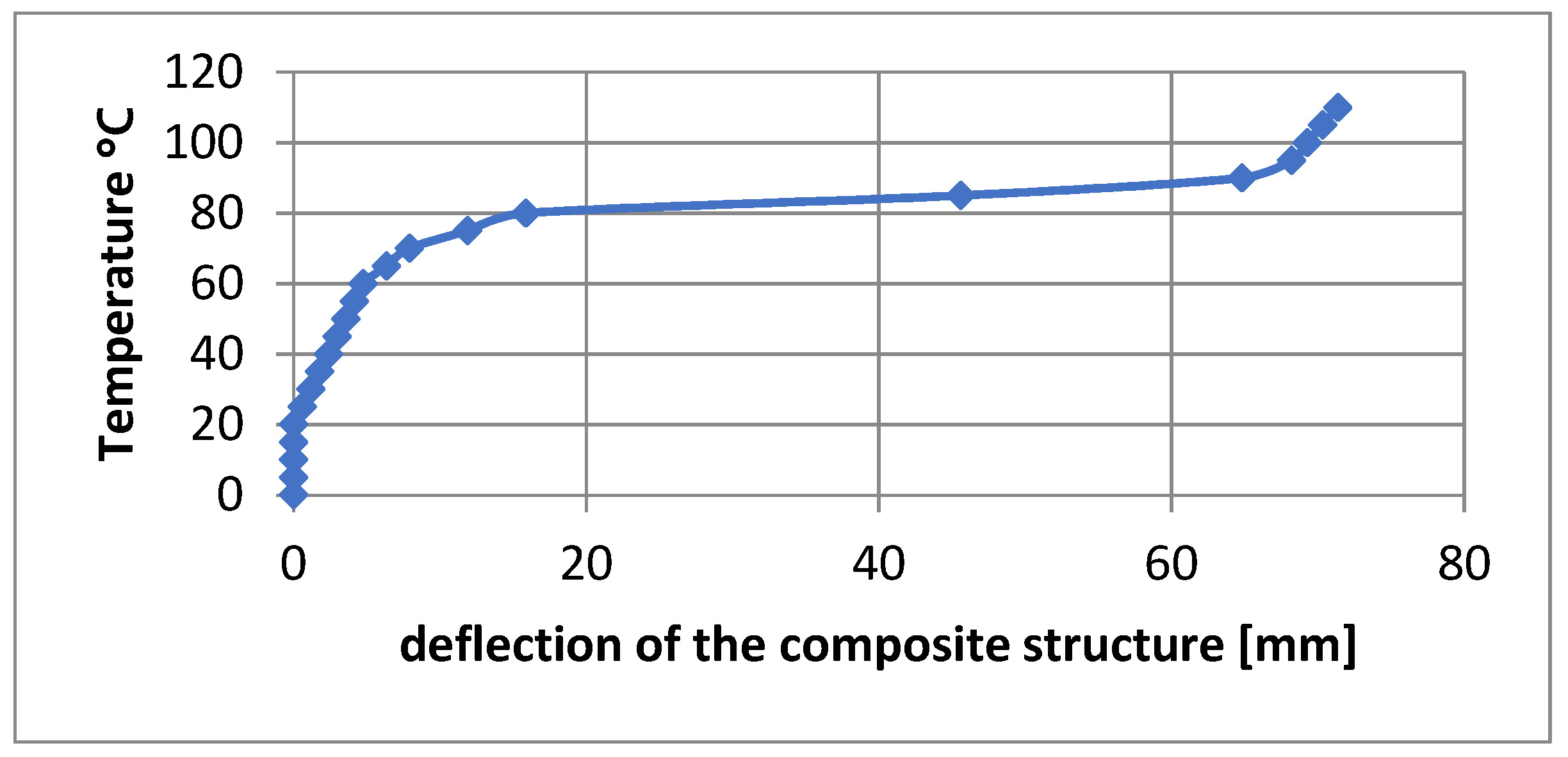
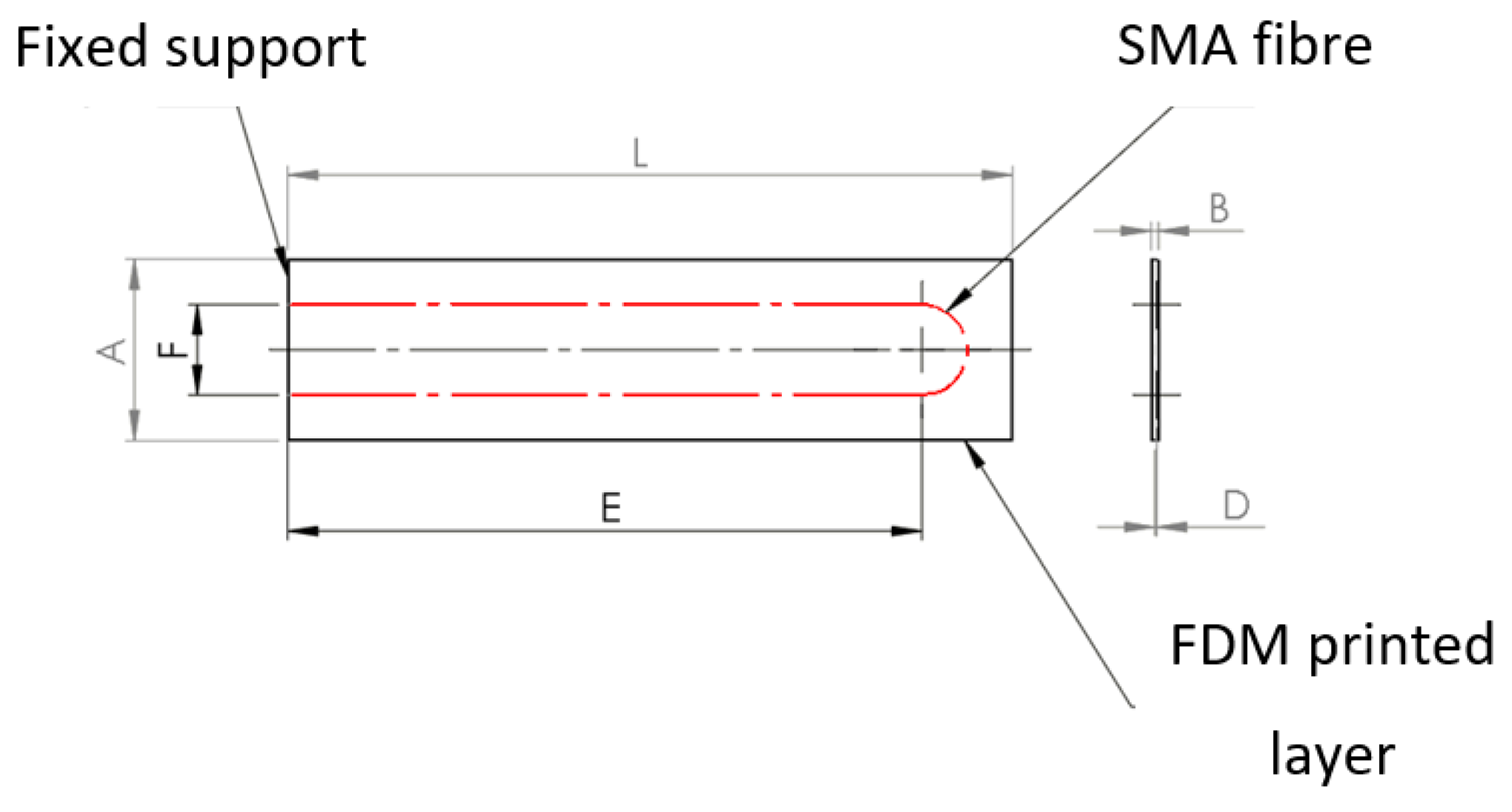
5. Sample of Actuator
6. Conclusions
7. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tibbits, T.; McKnelly, C.; Olguin, C.; Dikovsky, D. 4D printing and universal transformation. In Proceedings of the 34th Annual Conference of the Association for Computer Aided Design in Architecture, 23–25 October 2014; pp. 539–548. [Google Scholar]
- Tibbits, S. The emergence of 4D printing. In Proceedings of the Paper Presented at the TED Conference, Long Beach, CA, USA, 27 February 2013. [Google Scholar]
- Sadasivuni, K.K.; Deshmukh, K.; Almaadeed, M.A. 3D and 4D Printing of Polymer Nanocomposite Materials; Elsevier: Amsterdam, The Netherlands, 2020; pp. 1–24. ISBN 9780128168059. [Google Scholar]
- Alshahrani, H.A. Review of 4D printing materials and reinforced composites: Behaviors, applications and challenges. J. Sci. Adv. Mater. Devices 2021, 6, 167–185. [Google Scholar] [CrossRef]
- Momeni, F.; Liu, X.; Ni, J. A review of 4D printing. Mater. Des. 2017, 122, 42–79. [Google Scholar] [CrossRef]
- Mu, T.; Liu, L.; Lan, X.; Liu, Y.; Leng, J. Shape memory polymers for composites. Compos. Sci. Technol. 2018, 160, 169–198. [Google Scholar] [CrossRef]
- Ali, H.; Abilgaziyev, A.; Adair, D. 4D printing: A critical review of current developments, and future prospects. Int. J. Adv. Manuf. Technol. 2019, 105, 701–717. [Google Scholar] [CrossRef]
- Joshi, S.; Rawat, K.; Karunakaran, C.; Rajamohan, V.; Mathew, A.T.; Koziol, K.; Thakur, V.K.; Balan, A.S.S. 4D printing of materials for the future: Opportu-nities and challenges. Appl. Mater. Today 2020, 18, 100490. [Google Scholar] [CrossRef]
- Park, J.; Headings, L.M.; Dapino, M.J.; Baur, J.W.; Tandon, G.P. Investigation of interfacial shear stresses, shape fixity, and actuation strain in composites incorporating shape memory polymers and shape memory alloys. Front. Mater. 2015, 2, 12. [Google Scholar] [CrossRef][Green Version]
- Leist, S.K.; Zhou, J. Current status of 4D printing technology and the potentialof light-reactive smart materials as 4D printable materials materials as 4Dprintable materials. Virtual Phys. Prototyp. 2016, 11, 249–262. [Google Scholar] [CrossRef]
- Zhou, J.; Sheiko, S.S. Reversibleshape-shiftingin polymeric materials. J. Polym. Sci. Part B Polym. Phys. 2016, 54, 1365–1380. [Google Scholar] [CrossRef]
- Otsuka, K.; Wayman, C. Mechanism of Shape Memory Effect and Superelasticity Shape Memory Materials, 1st ed.; Cambridge University Press: Cambridge, UK, 1999; pp. 27–48. [Google Scholar]
- Bellouard, Y. Microrobotics, Microdevices Based on Shape Memory Alloys Encyclopedia of Smart Materials; John Wiley and Sons Inc.: New York, NY, USA, 2002; pp. 620–643. [Google Scholar]
- Khan, A. Characterization and Application of Shape Memory Alloy Wires for Micro and Meso Positioning Systems. Ph.D. Thesis, UMI, Washington, DC, USA, 2008. [Google Scholar]
- Bojarski, Z.; Morawiec, H. Metale z Pamięcią Kształtu; Państwowe Wydawnictwo Naukowe: Warszawa, Poland, 1989. [Google Scholar]
- Lester, B.; Baxevanis, T.; Chemisky, Y.; Lagouda, D. Review and perspectives: Shape memory alloy composite systems. Acta Mech. 2015, 226, 3907–3960. [Google Scholar] [CrossRef]
- Aboudi, J. The response of shape memory alloy composites. Smart Mater. Struct. 1997, 6, 1. [Google Scholar] [CrossRef]
- Ni, D.; Ma, Z. Shape Memory Alloy-Reinforced Metal-Matrix Composites: A Review. Acta Metall. Sin. 2014, 27, 739–761. [Google Scholar] [CrossRef]
- Asadi, H.; Bodaghi, M.; Shakeri, M.; Aghdam, M. Nonlinear dynamics of SMA-fiber-reinforced composite beams subjected to a primary/secondary-resonance excitation. Acta Mech. 2014, 226, 437–455. [Google Scholar] [CrossRef]
- Mężyk, A.; Klein, W.; Pawlak, M.; Dudek, O. Preliminary tests of new composite material based on shape memory alloys for artificial aortic valve leaflets. In Proceedings of the International Conference on Bio-Engineering for Smart Technologies, BioSMART 2016, Dubai, United Arab Emirates, 4–7 December 2016. [Google Scholar]
- Klein, W.; Dudek, O. Preliminary investigation of fabrication composite structures by using shape memory alloys. IOP Conf. Ser. Mater. Sci. Eng. 2017, 244, 012011. [Google Scholar] [CrossRef]
- Ma, J.; Franco, B.; Tapia, G.; Karayagiz, K.; Johnson, L.; Liu, J.; Arroyave, R.; Karaman, I.; Elwany, A. Spatial control of functional response in 4D-printed active metallic structures. Sci. Rep. 2017, 7, 46707. [Google Scholar] [CrossRef]
- Wei, Z.; Sandstroröm, R.; Miyazaki, S. Shape-memory materials and hybrid composites for smart systems: Part I Shape-memory materials. J. Mater. Sci. 1998, 33, 3743–3762. [Google Scholar] [CrossRef]
- Available online: http://hackaday.com/2016/09/07/3d-printering-xt-cf20-carbon-fiber-filament-review/ (accessed on 24 May 2019).
- Available online: http://colorfabb.com/files/amphora_pds_en.pdf (accessed on 24 May 2019).
- Available online: http://tworzywa.com.pl/Wiadomo%C5%9Bci/Kopoliestry-nowe-stare-polimery-transparentne-20892.html (accessed on 24 May 2019).
- Available online: http://www.dynalloy.com/pdfs/TCF1140.pdf (accessed on 24 May 2019).
- Available online: http://www.sms.am.put.poznan.pl/eskrypty_pliki/podstawymechaniki/13wytrzymalosczlozona.pdf (accessed on 24 May 2019).
- Banasiak, M.; Grossman, K.; Trombski, M. Zbiór Zadań z Wytrzymałości Materiałów; Wydawnictwo Naukowe PWN: Warszawa, Poland, 2021; ISBN 83-01-12483-0. [Google Scholar]
- Frowd, C.D.; Hancock, P.J.B.; Carson, D. A Holistic, Evolutionary Facial Imaging Technique for Creating Composites. ACM Trans. Appl. Percept. 2004, 1, 19–39. [Google Scholar] [CrossRef]
- Fotsch, D.; Ewins, D.J. Application of MAC in the Frequency Domain; Mechanical Engineering Department, Imperial College of Science, Technology and Medicine: London, UK, 1989. [Google Scholar]
- Pastor, M.; Binda, M.; Harčarik, T. Modal Assurance Criterion. Procedia Eng. 2012, 48, 543–548. [Google Scholar] [CrossRef]
- Allemang, R. The Modal Assurance Criterion—Twenty Years of Use and Abuse. Sound Vib. 2003, 37, 14–21. [Google Scholar]

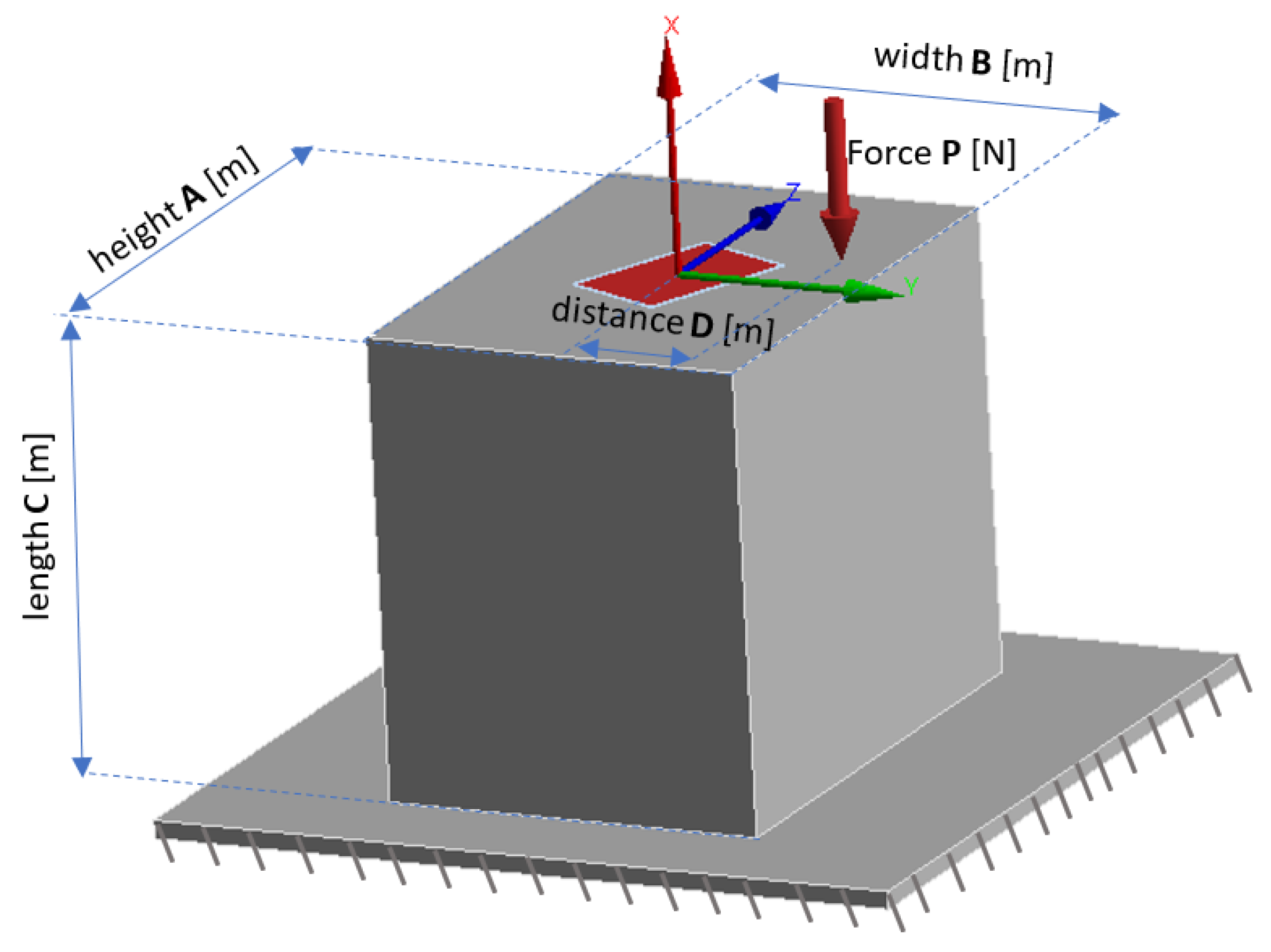
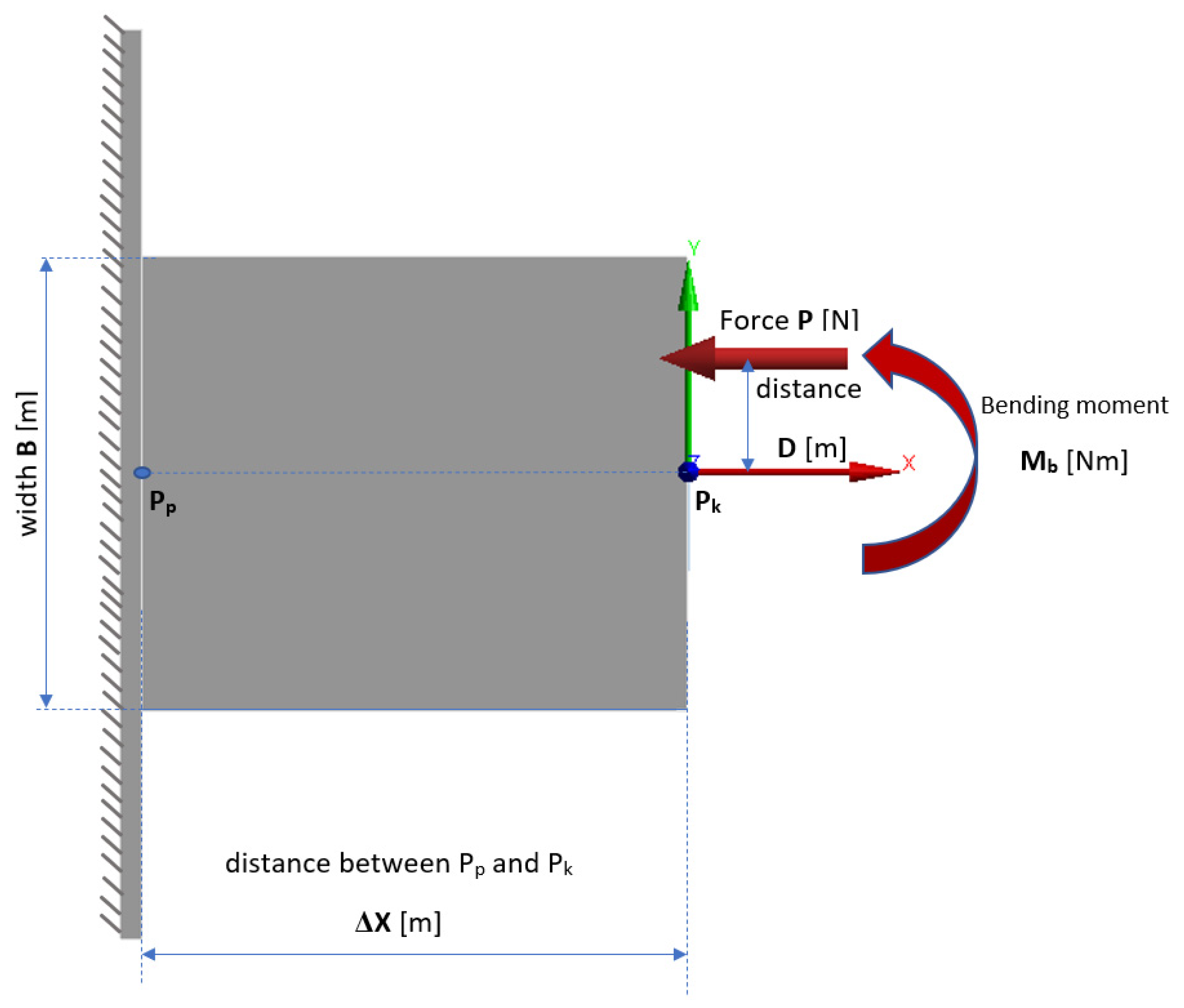






| Simulation number | 1 | 2 |
| Population size | 10 | 100 |
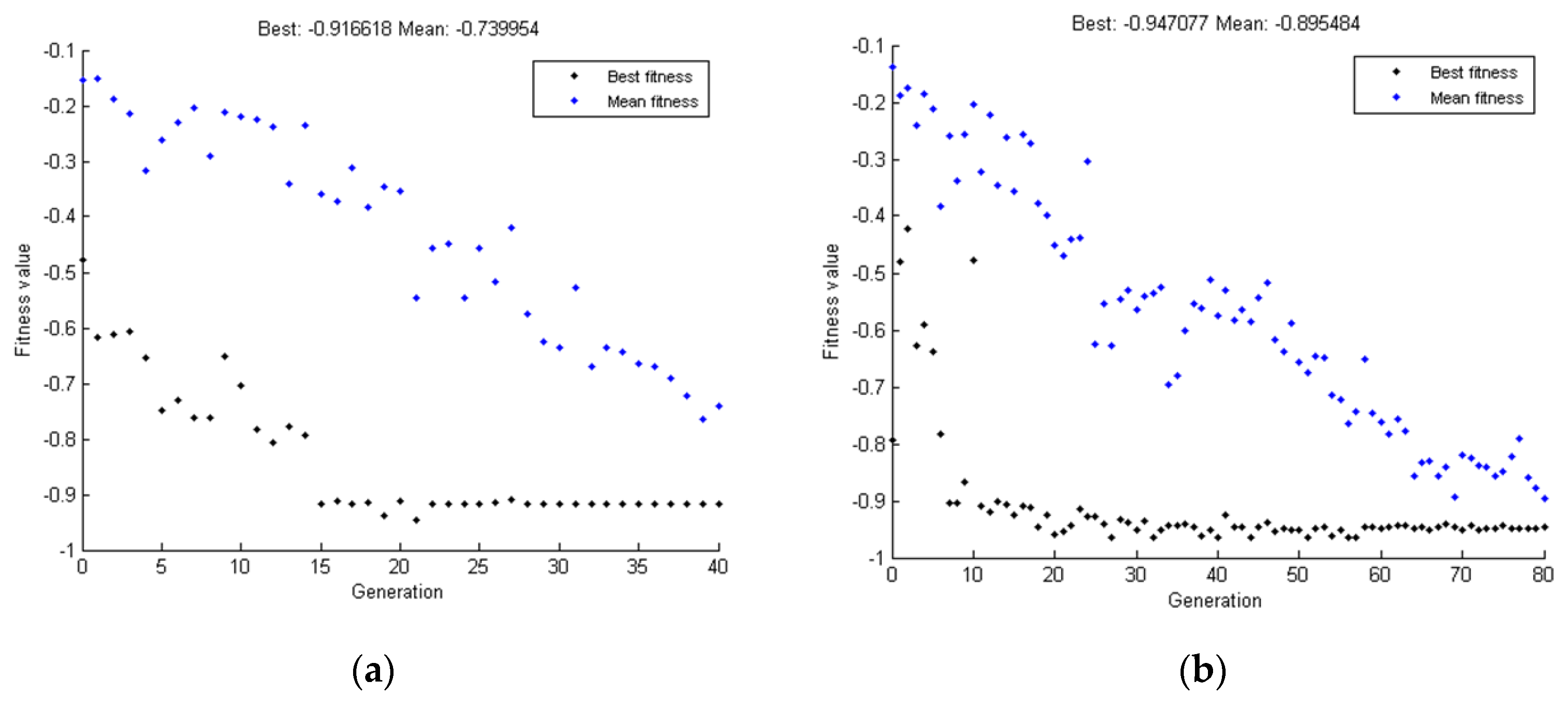
| Number of generations | 40 | 80 |
| Value of objective function | 0.92 | 0.95 |
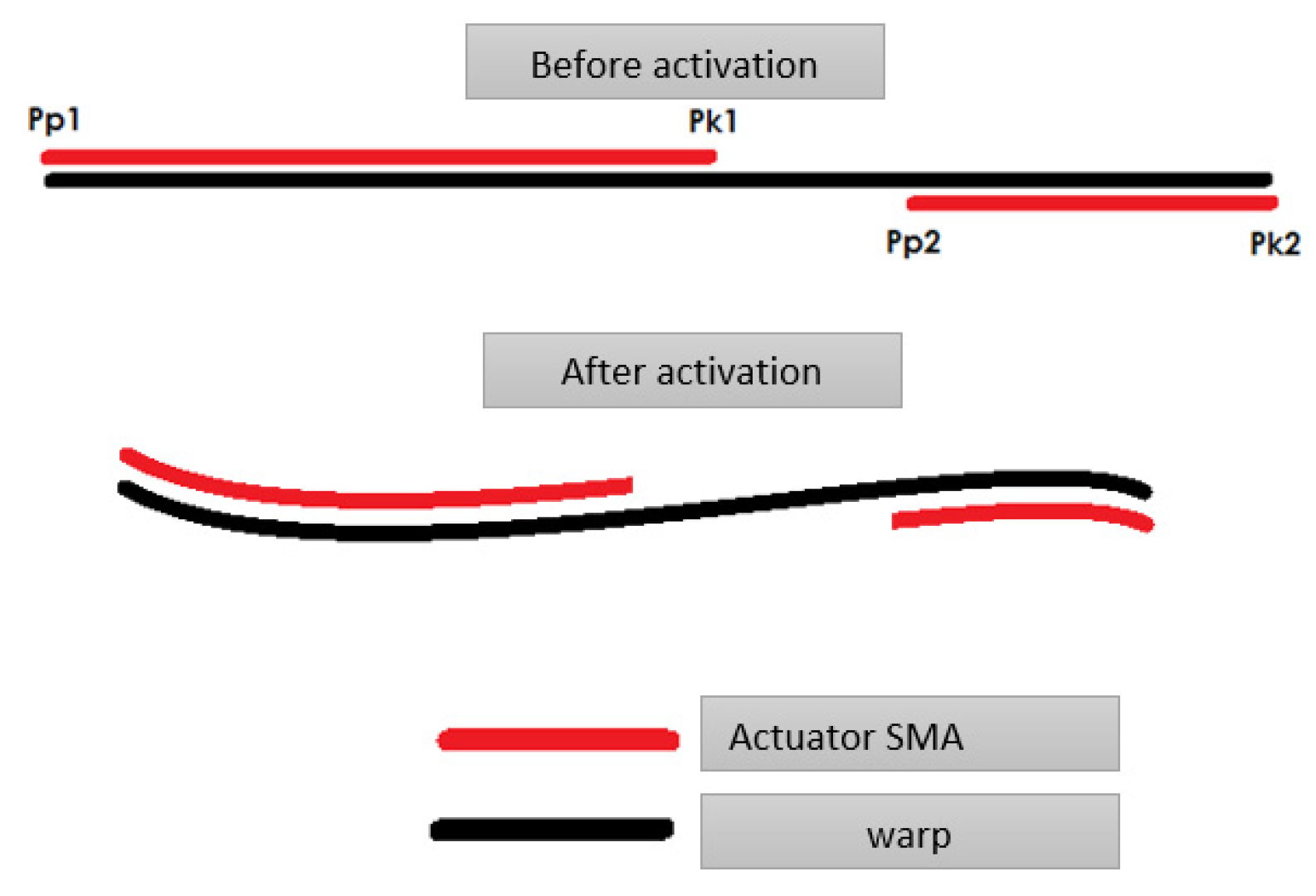
| Point Pp1 | 31 | 22 |
| Point Pk1 | 44 | 38 |
| Point Pp2 | 61 | 71 |
| Point Pk2 | 84 | 87 |
| Simulation Variant | ‘Sinus’ |
|---|---|
| Population size | 100 |
| Number of generations | 80 |
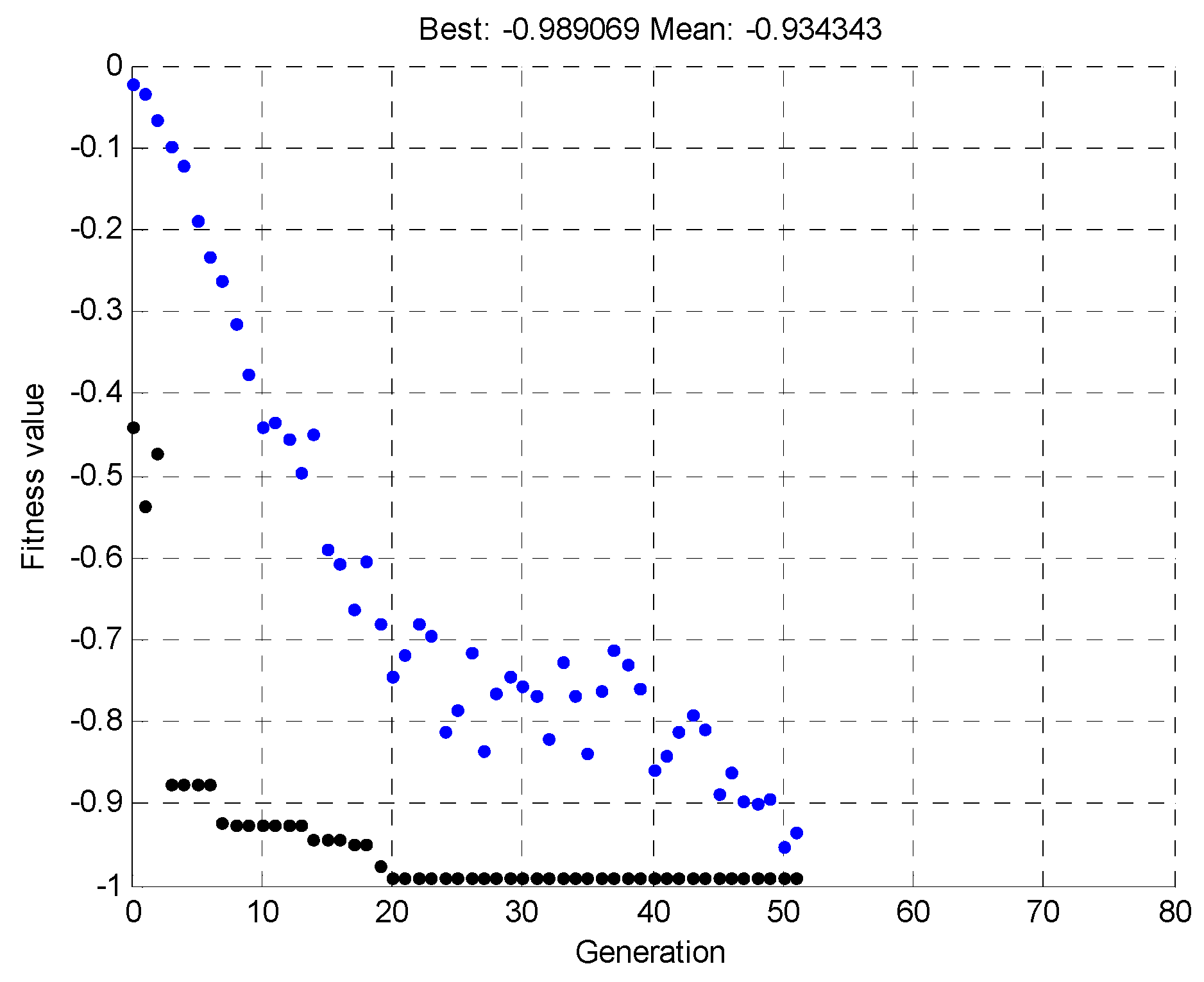
| Generation with the best solution | 52 |
| Value of objective function | 0.989 |
| Point Pp1 | 17 |
| Point Pk1 | 44 |
| Point Pp2 | 63 |
| Point Pk2 | 93 |
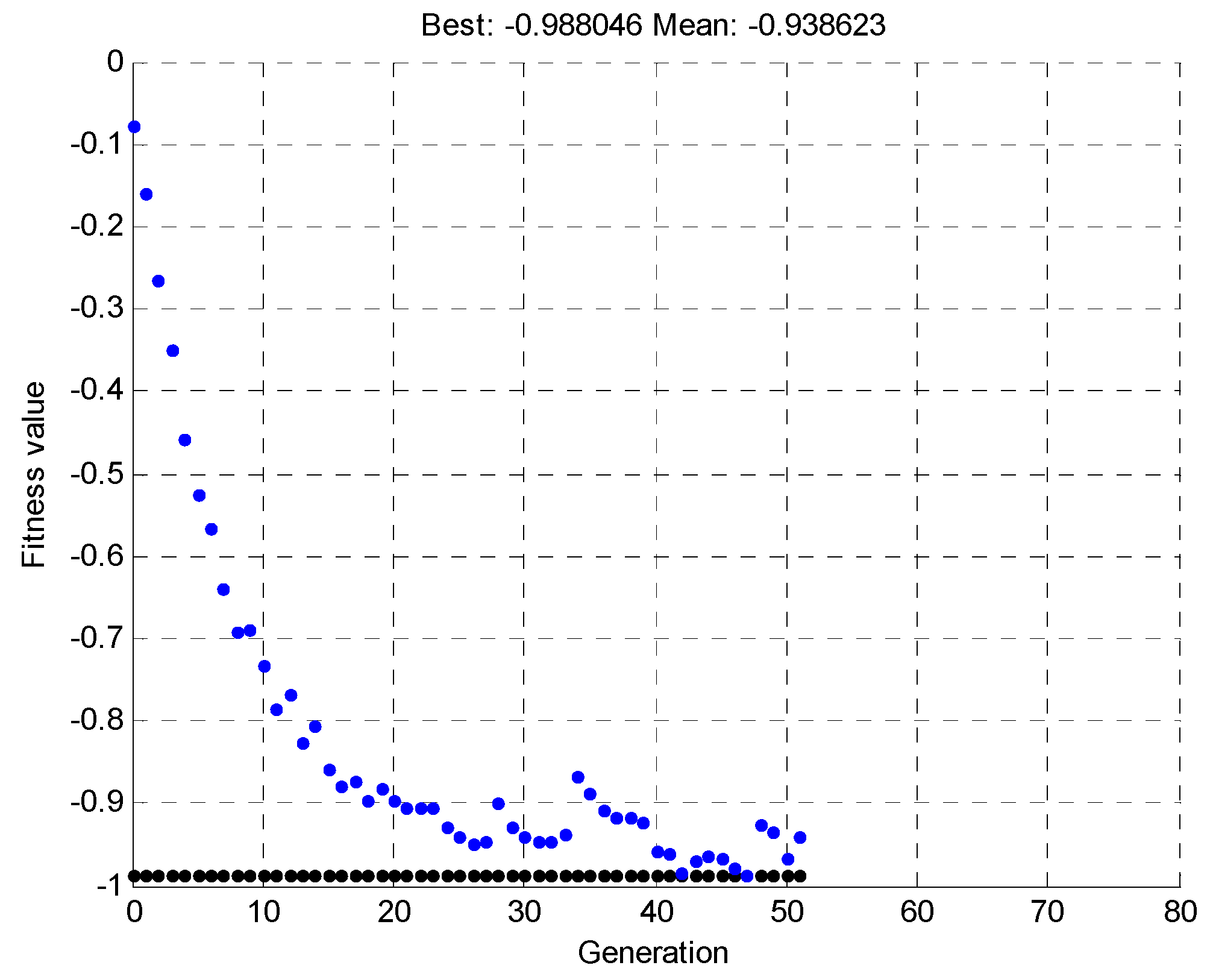
| Simulation Variant | ‘U’ |
|---|---|
| Population size | 100 |
| Number of generations | 80 |
| Generation with the best solution | 52 |
| Value of objective function | 0.988 |
| Point Pp1 | 78 |
| Point Pk1 | 100 |
| Point Pp2 | 28 |
| Point Pk2 | 54 |
| Simulation Variant | “Trapezium” |
|---|---|
| Population size | 100 |
| Number of generations | 80 |
| Generation with the best solution | 52 |
| Value of objective function | 0.993 |
| Point Pp1 | 33 |
| Point Pk1 | 56 |
| Point Pp2 | 66 |
| Point Pk2 | 90 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dudek, O.; Klein, W.; Gąsiorek, D.; Pawlak, M. Additive Manufacturing of Smart Composite Structures Based on Flexinol Wires. Materials 2022, 15, 499. https://doi.org/10.3390/ma15020499
Dudek O, Klein W, Gąsiorek D, Pawlak M. Additive Manufacturing of Smart Composite Structures Based on Flexinol Wires. Materials. 2022; 15(2):499. https://doi.org/10.3390/ma15020499
Chicago/Turabian StyleDudek, Olaf, Wojciech Klein, Damian Gąsiorek, and Mariusz Pawlak. 2022. "Additive Manufacturing of Smart Composite Structures Based on Flexinol Wires" Materials 15, no. 2: 499. https://doi.org/10.3390/ma15020499
APA StyleDudek, O., Klein, W., Gąsiorek, D., & Pawlak, M. (2022). Additive Manufacturing of Smart Composite Structures Based on Flexinol Wires. Materials, 15(2), 499. https://doi.org/10.3390/ma15020499







