Concurrent Topology Optimization of Composite Plates for Minimum Dynamic Compliance
Abstract
:1. Introduction
- A concurrent TO method that can optimize the dynamic compliance of a two-scale composite plate subjected to harmonic loading in a specified frequency range is developed based on the density method.
- The complex stiffness model is used to describe the material damping and accurately consider the variation of structural response due to the change of damping material configurations. The mode superposition method is used to calculate the frequency response of the composite plates to reduce the heavy computational burden caused by a large number of sample points in the frequency range during each iteration.
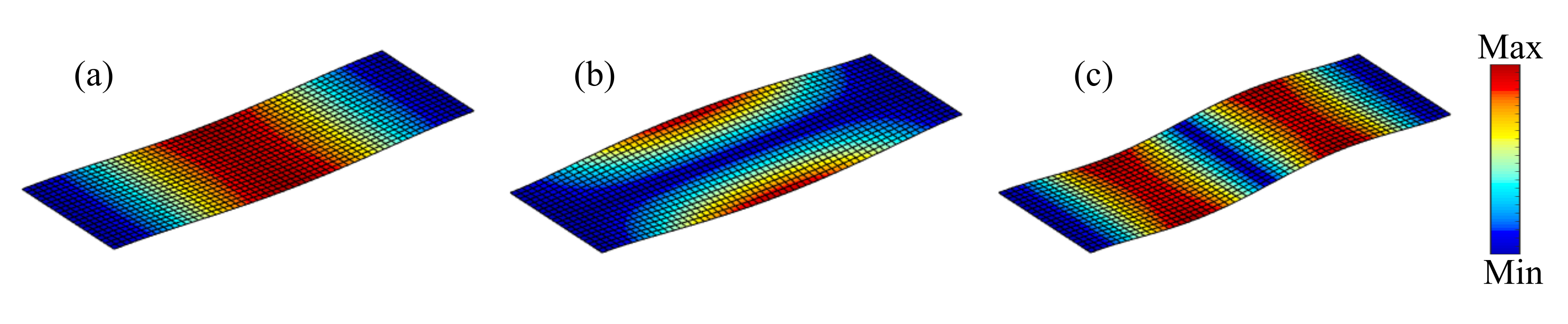
- In the numerical examples, the effects of the excitation frequency range and positions on the optimal composite plate configurations are investigated. It is found that the damping composite material layout is beneficial to resist the deformation of the eigenmode. Finally, some general design rules for the design of composite structures to improve vibration performance are also summarized.

2. Dynamic Compliance of the Composite Plate
2.1. The Complex Stiffness Model for the Damping Material
2.2. Complex Frequency Response of the Composite Plate
2.3. Dynamic Compliance of the Composite Plate
3. Concurrent Topology Optimization and Sensitivity Analysis
3.1. Multi-Scale Modeling Procedure
3.2. Mathematical Model for the Concurrent to Problem
3.3. Sensitivity Analysis
3.3.1. Material Interpolation Scheme
3.3.2. Sensitivity Analysis at the Macro-Scale
3.3.3. Sensitivity Analysis at the Micro-Scale
3.4. Design Process
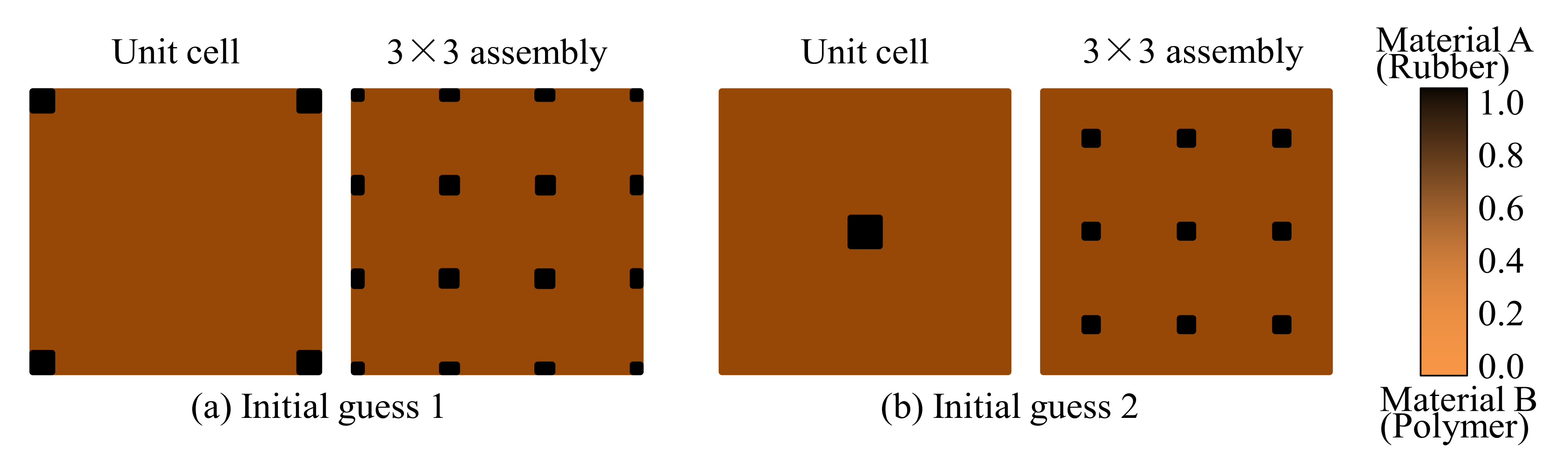
- Construct the initial configurations in micro- and macro-scales. Set the initial guess for design variables x and y. In this study, the initial value of the iteration number is N = 0;
- Calculate the effective properties of the damping composite material. The homogenization method is used to calculate the effective material properties DH and ρH;
- Perform the finite element analysis on a macro-scale, using DH and ρH to calculate the frequency response of the macrostructure;
- Compute the objective and constraints;
- Analyze the sensitivity of the design variables in both macro-and micro-scales and apply the sensitivity filter to avoid checkboard patterns or gray-scale elements;
- Update the design variables X(x,y) by the MMA method;
- Repeat steps 2–6 until the objective function is convergent or the iteration number N reaches the predefined maximum value Nmax (in this paper, Nmax = 200).

4. Model Verification and Numerical Examples
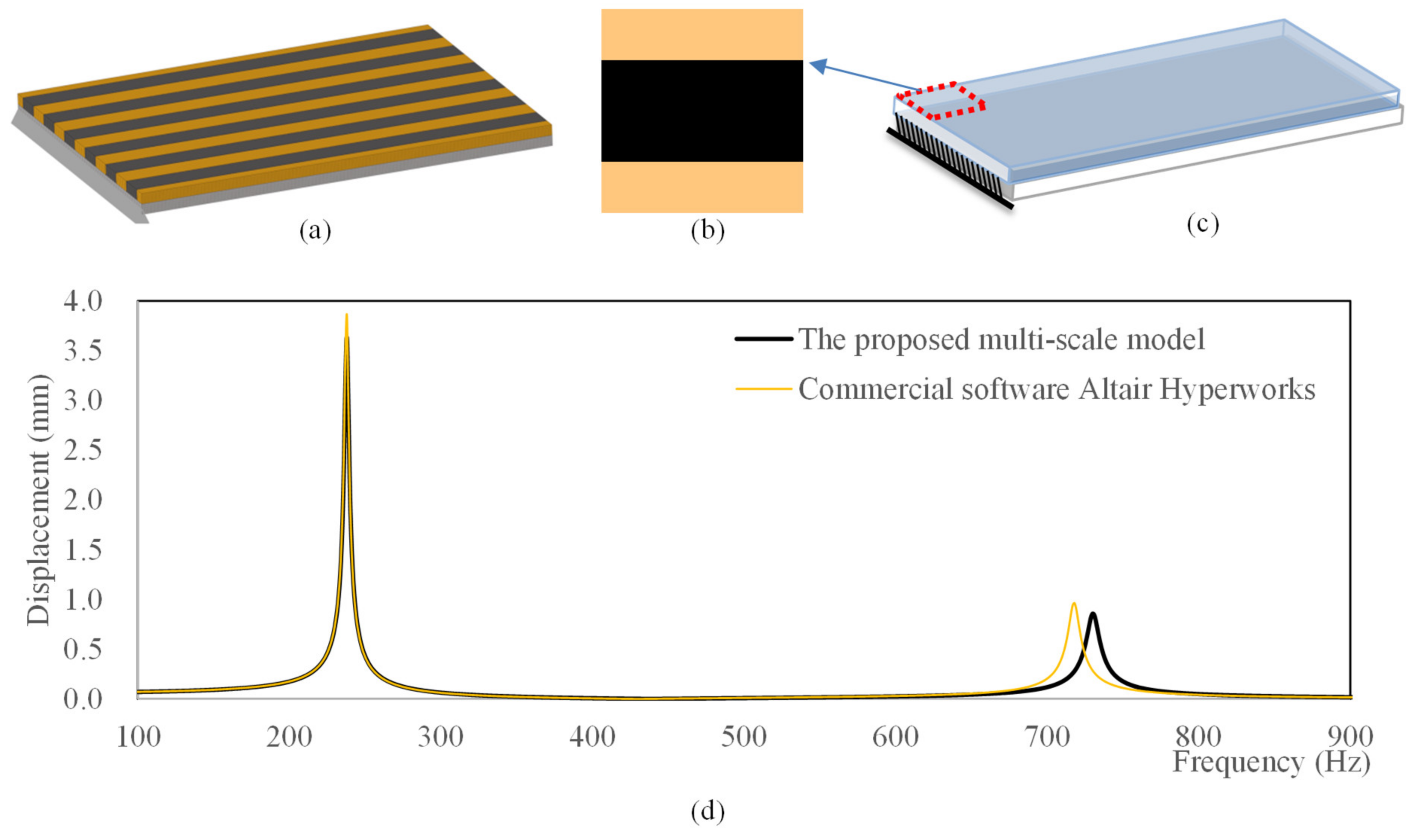
4.1. Model Verification of Frequency Response of Composite Plates
4.2. Numerical Examples
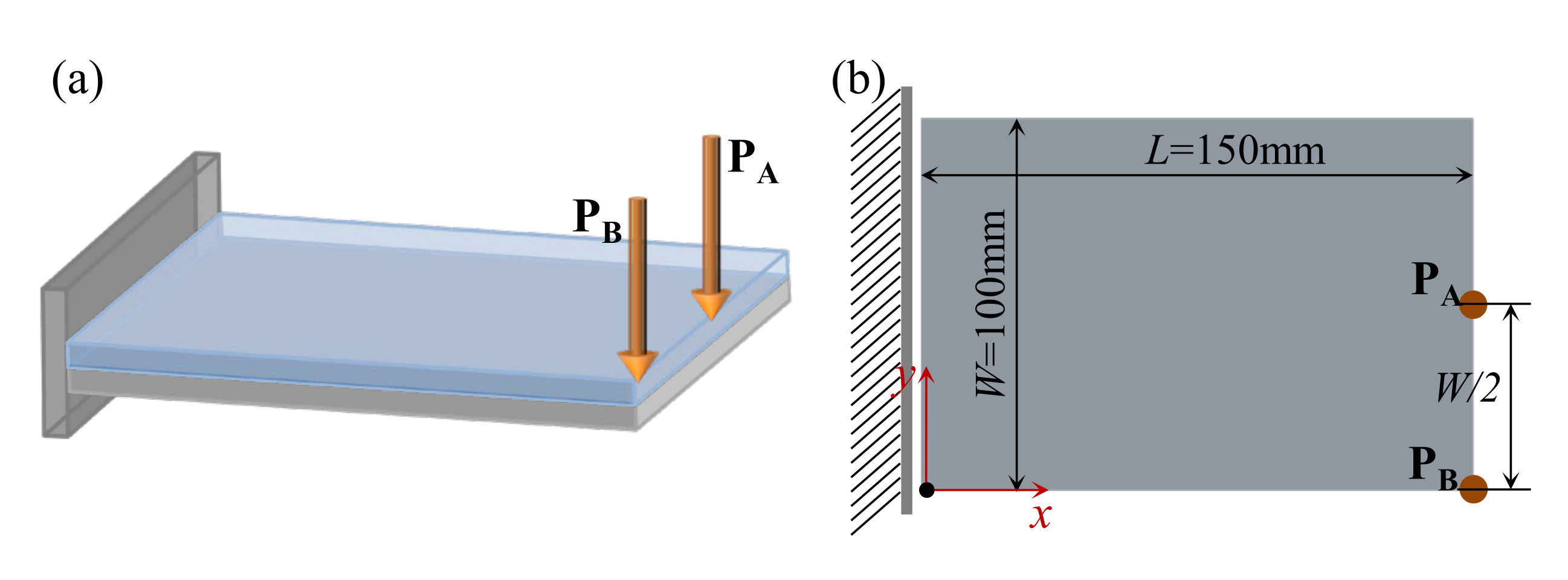
4.2.1. Cantilever Composite Plate
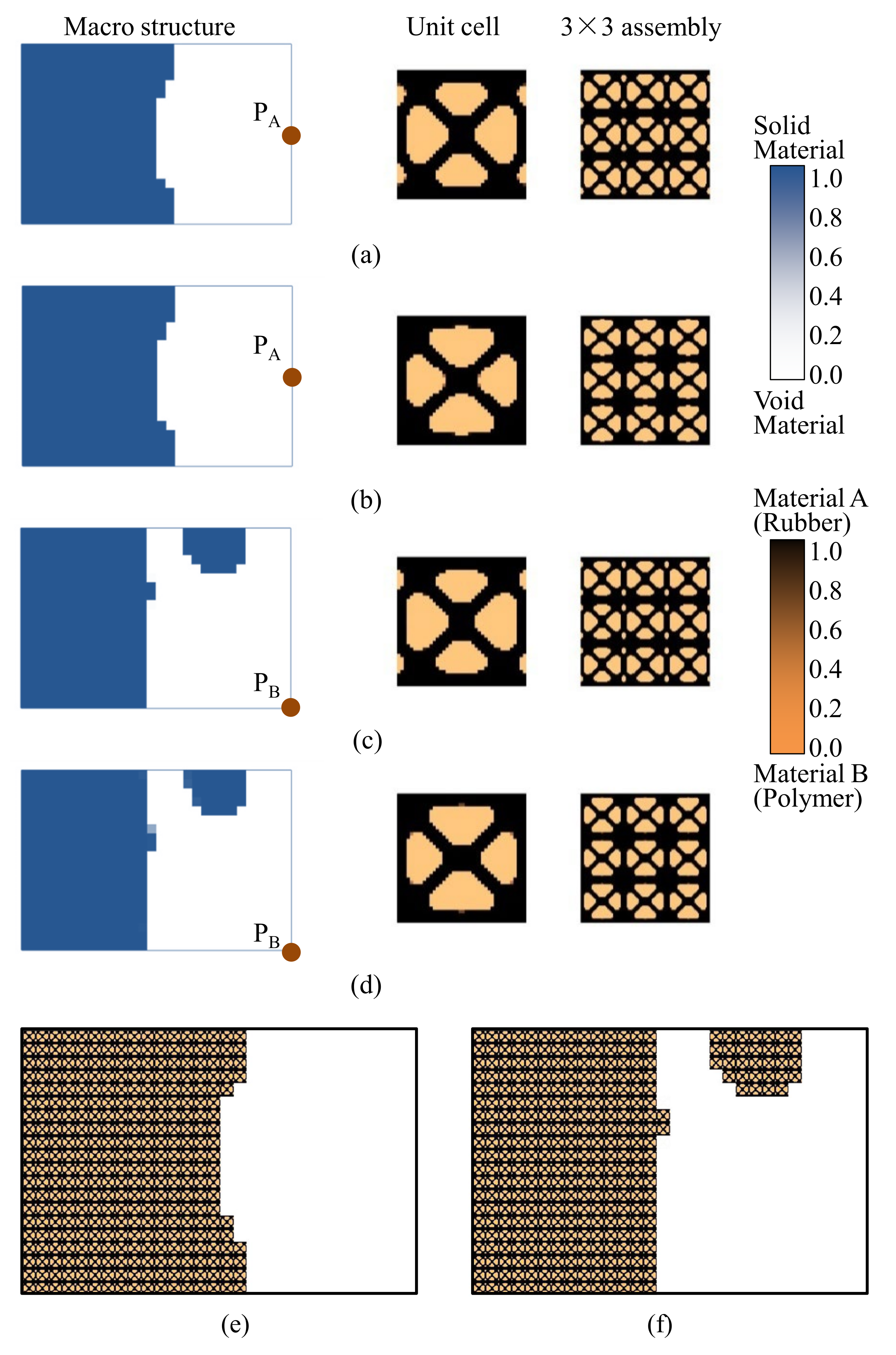
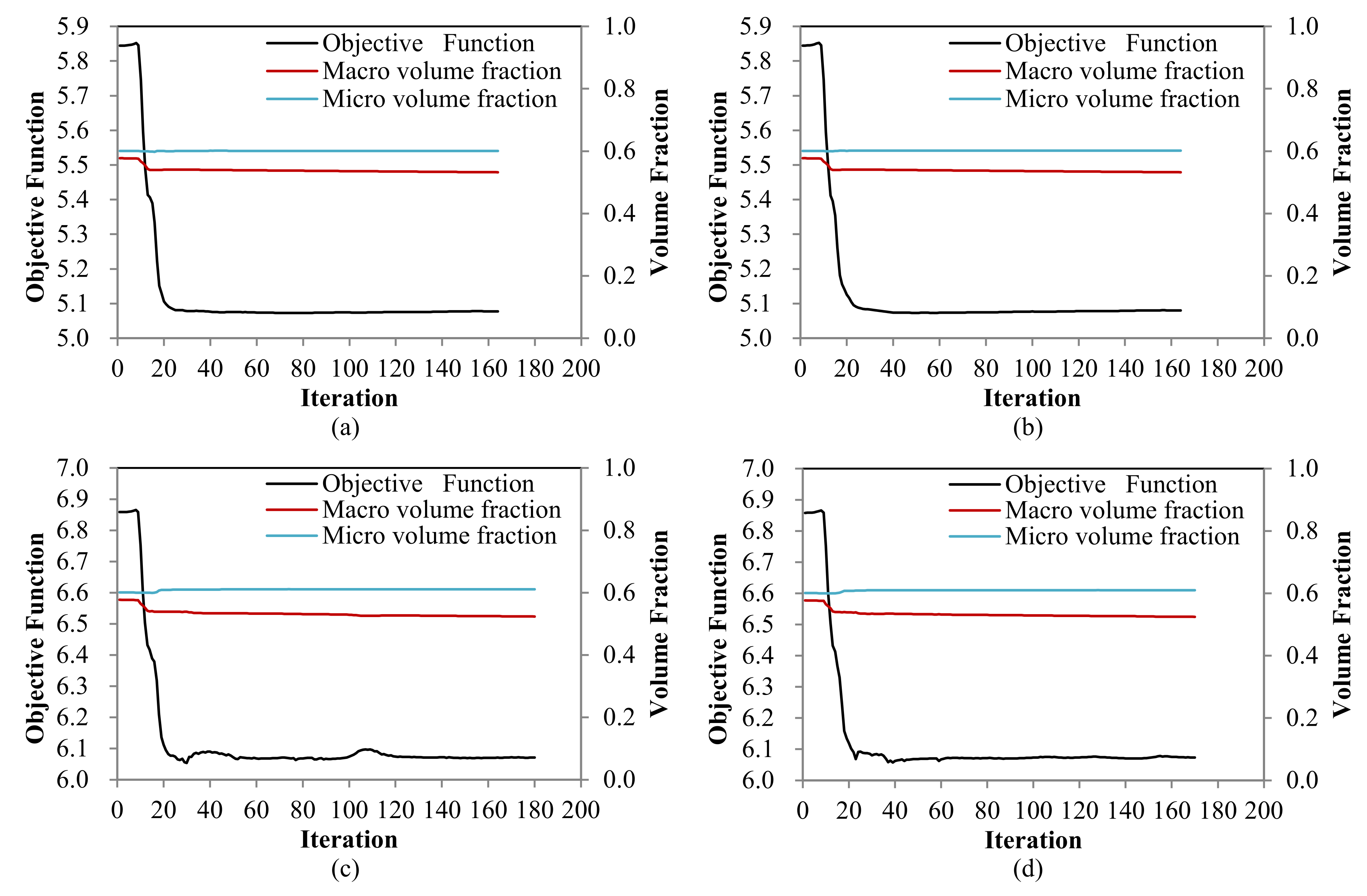
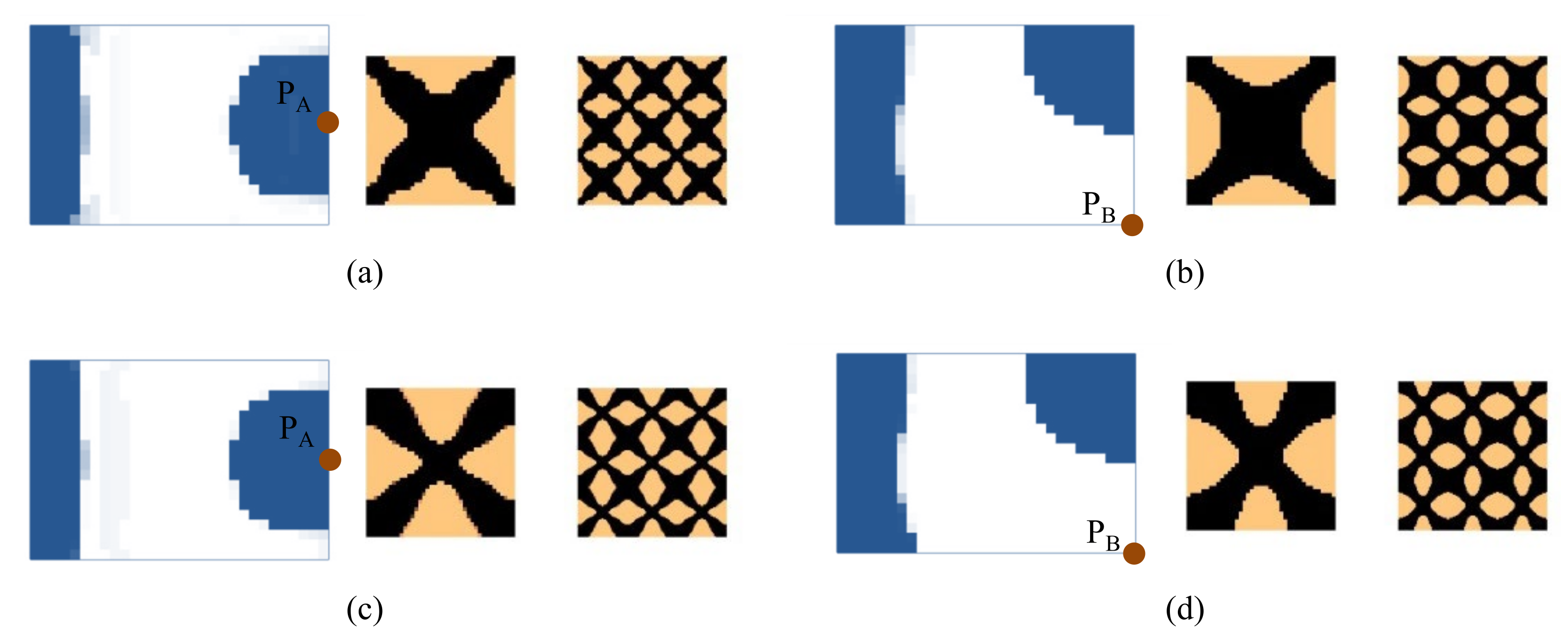
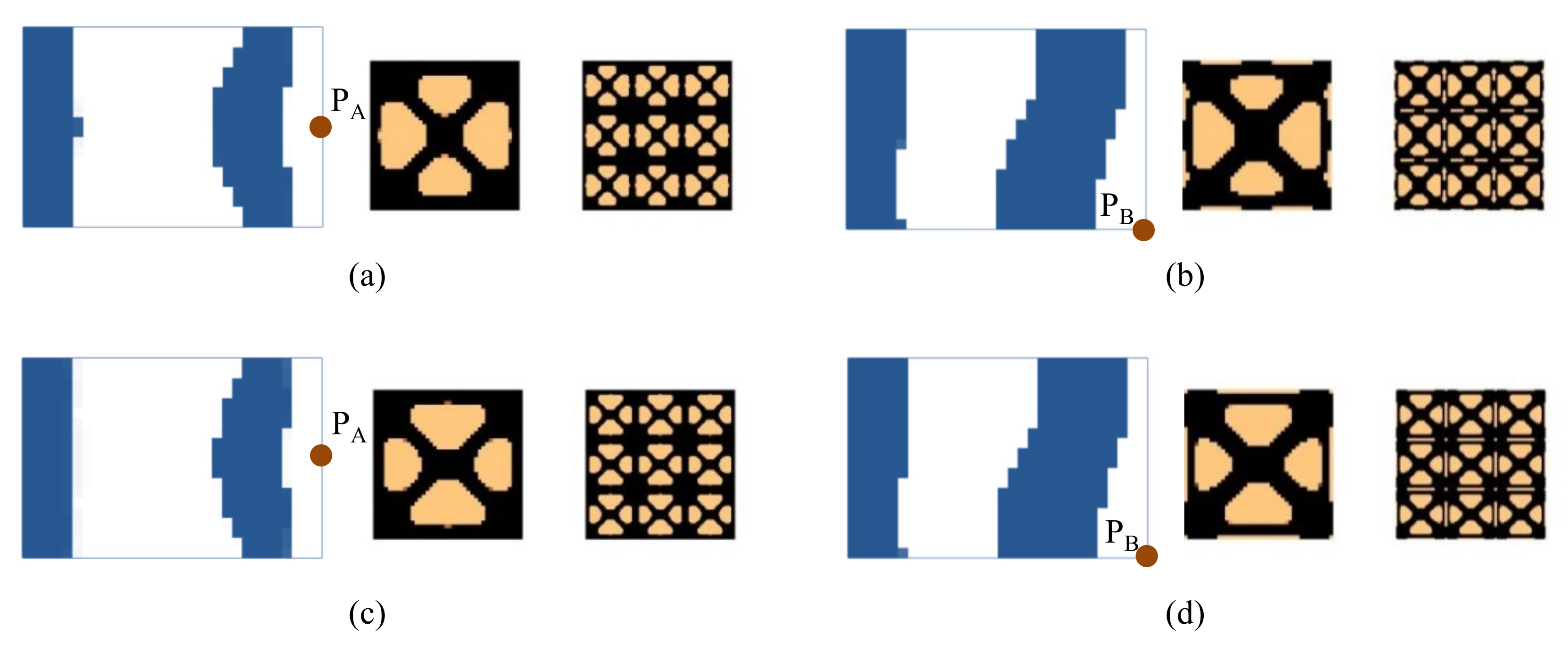
| Examples | Natural Frequency (Hz) | Total Mass (g) | Mass of Damping Layer (g) | Mass Ratio of the Damping Layer | ||
|---|---|---|---|---|---|---|
| First | Second | Third | ||||
| Base plate | 75.1 | 254.7 | 467.4 | 81.00 | 0.00 | 0.00% |
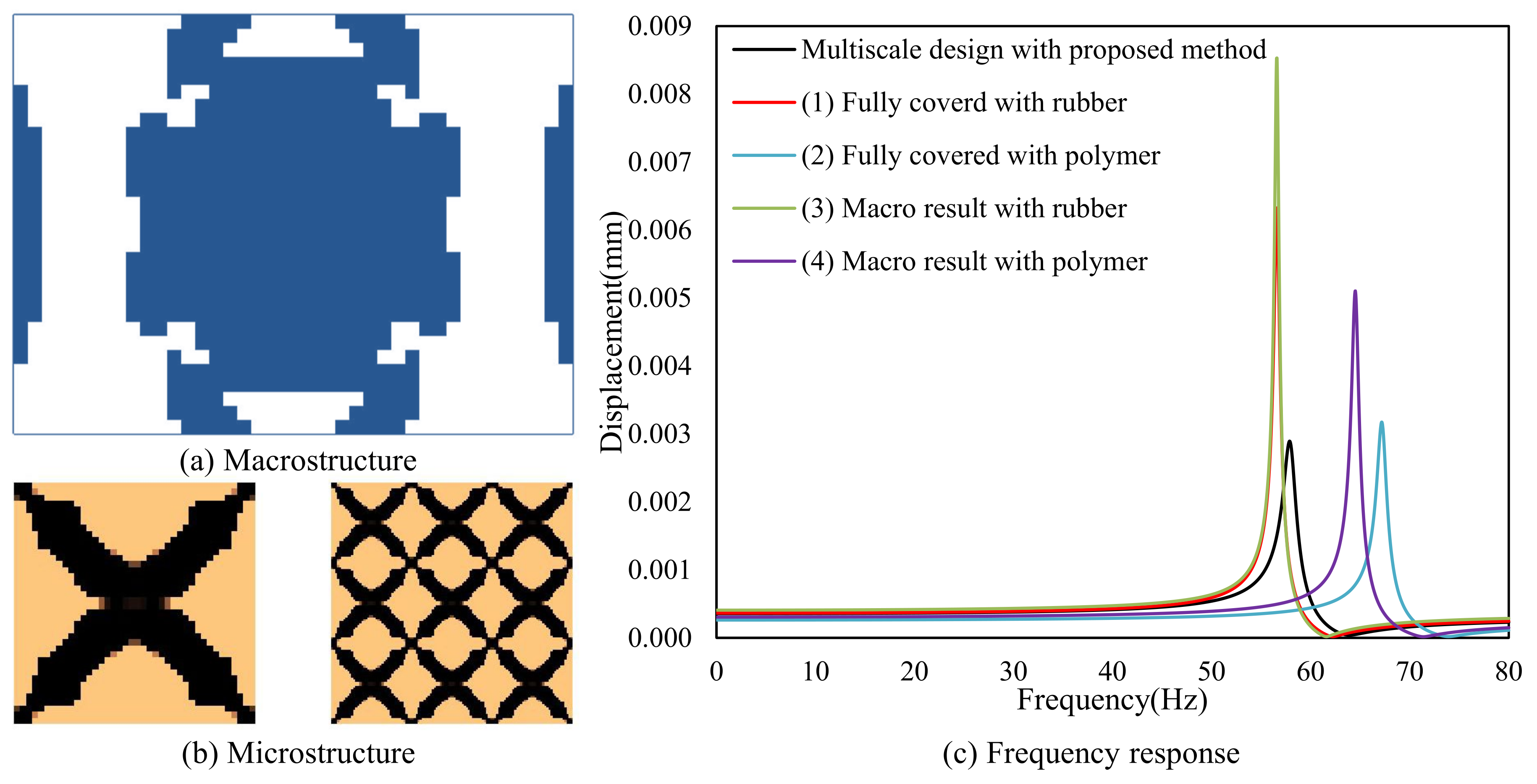
| Fully covered with Rubber | 60.5 | 205.1 | 376.6 | 126.00 | 45.00 | 55.56% |
| Fully covered with Polymer | 75.7 | 253.1 | 470.1 | 111.02 | 30.02 | 37.06% |
| Figure 7a | 75.3 | 248.9 | 425.3 | 101.76 | 20.76 | 25.63% |
| Figure 7c | 74.3 | 244.4 | 432.8 | 101.43 | 20.43 | 25.22% |
| Figure 9a | 68.1 | 244.3 | 450.7 | 95.75 | 14.75 | 18.21% |
| Figure 9b | 69.6 | 238.6 | 450.9 | 96.36 | 15.36 | 18.96% |
| Figure 10a | 69.0 | 235.4 | 462.8 | 96.17 | 15.17 | 18.73% |
| Figure 10b | 67.7 | 228.7 | 450.0 | 101.08 | 20.08 | 24.79% |
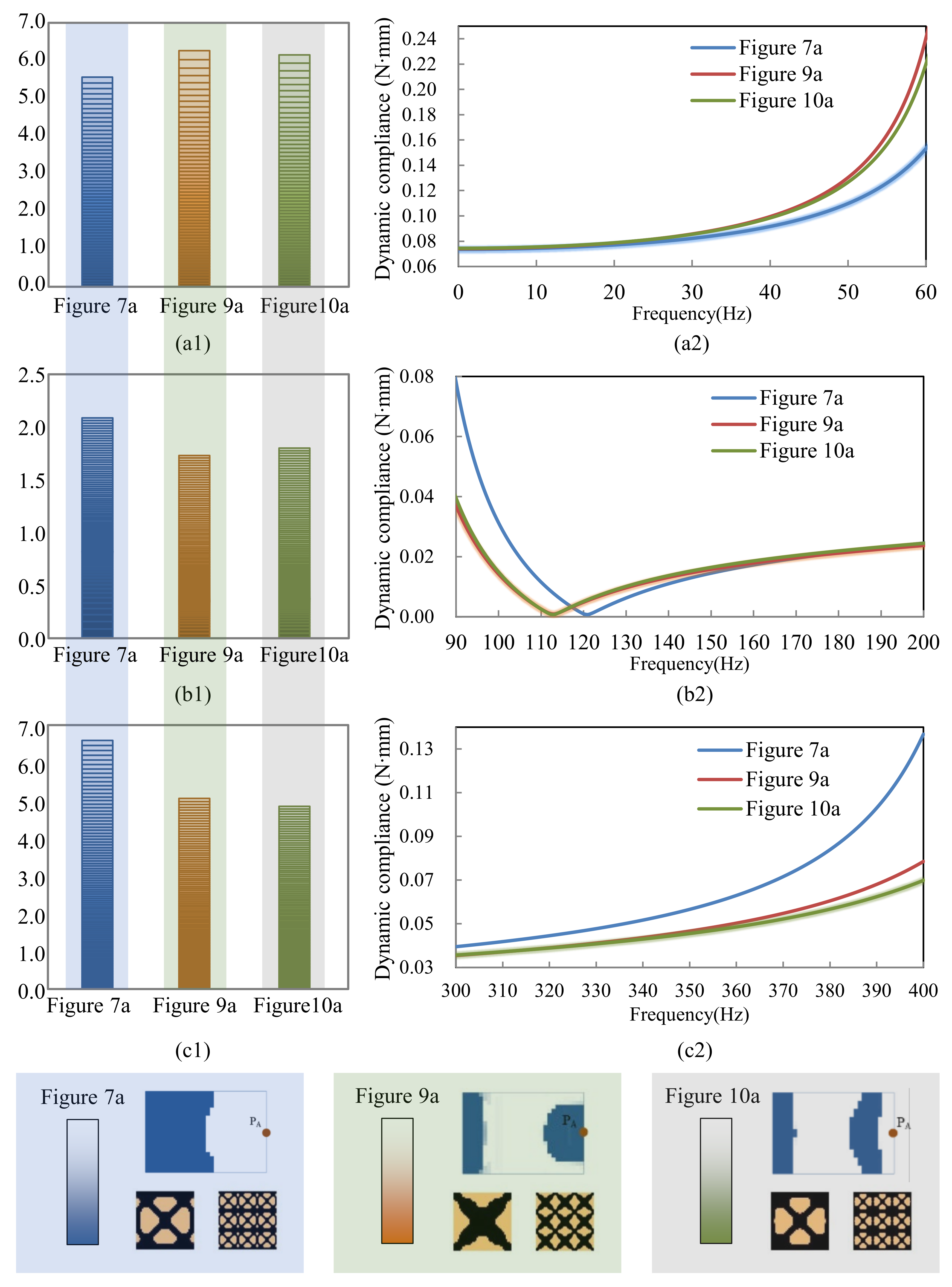
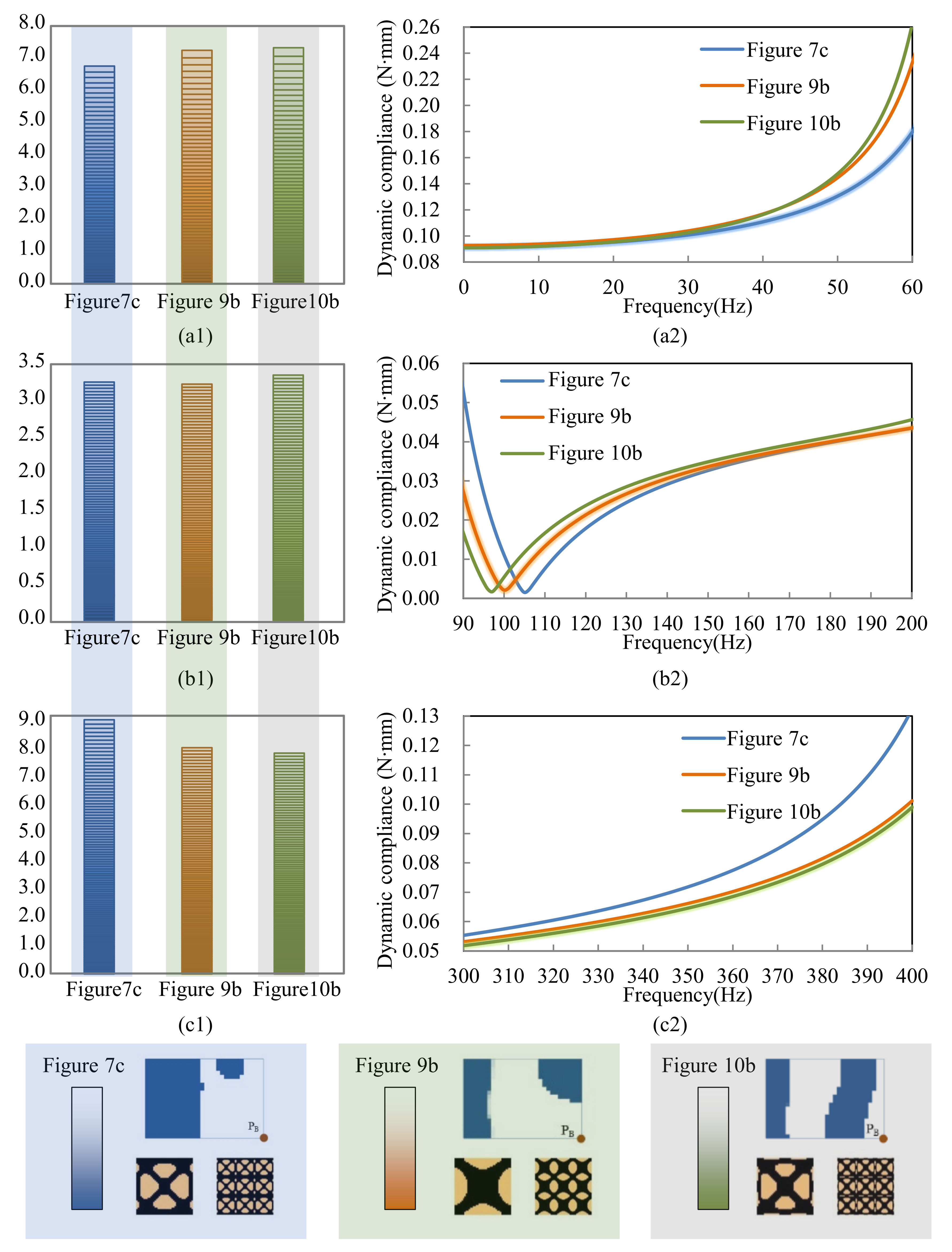
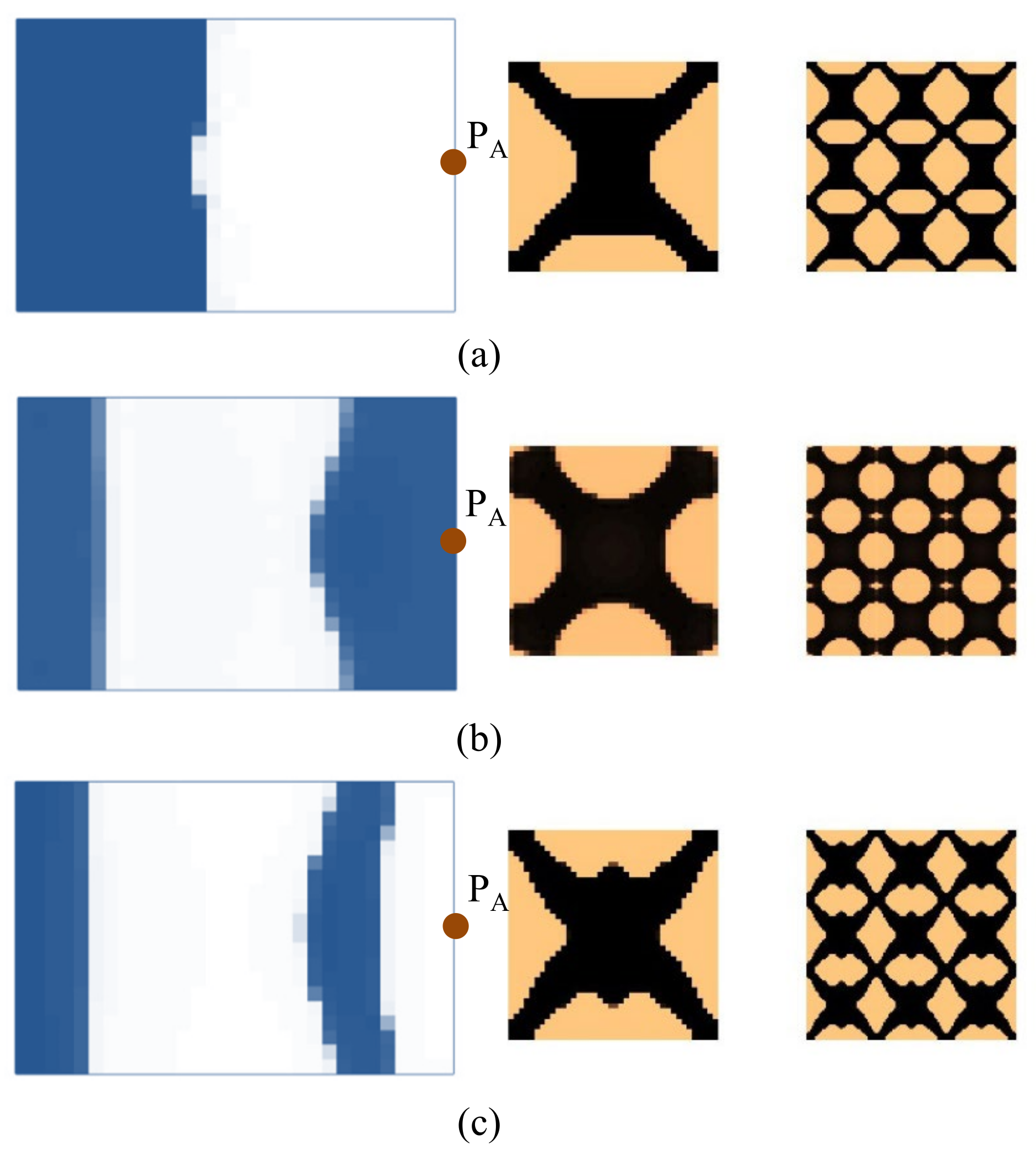

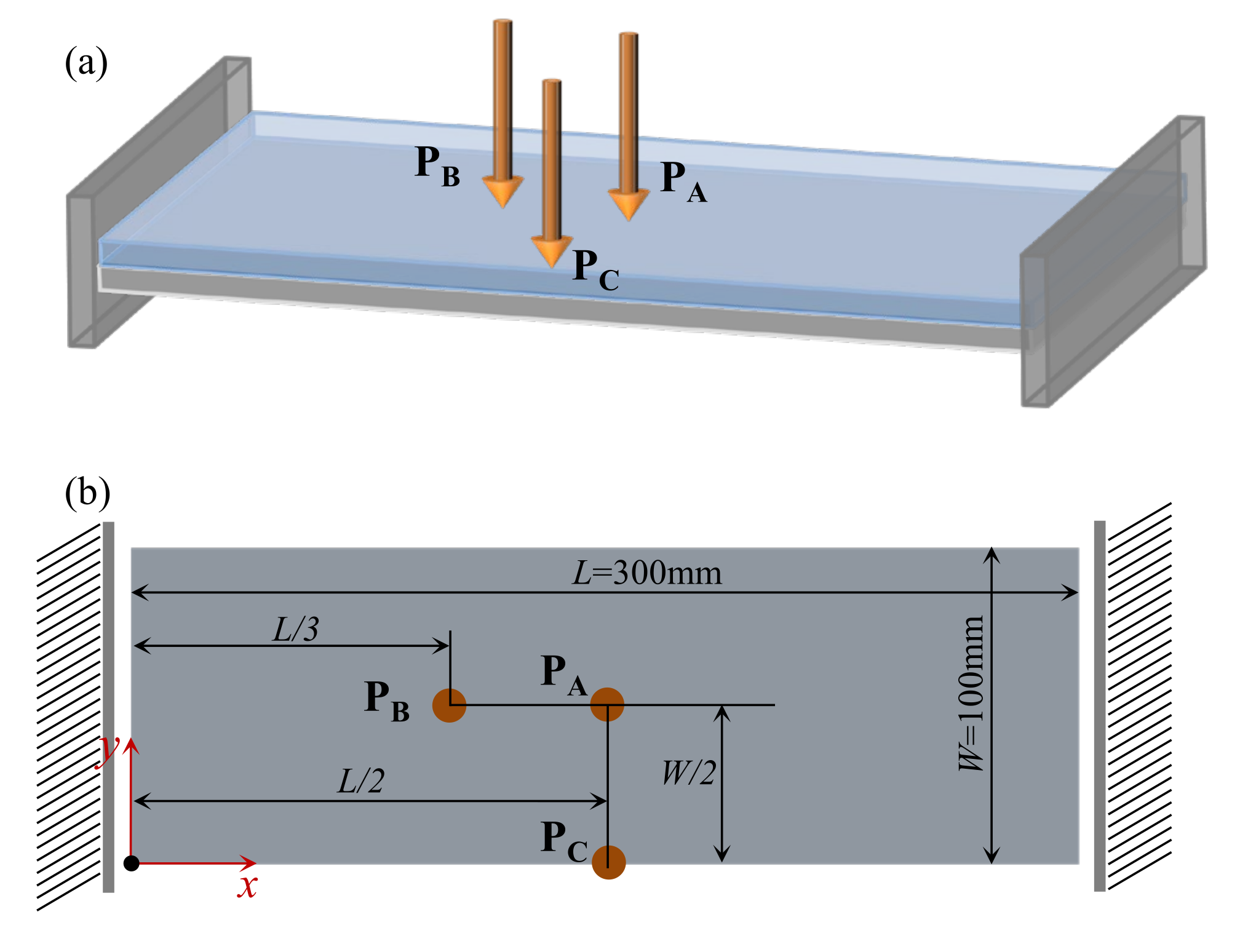
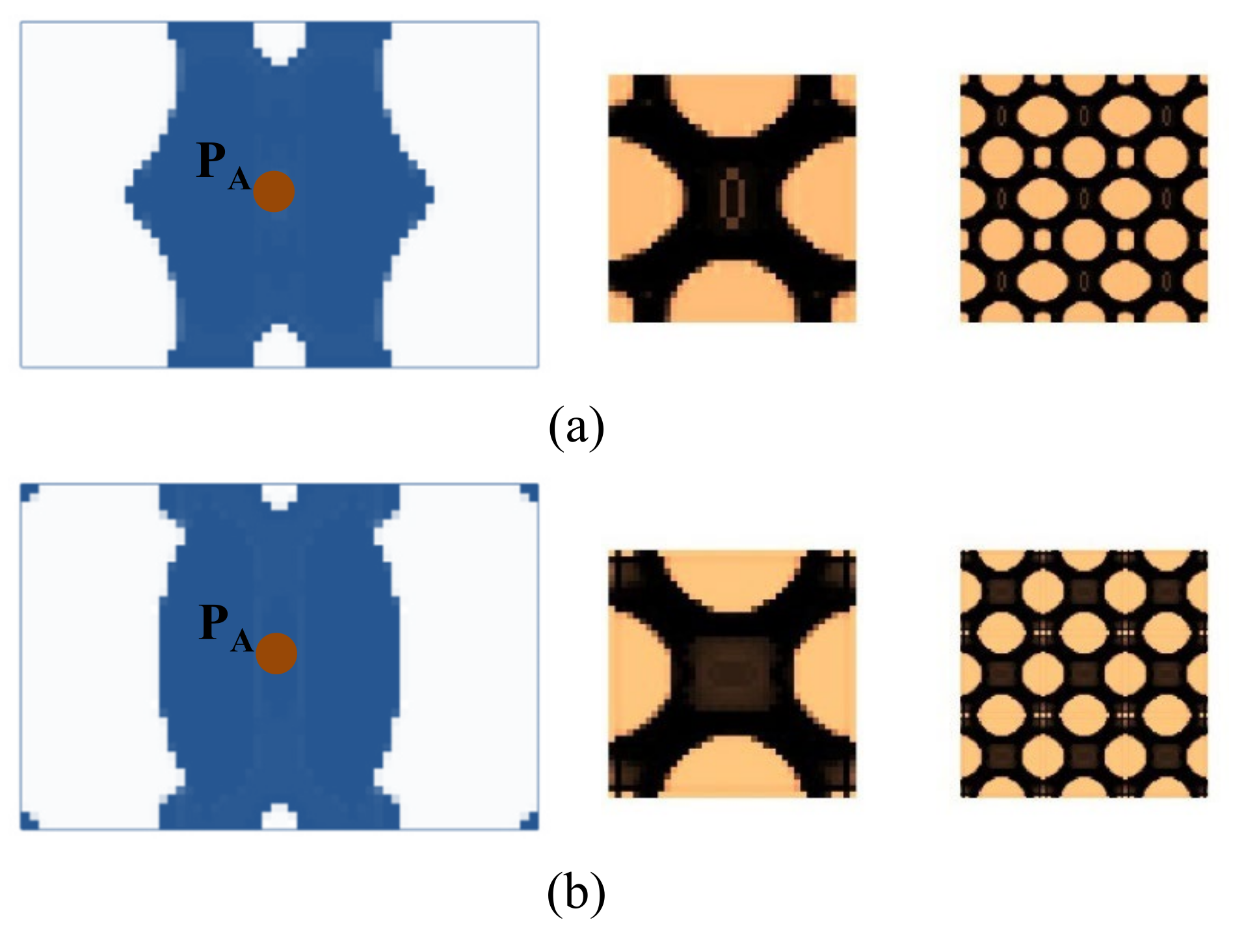
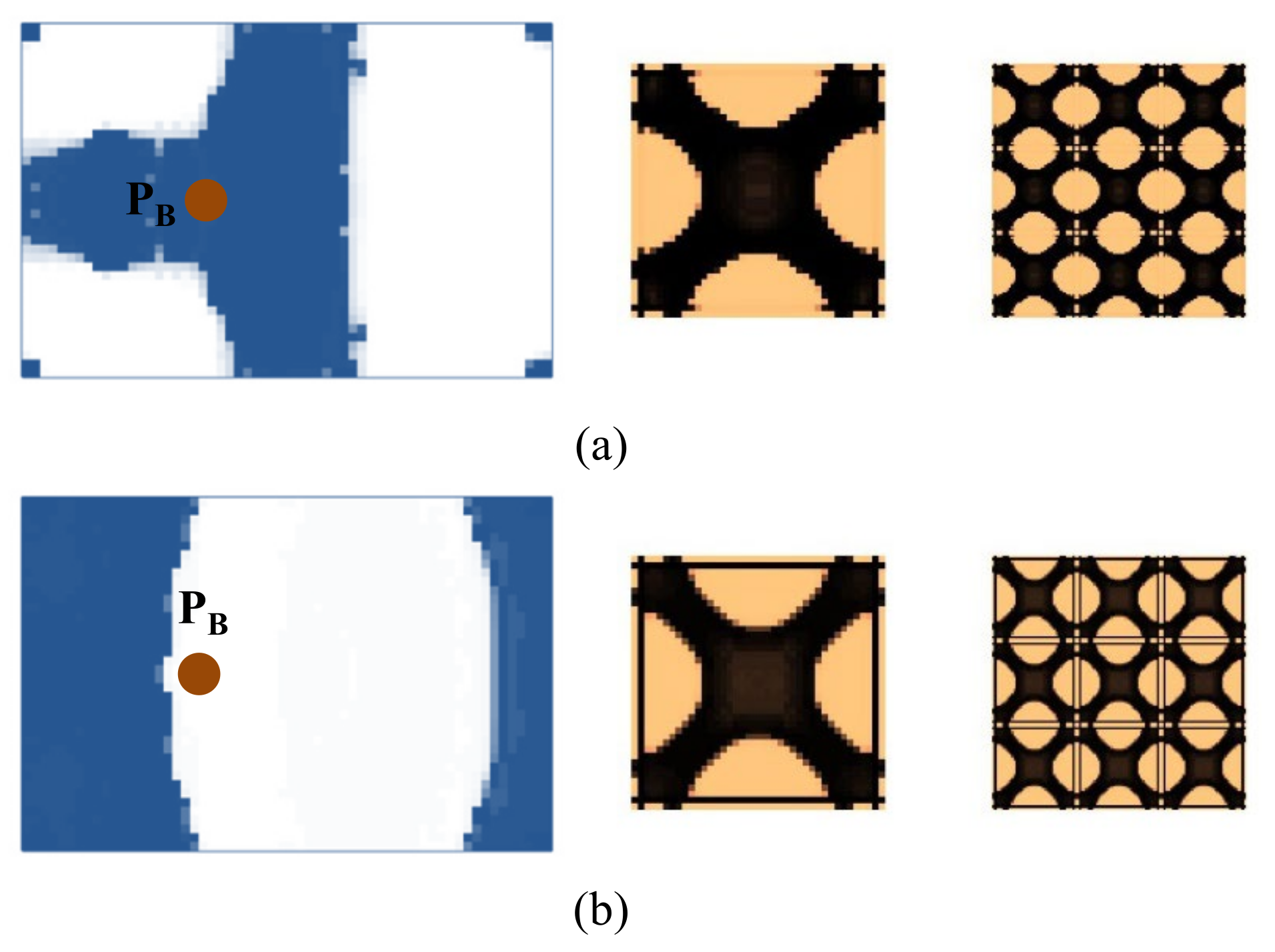
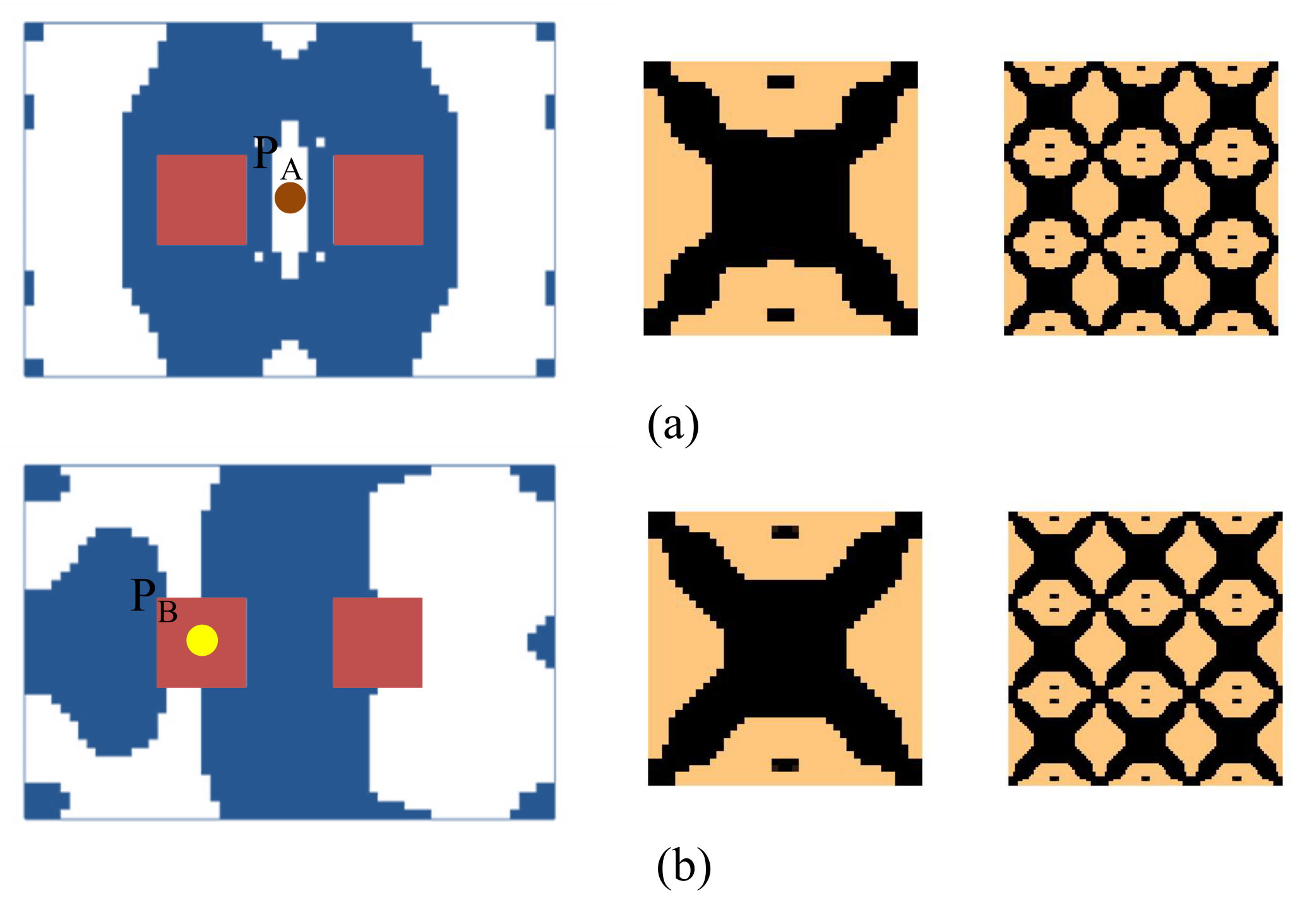
4.2.2. Composite Plate Clamped with Two Opposite Edges
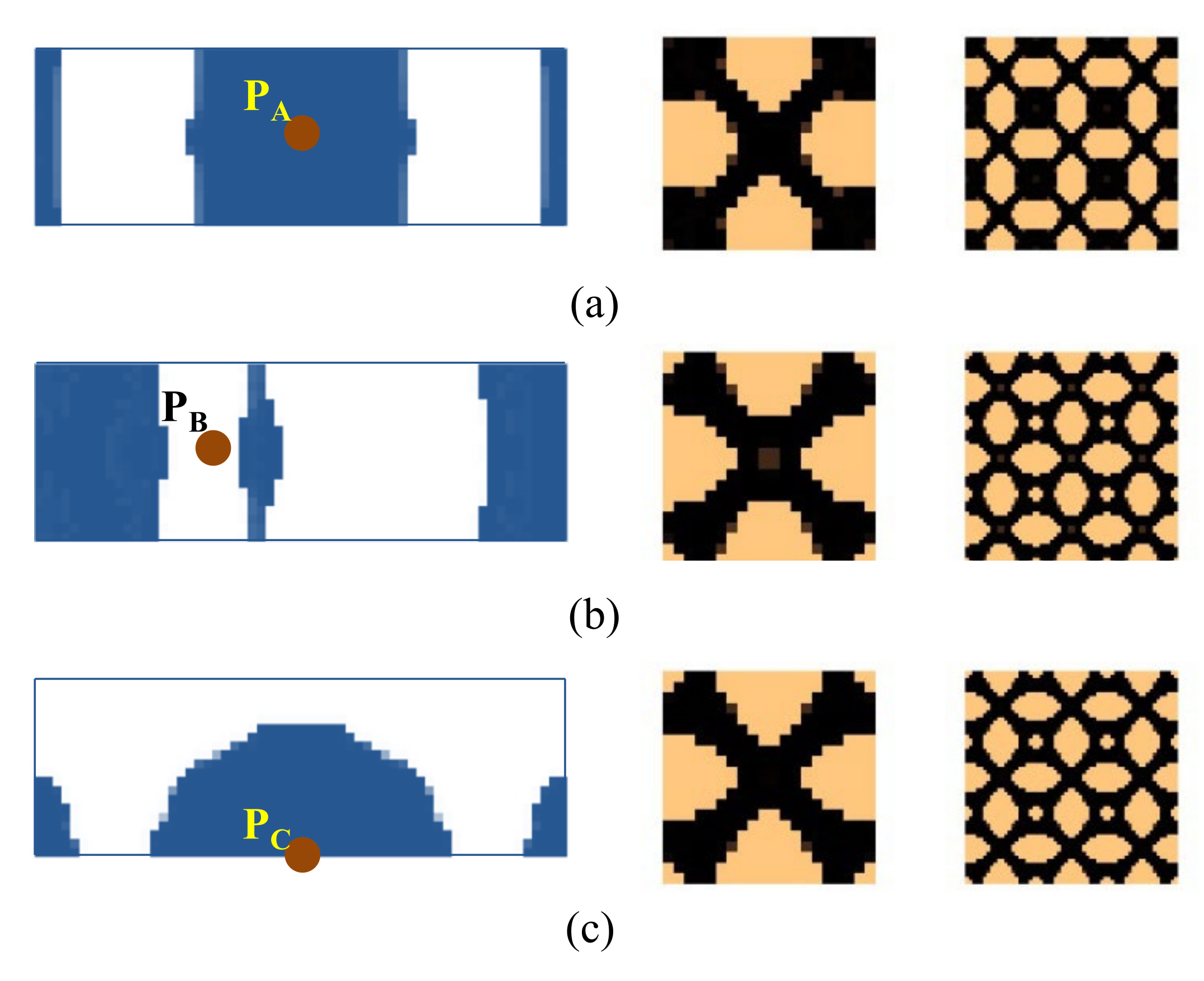
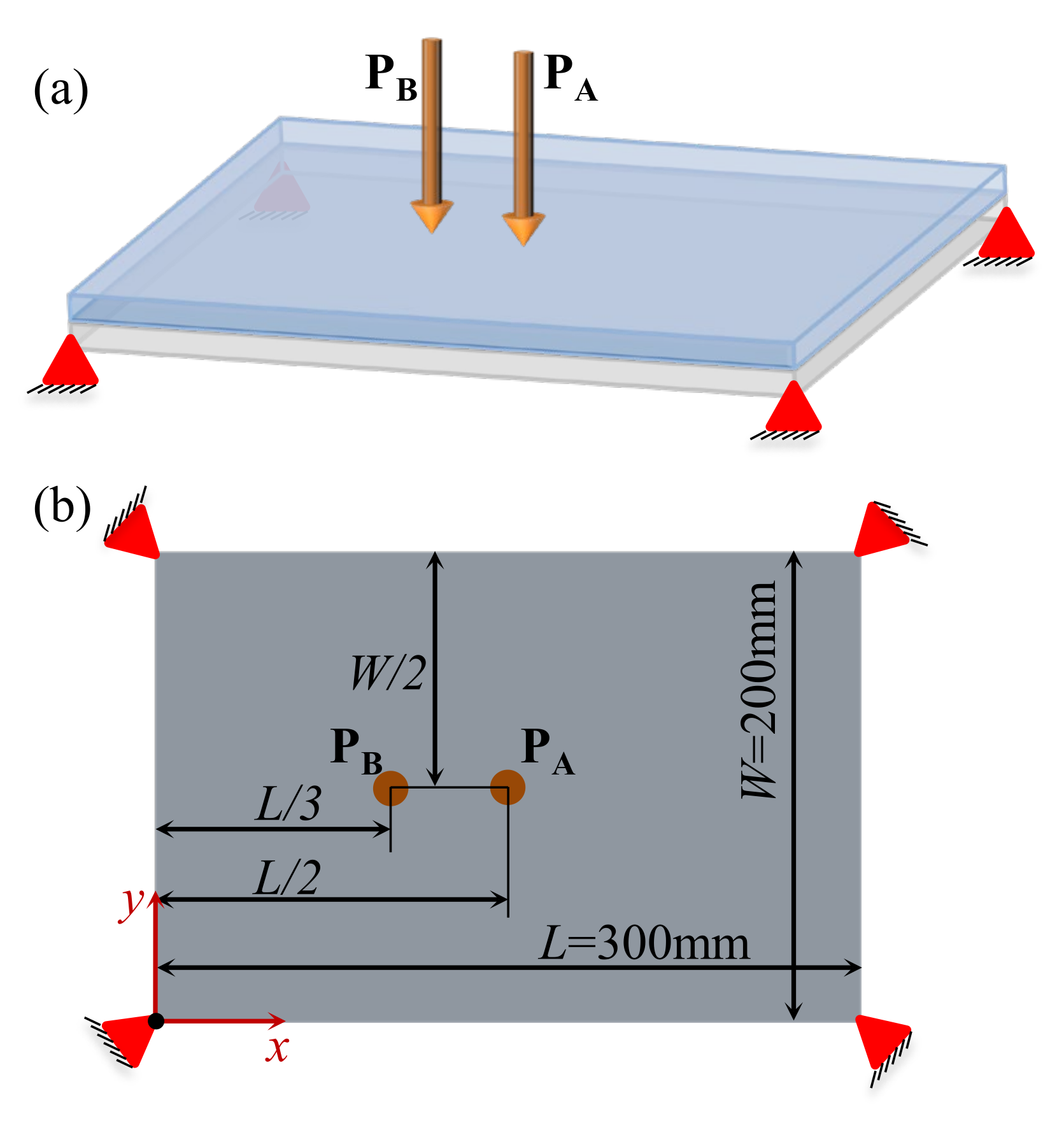
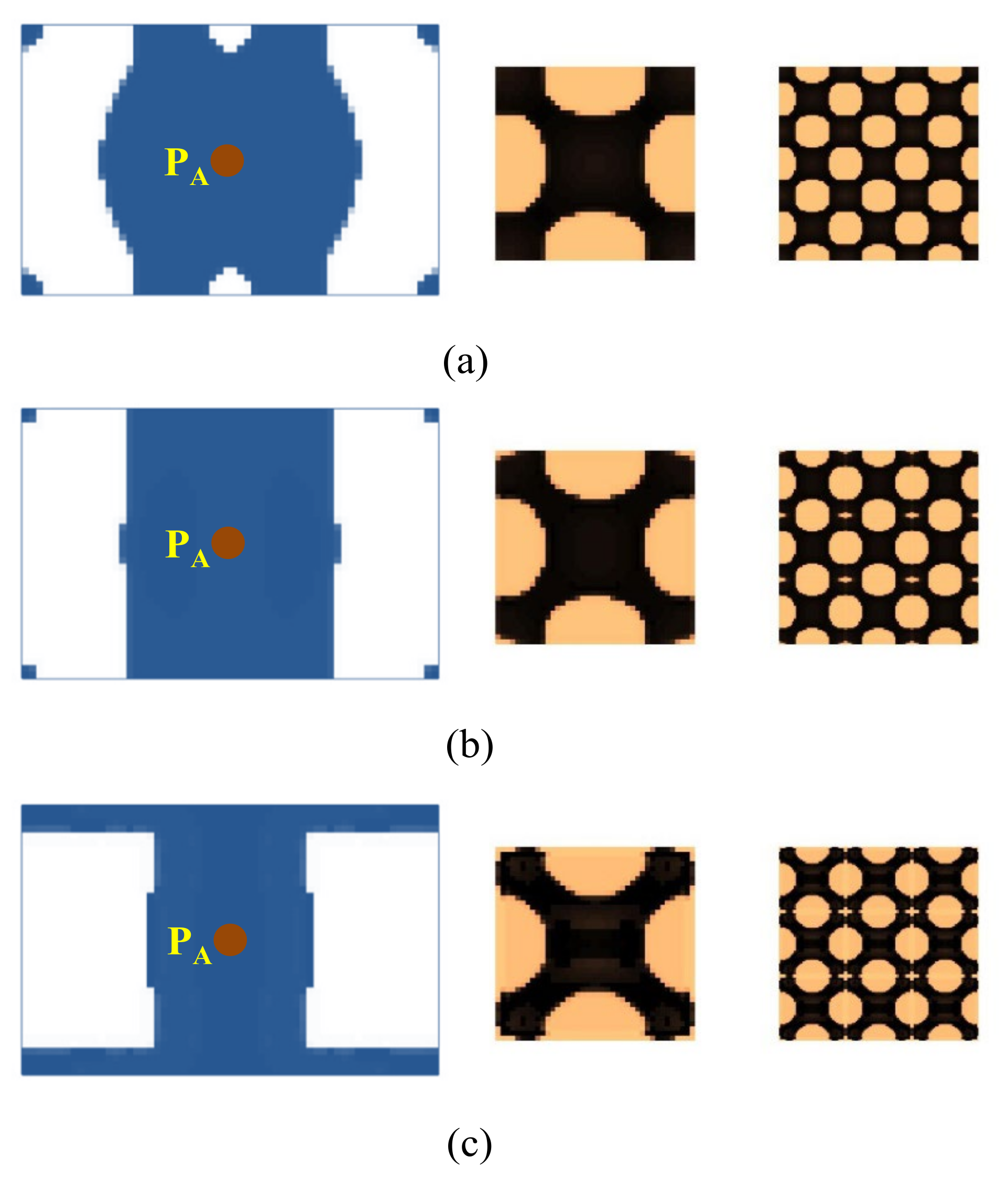
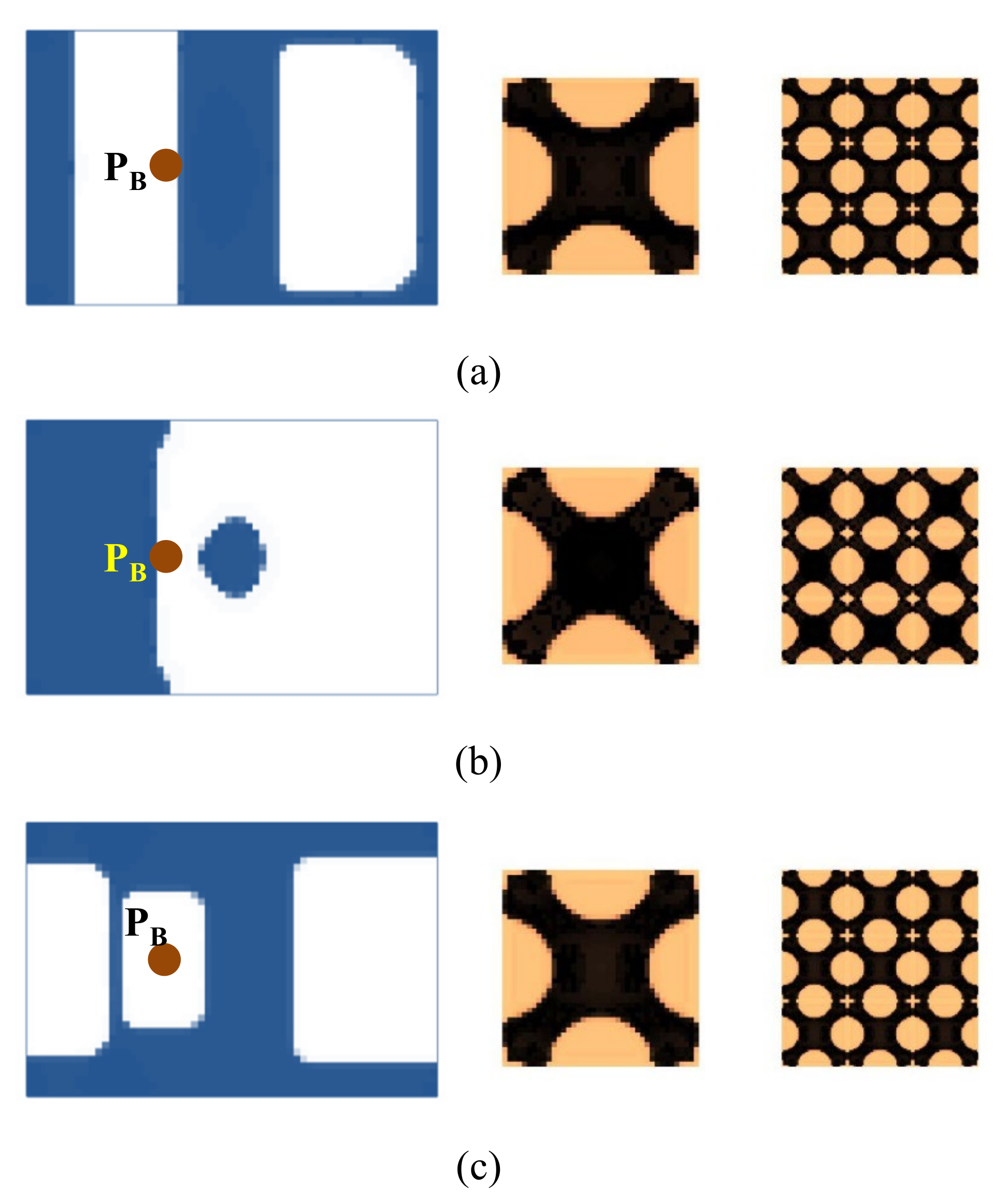
4.2.3. Composite Plate with Four Corners Fixed
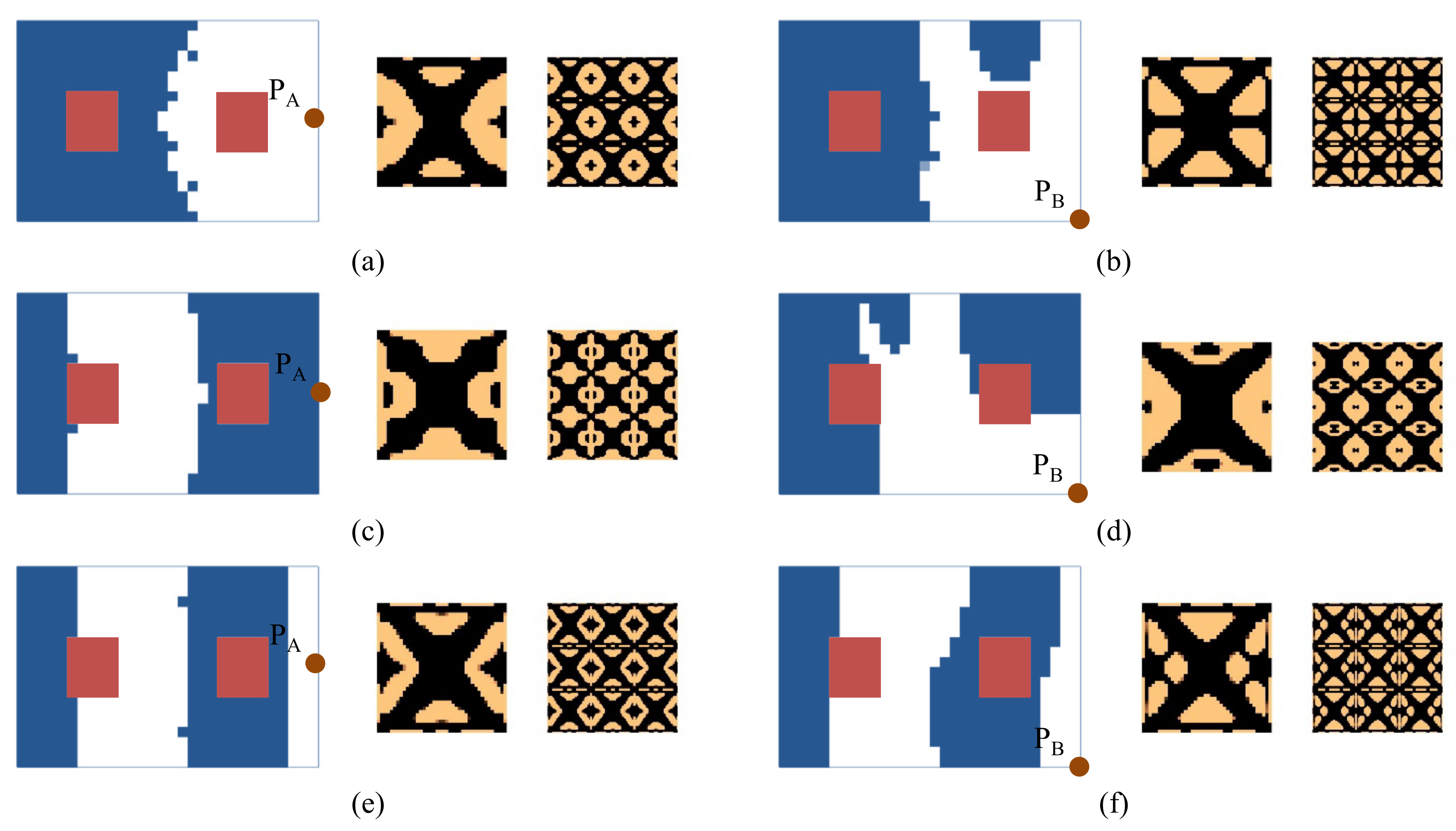
4.2.4. Composite Plate with Non-Design Domain
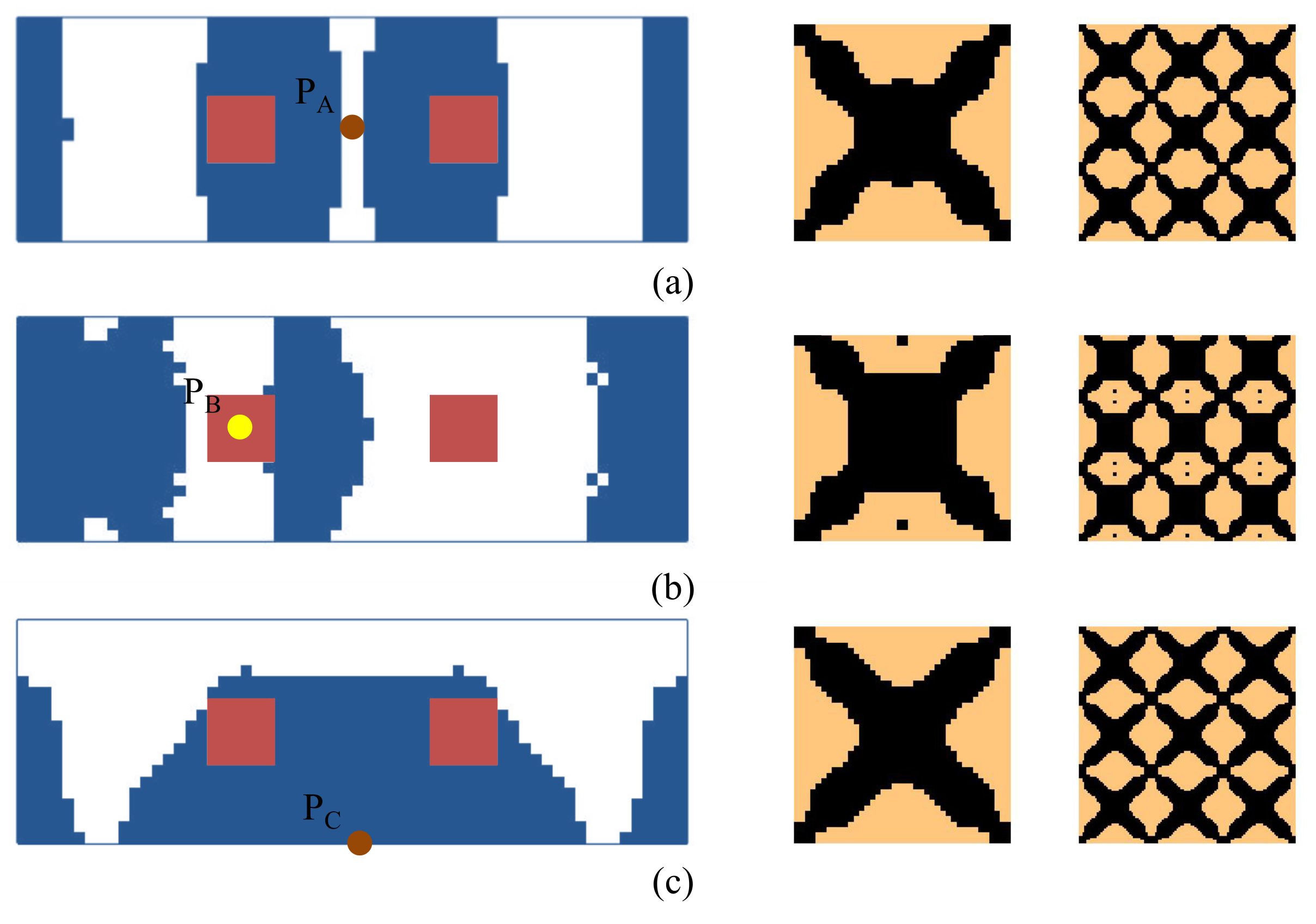
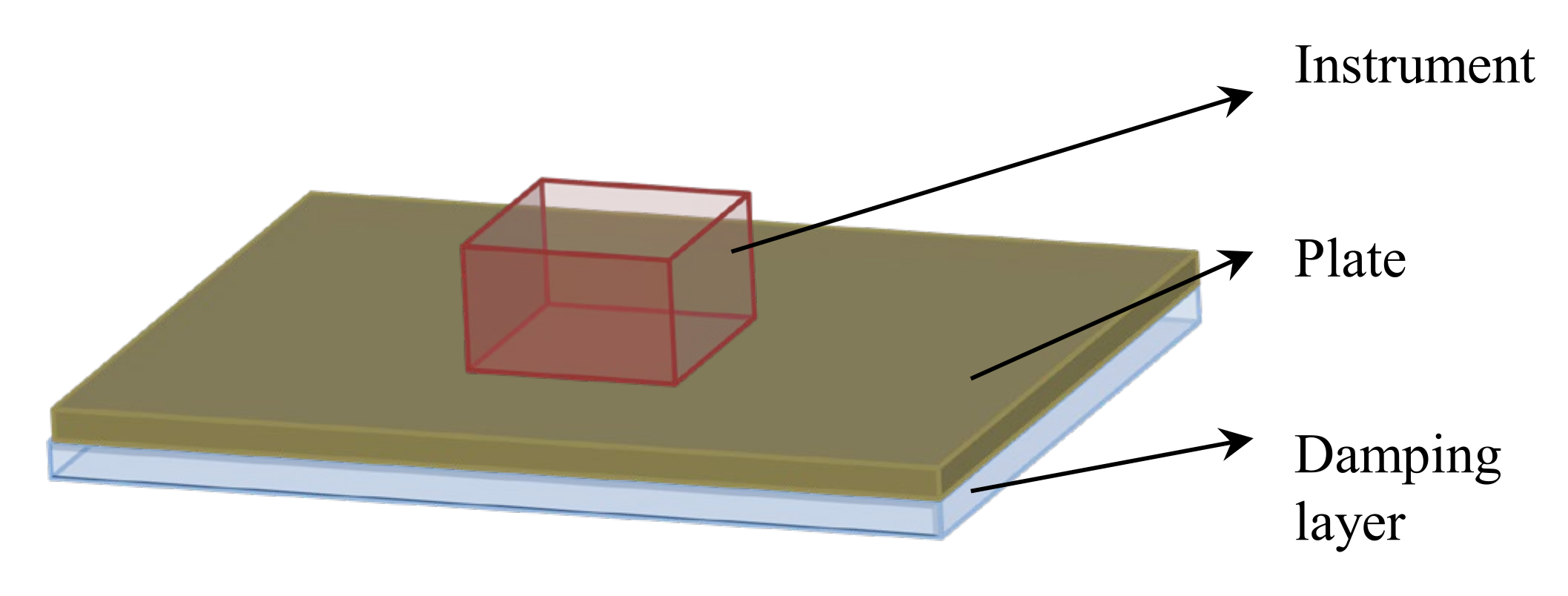
4.2.5. Composite Plate with Instrument Installed on It
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, B.; Huang, C.; Xuan, C.; Liu, X. Dynamic stiffness design of plate/shell structures using explicit topology optimization. Thin-Walled Struct. 2019, 140, 542–564. [Google Scholar] [CrossRef]
- Nakra, B. Vibration Control in Machines and Structures Using Viscoelastic Damping. J. Sound Vib. 1998, 211, 449–466. [Google Scholar] [CrossRef]
- Qatu, M.S.; Sullivan, R.W.; Wang, W. Recent research advances on the dynamic analysis of composite shells: 2000–2009. Compos. Struct. 2010, 93, 14–31. [Google Scholar] [CrossRef]
- Rao, M.D. Recent applications of viscoelastic damping for noise control in automobiles and commercial airplanes. J. Sound Vib. 2003, 262, 457–474. [Google Scholar] [CrossRef]
- Zhou, X.; Yu, D.; Shao, X.; Zhang, S.; Wang, S. Research and applications of viscoelastic vibration damping materials: A review. Compos. Struct. 2016, 136, 460–480. [Google Scholar] [CrossRef]
- Danti, M.; Vigè, D.; Nierop, G.V. Modal Methodology for the Simulation and Optimization of the Free-Layer Damping Treatment of a Car Body. J. Vib. Acoust. 2010, 132, 021001. [Google Scholar] [CrossRef]
- Alvelid, M.; Enelund, M. Modelling of constrained thin rubber layer with emphasis on damping. J. Sound Vib. 2007, 300, 662–675. [Google Scholar] [CrossRef]
- Balmès, E.; Corus, M.; Baumhauer, S.; Jean, P.; Lombard, J.-P. Constrained viscoelastic damping, test/analysis correlation on an aircraft engine. Conf. Proc. Soc. Exp. Mech. Ser. 2011, 3, 1177–1185. [Google Scholar] [CrossRef]
- Alvelid, M. Optimal position and shape of applied damping material. J. Sound Vib. 2008, 310, 947–965. [Google Scholar] [CrossRef]
- Zheng, H.; Cai, C.; Pau, G.; Liu, G. Minimizing vibration response of cylindrical shells through layout optimization of passive constrained layer damping treatments. J. Sound Vib. 2005, 279, 739–756. [Google Scholar] [CrossRef]
- Bendsøe, M.P.; Kikuchi, N. Generating optimal topologies in structural design using a homogenization method. Comput. Methods Appl. Mech. Eng. 1988, 71, 197–224. [Google Scholar] [CrossRef]
- Bendsøe, M.P.; Sigmund, O. Material interpolation schemes in topology optimization. Ingenieur-Archiv 1999, 69, 635–654. [Google Scholar] [CrossRef]
- Alfouneh, M.; Tong, L. Maximizing modal damping in layered structures via multi-objective topology optimization. Eng. Struct. 2017, 132, 637–647. [Google Scholar] [CrossRef]
- Kim, S.Y.; Mechefske, C.K.; Kim, I.Y. Optimal damping layout in a shell structure using topology optimization. J. Sound Vib. 2013, 332, 2873–2883. [Google Scholar] [CrossRef]
- Yamamoto, T.; Yamada, T.; Izui, K.; Nishiwaki, S. Topology optimization of free-layer damping material on a thin panel for maximizing modal loss factors expressed by only real eigenvalues. J. Sound Vib. 2015, 358, 84–96. [Google Scholar] [CrossRef]
- Ding, H.; Xu, B. Optimal design of vibrating composite plate considering discrete–continuous parameterization model and resonant peak constraint. Int. J. Mech. Mater. Des. 2021, 17, 679–705. [Google Scholar] [CrossRef]
- Chen, W.; Liu, S. Microstructural topology optimization of viscoelastic materials for maximum modal loss factor of macrostructures. Struct. Multidiscip. Optim. 2016, 53, 1–14. [Google Scholar] [CrossRef]
- Huang, X.; Zhou, S.; Sun, G.; Li, G.; Xie, Y.M. Topology optimization for microstructures of viscoelastic composite materials. Comput. Methods Appl. Mech. Eng. 2015, 283, 503–516. [Google Scholar] [CrossRef]
- Zhang, H.; Ding, X.; Wang, Q.; Ni, W.; Li, H. Topology optimization of composite material with high broadband damping. Comput. Struct. 2020, 239, 106331. [Google Scholar] [CrossRef]
- Ding, H.; Xu, B. Material microstructure topology optimization of piezoelectric composite beam under initial disturbance for vibration suppression. J. Vib. Control. 2021, 2021. [Google Scholar] [CrossRef]
- Andreassen, E.; Andreasen, C.S. How to determine composite material properties using numerical homogenization. Comput. Mater. Sci. 2014, 83, 488–495. [Google Scholar] [CrossRef] [Green Version]
- Liang, X.; Du, J. Concurrent multi-scale and multi-material topological optimization of vibro-acoustic structures. Comput. Methods Appl. Mech. Eng. 2019, 349, 117–148. [Google Scholar] [CrossRef]
- Fang, Z.; Yao, L.; Tian, S.; Hou, J. Microstructural Topology Optimization of Constrained Layer Damping on Plates for Maximum Modal Loss Factor of Macrostructures. Shock. Vib. 2020, 2020, 1–13. [Google Scholar] [CrossRef]
- Banh, T.T.; Luu, N.G.; Lee, D. A non-homogeneous multi-material topology optimization approach for functionally graded structures with cracks. Compos. Struct. 2021, 273, 114230. [Google Scholar] [CrossRef]
- Zhu, J.-H.; Liu, T.; Zhang, W.-H.; Wang, Y.-L.; Wang, J.-T. Concurrent optimization of sandwich structures lattice core and viscoelastic layers for suppressing resonance response. Struct. Multidiscip. Optim. 2021, 64, 1801–1824. [Google Scholar] [CrossRef]
- Zhang, H.; Ding, X.; Li, H.; Xiong, M. Multi-scale structural topology optimization of free-layer damping structures with damping composite materials. Compos. Struct. 2019, 212, 609–624. [Google Scholar] [CrossRef]
- Olhoff, N.; Du, J. Generalized incremental frequency method for topological designof continuum structures for minimum dynamic compliance subject to forced vibration at a prescribed low or high value of the excitation frequency. Struct. Multidiscip. Optim. 2016, 54, 1113–1141. [Google Scholar] [CrossRef] [Green Version]
- Takezawa, A.; Daifuku, M.; Nakano, Y.; Nakagawa, K.; Yamamoto, T.; Kitamura, M. Topology optimization of damping material for reducing resonance response based on complex dynamic compliance. J. Sound Vib. 2016, 365, 230–243. [Google Scholar] [CrossRef] [Green Version]
- Xu, B.; Jiang, J.S.; Xie, Y.M. Concurrent design of composite macrostructure and multi-phase material microstructure for minimum dynamic compliance. Compos. Struct. 2015, 128, 221–233. [Google Scholar] [CrossRef]
- Yang, X.; Li, Y. Topology optimization to minimize the dynamic compliance of a bi-material plate in a thermal environment. Struct. Multidiscip. Optim. 2012, 47, 399–408. [Google Scholar] [CrossRef]
- Kang, Z.; Zhang, X.; Jiang, S.; Cheng, G. On topology optimization of damping layer in shell structures under harmonic excitations. Struct. Multidiscip. Optim. 2012, 46, 51–67. [Google Scholar] [CrossRef]
- Olhoff, N.; Niu, B. Minimizing the vibrational response of a lightweight building by topology and volume optimization of a base plate for excitatory machinery. Struct. Multidiscip. Optim. 2016, 53, 567–588. [Google Scholar] [CrossRef]
- Zhang, X.; Kang, Z. Dynamic topology optimization of piezoelectric structures with active control for reducing transient response. Comput. Methods Appl. Mech. Eng. 2014, 281, 200–219. [Google Scholar] [CrossRef]
- Sigmund, O. A 99 line topology optimization code written in Matlab. Struct. Multidiscip. Optim. 2001, 21, 120–127. [Google Scholar] [CrossRef]
- Svanberg, K. A Class of Globally Convergent Optimization Methods Based on Conservative Convex Separable Approximations. SIAM J. Optim. 2002, 12, 555–573. [Google Scholar] [CrossRef] [Green Version]
- Long, K.; Han, D.; Gu, X. Concurrent topology optimization of composite macrostructure and microstructure constructed by constituent phases of distinct Poisson’s ratios for maximum frequency. Comput. Mater. Sci. 2017, 129, 194–201. [Google Scholar] [CrossRef]



| Material | Density (kg/m3) | Young’s Modulus (GPa) | Poisson’s Ratio | Loss Factor |
|---|---|---|---|---|
| Metal (Aluminum alloy) | 2700 | 70 | 0.29 | |
| Material A (Rubber) | 1500 | 0.05 | 0.4 | 1 |
| Material B (Polymer) | 1000 | 2 | 0.4 | 0.05 |
| Properties | Fully Covered with Polymer | Fully Covered with Rubber | The Structure in Figure 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Commercial | Proposed | Error | Commercial | Proposed | Error | Commercial | Proposed | Error | |
| The first modal loss factor | 0.01342 | 0.01412 | 5.21% | 0.00973 | 0.00977 | 0.42% | 0.01189 | 0.01288 | 8.38% |
| The second modal loss factor | 0.01238 | 0.01310 | 5.83% | 0.00870 | 0.00881 | 1.30% | 0.01063 | 0.01151 | 8.26% |
| The third modal loss factor | 0.01320 | 0.01395 | 5.68% | 0.00955 | 0.00963 | 0.85% | 0.01169 | 0.01258 | 7.60% |
| The first eigenfrequency (Hz) | 265.2 | 266.8 | 0.60% | 212.8 | 213.1 | 0.18% | 238.7 | 237.9 | 0.35% |
| The second eigenfrequency (Hz) | 796.0 | 810.5 | 1.82% | 647.4 | 656.3 | 1.38% | 718.7 | 730.4 | 1.62% |
| The third eigenfrequency (Hz) | 1634.6 | 1654.7 | 1.23% | 1313.9 | 1324.7 | 0.82% | 1473.2 | 1479.9 | 0.46% |
| CPU time (s) | 108 | 1.03 | 100 | 1.04 | 99 | 1.16 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Ding, X.; Ni, W.; Chen, Y.; Zhang, X.; Li, H. Concurrent Topology Optimization of Composite Plates for Minimum Dynamic Compliance. Materials 2022, 15, 538. https://doi.org/10.3390/ma15020538
Zhang H, Ding X, Ni W, Chen Y, Zhang X, Li H. Concurrent Topology Optimization of Composite Plates for Minimum Dynamic Compliance. Materials. 2022; 15(2):538. https://doi.org/10.3390/ma15020538
Chicago/Turabian StyleZhang, Heng, Xiaohong Ding, Weiyu Ni, Yanyu Chen, Xiaopeng Zhang, and Hao Li. 2022. "Concurrent Topology Optimization of Composite Plates for Minimum Dynamic Compliance" Materials 15, no. 2: 538. https://doi.org/10.3390/ma15020538
APA StyleZhang, H., Ding, X., Ni, W., Chen, Y., Zhang, X., & Li, H. (2022). Concurrent Topology Optimization of Composite Plates for Minimum Dynamic Compliance. Materials, 15(2), 538. https://doi.org/10.3390/ma15020538








