Influence of (Sub) Structure Development within Rotary Swaged Al–Cu Clad Conductors on Skin Effect during Transfer of Alternating Current
Abstract
:1. Introduction
2. Materials and Methods
2.1. Preparation of Material
2.2. Experimental Determination of Electric Characteristics
2.3. Numerical Predictions of Electric Characteristics
2.4. Analyses of Experimental Material
3. Results
3.1. Electric Characteristics
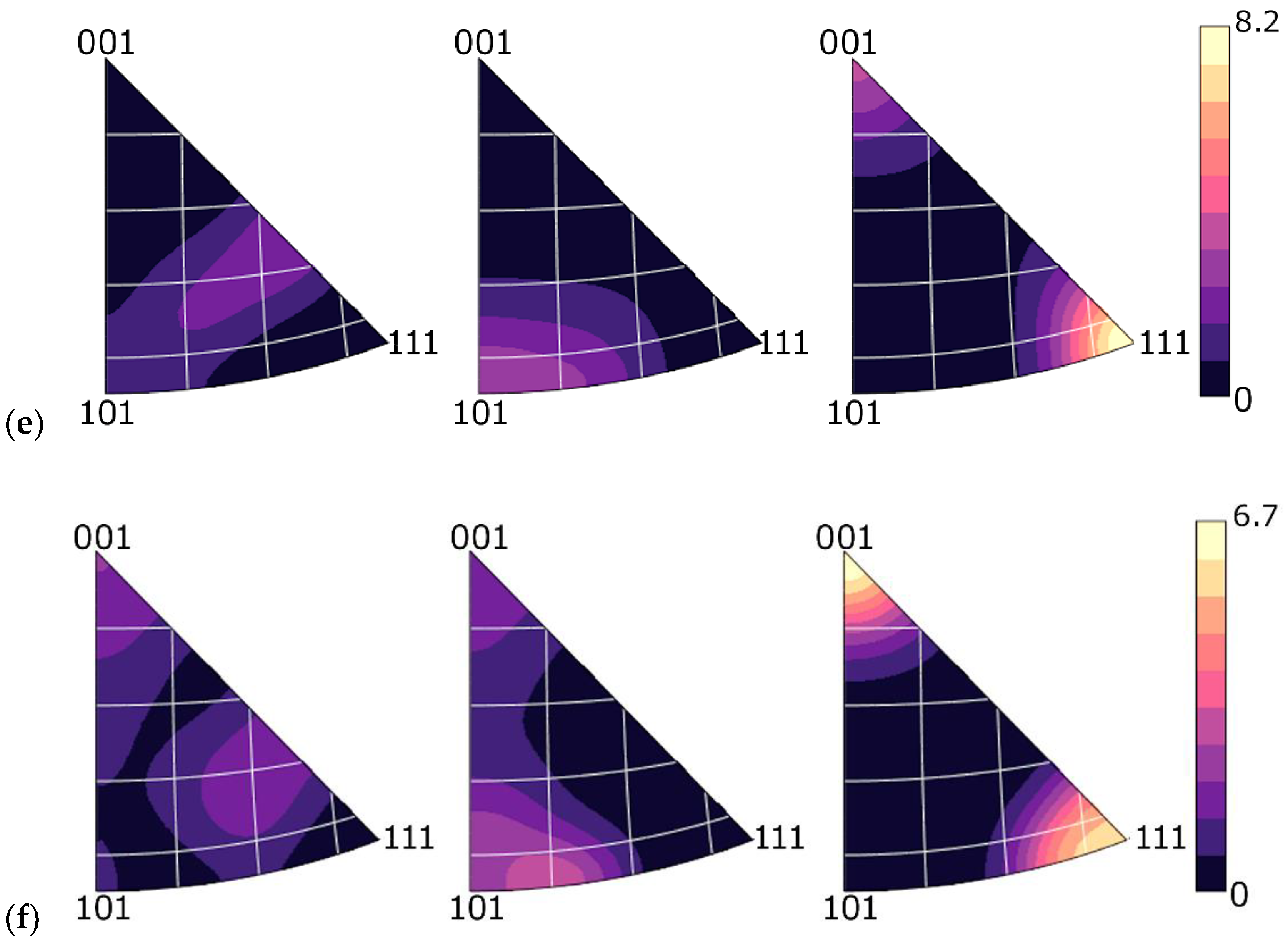
3.2. (Sub) Structure Development
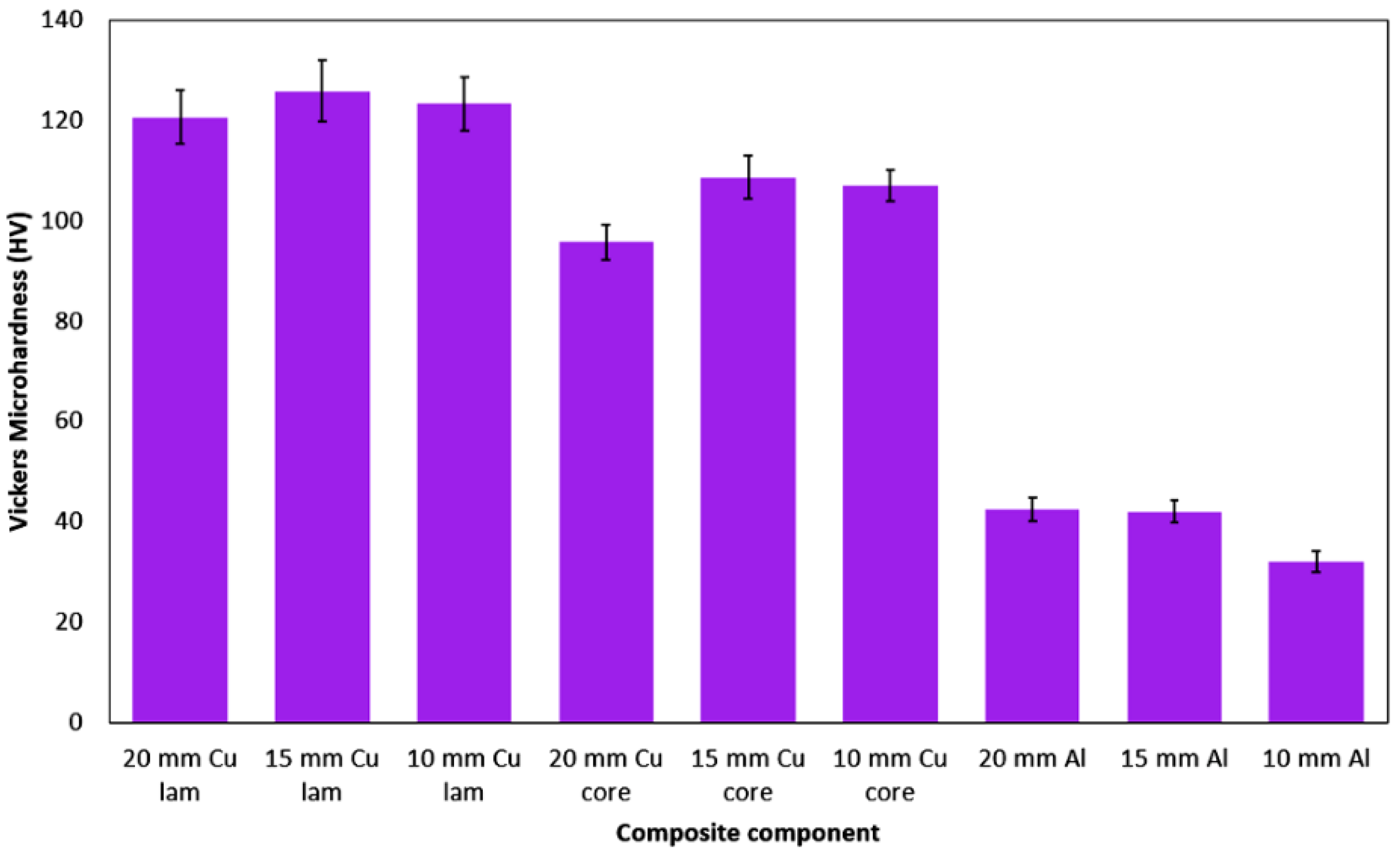
3.3. Microhardness Measurements
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ling, K.; Mo, Q.; Lv, X.; Qin, G.; Yang, W.; Li, L.; Li, W. Growth characteristics and corrosion resistance of micro-arc oxidation coating on Al–Mg composite plate. Vacuum 2022, 195, 110640. [Google Scholar] [CrossRef]
- Mozaffari, A.; Danesh Manesh, H.; Janghorban, K. Evaluation of mechanical properties and structure of multilayered Al/Ni composites produced by accumulative roll bonding (ARB) process. J. Alloys Compd. 2010, 489, 103–109. [Google Scholar] [CrossRef]
- Ghalandari, L.; Mahdavian, M.M.; Reihanian, M.; Mahmoudiniya, M. Production of Al/Sn multilayer composite by accumulative roll bonding (ARB): A study of microstructure and mechanical properties. Mater. Sci. Eng. A 2016, 661, 179–186. [Google Scholar] [CrossRef]
- Hosseini, M.; Danesh Manesh, H. Bond strength optimization of Ti/Cu/Ti clad composites produced by roll-bonding. Mater. Des. 2015, 81, 122–132. [Google Scholar] [CrossRef]
- Tayyebi, M.; Eghbali, B. Study on the microstructure and mechanical properties of multilayer Cu/Ni composite processed by accumulative roll bonding. Mater. Sci. Eng. A 2013, 559, 759–764. [Google Scholar] [CrossRef]
- Gladkovsky, S.V.; Kuteneva, S.V.; Sergeev, S.N. Microstructure and mechanical properties of sandwich copper/steel composites produced by explosive welding. Mater. Charact. 2019, 154, 294–303. [Google Scholar] [CrossRef]
- Motevalli, P.D.; Eghbali, B. Microstructure and mechanical properties of laminated Al–Cu–Mg composite fabricated by accumulative roll bonding. Bull. Mater. Sci. 2017, 40, 1481–1488. [Google Scholar] [CrossRef] [Green Version]
- Mahdavian, M.M.; Ghalandari, L.; Reihanian, M. Accumulative roll bonding of multilayered Cu/Zn/Al: An evaluation of microstructure and mechanical properties. Mater. Sci. Eng. A Struct. Mater. Prop. Microstruct. Process. 2013, 579, 99–107. [Google Scholar] [CrossRef]
- Akgul, B.; Erden, F.; Ozbay, S. Porous Cu/Al composites for cost-effective thermal management. Powder Technol. 2021, 391, 11–19. [Google Scholar] [CrossRef]
- Wang, Y.; Li, X.; Wang, X.; Yan, H. Fabrication of a thick copper-stainless steel clad plate for nuclear fusion equipment by explosive welding. Fusion Eng. Des. 2018, 137, 91–96. [Google Scholar] [CrossRef]
- Shen, W.; Yu, L.; Liu, H.; He, Y.; Zhou, Z.; Zhang, Q. Diffusion welding of powder metallurgy high speed steel by spark plasma sintering. J. Mater. Process. Technol. 2020, 275, 116383. [Google Scholar] [CrossRef]
- Jamili, A.M.; Zarei-Hanzaki, A.; Abedi, H.R.; Mosayebi, M.; Kocich, R.; Kunčická, L. Development of fresh and fully recrystallized microstructures through friction stir processing of a rare earth bearing magnesium alloy. Mater. Sci. Eng. A 2019, 775, 138837. [Google Scholar] [CrossRef]
- Kocich, R.; Kunčická, L.; Macháčková, A.; Šofer, M. Improvement of mechanical and electrical properties of rotary swaged Al-Cu clad composites. Mater. Des. 2017, 123, 137–146. [Google Scholar] [CrossRef]
- Kocich, R.; Macháčková, A.; Kunčická, L.; Fojtík, F. Fabrication and characterization of cold-swaged multilayered Al-Cu clad composites. Mater. Des. 2015, 71, 36–47. [Google Scholar] [CrossRef]
- Kunčická, L.; Lowe, T.C.; Davis, C.F.; Kocich, R.; Pohludka, M. Synthesis of an Al/Al2O3 composite by severe plastic deformation. Mater. Sci. Eng. A 2015, 646, 234–241. [Google Scholar] [CrossRef]
- Awang Sh’ri, D.N.; Zahari, Z.S.; Yamamoto, A. Effect of ECAP Die Angle on Mechanical Properties and Biocompatibility of SS316L. Metals 2021, 11, 1513. [Google Scholar] [CrossRef]
- Hlaváč, L.M.; Kocich, R.; Gembalová, L.; Jonšta, P.; Hlaváčová, I.M. AWJ cutting of copper processed by ECAP. Int. J. Adv. Manuf. Technol. 2016, 86, 885–894. [Google Scholar] [CrossRef]
- Kunčická, L.; Kocich, R.; Drápala, J.; Andreyachshenko, V.A. FEM simulations and comparison of the ecap and ECAP-PBP influence on Ti6Al4V alloy’s deformation behaviour. In Proceedings of the METAL 2013—22nd International Conference on Metallurgy and Materials, Brno, Czech Republic, 15–17 May 2013; pp. 391–396. [Google Scholar]
- Derakhshan, J.F.; Parsa, M.H.; Jafarian, H.R. Microstructure and mechanical properties variations of pure aluminum subjected to one pass of ECAP-Conform process. Mater. Sci. Eng. A 2019, 747, 120–129. [Google Scholar] [CrossRef]
- Kunčická, L.; Kocich, R.; Ryukhtin, V.; Cullen, J.C.T.; Lavery, N.P. Study of structure of naturally aged aluminium after twist channel angular pressing. Mater. Charact. 2019, 152, 94–100. [Google Scholar] [CrossRef] [Green Version]
- Kocich, R.; Kunčická, L.; Macháčková, A. Twist Channel Multi-Angular Pressing ( TCMAP ) as a method for increasing the efficiency of SPD. IOP Conf. Ser. Mater. Sci. Eng. 2014, 63, 012006. [Google Scholar] [CrossRef]
- Deb, S.; Panigrahi, S.K.; Weiss, M. Development of bulk ultrafine grained Al-SiC nano composite sheets by a SPD based hybrid process: Experimental and theoretical studies. Mater. Sci. Eng. A 2018, 738, 323–334. [Google Scholar] [CrossRef]
- Shahabi, H.S.; Eizadjou, M.; Manesh, H.D. Evolution of mechanical properties in SPD processed Cu/Nb nano-layered composites. Mater. Sci. Eng. A 2010, 527, 5790–5795. [Google Scholar] [CrossRef]
- Chlupová, A.; Šulák, I.; Kunčická, L.; Kocich, R.; Svoboda, J. Microstructural aspects of new grade ODS alloy consolidated by rotary swaging. Mater. Charact. 2021, 181, 111477. [Google Scholar] [CrossRef]
- Kunčická, L.; Kocich, R. Deformation behaviour of Cu-Al clad composites produced by rotary swaging. IOP Conf. Ser. Mater. Sci. Eng. 2018, 369, 012029. [Google Scholar] [CrossRef]
- Kunčická, L.; Macháčková, A.; Lavery, N.P.; Kocich, R.; Cullen, J.C.T.; Hlaváč, L.M. Effect of thermomechanical processing via rotary swaging on properties and residual stress within tungsten heavy alloy. Int. J. Refract. Met. Hard Mater. 2020, 87, 1–15. [Google Scholar] [CrossRef]
- Kocich, R.; Kunčická, L.; Král, P.; Strunz, P. Characterization of innovative rotary swaged Cu-Al clad composite wire conductors. Mater. Des. 2018, 160, 828–835. [Google Scholar] [CrossRef]
- Beygi, R.; Kazeminezhad, M.; Mehrizi, M.Z.; Eisaabadi, B.G.; Loureiro, A. Friction stir butt welding of Al-Cu bilayer laminated composites: Analysis of force, torque, and temperature. Int. J. Adv. Manuf. Technol. 2017, 88, 393–400. [Google Scholar] [CrossRef]
- Danilenko, V.N.N.; Sergeev, S.N.N.; Baimova, J.A.A.; Korznikova, G.F.F.; Nazarov, K.S.S.; Khisamov, R.K.; Glezer, A.M.M.; Mulyukov, R.R.R. An approach for fabrication of Al-Cu composite by high pressure torsion. Mater. Lett. 2019, 236, 51–55. [Google Scholar] [CrossRef]
- Kocich, R.; Kunčická, L.; Davis, C.F.; Lowe, T.C.; Szurman, I.; Macháčková, A. Deformation behavior of multilayered Al-Cu clad composite during cold-swaging. Mater. Des. 2016, 90, 379–388. [Google Scholar] [CrossRef]
- Yousefi Mehr, V.; Toroghinejad, M.R.; Rezaeian, A.; Asgari, H.; Szpunar, J.A. A texture study of nanostructured Al–Cu multi-layered composite manufactured via the accumulative roll bonding (ARB). J. Mater. Res. Technol. 2021, 14, 2909–2919. [Google Scholar] [CrossRef]
- Kunčická, L.; Kocich, R.; Strunz, P.; Macháčková, A. Texture and residual stress within rotary swaged Cu/Al clad composites. Mater. Lett. 2018, 230, 88–91. [Google Scholar] [CrossRef]
- Kocich, R.; Kunčická, L. Development of structure and properties in bimetallic Al/Cu sandwich composite during cumulative severe plastic deformation. J. Sandw. Struct. Mater. 2021, 23, 4252–4275. [Google Scholar] [CrossRef]
- Kim, I.-K.; Hong, S.I. Effect of heat treatment on the bending behavior of tri-layered Cu/Al/Cu composite plates. Mater. Des. 2013, 47, 590–598. [Google Scholar] [CrossRef]
- Kunčická, L.; Kocich, R.; Dvořák, K.; Macháčková, A. Rotary swaged laminated Cu-Al composites: Effect of structure on residual stress and mechanical and electric properties. Mater. Sci. Eng. A 2019, 742, 743–750. [Google Scholar] [CrossRef]
- Koo, G.M.; Tallman, T.N. Frequency-dependent alternating current piezoresistive switching behavior in self-sensing carbon nanofiber composites. Carbon N. Y. 2021, 173, 384–394. [Google Scholar] [CrossRef]
- Jouni, M.; Buzlukov, A.; Bardet, M.; Da Cruz-Boisson, F.; Eddarir, A.; Massardier, V.; Boiteux, G. Skin effect of conductive polymer composites observed by high-resolution solid-state NMR. Compos. Sci. Technol. 2014, 104, 104–110. [Google Scholar] [CrossRef]
- Webster, J.G. Electrical Measurement, Signal Processing, and Displays (Principles and Applications in Engineering), 1st ed.; CRC Press: Boca Raton, FL, USA, 2003; Available online: https://www.amazon.com/Electrical-Measurement-Processing-Applications-Engineering/dp/0849317339 (accessed on 25 August 2021).
- Dugdale, J.S. The Electrical Properties of Metals and Alloys; Dover Publication: Garden City, NY, USA, 2016. [Google Scholar]
- Gennesson, M.; Zollinger, J.; Daloz, D.; Rouat, B.; Demurger, J.; Combeau, H. Three Dimensional Methodology to Characterize Large Dendritic Equiaxed Grains in Industrial Steel Ingots. Materials 2018, 11, 1007. [Google Scholar] [CrossRef] [Green Version]
- Toth, L.S.; Biswas, S.; Gu, C.; Beausir, B. Notes on representing grain size distributions obtained by electron backscatter diffraction. Mater. Charact. 2013, 84, 67–71. [Google Scholar] [CrossRef]
- Russell, A.; Lee, K.L. Structure-Property Relations in Nonferrous Metals, 1st ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2005. [Google Scholar]


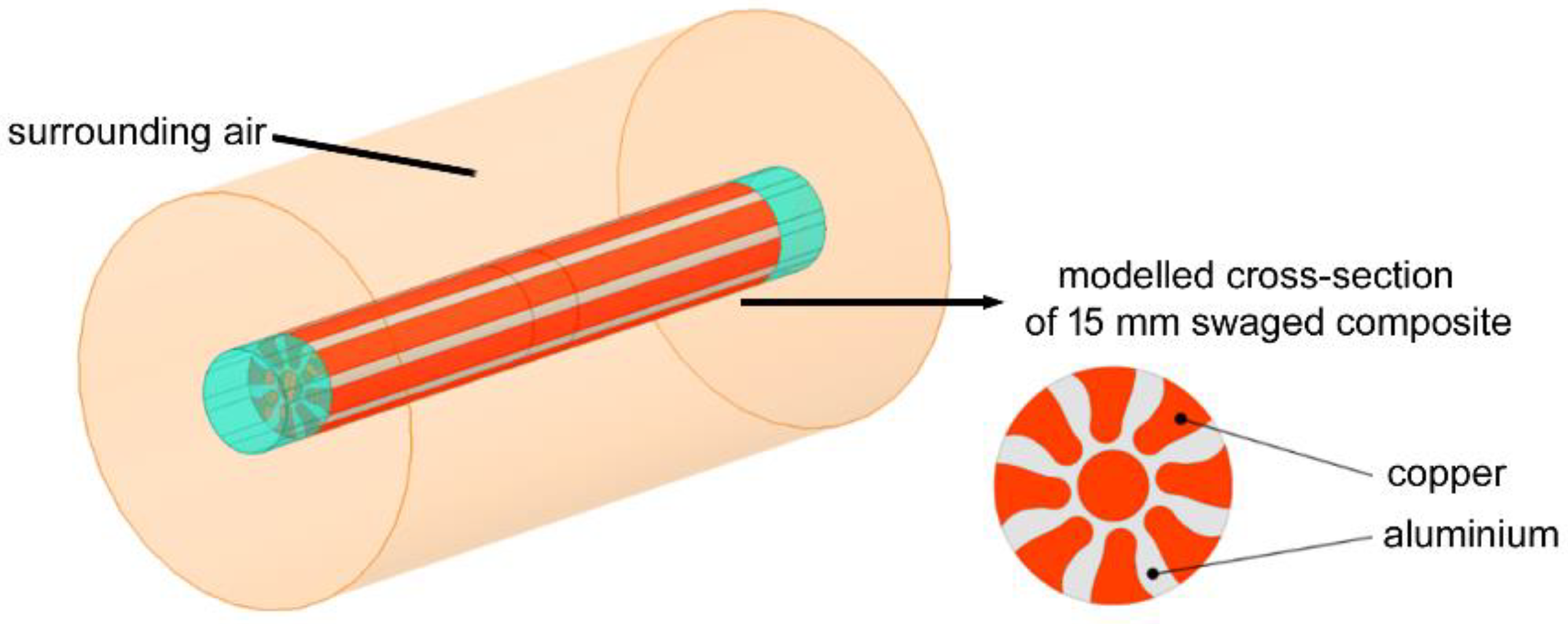
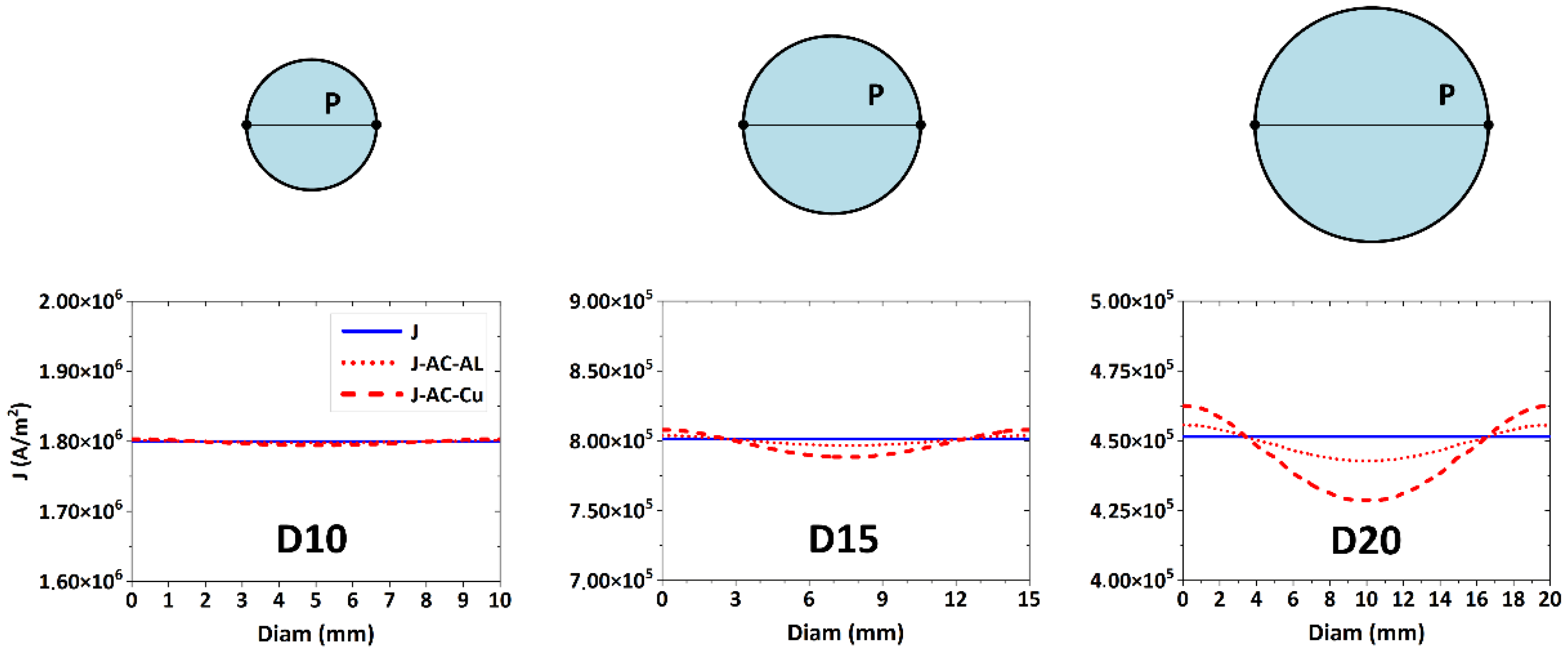
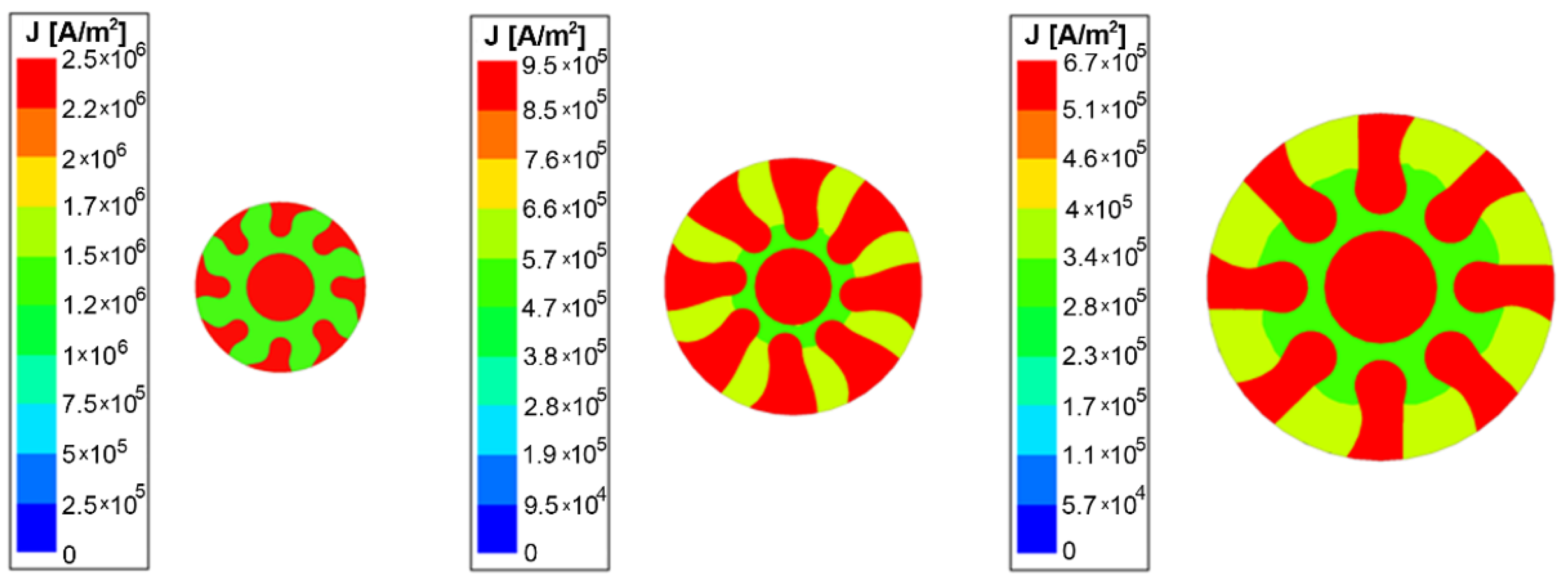
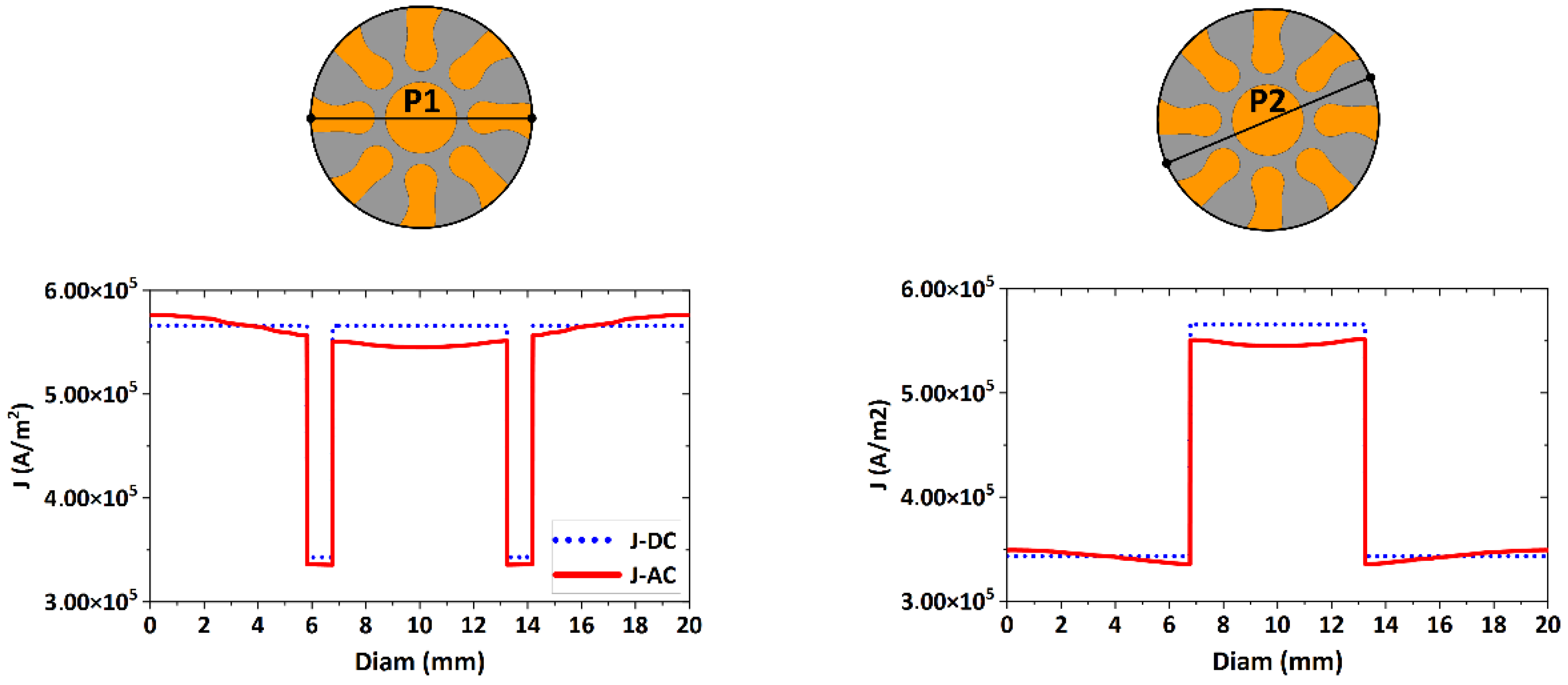
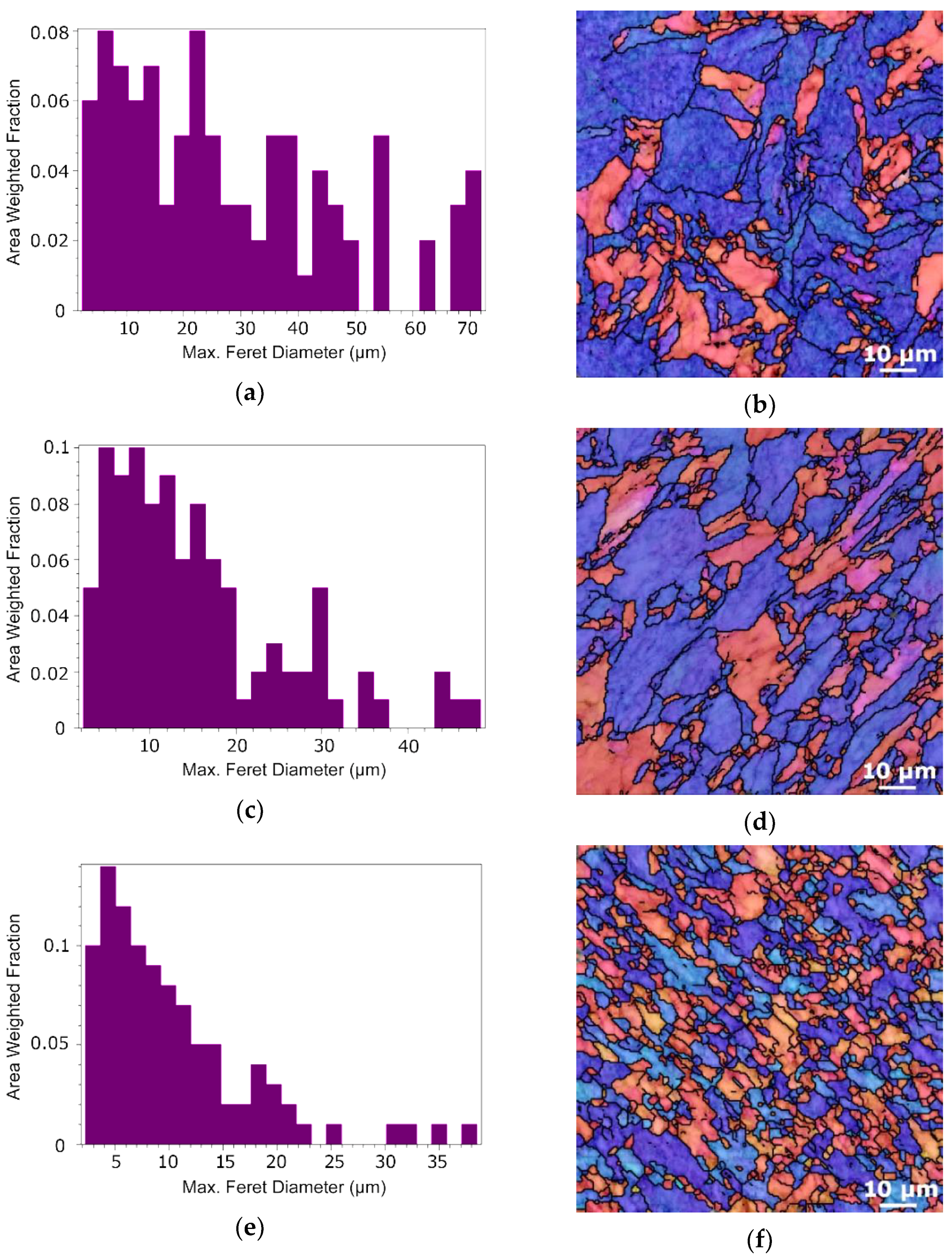

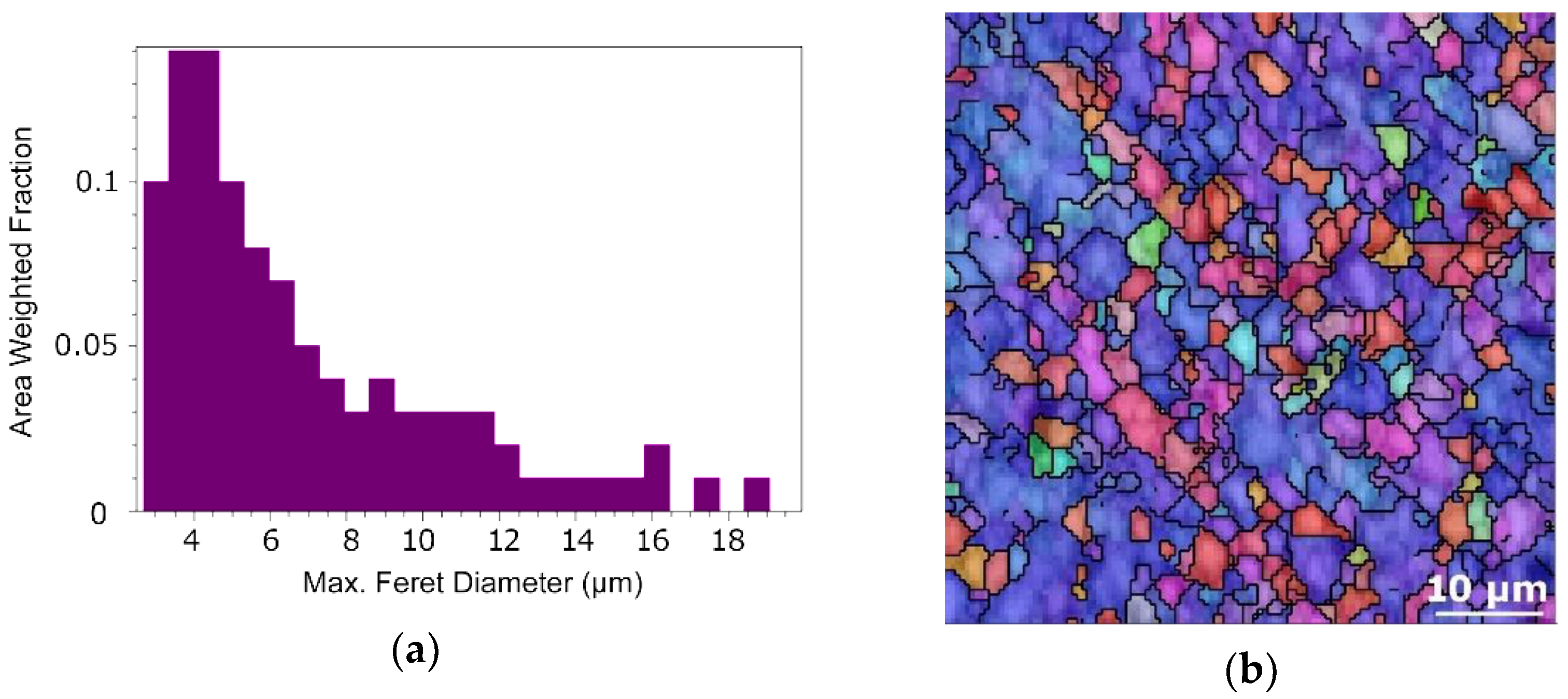
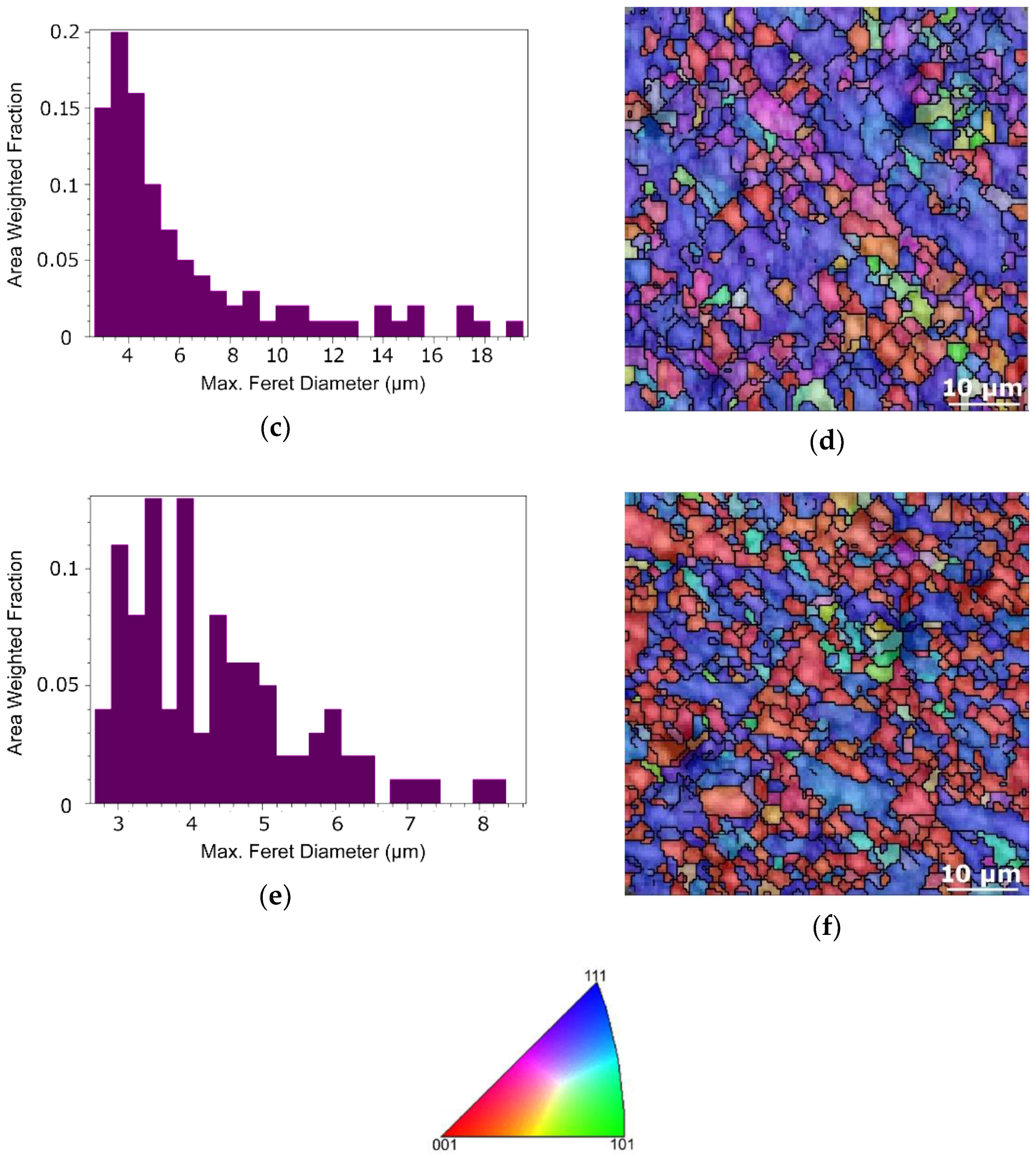
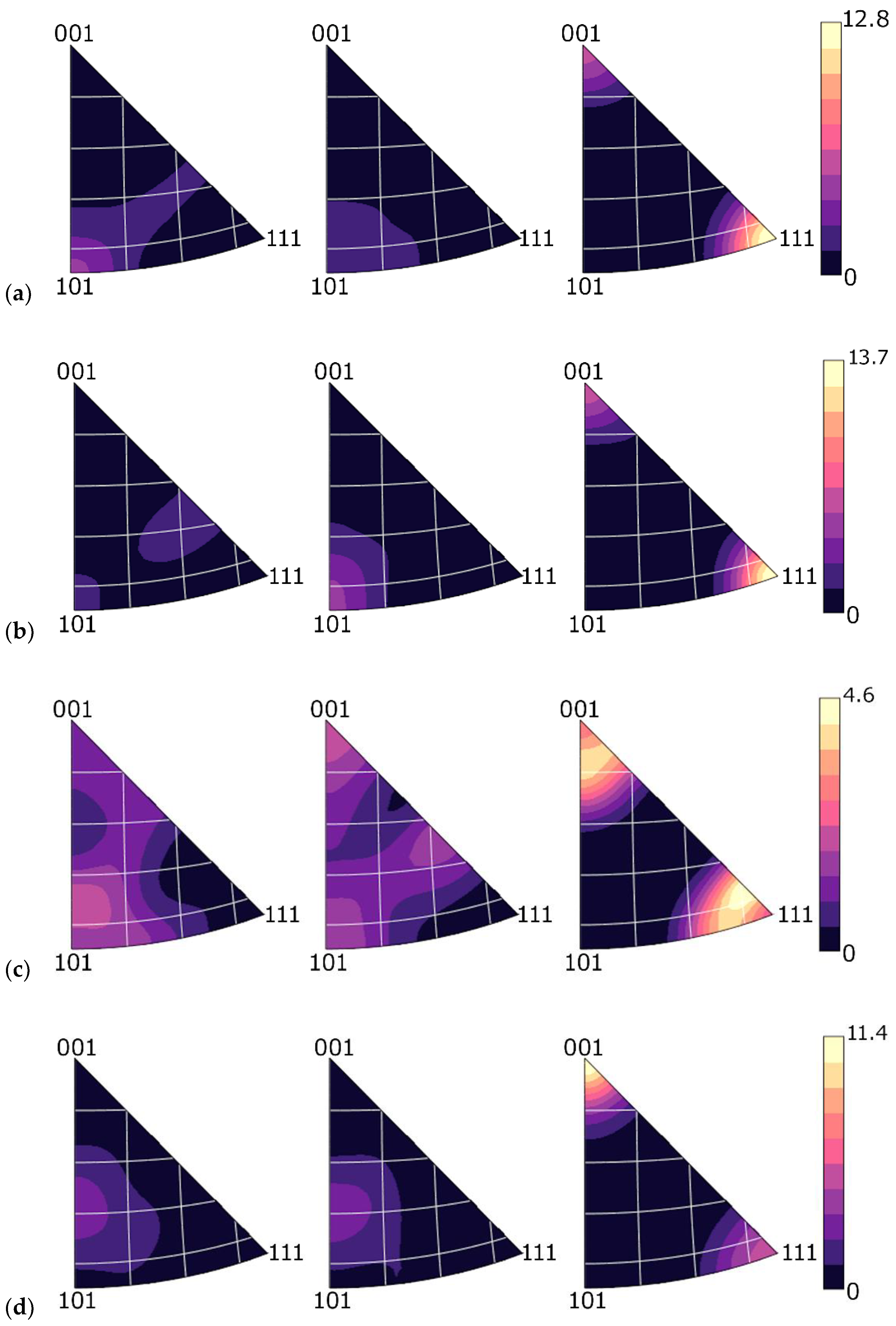


| Material | Permeability μr (-) | Specific Electric Resistivity ρ (Ω·m)·10−9 | Skin Depth δ (m)·10−3 |
|---|---|---|---|
| ETC Aluminium | 1.000021 | 28.772 | 12.07 |
| ETC Copper | 0.999991 | 17.468 | 9.41 |
| Material | DC Power Losses dPDC (W) | AC Power Losses dPAC (W) | Coefficient ks (-) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| D10 | D15 | D20 | D10 | D15 | D20 | D10 | D15 | D20 | |
| ETC Aluminium | 3.664 | 1.631 | 0.919 | 3.666 | 1.636 | 0.928 | 1.001 | 1.003 | 1.009 |
| ETC Copper | 2.222 | 0.989 | 0.557 | 2.225 | 0.997 | 0.571 | 1.002 | 1.008 | 1.025 |
| Clad composite | 2.821 | 1.165 | 0.698 | 2.824 | 1.173 | 0.711 | 1.001 | 1.006 | 1.018 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kunčická, L.; Kocich, R.; Kačor, P.; Jambor, M.; Jopek, M. Influence of (Sub) Structure Development within Rotary Swaged Al–Cu Clad Conductors on Skin Effect during Transfer of Alternating Current. Materials 2022, 15, 650. https://doi.org/10.3390/ma15020650
Kunčická L, Kocich R, Kačor P, Jambor M, Jopek M. Influence of (Sub) Structure Development within Rotary Swaged Al–Cu Clad Conductors on Skin Effect during Transfer of Alternating Current. Materials. 2022; 15(2):650. https://doi.org/10.3390/ma15020650
Chicago/Turabian StyleKunčická, Lenka, Radim Kocich, Petr Kačor, Michal Jambor, and Miroslav Jopek. 2022. "Influence of (Sub) Structure Development within Rotary Swaged Al–Cu Clad Conductors on Skin Effect during Transfer of Alternating Current" Materials 15, no. 2: 650. https://doi.org/10.3390/ma15020650
APA StyleKunčická, L., Kocich, R., Kačor, P., Jambor, M., & Jopek, M. (2022). Influence of (Sub) Structure Development within Rotary Swaged Al–Cu Clad Conductors on Skin Effect during Transfer of Alternating Current. Materials, 15(2), 650. https://doi.org/10.3390/ma15020650







