Analytical Determination of the Bending Stiffness of a Five-Layer Corrugated Cardboard with Imperfections
Abstract
:1. Introduction
2. Materials and Methods
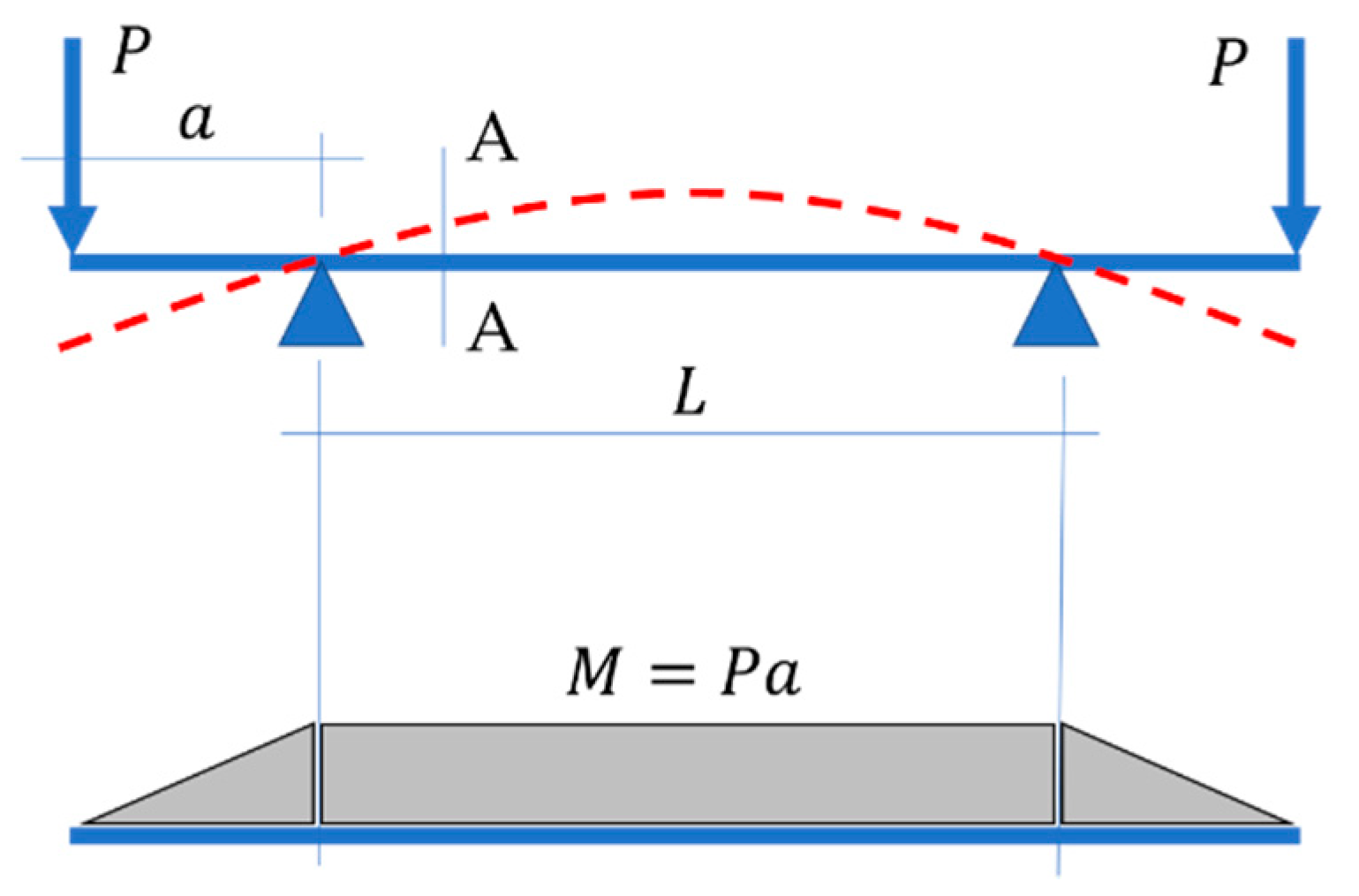
2.1. The Four-Point Bending Test of a Sample with an Asymmetric Cross-Section
2.2. Corrugated Cardboard-Samples
2.3. Bending Stiffness of Assymetric Corrugated Board with Imperfections
3. Results
- FEM-1 (1-wave), number of nodes: 375, number of elements: 377;
- FEM-2 (2-waves), number of nodes: 746, number of elements: 754;
- FEM-3 (3-waves); number of nodes: 1118, number of elements: 1131;
- FEM-4 (4-waves); number of nodes: 1489, number of elements: 1508.
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Baum, G.A.; Brennan, D.C.; Habeger, C.C. Orthotropic elastic constants of paper. Tappi 1981, 64, 97–101. [Google Scholar]
- Mann, R.W.; Baum, G.A.; Habeger, C.C. Determination of all nine orthotropic elastic constants for machine-made paper. Tappi 1980, 63, 163–166. [Google Scholar]
- Frank, B. Corrugated box compression—A literature survey. Packag. Technol. Sci. 2014, 27, 105–128. [Google Scholar] [CrossRef]
- Zhang, Y.-L.; Chen, J.; Wu, Y.; Sun, J. Analysis of hazard factors of the use of corrugated carton in packaging low-temperature yogurt during logistics. Procedia Environ. Sci. 2011, 10, 968–973. [Google Scholar] [CrossRef] [Green Version]
- Hung, D.; Nakano, Y.; Tanaka, F.; Hamanaka, D.; Uchino, T. Preserving the strength of corrugated cardboard under high humidity condition using nano-sized mists. Compos. Sci. Technol. 2010, 70, 2123–2127. [Google Scholar] [CrossRef]
- Gallo, J.; Cortés, F.; Alberdi, E.; Goti, A. Mechanical behavior modeling of containers and octabins made of corrugated cardboard subjected to vertical stacking loads. Materials 2021, 14, 2392. [Google Scholar] [CrossRef]
- Böröcz, P.; Molnár, B. Measurement and analysis of vibration levels in stacked small package shipments in delivery vans as a function of free movement space. Appl. Sci. 2020, 10, 7821. [Google Scholar] [CrossRef]
- Quesenberry, C.; Horvath, L.; Bouldin, J.; White, M.S. The Effect of pallet top deck stiffness on the compression strength of asymmetrically supported corrugated boxes. Packag. Technol. Sci. 2020, 33, 547–558. [Google Scholar] [CrossRef]
- Garbowski, T.; Gajewski, T.; Grabski, J.K. Estimation of the compressive strength of corrugated cardboard boxes with various openings. Energies 2021, 14, 155. [Google Scholar] [CrossRef]
- Garbowski, T.; Gajewski, T.; Grabski, J.K. Estimation of the compressive strength of corrugated cardboard boxes with various perforations. Energies 2021, 14, 1095. [Google Scholar] [CrossRef]
- Garbowski, T.; Knitter-Piątkowska, A.; Mrówczyński, D. Numerical homogenization of multi-layered corrugated cardboard with creasing or perforation. Materials 2021, 14, 3786. [Google Scholar] [CrossRef]
- Gong, G.; Liu, Y.; Fan, B.; Sun, D. Deformation and compressive strength of corrugated cartons under different indentation shapes: Experimental and simulation study. Packag. Technol. Sci. 2020, 33, 215–226. [Google Scholar] [CrossRef]
- Fadiji, T.; Coetzee, C.J.; Opara, U.L. Compression strength of ventilated corrugated paperboard packages: Numerical modelling, experimental validation and effects of vent geometric design. Biosyst. Eng. 2016, 151, 231–247. [Google Scholar] [CrossRef]
- Fadiji, T.; Ambaw, A.; Coetzee, C.J.; Berry, T.M.; Opara, U.L. Application of finite element analysis to predict the mechanical strength of ventilated corrugated paperboard packaging for handling fresh produce. Biosyst. Eng. 2018, 174, 260–281. [Google Scholar] [CrossRef]
- Mrówczyński, D.; Garbowski, T.; Knitter-Piątkowska, A. Estimation of the compressive strength of corrugated board boxes with shifted creases on the flaps. Materials 2021, 14, 5181. [Google Scholar] [CrossRef]
- Tutak, D.; Keskin, B.; Abubakr, S.; Fleming, P.D. Investigation of the effect of rubber based offset ink printed on packaging cardboard on the strength properties of packing cartons. Int. J. Appl. Sci. Technol. 2019, 9, 9–17. [Google Scholar] [CrossRef]
- Kellicutt, K.; Landt, E. Development of design data for corrugated fibreboard shipping containers. Tappi J. 1952, 35, 398–402. [Google Scholar]
- Allerby, I.M.; Laing, G.N.; Cardwell, R.D. Compressive strength—From components to corrugated containers. Appita Conf. Notes 1985, 1–11. [Google Scholar]
- Schrampfer, K.E.; Whitsitt, W.J.; Baum, G.A. Combined Board Edge Crush (ECT) Technology; Institute of Paper Chemistry: Appleton, WI, USA, 1987. [Google Scholar]
- Batelka, J.J.; Smith, C.N. Package Compression Model; Institute of Paper Science and Technology: Atlanta, GA, USA, 1993. [Google Scholar]
- Urbanik, T.J.; Frank, B. Box compression analysis of world-wide data spanning 46 years. Wood Fiber Sci. 2006, 38, 399–416. [Google Scholar]
- Zaheer, M.; Awais, M.; Rautkari, L.; Sorvari, J. Finite element analysis of paperboard package under compressional load. Procedia Manuf. 2018, 17, 1162–1170. [Google Scholar] [CrossRef]
- Garbowski, T.; Gajewski, T.; Grabski, J.K. The role of buckling in the estimation of compressive strength of corrugated cardboard boxes. Materials 2020, 13, 4578. [Google Scholar] [CrossRef] [PubMed]
- Czechowski, L.; Bieńkowska, M.; Szewczyk, W. Paperboard tubes failure due to lateral compression—Experimental and numerical study. Compos. Struct. 2018, 203, 132–141. [Google Scholar] [CrossRef]
- Garbowski, T.; Jarmuszczak, M. Numerical Strength Estimate of Corrugated Board Packages. Part 1. Theoretical Assumptions in Numerical Modeling of Paperboard Packages. Pol. Pap. Rev. 2014, 70, 219–222. (In Polish) [Google Scholar]
- Garbowski, T.; Jarmuszczak, M. Numerical Strength Estimate of Corrugated Board Packages. Part 2. Experimental tests and numerical analysis of paperboard packages. Pol. Pap. Rev. 2014, 70, 277–281. (In Polish) [Google Scholar]
- Park, J.; Chang, S.; Jung, H.M. Numerical prediction of equivalent mechanical properties of corrugated paperboard by 3D finite element analysis. Appl. Sci. 2020, 10, 7973. [Google Scholar] [CrossRef]
- Park, J.; Park, M.; Choi, D.S.; Jung, H.M.; Hwang, S.W. Finite element-based simulation for edgewise compression behavior of corrugated paperboard for packing of agricultural products. Appl. Sci. 2020, 10, 6716. [Google Scholar] [CrossRef]
- Czechowski, L.; Kmita-Fudalej, G.; Szewczyk, W.; Gralewski, J.; Bieńkowska, M. Numerical and experimental study of five-layer non-symmetrical paperboard panel stiffness. Materials 2021, 14, 7453. [Google Scholar] [CrossRef]
- Jamsari, M.A.; Kueh, C.; Gray-Stuart, E.M.; Dahm, K.; Bronlund, J.E. Experimental and numerical performance of corrugated fibreboard at different orientations under four-point bending test. Packag. Technol. Sci. 2019, 32, 555–565. [Google Scholar] [CrossRef]
- Urbanik, T.J.; Saliklis, E.P. Finite element corroboration of buckling phenomena observed in corrugated boxes. Wood Fiber Sci. 2003, 35, 322–333. [Google Scholar]
- Nordstrand, T. Basic Testing and Strength Design of Corrugated Board and Containers. Ph.D. Thesis, Lund University, Lund, Sweden, 2003. [Google Scholar]
- Nordstrand, T.; Carlsson, L. Evaluation of transverse shear stiffness of structural core sandwich plates. Compos. Struct. 1997, 37, 145–153. [Google Scholar] [CrossRef]
- Garbowski, T.; Gajewski, T. Determination of Transverse Shear Stiffness of Sandwich Panels with a Corrugated Core by Numerical Homogenization. Materials 2021, 14, 1976. [Google Scholar] [CrossRef]
- Avilés, F.; Carlsson, L.A.; May-Pat, A. A shear-corrected formulation of the sandwich twist specimen. Exp. Mech. 2012, 52, 17–23. [Google Scholar] [CrossRef]
- Słonina, M.; Dziurka, D.; & Smardzewski, J. Experimental research and numerical analysis of the elastic properties of paper cell cores before and after impregnation. Materials 2020, 13, 2058. [Google Scholar] [CrossRef]
- Domaneschi, M.; Perego, U.; Borgqvist, E.; Borsari, R. An industry-oriented strategy for the finite element simulation of paperboard creasing and folding. Packag. Technol. Sci. 2017, 30, 269–294. [Google Scholar] [CrossRef]
- Awais, M.; Tanninen, P.; Leppänen, T.; Matthews, S.; Sorvari, J.; Varis, J.; Backfol, K. A computational and experimental analysis of crease behavior in press forming process. Procedia Manuf. 2018, 17, 835–842. [Google Scholar] [CrossRef]
- Thakkar, B.K.; Gooren, L.G.J.; Peerlings, R.H.J.; Geers, M.G.D. Experimental and numerical investigation of creasing in corrugated paperboard. Philos. Mag. 2008, 88, 3299–3310. [Google Scholar] [CrossRef] [Green Version]
- Beex, L.A.A.; Peerlings, R.H.J. An experimental and computational study of laminated paperboard creasing and folding. Int. J. Solids Struct. 2009, 46, 4192–4207. [Google Scholar] [CrossRef] [Green Version]
- Giampieri, A.; Perego, U.; Borsari, R. A constitutive model for the mechanical response of the folding of creased paperboard. Int. J. Solids Struct. 2011, 48, 2275–2287. [Google Scholar] [CrossRef] [Green Version]
- Leminena, V.; Tanninena, P.; Pesonena, A.; Varis, J. Effect of mechanical perforation on the press-forming process of paperboard. Procedia Manuf. 2019, 38, 1402–1408. [Google Scholar] [CrossRef]
- Biancolini, M.E. Evaluation of equivalent stiffness properties of corrugated board. Compos. Struct. 2005, 69, 322–328. [Google Scholar] [CrossRef]
- Garbowski, T.; Jarmuszczak, M. Homogenization of corrugated paperboard. Part 1. Analytical homogenization. Pol. Pap. Rev. 2014, 70, 345–349. (In Polish) [Google Scholar]
- Garbowski, T.; Jarmuszczak, M. Homogenization of corrugated paperboard. Part 2. Numerical homogenization. Pol. Pap. Rev. 2014, 70, 390–394. (In Polish) [Google Scholar]
- Garbowski, T.; Marek, A. Homogenization of corrugated boards through inverse analysis. In Proceedings of the 1st International Conference on Engineering and Applied Sciences Optimization, Kos Island, Greece, 4–6 June 2014; pp. 1751–1766. [Google Scholar]
- Hohe, J. A direct homogenization approach for determination of the stiffness matrix for microheterogeneous plates with application to sandwich panels. Compos. Part B Eng. 2003, 34, 615–626. [Google Scholar] [CrossRef]
- Buannic, N.; Cartraud, P.; Quesnel, T. Homogenization of corrugated core sandwich panels. Compos. Struct. 2003, 59, 299–312. [Google Scholar] [CrossRef] [Green Version]
- Abbès, B.; Guo, Y.Q. Analytic homogenization for torsion of orthotropic sandwich plates: Appl. Compos. Struct. 2010, 92, 699–706. [Google Scholar] [CrossRef]
- Marek, A.; Garbowski, T. Homogenization of sandwich panels. Comput. Assist. Methods Eng. Sci. 2015, 22, 39–50. [Google Scholar]
- Suarez, B.; Muneta, M.L.M.; Sanz-Bobi, J.D.; Romero, G. Application of homogenization approaches to the numerical analysis of seating made of multi-wall corrugated cardboard. Compos. Struct. 2021, 262, 113642. [Google Scholar] [CrossRef]
- Nguyen-Minh, N.; Tran-Van, N.; Bui-Xuan, T.; Nguyen-Thoi, T. Static analysis of corrugated panels using homogenization models and a cell-based smoothed mindlin plate element (CS-MIN3). Front. Struct. Civ. Eng. 2019, 13, 251–272. [Google Scholar] [CrossRef]
- Allaoui, S.; Benzeggagh, M.L.; Aboura, Z.; Talbi, N. Elastic behaviour of corrugated cardboard: Experiments and modeling. Compos. Struct. 2004, 63, 53–62. [Google Scholar]
- Ramírez-Torres, A.; Di Stefano, S.; Grillo, A.; Rodríguez-Ramos, R.; Merodio, J.; Penta, R. An asymptotic homogenization approach to the microstructural evolution of heterogeneous media. Int. J. Non-Lin. Mech. 2018, 106, 245–257. [Google Scholar] [CrossRef] [Green Version]
- Ramírez-Torres, A.; Penta, R.; Rodríguez-Ramos, R.; Merodio, J.; Sabina, F.J.; Bravo-Castillero, J.; Guinovart-Díaz, R.; Preziosi, L.; Grillo, A. Three scales asymptotic homogenization and its application to layered hierarchical hard tissues. Int. J. Solids Struct. 2018, 130, 190–198. [Google Scholar] [CrossRef]
- Garbowski, T.; Grabski, J.K.; Marek, A. Full-field measurements in the edge crush test of a corrugated board—Analytical and numerical predictive models. Materials 2021, 14, 2840. [Google Scholar] [CrossRef]
- Garbowski, T.; Knitter-Piątkowska, A.; Marek, A. New edge crush test configuration enhanced with full-field strain measurements. Materials 2021, 14, 5768. [Google Scholar] [CrossRef]
- Hägglund, R.; Åslund, P.E.; Carlsson, L.A.; Isaksson, P. Measuring thickness changes of edgewise compression loaded corrugated board panels using digital image correlation. J. Sandw. Struct. Mater. 2010, 14, 75–94. [Google Scholar] [CrossRef]
- Viguié, J.; Dumont, P.J.J.; Vacher, P.; Orgéas, L.; Desloges, I.; Mauret, E. Analysis of the strain and stress field of cardboard box during compression by 3D Digital Image Correlation. Appl. Mech. Mater. 2010, 24–25, 103–108. [Google Scholar] [CrossRef] [Green Version]
- Viguié, J.; Dumont, P.J.J.; Orgéas, L.; Vacher, P.; Desloges, I.; Mauret, E. Surface stress and strain fields on compressed panels of corrugated board boxes. An experimental analysis by using Digital Image Stereocorrelation. Compos. Struct. 2011, 93, 2861–2873. [Google Scholar] [CrossRef]
- Viguié, J.; Dumont, P.J.J. Analytical post-buckling model of corrugated board panels using digital image correlation measurements. Compos. Struct. 2013, 101, 243–254. [Google Scholar] [CrossRef]
- Garbowski, T.; Maier, G.; Novati, G. On calibration of orthotropic elastic-plastic constitutive models for paper foils by biaxial tests and inverse analyses. Struct. Multidisc. Optim. 2012, 46, 111–128. [Google Scholar] [CrossRef] [Green Version]
- Fadiji, T.; Coetzee, C.J.; Opara, U.L. Evaluating the displacement field of paperboard packages subjected to compression loading using digital image correlation (DIC). Food Bioprod. Process. 2020, 123, 60–71. [Google Scholar] [CrossRef]
- Maier, G.; Bolzon, G.; Buljak, V.; Garbowski, T.; Miller, B. Synergic Combinations of Computational Methods and Experiments for Structural Diagnoses. In Computer Methods in Mechanics; Advanced Structured Materials Book Series; Kuczma, M., Wilmanski, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 1, pp. 453–476. [Google Scholar] [CrossRef]
- Mathworks Inc. Available online: www.mathworks.com (accessed on 25 December 2021).
- Östlund, S.; Niskanen, K. Mechanics of Paper Products; De Gruyter: Berlin, Germany; Boston, MA, USA, 2021. [Google Scholar] [CrossRef]
- Garbowski, T.; Gajewski, T.; Mrówczyński, D.; Jędrzejczak, R. Crushing of Single-Walled Corrugated Board during Converting: Experimental and Numerical Study. Energies 2021, 14, 3203. [Google Scholar] [CrossRef]
- Gajewski, T.; Garbowski, T.; Staszak, N.; Kuca, M. Crushing of Double-Walled Corrugated Board and Its Influence on the Load Capacity of Various Boxes. Energies 2021, 14, 4321. [Google Scholar] [CrossRef]












| Mode ID | |||
|---|---|---|---|
| Liner 1 | Liner 2 | Liner 3 | |
| Board 1 | 5700 | 6460 | 5650 |
| Board 2 | 6690 | 5200 | 5520 |
| Board 3 | 5700 | 6460 | 5650 |
| Board 4 | 5700 | 5720 | 5650 |
| Board 5 | 6690 | 5200 | 5520 |
| Board 6 | 5700 | 5730 | 5520 |
| Layer | Take-Up Factor | ||
|---|---|---|---|
| Flute E | 3.40 | 1.20 | 1.262 1 |
| Flute B | 6.10 | 2.58 | 1.362 1 |
| Mode ID | Height (mm) | ||||||
|---|---|---|---|---|---|---|---|
| Liner 1 | Flute E | Liner 2 | Flute B | Liner 3 | |||
| Board 1 | 142 | 164 | 126 | 164 | 146 | 1.498 | 2.880 |
| Board 2 | 185 | 227 | 177 | 199 | 186 | 1.608 | 2.961 |
| Board 3 | 142 | 199 | 126 | 139 | 146 | 1.523 | 2.855 |
| Board 4 | 142 | 177 | 139 | 177 | 146 | 1.518 | 2.899 |
| Board 5 | 185 | 199 | 177 | 199 | 186 | 1.580 | 2.961 |
| Board 6 | 142 | 177 | 164 | 177 | 186 | 1.530 | 2.930 |
| Name | ||||
|---|---|---|---|---|
| FEM-1 | FEM-2 | FEM-3 | FEM-4 | |
| Board 1 | 8.187 | 8.198 | 8.160 | 8.160 |
| Board 2 | 12.129 | 12.135 | 12.069 | 12.069 |
| Board 3 | 8.213 | 8.231 | 8.182 | 8.182 |
| Board 4 | 8.322 | 8.332 | 8.292 | 8.293 |
| Board 5 | 11.983 | 11.991 | 11.926 | 11.926 |
| Board 6 | 9.652 | 9.669 | 9.625 | 9.626 |
| Title 1 | Face-up | EXP (Mean) | Theoretical | FEM-Beam | FEM [29] | Analytical |
|---|---|---|---|---|---|---|
| Board 1 | EB | 8.32 | 8.11 | 8.20 (8.14) | 7.62 | 7.13 |
| BE | 8.47 | 7.58 | 7.84 | |||
| Board 2 | EB | 10.97 | 11.92 | 12.14 (12.02) | 9.88 | 11.15 |
| BE | 11.58 | 9.81 | 11.65 | |||
| Board 3 | EB | 7.25 | 8.12 | 8.23 (8.15) | 7.61 | 7.15 |
| BE | 9.50 | 7.53 | 7.85 | |||
| Board 4 | EB | 9.10 | 8.24 | 8.32 (8.27) | 7.53 | 7.24 |
| BE | 11.10 | 7.45 | 7.98 | |||
| Board 5 | EB | 11.46 | 11.78 | 11.99 (11.89) | 10.42 | 10.89 |
| BE | 12.97 | 10.37 | 11.52 | |||
| Board 6 | EB | 8.20 | 9.60 | 9.67 (9.60) | 8.45 | 8.86 |
| BE | 9.12 | 8.40 | 9.27 |
| Title 1 | Face-up | FEM [29] | Analytical |
|---|---|---|---|
| Board 1 | EB | 9.18 | 16.69 |
| BE | 11.74 | 8.04 | |
| Board 2 | EB | 11.03 | 1.61 |
| BE | 18.04 | 0.60 | |
| Board 3 | EB | 4.73 | 1.40 |
| BE | 26.16 | 21.02 | |
| Board 4 | EB | 20.85 | 25.69 |
| BE | 48.99 | 39.10 | |
| Board 5 | EB | 9.98 | 5.23 |
| BE | 25.07 | 12.59 | |
| Board 6 | EB | 2.95 | 7.45 |
| BE | 8.57 | 1.62 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garbowski, T.; Knitter-Piątkowska, A. Analytical Determination of the Bending Stiffness of a Five-Layer Corrugated Cardboard with Imperfections. Materials 2022, 15, 663. https://doi.org/10.3390/ma15020663
Garbowski T, Knitter-Piątkowska A. Analytical Determination of the Bending Stiffness of a Five-Layer Corrugated Cardboard with Imperfections. Materials. 2022; 15(2):663. https://doi.org/10.3390/ma15020663
Chicago/Turabian StyleGarbowski, Tomasz, and Anna Knitter-Piątkowska. 2022. "Analytical Determination of the Bending Stiffness of a Five-Layer Corrugated Cardboard with Imperfections" Materials 15, no. 2: 663. https://doi.org/10.3390/ma15020663







