Injection Molding Process Simulation of Polycaprolactone Sticks for Further 3D Printing of Medical Implants
Abstract
:1. Introduction
2. Materials and Methods
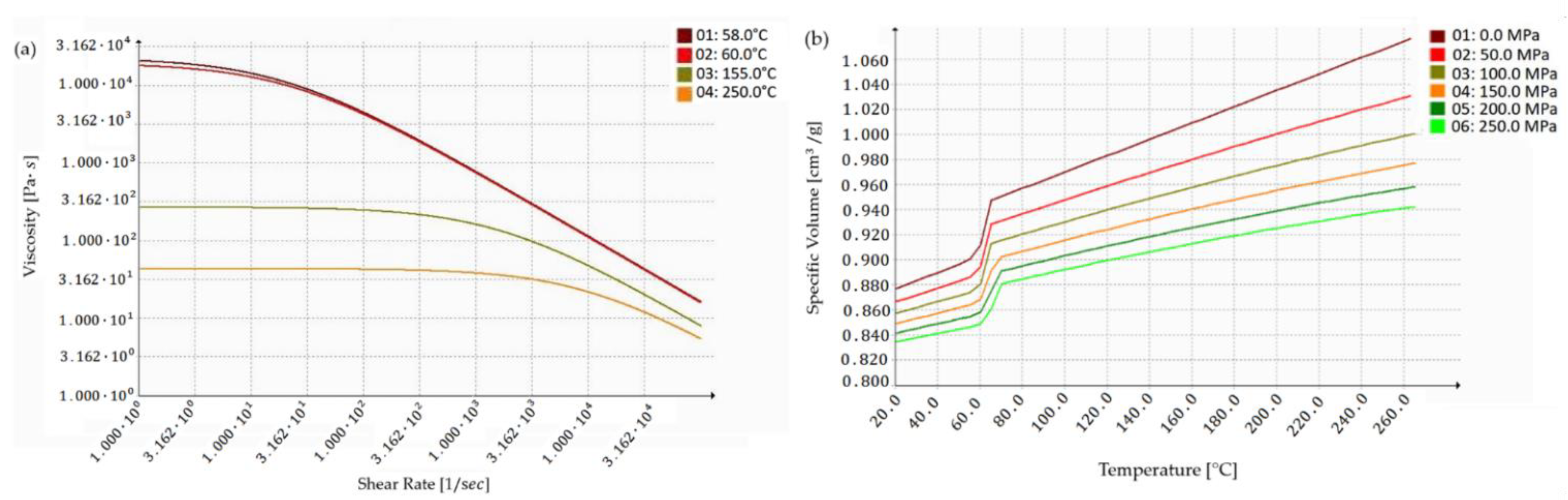
2.1. Material Data Collection
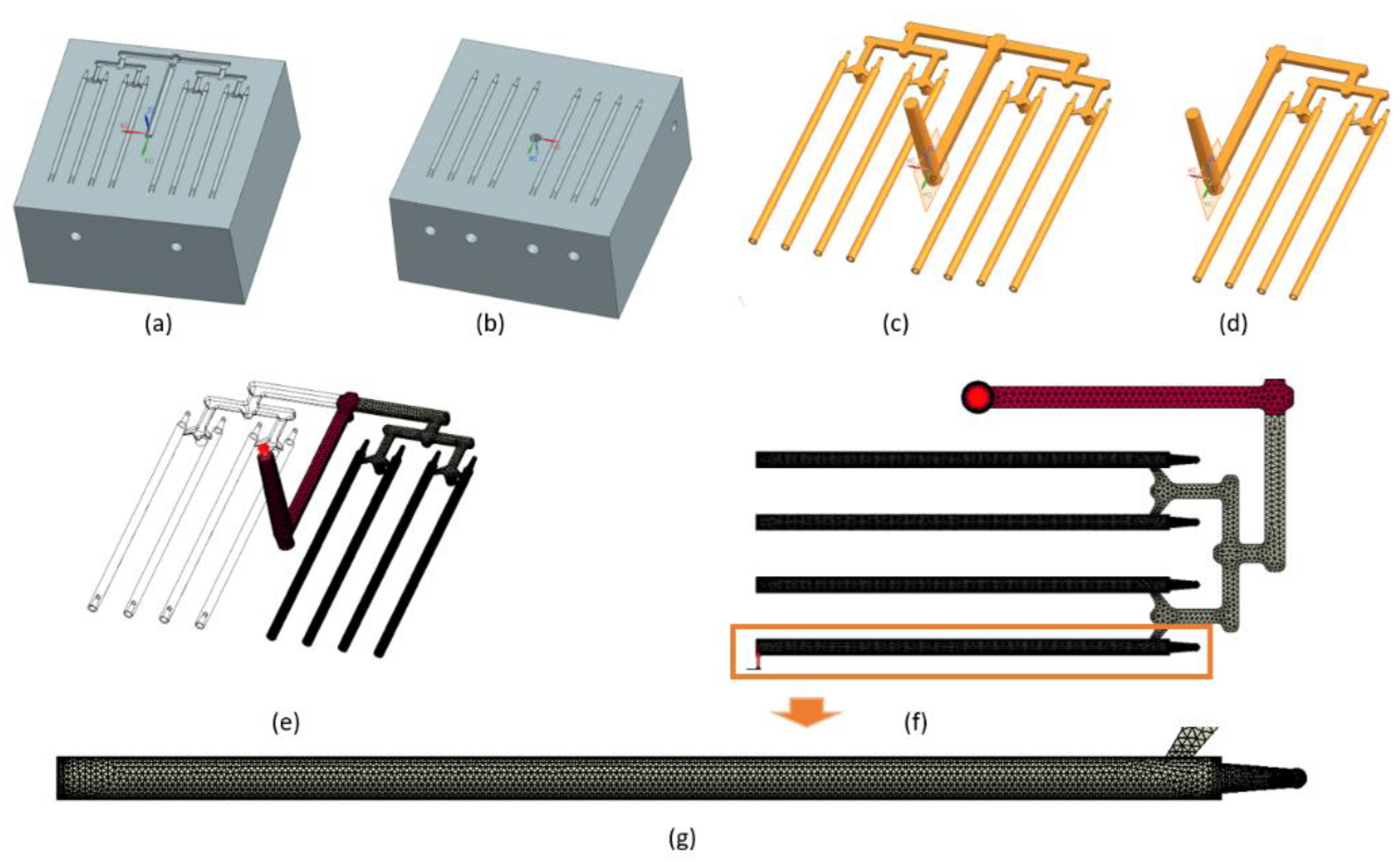
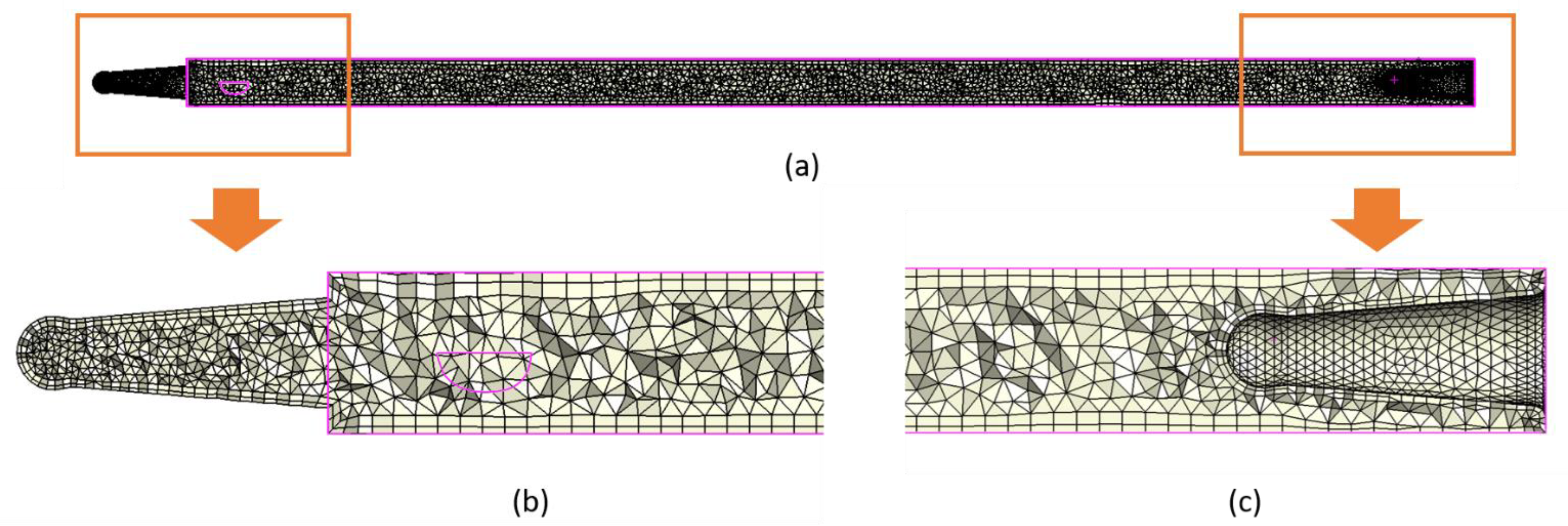
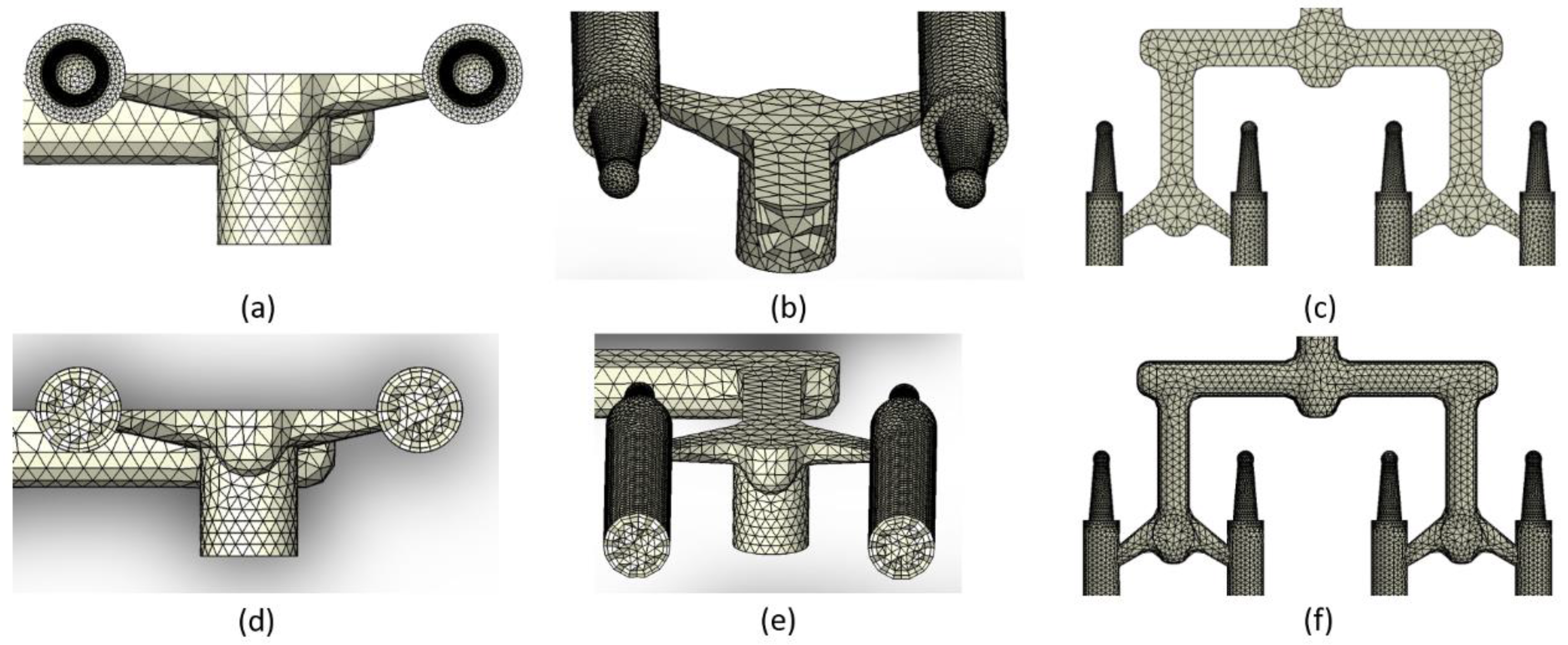
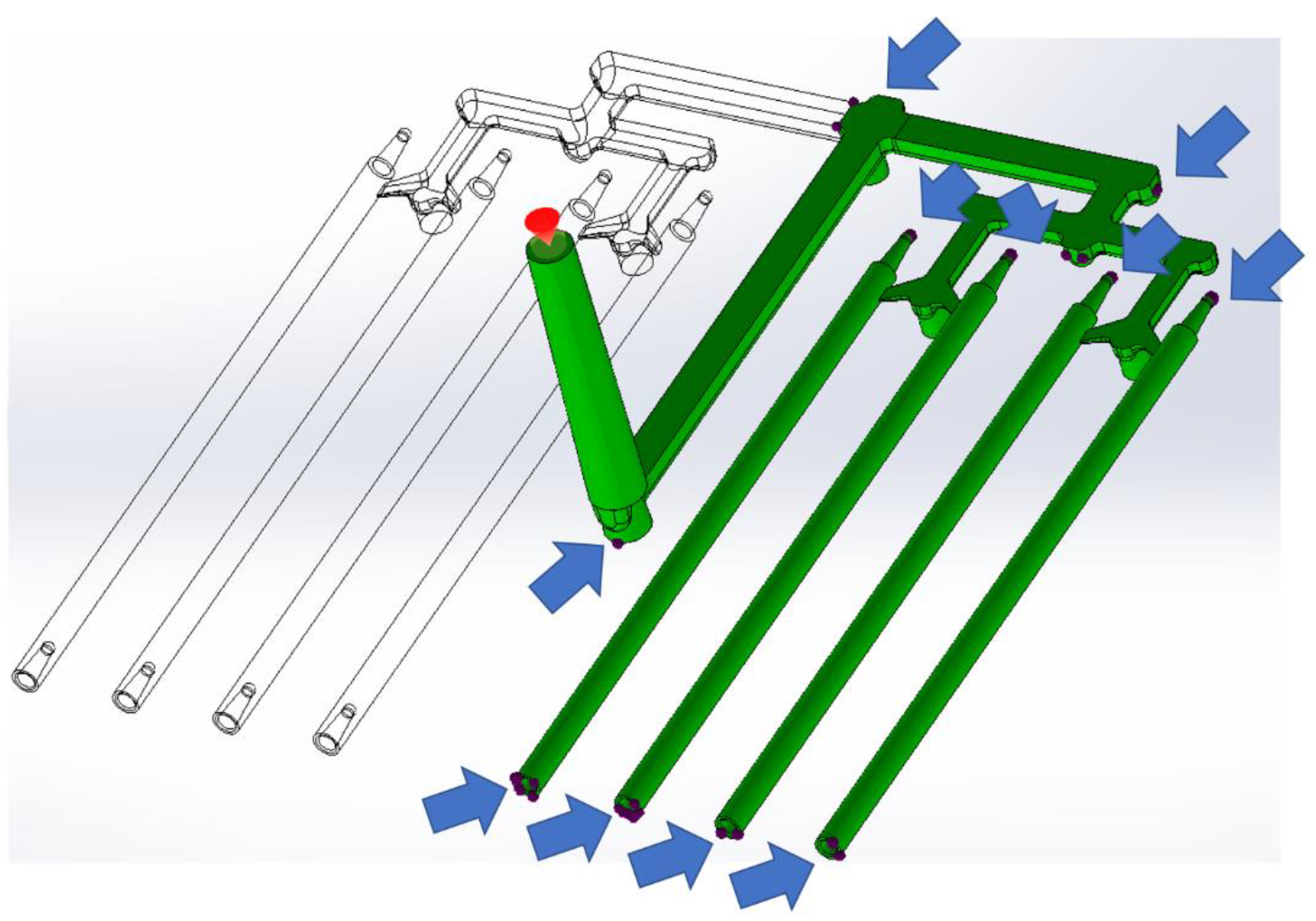
2.2. Injection Molding Simulation
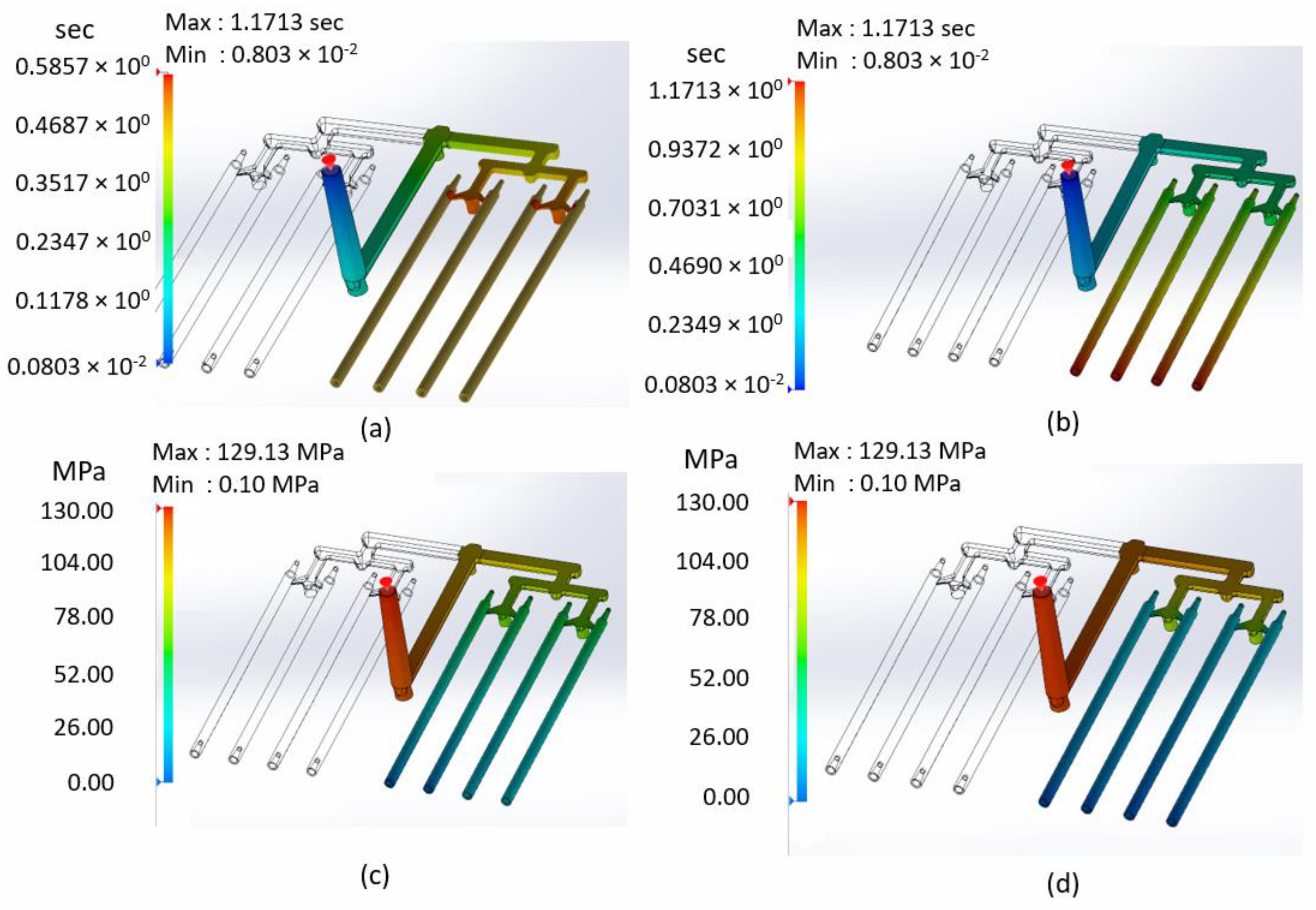
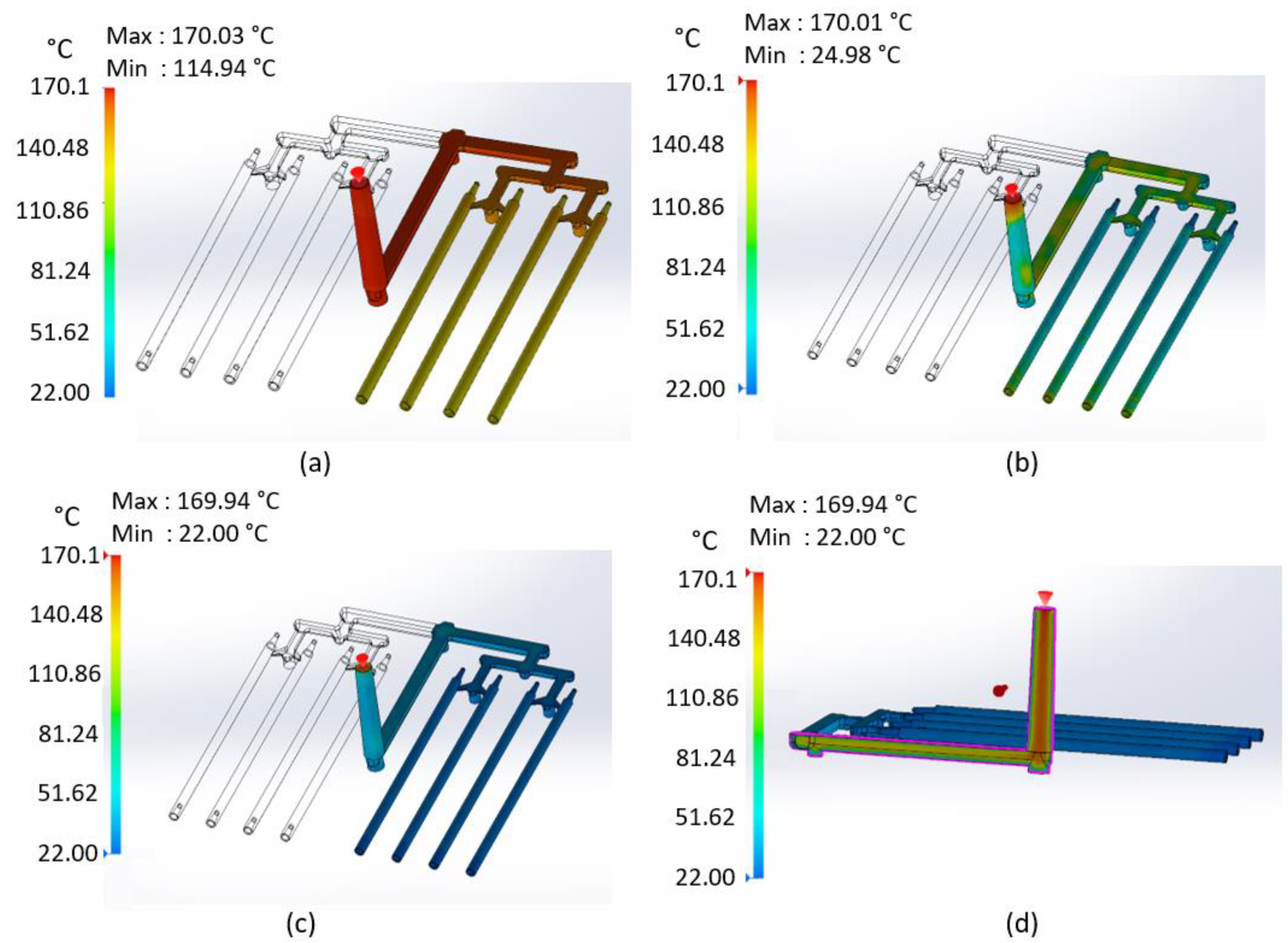
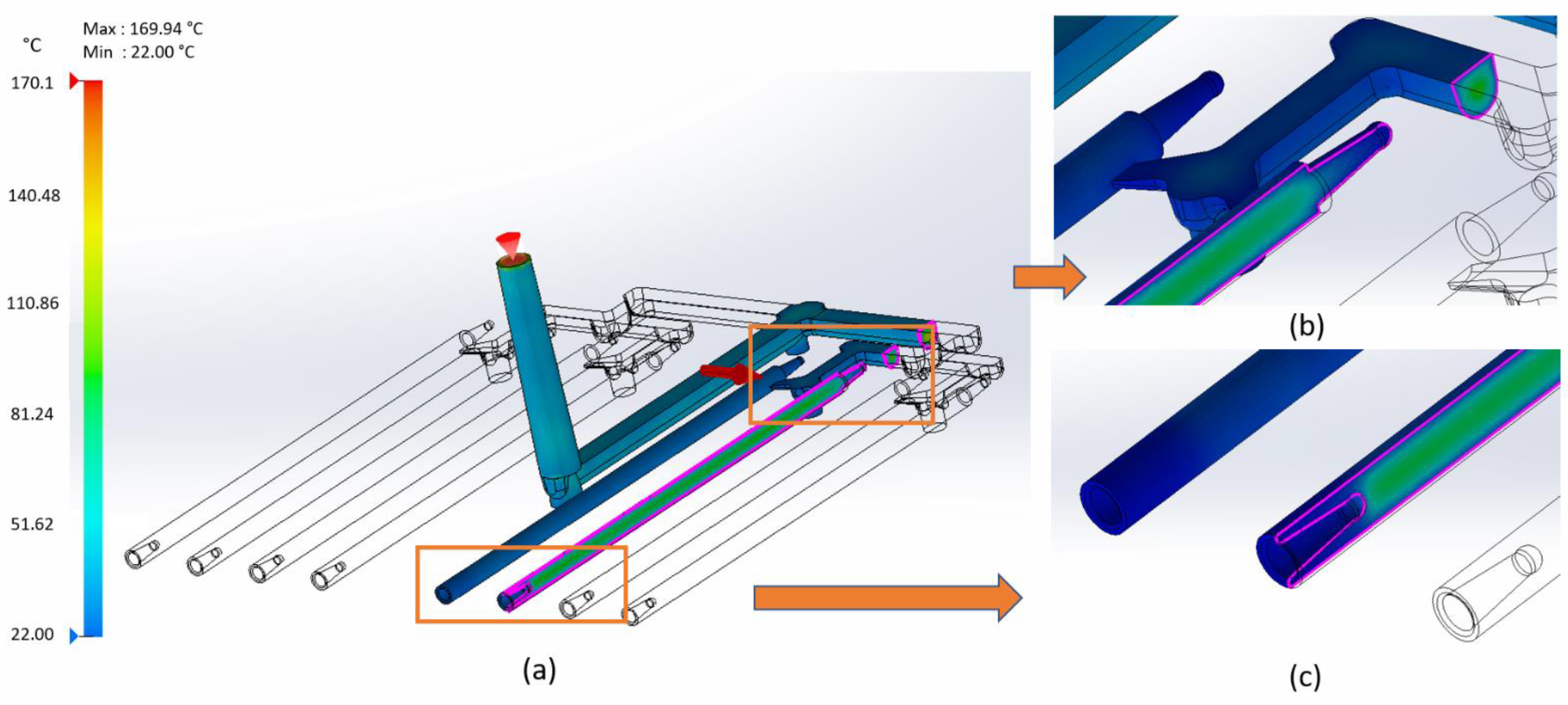
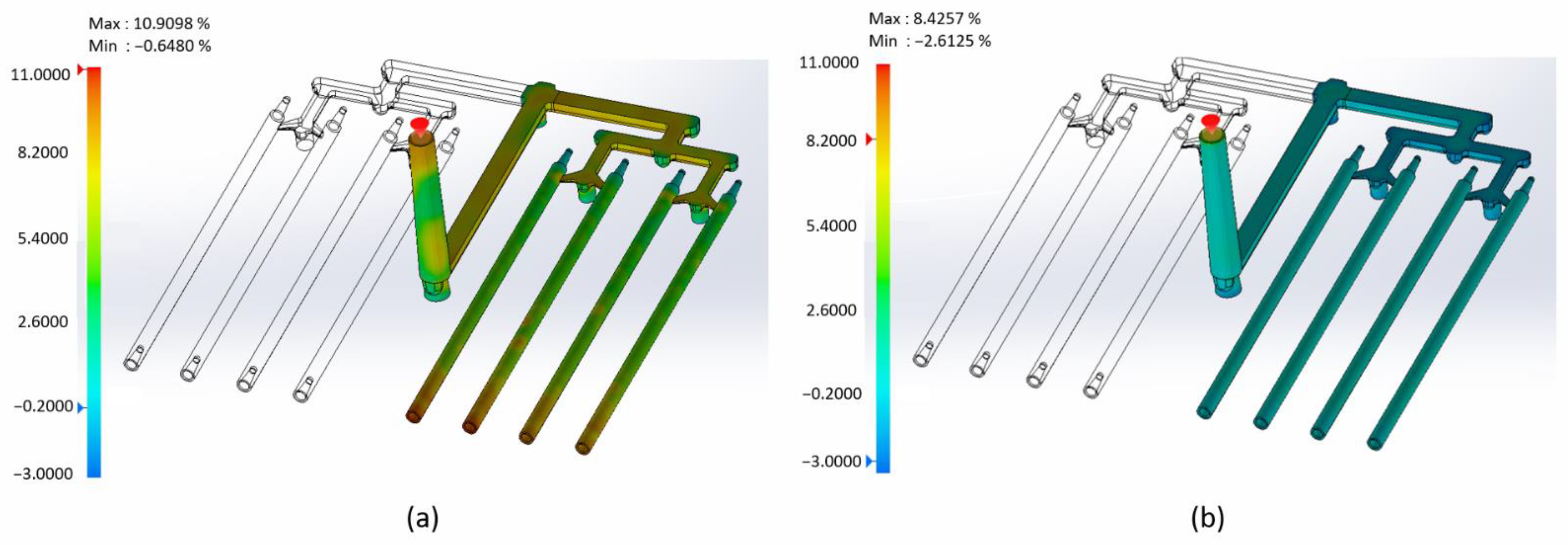
3. Results
4. Discussion
5. Conclusions
6. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rajzer, I.; Kurowska, A.; Jabłoński, A.; Kwiatkowski, R.; Piekarczyk, W.; Hajduga, M.B.; Kopeć, J.; Sidzina, M.; Menaszek, E. Scaffolds modified with graphene as future implants for nasal cartilage. J. Mater. Sci. 2020, 55, 4030–4042. [Google Scholar] [CrossRef]
- Fuenmayor, E.; O’Donnell, C.; Gately, N.; Doran, P.; Devine, D.M.; Lyons, J.G.; McConville, C.; Major, I. Mass-customization of oral tablets via the combination of 3D printing and injection molding. Int. J. Pharm. 2019, 569, 118611. [Google Scholar] [CrossRef] [PubMed]
- Yizong, T.; Ariff, Z.M.; Khalil, A.M. Influence of processing parameters on injection molded polystyrene using Taguchi method as design of experiment. Procedia Eng. 2017, 184, 350–359. [Google Scholar] [CrossRef]
- Heidari, B.S.; Oliaei, E.; Shayesteh, H.; Davachi, S.M.; Hejazi, I.; Seyfi, J.; Bahrami, M.; Rashedi, H. Simulation of mechanical behavior and optimization of simulated injection molding process for PLA based antibacterial composite and nanocomposite bone screws using central composite design. J. Mech. Behav. Biomed. Mater. 2017, 65, 160–176. [Google Scholar] [CrossRef] [PubMed]
- Surace, R.; Bellantone, V.; Trotta, G.; Fassi, I. Replicating capability investigation of micro features in injection moulding process. J. Manuf. Process. 2017, 28, 351–361. [Google Scholar] [CrossRef]
- Tosello, G.; Costa, F.S. High precision validation of micro injection molding process simulations. J. Manuf. Process. 2019, 48, 236–248. [Google Scholar] [CrossRef]
- Rajzer, I.; Rom, M.; Menaszek, E.; Fabia, J.; Kwiatkowski, R. Conductive polyaniline patterns on electrospun polycaprolactone/hydroxyapatite scaffolds for bone tissue engineering. Materials 2021, 14, 4837. [Google Scholar] [CrossRef] [PubMed]
- Hajduga, M.B.; Bobiński, R.; Dutka, M.; Ulman-Włodarz, I.; Bujok, J.; Pająk, C.; Ćwiertnia, M.; Kurowska, A.; Dziadek, M.; Rajzer, I. Analysis of the antibacterial properties of polycaprolactone modified with graphene, bioglass and zinc doped bioglass. Acta. Bioeng. Biomech. 2021, 23, 131–138. [Google Scholar] [CrossRef] [PubMed]
- Woodruff, M.A.; Hutmacher, D.W. The return of a forgotten polymer—Polycaprolactone in the 21st century. Prog. Polym. Sci. 2010, 35, 1217–1256. [Google Scholar] [CrossRef] [Green Version]
- Kelly, C.A.; Murphy, S.H.; Leeke, G.A.; Howdle, S.M.; Shakesheff, K.M.; Jenkins, M.J. Rheological studies of polycaprolactone in supercritical CO2. Eur. Polym. J. 2013, 49, 464–470. [Google Scholar] [CrossRef]
- Domalik-Pyzik, P.; Morawska-Chochół, A.; Chłopek, J.; Rajzer, I.; Wrona, A.; Menaszek, E.; Ambroziak, M. Polylactide/polycaprolactone asymmetric membranes for guided bone regeneration. E-Polymers 2016, 16, 351–358. [Google Scholar] [CrossRef]
- Rajzer, I.; Menaszek, E.; Kwiatkowski, R.; Planell, J.A.; Castano, O. Electrospun gelatin/poly(ε-caprolactone) fibrous scaffold modified with calcium phosphate for bone tissue engineering. Mater. Sci. Eng. C 2014, 44, 183–190. [Google Scholar] [CrossRef] [PubMed]
- Koch, F.; Thaden, O.; Conrad, S.; Tröndle, K.; Finkenzeller, G.; Zengerle, R.; Kartmann, S.; Zimmermann, S.; Koltay, P. Mechanical properties of polycaprolactone (PCL) scaffolds for hybrid 3D-bioprinting with alginate-gelatin hydrogel. J. Mech. Behav. Biomed. Mater. 2022, 130, 105219. [Google Scholar] [CrossRef] [PubMed]
- Noroozi, N.; Thomson, J.A.; Noroozi, N.; Schafer, L.L.; Hatzikiriakos, S.G. Viscoelastic behaviour and flow instabilities of biodegradable polycaprolactone polyesters. Rheol. Acta. 2012, 51, 179–192. [Google Scholar] [CrossRef]
- Schaible, S.; Bernet, C.; Ledergeber, P.; Balmer, T.; Brändli, C. Basic study on the evaluation of thermoplastic polymers as hot-melt adhesives for mixed-substrate joining. Open J. Appl. Sci. 2016, 6, 579–592. [Google Scholar] [CrossRef] [Green Version]
- Wunderlich, B. Thermal Analysis of Polymeric Materials; Springer: Berlin/Heidelberg, Germany, 2005; p. 381. [Google Scholar]
- Gumede, T.P.; Luyt, A.S.; Hassan, M.K.; Pérez-Camargo, R.A.; Tercjak, A.; Müller, A.J. Morphology, nucleation, and isothermal crystallization kinetics of poly(ε-caprolactone) mixed with a polycarbonate/MWCNTs masterbatch. Polymers 2017, 9, 709. [Google Scholar] [CrossRef] [Green Version]
- Properties & Processing of CAPA® Thermoplastics. Available online: http://www.rapstrap.com/TDS-CAPA6500.pdf (accessed on 26 September 2022).
- Density of Plastics: Technical Properties. Available online: https://omnexus.specialchem.com/polymer-properties/properties/density (accessed on 26 September 2022).
- Lu, L.; Zhang, Q.; Wootton, D.M.; Chiou, R.; Li, D.; Lu, B.; Lelkes, P.I.; Zhou, J. Mechanical study of polycaprolactone-hydroxyapatite porous scaffolds created by porogen-based solid freeform fabrication method. J. Appl. Biomater. Funct Mater. 2014, 12, 145–154. [Google Scholar] [CrossRef] [PubMed]
- Pionteck, J. Determination of pressure dependence of polymer phase transitions by pVT analysis. Polymers 2018, 10, 578. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Oliaei, E.; Heidari, B.S.; Davachi, S.M.; Bahrami, M.; Davoodi, S.; Hejaz, I.; Seyfi, J. Warpage and shrinkage optimization of injection-molded plastic spoon parts for biodegradable polymers using Taguchi, ANOVA and artificial neural network methods. J. Mater. Sci. Technol. 2016, 32, 710–720. [Google Scholar] [CrossRef]
- Wang, X.; Li, H.; Gu, J.; Li, Z.; Ruan, S.; Shen, C.; Wang, M. Pressure analysis of dynamic injection molding and process parameter optimization for reducing warpage of injection molded products. Polymers 2017, 9, 85. [Google Scholar] [CrossRef]
- Wang, J.; Hopmann, C.; Schmitz, M.; Hohlweck, T.; Wipperfürth, J. Modeling of pvT behavior of semi-crystalline polymer based on the two-domain Tait equation of state for injection molding. Mater. Des. 2019, 183, 108149. [Google Scholar] [CrossRef]
- Formas, K.; Rajzer, I.; Wróbel, I. Symulacja procesów wtrysku sztyftów używanych w druku 3D. Tworzywa Sztuczne w Przemyśle 2020, 5, 58–64. [Google Scholar]
- Tran, N.T.; Gehde, M. Creating material data for thermoset injection molding simulation process. Polym. Test. 2019, 73, 284–292. [Google Scholar] [CrossRef]


| Parameter | Value | Literature |
|---|---|---|
| Rheological properties. Viscosity model: Cross-WLF | ||
| D2 [K] | 243.15 | [10,14,15] |
| n | 0.1547 | |
| D1 [Pa∙s] | 2.21915 × 1012 | |
| τ* [Pa] | 429,551 | |
| A1 | 29.20632 | |
| A2 [K] | 51.6 | |
| Physical Properties | ||
| Solid density, kg/m3 | 1140 | [19] |
| Thermal Properties | ||
| Glass transition, °C | −60 | [16,17,18] |
| Specific heat, [J/kgK] | 2100 | |
| Melt flow rate (MFR), g/10 min (190 °C/2.16 kg) | 28 | |
| Thermal conductivity, [W/m·K] (20 °C) | 0.1 | |
| Melting point [°C] | 60–62 | |
| Mechanical properties | ||
| Yield stress, σy, [MPa] | 17.5 | [20] |
| Tensile modulus [MPa] | 430 | [18] |
| Poisson’s ratio | 0.44 | [20] |
| P–V–T (Pressure–Volume–Temperature) Properties 13-Parameter Modified Tait Equation | |
|---|---|
| Parameter | Value |
| b1m [m3/kg] | 9.463 × 10−4 |
| b2m [m3/(kg-K)] | 6.514 × 10−7 |
| b3m [Pa] | 2.030180 × 108 |
| b4m [1/K] | 4.521 × 10−3 |
| b1s [m3/kg] | 9.045 × 10−4 |
| b2s [m3/(kg-K)] | 6.291 × 10−7 |
| b3s [Pa] | 2.52593 × 108 |
| b4s [1/K] | 7.368 × 10−3 |
| b5 [K] | 336.77 |
| b6 [K/Pa] | 1.497 × 10−8 |
| b7 [m3/kg] | 4.181 × 10−5 |
| b8 [1/K] | 4.042 × 10−1 |
| b9 [1/Pa] | 7.393 × 10−9 |
| Mesh Details | |
|---|---|
| solver type | AMG (algebraic multigrid) |
| mesh type | solid mesh |
| mesh volume, [mm3] | 955 |
| mesh type | tetrahedral hybrid |
| total elements of surface mesh | 59,756 |
| total nodes of surface mesh | 29,857 |
| total elements of solid mesh | 394,602 |
| total nodes of solid mesh | 119,344 |
| analyze type | fill and pack |
| Process Details | |
|---|---|
| Process Parameter | Value |
| ambient temperature, [°C] | 22 |
| melt temperature, [°C] | 170 |
| mold temperature, [°C] | 22 |
| filling time, [sec] | 1 |
| injection pressure at the nozzle (filling), [MPa] | 130 |
| packing time, [sec] | 2.5 |
| injection pressure at the nozzle (packing), [MPa] | 20 |
| cooling time, [sec] | 25 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Formas, K.; Kurowska, A.; Janusz, J.; Szczygieł, P.; Rajzer, I. Injection Molding Process Simulation of Polycaprolactone Sticks for Further 3D Printing of Medical Implants. Materials 2022, 15, 7295. https://doi.org/10.3390/ma15207295
Formas K, Kurowska A, Janusz J, Szczygieł P, Rajzer I. Injection Molding Process Simulation of Polycaprolactone Sticks for Further 3D Printing of Medical Implants. Materials. 2022; 15(20):7295. https://doi.org/10.3390/ma15207295
Chicago/Turabian StyleFormas, Krzysztof, Anna Kurowska, Jarosław Janusz, Piotr Szczygieł, and Izabella Rajzer. 2022. "Injection Molding Process Simulation of Polycaprolactone Sticks for Further 3D Printing of Medical Implants" Materials 15, no. 20: 7295. https://doi.org/10.3390/ma15207295
APA StyleFormas, K., Kurowska, A., Janusz, J., Szczygieł, P., & Rajzer, I. (2022). Injection Molding Process Simulation of Polycaprolactone Sticks for Further 3D Printing of Medical Implants. Materials, 15(20), 7295. https://doi.org/10.3390/ma15207295







