Mixing Enthalpies of Liquid Ag–Mg–Pb Alloys: Experiment vs. Thermodynamic Modeling
Abstract
:1. Introduction
2. Materials and Methods
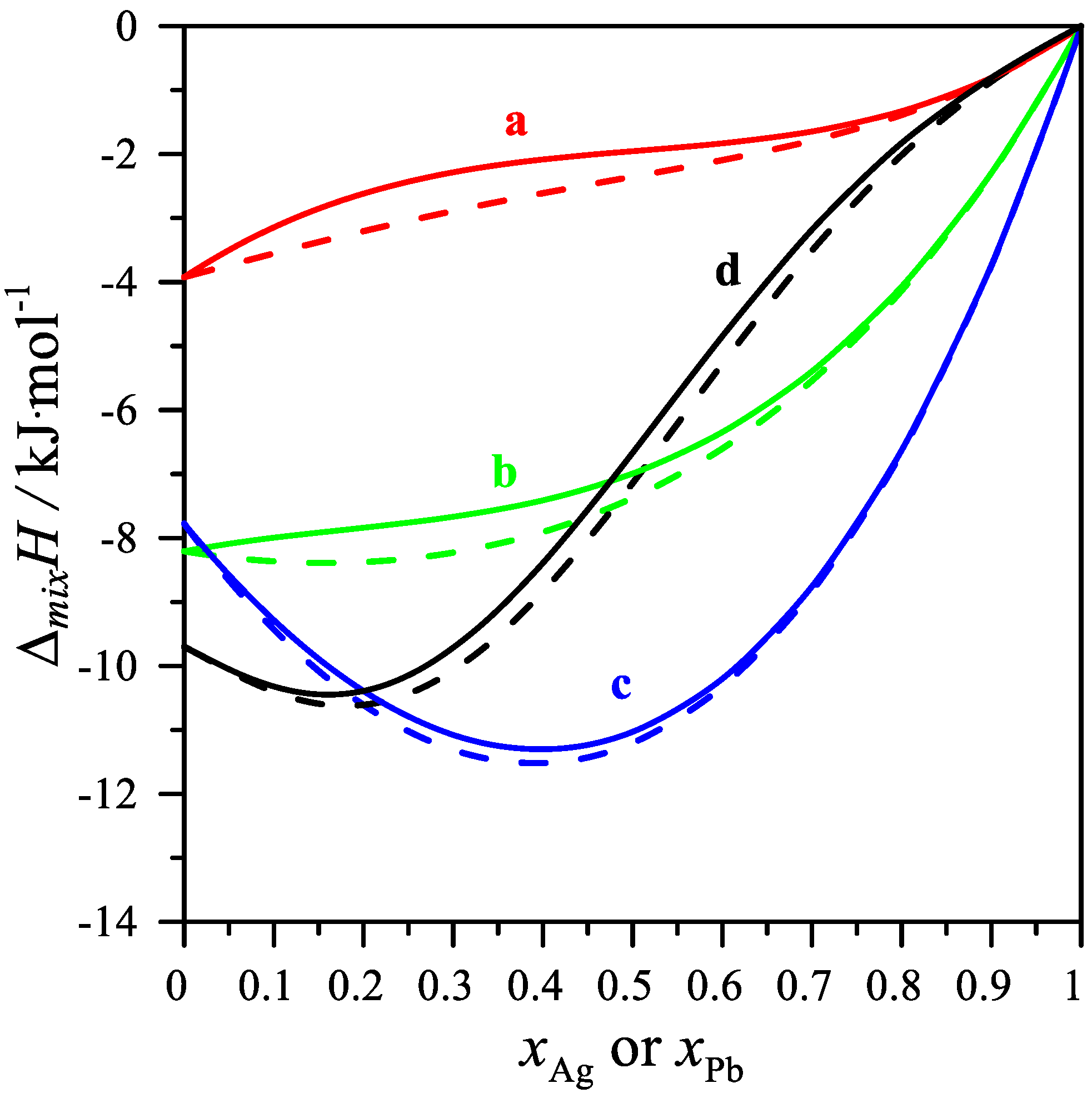
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mordike, B.L.; Ebert, T. Magnesium: Properties—Applications—Potential. Mater. Sci. Eng. A 2001, 302, 37. [Google Scholar] [CrossRef]
- Plevachuk, Y. Electrophysical Properties of Mg-Pb Based Liquid Alloys and Their Application; Kainer, K.U., Ed.; Wiley: Hoboken, NJ, USA, 2000. [Google Scholar]
- Singh, P.; Rana, P.J.S.; Mukherejee, R.; Srivastava, P. A step towards environmental benign Mg/Pb based binary metal mixed halide perovskite material. Sol. Energy 2018, 170, 769. [Google Scholar] [CrossRef]
- Ouyang, L.; Liu, F.; Wang, H.; Liu, J.; Yang, X.-S.; Sun, L.; Zhu, M. Magnesium-based hydrogen storage compounds: A review. J. Alloy. Compd. 2020, 832, 154865. [Google Scholar] [CrossRef]
- Baran, A.; Polański, M. Magnesium-based materials for hydrogen storage—A scope review. Materials 2020, 13, 3993. [Google Scholar] [CrossRef] [PubMed]
- Mendis, C.L.; Oh-ishi, K.; Hono, K. Enhanced age hardening in a Mg–2.4 at.% Zn alloy by trace additions of Ag and Ca. Scr. Mater. 2007, 57, 485. [Google Scholar] [CrossRef]
- Adams, B.D.; Chen, A. The role of palladium in a hydrogen economy. Mater. Today 2011, 14, 282. [Google Scholar] [CrossRef]
- Pęska, M.; Smektalska, K.; Dworecka-Wójcik, J.; Terlicka, S.; Gąsior, W.; Gierlotka, W.; Dębski, A.; Polański, M. Hydrogen sorption behavior of mechanically synthesized Mg–Ag alloys. Int. J. Hydrogen Energy 2021, 46, 33152. [Google Scholar] [CrossRef]
- Dębski, A.; Terlicka, S.; Sypien, A.; Gąsior, W.; Pęska, M.; Polański, M. Hydrogen Sorption Behavior of Cast Ag-Mg Alloys. Materials 2022, 15, 270. [Google Scholar] [CrossRef]
- Dębski, A.; Gierlotka, W.; Gąsior, W. Calorimetric studies and thermodynamic calculations of the Ag-Mg system. J. Alloys Compd. 2022, 891, 161937. [Google Scholar] [CrossRef]
- Terlicka, S.; Dębski, A.; Sypien, A.; Gąsior, W.; Budziak, A. Determination of thermophysical and thermodynamic properties, of Ag-Mg alloys. Mater. Today Commun. 2021, 29, 102946. [Google Scholar] [CrossRef]
- Dębski, A.; Gierlotka, W.; Terlicka, S.; Gąsior, W. On the Mg-Pb system. Calorimetric studies and thermodynamic calculations. J. Alloys Compd. 2021, 861, 158396. [Google Scholar] [CrossRef]
- Zimmermann, B. Calculative and Experimental Optimization of Binary and Ternary Ag, Bi, Pb and T1 Systems. Ph.D. Thesis, Universitat Stuttgart, Stuttgart, German, 1976. [Google Scholar]
- Elliott, R.P.; Shunk, F.A. The Ag–Pb (Silver-Lead) System. Bull. Alloy Phase Diagr. 1980, 1, 56. [Google Scholar] [CrossRef]
- Ashtakala, S.; Pelton, A.D.; Bale, C.W. The Ag-Pb (Silver-Lead) System. Bull. Alloy Phase Diagr. 1981, 2, 81. [Google Scholar] [CrossRef]
- Karakaya, I.; Thompson, W.T. The Ag-Pb (Silver-Lead) system. Bull. Alloy Phase Diagr. 1987, 8, 326. [Google Scholar] [CrossRef]
- Gierlotka, W.; Łapsa, J.; Fitzner, K. Thermodynamic Description of the Ag-Pb-Te Ternary System. J. Phase Equlib. Diff. 2010, 31, 509. [Google Scholar] [CrossRef] [Green Version]
- Hassam, S.; Boa, D.; Rogez, B.P.J. Critical assessment and optimization of the Ag–Au–Pb system. Thermochim. Acta 2010, 510, 37. [Google Scholar] [CrossRef]
- Du, J.-Y.; Zemanova, A.; Hutabalian, Y.; Kroupa, A.; Chen, S.-W. Phase diagram of Ag–Pb–Sn system. Calphad 2020, 71, 101997. [Google Scholar] [CrossRef]
- Heycock, C.T.; Neville, F.H. Complete Freezing-point Curves of Binary Alloys, containing Silver or Copper together with another metal. Philos. Trans. R. Soc. Lond. Ser. A 1897, 189, 25. [Google Scholar]
- Petrenko, G.J. On the Alloying of Silver with Lead and Tin. Z. Anorg. Chem. 1907, 53, 200. [Google Scholar]
- Friedrich, K. Lead and Silver. Metallurgie 1906, 3, 396. [Google Scholar]
- Yoldi, F. The Lead-Silver System. An. Soc. Espan. Fis. Quim. 1930, 28, 1055. [Google Scholar]
- Kleppa, O.J. Thermodynamic Properties of Moderately Dilute Liquid Solutions of Copper, Silver and Gold in Thallium, Lead and Bismuth. J. Phys. Chem. 1956, 60, 446. [Google Scholar] [CrossRef]
- Preckshot, G.W.; Hudrlik, R.E. Diffusion in the solid silver-molten lead system. Trans. AIME 1960, 218, 516. [Google Scholar]
- Glazov, V.M.; Akopyan, R.A.; Timoshina, G.G. Determination of the Position of the Retrograde Solidus in the Ag-Pb and Ag-Bi Systems. Izvest. Akad. Nauk SSSR Met. 1975, 1, 162. [Google Scholar]
- Akopyan, R.A.; Mamedova, S.K.; Kerimov, E.R. A Study of the Retrograde Solidus Curves in the Systems Ag−Pb and Ag−Bi. Izv V. U. Z. Tsvetn. Metall. 1983, 6, 83. [Google Scholar]
- Pollock, D.D. Solubility Limits of Some Silver-Rich Binary Solid Solutions near Room Temperature. Trans. AIME 1967, 239, 1768. [Google Scholar]
- Kusunoki, K.; Tsumuraya, K.; Nishikawa, S. Diffusion of Ag in dilute Pb (Ag) alloys. Trans. Jpn. Inst. Met. 1981, 22, 501. [Google Scholar] [CrossRef] [Green Version]
- Kawakami, M. A Further Investigation of the Heat of Mixture in Molten Metals. Sci. Rep. Tohoku Imp. Univ. 1930, 19, 521. [Google Scholar]
- von Samson-Himmelstjerna, H.O. Heat capacity and heat of formation of molten alloys. Z. Metallkd. 1936, 28, 197. [Google Scholar]
- Ehrlich, K. The Enthalpy of Mixing of Silver and Magnesium with Some B Metals in Liquid Binary Systems. Inaugural Thesis, Ludwig-Maximilians-Universität, München, Germany, 1965. [Google Scholar]
- Kozuka, Z.; Oishi, T.; Moriyama, J. Measurements of the Thermodynamic Properties of Molten Ag-Pb Alloys by Calorimetry. Nippon Kihz. Gakk. 1968, 32, 136. [Google Scholar]
- Castanet, R.; Claire, Y.; Lafitte, M. Enthalpie de formation à 1 280 k des alliages liquides d’argent avec le germanium, l’étain et le plomb. J. Chim. Phys. 1969, 66, 1276. [Google Scholar] [CrossRef]
- Itagaki, K.; Yazawa, A. Measurements of Heats of Mixing in Liquid Silver Binary Alloys. J. Jpn. Inst. Met. 1968, 32, 1294. [Google Scholar] [CrossRef] [Green Version]
- Hultgren, R.; Sommelet, P. The magnitude of some of the errors in determining heats of formation of liquid alloys by drop calorimetry; the silver-lead system. In Proceedings of the First International Conference on Calorimetry and Thermodynamics, Warsaw, Poland, 31 August–4 September 1969; p. 1027. [Google Scholar]
- Hager, J.P.; Wilkomirsky, I.A. Galvanic cell studies using a molten oxide electrolyte. Pt. 1. Thermodynamic properties of the lead-silver system. Trans. AIME 1968, 242, 183. [Google Scholar]
- Terpilowski, J. Thermodynamic Properties of Liquid Metallic Solutions. (I) Ag−Pb System. Arch. Hutnictwa 1957, 2, 289. [Google Scholar]
- Eremenko, V.N. Thermodynamic Activity of Pb in Melted Pb−Ag Alloys. Ukr. Khim. Zh. 1957, 23, 6. [Google Scholar]
- Iwase, M.; Fujimura, K.; Mori, T. Thermodynamic study of liquid lead-silver alloys by means of solid-oxide galvanic cell. Trans. Jpn. Inst. Met. 1978, 19, 377. [Google Scholar] [CrossRef] [Green Version]
- Jacob, K.T.; Jeffes, J.H.E. Activities of oxygen and lead in liquid Pb + Ag + O solutions. J. Chem. Thermodyn. 1971, 3, 433. [Google Scholar] [CrossRef]
- Aldred, A.T.; Pratt, J.N. Thermodynamic properties of liquid silver-lead alloys. With an appendix on the vapour pressure of lead. Trans. Faraday Soc. 1961, 57, 611. [Google Scholar] [CrossRef]
- Khobdabergenov, R.Z.; Nesterov, V.I.; Ivragimov, E.T.; Shendyapin, A.S.; Vasharatyan, E.I.; Kalinin, E.I. The Vapour Pressure of Lead in the Silver-Lead System. Trans. Inst. Met. i Obogashch. Akad. Nauk Kaz. SSR 1967, 26, 37. [Google Scholar]
- Granovskaya, A.P.; Lyubimov, A.P. Measurement of Small Vapor Pressures at High Temperatures (IV) Partial Vapor Pressures of Components of the Ag− Pb System. Z. Fiz. Khim. 1953, 27, 1437. [Google Scholar]
- Scientific Group Thermodata Europe. Unary SGTE Database 5.0. Available online: https://www.sgte.net/en/free-pure-substance-database (accessed on 19 September 2022).
- Muggianu, Y.M.; Gambino, M.; Bros, J.-P. Enthalpies de formation des alliages liquides bismuth-etain-gallium a 723 k. choix d’une representation analytique des grandeurs d’exces integrales e t partielles de melange. J. Chim. Phys. 1975, 72, 83. [Google Scholar] [CrossRef]
- Redlich, O.; Kister, A.T. Algebraic representation of thermodynamic properties and the classification of solutions. Ind. Eng. Chem. 1948, 40, 345. [Google Scholar] [CrossRef]
- Gąsior, W.; Dębski, A.; Zabrocki, M. Thermodynamic description of the Ge-In-Li liquid alloys. J. Mol. Liq. 2018, 260, 415. [Google Scholar] [CrossRef]
| Chemical Name | Source | Purity [Mass%] | Purification Method | Analysis Method |
|---|---|---|---|---|
| Magnesium | Alfa Aesar | 99.9 | None | Certified purity |
| Lead | POCH | 99.999 | None | Certified purity |
| Silver | Innovator Sp. z o.o. | 99.9 | None | Certified purity |
| Argon | Air Products | 99.9999 | None | Certified purity |
| Number of Dropped Moles of Ag [mol] | Heat Effect ΔHSignal·K [kJ] | Mole Fraction xAg | Integral Molar Enthalpy ΔmixH [kJ/mol] | Standard Uncertainties u(ΔmixH) [kJ/mol] | ||
|---|---|---|---|---|---|---|
| = 0.04 kJ/mol. | ||||||
| 0.000929 | 0.034250 | 0.003 | 0.0677 | −3.7 | 3.1 | 0.06 |
| 0.000959 | 0.033922 | 0.002 | 0.1287 | −3.4 | 1.6 | 0.08 |
| 0.000996 | 0.035925 | 0.002 | 0.1840 | −3.0 | 2.3 | 0.11 |
| 0.001044 | 0.036470 | 0.001 | 0.2350 | −2.7 | 1.2 | 0.13 |
| 0.001137 | 0.039690 | 0.001 | 0.2837 | −2.5 | 1.1 | 0.15 |
| 0.001119 | 0.038816 | 0.001 | 0.3260 | −2.3 | 0.9 | 0.16 |
| 0.001072 | 0.039129 | 0.003 | 0.3620 | −2.0 | 2.8 | 0.18 |
| 0.001115 | 0.039747 | 0.002 | 0.3956 | −1.8 | 1.9 | 0.20 |
| 0.001077 | 0.038824 | 0.002 | 0.4249 | −1.6 | 2.3 | 0.22 |
| 0.001353 | 0.049990 | 0.004 | 0.4579 | −1.3 | 3.2 | 0.24 |
| = 0.16 kJ/mol. | ||||||
| 0.001148 | 0.032040 | −0.007 | 0.0596 | −7.6 | −5.8 | 0.19 |
| 0.000980 | 0.023487 | −0.010 | 0.1051 | −7.7 | −9.8 | 0.21 |
| 0.000974 | 0.024040 | −0.009 | 0.1462 | −7.8 | −9.1 | 0.23 |
| 0.001192 | 0.028836 | −0.011 | 0.1916 | −7.8 | −9.6 | 0.25 |
| 0.001446 | 0.035855 | −0.013 | 0.2407 | −7.9 | −9.0 | 0.28 |
| 0.001457 | 0.040151 | −0.009 | 0.2844 | −7.8 | −6.2 | 0.30 |
| 0.001494 | 0.044598 | −0.006 | 0.3243 | −7.6 | −3.9 | 0.33 |
| 0.001521 | 0.040084 | −0.011 | 0.3606 | −7.6 | −7.4 | 0.36 |
| 0.001724 | 0.046074 | −0.012 | 0.3973 | −7.6 | −7.0 | 0.39 |
| 0.001727 | 0.049376 | −0.009 | 0.4300 | −7.4 | −5.2 | 0.41 |
| 0.001647 | 0.050232 | −0.005 | 0.4581 | −7.2 | −3.3 | 0.44 |
| 0.001765 | 0.051050 | −0.009 | 0.4853 | −7.1 | −4.8 | 0.47 |
| = 0.44 kJ/mol. | ||||||
| 0.0011199 | 0.003841 | −0.034 | 0.0317 | −8.2 | −30.3 | 0.44 |
| 0.0014406 | 0.007875 | −0.041 | 0.0697 | −9.0 | −28.3 | 0.44 |
| 0.0016789 | 0.010824 | −0.046 | 0.1104 | −9.8 | −27.3 | 0.45 |
| 0.0020599 | 0.018174 | −0.051 | 0.1557 | −10.6 | −24.9 | 0.46 |
| 0.0020673 | 0.023159 | −0.047 | 0.1967 | −11.2 | −22.5 | 0.47 |
| 0.0021758 | 0.032061 | −0.041 | 0.2358 | −11.5 | −19.0 | 0.48 |
| 0.0022833 | 0.034419 | −0.043 | 0.2729 | −11.9 | −18.7 | 0.49 |
| 0.0022861 | 0.034784 | −0.042 | 0.3067 | −12.2 | −18.5 | 0.51 |
| 0.0029063 | 0.049882 | −0.048 | 0.3453 | −12.4 | −16.6 | 0.52 |
| 0.0031056 | 0.057853 | −0.047 | 0.3820 | −12.6 | −15.1 | 0.54 |
| 0.0032734 | 0.065761 | −0.045 | 0.4166 | −12.7 | −13.7 | 0.56 |
| 0.0037230 | 0.085006 | −0.041 | 0.4515 | −12.6 | −10.9 | 0.59 |
| Number of Dropped Moles of Pb [mol] | Heat Effect ΔHSignal·K [kJ] | Mole Fraction xPb | Integral Molar Enthalpy ΔmixH [kJ/mol] | Standard Uncertainties u(ΔmixH) [kJ/mol] | ||
|---|---|---|---|---|---|---|
| = 0.54 kJ/mol. | ||||||
| 0.0006636 | −0.012041 | −0.031 | 0.0200 | −9.3 | −46.8 | 0.55 |
| 0.0010212 | 0.010405 | −0.019 | 0.0494 | −9.6 | −18.5 | 0.56 |
| 0.0014334 | 0.018966 | −0.022 | 0.0877 | −9.8 | −15.4 | 0.57 |
| 0.0014633 | 0.020177 | −0.022 | 0.1237 | −10.0 | −14.9 | 0.58 |
| 0.0014899 | 0.022766 | −0.020 | 0.1576 | −10.1 | −13.4 | 0.59 |
| 0.0015642 | 0.023316 | −0.022 | 0.1905 | −10.3 | −13.8 | 0.60 |
| 0.0017505 | 0.045275 | −0.005 | 0.2244 | −10.0 | −2.8 | 0.62 |
| 0.0025801 | 0.069316 | −0.005 | 0.2695 | −9.5 | −1.8 | 0.65 |
| 0.0044069 | 0.128546 | 0.002 | 0.3354 | −8.6 | 0.5 | 0.70 |
| 0.0054725 | 0.174444 | 0.018 | 0.4024 | −7.4 | 3.2 | 0.76 |
| 0.0084517 | 0.253278 | 0.011 | 0.4829 | −6.2 | 1.3 | 0.84 |
| 0.0094570 | 0.306745 | 0.036 | 0.5506 | −4.9 | 3.8 | 0.92 |
| System | References | |
|---|---|---|
| Ag–Mg | 53,346.5 −3694 905.8 | [10] |
| Ag–Pb | 12,902.274 | [17] |
| −4008.088 −2576.139 | ||
| Mg–Pb | −39,272.641-5.773712·T | [12] |
| −43,546.211-16.706741·T | ||
| −4329.298-8.616737·T | ||
| 17,406.133 | ||
| 4967.802 | ||
| Ag–Mg–Pb | 4700.8075 | This study |
| 518.60761 | ||
| 39,007.392 |
| xAg | xMg | xPb | ΔmixH | |||
|---|---|---|---|---|---|---|
| kJ/mol | ||||||
| (Mg0.25Pb0.75)1−xAgx alloys at T = 1116 K | ||||||
| 0 | 0.25 | 0.75 | 5.318 | −17.286 | 0.532 | −3.923 |
| 0.05 | 0.2375 | 0.7125 | 3.880 | −18.909 | 1.121 | −3.498 |
| 0.1 | 0.225 | 0.675 | 2.646 | −20.519 | 1.790 | −3.144 |
| 0.2 | 0.2 | 0.6 | 0.744 | −23.735 | 3.302 | −2.617 |
| 0.3 | 0.175 | 0.525 | −0.490 | −27.000 | 4.930 | −2.284 |
| 0.4 | 0.15 | 0.45 | −1.161 | −30.386 | 6.529 | −2.084 |
| 0.5 | 0.125 | 0.375 | −1.379 | −33.969 | 7.949 | −1.955 |
| 0.6 | 0.1 | 0.3 | −1.261 | −37.832 | 9.027 | −1.832 |
| 0.7 | 0.075 | 0.225 | −0.929 | −42.063 | 9.594 | −1.647 |
| 0.8 | 0.05 | 0.15 | −0.514 | −46.756 | 9.465 | −1.330 |
| 0.9 | 0.025 | 0.075 | −0.155 | −52.013 | 8.444 | −0.806 |
| 1 | 0 | 0 | 0 | −57.946 | 6.318 | 0 |
| (Mg0.50Pb0.50)1−xAgx alloys at T = 1116 K | ||||||
| 0 | 0.5 | 0.5 | −5.584 | −14.433 | −1.982 | −8.207 |
| 0.05 | 0.475 | 0.475 | −6.112 | −15.669 | −0.720 | −8.090 |
| 0.1 | 0.45 | 0.45 | −6.450 | −16.889 | 0.553 | −7.996 |
| 0.2 | 0.4 | 0.4 | −6.624 | −19.354 | 3.066 | −7.840 |
| 0.3 | 0.35 | 0.35 | −6.246 | −21.982 | 5.427 | −7.669 |
| 0.4 | 0.3 | 0.3 | −5.455 | −24.926 | 7.500 | −7.410 |
| 0.5 | 0.25 | 0.25 | −4.392 | −28.340 | 9.152 | −6.993 |
| 0.6 | 0.2 | 0.2 | −3.199 | −32.379 | 10.248 | −6.346 |
| 0.7 | 0.15 | 0.15 | −2.018 | −37.201 | 10.651 | −5.396 |
| 0.8 | 0.1 | 0.1 | −0.995 | −42.964 | 10.223 | −4.070 |
| 0.9 | 0.05 | 0.05 | −0.273 | −49.826 | 8.825 | −2.296 |
| 1 | 0 | 0 | 0 | −57.946 | 6.318 | 0 |
| (Mg0.75Pb0.25)1−xAgx alloys at T = 1116 K | ||||||
| 0 | 0.75 | 0.25 | −24.819 | −2.974 | −22.182 | −7.776 |
| 0.05 | 0.7125 | 0.2375 | −22.916 | −4.358 | −18.227 | −8.579 |
| 0.1 | 0.675 | 0.225 | −21.085 | −5.781 | −14.551 | −9.285 |
| 0.2 | 0.6 | 0.2 | −17.600 | −8.792 | −7.987 | −10.393 |
| 0.3 | 0.525 | 0.175 | −14.311 | −12.114 | −2.420 | −11.077 |
| 0.4 | 0.45 | 0.15 | −11.210 | −15.881 | 2.177 | −11.304 |
| 0.5 | 0.375 | 0.125 | −8.320 | −20.248 | 5.791 | −11.030 |
| 0.6 | 0.3 | 0.1 | −5.699 | −25.395 | 8.372 | −10.201 |
| 0.7 | 0.225 | 0.075 | −3.433 | −31.518 | 9.838 | −8.757 |
| 0.8 | 0.15 | 0.05 | −1.634 | −38.831 | 10.080 | −6.627 |
| 0.9 | 0.075 | 0.025 | −0.437 | −47.560 | 8.960 | −3.736 |
| 1 | 0 | 0 | 0 | −57.946 | 6.318 | 0 |
| (Ag0.25Mg0.75)1−xPbx alloys at T = 1116 K | ||||||
| 0.25 | 0.75 | 0 | −29.880 | −2.972 | −17.047 | −9.699 |
| 0.2375 | 0.7125 | 0.05 | −27.155 | −3.919 | −16.231 | −10.053 |
| 0.225 | 0.675 | 0.1 | −23.995 | −5.219 | −14.018 | −10.323 |
| 0.2 | 0.6 | 0.2 | −17.600 | −8.792 | −7.987 | −10.393 |
| 0.175 | 0.525 | 0.3 | −12.104 | −13.056 | −2.478 | −9.716 |
| 0.15 | 0.45 | 0.4 | −7.707 | −17.004 | 1.042 | −8.391 |
| 0.125 | 0.375 | 0.5 | −3.991 | −19.697 | 2.432 | −6.669 |
| 0.1 | 0.3 | 0.6 | −0.384 | −20.577 | 2.273 | −4.847 |
| 0.075 | 0.225 | 0.7 | 3.502 | −19.653 | 1.398 | −3.181 |
| 0.05 | 0.15 | 0.8 | 7.656 | −17.564 | 0.532 | −1.826 |
| 0.025 | 0.075 | 0.9 | 11.581 | −15.514 | 0.075 | −0.806 |
| 0 | 0 | 1 | 14.334 | −15.079 | 0 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dębski, A.; Gąsior, W.; Gierlotka, W.; Polański, M. Mixing Enthalpies of Liquid Ag–Mg–Pb Alloys: Experiment vs. Thermodynamic Modeling. Materials 2022, 15, 7360. https://doi.org/10.3390/ma15207360
Dębski A, Gąsior W, Gierlotka W, Polański M. Mixing Enthalpies of Liquid Ag–Mg–Pb Alloys: Experiment vs. Thermodynamic Modeling. Materials. 2022; 15(20):7360. https://doi.org/10.3390/ma15207360
Chicago/Turabian StyleDębski, Adam, Władysław Gąsior, Wojciech Gierlotka, and Marek Polański. 2022. "Mixing Enthalpies of Liquid Ag–Mg–Pb Alloys: Experiment vs. Thermodynamic Modeling" Materials 15, no. 20: 7360. https://doi.org/10.3390/ma15207360






