DDSM: Design-Oriented Dual-Scale Shape-Material Model for Lattice Material Components
Abstract
:1. Introduction
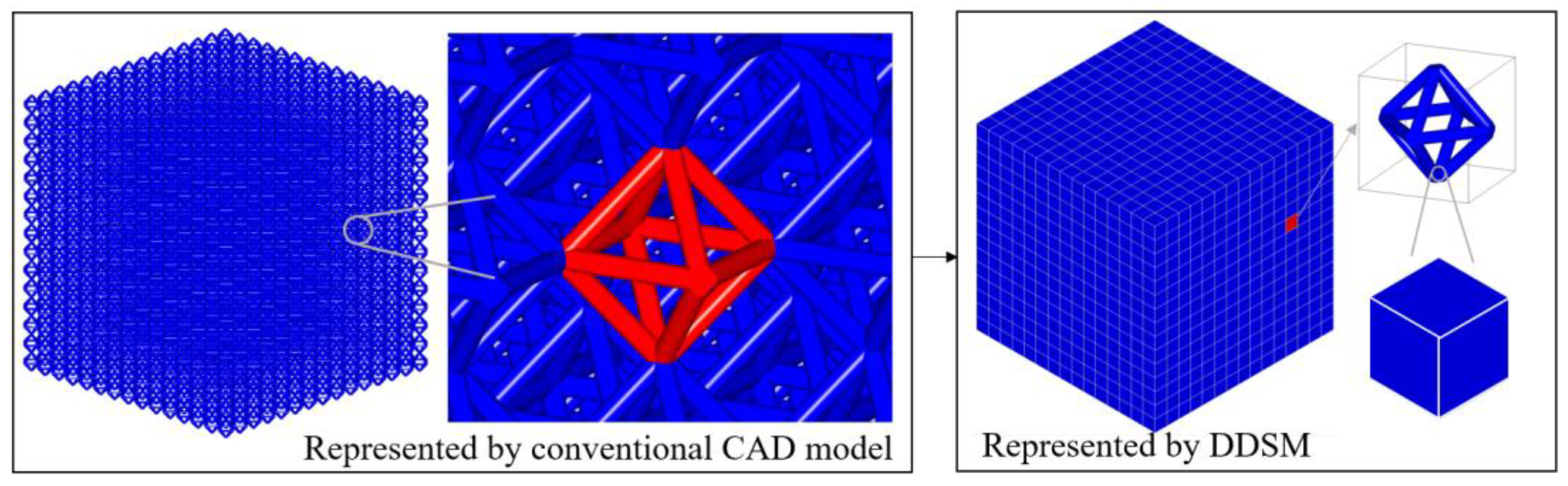
- Lack of dual-material model representation: Due to the dual-material properties on the lattice CAD model, the geometric model based on STL file format does not provide a complete representation of the material information. Moreover, this renders the model computationally expensive for the material query. Therefore, there is an urgent need to propose a dual-scale shape-material model, which supports material information queries on two scales.
- Large storage cost. As mentioned before, most lattice structures are stored in the STL format. A large number of hollowed-out structures produce huge triangular facets to store geometry information. These triangular facets take up large memory and make the information redundant extremely.
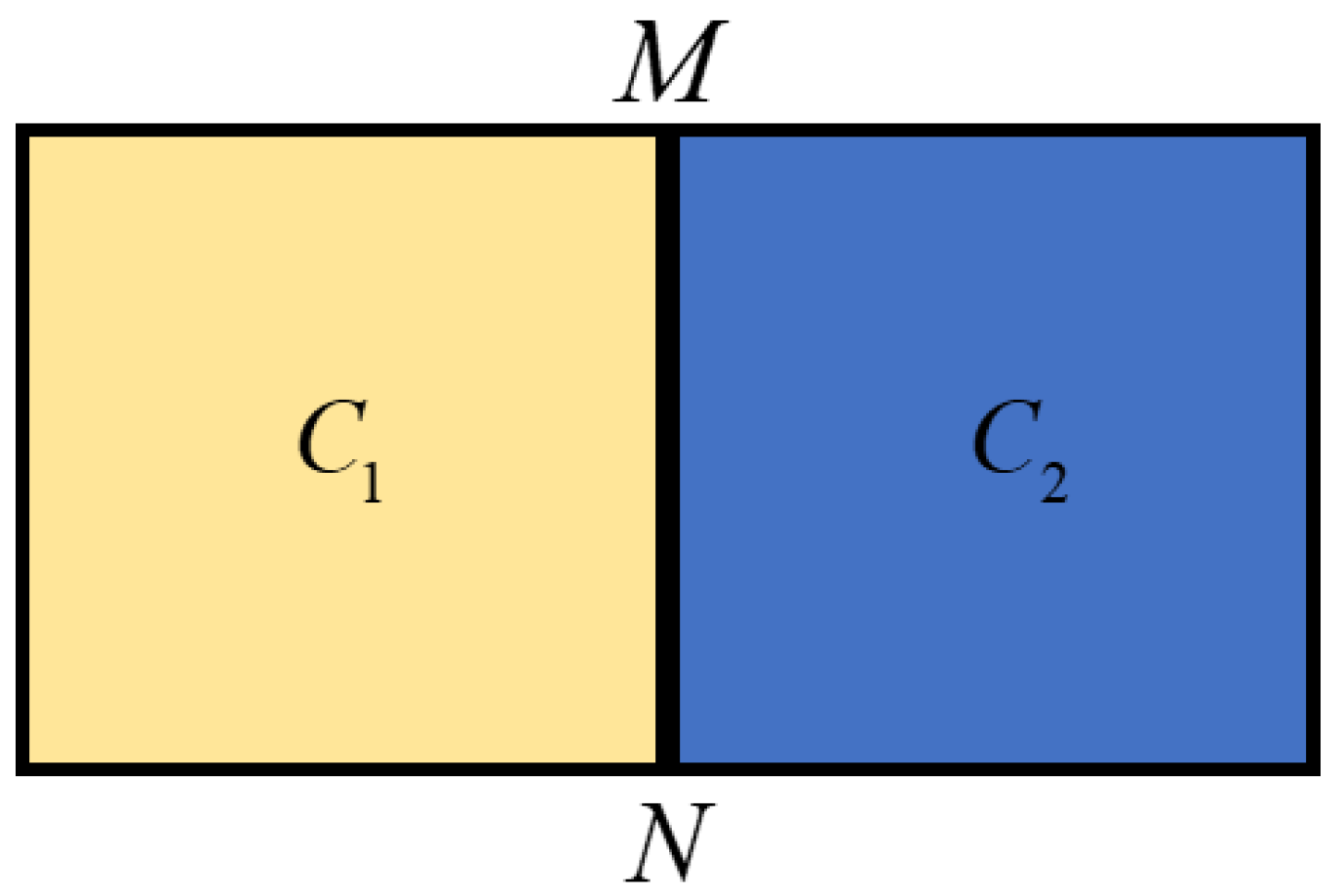
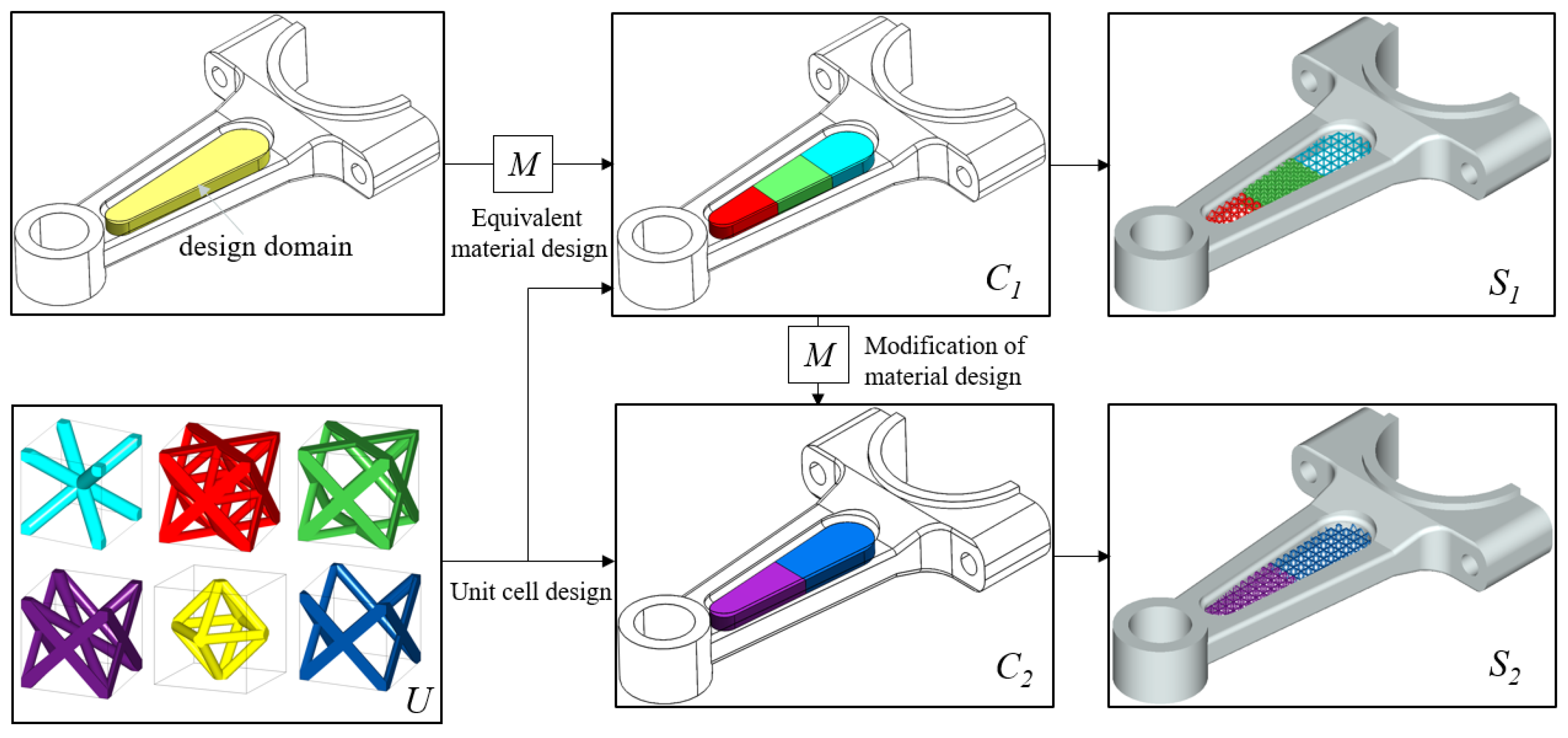
- Missing design intent: In the design-oriented process, designers prefer to focus on the overall equivalent material properties (elastic modulus, Poisson’s ratio, etc.) embodied in design domain, rather than on the specific configuration and manufacturing material of the unit cell. However, the existing CAD tools and model representation format (e.g., Delaunay triangulation) lack equivalent macroscopic material properties, which makes CAD models poorly designable and revisable.
2. Mathematical Frameworks for the DDSM
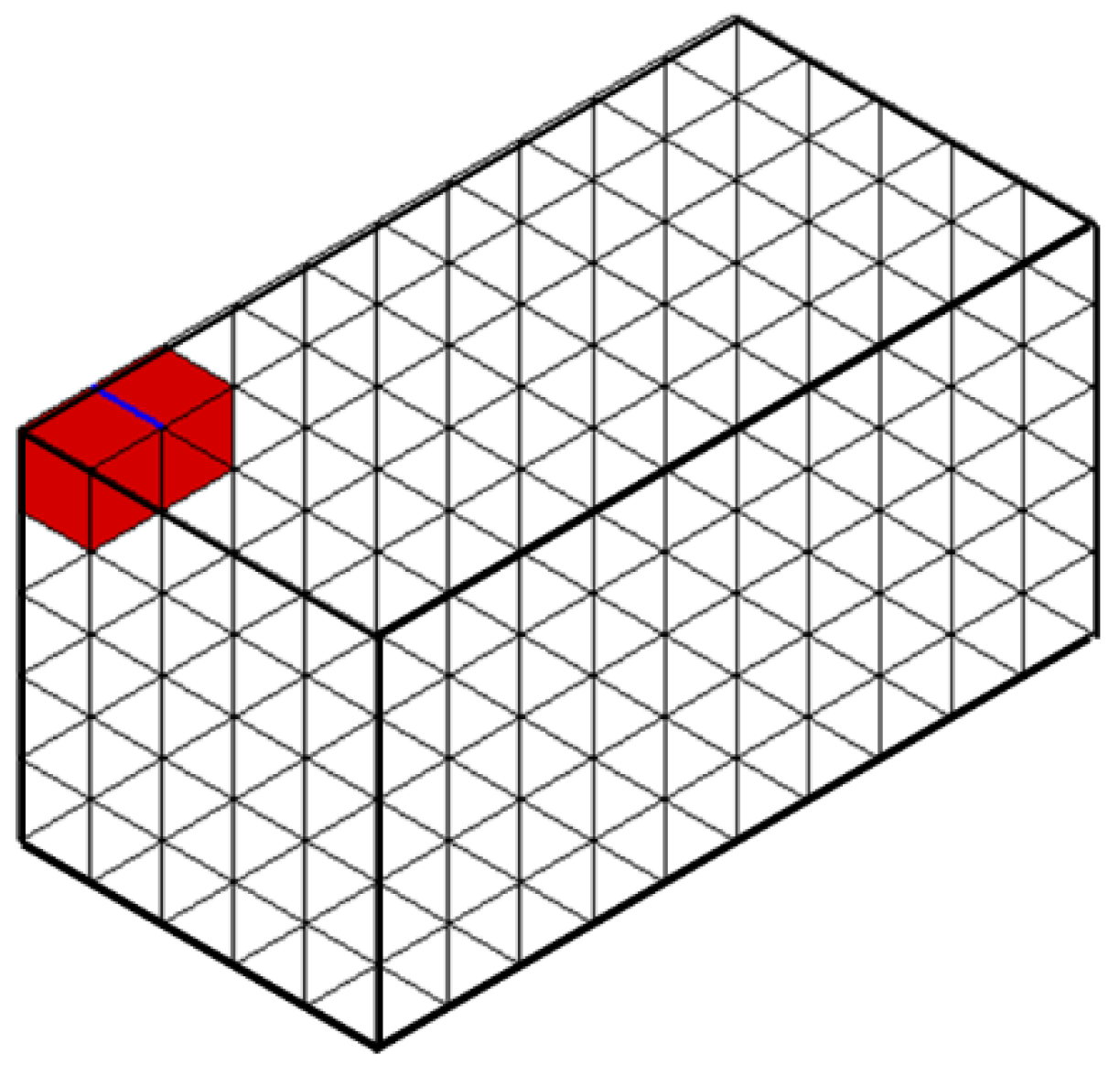
3. Macroscopic Scale: A Compact Face-Based Topological Data Structure
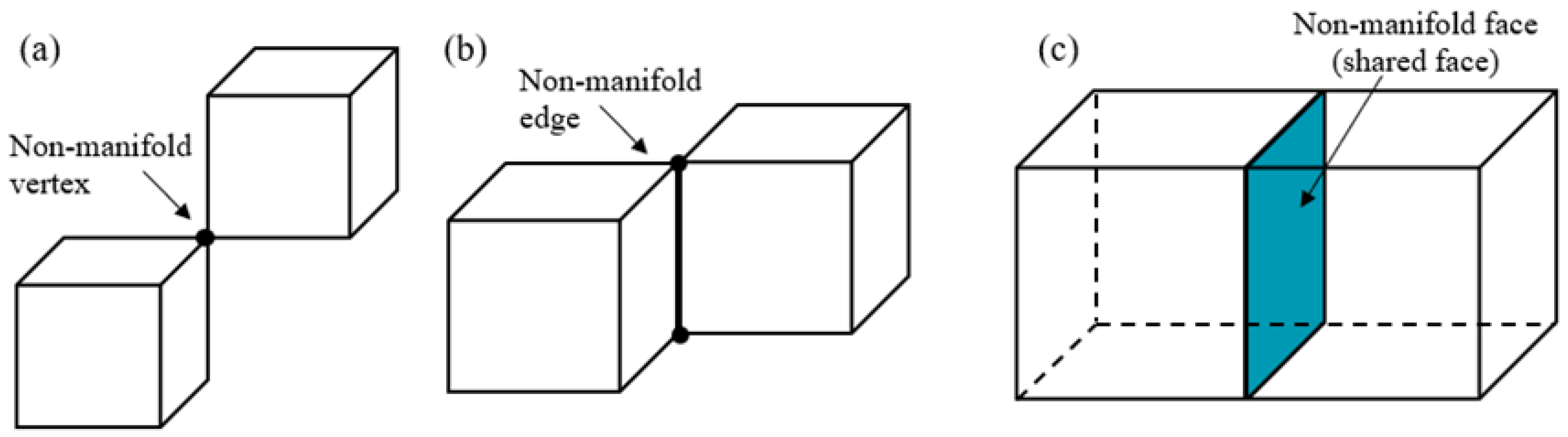
3.1. Finite Non-Manifold Characteristic
3.2. A compact Half-Face Data Structure Design
- Generality: support for macroscopic non-manifold geometry CAD representations.
- Time efficiency: support specific topology queries without performing global search.
- Memory overhead: require a minimal amount of storage.
3.3. Macroscopic CAD Model Topology Reconstruction
- m2hfs: Map each half-face to the ID of its twin half-face;
- v2hfs: Map each non-manifold vertex to its incident half-face;
- b2hfs: Map manifold border vertex to its incident element ID and its local ID;
- bhfsm: Map each border half-face to its incident element ID and its local ID.
| Algorithm 1: Construction of twin half-faces |
| Input: element connectivity, CElement Output: mutual mapping of twin half-faces, m2hfs begin Allocate the initial Element and define m2hfs zeros for each e in CElement do f←traverse each face in e; ←get the maximum node identification on f; set mapping to the corresponding face into v2fs; set mapping to adjacent vertices into v2adj; end for for each e in CElement do f←traverse each face in e; if m2hfs (f) = 0 then ←get the maximum node identification on f; get candidate faces of mutual mapping on f; match twin half-face of f in v2adj; end if end for end |
| Algorithm 2: Construction of topological relationship |
| Input: element connectivity, CElement mutual mapping of twin half-faces, m2hfs Output: vertex to incident half-faces, v2hfs border vertex to incident half-faces, b2hfs border half-faces mapping, bhfsm begin Allocate array marked initialized to false and it is the same size as m2hfs; for each e in CElement do f ←traverse each face in e; if not m2hfs (f) and not marked(f) then set mapping vertices on face to f into v2hfs; end if end for for each e in CElement do f ←traverse each face in e; if not m2hfs(f) then set mapping f into bhfsm; v ←traverse each vertex in f; V ←set of elements incident on v in v2hfs; if not V then append f to b2hfs; end if end if end for end |
3.4. Topology Information Query
- 1.
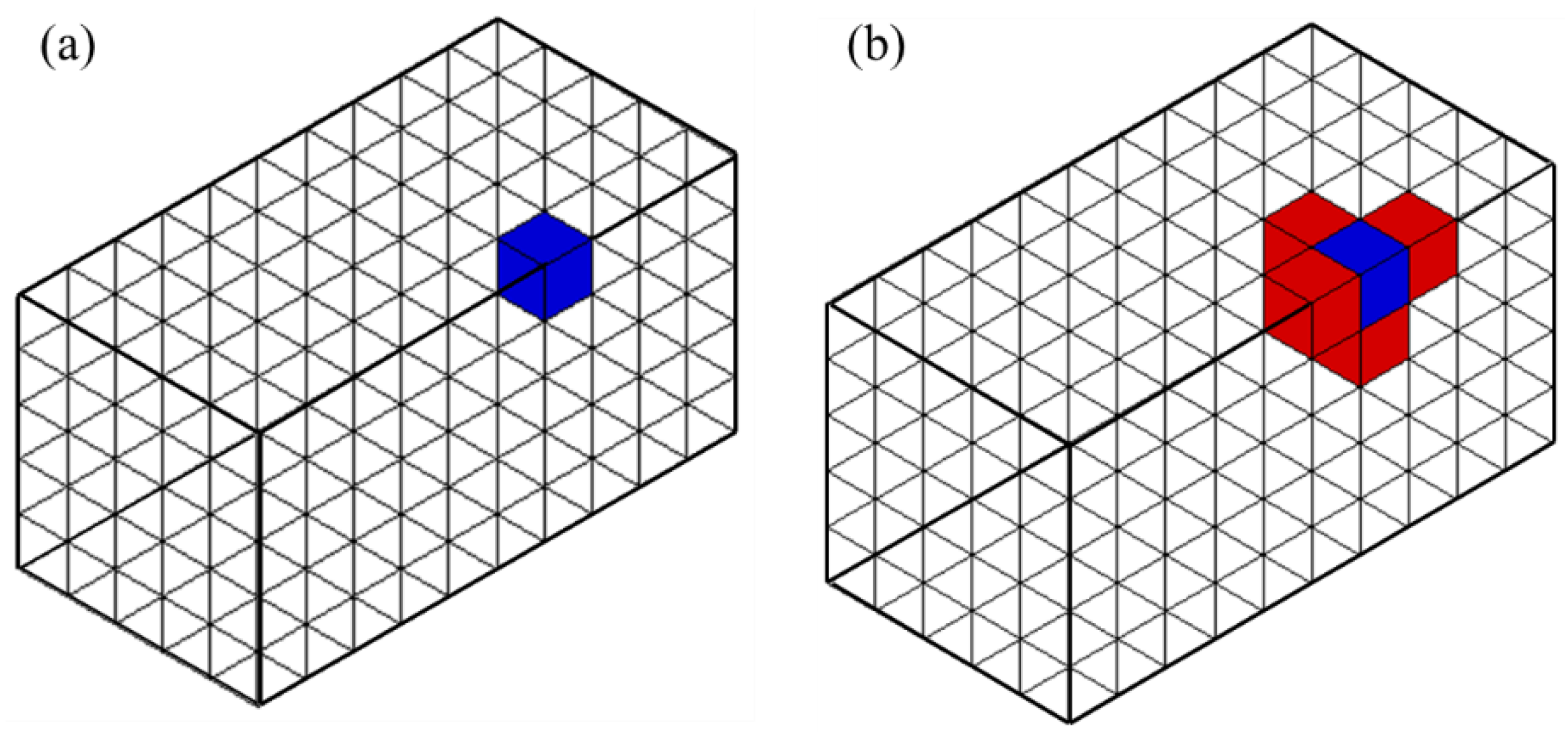
- Adjacency query:
- Given an edge, return vertex-connected adjacent edges;
- Given a face, return edge-connected adjacent faces;
- Given an element, return face-connected adjacent elements;
| Algorithm 3: Adjacency query for shared sub-entity |
| Input: element identification number, elem mutual mapping of twin half-faces, m2hfs Output: adjacent three-dimensional entities, cadj begin for each face f in elem do if m2hfs (f) then e←decode to obtain face-connected adjacent elements; append e to cadj; end if end for end |
- 2.
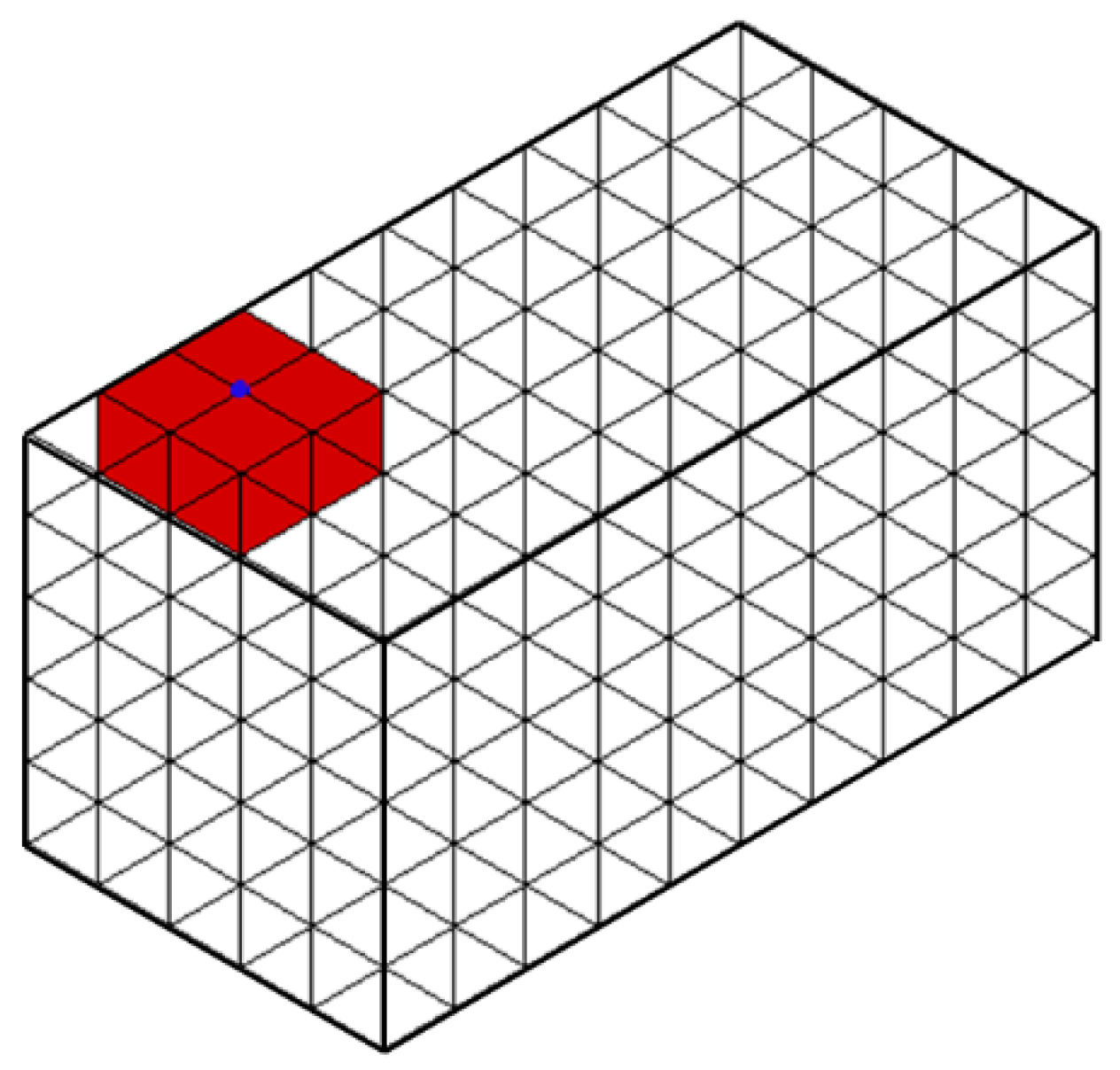
- Incidence query:
- Given a vertex, return incident elements;
- Given an edge, return incident elements;
| Algorithm 4: Upscaling incidence query |
| Input: An edge defined by two vertices, s vertex to incident half-faces, v2hfs border vertex to incident half-faces, b2hfs Output: incident three-dimensional entities, cinc begin v1←vertex with larger ID in s; V1←set of elements incident on v1 found in v2hfs(v); if not V1 then V1←set of elements incident on v1 found in b2hfs(v); end if v2←adjacent vertex to v1 in s; V2←set of elements incident on v2 found in v2hfs(v); if not V2 then V2←set of elements incident on v2 found in b2hfs(v); end if cinc←the intersection of V1 and V2; end |
4. Microscopic Scale: Lattice Unit Cell Based on Implicit Representation
4.1. Implicit Function of Truss-like Struts
4.2. Generation of Lattice Unit Cell
5. Dual-Scale Shape-Material Model Representation
5.1. Data Structure of the DDSM
- Vertices array : The array records the node information of the mesh model at the macroscopic scale. It consists of node index and node coordinates.
- Material library : The material library contains homogenized equivalent materials and unit cell fabrication materials (i.e., microscopic materials) . It consists of material index and material properties. Depending on the functional requirement, the material properties on each scale can be elastic modulus , Poisson’s ratio , shear modulus and thermal expansion coefficient , etc. Additional parameters can be attached to the columns of the array.
- The macroscopic model C: Each mesh has three attributes, the mesh identification number, eight primary nodes, and equivalent material properties. Mi corresponds to equivalent material index from (19). The eight primary node storage order follows the convention in Figure 4.
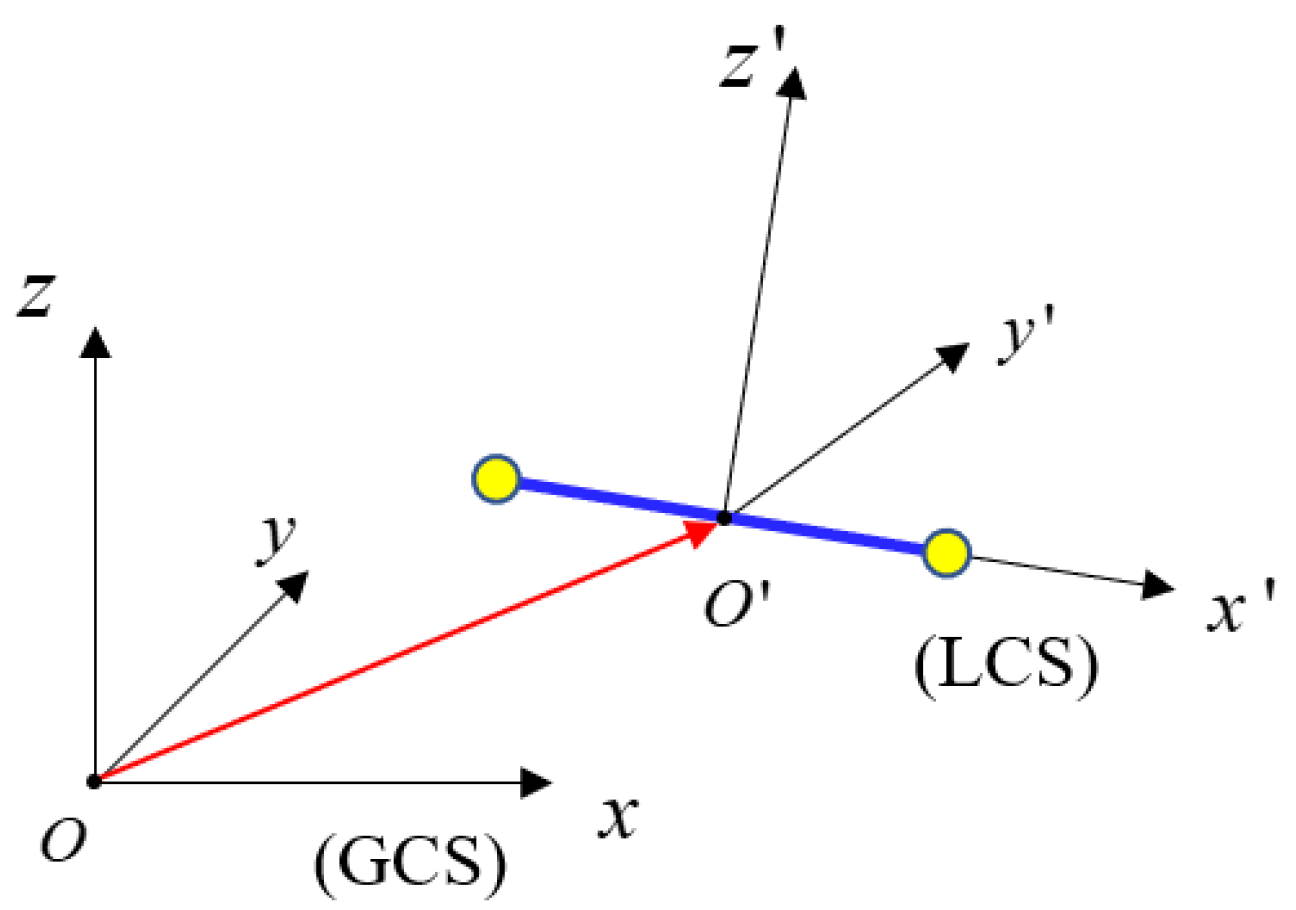
- The microscopic model U: Each unit cell is composed of Nk struts and its fabrication materials. corresponds to fabrication material index from (20). The strut has two attributes, two nodes ID connecting the strut and strut geometric parameters. The geometry of the strut is determined by the three parameters r1, r2, t. All the implicit functions of struts are expressed in LCS.
5.2. Prototype Implementation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bai, L.; Yi, C.; Chen, X.; Sun, Y.; Zhang, J. Effective design of the graded strut of bcc lattice structure for improving mechanical properties. Materials 2019, 12, 2192. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, M.; Liu, F.; Fu, G.; Zhang, D.Z.; Zhang, T.; Zhou, H. Improved mechanical properties and energy absorption of bcc lattice structures with triply periodic minimal surfaces fabricated by slm. Materials 2018, 11, 2411. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Y.; Zhuo, S.; Xiao, Y.; Zheng, G.; Dong, G.; Zhao, Y.F. Rapid modeling and design optimization of multi-topology lattice structure based on unit-cell library. J. Mech. Des. 2020, 142, 091705. [Google Scholar] [CrossRef]
- Liu, Y.; Zheng, G.; Letov, N.; Zhao, Y. A survey of modeling and optimization methods for multi-scale heterogeneous lattice structures. J. Mech. Des. 2020, 143, 040803. [Google Scholar] [CrossRef]
- Azman, A.H.; Vignat, F.; Villeneuve, F. Cad tools and file format performance evaluation in designing lattice structures for additive manufacturing. J. Teknol. 2018, 80, 87–95. [Google Scholar] [CrossRef] [Green Version]
- Kladovasilakis, N.; Tsongas, K.; Karalekas, D.; Tzetzis, D. Architected materials for additive manufacturing: A comprehensive review. Materials 2022, 15, 5919. [Google Scholar] [CrossRef]
- Plocher, J.; Panesar, A. Review on design and structural optimisation in additive manufacturing: Towards next-generation lightweight structures. Mater. Des. 2019, 183, 108164. [Google Scholar] [CrossRef]
- Savio, G.; Meneghello, R.; Concheri, G. Geometric modeling of lattice structures for additive manufacturing. Rapid Prototyp. J. 2018, 24, 351–360. [Google Scholar] [CrossRef]
- Aremu, A.O.; Brennan-Craddock, J.P.J.; Panesar, A.; Ashcroft, I.A.; Hague, R.J.M.; Wildman, R.D.; Tuck, C. A voxel-based method of constructing and skinning conformal and functionally graded lattice structures suitable for additive manufacturingt. Addit. Manuf. 2017, 13, 1–13. [Google Scholar]
- Mustafa, S.S.; Lazoglu, I. A new model and direct slicer for lattice structures. Struct. Multidiscip. Optim. 2021, 63, 2211–2230. [Google Scholar] [CrossRef]
- Liu, H. Algorithms for Design and Interrogation of Functionally Graded Material Solids. PhD Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2000. [Google Scholar]
- Cirillo, E.; Elber, G. Handling heterogeneous structures and materials using blending schemes in v-reps. Comput. Aided Geom. Des. 2020, 83, 101942. [Google Scholar] [CrossRef]
- Hong, Q.Y.; Elber, G. Conformal microstructure synthesis in trimmed trivariate based v-reps. Comput. Aided Des. 2021, 140, 11. [Google Scholar] [CrossRef]
- Mandad, M.; Chen, R.; Bommes, D.; Campen, M. Intrinsic mixed-integer polycubes for hexahedral meshing. Comput. Aided Geom. Des. 2022, 94, 102078. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Chen, D.F.; Hu, J.Q.; Wang, X.P.; Chen, P. Representation and fabrication method for multiple gradients fgm part based on additive manufacturing. Appl. Mech. Mater. 2013, 433-435, 2076–2080. [Google Scholar] [CrossRef]
- Tereshin, A.; Pasko, A.; Fryazinov, O.; Adzhiev, V. Hybrid function representation for heterogeneous objects. Graph. Models 2021, 114, 101098. [Google Scholar] [CrossRef]
- Zang, T.; Zhu, D.; Mu, G. Inverse construction methods of heterogeneous nurbs object based on additive manufacturing. Comput. Modeling Eng. Sci. 2020, 125, 597–610. [Google Scholar] [CrossRef]
- Li, B.; Fu, J. Solid modeling and slicing process of heterogeneous materials based on trivariate t-splines. J. Zhejiang Univ. (Eng. Sci.) 2021, 55, 10. [Google Scholar]
- Kambampati, S.; Jauregui, C.; Museth, K.; Kim, H.A. Geometry design using function representation on a sparse hierarchical data structure. Comput.-Aided Des. 2021, 133, 102989. [Google Scholar] [CrossRef]
- Kou, X.Y.; Tan, S.T.; Sze, W.S. Modeling complex heterogeneous objects with non-manifold heterogeneous cells. Comput. Aided Des. 2006, 38, 457–474. [Google Scholar] [CrossRef]
- Qian, X.; Dutta, D. Heterogeneous object modeling through direct face neighborhood alteration. Comput. Graph. 2003, 27, 943–961. [Google Scholar] [CrossRef]
- Mueller-Karger, C.M.; Rank, E.; Cerrolaza, M. P-version of the finite-element method for highly heterogeneous simulation of human bone. Finite Elem. Anal. Des. 2004, 40, 757–770. [Google Scholar] [CrossRef]
- Opgenoord, M.M.J.; Willcox, K.E. Design for additive manufacturing: Cellular structures in early-stage aerospace design. Struct. Multidiscip. Optim. 2019, 60, 411–428. [Google Scholar] [CrossRef]
- Schumacher, C.; Bickel, B.; Rys, J.; Marschner, S.; Daraio, C.; Gross, M. Microstructures to control elasticity in 3d printing. ACM Trans. Graph. 2015, 34, 136. [Google Scholar] [CrossRef] [Green Version]
- Deng, H.; Zhao, J.; Wang, C. Bionic design method of a non-uniform lattice structure for a landing footpad. Aerospace 2022, 9, 220. [Google Scholar] [CrossRef]
- Li, F.; Zhang, Q.; Shi, H.; Liu, Z. A modified three-dimensional negative-poisson-ratio metal metamaterial lattice structure. Materials 2022, 15, 3752. [Google Scholar] [CrossRef]
- Liu, P.; Liu, A.; Peng, H.; Tian, L.; Liu, J.; Lu, L. Mechanical property profiles of microstructures via asymptotic homogenization. Comput. Graph. 2021, 100, 106–115. [Google Scholar] [CrossRef]
- Liu, X.; Shapiro, V. Multiscale shape–material modeling by composition. Comput.-Aided Des. 2018, 102, 194–203. [Google Scholar] [CrossRef]
- Xia, H.; Meng, J.; Liu, J.; Ao, X.; Lin, S.; Yang, Y. Evaluation of the equivalent mechanical properties of lattice structures based on the finite element method. Materials 2022, 15, 2993. [Google Scholar] [CrossRef]
- Ellul, C. Functionality and Performance: Two Important Considerations when Implementing Topology in 3D; University of London: London, UK, 2008. [Google Scholar]
- Boguslawski, P. Modelling and Analysing 3D Building Interiors with the Dual Half-Edge Data Structure; University of South Wales: New Port, UK, 2011. [Google Scholar]
- Canino, D.; De Floriani, L.; Weiss, K. Ia*: An adjacency-based representation for non-manifold simplicial shapes in arbitrary dimensions. Comput. Graph. 2011, 35, 747–753. [Google Scholar] [CrossRef] [Green Version]
- Alumbaugh, T.J.; Jiao, X. Compact Array-Based Mesh Data Structures. In Proceedings of the 14th International Meshing Roundtable; Hanks, B.W., Ed.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 485–503. [Google Scholar]
- Dyedov, V.; Ray, N.; Einstein, D.; Jiao, X.; Tautges, T.J. Ahf: Array-based half-facet data structure for mixed-dimensional and non-manifold meshes. Eng. Comput. 2015, 31, 389–404. [Google Scholar] [CrossRef]
- Gupta, A.; Allen, G.; Rossignac, J. Quador: Quadric-of-revolution beams for lattices. Comput.-Aided Des. 2018, 102, 160–170. [Google Scholar] [CrossRef]




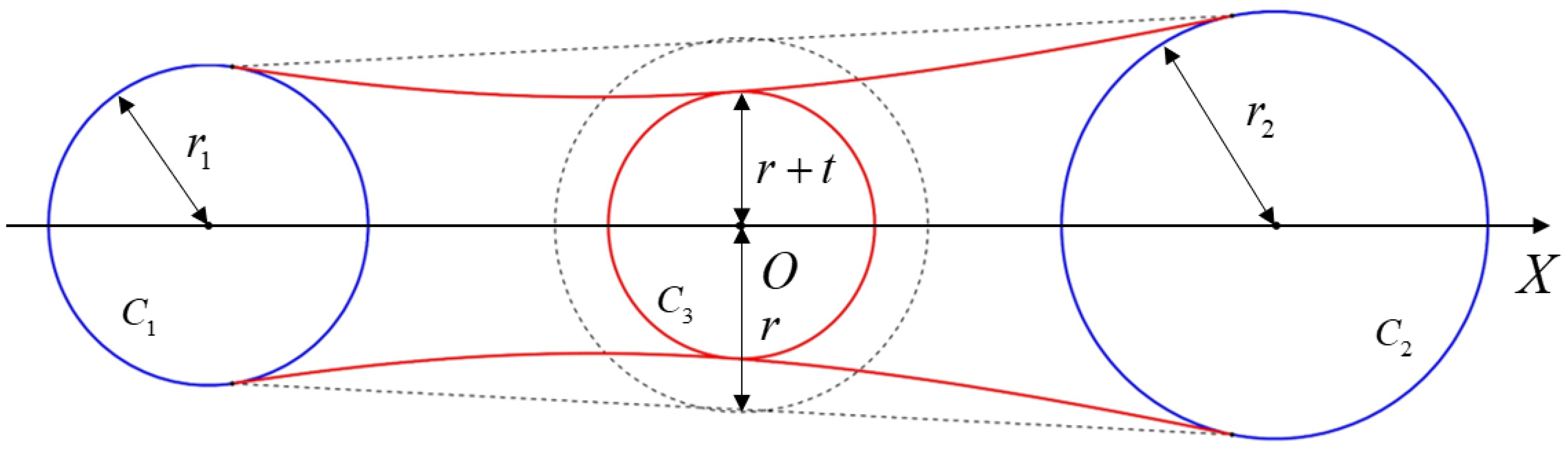


| Value of a | Shape |
|---|---|
| Hyperbola strut | |
| Cone strut | |
| Hyperbola strut | |
| Parabola strut | |
| Ellipse strut |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, C.; Yang, R.; Niu, B.; Meng, X. DDSM: Design-Oriented Dual-Scale Shape-Material Model for Lattice Material Components. Materials 2022, 15, 7428. https://doi.org/10.3390/ma15217428
Feng C, Yang R, Niu B, Meng X. DDSM: Design-Oriented Dual-Scale Shape-Material Model for Lattice Material Components. Materials. 2022; 15(21):7428. https://doi.org/10.3390/ma15217428
Chicago/Turabian StyleFeng, Chao, Rui Yang, Bin Niu, and Xiangpeng Meng. 2022. "DDSM: Design-Oriented Dual-Scale Shape-Material Model for Lattice Material Components" Materials 15, no. 21: 7428. https://doi.org/10.3390/ma15217428
APA StyleFeng, C., Yang, R., Niu, B., & Meng, X. (2022). DDSM: Design-Oriented Dual-Scale Shape-Material Model for Lattice Material Components. Materials, 15(21), 7428. https://doi.org/10.3390/ma15217428




