Point Defects Stability, Hydrogen Diffusion, Electronic Structure, and Mechanical Properties of Defected Equiatomic γ(U,Zr) from First-Principles
Abstract
1. Introduction
2. Computational Methods
2.1. Computational Details
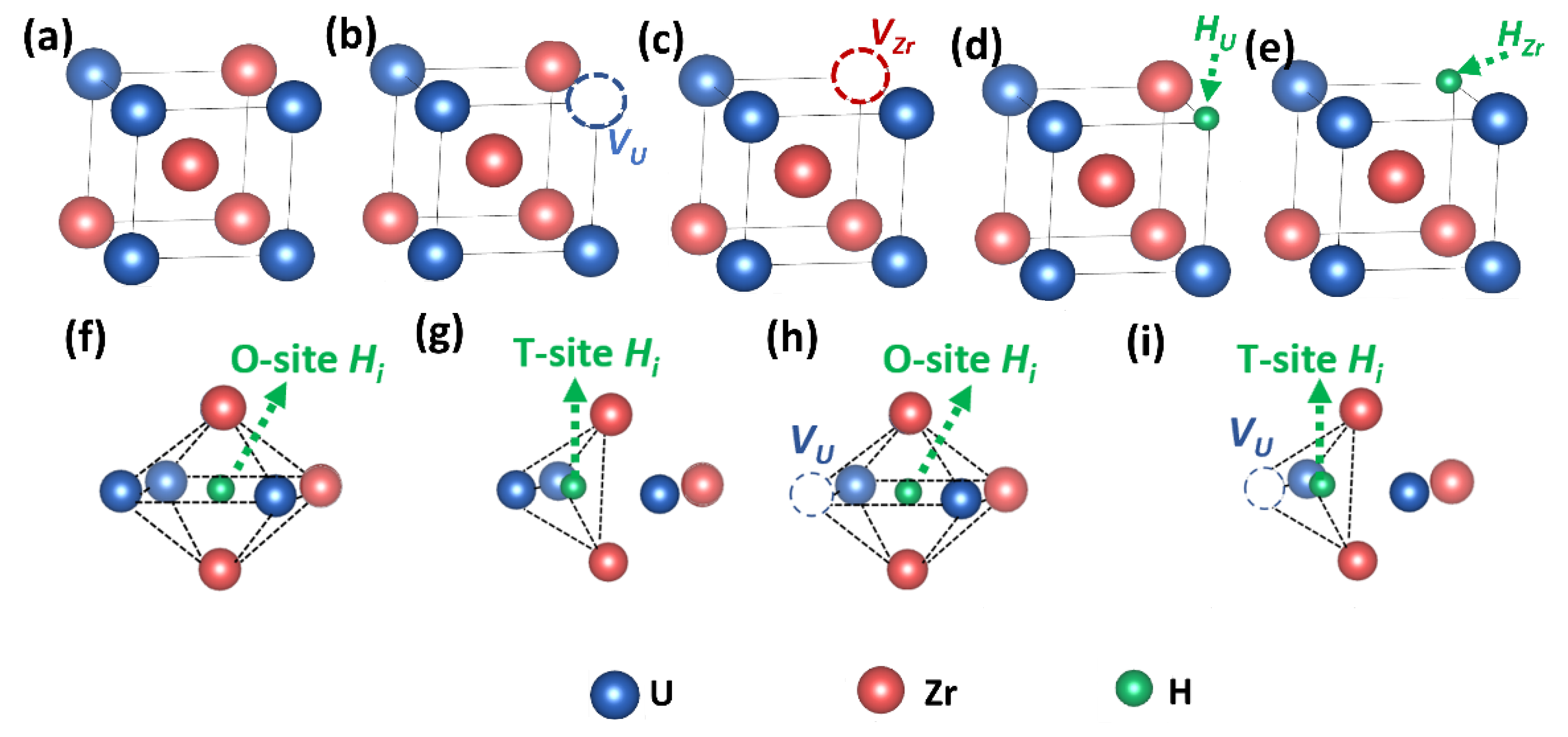
2.2. Simulation Models
3. Results and Discussion
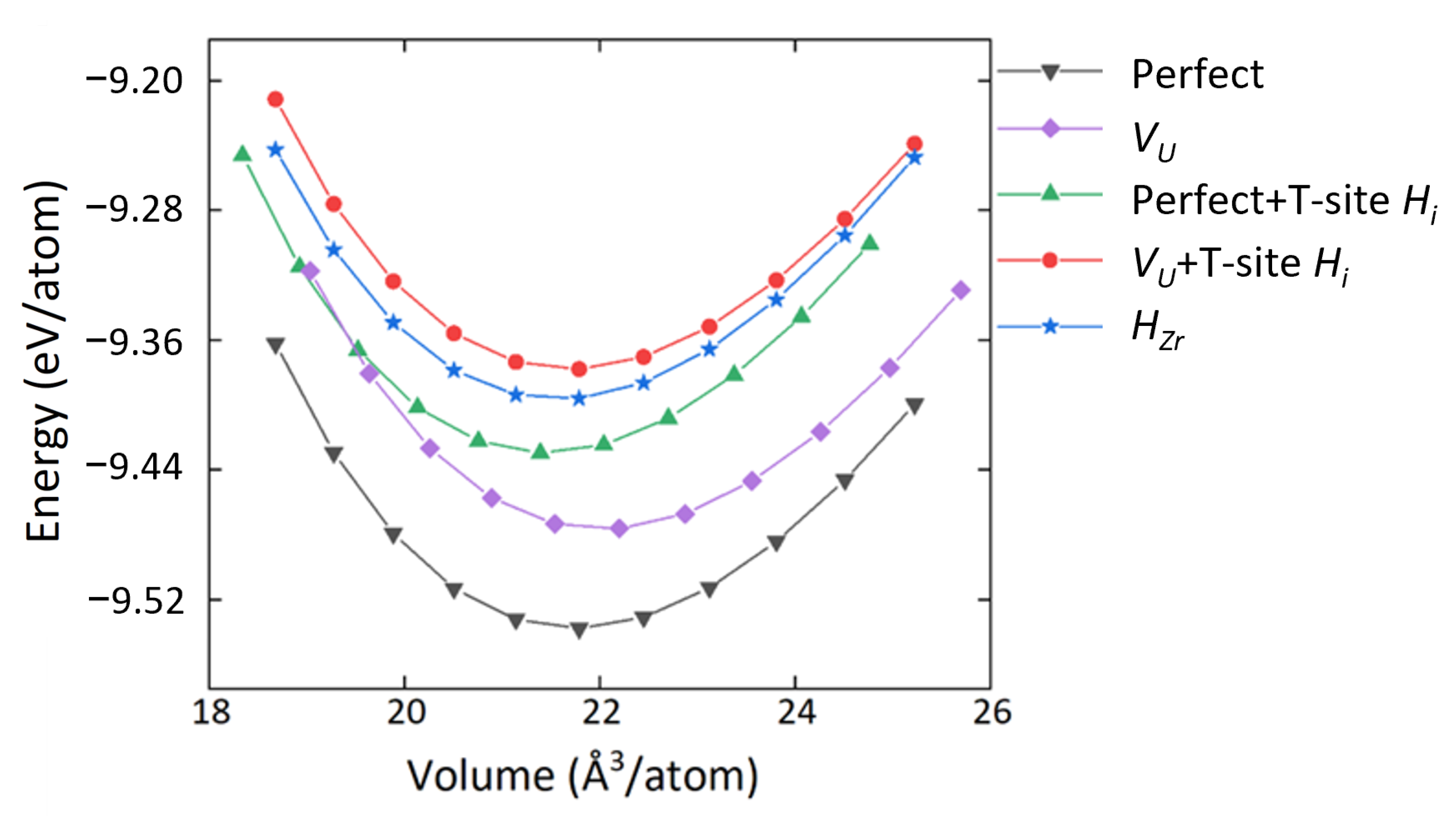
3.1. Structure and Defect Stabilities
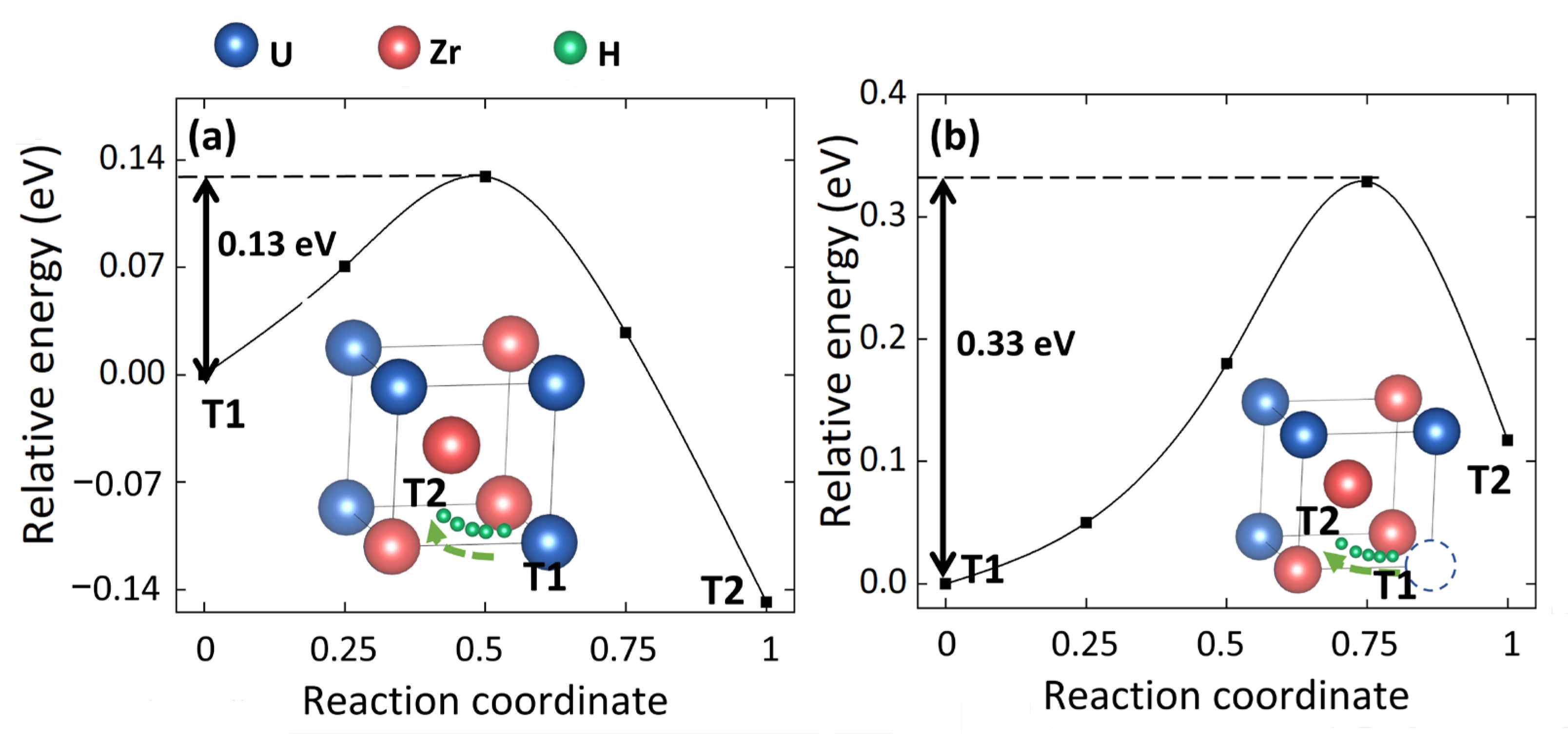
3.2. Effect of Uranium Vacancy on H Diffusion
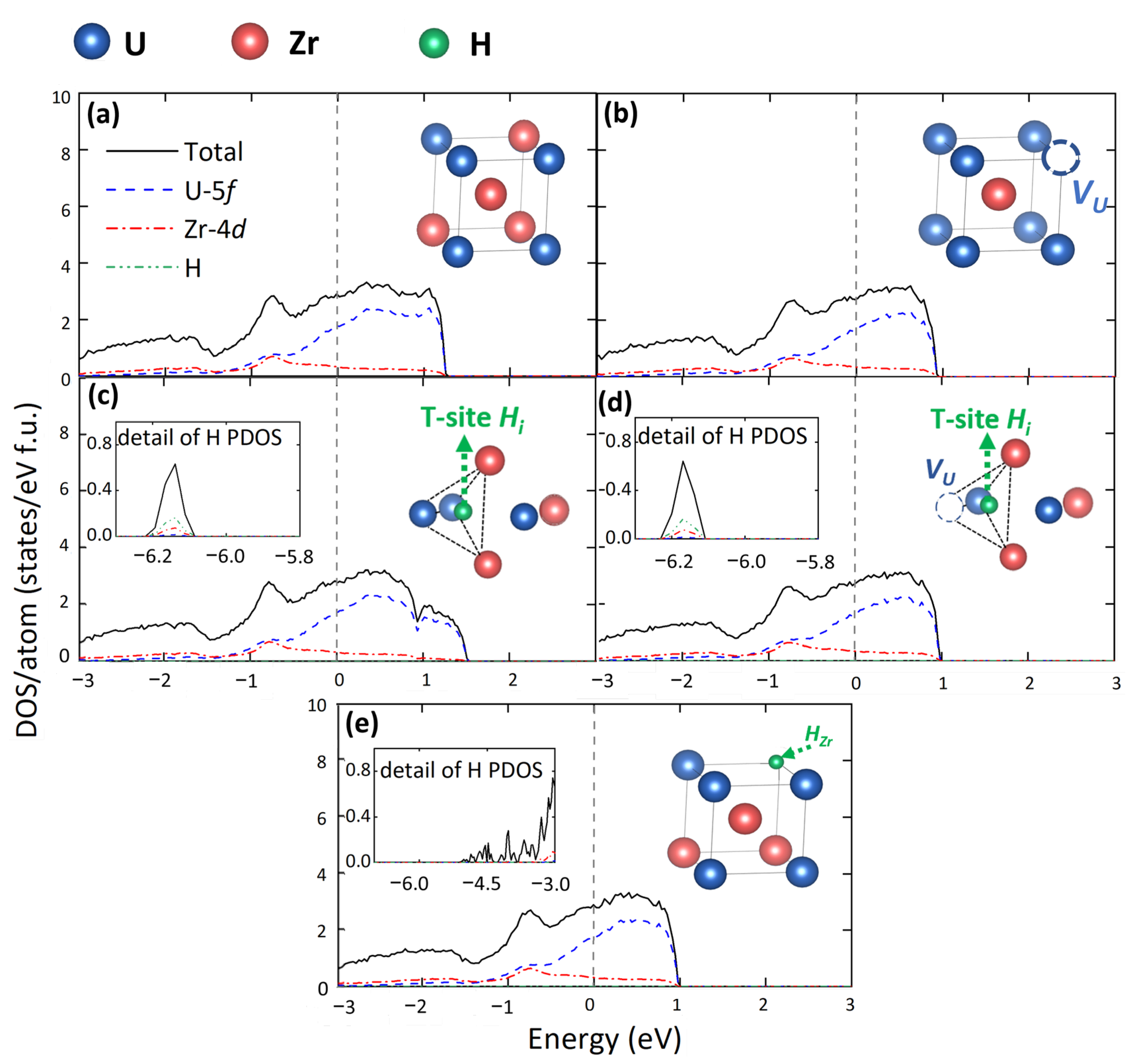
3.3. Electronic Structure
3.4. Mechanical Properties
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| U-Pu-Zr | Uranium-plutonium-zirconium |
| U-Zr | Uranium-zirconium |
| BCC | body-centered cubic |
| H | Hydrogen |
| DFT | Density functional theory |
| DFT + U | Density functional theory plus Hubbard parameter U |
| SOC | Spin-orbit coupling |
| Uranium vacancy | |
| Zirconium vacancy | |
| Uranium lattice occupied by hydrogen atom | |
| Zirconium lattice occupied by hydrogen atom | |
| Octahedral hydrogen interstitial in perfect cell | |
| Tetrahedral hydrogen interstitial in perfect cell | |
| Octahedral hydrogen interstitial in uranium vacancy-containing cell | |
| Tetrahedral hydrogen interstitial in uranium vacancy-containing cell | |
| CI-NEB | Climbing image nudged elastic band |
| SQS | Special quasi-random structure |
| Ecohesive | Cohesive energy |
| Number of uranium atoms | |
| Number of zirconium atoms | |
| Energy of an isolated uranium atom | |
| Energy of an isolated zirconium atom | |
| E[γ(U,Zr)] | Total energy of the γ(U,Zr) supercells |
| Formation energy of X type vacancy, X can be uranium or zirconium | |
| Total energy of γ(U,Zr) supercells with a vacancy | |
| Energy of an isolated X atom, X can be uranium or zirconium | |
| Hydrogen solution energy | |
| E[γ(U,Zr),H] | Total energy of the γ(U,Zr) supercells with H atom |
| Energy of H2 molecular | |
| Total energy of the γ(U,Zr) supercells with both X type vacancy and H atom, X can be uranium or zirconium | |
| Trapping energy of uranium vacancy on T-site | |
| TDOS | Total densities of states |
| PDOS | Partial densities of states |
| TDOS at the Fermi level | |
| Number of valence electrons of U element at the Fermi energy level | |
| Number of valence electrons of Zr element at the Fermi energy level | |
| EOS | Equation of state |
| VRH approximations | Voight-Reuss-Hill approximations |
References
- Hatala, B. Gas cooled fast reactor system (GFR). Encycl. Nucl. Energy 2021, 545–552. [Google Scholar]
- Carmack, W.; Porter, D.; Chang, Y.; Hayes, S.; Meyer, M.; Burkes, D.; Lee, C.; Mizuno, T.; Delage, F.; Somers, J. Metallic fuels for advanced reactors. J. Nucl. Mater. 2009, 392, 139–150. [Google Scholar] [CrossRef]
- Stevenson, C.E. The EBR-II Fuel Cycle Story; American Nuclear Society: LaGrange Park, IL, USA, 1987. [Google Scholar]
- Chang, Y.I. The integral fast reactor. Nucl. Technol. 1989, 88, 129–138. [Google Scholar] [CrossRef]
- Ogata, T. 5.01—Metal Fuel. In Comprehensive Nuclear Materials, 2nd ed.; Konings, R.J.M., Stoller, R.E., Eds.; Elsevier: Oxford, UK, 2020; pp. 1–42. [Google Scholar]
- Hofman, G.L.; Walters, L.C.; Bauer, T.H. Metallic fast reactor fuels. Prog. Nucl. Energy 1997, 31, 83–110. [Google Scholar] [CrossRef]
- Jerred, N.; Khanal, R.; Benson, M.; Perez, E.; King, J.A.; Dubey, M.; Burns, J.; Charit, I.; Choudhury, S.; Mariani, R.D. Evaluation of tellurium as a fuel additive in neodymium-containing U-Zr Metallic Fuel. Sci. Rep. 2019, 9, 16043. [Google Scholar] [CrossRef] [PubMed]
- Crawford, D.C.; Porter, D.L.; Hayes, S.L. Fuels for sodium-cooled fast reactors: US perspective. J. Nucl. Mater. 2007, 371, 202–231. [Google Scholar] [CrossRef]
- Lagerberg, G. Phase transformations in a uranium-zirconium alloy containing 2 weight per cent zirconium. J. Nucl. Mater. 1963, 9, 261–276. [Google Scholar] [CrossRef]
- Ogata, T. 3.01—Metal Fuel. In Comprehensive Nuclear Materials; Konings, R.J.M., Ed.; Elsevier: Oxford, UK, 2012; pp. 1–40. [Google Scholar]
- Basak, C.B. Microstructural evaluation of U-rich U–Zr alloys under near-equilibrium condition. J. Nucl. Mater. 2011, 416, 280–287. [Google Scholar] [CrossRef]
- Landa, A.; Söderlind, P.; Turchi, P.E.A. Density-functional study of the U–Zr system. J. Alloys Compd. 2009, 478, 103–110. [Google Scholar] [CrossRef]
- Zhou, S.; Zhang, Y.; Jiang, C.; Morgan, D. A combined ab-initio and empirical model for thermal conductivity of concentrated metal alloys with the focus on binary uranium alloys. Materialia 2021, 15, 100990. [Google Scholar] [CrossRef]
- Moore, A.; Beeler, B.; Deo, C.; Baskes, M.; Okuniewski, M. Atomistic modeling of high temperature uranium–zirconium alloy structure and thermodynamics. J. Nucl. Mater. 2015, 467, 802–819. [Google Scholar] [CrossRef]
- Moore, A.; Deo, C.; Baskes, M.; Okuniewski, M. Atomistic mechanisms of morphological evolution and segregation in U-Zr alloys. Acta Mater. 2016, 115, 178–188. [Google Scholar] [CrossRef]
- Aly, A.; Beeler, B.; Avramova, M. Ab initio molecular dynamics investigation of γ-(U,Zr) structural and thermal properties as a function of temperature and composition. J. Nucl. Mater. 2022, 561, 153523. [Google Scholar] [CrossRef]
- Powell, G.L.; Koger, J.W.; Bennett, R.K.; Williamson, A.L.; Hemperly, V.C. Internal hydrogen embrittlement of gamma-stabilized uranium alloys. Corrosion 2013, 32, 442–450. [Google Scholar] [CrossRef]
- Stoller, R.E. Primary radiation damage formation. Compr. Nucl. Mater. 2012, 1, 293–332. [Google Scholar]
- Zhao, Q.; Zhang, Z.; Ouyang, X. Formation energy and diffusion barrier of point defects in three uranium compounds as nuclear fuels. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2019, 450, 114–117. [Google Scholar] [CrossRef]
- Was, G.S. Fundamentals of Radiation Materials Science: Metals and Alloys; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Najafi, A.; Sharifi, F.; Mesgari-Abbasi, S.; Khalaj, G. Influence of pH and temperature parameters on the sol-gel synthesis process of meso porous ZrC nanopowder. Ceram. Int. 2022, 48, 26725–26731. [Google Scholar] [CrossRef]
- Kiritani, M. Similarity and difference between fcc, bcc and hcp metals from the view point of point defect cluster formation. J. Nucl. Mater. 2000, 276, 41–49. [Google Scholar] [CrossRef]
- Cersullo, N.; Mardaras, J.; Emile, P.; Nickel, K.; Holzinger, V.; Hühne, C. Effect of Internal Defects on the Fatigue Behavior of Additive Manufactured Metal Components: A Comparison between Ti6Al4V and Inconel 718. Materials 2022, 15, 6882. [Google Scholar] [CrossRef]
- Su, Z.; Quan, Z.; Shen, T.; Jin, P.; Li, J.; Hu, S.; Liu, D. A Novel BCC-Structure Zr-Nb-Ti Medium-Entropy Alloys (MEAs) with Excellent Structure and Irradiation Resistance. Materials 2022, 15, 6565. [Google Scholar] [CrossRef]
- Starikov, S.; Korneva, M. Description of phase transitions through accumulation of point defects: UN, UO2 and UC. J. Nucl. Mater. 2018, 510, 373–381. [Google Scholar] [CrossRef]
- Seshadri, A.; Jokisaari, A.M.; Sun, C. A Review of Irradiation Damage and Effects in α-Uranium. Materials 2022, 15, 4106. [Google Scholar] [CrossRef]
- Loomis, B.A.; Gerber, S.B. Length and electrical resistivity changes of neutron irradiated uranium. Philos. Mag. 1968, 18, 539–553. [Google Scholar] [CrossRef]
- Huang, G.-Y.; Wirth, B.D. First-principles study of diffusion of interstitial and vacancy in α U–Zr. J. Phys. Condens. Matter 2011, 23, 205402. [Google Scholar] [CrossRef]
- Huang, G.-Y.; Wirth, B.D. First-principles study of bubble nucleation and growth behaviors in α U–Zr. J. Phys. Condens. Matter 2012, 24, 415404. [Google Scholar] [CrossRef]
- Beeler, B.; Zhang, Y.; Okuniewski, M.; Deo, C. Calculation of the displacement energy of α and γ uranium. J. Nucl. Mater. 2018, 508, 181–194. [Google Scholar] [CrossRef]
- Vizoso, D.; Deo, C. Determination of vacancy formation energies in binary UZr alloys using special quasirandom structure methods. Front. Mater. 2021, 8, 692660.0. [Google Scholar] [CrossRef]
- Grabovetskaya, G.; Mishin, I.; Stepanova, E.; Zabudchenko, O. Effect of Structure and Hydrogen on the Short-Term Creep of Titanium Ti-2.9Al-4.5V-4.8Mo Alloy. Materials 2022, 15, 3905. [Google Scholar] [CrossRef]
- Lloyd, A.L.; Smith, R.; Wootton, M.J.; Andrews, J.; Arul, J.; Muruva, H.P.; Vinod, G. Modelling the effect of hydrogen on crack growth in zirconium. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2019, 455, 13–20. [Google Scholar] [CrossRef]
- Asada, K.; Ono, K.; Yamaguchi, K.; Yamamoto, T.; Maekawa, A.; Oe, S.; Yamawaki, M. Hydrogen absorption properties of uranium alloys. J. Alloys Compd. 1995, 231, 780–784. [Google Scholar] [CrossRef]
- Adamson, P.; Orman, S.; Picton, G. The effects of hydrogen on the tensile properties of uranium when tested in different environments. J. Nucl. Mater. 1969, 33, 215–224. [Google Scholar] [CrossRef]
- Tuli, V.; Claisse, A.; Burr, P.A. Hydrogen solubility in Zr–Nb alloys. Scr. Mater. 2022, 214, 114652. [Google Scholar] [CrossRef]
- Xie, W.; Xiong, W.; Marianetti, C.A.; Morgan, D. Correlation and relativistic effects in U metal and U-Zr alloy: Validation ofab initioapproaches. Phys. Rev. B 2013, 88, 235128. [Google Scholar] [CrossRef]
- Söderlind, P.; Landa, A.; Turchi, P. Comment on Correlation and relativistic effects in U metal and U-Zr alloy: Validation of ab initio approaches. Phys. Rev. B 2014, 90, 157101. [Google Scholar] [CrossRef]
- Söderlind, P.; Sadigh, B.; Lordi, V.; Landa, A.; Turchi, P. Electron correlation and relativity of the 5f electrons in the U–Zr alloy system. J. Nucl. Mater. 2014, 444, 356–358. [Google Scholar] [CrossRef]
- Zhang, C.-B.; Li, X.-P.; Li, W.-D.; Zhang, P.; Yin, W.; Wang, F.; Wang, B.-T. Structural, electronic, and elastic properties of equiatomic UZr alloys from first-principles. J. Nucl. Mater. 2017, 496, 333–342. [Google Scholar] [CrossRef]
- Okamoto, H. U-zr (uranium-zirconium). J. Phase Equilibria Diffus. 2007, 28, 499. [Google Scholar] [CrossRef]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671–6687, Erratum in Phys. Rev. B 1993, 48, 4978. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Henkelman, G.; Uberuaga, B.P.; Jónsson, H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 2000, 113, 9901–9904. [Google Scholar] [CrossRef]
- Zunger, A.; Wei, S.-H.; Ferreira, L.G.; Bernard, J.E. Special quasirandom structures. Phys. Rev. Lett. 1990, 65, 353–356. [Google Scholar] [CrossRef]
- Matar, S.F. First principles studies of hydrogen insertion effects on magnetic properties, bonding and structure reordering of UZr 2. Comput. Condens. Matter 2017, 12, 19–24. [Google Scholar] [CrossRef]
- Qin, S.-Y.; Jin, S.; Sun, L.; Zhou, H.-B.; Zhang, Y.; Lu, G.-H. Hydrogen assisted vacancy formation in tungsten: A first-principles investigation. J. Nucl. Mater. 2015, 465, 135–141. [Google Scholar] [CrossRef]
- Alay-E-Abbas, S.M.; Nazir, S.; Noor, N.A.; Amin, N.; Shaukat, A. Thermodynamic Stability and Vacancy Defect Formation Energies in SrHfO3. J. Phys. Chem. C 2014, 118, 19625–19634. [Google Scholar] [CrossRef]
- Yang, X.; Yang, Y.; Liu, Y.; Wang, Z.; Wärnå, J.; Xu, Z.; Zhang, P. Investigating the solution and diffusion properties of hydrogen in α-Uranium by first-principles calculations. Prog. Nucl. Energy 2020, 122, 362–370. [Google Scholar] [CrossRef]
- Ferrin, P.; Kandoi, S.; Nilekar, A.U.; Mavrikakis, M. Hydrogen adsorption, absorption and diffusion on and in transition metal surfaces: A DFT study. Surf. Sci. 2012, 606, 679–689. [Google Scholar] [CrossRef]
- Ma, B.-L.; Wu, Y.-Y.; Guo, Y.-H.; Yin, W.; Zhan, Q.; Yang, H.-G.; Wang, S.; Wang, B.-T. Effects of Monovacancy and Divacancies on Hydrogen Solubility, Trapping and Diffusion Behaviors in fcc-Pd by First Principles. Materials 2020, 13, 4876. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Zhao, J.; Wen, B. Trapping of multiple hydrogen atoms in a vanadium monovacancy: A first-principles study. J. Nucl. Mater. 2012, 429, 216–220. [Google Scholar] [CrossRef]
- Jiménez, G.C.; Morinson-Negrete, J.D.; Blanquicett, F.P.; Ortega-López, C.; Espitia-Rico, M.J. Effects of Mono-Vacancies and Co-Vacancies of Nitrogen and Boron on the Energetics and Electronic Properties of Heterobilayer h-BN/graphene. Materials 2022, 15, 6369. [Google Scholar] [CrossRef] [PubMed]
- Birch, F. Finite Elastic Strain of Cubic Crystals. Phys. Rev. 1947, 71, 809–824. [Google Scholar] [CrossRef]
- Voigt, W. Lehrbuch der Kristallphysik:(Mit Ausschluss der Kristalloptik); BG Teubner: Leipzig, Germany, 1910; Volume 34. [Google Scholar]
- Hill, R. The Elastic Behaviour of a Crystalline Aggregate. Proc. Phys. Soc. Sect. A 1952, 65, 349. [Google Scholar] [CrossRef]
- Reuss, A. Berechnung der fließgrenze von mischkristallen auf grund der plastizitätsbedingung für einkristalle. ZAMM—J. Appl. Math. Mech. 1929, 9, 49–58. [Google Scholar] [CrossRef]
- Watt, J.P.; Peselnick, L. Clarification of the Hashin-Shtrikman bounds on the effective elastic moduli of polycrystals with hexagonal, trigonal, and tetragonal symmetries. J. Appl. Phys. 1980, 51, 1525–1531. [Google Scholar] [CrossRef]
- Huber, J.G.; Ansari, P.H. The superconductivity of BCC U-Zr alloys. Phys. B+C 1985, 135, 441–444. [Google Scholar] [CrossRef]
- Beeler, B.; Deo, C.; Baskes, M.; Okuniewski, M. First principles calculations of the structure and elastic constants of α, β and γ uranium. J. Nucl. Mater. 2013, 433, 143–151. [Google Scholar] [CrossRef]
- Iasir, A.R.M.; Hammond, K.D. Pseudopotential for plane-wave density functional theory studies of metallic uranium. Comput. Mater. Sci. 2019, 171, 109221. [Google Scholar] [CrossRef]
- Zhang, H.J.; Li, S.N.; Zheng, J.J.; Li, W.D.; Wang, B.T. Effects of pressure on structural, electronic, and mechanical properties of α, β, and γ uranium. Chin. Phys. B 2017, 26, 066104. [Google Scholar] [CrossRef]
- Wang, B.-T.; Zhang, P.; Liu, H.-Y.; Li, W.-D. First-principles calculations of phase transition, elastic modulus, and superconductivity under pressure for zirconium. J. Appl. Phys. 2011, 109, 063514. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, X.; Zhu, Y.; Zhang, S.; Qi, L.; Liu, R. First-principles investigations on elastic and thermodynamic properties of zirconium under pressure. Comput. Mater. Sci. 2012, 61, 42–49. [Google Scholar] [CrossRef]
- Moore, K.T.; Van der Laan, G. Nature of the 5f states in actinide metals. Rev. Mod. Phys. 2009, 81, 235–298. [Google Scholar] [CrossRef]
- Adak, S.; Nakotte, H.; De Châtel, P.F.; Kieder, B. Uranium at high pressure from first principles. Phys. B Condens. 2011, 406, 3342–3347. [Google Scholar] [CrossRef]
- Tateiwa, N.; Pospíšil, J.; Haga, Y.; Sakai, H.; Matsuda, T.D.; Yamamoto, E. Itinerant ferromagnetism in actinide 5f-electron systems: Phenomenological analysis with spin fluctuation theory. Phys. Rev. B. 2017, 96, 035125. [Google Scholar] [CrossRef]
- Kaneko, K.; Metoki, N.; Bernhoeft, N.; Lander, G.H.; Ishii, Y.; Ikeda, S.; Tokiwa, Y.; Haga, Y.; Ōnuki, Y. Large orbital magnetic moment and its quenching in the itinerant uranium intermetallic compounds U T Ga 5 (T = Ni, Pd, Pt). Phys. Rev. B 2003, 68, 214419. [Google Scholar] [CrossRef]
- Fujimori, S.I.; Kawasaki, I.; Yasui, A.; Takeda, Y.; Okane, T.; Saitoh, Y.; Fujimori, A.; Yamagami, H.; Haga, Y.; Yamamoto, E.; et al. Itinerant magnetism in URhGe revealed by angle-resolved photoelectron spectroscopy. Phys. Rev. B 2014, 89, 104518. [Google Scholar] [CrossRef]
- Schneider, W.D.; Laubschat, C. Actinide—Noble-metal systems: An x-ray-photoelectron-spectroscopy study of thorium-platinum, uranium-platinum, and uranium-gold intermetallics. Phys. Rev. B 1981, 23, 997. [Google Scholar] [CrossRef]
| Disordered Es (eV) | |
|---|---|
| −0.52 | |
| −0.67 | |
| perfect + T-site | −0.89 |
| perfect + O-site | −0.64 |
| + T-site | −1.13 |
| + O-site | −0.76 |
| 2.83 | 1.72 | 0.35 | |
| 2.52 [37] | 1.58 [37], 1.63 [13] | 0.37 [37] | |
| 2.86 | 1.70 | 0.35 | |
| perfect + T-site | 2.82 | 1.68 | 0.33 |
| + T-site | 2.81 | 1.64 | 0.34 |
| 2.90 | 1.71 | 0.32 |
| 21.93 | 75.2 | 120.8 | 36.7 | 105.6 | 103.2 | |
| 21.97 [37], 21.81 [13], 22.29 [62] | - | - | - | - | - | |
| 22.22 | 67.3 | 114.9 | 34.8 | 99.0 | 99.5 | |
| perfect + T-site | 21.65 | 73.8 | 122.6 | 38.7 | 106.3 | 103.6 |
| 21.89 | 69.3 | 116.9 | 34.7 | 101.0 | 100.2 | |
| 21.78 | 73.3 | 112.6 | 38.7 | 99.5 | 100.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, S.; Ma, J.-J.; Lai, K.; Zhang, C.-B.; Yin, W.; Qiu, R.; Zhang, P.; Wang, B.-T. Point Defects Stability, Hydrogen Diffusion, Electronic Structure, and Mechanical Properties of Defected Equiatomic γ(U,Zr) from First-Principles. Materials 2022, 15, 7452. https://doi.org/10.3390/ma15217452
Huang S, Ma J-J, Lai K, Zhang C-B, Yin W, Qiu R, Zhang P, Wang B-T. Point Defects Stability, Hydrogen Diffusion, Electronic Structure, and Mechanical Properties of Defected Equiatomic γ(U,Zr) from First-Principles. Materials. 2022; 15(21):7452. https://doi.org/10.3390/ma15217452
Chicago/Turabian StyleHuang, Shasha, Jiang-Jiang Ma, Kan Lai, Cheng-Bin Zhang, Wen Yin, Ruizhi Qiu, Ping Zhang, and Bao-Tian Wang. 2022. "Point Defects Stability, Hydrogen Diffusion, Electronic Structure, and Mechanical Properties of Defected Equiatomic γ(U,Zr) from First-Principles" Materials 15, no. 21: 7452. https://doi.org/10.3390/ma15217452
APA StyleHuang, S., Ma, J.-J., Lai, K., Zhang, C.-B., Yin, W., Qiu, R., Zhang, P., & Wang, B.-T. (2022). Point Defects Stability, Hydrogen Diffusion, Electronic Structure, and Mechanical Properties of Defected Equiatomic γ(U,Zr) from First-Principles. Materials, 15(21), 7452. https://doi.org/10.3390/ma15217452







