Numerical Simulation and Analytical Prediction of Residual Strength for Elbow Pipes with Erosion Defects
Abstract
:1. Introduction
2. Erosion Rate Analysis of 90° Elbow
2.1. Predictive Model for Erosion Wear
2.2. Model Parameters and Boundary Conditions
2.3. Mesh Division and Mesh Independence Verification
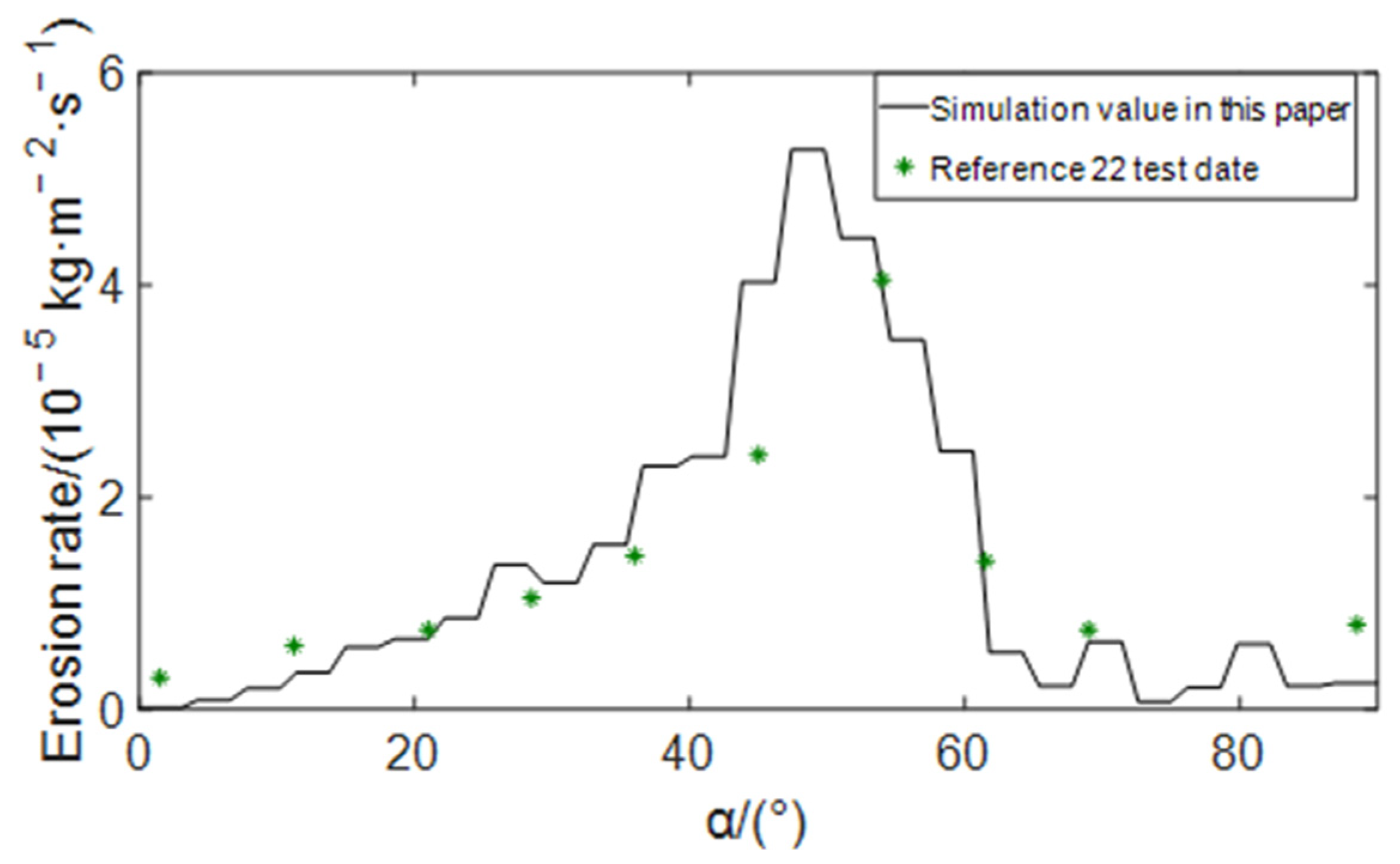
2.4. Validation of Numerical Methods
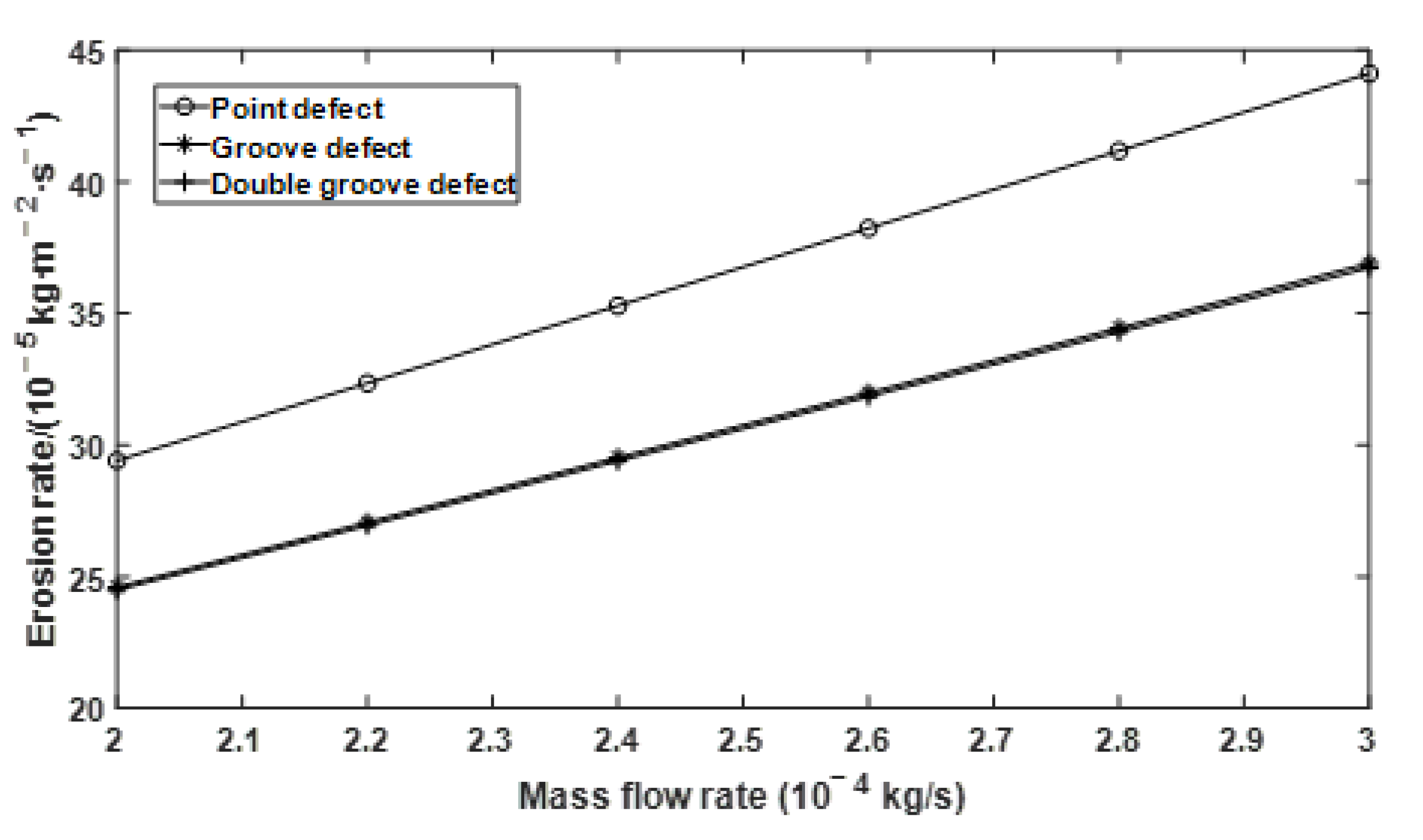
3. Erosion Rate Analysis of Defective Elbow Pipes
3.1. Model Parameters
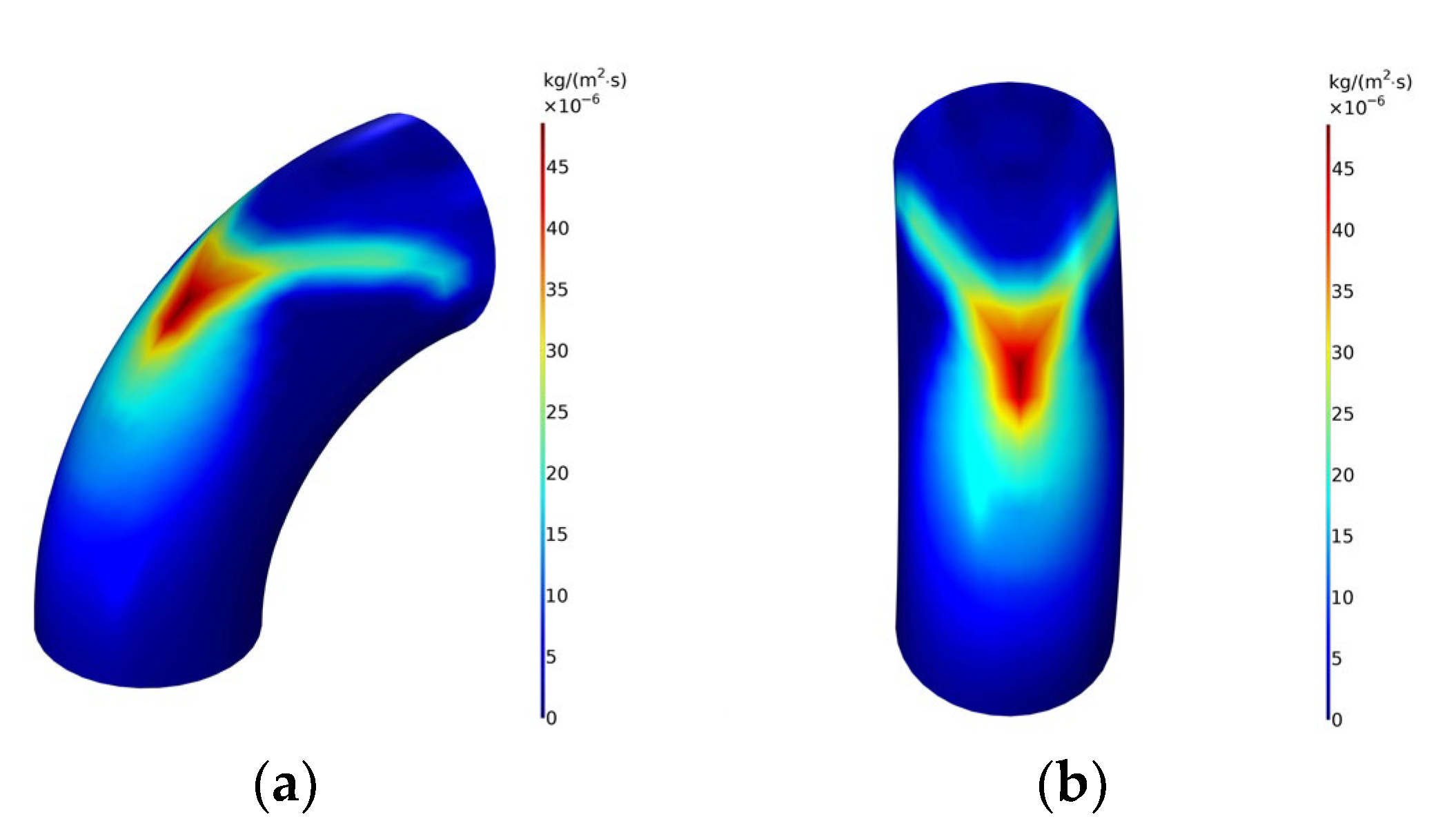
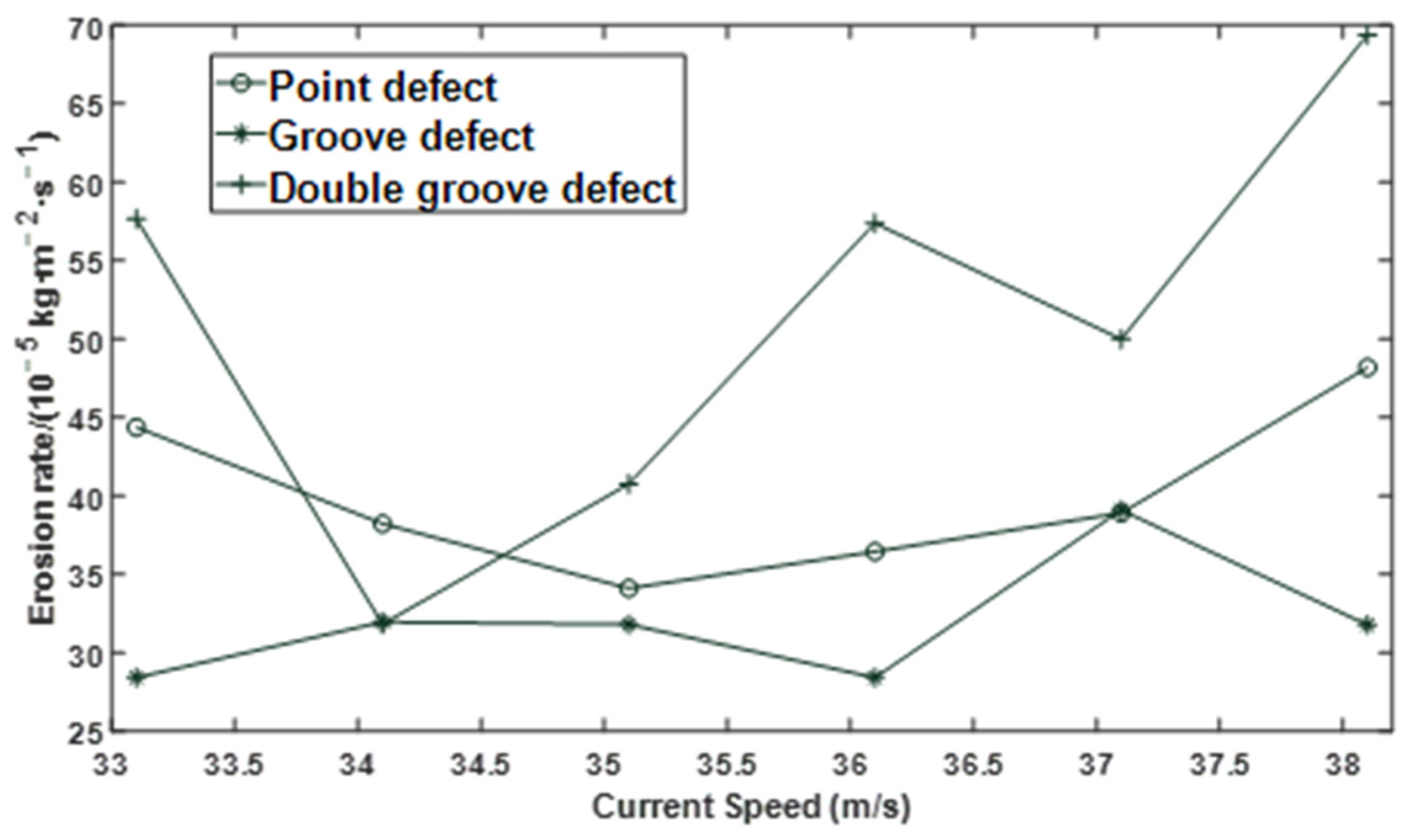
3.2. Analysis of Simulation Results
4. Analysis of Residual Strength of Defective Elbow Pipes
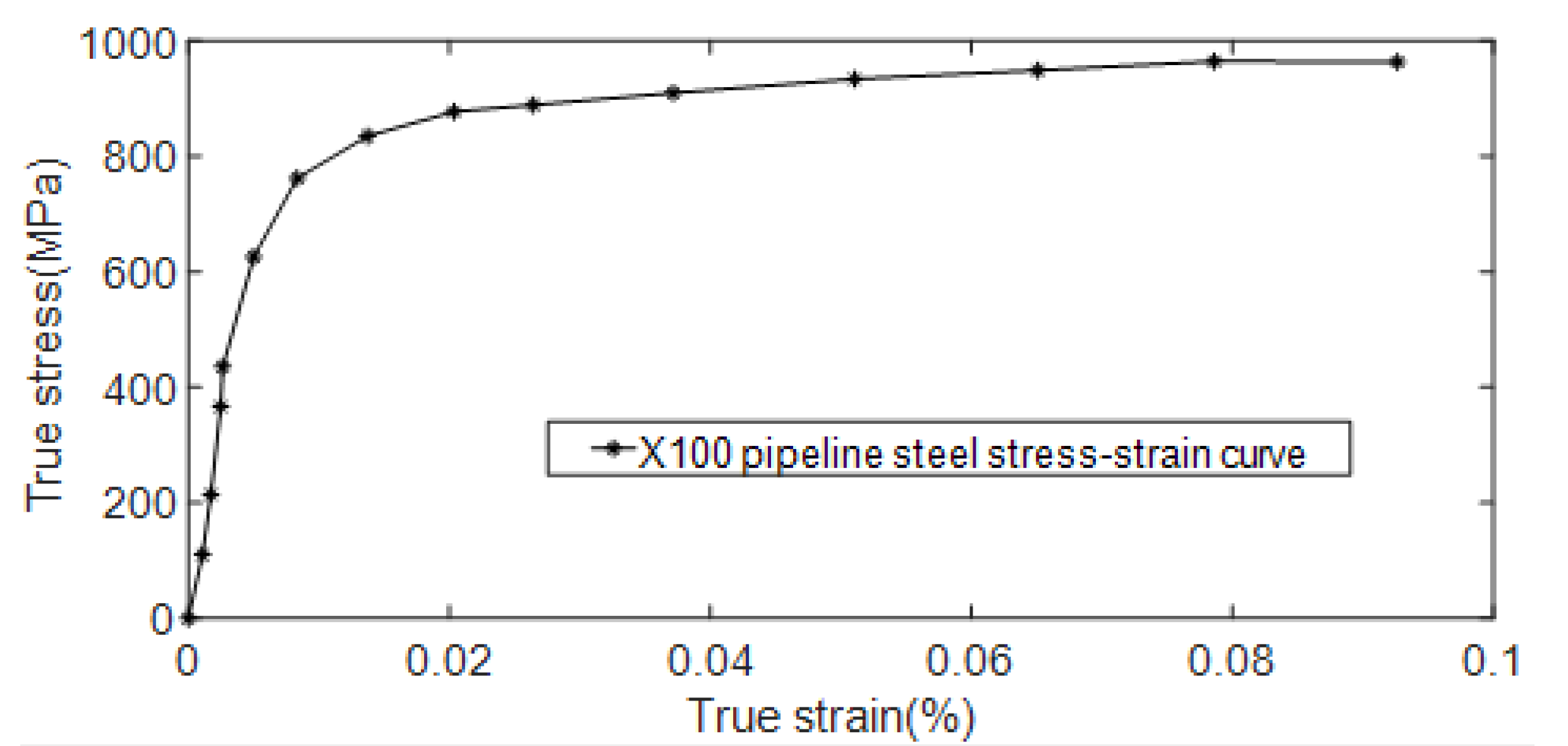
4.1. Model Parameters and Boundary Conditions
- (1)
- The coupling effect of pipe gas and pipe soil (such as the friction between pipe gas and pipe soil, the velocity of the medium in the pipe, etc.) during the operation of the pipelines is not considered; the thermal expansion and cold contraction due to changes in ambient temperature are not considered The thermal stress generated in the pipelines when the phenomenon is limited by the internal and external constraints of the pipelines; the force generated by the anti-erosion protection measures of the pipelines are not considered.
- (2)
- Only the effect of the internal pressure on the pipelines during the operation of the pipelines is considered, and the direction of the force is perpendicular to the inner surface of the pipelines; the forces generated by the pipelines’ own weight, bending moment, and seismic load are not considered.
- (3)
- Displacement constraints are imposed on the left and right ends of the model; that is, the ends are completely fixed. The elbow model is shown in Figure 10.
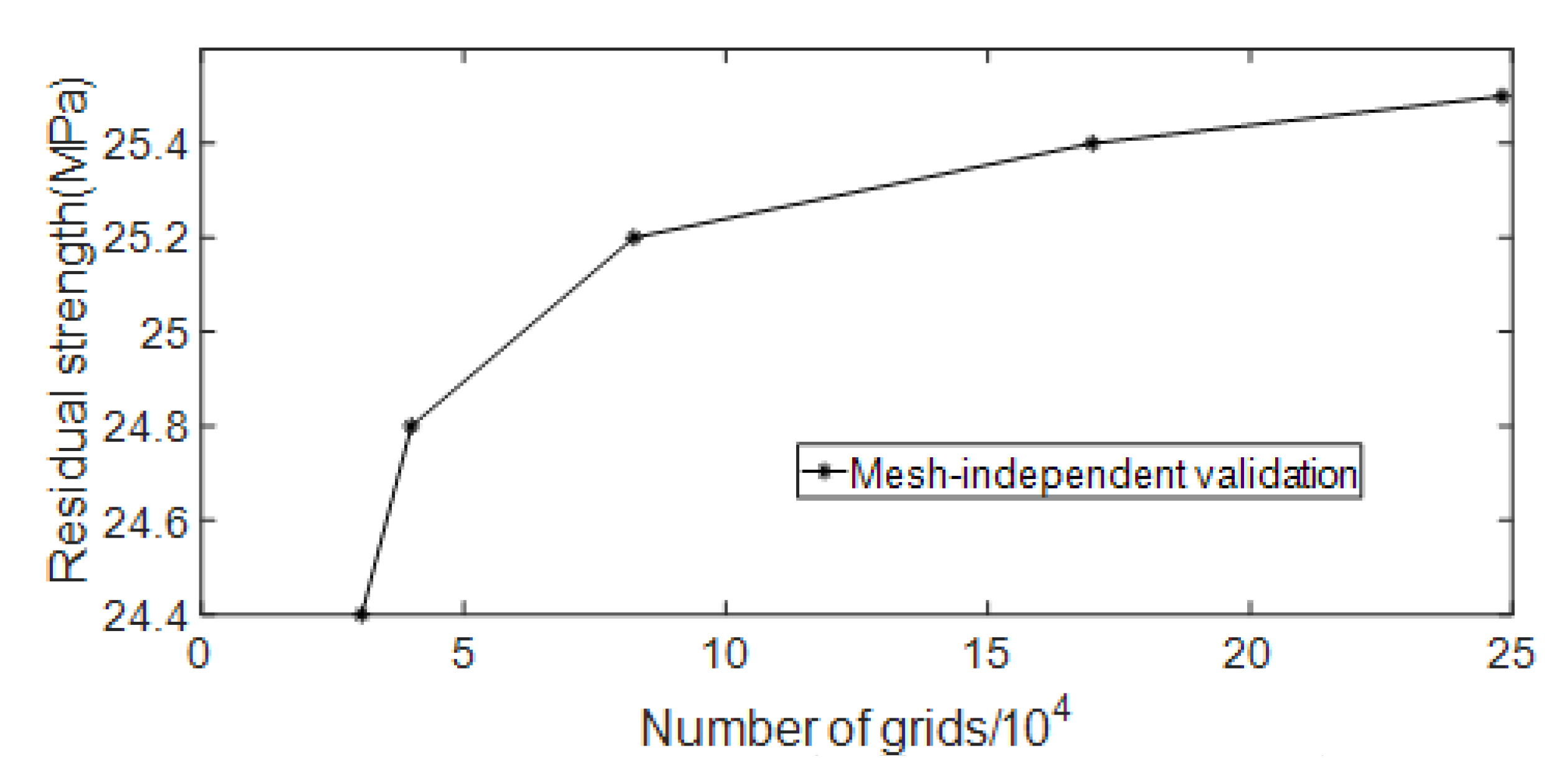
4.2. Meshing and Mesh Independence Verification
4.3. Numerical Method Validation
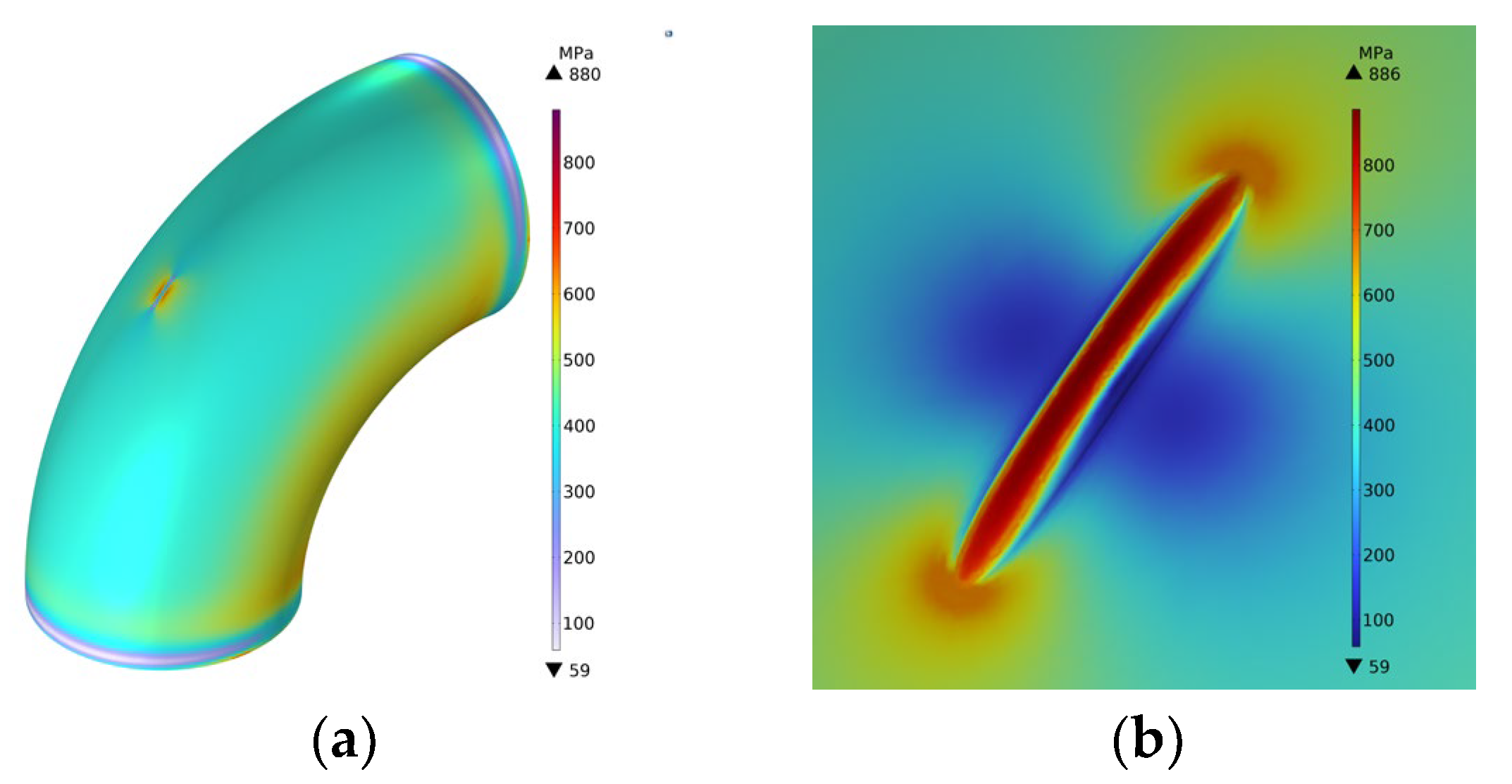
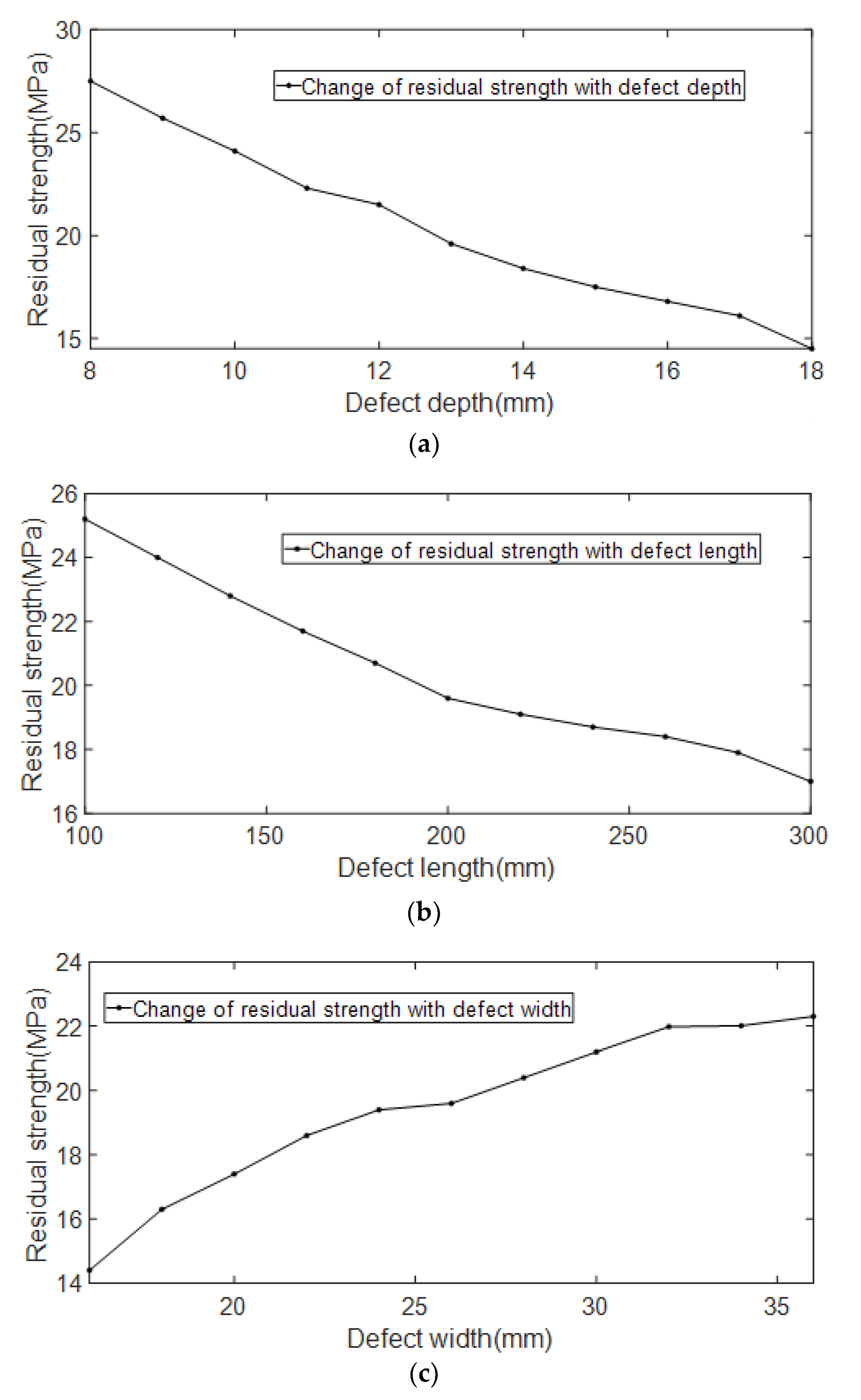
4.4. Analysis of Simulation Results
5. Prediction of Erosion Life and Residual Strength
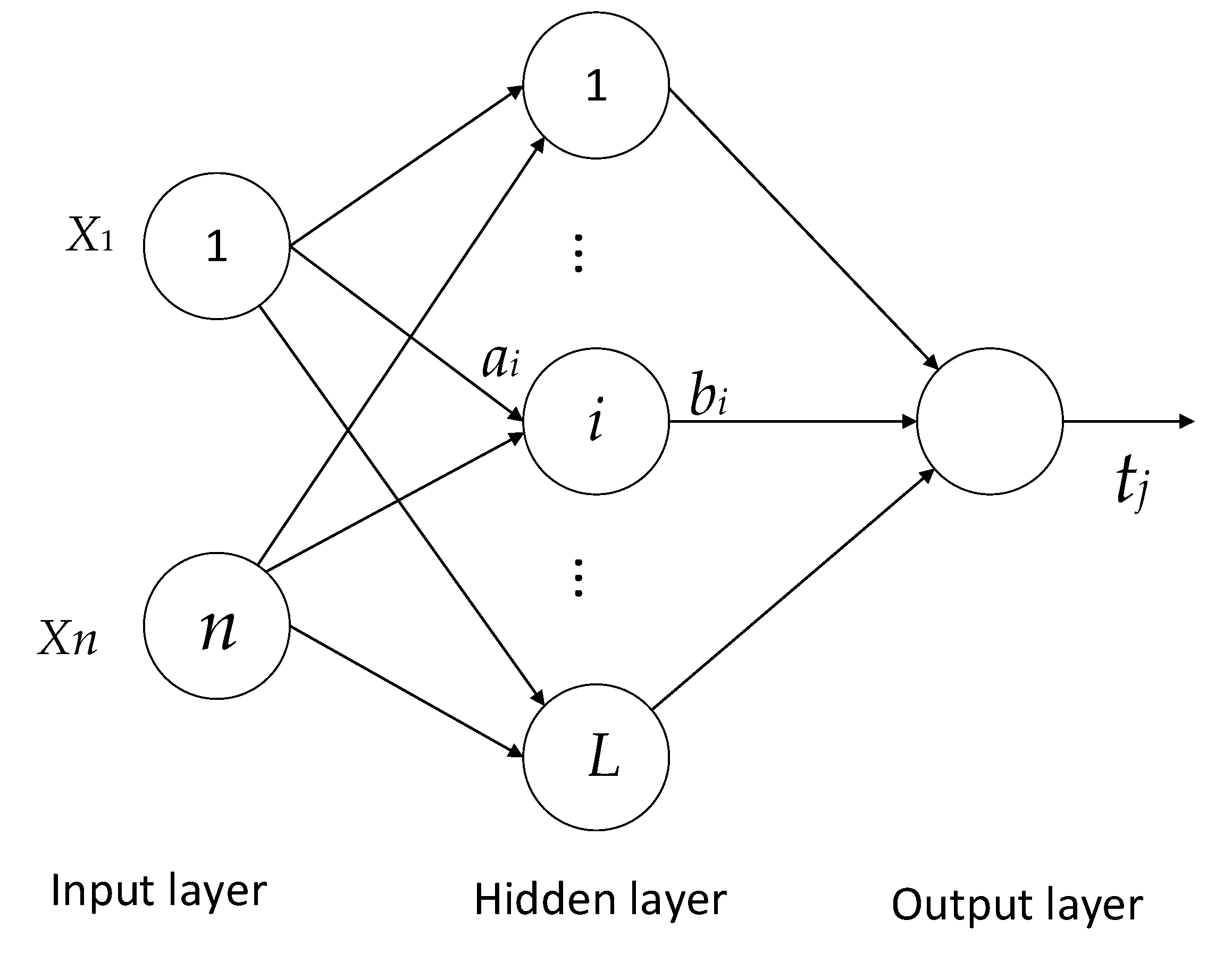
5.1. Extreme Learning Machine
- (1)
- Set the hidden layer activation function and the number of hidden layer nodes L;
- (2)
- Randomly generate hidden layer node parameters , ;
- (3)
- Calculate the hidden layer output matrix H;
- (4)
- Calculate the output weight , where is the generalized inverse of Moore–Penrose of the matrix H.
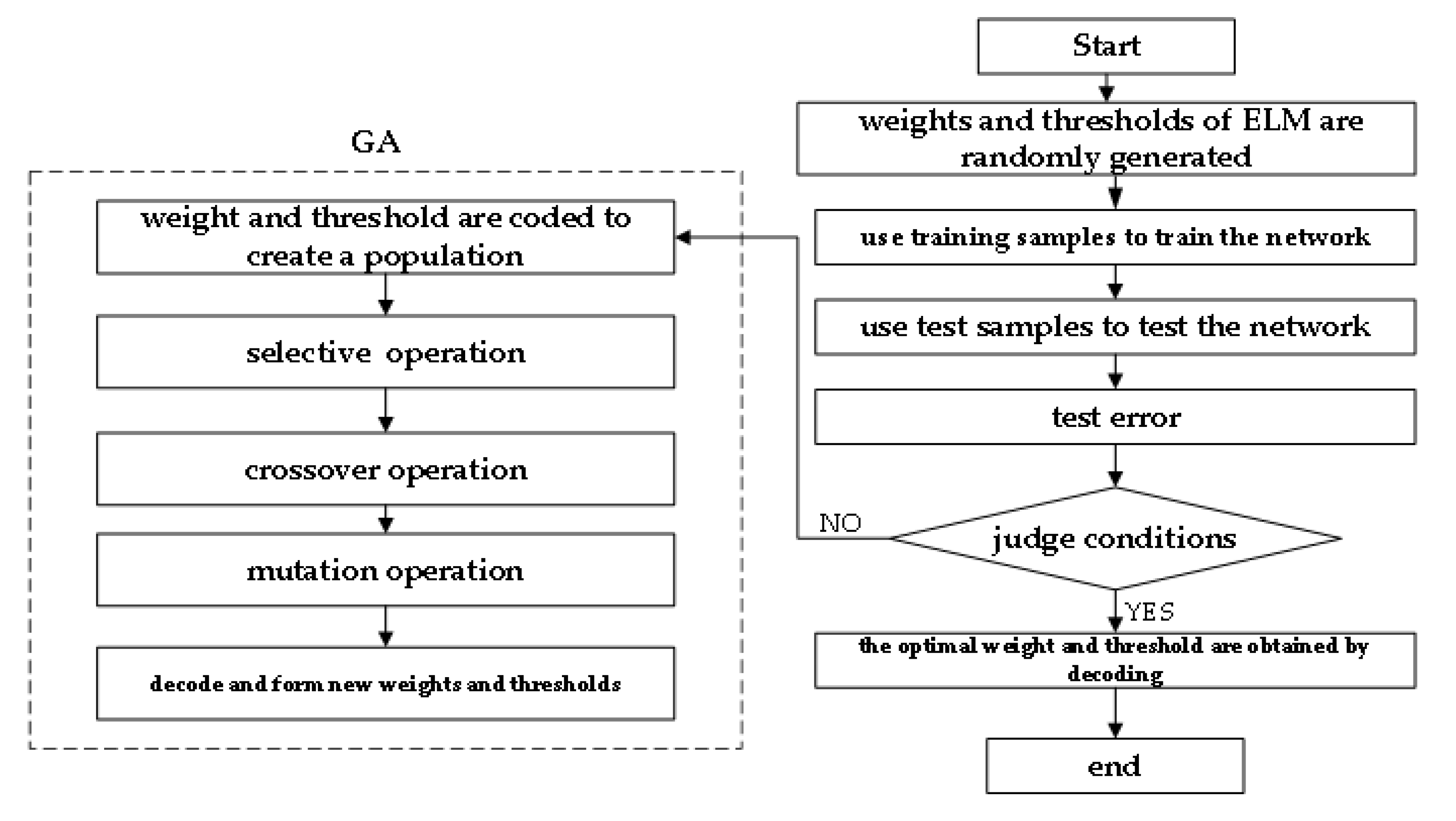
5.2. Genetic Algorithm
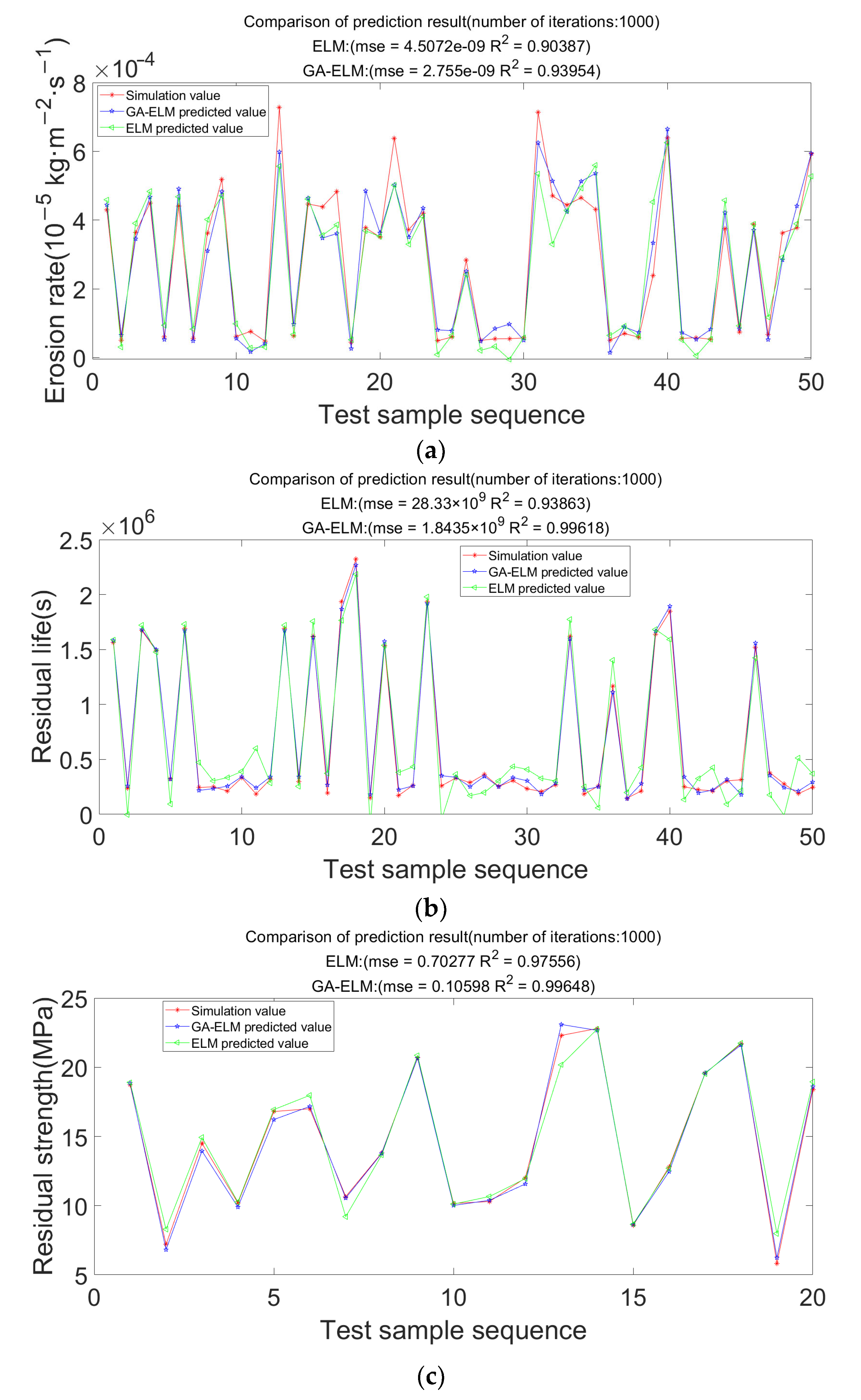
5.3. Prediction Results and Analysis of Test Data
5.4. Prediction Results and Analysis of Simulation Data
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| corrosion rate (kg/m2·s) | |
| function of impact angle | |
| reference wear rate (kg/m2·s) | |
| Vickers hardness of the eroded material | |
| relative velocity between particle and wall (m/s) | |
| particle size of erosion particles (μm) | |
| particle reference velocity constant | |
| reference particle size | |
| Von Mises equivalent stress (MPa) | |
| the stress along the X-axis (MPa) | |
| the stress along the Y-axis (MPa) | |
| the stress along the Z-axis (MPa) | |
| defect length (mm) | |
| defect width (mm) | |
| defect depth (mm) | |
| extreme learning machine optimized by genetic algorithm | |
| number of input layers | |
| number of hidden layer neurons | |
| , | hidden layer node parameters |
| outer weight between the i-th hidden layer node and the network output | |
| activation function | |
| hidden layer output matrix | |
| squared loss function | |
| determine population size | |
| cross probability | |
| mutation probability | |
| initial population | |
| current evolutionary algebra | |
| maximum evolutionary algebra | |
| safe allowable wall thickness of the pipe wall (m) | |
| density of X100 steel (kg/m3) | |
| erosion life (s) |
References
- Zhang, H. Research on Corrosion Fatigue Life Prediction Method of Submarine Pipeline; Southwest Petroleum University: Chengdu, China, 2018. (In Chinese) [Google Scholar]
- Zhao, J. Risk assessment of oil and gas submarine pipeline. Oil Gas Storage Transp. 2007, 11, 5–8, 62, 65. (In Chinese) [Google Scholar]
- Lin, N.; Ju, J.; Zhang, H. Effect of flow field on particle erosion in eroded square elbows. J. IOP Conf. Ser. Earth Environ. Sci. 2022, 984, 012008. [Google Scholar] [CrossRef]
- Li, B.; Zeng, M.; Wang, Q. Numerical Simulation of Erosion Wear for Continuous Elbows in Different Directions. Energies 2022, 15, 1901. [Google Scholar] [CrossRef]
- Bilal, F.S.; Sedrez, T.A.; Shirazi, S.A. Experimental and CFD investigations of 45 and 90 degrees bends and various elbow curvature radii effects on solid particle erosion. J. Wear 2021, 476, 203646. [Google Scholar] [CrossRef]
- Hong, B.; Li, Y.; Li, X.; Ji, S.; Yu, Y.; Fan, D.; Qian, Y.; Guo, J.; Gong, J. Numerical Simulation of Gas-Solid Two-Phase Erosion for Elbow and Tee Pipe in Gas Field. Energies 2021, 14, 6609. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, L.; Fan, J.; Sun, B. Experimental study on erosion behavior of fracturing pipeline involving tensile stress and erosion prediction using random forest regression. J. Nat. Gas Sci. Eng. 2021, 87, 103760. [Google Scholar] [CrossRef]
- Wang, W.; Sun, Y.; Wang, B.; Mei, D. CFD-Based Erosion and Corrosion Modeling of a Pipeline with CO2-Containing Gas–Water Two-Phase Flow. Energies 2022, 15, 1694. [Google Scholar] [CrossRef]
- Parancheerivilakkathil, M.S.; Parapurath, S.; Ainane, S.; Yap, Y.F.; Rostron, P. Flow Velocity and Sand Loading Effect on Erosion–Corrosion during Liquid-Solid Impingement on Mild Steel. Appl. Sci. 2022, 12, 2530. [Google Scholar] [CrossRef]
- Varaksin, A.Y. Collision of Particles and Droplets in Turbulent Two-Phase Flows. High Temp. 2019, 4, 555–572. [Google Scholar] [CrossRef]
- Hong, B.; Li, Y.; Li, X.; Li, G.; Huang, A.; Ji, S.; Li, W.; Gong, J.; Guo, J. Experimental investigation of erosion rate for gas-solid two-phase flow in 304 stainless/L245 carbon steel. J. Pet. Sci. 2022, 19, 1347–1360. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, X. Solid particle erosion rate predictions through LSBoost. J. Powder Technol. 2021, 388, 517–525. [Google Scholar] [CrossRef]
- Ou, G.; Xu, G.; Zhu, Z.; Yang, J.; Wang, Y. Fluid structure coupling mechanism and numerical simulation of elbow erosion failure. J. Mech. Eng. 2009, 11, 7. (In Chinese) [Google Scholar]
- Yang, Y. Study on Residual Strength and Failure Probability of High Steel Grade X100 with Corrosion Defects; Yangtze University: Jinzhou, China, 2021. (In Chinese) [Google Scholar]
- Zaidi, R.; Sedmak, A.; Kirin, S. Risk assessment of oil drilling rig welded pipe based on structural integrity and life estimation. J. Eng. Fail. Anal. 2020, 112, 104508. [Google Scholar] [CrossRef]
- Muhammad, H.A.; Rosemary, N.; Alasdair, C. Neural network modelling of high pressure CO2 corrosion in pipeline steels. J. Process Saf. Environ. Prot. 2018, 119, 36–45. [Google Scholar]
- Khalaj, G.; Azimzadegan, T.; Khoeini, M.; Etaat, M. Artificial neural networks application to predict the ultimate tensile strength of X70 pipeline steels. J. Neural Comput. Appl. 2013, 23, 2301–2308. [Google Scholar] [CrossRef]
- Gholamreza, K.; Hesam, P.; Kaveh, R.M.; Mohammad-Javad, K. Modeling the Correlation between Heat Treatment, Chemical Composition and Bainite Fraction of Pipeline Steels by Means of Artificial Neural Networks. J. Neural Netw. World 2013, 23, 351. [Google Scholar]
- Oka, Y.I.; Okamura, K.; Yoshida, T. Practical estimation of erosion damage caused by solid particle impact Part 1: Effects of impact parameters on a predictive equation. J. Wear 2005, 259, 95–101. [Google Scholar] [CrossRef]
- Oka, Y.I.; Yoshida, T. Practical estimation of erosion damage caused by solid particle impact Part 2: Mechanical properties of materials directly associated with erosion damage. J. Wear 2005, 259, 102–109. [Google Scholar] [CrossRef]
- Zhuo, K.; Qiu, Y.; Zhang, Y.; Wu, D. Influence of particle parameters on erosion wear of gas-solid two-phase flow. J. Xi’an Univ. Pet. 2020, 35, 100–106. (In Chinese) [Google Scholar]
- Mazumder, Q.H.; Shirazi, S.A.; Mclaury, B. Experimental investigation of the location of maximum erosive wear damage in elbows. J. Press. Vessel Technol. 2008, 130, 011303. [Google Scholar] [CrossRef]
- Li, Y.; Wang, W.; Chen, Z.; Chu, W.; Wang, H.; Yang, H.; Wang, C.; Li, Y. Burst Pressure Prediction of Subsea Supercritical CO2 Pipelines. Materials 2022, 15, 3465. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Liu, X.; Yang, H.; Fang, W.; Chen, P.; Li, R.; Gao, H.; Zhang, H. A Semi Empirical Regression Model for Critical Dent Depth of Externally Corroded X65 Gas Pipeline. Materials 2022, 15, 5492. [Google Scholar] [CrossRef] [PubMed]
- Su, W.; Liu, Z. Numerical Simulation of Damage Evolution and Electrode Deformation of X100 Pipeline Steel during Crevice Corrosion. Materials 2022, 15, 2329. [Google Scholar] [CrossRef] [PubMed]
- Zang, X.; Gu, X.; Wang, Q. Study on residual strength of X100 gas pipeline with corrosion defects. Mater. Prot. 2019, 52, 125–131. (In Chinese) [Google Scholar]
- Zhao, L. Quantitative evaluation of parameters affecting residual strength of long-distance pipelines with corrosion defects. Contemp. Chem. Ind. 2016, 45, 639–641. (In Chinese) [Google Scholar]
- Ma, T.; Pan, Y.; Huang, W.; Wang, L. Residual strength evaluation of oil and gas pipelines with constant wall thickness volume defects. Mater. Prot. 2020, 53, 34–41. (In Chinese) [Google Scholar]
- Gao, J.; Yang, P.; Li, X.; Zhou, J.; Liu, J. Analytical prediction of failure pressure for pipeline with long corrosion defect. Ocean. Eng. 2019, 191, 106497. [Google Scholar] [CrossRef]
- Pan, L. Failure Analysis and Life Prediction of T-Type Tee for Fracturing Manifold; Yangtze University: Jinzhou, China, 2019. (In Chinese) [Google Scholar]







| Minimum Yield Strength (MPa) | Minimum Tensile Strength (MPa) | Ultimate Tensile Strength (MPa) | Young’s Modulus (MPa) | Poisson’s Ratio |
|---|---|---|---|---|
| 690 | 760 | 886 | 210,000 | 0.3 |
| C | Si | Mn | P | S | Cr | Ni | Mo | Fe |
|---|---|---|---|---|---|---|---|---|
| 0.065 | 0.95 | 1.69 | 0.015 | 0.002 | 0.04 | 0.03 | 0.27 | allowance |
| Number | Pipe Diameter (mm) | Wall Thickness (mm) | Defect Length (mm) | Defect Depth (mm) | Residual Strength (MPa) (Literature Test Value) | Residual Strength (MPa) (Simulation Results) | Error (%) |
|---|---|---|---|---|---|---|---|
| 1 | 1320 | 22.9 | 200 | 4.58 | 27.79 | 27.87 | 0.3 |
| 2 | 1320 | 22.9 | 1000 | 11.45 | 16.59 | 16.64 | 0.3 |
| 3 | 1320 | 22.9 | 514.98 | 11.45 | 17.9 | 17.72 | 1.0 |
| 4 | 1320 | 22.9 | 1109.93 | 11.45 | 15.4 | 16.01 | 4.0 |
| 5 | 1320 | 22.9 | 556.88 | 11.36 | 18.1 | 17.3 | 4.4 |
| 6 | 1320 | 22.9 | 1012.74 | 11.45 | 15 | 15.97 | 6.4 |
| 7 | 1320 | 22.9 | 800 | 41.2 | 18.76 | 16.97 | 9.5 |
| Pipe Diameter (mm) | Wall Thickness (mm) | Defect Length (mm) | Defect Depth (mm) | Defect Width (mm) | Yield Strength (MPa) | Tensile Strength (MPa) | Residual Strength (MPa) |
|---|---|---|---|---|---|---|---|
| 458.8 | 8.1 | 39.6 | 5.39 | 31.9 | 601 | 684 | 22.68 |
| 459.4 | 8 | 40.05 | 3.75 | 32 | 589 | 730.5 | 24.2 |
| 323.9 | 9.8 | 255.6 | 7.08 | 95.3 | 452 | 542 | 14.4 |
| 323.9 | 9.66 | 305.6 | 6.76 | 95.3 | 452 | 542 | 14.07 |
| 508 | 14.6 | 500 | 10.35 | 97 | 478 | 600 | 14.6 |
| 508 | 14.3 | 500 | 10.3 | 97 | 478 | 600 | 13.4 |
| 76.2 | 2 | 75 | 1.4 | 16 | 391 | 458 | 9.4 |
| 76.2 | 2.04 | 75 | 1.44 | 16 | 260 | 309 | 5.45 |
| 762 | 17.5 | 200 | 9 | 200 | 474.1 | 556.6 | 22.64 |
| 426 | 6.95 | 160 | 2.7 | 25 | 240 | 390 | 10.8 |
| … | … | … | … | … | … | … | … |
| 426 | 7 | 150 | 3.8 | 21 | 240 | 390 | 9.81 |
| 529 | 9 | 350 | 4.7 | 25 | 285 | 415 | 8.83 |
| 529 | 9 | 160 | 4.7 | 25 | 285 | 415 | 15.7 |
| 720 | 8 | 320 | 4.4 | 26 | 425 | 535 | 8.83 |
| 720 | 8 | 180 | 6.2 | 26 | 425 | 535 | 7.55 |
| 304.8 | 6.35 | 26 | 4.95 | 20 | 351 | 543 | 15.36 |
| 304.8 | 6.35 | 33 | 4.25 | 21 | 382 | 570 | 16.29 |
| 323.9 | 9.74 | 527.8 | 7.06 | 95.3 | 422.5 | 589.6 | 11.3 |
| 1422.4 | 19.25 | 180 | 10.4 | 0.5 | 740 | 774 | 15.35 |
| 914.4 | 16.4 | 450 | 6 | 0.5 | 739 | 813 | 24.02 |
| … | … | … | … | … | … | … | … |
| 304.8 | 6.35 | 37 | 4.64 | 30 | 351 | 463 | 14.29 |
| 324 | 6.01 | 19.35 | 3.6 | 19 | 382 | 570 | 16.22 |
| 324 | 10.3 | 243 | 5.15 | 154.5 | 380 | 514 | 23.2 |
| 324 | 10.3 | 243 | 5.15 | 30.9 | 380 | 514 | 22 |
| 508 | 6.6 | 381 | 2.62 | 35.4 | 443.4 | 598.9 | 11.25 |
| 508 | 6.35 | 900 | 3.43 | 25.4 | 429.6 | 572.5 | 8 |
| 323.9 | 9.79 | 500 | 6.99 | 95.3 | 452 | 542 | 11.99 |
| 323.9 | 9.74 | 527.8 | 7.14 | 95.3 | 452 | 542 | 11.3 |
| 762 | 17.5 | 200 | 8.4 | 100 | 474.1 | 556.6 | 23.42 |
| 762 | 17.5 | 200 | 9 | 200 | 474.1 | 556.6 | 22.64 |
| Number | Test Values in Literature (MPa) | Predicted Value of GA-ELM (MPa) | Error (%) |
|---|---|---|---|
| 1 | 15.36 | 15.7528 | 2.56 |
| 2 | 24.3 | 23.7243 | 2.37 |
| 3 | 11.91 | 12.5701 | 5.55 |
| 4 | 11.99 | 12.4956 | 4.22 |
| 5 | 22.64 | 23.2093 | 2.51 |
| 6 | 24.3 | 23.7668 | 2.19 |
| 7 | 11.3 | 12.0015 | 6.21 |
| 8 | 8 | 8.7686 | 9.61 |
| 9 | 11.25 | 11.4471 | 1.75 |
| 10 | 5.45 | 6.2013 | 13.78 |
| 11 | 14.4 | 15.0982 | 4.85 |
| Defect | Velocity of Flow (m/s) | Mass Flow Rate (10−4 kg/s) | Grain Size (µm) | Maximum Erosion Rate (10−5 kg∙m−2∙s−1) | Residual Life Span (105 s) |
|---|---|---|---|---|---|
| 0 | 34.1 | 2.60 | 152 | 5.10 | 18.5 |
| 0 | 34.1 | 2.80 | 152 | 5.49 | 17.1 |
| 0 | 33.1 | 2.60 | 152 | 4.74 | 19.9 |
| 0 | 33.1 | 2.60 | 152 | 5.10 | 18.5 |
| 0 | 35.1 | 2.60 | 152 | 5.44 | 17.3 |
| … | … | … | … | … | … |
| 0 | 37.1 | 2.20 | 202 | 5.56 | 17.0 |
| 0 | 37.1 | 2.40 | 202 | 6.06 | 15.5 |
| 0 | 38.1 | 2.60 | 202 | 6.99 | 13.5 |
| 0 | 38.1 | 2.80 | 202 | 7.53 | 12.5 |
| 0 | 38.1 | 3.00 | 202 | 8.06 | 11.7 |
| 1 | 33.1 | 2.60 | 142 | 83.0 | 1.13 |
| 1 | 34.1 | 2.60 | 142 | 35.8 | 2.63 |
| 1 | 35.1 | 2.60 | 142 | 28.7 | 3.28 |
| 1 | 36.1 | 2.60 | 142 | 54.8 | 1.72 |
| 1 | 33.1 | 2.80 | 142 | 27.6 | 3.41 |
| … | … | … | … | … | … |
| 1 | 37.1 | 2.00 | 202 | 35.4 | 2.66 |
| 1 | 37.1 | 2.20 | 202 | 39.0 | 2.42 |
| 1 | 37.1 | 2.40 | 202 | 42.5 | 2.22 |
| 1 | 38.1 | 2.80 | 202 | 52.6 | 1.79 |
| 1 | 38.1 | 3.00 | 202 | 56.4 | 1.67 |
| 2 | 35.1 | 2.60 | 142 | 47.3 | 1.99 |
| 2 | 36.1 | 2.60 | 142 | 72.8 | 1.29 |
| 2 | 33.1 | 2.60 | 142 | 59.3 | 1.59 |
| 2 | 34.1 | 2.60 | 142 | 66.2 | 1.42 |
| 2 | 34.1 | 2.80 | 142 | 71.3 | 1.32 |
| … | … | … | … | … | … |
| 2 | 37.1 | 3.20 | 202 | 45.9 | 2.05 |
| 2 | 37.1 | 3.00 | 202 | 43.0 | 2.19 |
| 2 | 38.1 | 2.80 | 202 | 44.4 | 2.12 |
| 2 | 38.1 | 2.40 | 202 | 38.1 | 2.48 |
| 2 | 38.1 | 2.20 | 202 | 34.9 | 2.70 |
| Pipe Diameter (mm) | Wall Thickness (mm) | Defect Length (mm) | Defect Depth (mm) | Defect Width (mm) | Yield Strength (MPa) | Tensile Strength (MPa) | Residual Strength (MPa) |
|---|---|---|---|---|---|---|---|
| 1320 | 22.9 | 100 | 13 | 26 | 690 | 886 | 25.2 |
| 1320 | 22.9 | 120 | 13 | 26 | 690 | 886 | 24 |
| 1320 | 22.9 | 140 | 13 | 26 | 690 | 886 | 22.8 |
| 1320 | 22.9 | 160 | 13 | 26 | 690 | 886 | 21.7 |
| 1320 | 22.9 | 180 | 13 | 26 | 690 | 886 | 20.7 |
| … | … | … | … | … | … | … | … |
| 1320 | 22.9 | 200 | 14 | 26 | 690 | 886 | 18.4 |
| 1320 | 22.9 | 200 | 15 | 26 | 690 | 886 | 17.5 |
| 1320 | 22.9 | 200 | 16 | 26 | 690 | 886 | 16.8 |
| 1320 | 22.9 | 200 | 17 | 26 | 690 | 886 | 16.1 |
| 1320 | 22.9 | 200 | 18 | 26 | 690 | 886 | 14.5 |
| 1422.4 | 20.1 | 100 | 11 | 22 | 795 | 840 | 15.7 |
| 1422.4 | 20.1 | 120 | 11 | 22 | 795 | 840 | 14.67 |
| 1422.4 | 20.1 | 140 | 11 | 22 | 795 | 840 | 13.8 |
| 1422.4 | 20.1 | 160 | 11 | 22 | 795 | 840 | 12.78 |
| 1422.4 | 20.1 | 180 | 11 | 22 | 795 | 840 | 12.3 |
| … | … | … | … | … | … | … | … |
| 1422.4 | 20.1 | 200 | 12 | 22 | 795 | 840 | 11.2 |
| 1422.4 | 20.1 | 200 | 13 | 22 | 795 | 840 | 10.01 |
| 1422.4 | 20.1 | 200 | 14 | 22 | 795 | 840 | 9.31 |
| 1422.4 | 20.1 | 200 | 15 | 22 | 795 | 840 | 8.57 |
| 1422.4 | 20.1 | 200 | 16 | 22 | 795 | 840 | 8.2 |
| 914.4 | 16.4 | 100 | 10 | 20 | 739 | 813 | 15.4 |
| 914.4 | 16.4 | 120 | 10 | 20 | 739 | 813 | 14.1 |
| 914.4 | 16.4 | 140 | 10 | 20 | 739 | 813 | 13.21 |
| 914.4 | 16.4 | 160 | 10 | 20 | 739 | 813 | 12.5 |
| 914.4 | 16.4 | 180 | 10 | 20 | 739 | 813 | 12.2 |
| … | … | … | … | … | … | … | … |
| 914.4 | 16.4 | 200 | 11 | 20 | 739 | 813 | 10.2 |
| 914.4 | 16.4 | 200 | 12 | 20 | 739 | 813 | 9.4 |
| 914.4 | 16.4 | 200 | 13 | 20 | 739 | 813 | 8.7 |
| 914.4 | 16.4 | 200 | 14 | 20 | 739 | 813 | 7.2 |
| 914.4 | 16.4 | 200 | 15 | 20 | 739 | 813 | 5.83 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, C.; Wang, Q.; Li, Y.; Li, Y.; Liu, Y. Numerical Simulation and Analytical Prediction of Residual Strength for Elbow Pipes with Erosion Defects. Materials 2022, 15, 7479. https://doi.org/10.3390/ma15217479
Sun C, Wang Q, Li Y, Li Y, Liu Y. Numerical Simulation and Analytical Prediction of Residual Strength for Elbow Pipes with Erosion Defects. Materials. 2022; 15(21):7479. https://doi.org/10.3390/ma15217479
Chicago/Turabian StyleSun, Chao, Qi Wang, Yuelin Li, Yingqi Li, and Yuechan Liu. 2022. "Numerical Simulation and Analytical Prediction of Residual Strength for Elbow Pipes with Erosion Defects" Materials 15, no. 21: 7479. https://doi.org/10.3390/ma15217479
APA StyleSun, C., Wang, Q., Li, Y., Li, Y., & Liu, Y. (2022). Numerical Simulation and Analytical Prediction of Residual Strength for Elbow Pipes with Erosion Defects. Materials, 15(21), 7479. https://doi.org/10.3390/ma15217479







