In-Depth Analysis of Cement-Based Material Incorporating Metakaolin Using Individual and Ensemble Machine Learning Approaches
Abstract
1. Introduction
2. Data Description
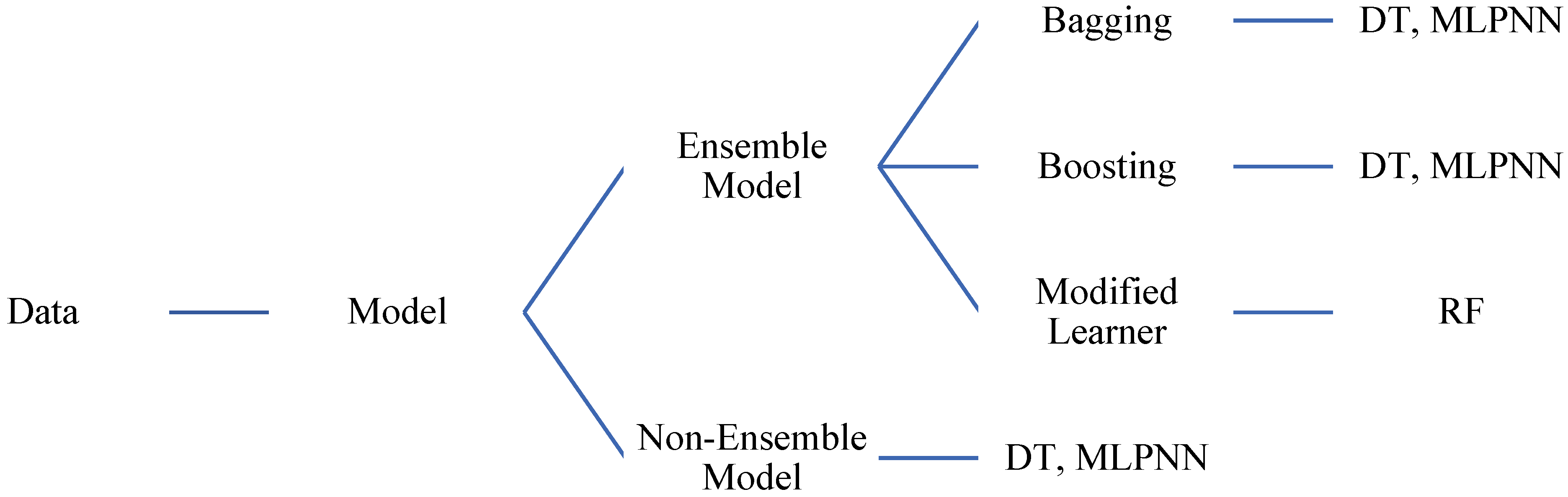
3. Methodology
3.1. Machine Learning Methods
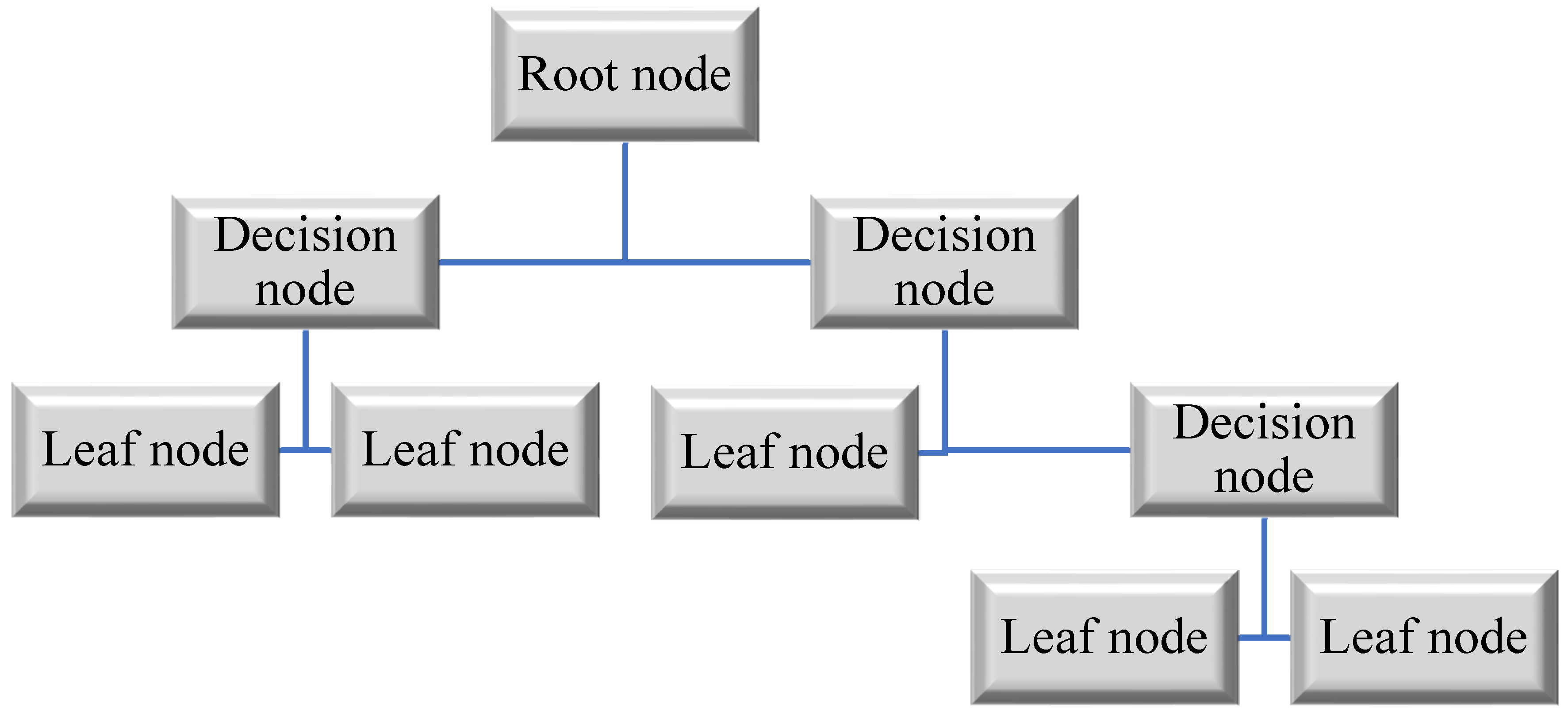
3.1.1. Decision Tree-Based Machine Learning
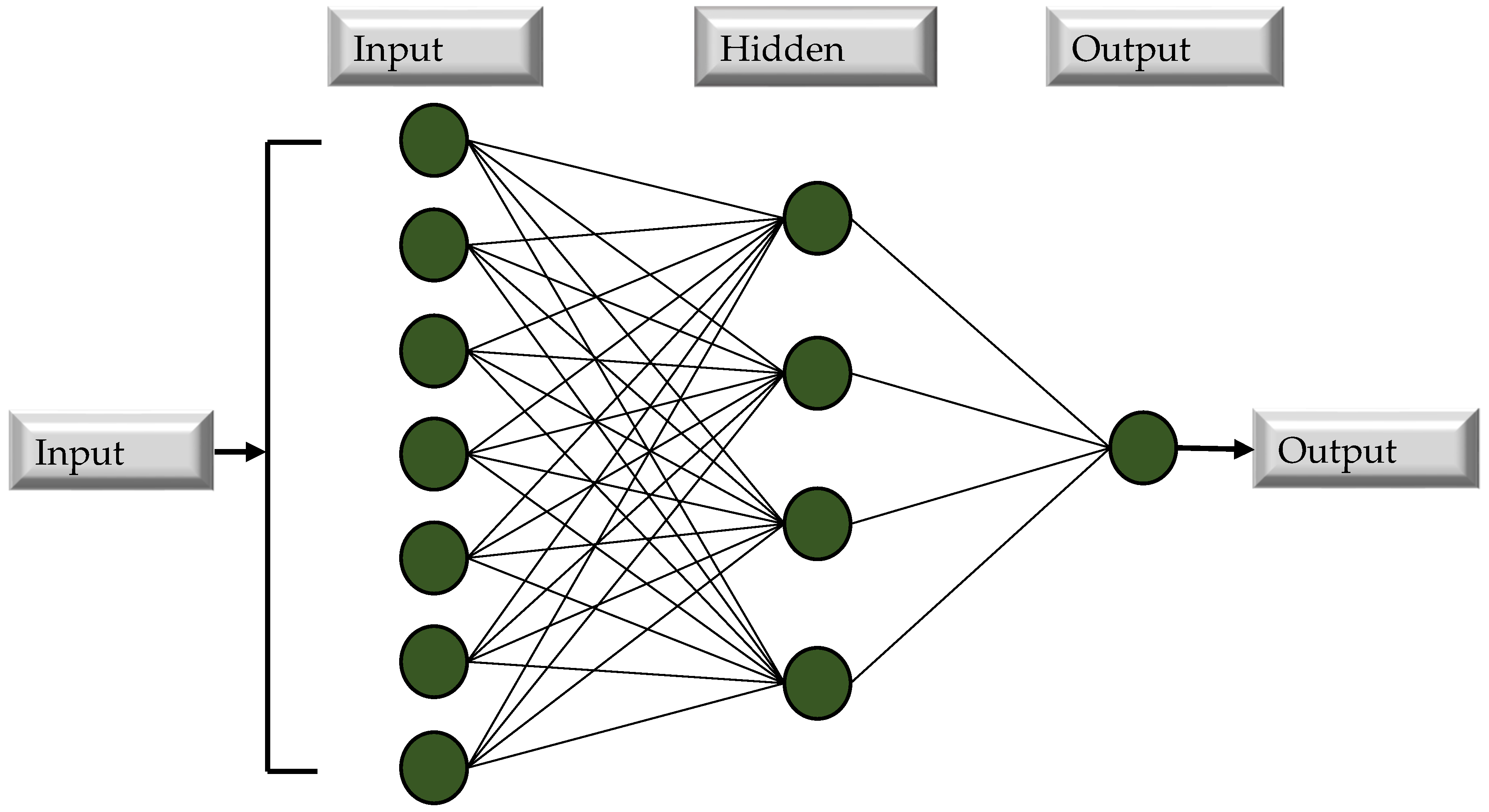
3.1.2. Artificial Neural Network-Based Machine Learning
3.2. Bagging and Boosting for Ensemble Approaches
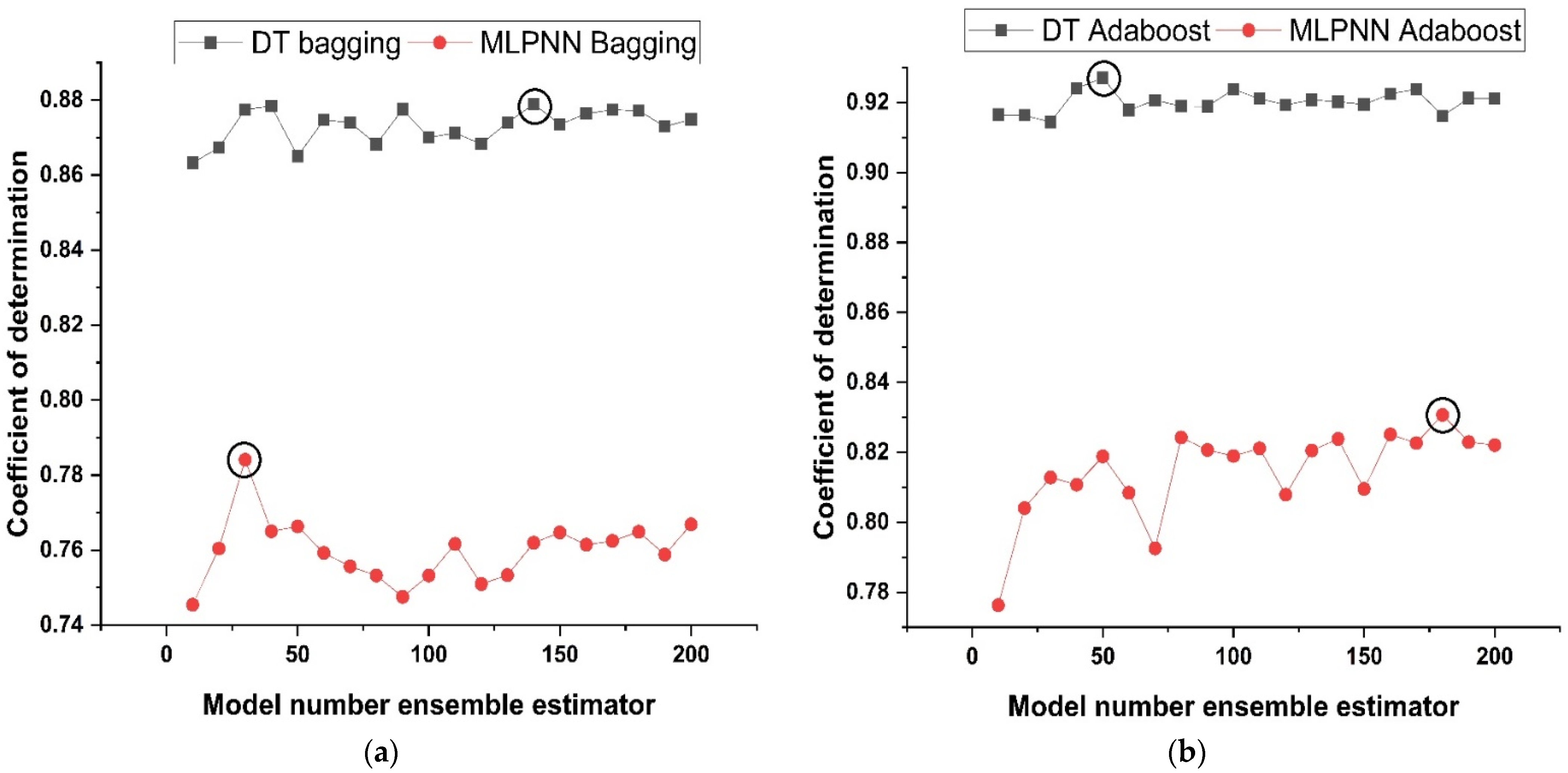
3.3. Ensemble Learner’s Parameter Tuning
3.4. Random Forest Regression Based Machine Learning
- The equivalent of two-thirds of the entire dataset is chosen for each tree at random. Bagging is the term used to describe this practise. Predictor variables are picked, and node splitting is done based on the best possible node split on these variables.
- The remaining data are used to estimate the out-of-bag error for each and every tree. To get the most accurate estimation of the out-of-bag error rate, errors from each tree are then added together.
- Every tree in the RF algorithm provides a regression, but the model prioritizes the forest that receives the most votes over all of the individual trees in the forest. The votes might be either zeros or ones. As a prediction probability, the fraction of 1s achieved is provided.
3.5. 10 K Fold Method for Cross Validation
3.6. Evaluation Criteria for Models
4. Model Result
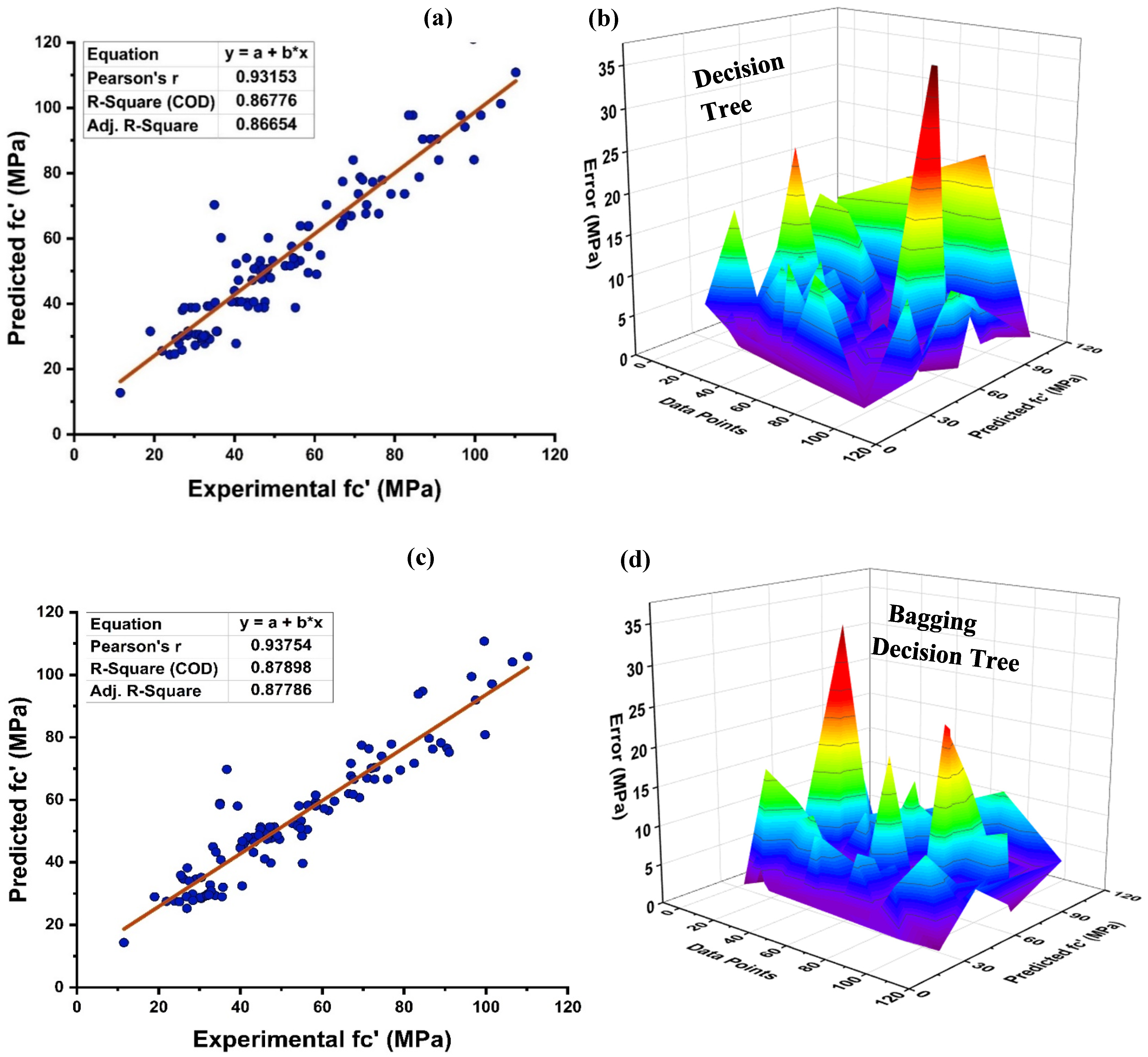
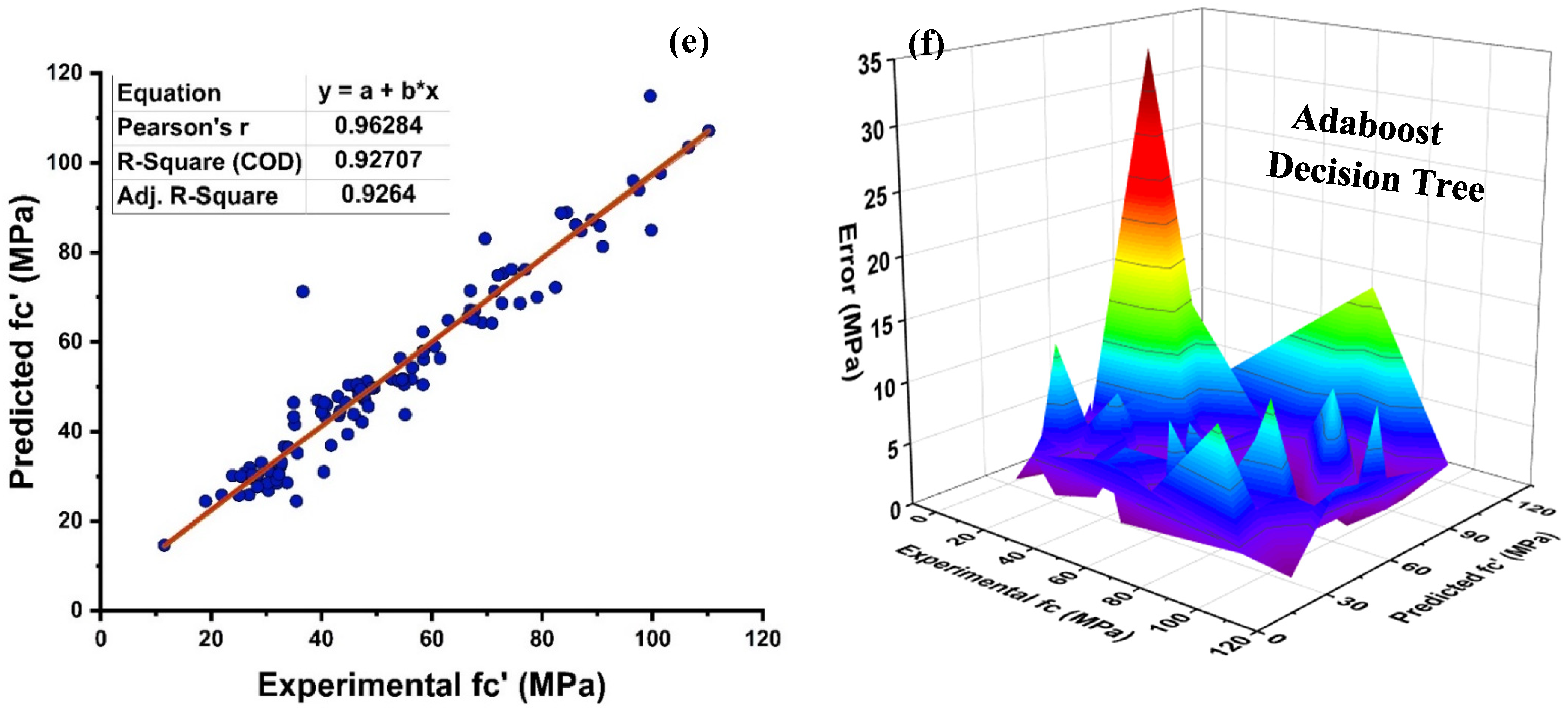
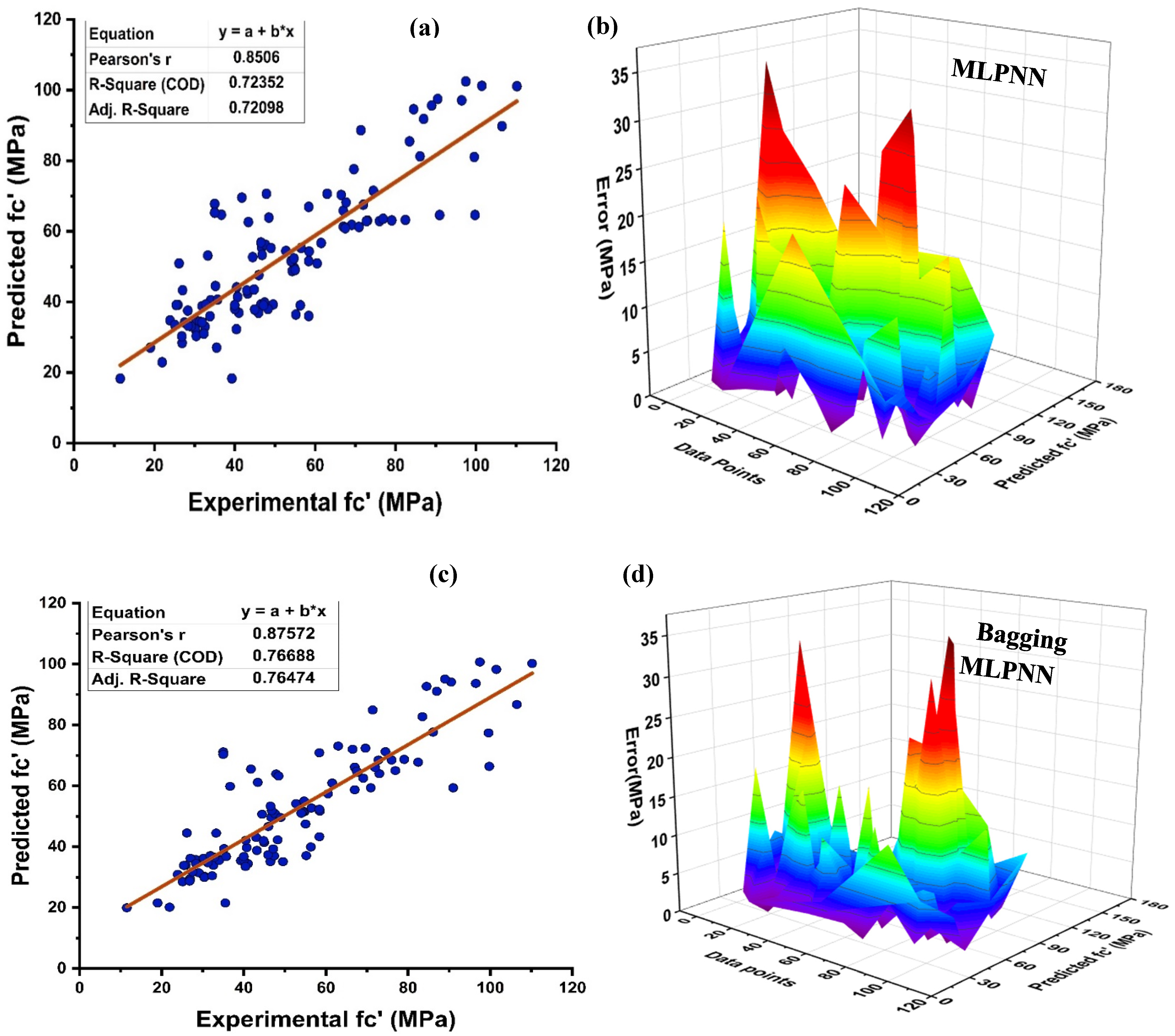
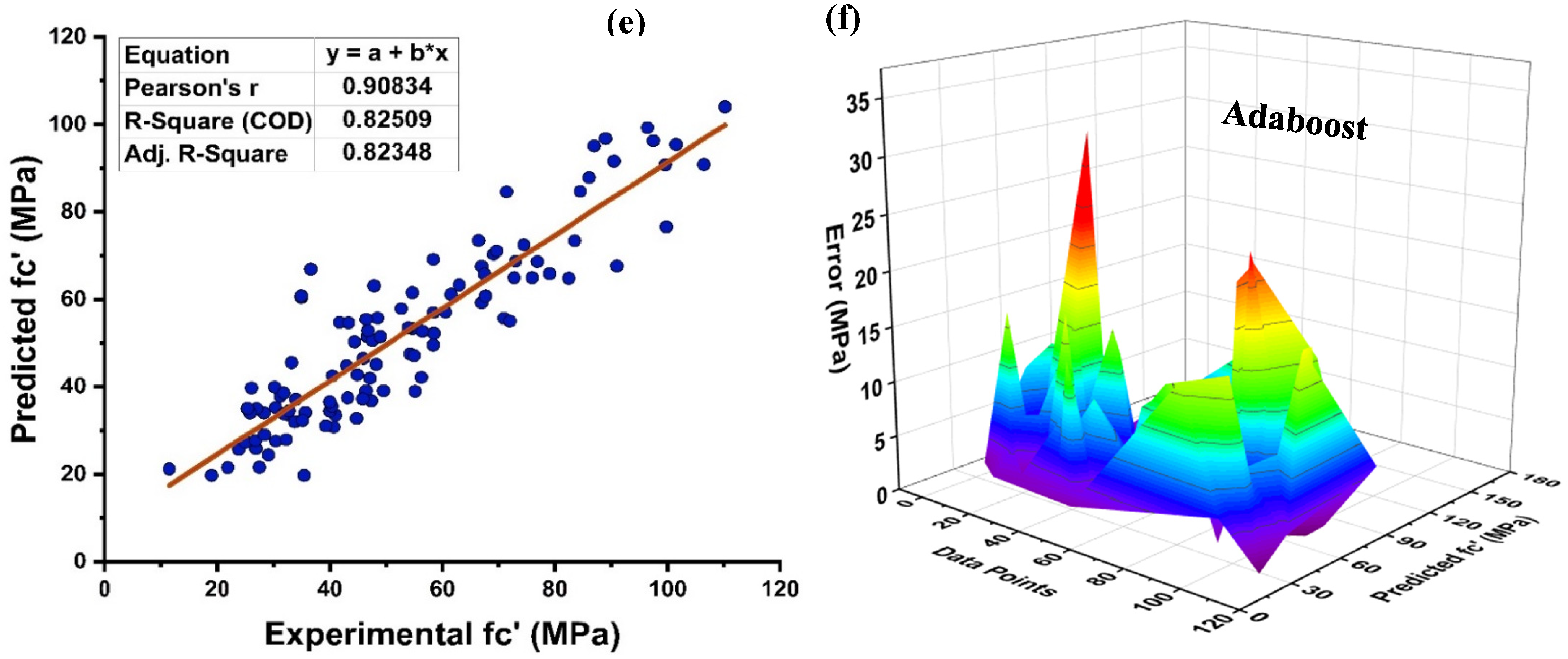
4.1. Decision Tree Model Outcomes
4.2. MLPNN Model Outcomes
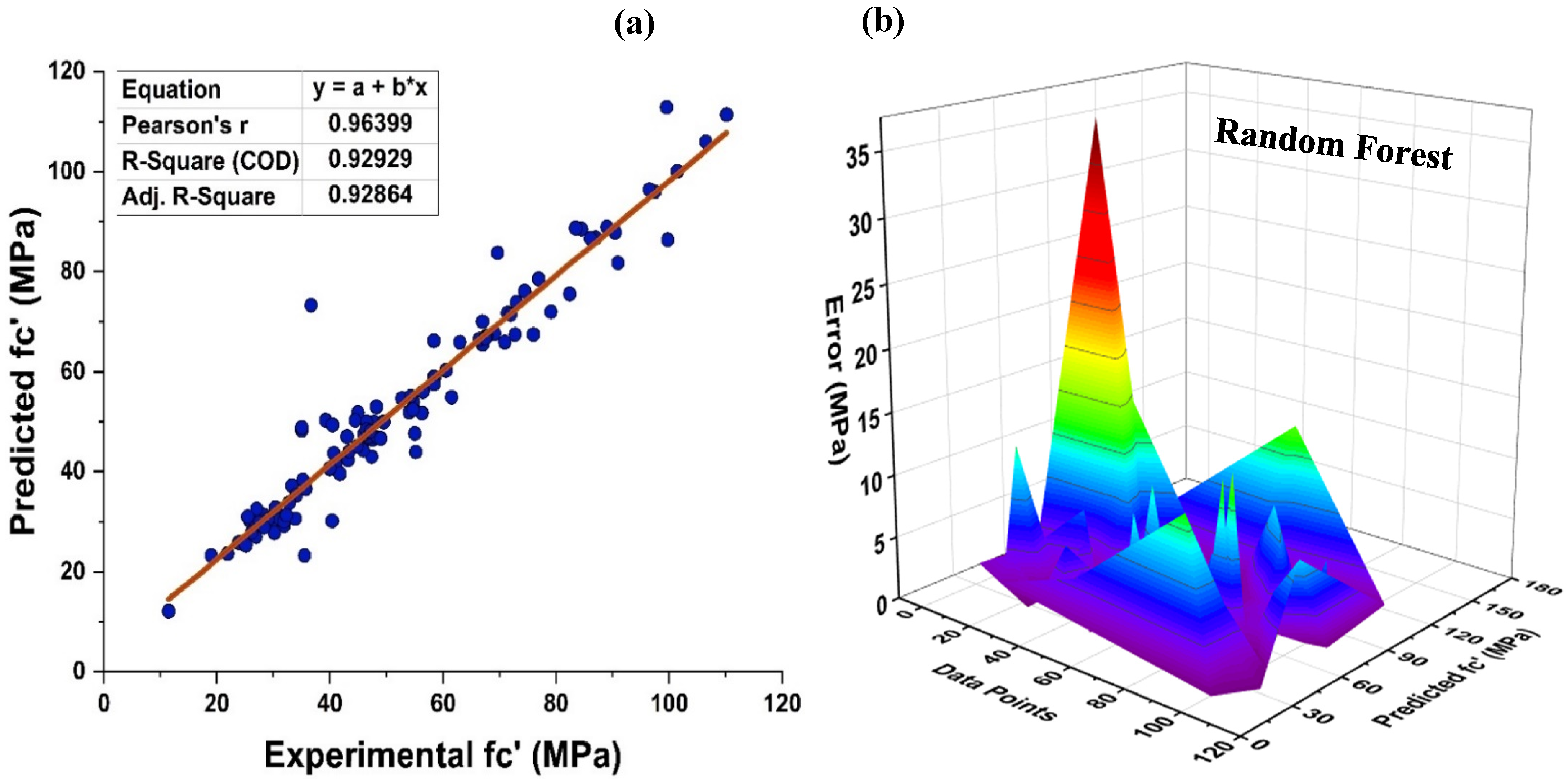
4.3. Random Forest Model Outcomes
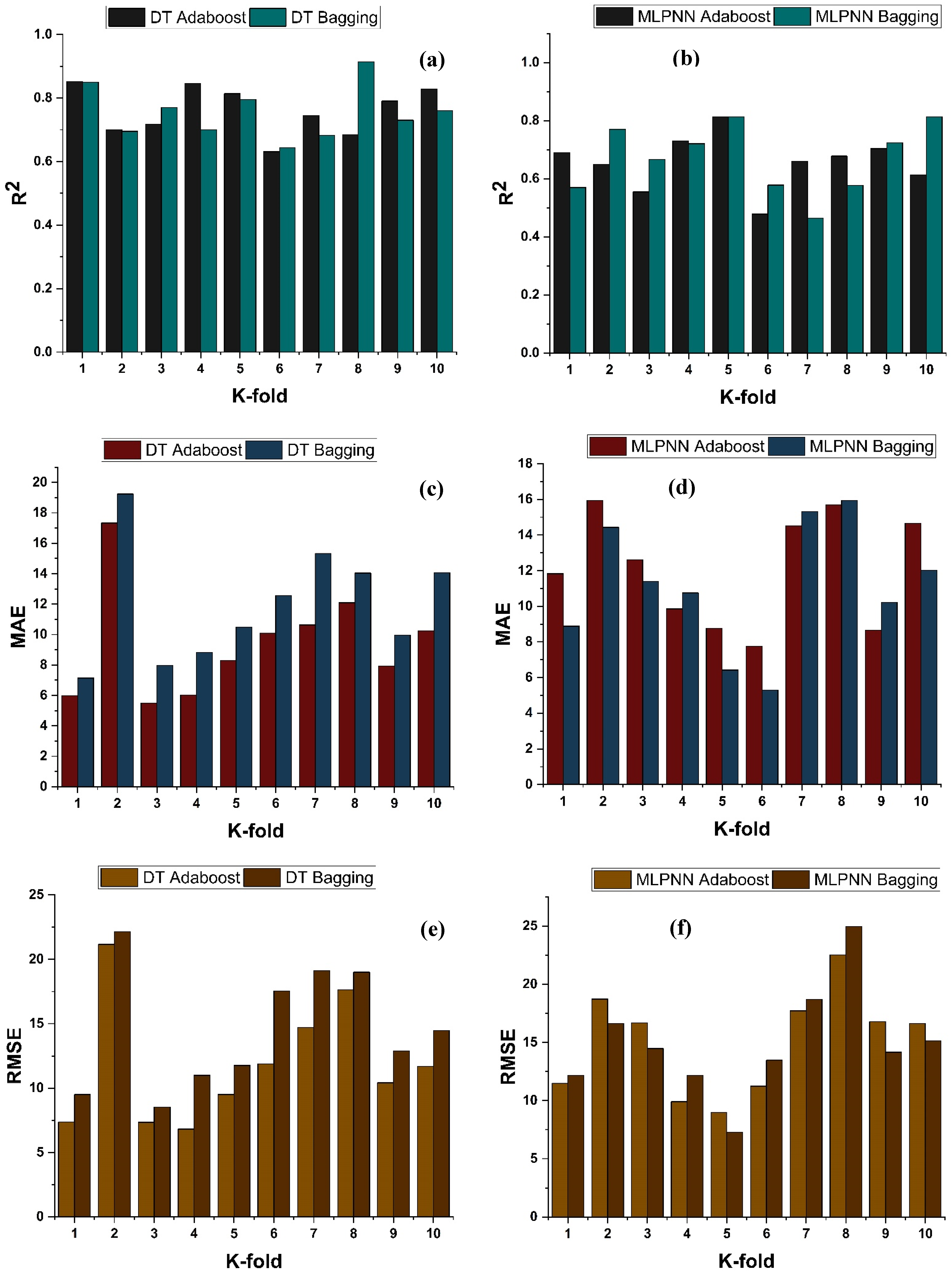
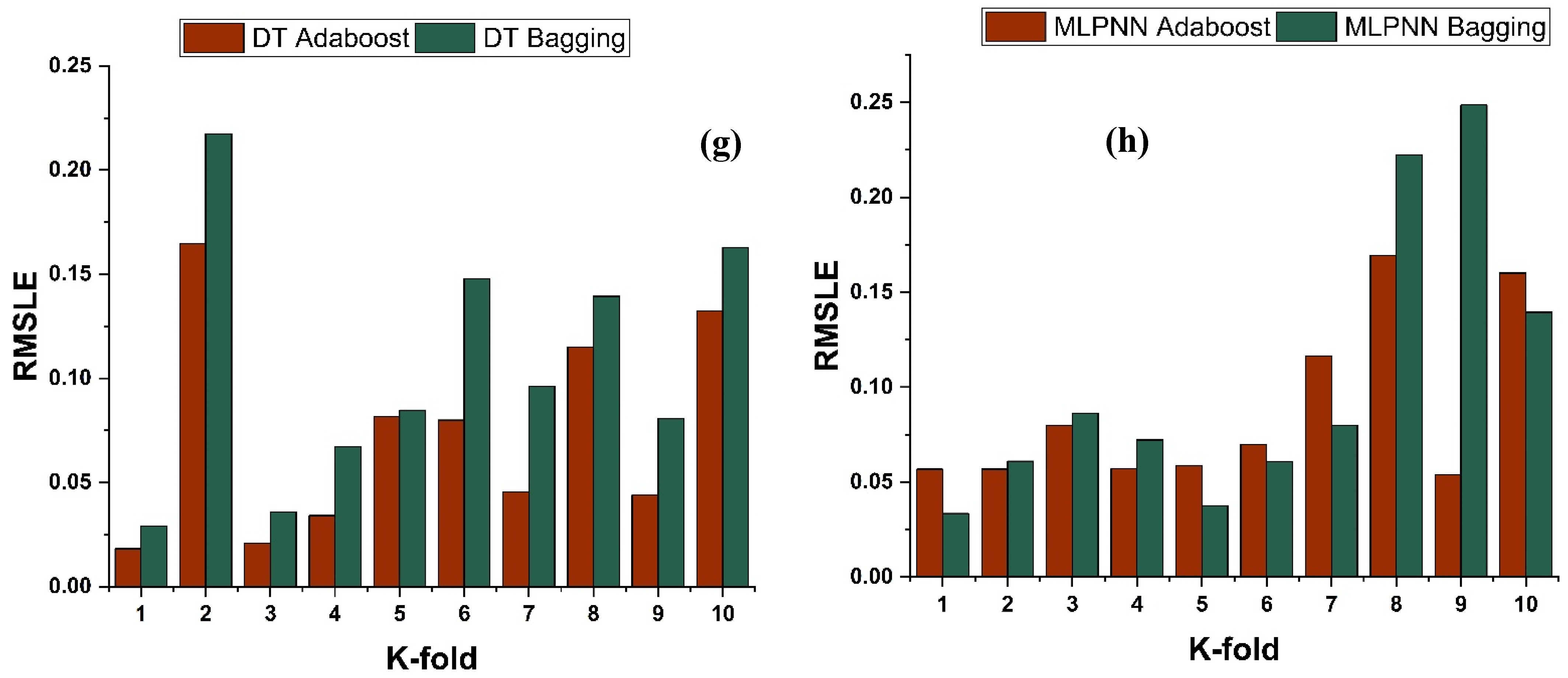
4.4. K-Fold Results
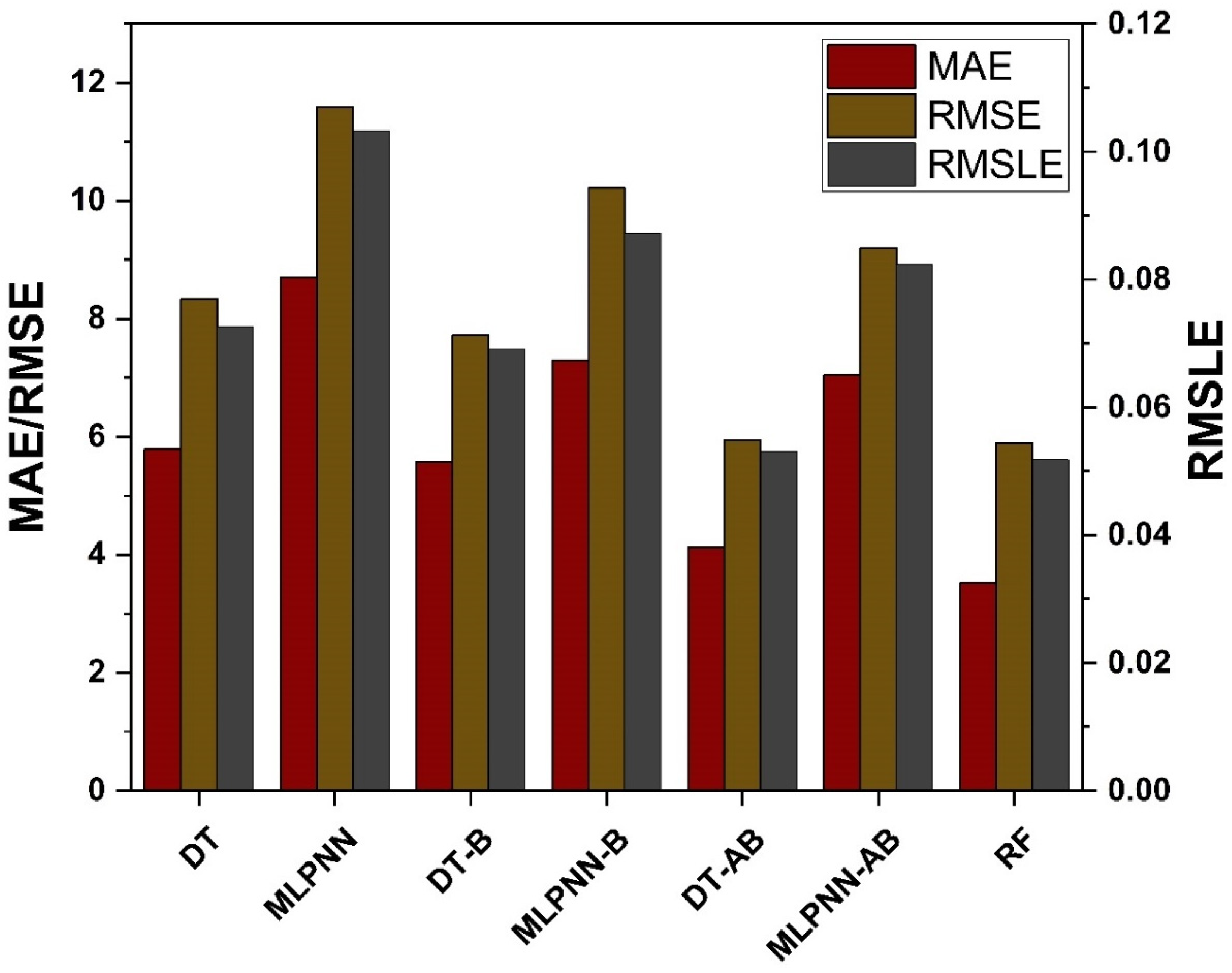
4.5. Model Evaluation and Discussion Based on Statistical Metrics
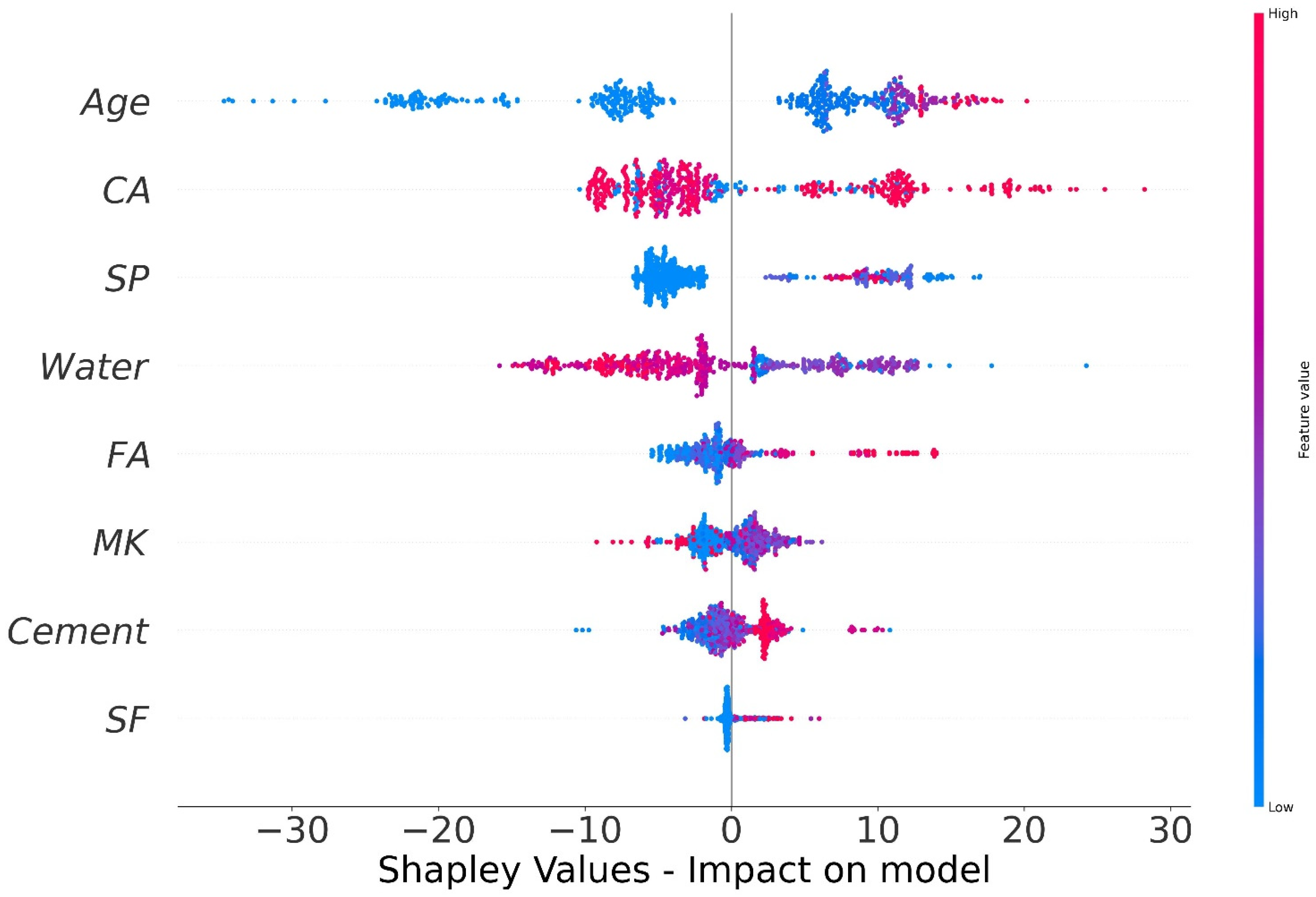
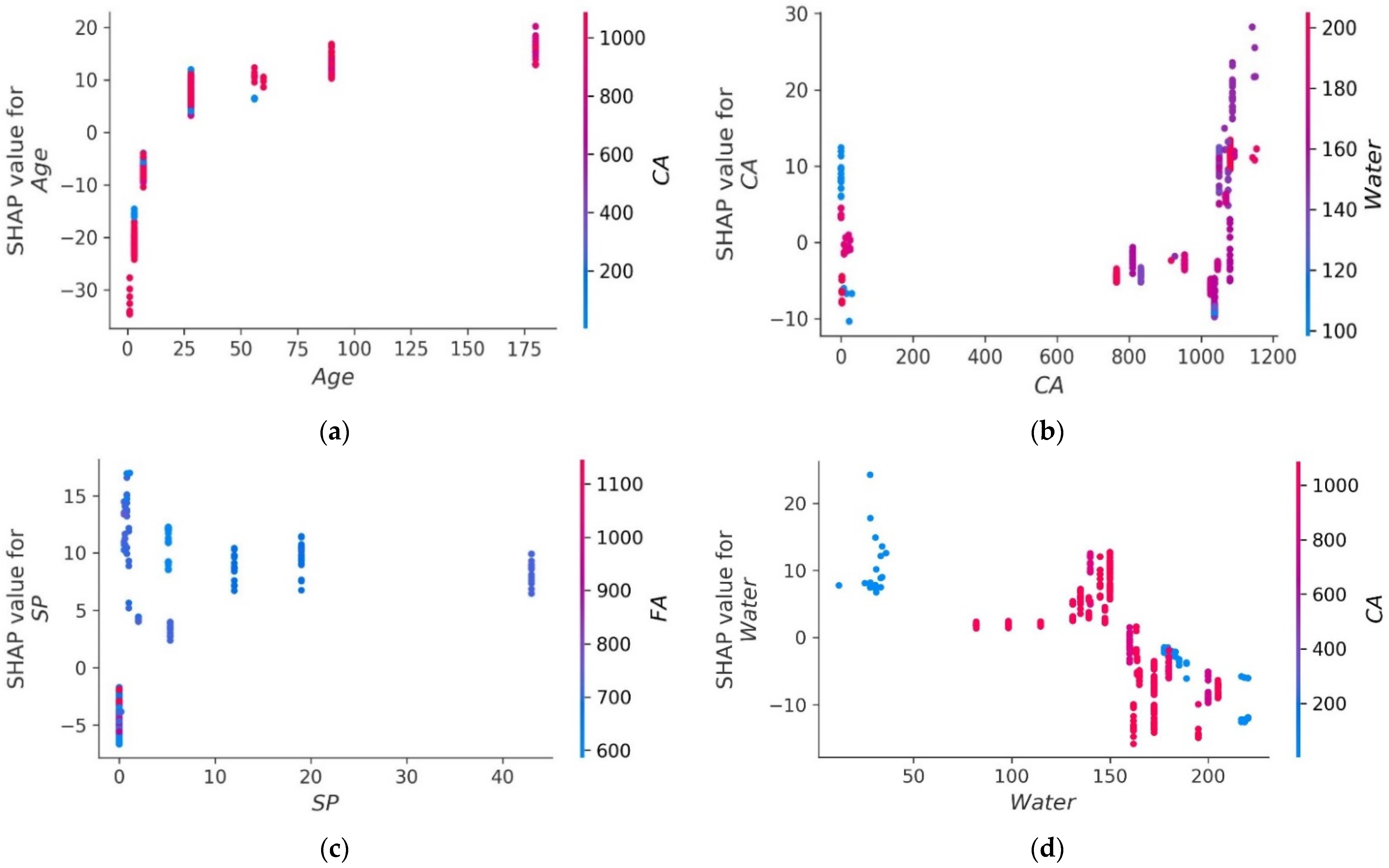
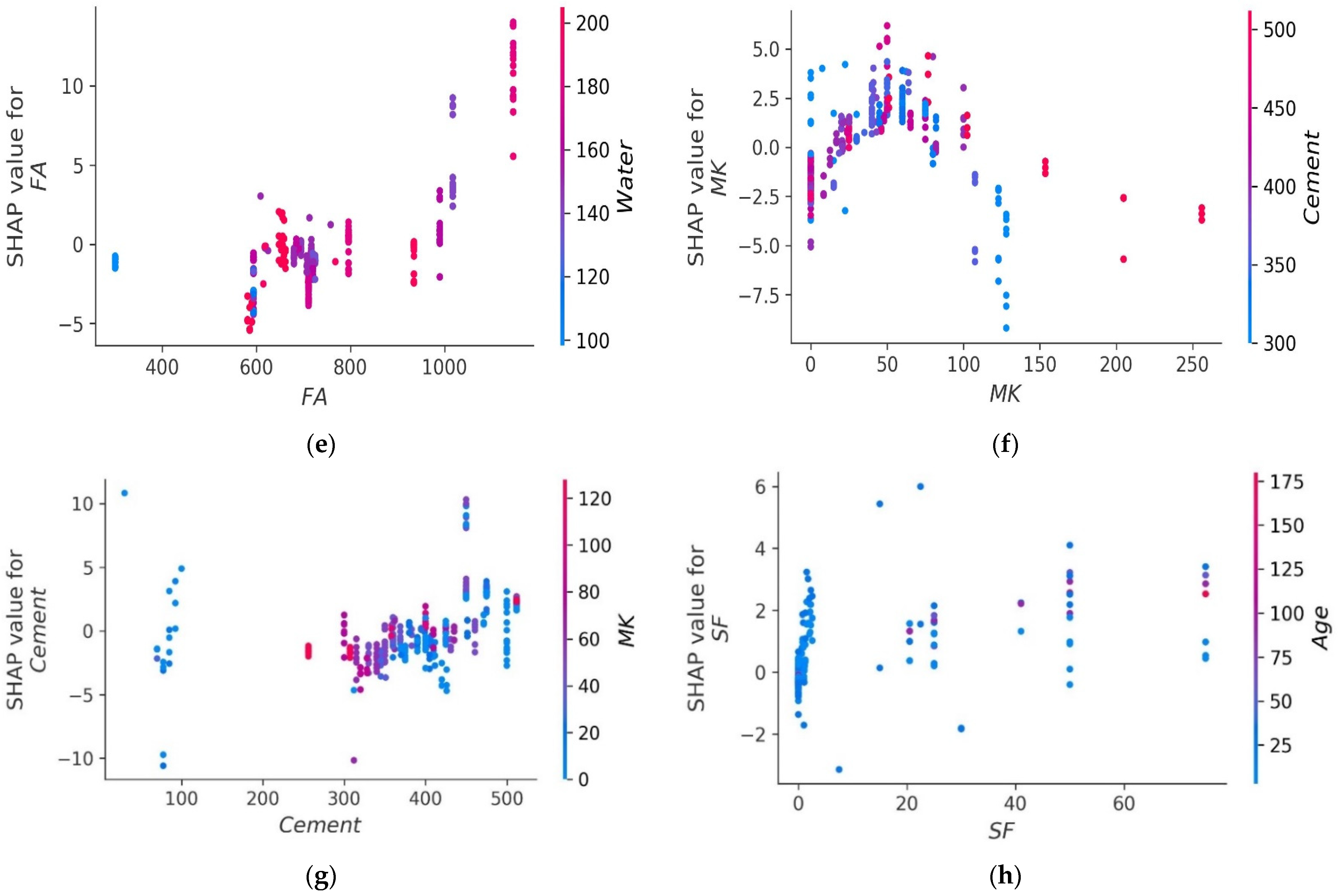
4.6. SHAP Analysis
5. Conclusions
- Bagging and AdaBoost models outperform the individual models. As compared to the standalone DT model, the ensemble DT model with boosting and RF demonstrates a 7% improvement. Both techniques have a significant correlation with R2 equal to 0.92. Similarly, an improvement of 14 %, 6%, and 29% was observed in MLPNN AdaBoost, MLPNN bagging, and RF model, respectively, when compared with individual DT model;
- Statistical measures using MAE, RMSE, RMSLE, and R2 were also performed. Ensemble learner DT bagging and boosting depicts a smaller error of about 4%, and 29% for MAE, 8% and 29% for RMSE, 5% and 27% for RMSLE, respectively, when compared to the individual DT model. Similarly, enhancements of 16% and 19% in MAE, 12% and 21% in RMSE, and 16% and 20% in RMSLE were observed for MLPNN bagging and AdaBoost models, respectively, when compared to the individual base learner DT model;
- RF shows improvements of 60%, 49%, and 50% in MAE, RMSE, and RMSLE when compared to the MLPNN individual model. Similarly, improvements of 39%, 29%, and 29% for the RF model, in MAE, RMSE and RMSLE, were observed in comparison to DT individual model;
- The validity of models using R2, MAE, RMSE, and RMSLE were tested using k-fold cross-validation. Fewer inaccuracies with strong correlations were examined;
- The DT AdaBoost model and the modified bagging model are the best techniques for forecasting MK concrete fc’ among all of the ML approaches;
- Age has the greatest impact on calculating MK concrete fc’, followed by coarse aggregate and superplasticizer, according to the SHAP assessment. However, silica fume has the least impact on the fc’ of MK concrete. SHAP dependency feature graphs can illustrate the relationship between input parameters for various ranges;
- Sensitivity analyses depicted that FA contributed moderately to the development of the fc’ models and fsts models. Moreover, cement, SF, CA, and age played vital roles in the development of fc’ models. Tensile strength models showed to be affected least by water and CA;
6. Limitations and Directions for Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, T.; Nafees, A.; Khan, S.; Javed, M.F.; Aslam, F.; Alabduljabbar, H.; Xiong, J.-J.; Khan, M.I.; Malik, M. Comparative study of mechanical properties between irradiated and regular plastic waste as a replacement of cement and fine aggregate for manufacturing of green concrete. Ain Shams Eng. J. 2021, 13, 101563. [Google Scholar] [CrossRef]
- Khan, K.; Ahmad, A.; Amin, M.N.; Ahmad, W.; Nazar, S.; Abu Arab, A.M. Comparative Study of Experimental and Modeling of Fly Ash-Based Concrete. Materials 2022, 15, 3762. [Google Scholar] [CrossRef]
- Khan, K.; Ahmad, W.; Amin, M.N.; Ahmad, A.; Nazar, S.; Alabdullah, A.A.; Abu Arab, A.M. Exploring the Use of Waste Marble Powder in Concrete and Predicting Its Strength with Different Advanced Algorithms. Materials 2022, 15, 4108. [Google Scholar] [CrossRef] [PubMed]
- Vu, D.; Stroeven, P.; Bui, V. Strength and durability aspects of calcined kaolin-blended Portland cement mortar and concrete. Cem. Concr. Compos. 2001, 23, 471–478. [Google Scholar] [CrossRef]
- Batis, G.; Pantazopoulou, P.; Tsivilis, S.; Badogiannis, E. The effect of metakaolin on the corrosion behavior of cement mortars. Cem. Concr. Compos. 2005, 27, 125–130. [Google Scholar] [CrossRef]
- Khatib, J.; Negim, E.; Gjonbalaj, E. High volume metakaolin as cement replacement in mortar. World J. Chem. 2012, 7, 7–10. [Google Scholar]
- Ameri, F.; Shoaei, P.; Zareei, S.A.; Behforouz, B. Geopolymers vs. alkali-activated materials (AAMs): A comparative study on durability, microstructure, and resistance to elevated temperatures of lightweight mortars. Constr. Build. Mater. 2019, 222, 49–63. [Google Scholar] [CrossRef]
- Pavlikova, M.; Brtník, T.; Keppert, M.; Černý, R. Effect of metakaolin as partial Portland-cement replacement on properties of high performance mortars. Cem. Wapno Beton 2009, 3, 115–122. [Google Scholar]
- Kadri, E.-H.; Kenai, S.; Ezziane, K.; Siddique, R.; De Schutter, G. Influence of metakaolin and silica fume on the heat of hydration and compressive strength development of mortar. Appl. Clay Sci. 2011, 53, 704–708. [Google Scholar] [CrossRef]
- Wianglor, K.; Sinthupinyo, S.; Piyaworapaiboon, M.; Chaipanich, A. Effect of alkali-activated metakaolin cement on compressive strength of mortars. Appl. Clay Sci. 2017, 141, 272–279. [Google Scholar] [CrossRef]
- Khatib, J.; Wild, S. Sulphate Resistance of Metakaolin Mortar. Cem. Concr. Res. 1998, 28, 83–92. [Google Scholar] [CrossRef]
- Van Fan, Y.; Chin, H.H.; Klemeš, J.J.; Varbanov, P.S.; Liu, X. Optimisation and process design tools for cleaner production. J. Clean. Prod. 2019, 247, 119181. [Google Scholar] [CrossRef]
- Apostolopoulou, M.; Asteris, P.G.; Armaghani, D.J.; Douvika, M.G.; Lourenço, P.B.; Cavaleri, L.; Bakolas, A.; Moropoulou, A. Mapping and holistic design of natural hydraulic lime mortars. Cem. Concr. Res. 2020, 136, 106167. [Google Scholar] [CrossRef]
- Asteris, P.G.; Douvika, M.G.; Karamani, C.A.; Skentou, A.D.; Chlichlia, K.; Cavaleri, L.; Daras, T.; Armaghani, D.J.; Zaoutis, T.E. A Novel Heuristic Algorithm for the Modeling and Risk Assessment of the COVID-19 Pandemic Phenomenon. Comput. Model. Eng. Sci. 2020, 125, 815–828. [Google Scholar] [CrossRef]
- Banan, A.; Nasiri, A.; Taheri-Garavand, A. Deep learning-based appearance features extraction for automated carp species identification. Aquac. Eng. 2020, 89, 102053. [Google Scholar] [CrossRef]
- Fan, Y.; Xu, K.; Wu, H.; Zheng, Y.; Tao, B. Spatiotemporal Modeling for Nonlinear Distributed Thermal Processes Based on KL Decomposition, MLP and LSTM Network. IEEE Access 2020, 8, 25111–25121. [Google Scholar] [CrossRef]
- Taormina, R.; Chau, K.-W. ANN-based interval forecasting of streamflow discharges using the LUBE method and MOFIPS. Eng. Appl. Artif. Intell. 2015, 45, 429–440. [Google Scholar] [CrossRef]
- Wu, C.; Chau, K. Prediction of rainfall time series using modular soft computingmethods. Eng. Appl. Artif. Intell. 2013, 26, 997–1007. [Google Scholar] [CrossRef]
- Armaghani, D.; Momeni, E.; Asteris, P. Application of group method of data handling technique in assessing deformation of rock mass. Metaheuristic Comput. Appl. 2020, 1, 1–18. [Google Scholar]
- Nafees, A.; Khan, S.; Javed, M.F.; Alrowais, R.; Mohamed, A.M.; Mohamed, A.; Vatin, N.I. Forecasting the Mechanical Properties of Plastic Concrete Employing Experimental Data Using Machine Learning Algorithms: DT, MLPNN, SVM, and RF. Polymers 2022, 14, 1583. [Google Scholar] [CrossRef]
- Nafees, A.; Javed, M.F.; Khan, S.; Nazir, K.; Farooq, F.; Aslam, F.; Musarat, M.A.; Vatin, N.I. Predictive Modeling of Mechanical Properties of Silica Fume-Based Green Concrete Using Artificial Intelligence Approaches: MLPNN, ANFIS, and GEP. Materials 2021, 14, 7531. [Google Scholar] [CrossRef] [PubMed]
- Nafees, A.; Amin, M.N.; Khan, K.; Nazir, K.; Ali, M.; Javed, M.F.; Aslam, F.; Musarat, M.A.; Vatin, N.I. Modeling of Mechanical Properties of Silica Fume-Based Green Concrete Using Machine Learning Techniques. Polymers 2021, 14, 30. [Google Scholar] [CrossRef] [PubMed]
- Amin, M.N.; Ahmad, W.; Khan, K.; Ahmad, A.; Nazar, S.; Alabdullah, A.A. Use of Artificial Intelligence for Predicting Parameters of Sustainable Concrete and Raw Ingredient Effects and Interactions. Materials 2022, 15, 5207. [Google Scholar] [CrossRef] [PubMed]
- Khan, K.; Ahmad, W.; Amin, M.N.; Ahmad, A. A Systematic Review of the Research Development on the Application of Machine Learning for Concrete. Materials 2022, 15, 4512. [Google Scholar] [CrossRef]
- Khan, K.; Ahmad, W.; Amin, M.N.; Aslam, F.; Ahmad, A.; Al-Faiad, M.A. Comparison of Prediction Models Based on Machine Learning for the Compressive Strength Estimation of Recycled Aggregate Concrete. Materials 2022, 15, 3430. [Google Scholar] [CrossRef]
- Khan, K.; Ahmad, W.; Amin, M.N.; Ahmad, A.; Nazar, S.; Al-Faiad, M.A. Assessment of Artificial Intelligence Strategies to Estimate the Strength of Geopolymer Composites and Influence of Input Parameters. Polymers 2022, 14, 2509. [Google Scholar] [CrossRef]
- Khan, K.; Ahmad, W.; Amin, M.N.; Ahmad, A.; Nazar, S.; Alabdullah, A.A. Compressive Strength Estimation of Steel-Fiber-Reinforced Concrete and Raw Material Interactions Using Advanced Algorithms. Polymers 2022, 14, 3065. [Google Scholar] [CrossRef]
- Dai, L.; Wu, X.; Zhou, M.; Ahmad, W.; Ali, M.; Sabri, M.M.S.; Salmi, A.; Ewais, D.Y.Z. Using Machine Learning Algorithms to Estimate the Compressive Property of High Strength Fiber Reinforced Concrete. Materials 2022, 15, 4450. [Google Scholar] [CrossRef]
- Amin, M.N.; Ahmad, A.; Khan, K.; Ahmad, W.; Nazar, S.; Faraz, M.I.; Alabdullah, A.A. Split Tensile Strength Prediction of Recycled Aggregate-Based Sustainable Concrete Using Artificial Intelligence Methods. Materials 2022, 15, 4296. [Google Scholar] [CrossRef]
- González-Taboada, I.; González-Fonteboa, B.; Martínez-Abella, F.; Pérez-Ordóñez, J.L. Prediction of the mechanical properties of structural recycled concrete using multivariable regression and genetic programming. Constr. Build. Mater. 2016, 106, 480–499. [Google Scholar] [CrossRef]
- Asteris, P.G.; Moropoulou, A.; Skentou, A.D.; Apostolopoulou, M.; Mohebkhah, A.; Cavaleri, L.; Rodrigues, H.; Varum, H. Stochastic Vulnerability Assessment of Masonry Structures: Concepts, Modeling and Restoration Aspects. Appl. Sci. 2019, 9, 243. [Google Scholar] [CrossRef]
- Asteris, P.G.; Apostolopoulou, M.; Skentou, A.D.; Moropoulou, A. Application of artificial neural networks for the prediction of the compressive strength of cement-based mortars. Comput. Concr. 2019, 24, 329–345. [Google Scholar]
- Ben Chaabene, W.; Flah, M.; Nehdi, M.L. Machine learning prediction of mechanical properties of concrete: Critical review. Constr. Build. Mater. 2020, 260, 119889. [Google Scholar] [CrossRef]
- Alkadhim, H.A.; Amin, M.N.; Ahmad, W.; Khan, K.; Nazar, S.; Faraz, M.I.; Imran, M. Evaluating the Strength and Impact of Raw Ingredients of Cement Mortar Incorporating Waste Glass Powder Using Machine Learning and SHapley Additive ExPlanations (SHAP) Methods. Materials 2022, 15, 7344. [Google Scholar] [CrossRef]
- Ghorbani, B.; Arulrajah, A.; Narsilio, G.; Horpibulsuk, S. Experimental and ANN analysis of temperature effects on the permanent deformation properties of demolition wastes. Transp. Geotech. 2020, 24, 100365. [Google Scholar] [CrossRef]
- Akkurt, S.; Tayfur, G.; Can, S. Fuzzy logic model for the prediction of cement compressive strength. Cem. Concr. Res. 2004, 34, 1429–1433. [Google Scholar] [CrossRef]
- Özcan, F.; Atis, C.; Karahan, O.; Uncuoğlu, E.; Tanyildizi, H. Comparison of artificial neural network and fuzzy logic models for prediction of long-term compressive strength of silica fume concrete. Adv. Eng. Softw. 2009, 40, 856–863. [Google Scholar] [CrossRef]
- Pérez, J.L.; Cladera, A.; Rabuñal, J.R.; Martínez-Abella, F. Optimization of existing equations using a new Genetic Programming algorithm: Application to the shear strength of reinforced concrete beams. Adv. Eng. Softw. 2012, 50, 82–96. [Google Scholar] [CrossRef]
- Mansouri, I.; Kisi, O. Prediction of debonding strength for masonry elements retrofitted with FRP composites using neuro fuzzy and neural network approaches. Compos. Part B Eng. 2015, 70, 247–255. [Google Scholar] [CrossRef]
- Nasrollahzadeh, K.; Nouhi, E. Fuzzy inference system to formulate compressive strength and ultimate strain of square concrete columns wrapped with fiber-reinforced polymer. Neural Comput. Appl. 2016, 30, 69–86. [Google Scholar] [CrossRef]
- Falcone, R.; Lima, C.; Martinelli, E. Soft computing techniques in structural and earthquake engineering: A literature review. Eng. Struct. 2020, 207, 110269. [Google Scholar] [CrossRef]
- Farooqi, M.U.; Ali, M. Effect of pre-treatment and content of wheat straw on energy absorption capability of concrete. Constr. Build. Mater. 2019, 224, 572–583. [Google Scholar] [CrossRef]
- Farooqi, M.U.; Ali, M. Effect of Fibre Content on Compressive Strength of Wheat Straw Reinforced Concrete for Pavement Applications. IOP Conf. Ser. Mater. Sci. Eng. 2018, 422, 012014. [Google Scholar] [CrossRef]
- Younis, K.H.; Amin, A.A.; Ahmed, H.G.; Maruf, S.M. Recycled Aggregate Concrete including Various Contents of Metakaolin: Mechanical Behavior. Adv. Mater. Sci. Eng. 2020, 2020, 8829713. [Google Scholar] [CrossRef]
- Poon, C.; Kou, S.; Lam, L. Compressive strength, chloride diffusivity and pore structure of high performance metakaolin and silica fume concrete. Constr. Build. Mater. 2006, 20, 858–865. [Google Scholar] [CrossRef]
- Qian, X.; Li, Z. The relationships between stress and strain for high-performance concrete with metakaolin. Cem. Concr. Res. 2001, 31, 1607–1611. [Google Scholar] [CrossRef]
- Li, Q.; Geng, H.; Shui, Z.; Huang, Y. Effect of metakaolin addition and seawater mixing on the properties and hydration of concrete. Appl. Clay Sci. 2015, 115, 51–60. [Google Scholar] [CrossRef]
- Ramezanianpour, A.; Jovein, H.B. Influence of metakaolin as supplementary cementing material on strength and durability of concretes. Constr. Build. Mater. 2012, 30, 470–479. [Google Scholar] [CrossRef]
- Shehab El-Din, H.K.; Eisa, A.S.; Abdel Aziz, B.H.; Ibrahim, A. Mechanical performance of high strength concrete made from high volume of Metakaolin and hybrid fibers. Constr. Build. Mater. 2017, 140, 203–209. [Google Scholar] [CrossRef]
- Roy, D.; Arjunan, P.; Silsbee, M. Effect of silica fume, metakaolin, and low-calcium fly ash on chemical resistance of concrete. Cem. Concr. Res. 2001, 31, 1809–1813. [Google Scholar] [CrossRef]
- Poon, C.S.; Shui, Z.; Lam, L. Compressive behavior of fiber reinforced high-performance concrete subjected to elevated temperatures. Cem. Concr. Res. 2004, 34, 2215–2222. [Google Scholar] [CrossRef]
- Sharaky, I.; Ghoneim, S.S.; Aziz, B.H.A.; Emara, M. Experimental and theoretical study on the compressive strength of the high strength concrete incorporating steel fiber and metakaolin. Structures 2021, 31, 57–67. [Google Scholar] [CrossRef]
- Gilan, S.S.; Jovein, H.B.; Ramezanianpour, A.A. Hybrid support vector regression—Particle swarm optimization for prediction of compressive strength and RCPT of concretes containing metakaolin. Constr. Build. Mater. 2012, 34, 321–329. [Google Scholar] [CrossRef]
- Silva, F.A.N.; Delgado, J.M.P.Q.; Cavalcanti, R.S.; Azevedo, A.C.; Guimarães, A.S.; Lima, A.G.B. Use of Nondestructive Testing of Ultrasound and Artificial Neural Networks to Estimate Compressive Strength of Concrete. Buildings 2021, 11, 44. [Google Scholar] [CrossRef]
- Poon, C.S.; Azhar, S.; Anson, M.; Wong, Y.-L. Performance of metakaolin concrete at elevated temperatures. Cem. Concr. Compos. 2003, 25, 83–89. [Google Scholar] [CrossRef]
- Nica, E.; Stehel, V. Internet of things sensing networks, artificial intelligence-based decision-making algorithms, and real-time process monitoring in sustainable industry 4. J. Self-Gov. Manag. Econ. 2021, 9, 35–47. [Google Scholar]
- Sierra, L.A.; Yepes, V.; Pellicer, E. A review of multi-criteria assessment of the social sustainability of infrastructures. J. Clean. Prod. 2018, 187, 496–513. [Google Scholar] [CrossRef]
- Kicinger, R.; Arciszewski, T.; De Jong, K. Evolutionary computation and structural design: A survey of the state-of-the-art. Comput. Struct. 2005, 83, 1943–1978. [Google Scholar] [CrossRef]
- Yin, Z.; Jin, Y.; Liu, Z. Practice of artificial intelligence in geotechnical engineering. J. Zhejiang Univ. A 2020, 21, 407–411. [Google Scholar] [CrossRef]
- Park, H.S.; Lee, E.; Choi, S.W.; Oh, B.K.; Cho, T.; Kim, Y. Genetic-algorithm-based minimum weight design of an outrigger system for high-rise buildings. Eng. Struct. 2016, 117, 496–505. [Google Scholar] [CrossRef]
- Villalobos Arias, L. Evaluating an Automated Procedure of Machine Learning Parameter Tuning for Software Effort Estimation; Universidad de Costa Rica: San Pedro, Costa Rica, 2021. [Google Scholar]
- Myles, A.J.; Feudale, R.N.; Liu, Y.; Woody, N.A.; Brown, S.D. An introduction to decision tree modeling. J. Chemom. A J. Chemom. Soc. 2004, 18, 275–285. [Google Scholar] [CrossRef]
- Debeljak, M.; Džeroski, S. Decision Trees in Ecological Modelling. In Modelling Complex Ecological Dynamics; Springer: Berlin/Heidelberg, Germany, 2011; pp. 197–209. [Google Scholar]
- Murthy, S.K. Automatic Construction of Decision Trees from Data: A Multi-Disciplinary Survey. Data Min. Knowl. Discov. 1998, 2, 345–389. [Google Scholar] [CrossRef]
- Kheir, R.B.; Greve, M.H.; Abdallah, C.; Dalgaard, T. Spatial soil zinc content distribution from terrain parameters: A GIS-based decision-tree model in Lebanon. Environ. Pollut. 2010, 158, 520–528. [Google Scholar] [CrossRef] [PubMed]
- Tso, G.K.F.; Yau, K.W.K. Predicting electricity energy consumption: A comparison of regression analysis, decision tree and neural networks. Energy 2007, 32, 1761–1768. [Google Scholar] [CrossRef]
- Cho, J.H.; Kurup, P.U. Decision tree approach for classification and dimensionality reduction of electronic nose data. Sens. Actuators B Chem. 2011, 160, 542–548. [Google Scholar] [CrossRef]
- Quinlan, J.R. C4. 5: Programs for Machine Learning; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Abidoye, L.; Mahdi, F.; Idris, M.; Alabi, O.; Wahab, A. ANN-derived equation and ITS application in the prediction of dielectric properties of pure and impure CO2. J. Clean. Prod. 2018, 175, 123–132. [Google Scholar] [CrossRef]
- Ozoegwu, C.G. Artificial neural network forecast of monthly mean daily global solar radiation of selected locations based on time series and month number. J. Clean. Prod. 2019, 216, 1–13. [Google Scholar] [CrossRef]
- Hafeez, A.; Taqvi, S.A.A.; Fazal, T.; Javed, F.; Khan, Z.; Amjad, U.S.; Bokhari, A.; Shehzad, N.; Rashid, N.; Rehman, S.; et al. Optimization on cleaner intensification of ozone production using Artificial Neural Network and Response Surface Methodology: Parametric and comparative study. J. Clean. Prod. 2019, 252, 119833. [Google Scholar] [CrossRef]
- Zhou, G.; Moayedi, H.; Bahiraei, M.; Lyu, Z. Employing artificial bee colony and particle swarm techniques for optimizing a neural network in prediction of heating and cooling loads of residential buildings. J. Clean. Prod. 2020, 254, 120082. [Google Scholar] [CrossRef]
- Shahin, M.A.; Maier, H.R.; Jaksa, M.B. Data Division for Developing Neural Networks Applied to Geotechnical Engineering. J. Comput. Civ. Eng. 2004, 18, 105–114. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. Experiments with a new boosting algorithm. In Proceedings of the ICML, Bari, Italy, 3–6 July 1996; pp. 148–156. [Google Scholar]
- Guo, L.; Ge, P.; Zhang, M.-H.; Li, L.-H.; Zhao, Y.-B. Pedestrian detection for intelligent transportation systems combining AdaBoost algorithm and support vector machine. Expert Syst. Appl. 2012, 39, 4274–4286. [Google Scholar] [CrossRef]
- Han, Q.; Gui, C.; Xu, J.; Lacidogna, G. A generalized method to predict the compressive strength of high-performance concrete by improved random forest algorithm. Constr. Build. Mater. 2019, 226, 734–742. [Google Scholar] [CrossRef]
- Han, J.; Pei, J.; Kamber, M. Data Mining: Concepts and Techniques; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Farooq, F.; Ahmed, W.; Akbar, A.; Aslam, F.; Alyousef, R. Predictive modeling for sustainable high-performance concrete from industrial wastes: A comparison and optimization of models using ensemble learners. J. Clean. Prod. 2021, 292, 126032. [Google Scholar] [CrossRef]
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. In Proceedings of the IJCAI, Montreal, QC, Canada, 20–25 August 1995; pp. 113–1145. [Google Scholar]
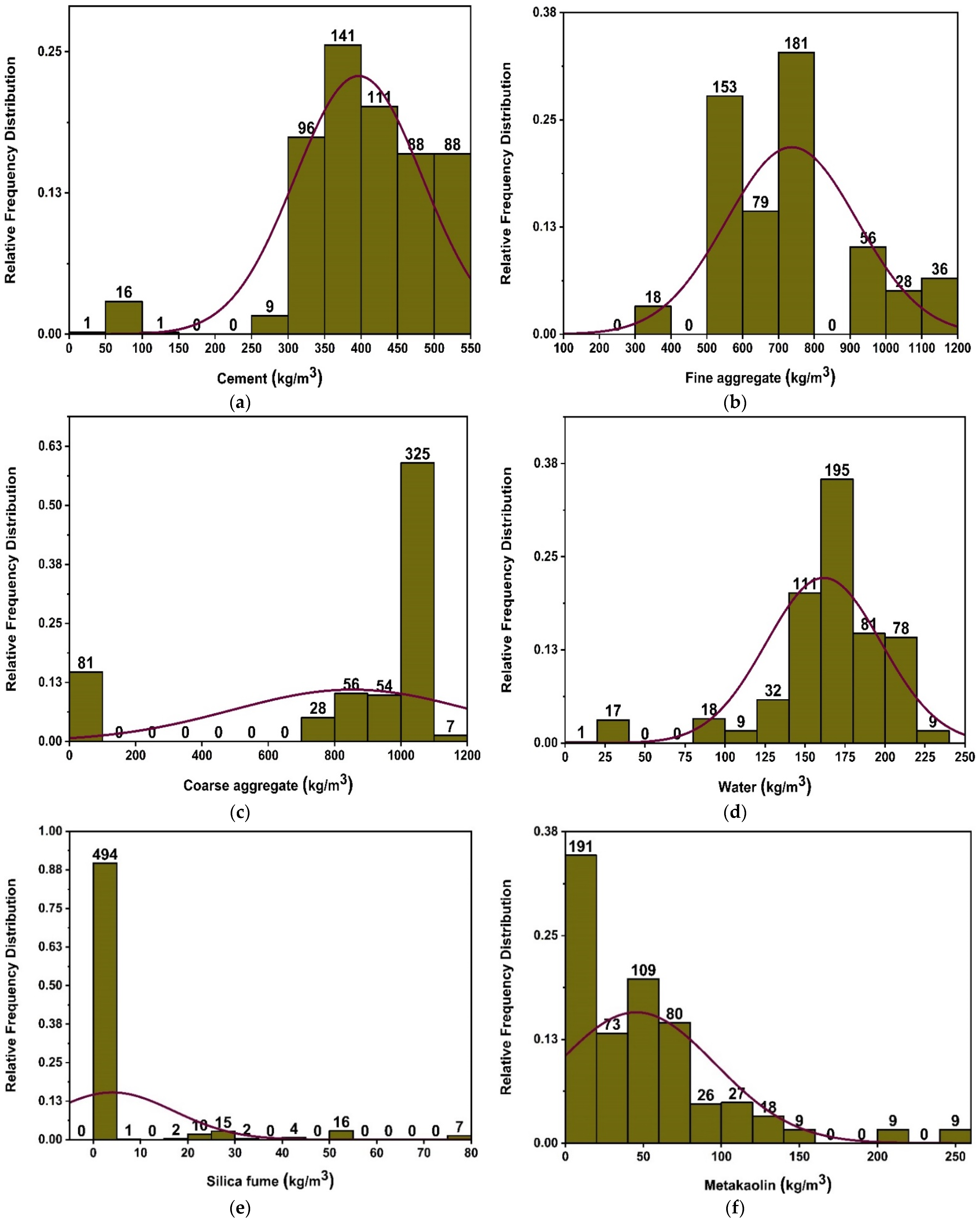
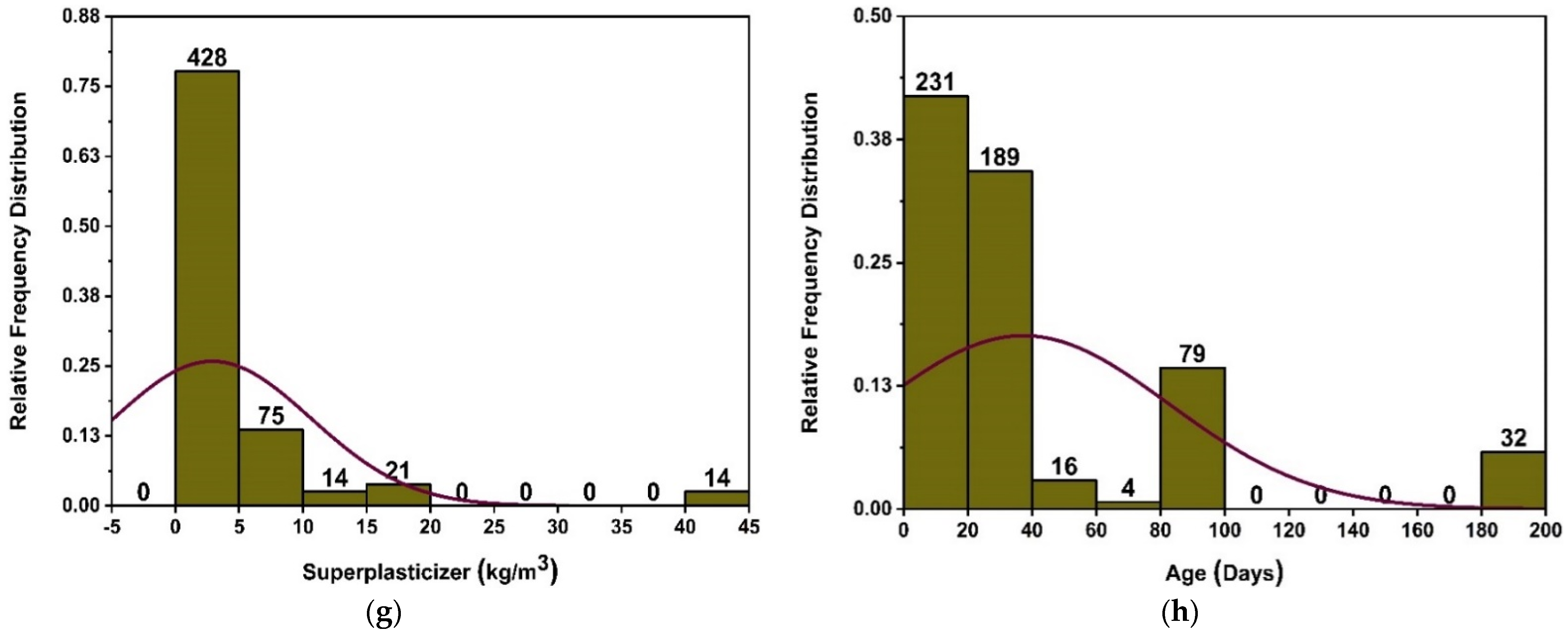


| Parameters | Acronym | Min | Max |
|---|---|---|---|
| Input Parameters | |||
| Cement | C | 30 | 512 |
| Fine aggregate | FA | 300 | 1146 |
| Coarse aggregate | CA | 0 | 1154 |
| Water | W | 12 | 220.30 |
| Silica fume | SF | 0 | 75 |
| Metakaolin | MK | 0 | 256 |
| Superplasticizer | SP | 0 | 43 |
| Age | Age | 1 | 180 |
| Output variable | |||
| Compressive strength | fc’ | 9.84 | 131.30 |
| Parameters | Cement | Fine Aggregate | Coarse Aggregate | Water | Silica Fume | Metakaolin | Superplasticizer | Age (Days) |
|---|---|---|---|---|---|---|---|---|
| Statistical description | ||||||||
| Mean | 396.64 | 737.24 | 853.09 | 161.71 | 4.05 | 45.48 | 2.90 | 37.29 |
| Std error | 3.72 | 7.79 | 15.47 | 1.53 | 0.55 | 2.16 | 0.33 | 1.93 |
| Median | 400 | 711 | 1037 | 163.40 | 0 | 40 | 0 | 28 |
| Std. dev | 87.28 | 182.93 | 363.13 | 36.00 | 13.02 | 50.59 | 7.73 | 45.34 |
| Variance | 7617.40 | 33,463.99 | 131,866.26 | 1295.65 | 169.49 | 2559.62 | 59.80 | 2056 |
| Kurtosis | 3.57 | 0.37 | 1.42 | 4.18 | 13.68 | 4.43 | 16.38 | 3.13 |
| Skewness | −1.34 | 0.52 | −1.75 | −1.58 | 3.68 | 1.85 | 3.92 | 1.90 |
| Range | 482.00 | 846 | 1154 | 208.30 | 75 | 256 | 43 | 179 |
| Min | 30 | 300 | 0 | 12 | 0 | 0 | 0 | 1 |
| Max | 512 | 1146 | 1154 | 220.30 | 75 | 256 | 43 | 180 |
| Sum | 218,548.70 | 406,217 | 470,050.80 | 89,099.50 | 2232.15 | 25,060.77 | 1597.30 | 20549 |
| Count | 551 | 551 | 551 | 551 | 551 | 551 | 551 | 551 |
| Training dataset | ||||||||
| Mean | 395.18 | 738.49 | 841.41 | 161.06 | 4.09 | 45.50 | 2.66 | 37.85 |
| Std error | 4.19 | 8.86 | 17.83 | 1.74 | 0.63 | 2.39 | 0.35 | 2.20 |
| Median | 400 | 711 | 1037 | 163.40 | 0 | 40 | 0 | 28 |
| Std. dev | 87.97 | 185.84 | 374.05 | 36.54 | 13.24 | 50.03 | 7.38 | 46.20 |
| Variance | 7738.04 | 34,538.02 | 139,915.86 | 1334.83 | 175.26 | 2503 | 54.44 | 2134.15 |
| Kurtosis | 3.65 | 0.33 | 1.04 | 4.08 | 13.61 | 4.56 | 18.52 | 2.92 |
| Skewness | −1.38 | 0.52 | −1.66 | −1.57 | 3.69 | 1.86 | 4.13 | 1.86 |
| Range | 482 | 846 | 1154 | 208.30 | 75 | 256 | 43 | 179 |
| Min | 30 | 300 | 0 | 12 | 0 | 0 | 0 | 1 |
| Max | 512 | 1146 | 1154 | 220.30 | 75 | 256 | 43 | 180 |
| Sum | 173,881.30 | 324,936.00 | 370,219.70 | 70,868.40 | 1798.72 | 20019.51 | 1171.52 | 16656 |
| Count | 440 | 440 | 440 | 440 | 440 | 440 | 440 | 440 |
| Testing Dataset | ||||||||
| Mean | 402.41 | 732.26 | 899.38 | 164.24 | 3.90 | 45.42 | 3.84 | 35.07 |
| Std error | 8.03 | 16.29 | 29.75 | 3.21 | 1.15 | 5.03 | 0.85 | 3.98 |
| Median | 400 | 708 | 1037 | 163.40 | 0 | 40 | 0 | 28 |
| Std. dev | 84.64 | 171.61 | 313.42 | 33.81 | 12.16 | 53 | 8.98 | 41.92 |
| Variance | 7163.11 | 29,450.55 | 98,231.83 | 1142.93 | 147.97 | 2808.83 | 80.63 | 1756.94 |
| Kurtosis | 3.30 | 0.59 | 3.85 | 4.79 | 14.25 | 4.19 | 11.32 | 4.29 |
| Skewness | −1.16 | 0.54 | −2.25 | −1.62 | 3.64 | 1.85 | 3.31 | 2.06 |
| Range | 434.50 | 846 | 1149 | 192.40 | 75 | 256 | 43 | 179 |
| Min | 77.50 | 300 | 0 | 27.90 | 0 | 0 | 0 | 1 |
| Max | 512 | 1146 | 1149 | 220.30 | 75 | 256 | 43 | 180 |
| Sum | 44,667.40 | 81,281.00 | 99,831.10 | 18,231.09 | 433.43 | 5041.26 | 425.78 | 3893 |
| Count | 111 | 111 | 111 | 111 | 111 | 111 | 111 | 111 |
| Statistical Analysis | DT | DT-Bagging | DT-AdaBoost |
|---|---|---|---|
| Average | 5.79 | 7.29 | 7.05 |
| Minimum | 0.08 | 0.11 | 0.07 |
| Maximum | 35.3 | 34.74 | 31.31 |
| No. of data points below 10 MPa | 92 | 94 | 103 |
| No. of data points between 10 and 20 MPa | 15 | 14 | 07 |
| No. of data points between 20 and 30 MPa | 02 | 02 | 00 |
| No. of data points between 30 and 40 MPa | 02 | 01 | 01 |
| No. of data points testing points | 111 | 111 | 111 |
| Average below 10 MPa | 82.88 | 84.68 | 92.79 |
| Average in range of 10 to 20 MPa | 13.51 | 12.61 | 6.31 |
| Average in range of 20 to 30 MPa | 1.80 | 3.60 | 00 |
| Average in range of 30 to 40 MPa | 1.80 | 2.70 | 0.90 |
| Statistical Analysis | MLPNN | MLPNN-Bagging | MLPNN-AdaBoost |
|---|---|---|---|
| Average | 8.70 | 7.29 | 7.05 |
| Minimum | 0.04 | 0.11 | 0.07 |
| Maximum | 35.15 | 34.74 | 31.31 |
| No. of data points below 10 MPa | 81 | 86 | 83 |
| No. of data points between 10 and 20 MPa | 20 | 18 | 23 |
| No. of data points between 20 and 30 MPa | 07 | 04 | 04 |
| No. of data points between 30 and 40 MPa | 03 | 03 | 01 |
| No. of data points between 10 and 20 MPa | 111 | 111 | 111 |
| Average below 10 MPa | 72.97 | 77.48 | 74.77 |
| Average in range of 10 to 20 MPa | 18.02 | 16.22 | 20.72 |
| Average in range of 20 to 30 MPa | 6.31 | 3.60 | 3.60 |
| Average in range of 30 to 40 MPa | 2.70 | 2.70 | 0.90 |
| Approach Employed | ML Methods | MAE | RMSE | RMSLE | R2 |
|---|---|---|---|---|---|
| Individual Learner | DT | 5.79072 | 8.34472 | 0.07261 | 0.868 |
| MLPNN | 8.70159 | 11.59452 | 0.10325 | 0.724 | |
| Ensemble Learner Bagging | DT | 5.57845 | 7.72089 | 0.06911 | 0.879 |
| MLPNN | 7.29168 | 10.21239 | 0.08721 | 0.767 | |
| Ensemble Learner Boosting | DT | 4.12636 | 5.93813 | 0.05303 | 0.924 |
| MLPNN | 7.04574 | 9.20414 | 0.08233 | 0.825 | |
| Modified Ensemble | Random Forest | 3.52232 | 5.89161 | 0.05179 | 0.929 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bulbul, A.M.R.; Khan, K.; Nafees, A.; Amin, M.N.; Ahmad, W.; Usman, M.; Nazar, S.; Arab, A.M.A. In-Depth Analysis of Cement-Based Material Incorporating Metakaolin Using Individual and Ensemble Machine Learning Approaches. Materials 2022, 15, 7764. https://doi.org/10.3390/ma15217764
Bulbul AMR, Khan K, Nafees A, Amin MN, Ahmad W, Usman M, Nazar S, Arab AMA. In-Depth Analysis of Cement-Based Material Incorporating Metakaolin Using Individual and Ensemble Machine Learning Approaches. Materials. 2022; 15(21):7764. https://doi.org/10.3390/ma15217764
Chicago/Turabian StyleBulbul, Abdulrahman Mohamad Radwan, Kaffayatullah Khan, Afnan Nafees, Muhammad Nasir Amin, Waqas Ahmad, Muhammad Usman, Sohaib Nazar, and Abdullah Mohammad Abu Arab. 2022. "In-Depth Analysis of Cement-Based Material Incorporating Metakaolin Using Individual and Ensemble Machine Learning Approaches" Materials 15, no. 21: 7764. https://doi.org/10.3390/ma15217764
APA StyleBulbul, A. M. R., Khan, K., Nafees, A., Amin, M. N., Ahmad, W., Usman, M., Nazar, S., & Arab, A. M. A. (2022). In-Depth Analysis of Cement-Based Material Incorporating Metakaolin Using Individual and Ensemble Machine Learning Approaches. Materials, 15(21), 7764. https://doi.org/10.3390/ma15217764







