Constitutive Model for Equivalent Stress-Plastic Strain Curves Including Full-Range Strain Hardening Behavior of High-Strength Steel at Elevated Temperatures
Abstract
1. Introduction
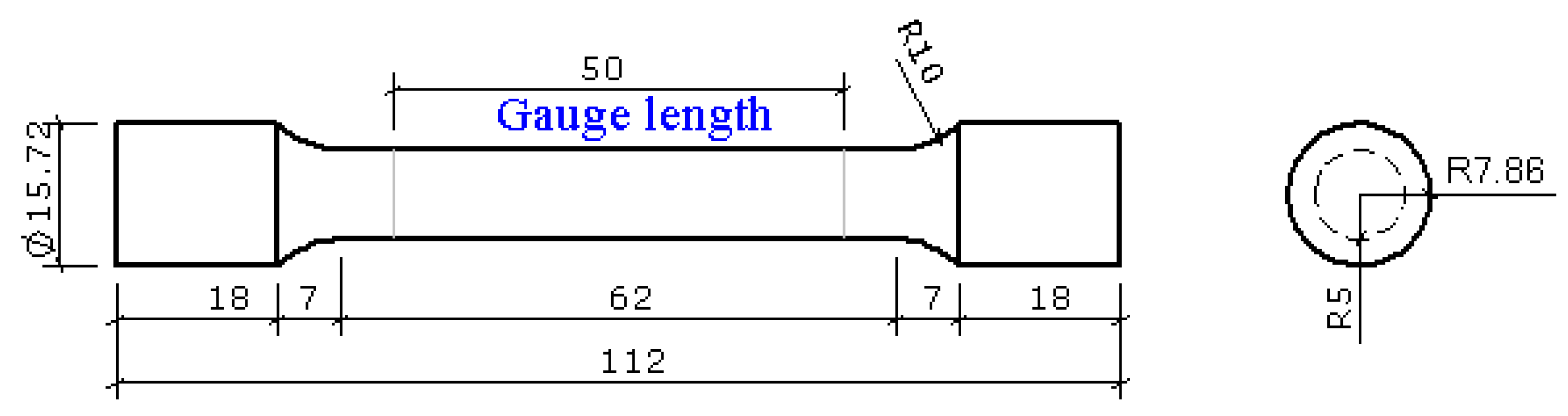
2. Summary of Tensile Tests of Q890 High Strength Steel at Elevated Temperatures
3. Procedure for Determining the Equivalent Stress-Plastic Strain Curves of Q890 Steel at Elevated Temperatures
3.1. Determination of Equivalent Stress-Plastic Strain Curves during the Pre-Necking Phase
3.2. Determination of Equivalent Stress-Plastic Strain Curves during the Post-Necking Phase
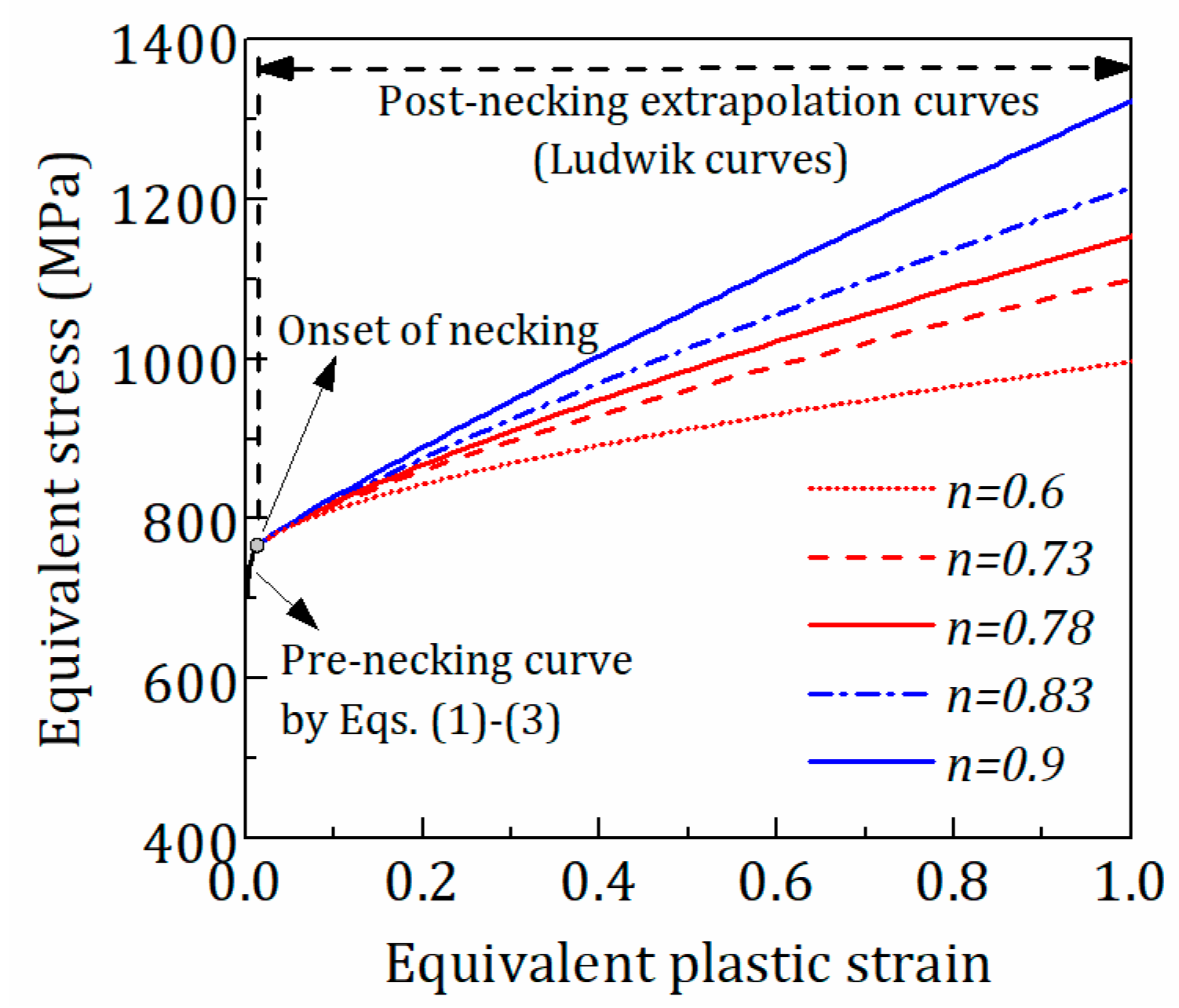
- Approach I—Iteration procedure for strain-hardening functions
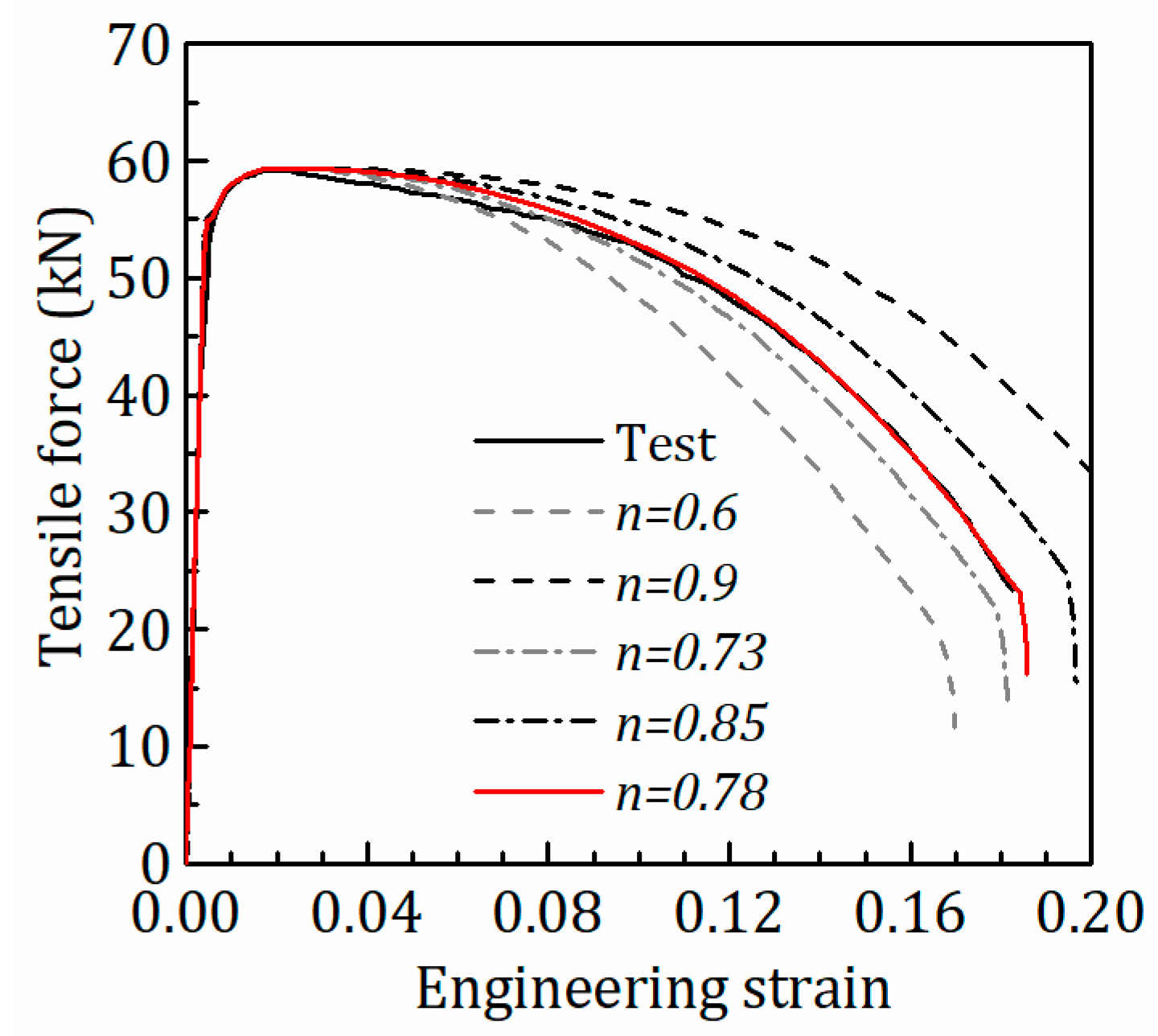
- Approach II—Iteration procedure for equivalent stress (Figure 5)
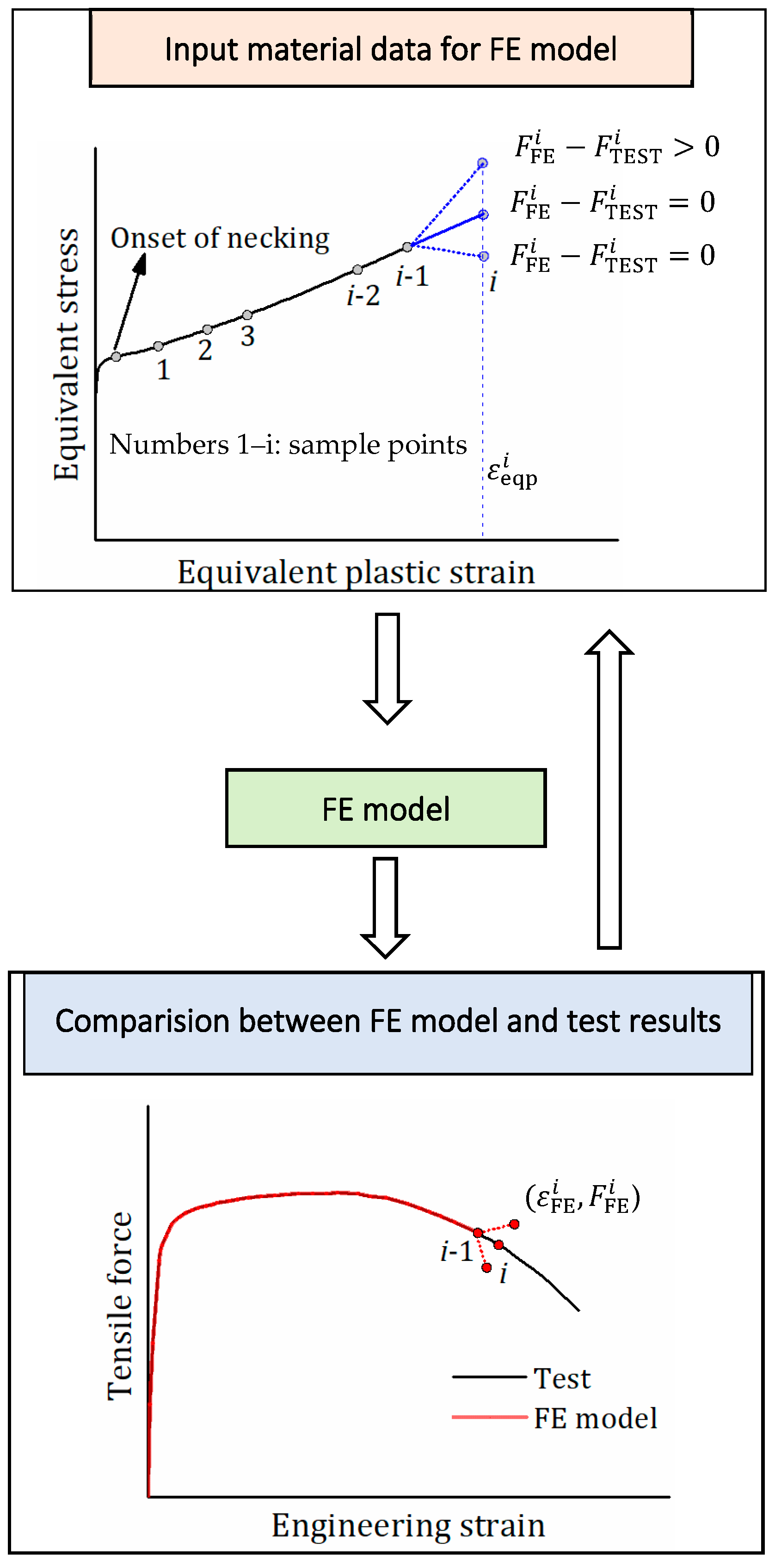
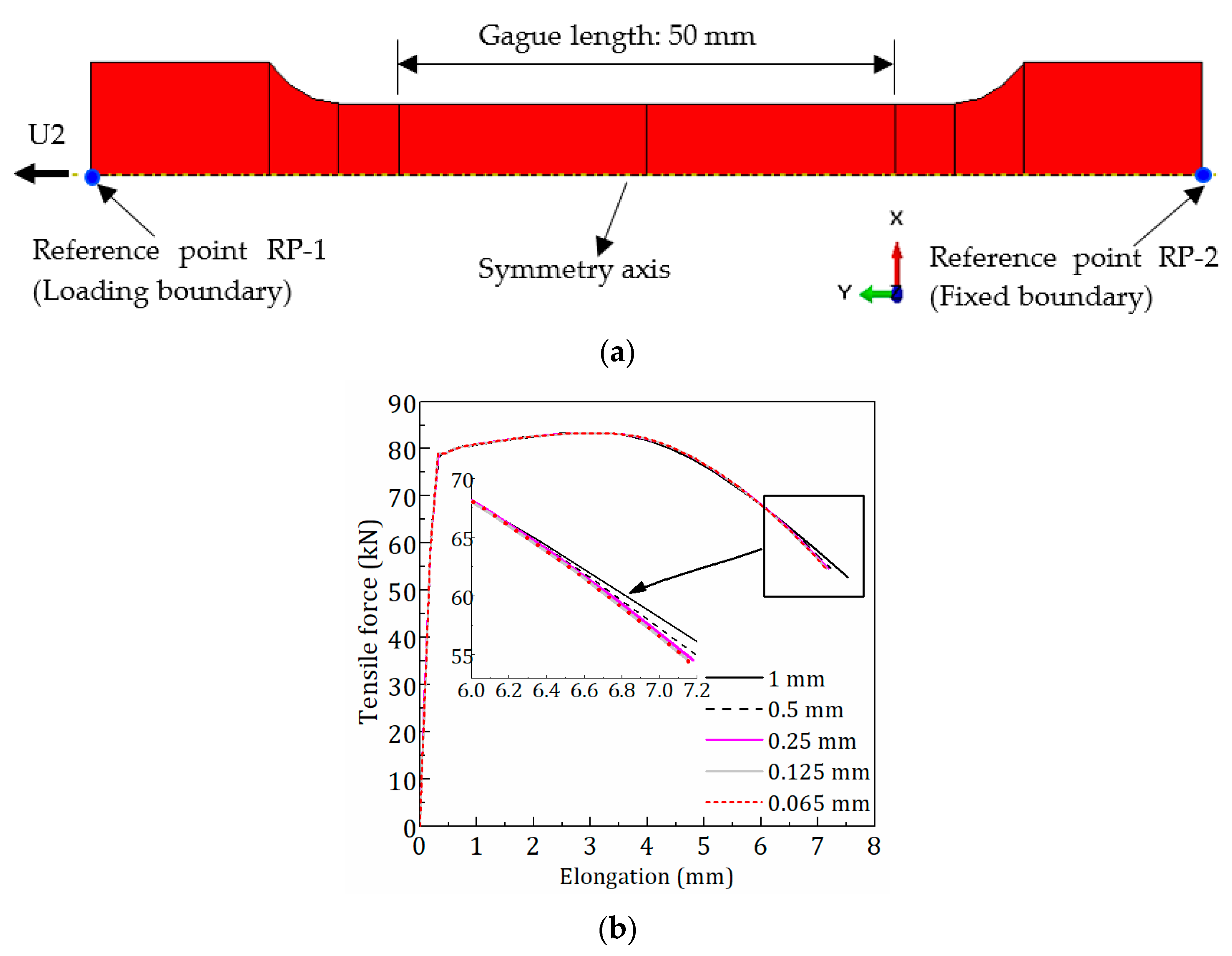
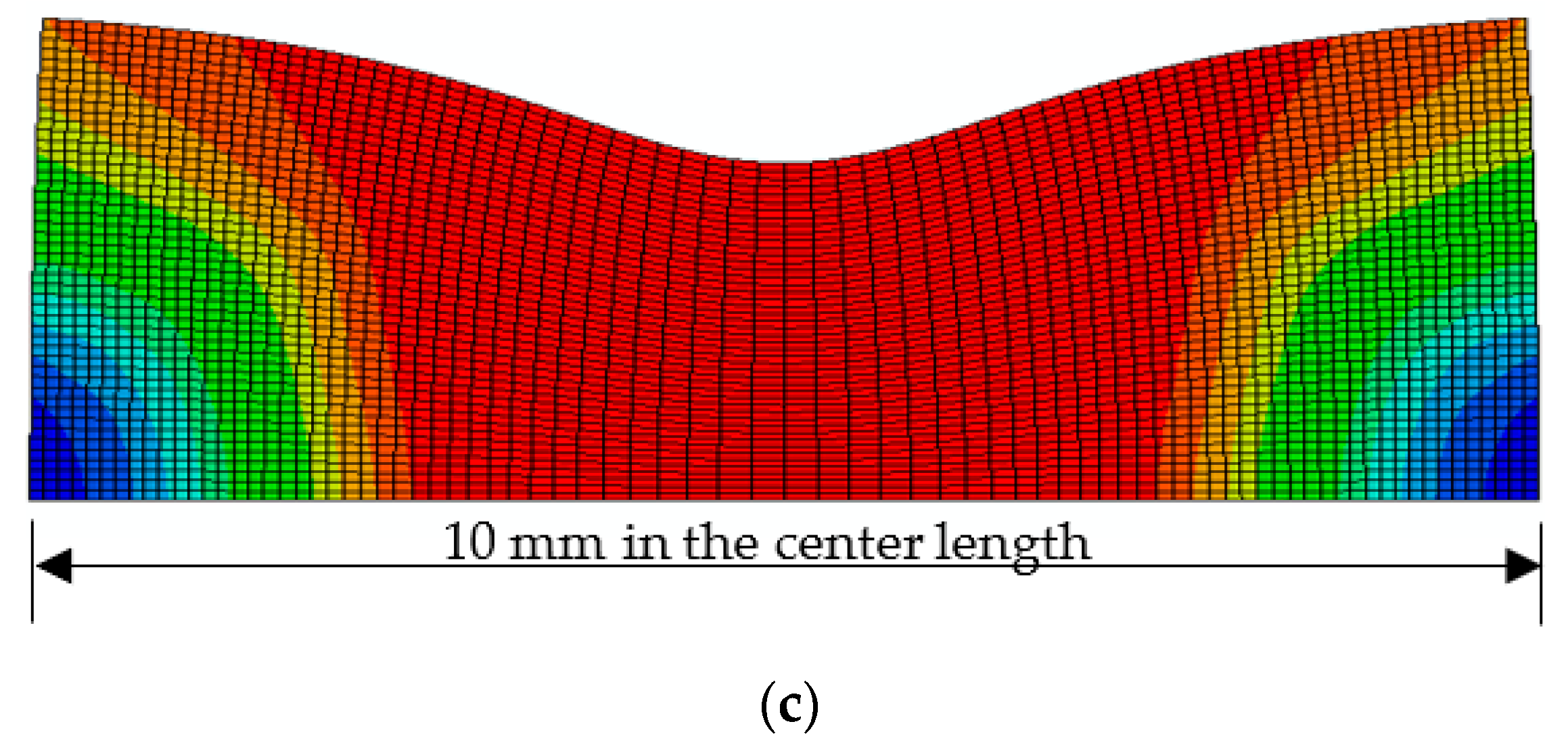
4. Description of FE Model
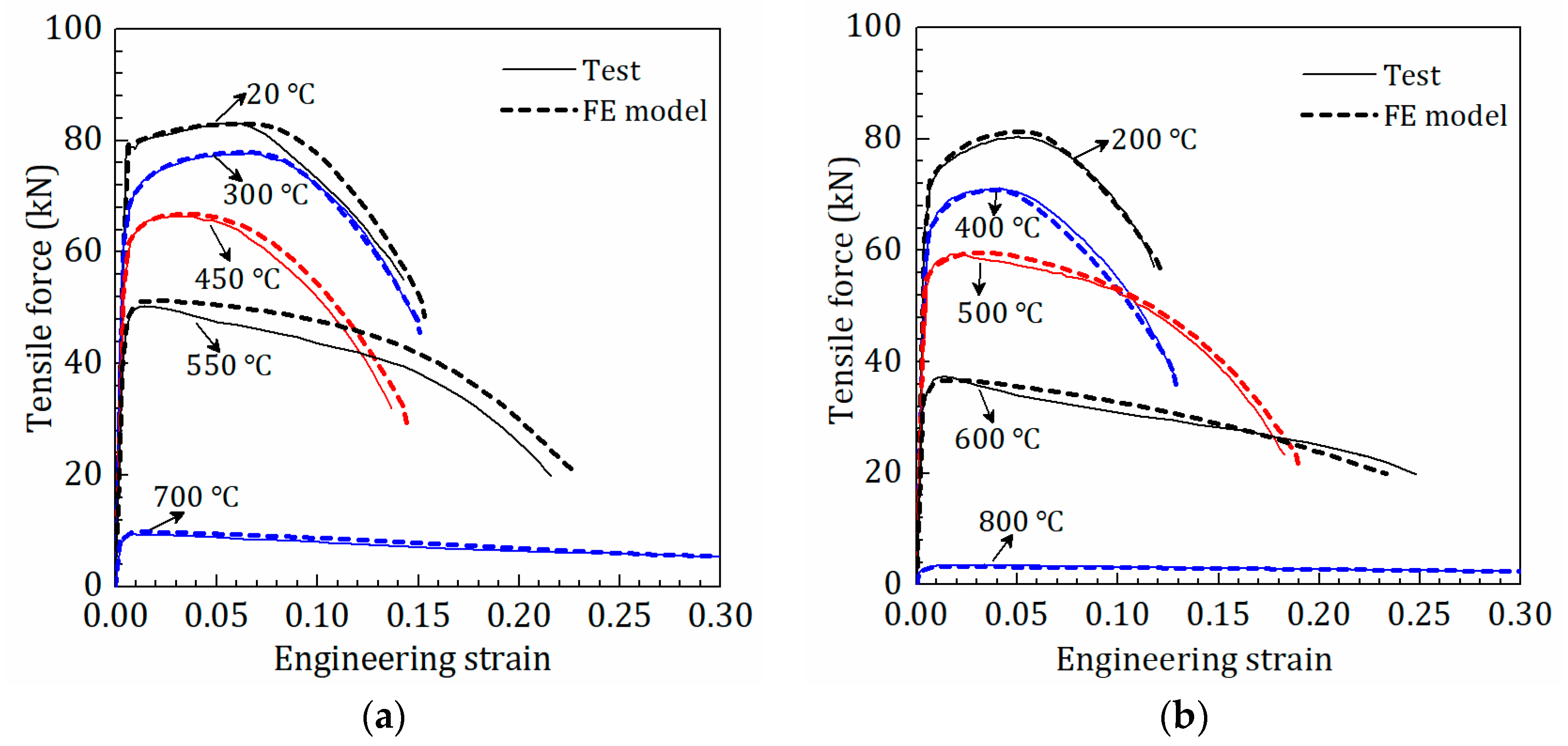
5. Constitutive Model for Equivalent Stress-Plastic Strain Curves of Q890 Steel at Different Temperatures
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nassiraei, H. Static strength of tubular T/Y-joints reinforced with collar plates at fire induced elevated temperature. Mar. Struct. 2019, 67, 102635. [Google Scholar] [CrossRef]
- Wang, Y.; Lennon, T.; Moore, D. The behaviour of steel frames subject to fire. J. Constr. Steel Res. 1995, 35, 291–322. [Google Scholar] [CrossRef]
- Li, G.Q.; Chen, K.; Jiang, S.C.; Yin, Y.Z. Experimental study on material properties of Q345 steel at high temperature. Build. Struct. 2001, 31, 53–55. (In Chinese) [Google Scholar]
- Chen, J.; Young, B.; Uy, B. Behavior of High Strength Structural Steel at Elevated Temperatures. J. Struct. Eng. 2006, 132, 1948–1954. [Google Scholar] [CrossRef]
- Qiang, X.; Bijlaard, F.; Kolstein, H. Dependence of mechanical properties of high strength steel S690 on elevated temperatures. Constr. Build. Mater. 2012, 30, 73–79. [Google Scholar] [CrossRef]
- Qiang, X.; Bijlaard, F.S.; Kolstein, H. Elevated-temperature mechanical properties of high strength structural steel S460N: Experimental study and recommendations for fire-resistance design. Fire Saf. J. 2013, 55, 15–21. [Google Scholar] [CrossRef]
- Chiew, S.; Zhao, M.; Lee, C.K. Mechanical properties of heat-treated high strength steel under fire/post-fire conditions. J. Constr. Steel Res. 2014, 98, 12–19. [Google Scholar] [CrossRef]
- Wang, W.Y.; Liu, B.; Li, G.Q. Experimental study on high temperature mechanical properties of high strength Q460 steel. J. Disaster Prev. Mitig. Eng. 2012, 32, 30–35. (In Chinese) [Google Scholar]
- Lee, J.; Engelhardt, M.D.; Choi, B.J. Constitutive model for ASTM A992 steel at elevated temperature. Int. J. Steel Struct. 2015, 15, 733–741. [Google Scholar] [CrossRef]
- Qiang, X.; Jiang, X.; Bijlaard, F.S.; Kolstein, H. Mechanical properties and design recommendations of very high strength steel S960 in fire. Eng. Struct. 2016, 112, 60–70. [Google Scholar] [CrossRef]
- Xiong, M.-X.; Liew, J.R. Mechanical properties of heat-treated high tensile structural steel at elevated temperatures. Thin-Walled Struct. 2016, 98, 169–176. [Google Scholar] [CrossRef]
- Li, G.Q.; Huang, L.; Zhang, C. Experimental study on high temperature elastic modulus of China made high strength structural steel. In Proceedings of the Eurosteel 2017, Copenhagen, Denmark, 13–15 September 2017. [Google Scholar]
- Neuenschwander, M.; Knobloch, M.; Fontana, M. Elevated temperature mechanical properties of solid section structural steel. Constr. Build. Mater. 2017, 149, 186–201. [Google Scholar] [CrossRef]
- Huang, L.; Li, G.-Q.; Wang, X.-X.; Zhang, C.; Choe, L.; Engelhardt, M. High Temperature Mechanical Properties of High Strength Structural Steels Q550, Q690 and Q890. Fire Technol. 2018, 54, 1609–1628. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Wang, K.; Kodur, V.; Wang, B. Mechanical Properties of High-Strength Q690 Steel at Elevated Temperature. J. Mater. Civ. Eng. 2018, 30, 04018062. [Google Scholar] [CrossRef]
- Fan, S.G.; Liu, P.; Shi, K.; Xiao, H.J.; Qian, F.; Fang, C. Experiment on mechanical properties of Q550D high-strength steel exposed to overall stage of fire exposure. J. Tianjin Univ. Sci. Technol. 2019, 52, 680–689. (In Chinese) [Google Scholar] [CrossRef]
- Wang, W.; Zhang, Y.; Xu, L.; Li, X. Mechanical properties of high-strength Q960 steel at elevated temperature. Fire Saf. J. 2020, 114, 103010. [Google Scholar] [CrossRef]
- Li, G.-Q.; Song, L.-X. Mechanical properties of TMCP Q690 high strength structural steel at elevated temperatures. Fire Saf. J. 2020, 116, 103190. [Google Scholar] [CrossRef]
- Kumar, W.; Sharma, U.K.; Shome, M. Mechanical properties of conventional structural steel and fire-resistant steel at elevated temperatures. J. Constr. Steel Res. 2021, 181, 106615. [Google Scholar] [CrossRef]
- Luecke, W.E.; Banovic, S.W.; McColskey, J.D. High-Temperature Tensile Constitutive Data and Models for Structural Steels in Fire; NIST Technical Note 1714; National Institute of Standards and Technology (NIST): Gaithersburg, MD, USA, 2011. [Google Scholar]
- EN 1993-1-2; Eurocode 3: Design of Steel Structures—Part 1–2: General Rules—Structural Fire Design. European Committee for Standardization (CEN): Brussels, Belgium, 2005.
- Lie, T.T. Structural Fire Protection. ASCE Manuals and Reports on Engineering Practice No. 78; American Society of Civil Engineers: New York, NY, USA, 1992. [Google Scholar]
- Poh, K.W. Stress-Strain-Temperature Relationship for Structural Steel. J. Mater. Civ. Eng. 2001, 13, 371–379. [Google Scholar] [CrossRef]
- Feng, C.Y.; Li, G.Q.; Jiang, B.H. The influence of high-temperature material model of steel on the simulation of collapse of steel frame structure under fire. Eng. Mech. 2019, 36, 24–36. (In Chinese) [Google Scholar] [CrossRef]
- Tu, S.; Ren, X.; He, J.; Zhang, Z. A method for determining material’s equivalent stress-strain curve with any axisymmetric notched tensile specimens without Bridgman correction. Int. J. Mech. Sci. 2018, 135, 656–667. [Google Scholar] [CrossRef]
- Yao, Z.; Wang, W. Full-range strain-hardening behavior of structural steels: Experimental identification and numerical simulation. J. Constr. Steel Res. 2022, 194, 107329. [Google Scholar] [CrossRef]
- Mirone, G. A new model for the elastoplastic characterization and the stress–strain determination on the necking section of a tensile specimen. Int. J. Solids Struct. 2004, 41, 3545–3564. [Google Scholar] [CrossRef]
- Bridgman, P.W. Studies in Large Plastic Flow and Fracture, 2nd ed.; Harvard University Press: Cambridge, MA, USA, 1964. [Google Scholar] [CrossRef]
- Joun, M.; Eom, J.G.; Lee, M.C. A new method for acquiring true stress–strain curves over a large range of strains using a tensile test and finite element method. Mech. Mater. 2008, 40, 586–593. [Google Scholar] [CrossRef]
- Kamaya, M.; Kawakubo, M. A procedure for determining the true stress–strain curve over a large range of strains using digital image correlation and finite element analysis. Mech. Mater. 2011, 43, 243–253. [Google Scholar] [CrossRef]
- Chen, J.; Li, J.; Li, Z. Experiment research on rate-dependent constitutive model of Q420 steel. Constr. Build. Mater. 2017, 153, 816–823. [Google Scholar] [CrossRef]
- Chen, J.; Shu, W.; Li, J. Constitutive model of Q345 steel at different intermediate strain rates. Int. J. Steel Struct. 2017, 17, 127–137. [Google Scholar] [CrossRef]
- Liu, X.; He, Z.; Ye, J.; Yan, L.; Li, S.; Tang, Y. Study on dynamic mechanical behavior of Q460JSC and HQ600 high strength steel. J. Constr. Steel Res. 2020, 173, 106232. [Google Scholar] [CrossRef]
- JGJ/T 483–2020; Standard for Design of High Strength Steel Structure. China Architecture & Building Press: Beijing, China, 2020. (In Chinese)
- Shi, G.; Hu, F.; Shi, Y. Recent research advances of high strength steel structures and codification of design specification in China. Int. J. Steel Struct. 2014, 14, 873–887. [Google Scholar] [CrossRef]
- Li, G.-Q.; Wang, Y.-B.; Chen, S.-W. The art of application of high-strength steel structures for buildings in seismic zones. Adv. Steel Constr. 2015, 11, 492–506. [Google Scholar] [CrossRef]
- Billingham, J.; Sharp, J.V.; Spurrier, J. Review of the Performance of High Strength Steels Used Offshore; Technical Report, RR-105; Health and Safety Executive: Bootle, UK, 2003. Available online: https://www.hse.gov.uk/research/rrpdf/rr105.pdf (accessed on 8 November 2022).
- Zeng, X.; Wu, W.; Huo, J.; Elchalakani, M. Residual mechanical properties of Q890 high-strength structural steel after exposure to fire. Constr. Build. Mater. 2021, 304, 124661. [Google Scholar] [CrossRef]
- Voce, E. The relationship between stress and strain for homogeneous deformation. J. Inst. Metals. 1948, 74, 537–562. [Google Scholar]
- Ludwik, P. Elemente der Technologischen Mechanik; Springer: Berlin/Heidelberg, Germany, 1909. [Google Scholar]


| Temperature (°C) | Elastic Modulus ET (MPa) | Yield Stress fy,T (MPa) | Ultimate Tensile Strength fu,T (MPa) |
|---|---|---|---|
| 20 | 204,976 | 1003 | 1057 |
| 200 | 204,400 | 893 | 1025 |
| 300 | 201,032 | 847 | 990 |
| 400 | 183,367 | 798 | 906 |
| 450 | 175,592 | 761 | 845 |
| 500 | 174,246 | 698 | 754 |
| 550 | 150,692 | 593 | 640 |
| 600 | 132,509 | 441 | 475 |
| 700 | 60,189 | 104 | 120 |
| 800 | 23,209 | 37 | 45 |
| T (°C) | Hardening Model | |
|---|---|---|
| 20 | Voce | |
| 200 | Voce | |
| 300 | Voce | |
| 400 | Voce | |
| 450 | Voce | |
| 500 | Ludwik |
| T (°C) | 800 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| at fracture | 1.006 | 0.719 | 0.985 | 1.08 | 1.35 | 1.95 | 2.29 | 2.22 | 2.92 | 2.3 |
| T (°C) | 20 | 200 | 300 | 400 | 450 | 500 | 550 | 600 | 700 | 800 | Mean | Standard Deviation |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.000 | 0.990 | 0.984 | 1.029 | 1.029 | 0.967 | 1.003 | 0.964 | 1.120 | 0.749 | 0.984 | 0.0889 | |
| 0.982 | 0.981 | 0.987 | 1.045 | 1.047 | 0.981 | 1.005 | 0.942 | 1.075 | 1.048 | 1.009 | 0.0397 | |
| 1.000 | 0.998 | 1.002 | 1.002 | 0.999 | 0.997 | 0.998 | 0.999 | 1.020 | 0.058 | 0.907 | 0.2832 | |
| 1.000 | 1.011 | 1.000 | 0.991 | 1.003 | 0.992 | 1.018 | 0.983 | 1.052 | 0.910 | 0.9960 | 0.0341 |
| T (°C) | |||||
|---|---|---|---|---|---|
| 20 | −87.62 | −115.96 | 203.58 | −24.10 | −9.47 |
| 200 | −14.39 | −192.18 | 206.57 | −136.43 | −42.54 |
| 300 | −81.13 | −175.81 | 256.94 | −123.61 | −20.24 |
| 400 | −128.7 | −28.96 | 157.66 | −82.17 | −35.40 |
| 450 | −89.1 | −109.76 | 198.86 | −137.55 | −8.53 |
| 500 | −1319.27 | −78.33 | 1397.6 | −0.34 | −104.93 |
| T (°C) | C | |||||
|---|---|---|---|---|---|---|
| 550 | −3.9496 | 52.397 | 0.00327 | 9.53 × 10−4 | −2682.4 | −0.1809 |
| 600 | −0.575 | 37.415 | 0.00394 | 6.82 × 10−4 | −350.94 | −0.764 |
| 700 | −0.5068 | 16.9 | 0.00341 | 6.33 × 10−4 | −72.98 | −0.9435 |
| 800 | −0.4473 | 7.606 | 0.00386 | 0.001 | −30.6 | −0.9442 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, X.; Wu, W.; Zou, J.; Elchalakani, M. Constitutive Model for Equivalent Stress-Plastic Strain Curves Including Full-Range Strain Hardening Behavior of High-Strength Steel at Elevated Temperatures. Materials 2022, 15, 8075. https://doi.org/10.3390/ma15228075
Zeng X, Wu W, Zou J, Elchalakani M. Constitutive Model for Equivalent Stress-Plastic Strain Curves Including Full-Range Strain Hardening Behavior of High-Strength Steel at Elevated Temperatures. Materials. 2022; 15(22):8075. https://doi.org/10.3390/ma15228075
Chicago/Turabian StyleZeng, Xiang, Wanbo Wu, Juan Zou, and Mohamed Elchalakani. 2022. "Constitutive Model for Equivalent Stress-Plastic Strain Curves Including Full-Range Strain Hardening Behavior of High-Strength Steel at Elevated Temperatures" Materials 15, no. 22: 8075. https://doi.org/10.3390/ma15228075
APA StyleZeng, X., Wu, W., Zou, J., & Elchalakani, M. (2022). Constitutive Model for Equivalent Stress-Plastic Strain Curves Including Full-Range Strain Hardening Behavior of High-Strength Steel at Elevated Temperatures. Materials, 15(22), 8075. https://doi.org/10.3390/ma15228075







