Selected Shear Models Based on the Analysis of the Critical Shear Crack for Slender Concrete Beams without Shear Reinforcement
Abstract
1. Introduction
2. Overview of Selected Theoretical Models
2.1. Muttoni and Ruiz 2008 [11]
2.2. Zhang et al., 2014 [12]
2.3. Yang 2014 [13]
2.4. Cladera et al., 2016 [14]
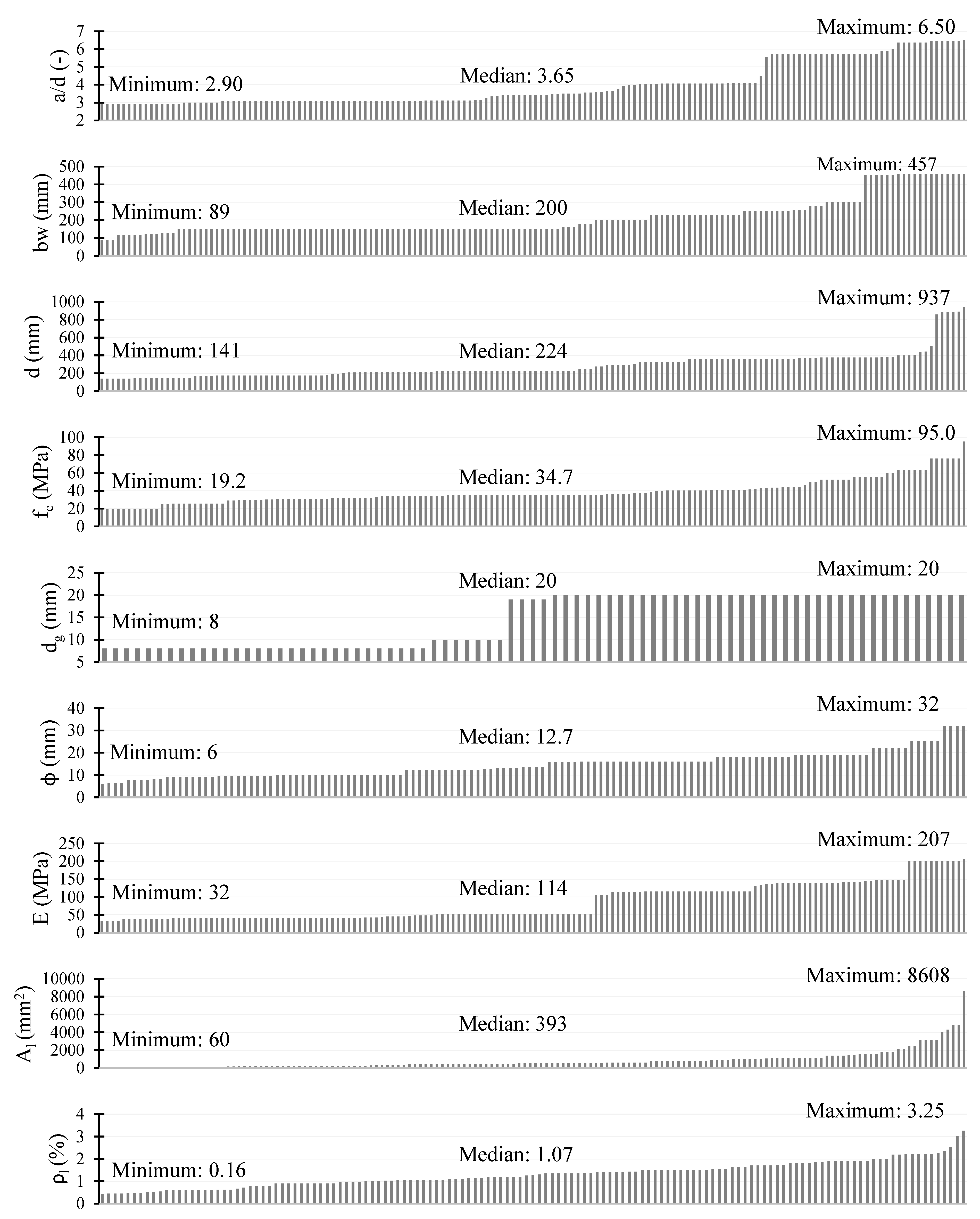
3. Test Database
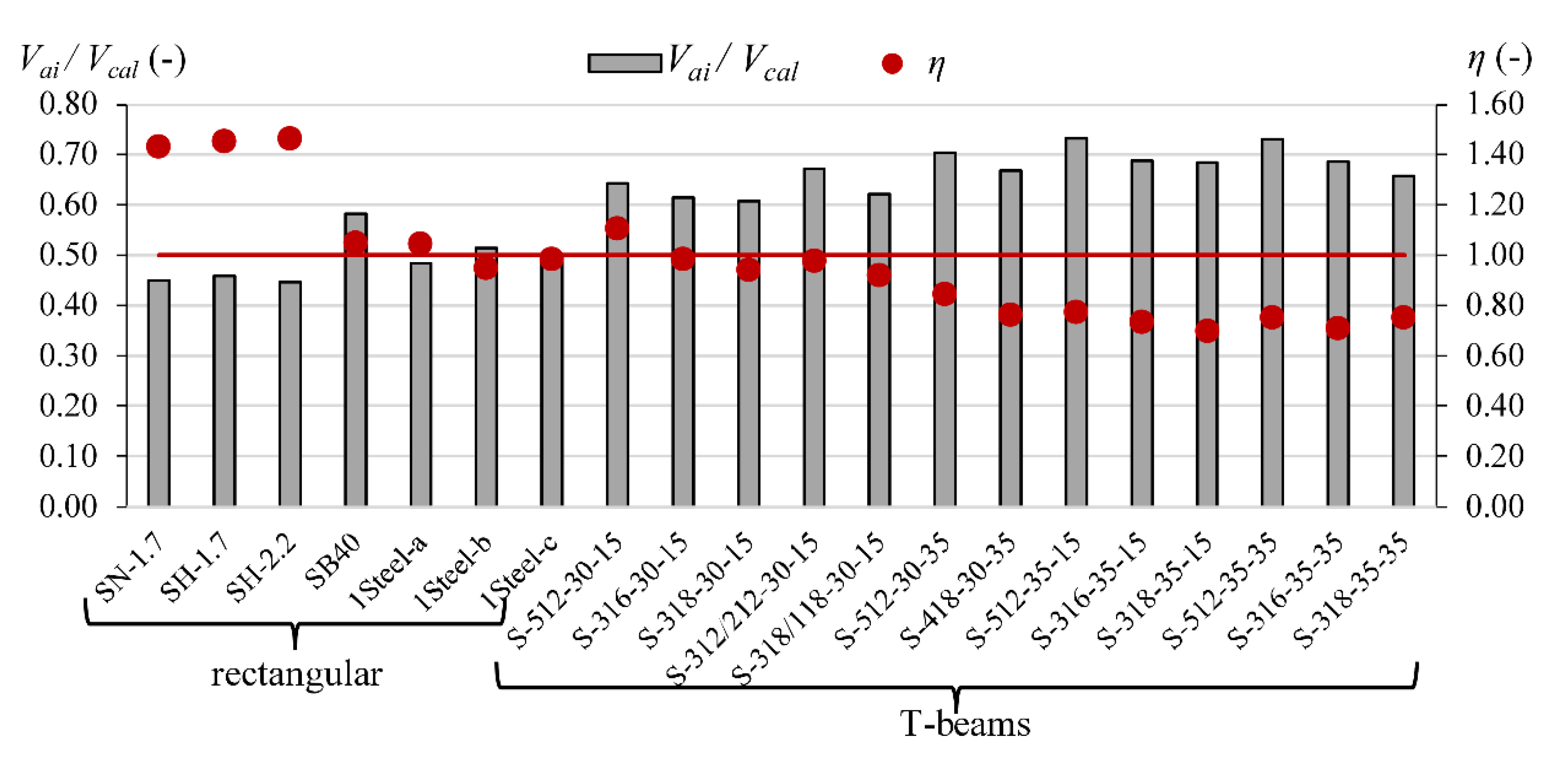
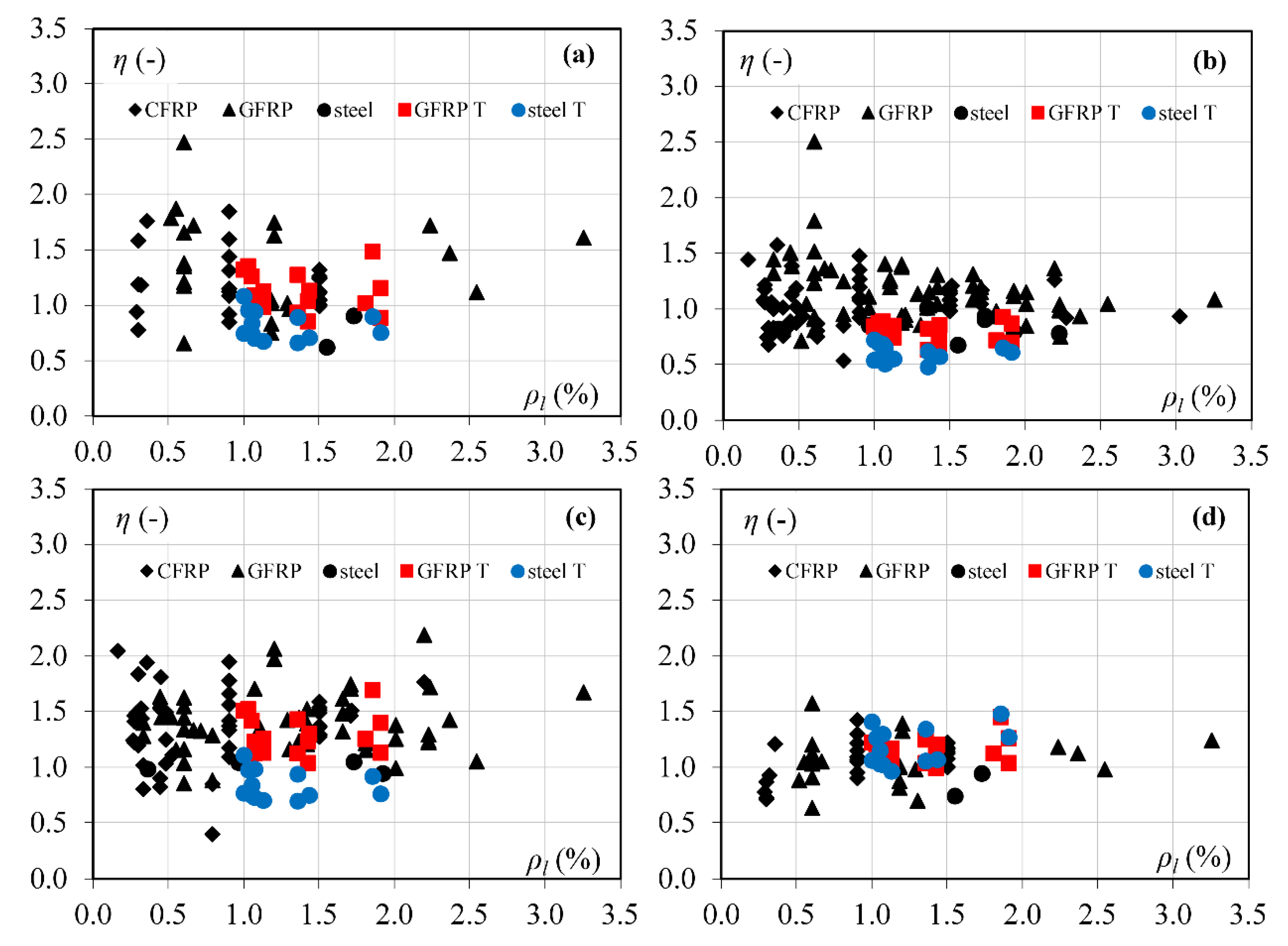
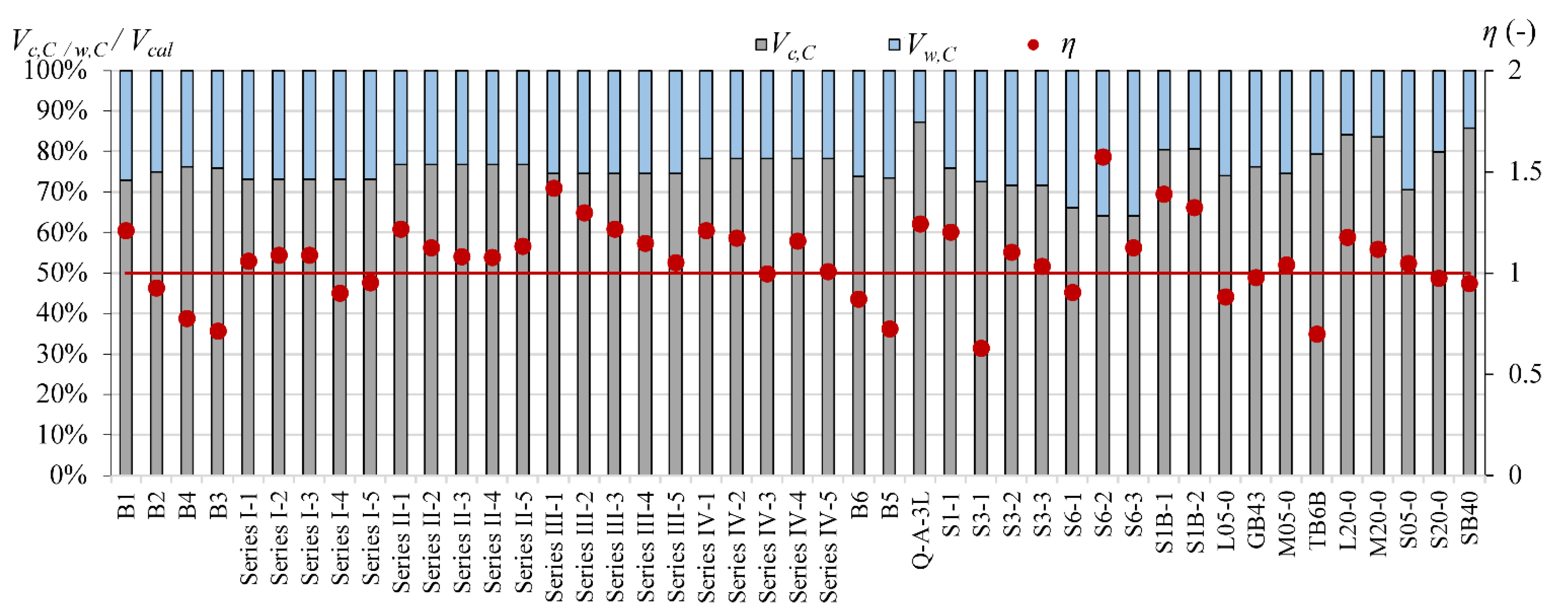
4. Results and Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| a | the distance from the support to the loading force [mm] |
| bw | the width of web in T-beams and the width in rectangular beams [mm] |
| d | the effective depth [mm] |
| dg | the maximum aggregate size [mm] |
| fc | the concrete compressive strength [MPa] |
| fctm | the mean concrete tensile strength [MPa] |
| hf | the height of flange in T-beams [mm] |
| n | the number of bars in longitudinal reinforcement [-] |
| x | the neutral axis depth [mm] |
| Al | the cross section longitudinal reinforcement [mm2] |
| E | the modulus of elasticity of longitudinal reinforcement [MPa] |
| Ec | the modulus of elasticity of concrete [MPa] |
| M | the bending moment in the critical section [kNm] |
| V | the shear force in critical section [kN] |
| ε | the strain in concrete [-] |
| the longitudinal reinforcement ratio [%] | |
| the diameter of longitudinal reinforcement [mm] |
Appendix A
| Specimen/Symbol | a/d | bw(mm) | d(mm) | fc(MPa) | dg (mm) | Type | ϕ (mm) | E (GPa) | Al (mm2) | ρl (%) | Vmax (kN) | [MR] | [Z] | [Y] | [C] | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Tureyen and Frosch [32] | V-A-1 | 3.4 | 457 | 360 | 40.3 | - | AFRP | - | 47.1 | 1579 | 1.0 | 115.6 | - | 105.5 | - | - |
| V-A-2 | 3.4 | 457 | 360 | 42.6 | - | AFRP | - | 130.0 | 3159 | 1.9 | 178.3 | - | 224.6 | - | - | |
| Zhao et al. [33] | I-No.1 | 3.00 | 150 | 250 | 34.3 | - | CFRP | - | 105.0 | 568 | 1.5 | 45.0 | - | 37.4 | - | - |
| II-No.6 | 3.00 | 150 | 250 | 34.3 | - | CFRP | - | 105.0 | 1136 | 3.0 | 46.0 | - | 49.1 | - | - | |
| IV-No.15 | 3.00 | 150 | 250 | 34.3 | - | CFRP | - | 105.0 | 852 | 2.3 | 40.5 | - | 44.0 | - | - | |
| El- Sayed et al. [34] | CN-1.7 | 3.10 | 250 | 326 | 43.6 | - | CFRP | 12.7 | 134 | 1393 | 1.7 | 124.5 | - | 106.3 | 82.4 | - |
| CH-1.7 | 3.10 | 250 | 326 | 63.0 | - | CFRP | 15.9 | 135 | 1390 | 1.7 | 130.0 | - | 124.8 | 88.8 | - | |
| CH-2.2 | 3.10 | 250 | 326 | 63.0 | - | CFRP | 15.9 | 135 | 1787 | 2.2 | 174.0 | - | 138.0 | 98.6 | - | |
| Jin et al. [35] | C-L-18-R1-1,2 | 3.10 | 200 | 215.5 | 33.6 | - | CFRP | 9 | 146.2 | 127 | 0.3 | 25.8 | - | 25.9 | 25.4 | - |
| C-L-18-R2-1,2 | 3.10 | 150 | 215.5 | 33.6 | - | CFRP | 9 | 146.2 | 127 | 0.4 | 18.9 | - | 22.1 | 22.9 | - | |
| C-L-18-R3-1,2 | 3.10 | 150 | 213.5 | 33.6 | - | CFRP | 13 | 147.9 | 265 | 0.8 | 15.3 | - | 28.6 | 38.6 | - | |
| C-L-27-R1-1,2 | 3.10 | 200 | 215.5 | 40.3 | - | CFRP | 9 | 146.2 | 127 | 0.3 | 23.2 | - | 27.9 | 28.9 | - | |
| C-L-27-R2-1,2 | 3.10 | 150 | 215.5 | 40.3 | - | CFRP | 9 | 146.2 | 127 | 0.4 | 21.1 | - | 23.8 | 23.4 | - | |
| C-L-27-R3-1,2 | 3.10 | 150 | 213.5 | 40.3 | - | CFRP | 13 | 147.9 | 265 | 0.8 | 26.2 | - | 30.8 | 30.7 | - | |
| Razaqpur et al. [36] | B1 | 3.50 | 300 | 200 | 52.3 | 20 | CFRP | 9.5 | 114 | 213 | 0.4 | 64.0 | 36.4 | 40.7 | 33.0 | 52.9 |
| B2 | 3.50 | 300 | 300 | 52.3 | 20 | CFRP | 9.5 | 114 | 284 | 0.3 | 61.0 | 51.6 | 57.8 | 39.9 | 65.8 | |
| B4 | 3.50 | 300 | 500 | 52.3 | 20 | CFRP | 9.5 | 114 | 425 | 0.3 | 68.0 | 72.6 | 91.8 | 45.7 | 87.4 | |
| B3 | 3.50 | 300 | 400 | 52.3 | 20 | CFRP | 9.5 | 114 | 354 | 0.3 | 55.0 | 70.8 | 74.8 | 46.1 | 77.2 | |
| Razaqpur et al. [37] | BA3 | 3.56 | 200 | 225 | 40.5 | - | CFRP | 8 | 145 | 201 | 0.4 | 47.0 | - | 34.0 | 26.0 | - |
| BA4 | 4.50 | 200 | 225 | 40.5 | - | CFRP | 8 | 145 | 201 | 0.4 | 38.5 | - | 34.0 | 25.3 | - | |
| Ashour and Kara [38] | B-300-2 | 3.60 | 200 | 276.117 | 29.8 | - | CFRP | 7.5 | 141.44 | 88 | 0.2 | 32.9 | - | 22.8 | 16.1 | - |
| B-300-4 | 3.60 | 200 | 276.117 | 29.8 | - | CFRP | 7.5 | 141.44 | 177 | 0.3 | 32.9 | - | 31.4 | 22.9 | - | |
| Olivito and Zuccarello [39] | Series I-1 | 5.71 | 150 | 175 | 19.2 | 20 | CFRP | 10 | 115 | 236 | 0.9 | 19.5 | 18.0 | 18.1 | 14.6 | 18.4 |
| Series I-2 | 5.71 | 150 | 175 | 19.2 | 20 | CFRP | 10 | 115 | 236 | 0.9 | 20.0 | 17.8 | 18.1 | 14.6 | 18.4 | |
| Series I-3 | 5.71 | 150 | 175 | 19.2 | 20 | CFRP | 10 | 115 | 236 | 0.9 | 20.0 | 17.8 | 18.1 | 14.6 | 18.4 | |
| Series I-4 | 5.71 | 150 | 175 | 19.2 | 20 | CFRP | 10 | 115 | 236 | 0.9 | 16.6 | 19.6 | 18.1 | 15.2 | 18.4 | |
| Series I-5 | 5.71 | 150 | 175 | 19.2 | 20 | CFRP | 10 | 115 | 236 | 0.9 | 17.6 | 19.0 | 18.1 | 15.0 | 18.4 | |
| Series II-1 | 5.71 | 150 | 175 | 19.2 | 20 | CFRP | 10 | 115 | 393 | 1.5 | 26.0 | 20.9 | 22.3 | 17.5 | 21.3 | |
| Series II-2 | 5.71 | 150 | 175 | 19.2 | 20 | CFRP | 10 | 115 | 393 | 1.5 | 24.0 | 21.6 | 22.3 | 17.7 | 21.3 | |
| Series II-3 | 5.71 | 150 | 175 | 19.2 | 20 | CFRP | 10 | 115 | 393 | 1.5 | 23.1 | 22.0 | 22.3 | 17.8 | 21.3 | |
| Series II-4 | 5.71 | 150 | 175 | 19.2 | 20 | CFRP | 10 | 115 | 393 | 1.5 | 23.0 | 22.0 | 22.3 | 17.8 | 21.3 | |
| Series II-5 | 5.71 | 150 | 175 | 19.2 | 20 | CFRP | 10 | 115 | 393 | 1.5 | 24.2 | 21.6 | 22.3 | 17.6 | 21.3 | |
| Series III-1 | 5.71 | 150 | 175 | 25.6 | 20 | CFRP | 10 | 115 | 236 | 0.9 | 29.9 | 16.2 | 20.2 | 15.3 | 21.3 | |
| Series III-2 | 5.71 | 150 | 175 | 25.6 | 20 | CFRP | 10 | 115 | 236 | 0.9 | 27.3 | 17.1 | 20.2 | 15.3 | 21.0 | |
| Series III-3 | 5.71 | 150 | 175 | 25.6 | 20 | CFRP | 10 | 115 | 236 | 0.9 | 25.6 | 17.8 | 20.2 | 15.4 | 21.0 | |
| Series III-4 | 5.71 | 150 | 175 | 25.6 | 20 | CFRP | 10 | 115 | 236 | 0.9 | 24.2 | 18.4 | 20.2 | 15.5 | 21.0 | |
| Series III-5 | 5.71 | 150 | 175 | 25.6 | 20 | CFRP | 10 | 115 | 236 | 0.9 | 22.2 | 19.3 | 20.2 | 15.7 | 21.0 | |
| Series IV-1 | 5.71 | 150 | 175 | 25.6 | 20 | CFRP | 10 | 115 | 393 | 1.5 | 29.7 | 22.5 | 25.0 | 18.7 | 21.0 | |
| Series IV-2 | 5.71 | 150 | 175 | 25.6 | 20 | CFRP | 10 | 115 | 393 | 1.5 | 28.7 | 22.8 | 25.0 | 18.7 | 24.5 | |
| Series IV-3 | 5.71 | 150 | 175 | 25.6 | 20 | CFRP | 10 | 115 | 393 | 1.5 | 24.5 | 24.6 | 25.0 | 19.2 | 24.5 | |
| Series IV-4 | 5.71 | 150 | 175 | 25.6 | 20 | CFRP | 10 | 115 | 393 | 1.5 | 28.4 | 22.9 | 25.0 | 18.7 | 24.5 | |
| Series IV-5 | 5.71 | 150 | 175 | 25.6 | 20 | CFRP | 10 | 115 | 393 | 1.5 | 24.7 | 24.5 | 25.0 | 19.2 | 24.5 | |
| Ashour and Kara [38] | B-200-2 | 5.90 | 200 | 169.918 | 24.7 | - | CFRP | 7.5 | 141.44 | 88 | 0.3 | 17.6 | - | 16.3 | 14.2 | |
| B-200-4 | 5.90 | 200 | 169.918 | 24.7 | - | CFRP | 7.5 | 141.44 | 177 | 0.5 | 20.8 | - | 22.2 | 18.7 | ||
| Razaqpur et al. [36] | B6 | 6.00 | 300 | 400 | 52.3 | 20 | CFRP | 9.5 | 114 | 354 | 0.3 | 62.0 | 39.2 | 74.8 | 33.8 | 71.2 |
| B5 | 6.50 | 300 | 400 | 52.3 | 20 | CFRP | 9.5 | 114 | 354 | 0.3 | 51.0 | 43.0 | 74.8 | 34.5 | 70.4 | |
| Gross et al. [40] | 8-2-1 | 6.36 | 127 | 143 | 55.0 | - | CFRP | 6.3 | 139.0 | 60 | 0.3 | 14.3 | - | 12.2 | 10.1 | - |
| 8-2-2 | 6.36 | 127 | 143 | 55.0 | - | CFRP | 6.3 | 139.0 | 60 | 0.3 | 12.9 | - | 12.2 | 10.5 | - | |
| 8-2-3 | 6.36 | 127 | 143 | 55.0 | - | CFRP | 6.3 | 139.0 | 60 | 0.3 | 14.7 | - | 12.2 | 10.1 | - | |
| 11-2-1 | 6.36 | 89 | 143 | 76.0 | - | CFRP | - | 139.0 | 60 | 0.4 | 8.8 | - | 11.5 | - | - | |
| 11-2-2 | 6.36 | 89 | 143 | 76.0 | - | CFRP | - | 139.0 | 60 | 0.4 | 11.7 | - | 11.5 | - | - | |
| 11-2-3 | 6.36 | 89 | 143 | 76.0 | - | CFRP | - | 139.0 | 60 | 0.4 | 8.9 | - | 11.5 | - | - | |
| 8-3-1 | 6.45 | 159 | 141 | 55.0 | - | CFRP | 9.5 | 139.0 | 130 | 0.5 | 19.8 | - | 19.5 | 15.9 | - | |
| 8-3-2 | 6.45 | 159 | 141 | 55.0 | - | CFRP | 9.5 | 139.0 | 130 | 0.5 | 23.1 | - | 19.5 | 15.5 | - | |
| 8-3-3 | 6.45 | 159 | 141 | 55.0 | - | CFRP | 9.5 | 139.0 | 130 | 0.5 | 17.0 | - | 19.5 | 16.5 | - | |
| 11-3-1 | 6.45 | 121 | 141 | 76.0 | - | CFRP | - | 139.0 | 130 | 0.6 | 14.3 | - | 19.0 | - | - | |
| 11-3-2 | 6.45 | 121 | 141 | 76.0 | - | CFRP | - | 139.0 | 130 | 0.6 | 15.3 | - | 19.0 | - | - | |
| 11-3-3 | 6.45 | 121 | 141 | 76.0 | - | CFRP | - | 139.0 | 130 | 0.6 | 16.6 | - | 19.0 | - | - | |
| Niewels [41] | Q-A-3L | 2.93 | 300 | 444 | 43.3 | 8 | GFRP | 32 | 43.968 | 4021 | 3.3 | 149.0 | 92.5 | 137.6 | 89.3 | 119.9 |
| El-Sayed et al. [34] | GN-1.7 | 3.10 | 250 | 326 | 43.6 | - | GFRP | 15.9 | 42 | 1390 | 1.7 | 77.5 | - | 65.0 | 45.4 | = |
| GH-1.7 | 3.10 | 250 | 326 | 63.0 | - | GFRP | 15.9 | 42 | 1390 | 1.7 | 87.0 | - | 75.8 | 50.0 | = | |
| GH-2.2 | 3.10 | 250 | 326 | 63.0 | - | GFRP | 15.9 | 42 | 1787 | 2.2 | 115.5 | - | 84.8 | 52.8 | = | |
| Steiner et al. [42] | A1 | 3.1 | 457 | 889 | 29.6 | - | GFRP | - | 41.0 | 2413 | 0.6 | 159.0 | - | 172.1 | - | - |
| Jin et al. [35] | G-L-18-R1-1,2 | 3.10 | 200 | 215.5 | 33.6 | - | GFRP | 9 | 41.0 | 127 | 0.3 | 20.7 | - | 14.3 | 14.8 | - |
| G-L-18-R2-1,2 | 3.10 | 150 | 215.5 | 33.6 | - | GFRP | 9 | 41.0 | 127 | 0.4 | 18.6 | - | 12.3 | 11.7 | - | |
| G-L-18-R3-1,2 | 3.10 | 150 | 213.5 | 33.6 | - | GFRP | 13 | 40.0 | 265 | 0.8 | 15.3 | - | 16.0 | 17.3 | - | |
| G-L-27-R1-1,2 | 3.10 | 200 | 215.5 | 40.3 | - | GFRP | 9 | 41.0 | 127 | 0.3 | 20.4 | - | 15.4 | 15.9 | - | |
| G-L-27-R2-1,2 | 3.10 | 150 | 215.5 | 40.3 | - | GFRP | 9.00 | 41.0 | 127 | 0.4 | 20.0 | - | 13.3 | 12.2 | - | |
| G-L-27-R3-1,2 | 3.10 | 150 | 213.5 | 40.3 | - | GFRP | 13.00 | 40.0 | 265 | 0.8 | 21.5 | - | 17.2 | 16.7 | - | |
| Matta et al. [43] | S3-0.24-1B | 3.10 | 114 | 292 | 40.6 | 19 | GFRP | - | 48.2 | 393 | 1.2 | 22.0 | 26.5 | 23.5 | - | 25.2 |
| S3-0.24-2B | 3.10 | 114 | 292 | 40.6 | 19 | GFRP | - | 48.2 | 393 | 1.2 | 20.6 | 27.6 | 23.5 | - | 25.2 | |
| S6-0.24-1B | 3.10 | 229 | 146 | 40.6 | 19 | GFRP | - | 48.2 | 395 | 1.2 | 33.0 | 31.6 | 23.6 | - | 32.6 | |
| S6-0.24-2B | 3.10 | 229 | 146 | 40.6 | 19 | GFRP | - | 48.2 | 395 | 1.2 | 32.5 | 31.9 | 23.6 | - | 32.6 | |
| Matta and Nanni [44] | S1-1 | 3.11 | 457 | 883 | 29.5 | 20 | GFRP | 32 | 40.7 | 2413 | 0.6 | 154.1 | 93.0 | 170.1 | 99.5 | 128.2 |
| S3-1 | 3.11 | 114 | 294 | 59.7 | 20 | GFRP | 16 | 40.8 | 201 | 0.6 | 15.2 | 23.2 | 18.9 | 17.7 | 24.1 | |
| S3-2 | 3.11 | 114 | 294 | 32.1 | 20 | GFRP | 16 | 40.8 | 201 | 0.6 | 19.3 | 14.3 | 14.7 | 13.4 | 17.5 | |
| S3-3 | 3.11 | 114 | 294 | 32.1 | 20 | GFRP | 16 | 40.8 | 201 | 0.6 | 18.1 | 15.0 | 14.7 | 13.5 | 17.5 | |
| S6-1 | 3.11 | 229 | 147 | 59.7 | 20 | GFRP | 16 | 40.8 | 201 | 0.6 | 28.6 | 24.4 | 18.9 | 27.5 | 31.6 | |
| S6-2 | 3.11 | 229 | 147 | 32.1 | 20 | GFRP | 16 | 40.8 | 201 | 0.6 | 36.8 | 14.9 | 14.7 | 22.7 | 23.4 | |
| S6-3 | 3.11 | 229 | 147 | 32.1 | 20 | GFRP | 16 | 40.8 | 201 | 0.6 | 26.3 | 19.1 | 14.7 | 22.6 | 23.4 | |
| S1B-1 | 3.12 | 457 | 880 | 29.5 | 20 | GFRP | 32 | 40.7 | 4825 | 1.2 | 220.7 | 126.2 | 234.0 | 107.1 | 158.7 | |
| S1B-2 | 3.12 | 457 | 880 | 30.7 | 20 | GFRP | 32 | 41.4 | 4825 | 1.2 | 216.2 | 132.8 | 239.6 | 109.6 | 163.1 | |
| Ashour [45] | Beam 3 | 3.14 | 150 | 212 | 28.9 | - | GFRP | 12 | 32 | 226 | 0.7 | 17.5 | - | 13.0 | 13.2 | 11.3 |
| Beam 9 | 3.14 | 150 | 212 | 50.2 | - | GFRP | 12 | 32 | 339 | 1.1 | 27.5 | - | 19.6 | 16.1 | 18.1 | |
| Bentz et al. [46] | L05-0 | 3.26 | 450 | 937 | 46.0 | 10 | GFRP | 25.4 | 37 | 2152 | 0.5 | 135.0 | 75.5 | 190.5 | 93.2 | 152.7 |
| M05-0 | 3.48 | 450 | 438 | 35.0 | 10 | GFRP | 25.4 | 37 | 1076 | 0.5 | 86.0 | 45.9 | 82.3 | 74.5 | 82.6 | |
| L20-0 | 3.56 | 450 | 857 | 36.0 | 10 | GFRP | 25.4 | 37 | 8608 | 2.2 | 232.0 | 134.6 | 309.2 | 135.2 | 196.8 | |
| M20-0 | 3.77 | 450 | 405 | 35.0 | 10 | GFRP | 25.4 | 37 | 4304 | 2.4 | 138.0 | 94.0 | 148.0 | 96.8 | 123.2 | |
| S05-0 | 3.93 | 450 | 194 | 35.0 | 10 | GFRP | 12.7 | 37 | 580 | 0.7 | 54.5 | 31.6 | 40.0 | 40.9 | 51.9 | |
| S20-0 | 4.05 | 450 | 188 | 35.0 | 10 | GFRP | 25.4 | 37 | 2152 | 2.5 | 74.0 | 66.2 | 71.0 | 70.3 | 75.8 | |
| Guadagnini et al. [47] | GB43 | 3.36 | 150 | 223 | 40.3 | 20 | GFRP | 13.5 | 45 | 429 | 1.3 | 27.2 | 26.7 | 24.0 | 19.1 | 27.7 |
| Tureyen and Frosch [32] | V-G1-1 | 3.4 | 457 | 360 | 39.7 | - | GFRP | - | 40.5 | 1579 | 1.0 | 108.9 | - | 97.9 | - | - |
| V-G2-1 | 3.4 | 457 | 360 | 39.8 | - | GFRP | - | 37.6 | 1579 | 1.0 | 95.4 | - | 94.7 | - | - | |
| V-G1-2 | 3.4 | 457 | 360 | 42.2 | - | GFRP | - | 32.0 | 3159 | 1.9 | 138.0 | - | 123.5 | - | - | |
| V-G2-2 | 3.4 | 457 | 360 | 42.5 | - | GFRP | - | 37.0 | 3159 | 1.9 | 153.7 | - | 132.1 | - | - | |
| Imjai [48] | TB6B | 3.49 | 150 | 220 | 95.0 | 10 | GFRP | 13.5 | 45 | 429 | 1.3 | 29.1 | 30.2 | 34.0 | 25.1 | 41.6 |
| Duranovic et al. [49] | GB2 | 3.65 | 150 | 210 | 38.1 | - | GFRP | 13.5 | 45 | 429 | 1.4 | 26.0 | - | 22.6 | 18.0 | - |
| GB6 | 3.65 | 150 | 210 | 32.9 | - | GFRP | 13.5 | 45 | 429 | 1.4 | 22.0 | - | 21.3 | 17.8 | - | |
| Ashour [45] | Beam 1 | 3.97 | 150 | 168 | 28.9 | - | GFRP | 6 | 38 | 113 | 0.4 | 12.5 | - | 9.0 | 8.6 | - |
| Beam 7 | 3.97 | 150 | 168 | 50.2 | - | GFRP | 12 | 32 | 339 | 1.3 | 17.5 | - | 17.3 | 15.5 | - | |
| Yost et al. [50] | 1FRP-a | 4.06 | 229 | 225 | 34.7 | - | GFRP | 19 | 40.336 | 567 | 1.1 | 39.1 | - | 30.9 | 28.9 | - |
| 1FRP-b | 4.06 | 229 | 225 | 34.7 | - | GFRP | 19 | 40.336 | 567 | 1.1 | 38.5 | - | 30.9 | 28.9 | - | |
| 1FRP-c | 4.06 | 229 | 225 | 34.7 | - | GFRP | 19 | 40.336 | 567 | 1.1 | 36.8 | - | 30.9 | 29.0 | - | |
| 2FRP-a | 4.06 | 178 | 225 | 34.7 | - | GFRP | 19 | 40.336 | 567 | 1.4 | 28.1 | - | 26.9 | 23.3 | - | |
| 2FRP-b | 4.06 | 178 | 225 | 34.7 | - | GFRP | 19 | 40.336 | 567 | 1.4 | 35.0 | - | 26.9 | 23.0 | - | |
| 2FRP-c | 4.06 | 178 | 225 | 34.7 | - | GFRP | 19 | 40.336 | 567 | 1.4 | 32.1 | - | 26.9 | 23.1 | - | |
| 3FRP-a | 4.06 | 229 | 225 | 34.7 | - | GFRP | 19 | 40.336 | 851 | 1.7 | 40.0 | - | 37.0 | 30.4 | - | |
| 3FRP-b | 4.06 | 229 | 225 | 34.7 | - | GFRP | 19 | 40.336 | 851 | 1.7 | 48.6 | - | 37.0 | 30.1 | - | |
| 3FRP-c | 4.06 | 229 | 225 | 34.7 | - | GFRP | 19 | 40.336 | 851 | 1.7 | 44.7 | - | 37.0 | 30.1 | - | |
| 4FRP-a | 4.06 | 279 | 225 | 34.7 | - | GFRP | 19 | 40.336 | 1134 | 1.8 | 43.8 | - | 46.9 | 38.0 | - | |
| 4FRP-b | 4.06 | 279 | 225 | 34.7 | - | GFRP | 19 | 40.336 | 1134 | 1.8 | 45.9 | - | 46.9 | 37.8 | - | |
| 4FRP-c | 4.06 | 279 | 225 | 34.7 | - | GFRP | 19 | 40.336 | 1134 | 1.8 | 46.1 | - | 46.9 | 37.7 | - | |
| 5FRP-a | 4.08 | 254 | 224 | 34.7 | - | GFRP | 22 | 40.336 | 1140 | 2.0 | 37.7 | - | 44.5 | 37.9 | - | |
| 5FRP-b | 4.08 | 254 | 224 | 34.7 | - | GFRP | 22 | 40.336 | 1140 | 2.0 | 51.0 | - | 44.5 | 37.0 | - | |
| 5FRP-c | 4.08 | 254 | 224 | 34.7 | - | GFRP | 22 | 40.336 | 1140 | 2.0 | 46.6 | - | 44.5 | 37.1 | - | |
| 6FRP-a | 4.08 | 229 | 224 | 34.7 | - | GFRP | 22 | 40.336 | 1140 | 2.2 | 43.5 | - | 42.0 | 33.7 | - | |
| 6FRP-b | 4.08 | 229 | 224 | 34.7 | - | GFRP | 22 | 40.336 | 1140 | 2.2 | 41.8 | - | 42.0 | 33.8 | - | |
| 6FRP-c | 4.08 | 229 | 224 | 34.7 | - | GFRP | 22 | 40.336 | 1140 | 2.2 | 41.3 | - | 42.0 | 33.8 | - | |
| El-Sayed et al. [34] | SN-1.7 | 3.10 | 250 | 326 | 43.6 | - | steel | 16 | 200 | 1407 | 1.7 | 144.5 | - | 124.7 | 101.1 | - |
| SH-1.7 | 3.10 | 250 | 326 | 63.0 | - | steel | 16 | 200 | 1407 | 1.7 | 160.0 | - | 146.5 | 110.3 | - | |
| SH-2.2 | 3.10 | 250 | 326 | 63.0 | - | steel | 16 | 200 | 1810 | 2.2 | 184.0 | - | 161.0 | 125.7 | - | |
| Guadagnini et al. [47] | SB40 | 3.35 | 150 | 224 | 43.4 | 20 | steel | 12 | 207 | 452 | 1.3 | 45.3 | 50.2 | 48.3 | 43.2 | 47.8 |
| Tureyen and Frosch [32] | V-S-1 | 3.4 | 457 | 360 | 40.9 | - | steel | - | 199.8 | 1579 | 1.0 | 180.5 | - | 198.6 | - | - |
| V-S-2 | 3.4 | 457 | 360 | 41.3 | - | steel | - | 200 | 3159 | 1.9 | 205.2 | - | 261.6 | - | - | |
| V-D-2 | 3.4 | 457 | 360 | 43.6 | - | steel | - | 200 | 592 | 0.4 | 135.7 | - | 134.3 | - | - | |
| Yost et al. [50] | 1Steel-a | 4.03 | 229 | 227 | 34.7 | - | steel | 16 | 200 | 804 | 1.5 | 60.7 | - | 70.7 | 58.2 | - |
| 1Steel-b | 4.03 | 229 | 227 | 34.7 | - | steel | 16 | 200 | 804 | 1.5 | 56.3 | - | 70.7 | 59.3 | - | |
| 1Steel-c | 4.03 | 229 | 227 | 34.7 | - | steel | 16 | 200 | 804 | 1.5 | 58.0 | - | 70.7 | 58.9 | - | |
| Olivito and Zuccarello [39] | S-1 | 5.56 | 150 | 180 | 19.2 | 20 | steel | - | 200 | 340 | 1.3 | 18.1 | 29.1 | 26.7 | - | 24.4 |
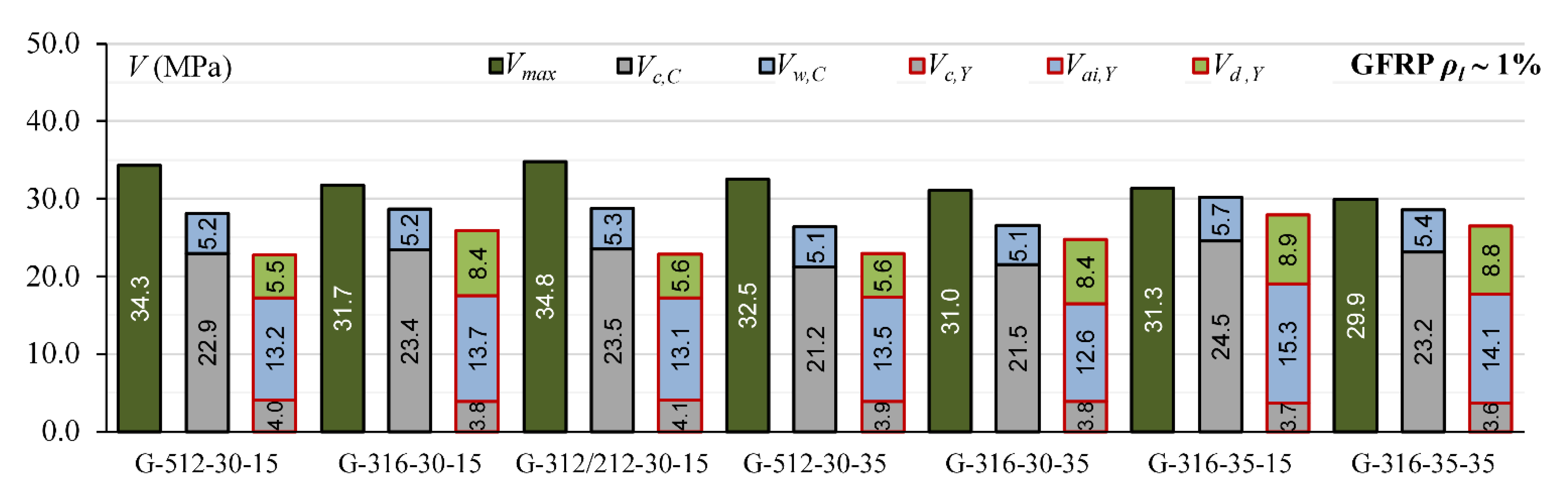
| Kotynia and Kaszubska [28] | G-512-30-15 | 2.90 | 150 | 379 | 30.10 | 8 | GFRP | 12 | 50.5 | 565 | 0.99 | 34.27 | 25.92 | 40.81 | 22.73 | 28.09 |
| G-316-30-15 | 2.92 | 150 | 377 | 31.10 | 8 | GFRP | 16 | 50.5 | 603 | 1.07 | 31.75 | 29.13 | 42.49 | 25.91 | 28.63 | |
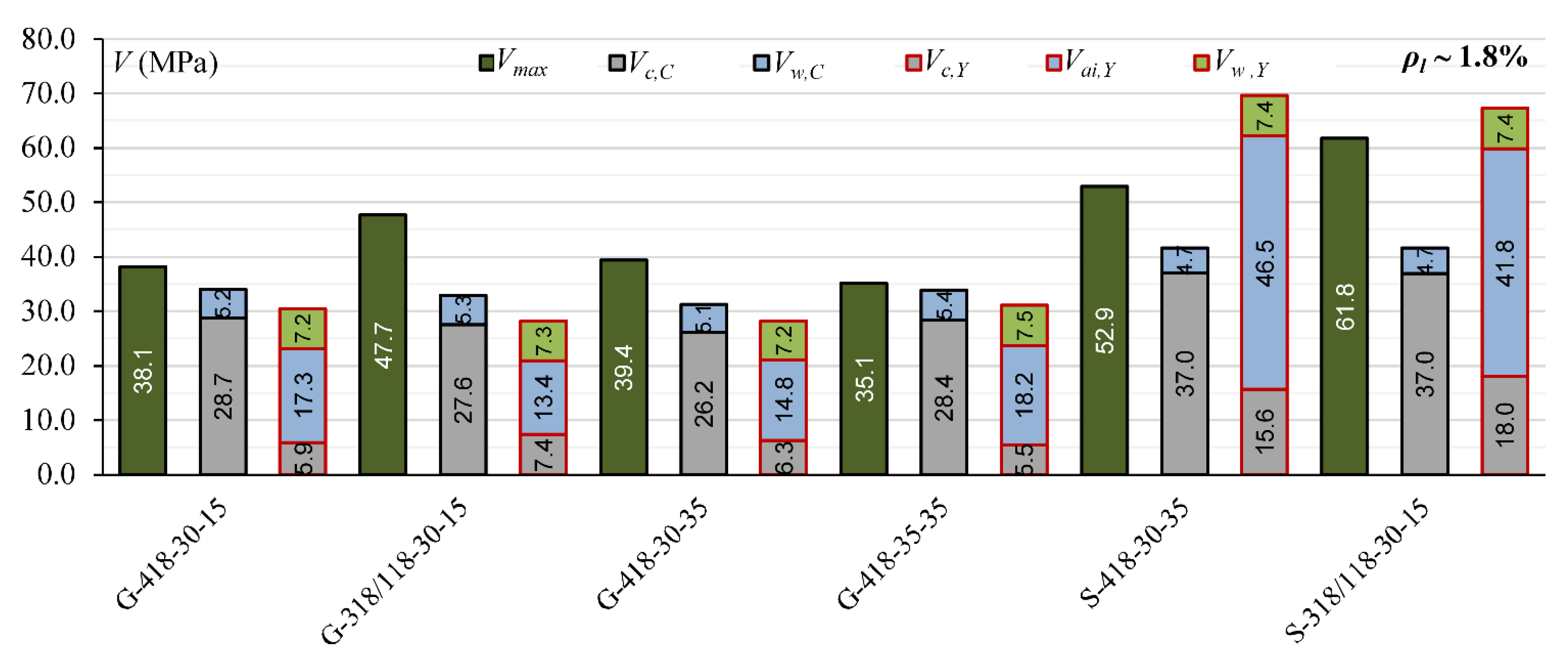
| G-318-30-15 | 2.93 | 150 | 376 | 31.10 | 8 | GFRP | 18 | 50.5 | 763 | 1.35 | 38.57 | 30.24 | 46.93 | 26.97 | 30.86 | |
| G-416-30-15 | 2.92 | 150 | 377 | 30.50 | 8 | GFRP | 16 | 50.5 | 804 | 1.42 | 34.77 | 33.57 | 47.67 | 28.25 | 31.52 | |
| G-418-30-15 | 2.93 | 150 | 376 | 31.10 | 8 | GFRP | 18 | 50.5 | 1018 | 1.80 | 38.14 | 37.61 | 53.33 | 30.41 | 33.97 | |
| G-312/212-30-15 | 2.99 | 150 | 367.8 | 32.30 | 8 | GFRP | 12 | 50.5 | 565 | 1.02 | 34.78 | 25.66 | 39.83 | 22.87 | 28.76 | |
| G-318/118-30-15 | 3.00 | 150 | 367 | 32.30 | 8 | GFRP | 18 | 50.5 | 1018 | 1.85 | 47.72 | 32.14 | 51.50 | 28.19 | 32.88 | |
| G-512-30-35 | 3.06 | 150 | 359 | 31.10 | 8 | GFRP | 12 | 50.5 | 565 | 1.05 | 32.47 | 25.82 | 36.47 | 22.90 | 26.37 | |
| G-316-30-35 | 3.08 | 150 | 357 | 30.50 | 8 | GFRP | 16 | 50.5 | 603 | 1.13 | 31.01 | 27.64 | 36.51 | 24.77 | 26.56 | |
| G-318-30-35 | 3.09 | 150 | 356 | 30.50 | 8 | GFRP | 18 | 50.5 | 763 | 1.43 | 34.42 | 30.57 | 40.28 | 26.54 | 28.60 | |
| G-418-30-35 | 3.09 | 150 | 356 | 30.10 | 8 | GFRP | 18 | 50.5 | 1018 | 1.91 | 39.41 | 34.19 | 45.25 | 28.26 | 31.23 | |
| G-316-35-15 | 2.92 | 150 | 377 | 37.05 | 8 | GFRP | 16 | 50.5 | 603 | 1.07 | 31.31 | 32.04 | 48.35 | 27.92 | 30.24 | |
| G-318-35-15 | 2.93 | 150 | 376 | 37.05 | 8 | GFRP | 18 | 50.5 | 763 | 1.35 | 33.76 | 36.13 | 53.43 | 30.15 | 32.56 | |
| G-416-35-15 | 2.92 | 150 | 377 | 36.02 | 8 | GFRP | 16 | 50.5 | 804 | 1.42 | 32.43 | 38.13 | 53.97 | 31.17 | 32.66 | |
| G-316-35-35 | 3.08 | 150 | 357 | 35.00 | 8 | GFRP | 16 | 50.5 | 603 | 1.13 | 29.90 | 30.34 | 40.26 | 26.48 | 28.59 | |
| G-418-35-35 | 3.09 | 150 | 356 | 35.00 | 8 | GFRP | 18 | 50.5 | 1018 | 1.91 | 35.14 | 39.56 | 50.43 | 31.17 | 33.85 | |
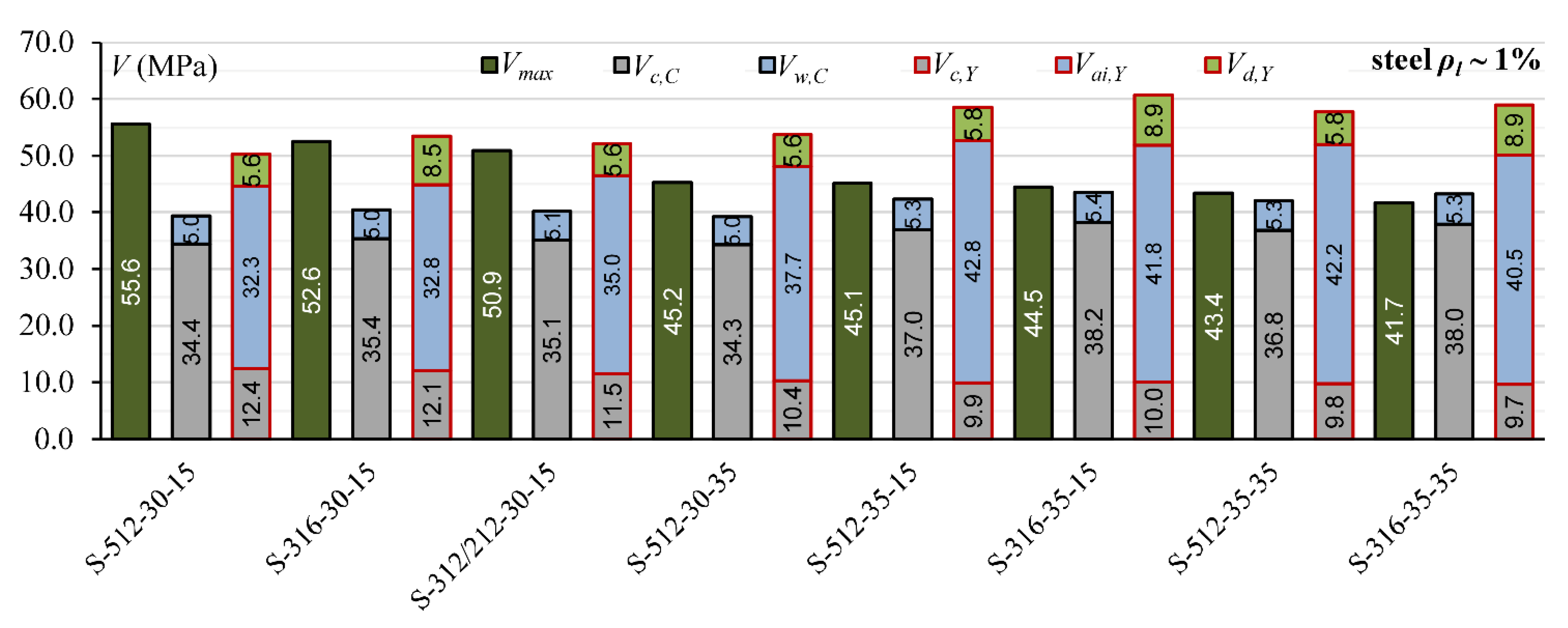
| Kotynia and Kaszubska [28] | S-512-30-15 | 2.90 | 150 | 379 | 31.10 | 8 | steel | 12 | 201 | 565 | 0.99 | 55.59 | 51.48 | 76.64 | 50.25 | 39.38 |
| S-316-30-15 | 2.92 | 150 | 377 | 32.30 | 8 | steel | 16 | 201 | 603 | 1.07 | 52.59 | 55.68 | 79.88 | 53.42 | 40.42 | |
| S-318-30-15 | 2.93 | 150 | 376 | 33.80 | 8 | steel | 18 | 201 | 763 | 1.35 | 56.10 | 62.81 | 90.37 | 59.59 | 41.77 | |
| S-312/212-30-15 | 2.99 | 150 | 367.8 | 32.30 | 8 | steel | 12 | 201 | 565 | 1.02 | 50.93 | 53.13 | 72.70 | 52.09 | 40.20 | |
| S-318/118-30-15 | 3.00 | 150 | 367 | 33.80 | 8 | steel | 18 | 201 | 1018 | 1.85 | 61.79 | 68.51 | 94.37 | 67.21 | 41.64 | |
| S-512-30-35 | 3.06 | 150 | 359 | 31.10 | 8 | steel | 12 | 201 | 565 | 1.05 | 45.24 | 53.90 | 66.21 | 53.67 | 39.16 | |
| S-418-30-35 | 3.09 | 150 | 356 | 33.80 | 8 | steel | 18 | 201 | 1018 | 1.91 | 52.94 | 70.18 | 86.62 | 69.58 | 41.66 | |
| S-512-35-15 | 2.90 | 150 | 379 | 34.95 | 8 | steel | 12 | 201 | 565 | 0.99 | 45.14 | 60.21 | 83.90 | 58.50 | 42.36 | |
| S-316-35-15 | 2.92 | 150 | 377 | 36.33 | 8 | steel | 16 | 201 | 603 | 1.07 | 44.52 | 63.55 | 87.47 | 60.67 | 43.55 | |
| S-318-35-15 | 2.93 | 150 | 376 | 37.35 | 8 | steel | 18 | 201 | 763 | 1.35 | 47.04 | 70.69 | 97.62 | 67.35 | 44.55 | |
| S-512-35-35 | 3.06 | 150 | 359 | 35.00 | 8 | steel | 12 | 201 | 565 | 1.05 | 43.40 | 58.10 | 72.27 | 57.74 | 42.13 | |
| S-316-35-35 | 3.08 | 150 | 357 | 36.33 | 8 | steel | 16 | 201 | 603 | 1.13 | 41.72 | 61.90 | 75.09 | 59.03 | 43.31 | |
| S-318-35-35 | 3.09 | 150 | 356 | 36.33 | 8 | steel | 18 | 201 | 763 | 1.43 | 46.89 | 66.23 | 81.85 | 62.60 | 43.70 |
References
- FIB Task Group 9.3. FRP Reinforcement in RC Structures. Bulletin No. 40, 2007, p. 160. Available online: https://re.public.polimi.it/handle/11311/661443 (accessed on 28 September 2007).
- JSCE. Recommendation for Design and Construction of Concrete Structures Using Continuous Fiber Reinforcing Materials; Japan Soc. of Civil Engineers: Tokyo, Japan, 1997; Volume 23. [Google Scholar]
- ACI 440.1R-15; Guide for the Design and Construction of Structural Concrete Reinforced with FRP Bars. American Concrete Institute: Farmington Hills, MI, USA, 2015; p. 88. [CrossRef]
- CAN/CSA-S806-12; Design and Construction of Building Structures with Fibre-Reinforced Polymers. Canadian Standards Association: Toronto, ON, Canada, 2012; p. 206.
- ISIS-M03-07; Reinforcing Concrete Structures with Fiber Reinforced Polymers. Canadian Network of Centers of Excellence on Intelligent Sensing for Innovative Structures. ISIS Canada: Winnipeg, MB, Canada, 2007.
- Kaszubska, M. Analysis of the Flexural Reinforcement on the Shear Strength of the Concrete Beams without Transverse Reinforcement. Ph.D. Thesis, Lodz University of Technology, Lodz, Poland, December 2018. [Google Scholar]
- Taylor, H.P.J. Investigation of the Dowel Shear Forces Carried by Tensile Steel in Reinforced Concrete Beams; Technical Report no. TRA 431; Cement and Concrete Association: London, UK, November 1969. [Google Scholar]
- Taylor, H.P.J. Investigation of the Forces Carried Across Cracks in Reinforced Concrete Beams in Shear by Interlock of Aggregate; Technical Report No. 42.77; Cement and Concrete Association: London, UK, 1970. [Google Scholar]
- Tottori, S.; Wakui, H. Shear capacity of RC and PC beams using FRP reinforcement. Proc. Aci Sp Detroit 1993, 138, 615–632. [Google Scholar] [CrossRef]
- Marí, A.; Bairán, J.; Cladera, A.; Oller, E.; Ribas, C. Shear-flexural strength mechanical model for the design and assessment of reinforced concrete beams. Struct. Infrastruct. Eng. 2015, 11, 1399–1419. [Google Scholar] [CrossRef]
- Muttoni, A.; Ruiz, M.F. Shear strength of members without transverse reinforcement as function of critical shear crack width. ACI Struct. J. 2008, 105, 163–172. [Google Scholar] [CrossRef]
- Zhang, T.; Oehlers, D.J.; Visintin, P. Shear Strength of FRP RC Beams and One-Way Slabs without Stirrups. J. Compos. Constr. 2014, 18, 5. [Google Scholar] [CrossRef]
- Yang, Y. Shear Behaviour of Reinforced Concrete Members without Shear Reinforcement, a New Look at an Old Problem. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, April 2014. [Google Scholar]
- Cladera, A.; Marí, A.; Bairán, J.M.; Ribas, C.; Oller, E.; Duarte, N. The compression chord capacity model for the shear design and assessment of reinforced and prestressed concrete beams. Struct. Concr. 2016, 17, 1017–1032. [Google Scholar] [CrossRef]
- Kani, M.W.; Huggins, M.W.; Wittkopp, R.R. Kani on Shear in Reinforced Concrete; Deptartment of Civil Engineering, University of Toronto: Toronto, ON, Canada, 1979. [Google Scholar]
- Lucas, W.; Oehlers, D.J.; Ali, M. Formulation of a Shear Resistance Mechanism for Inclined Cracks in RC Beams. J. Struct. Eng. 2011, 137, 12. [Google Scholar] [CrossRef]
- ACI 363. State-of-the-Art Report on High-Strength Concrete (ACI 363R-92). ACI J. Proc. 1992, 363, 92. [Google Scholar]
- Bažant, Z.P.; Ohtsubo, H. Stability conditions for propagation of a system of cracks in a brittle solid. Mech. Res. Commun. 1977, 4, 353–366. [Google Scholar] [CrossRef]
- Walraven, J. Aggregate Interlock: A Theoretical and Experimental Analysis. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, October 1980. [Google Scholar]
- Baumann, T.; Rüsch, H. Versuche zum Studium der Verdübelungswirkung der Biegezugbewehrung eines Stahlbetonbalkens (Heft 210); Ernst and Sohn: Berlin, Germany, 1970. [Google Scholar]
- Mörsch, E. Concrete-Steel Construction; Engineering News Publishing Company: London, UK, 1909. [Google Scholar]
- Marí, A.; Cladera, A.; Bairán García, J.M.; Oller, E.; Ribas, C. Shear-flexural strength mechanical model for the design and assessment of reinforced concrete beams subjected to point or distributed loads. Struct. Infrastruct. Eng. 2014, 8, 337–353. [Google Scholar] [CrossRef]
- Cladera, A.; Marí, A.; Ribas, C.; Bairán, J.; Oller, E. Predicting the shear-flexural strength of slender reinforced concrete T and I shaped beams. Eng. Struct. 2015, 101, 386–398. [Google Scholar] [CrossRef]
- Szczech, D.; Kotynia, R. Effect of shear reinforcement ratio on the shear capacity of GFRP reinforced concrete beams. Arch. Civ. Eng. 2021, 67, 1. [Google Scholar]
- Szczech, D.; Kotynia, R. Shear Tests on GFRP Reinforced Concrete Beams. In Proceedings of the MATEC Web of Conferences EDP Sciences, Lodz, Poland, 21–23 October 2020; Volume 323. [Google Scholar] [CrossRef]
- Kaszubska, M.; Kotynia, R.; Barros, J.A.O. Influence of Longitudinal GFRP Reinforcement Ratio on Shear Capacity of Concrete Beams without Stirrups. Procedia Eng. 2017, 193, 361–368. [Google Scholar] [CrossRef]
- Kaszubska, M.; Kotynia, R.; Barros, J.A.O.; Baghi, H. Shear behavior of concrete beams reinforced exclusively with longitudinal glass fiber reinforced polymer bars: Experimental research. Struct. Concr. 2017, 19, 152–161. [Google Scholar] [CrossRef]
- Kotynia, R.; Kaszubska, M. Research of the flexural reinforcement effect on the shear strength of concrete beams without transverse reinforcement. Report 2020, 23, 164. [Google Scholar]
- EN 1992-1-1; Eurocode 2: Design of Concrete Structures. Part 1: General Rules and Rules for Buildings. British Standard Institution: London, UK, 2004.
- Zhang, T.; Visintin, P.; Oehlers, D.J. Shear strength of RC beams without web reinforcement. Aust. J. Struct. Eng. 2016, 17, 87–96. [Google Scholar] [CrossRef]
- Kupfer, H. Erweiterung der Mörsch’schen Fachwerkanalogie mit Hilfe des Prinzips vom Minimum der Formänderungsarbeit; CEB Bulletin d’information: Paris, France, 1964. [Google Scholar]
- Tureyen, A.K.; Frosch, R.J. Shear tests of FRP-reinforced concrete beams without stirrups. ACI Struct. J. 2002, 99, 427–434. [Google Scholar] [CrossRef]
- Zhao, W.; Maruyama, K.; Suzuki, H. Shear behaviour of concrete beams reinforced by FRP rods as longitudinal and shear reinforcement. In Proceedings of the Non-Metallic (FRP) Reinforcement for Concrete Structures, Second International RILEM Symposium, Rilem, Ghent, 23–25 August 1995. [Google Scholar]
- El-Sayed, A.K.; El-Salakawy, E.; Benmokrane, B. Shear Capacity of High-Strength Concrete Beams Reinforced with FRP Bars. ACI Struct. J. 2006, 103, 383–389. [Google Scholar]
- Jin, M.H.; Jang, H.S.; Kim, C.H.; Baek, D.I. Concrete Shear Strength of Lightweight Concrete BEAM REINFORCED with FRP bar. In Proceedings of the APFIS, Seoul, Korea; 9–11 December 2009. [Google Scholar]
- Razaqpur, A.; Shedid, G.M.; Isgor, B. Shear Strength of Fiber-Reinforced Polymer Reinforced Concrete Beams Subject to Unsymmetric Loading. J. Compos. Constr. 2011, 15, 500–512. [Google Scholar] [CrossRef]
- Razaqpur, A.G.; Isgor, B.O.; Greenaway, S.; Selley, A. Concrete Contribution to the Shear Resistance of Fiber Reinforced Polymer Reinforced Concrete Members. J. Compos. Constr. 2004, 8, 452–460. [Google Scholar] [CrossRef]
- Ashour, A.F.; Kara, I.F. Shear Capacity of FRP Reinforced Concrete Beams. In Proceedings of the FRPRCS-11, Guimarães, Portugal; 26–28 June 2013. [Google Scholar]
- Olivito, R.S.; Zuccarello, F.A. On the shear behaviour of concrete beams reinforced by carbon fibre-reinforced polymer bars: An experimental investigation by means of acoustic emission technique. Strain 2010, 46, 5. [Google Scholar] [CrossRef]
- Gross, S.P.; Dinehart, D.W.; Yost, J.R.; Theisz, P.M. Experimental tests of high-strength concrete beams reinforced with CFRP bars. In Proceedings of the 4th International Conference on Advanced Composite Materials in Bridges and Structures (ACMBS-4), Calgary, AB, Canada; 20–23 July 2004. [Google Scholar]
- Niewels, J. Zum Tragverhalten von Betonbauteilen mit Faserverbundkunststoff-Bewehrung. Ph.D Thesis, Rheinisch-Westfälische Technische Hochschule Aachen, Aachen, Germany, November 2008. [Google Scholar]
- Steiner, S.; El-Sayed, A.K.; Benmokrane, B. Shear Behaviour of Large-Size Beams Reinforced with Glass FRP Bars. In Proceedings of the Annual Conference—Canadian Society for Civil Engineering, Quebec, Canada, 10–13 June 2008. [Google Scholar]
- Matta, F.; El-Sayed, A.K.; Nanni, A.; Benmokrane, B. Size effect on concrete shear strength in beams reinforced with fiber-reinforced polymer bars. ACI Struct. J. 2013, 110, 617–628. [Google Scholar]
- Matta, F.; Nanni, A. Scaling of strength of FRP reinforced concrete beams without shear reinforcement. In Proceedings of the Fourth International Conference on FRP Composites in Civil Engineering (CICE2008), Zurich, Shwitzerland, 22–24 July 2008. [Google Scholar]
- Ashour, A.F. Flexural and shear capacities of concrete beams reinforced with GFRP bars. Constr. Build. Mater. 2006, 20, 1005–1015. [Google Scholar] [CrossRef]
- Bentz, E.C.; Massam, L.; Collins, M.P. Shear Strength of Large Concrete Members with FRP Reinforcement. J. Compos. Constr. 2010, 14, 637–646. [Google Scholar] [CrossRef]
- Guadagnini, M.; Pilakoutas, K.; Waldron, P. Shear Resistance of FRP RC Beams: Experimental Study. J. Compos. Constr. 2006, 10, 464–473. [Google Scholar] [CrossRef]
- Imjai, T. Design and Analysis of Curved FRP Composites as Shear Reinforcement for Concrete Structures. Ph.D. Thesis, The University of Sheffield, Sheffield, UK, 2007. [Google Scholar]
- Duranovic, N.; Pilakoutas, K.; Waldron, P. Tests on Concrete Beams Reinforced with Glass Fibre Reinforced Plastic Bars. In Proceedings of the Third International Symposium on Non-Metallic (FRP) Reinforcement for Concrete Structures (FRPRCS-3), Sapporo, Japan, 14–16 October 1997. [Google Scholar]
- Yost, J.R.; Gross, S.P.; Dinehart, D.W. Shear Strength of Normal Strength Concrete Beams Reinforced with Deformed GFRP Bars. J. Compos. Constr. 2001, 5, 268–275. [Google Scholar] [CrossRef]






| Muttoni and Ruiz [11] | Zhang et al. [12] | Yang [13] | Cladera et al. [14] | |
|---|---|---|---|---|
| Number of specimens | 79 | 158 | 134 | 79 |
| ηmin | 0.62 | 0.48 | 0.40 | 0.63 |
| ηmax | 2.47 | 2.50 | 2.19 | 1.57 |
| ηm | 1.16 | 1.01 | 1.31 | 1.09 |
| median | 1.11 | 1.01 | 1.32 | 1.09 |
| ση | 0.35 | 0.27 | 0.31 | 0.18 |
| COV | 0.30 | 0.27 | 0.24 | 0.17 |
| Muttoni and Ruiz [11] | Zhang et al. [12] | Yang [13] | Cladera et al. [14] | |
|---|---|---|---|---|
| CFRP-reinforced rectangular beams | ||||
| Number of specimens | 26 | 56 | 47 | 26 |
| ηmin | 0.78 | 0.54 | 0.40 | 0.71 |
| ηmax | 1.85 | 1.57 | 2.04 | 1.42 |
| ηm | 1.20 | 1.04 | 1.38 | 1.06 |
| ση | 0.26 | 0.20 | 0.32 | 0.17 |
| COV | 0.22 | 0.20 | 0.23 | 0.16 |
| GFRP-reinforced rectangular beams | ||||
| Number of specimens | 22 | 60 | 51 | 22 |
| ηmin | 0.65 | 0.71 | 0.86 | 0.63 |
| ηmax | 2.47 | 2.50 | 2.19 | 1.57 |
| ηm | 1.37 | 1.16 | 1.39 | 1.05 |
| ση | 0.43 | 0.28 | 0.27 | 0.21 |
| COV | 0.31 | 0.24 | 0.19 | 0.20 |
| GFRP-reinforced T-beams | ||||
| Number of specimens | 16 | 16 | 16 | 16 |
| ηmin | 0.85 | 0.60 | 1.04 | 0.99 |
| ηmax | 1.48 | 0.93 | 1.69 | 1.45 |
| ηm | 1.12 | 0.78 | 1.30 | 1.15 |
| ση | 0.18 | 0.10 | 0.18 | 0.11 |
| COV | 0.16 | 0.13 | 0.14 | 0.10 |
| GFRP-reinforced beams (T-section and rectangular) | ||||
| Number of specimens | 38 | 76 | 67 | 38 |
| ηmin | 0.65 | 0.60 | 0.86 | 0.63 |
| ηmax | 2.47 | 2.50 | 2.19 | 1.57 |
| ηm | 1.26 | 1.08 | 1.37 | 1.10 |
| ση | 0.37 | 0.29 | 0.25 | 0.19 |
| COV | 0.29 | 0.27 | 0.18 | 0.17 |
| steel-reinforced rectangular beams | ||||
| Number of specimens | 2 | 11 | 7 | 2 |
| ηmin | - | 0.68 | 0.95 | - |
| ηmax | - | 1.16 | 1.46 | - |
| ηm | - | 0.93 | 1.20 | - |
| ση | - | 0.15 | 0.22 | - |
| COV | - | 0.16 | 0.19 | - |
| steel-reinforced T-beams | ||||
| Number of specimens | 13 | 13 | 13 | 13 |
| ηmin | 0.67 | 0.48 | 0.70 | 0.96 |
| ηmax | 1.08 | 0.73 | 1.11 | 1.48 |
| ηm | 0.82 | 0.61 | 0.84 | 1.19 |
| ση | 0.12 | 0.07 | 0.13 | 0.16 |
| COV | 0.15 | 0.12 | 0.15 | 0.14 |
| steel-reinforced beams (T-section and rectangular) | ||||
| Number of specimens | 15 | 24 | 20 | 15 |
| ηmin | 0.62 | 0.48 | 0.70 | 0.74 |
| ηmax | 1.08 | 1.16 | 1.46 | 1.48 |
| ηm | 0.81 | 0.75 | 0.97 | 1.14 |
| ση | 0.13 | 0.20 | 0.24 | 0.19 |
| COV | 0.16 | 0.26 | 0.24 | 0.17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaszubska, M.; Kotynia, R. Selected Shear Models Based on the Analysis of the Critical Shear Crack for Slender Concrete Beams without Shear Reinforcement. Materials 2022, 15, 8259. https://doi.org/10.3390/ma15228259
Kaszubska M, Kotynia R. Selected Shear Models Based on the Analysis of the Critical Shear Crack for Slender Concrete Beams without Shear Reinforcement. Materials. 2022; 15(22):8259. https://doi.org/10.3390/ma15228259
Chicago/Turabian StyleKaszubska, Monika, and Renata Kotynia. 2022. "Selected Shear Models Based on the Analysis of the Critical Shear Crack for Slender Concrete Beams without Shear Reinforcement" Materials 15, no. 22: 8259. https://doi.org/10.3390/ma15228259
APA StyleKaszubska, M., & Kotynia, R. (2022). Selected Shear Models Based on the Analysis of the Critical Shear Crack for Slender Concrete Beams without Shear Reinforcement. Materials, 15(22), 8259. https://doi.org/10.3390/ma15228259







