Study on Mix Proportion Optimization and Microstructure of Coal-Based Solid Waste (CSW) Backfill Material Based on Multi-Objective Decision-Making Model
Abstract
:1. Introduction
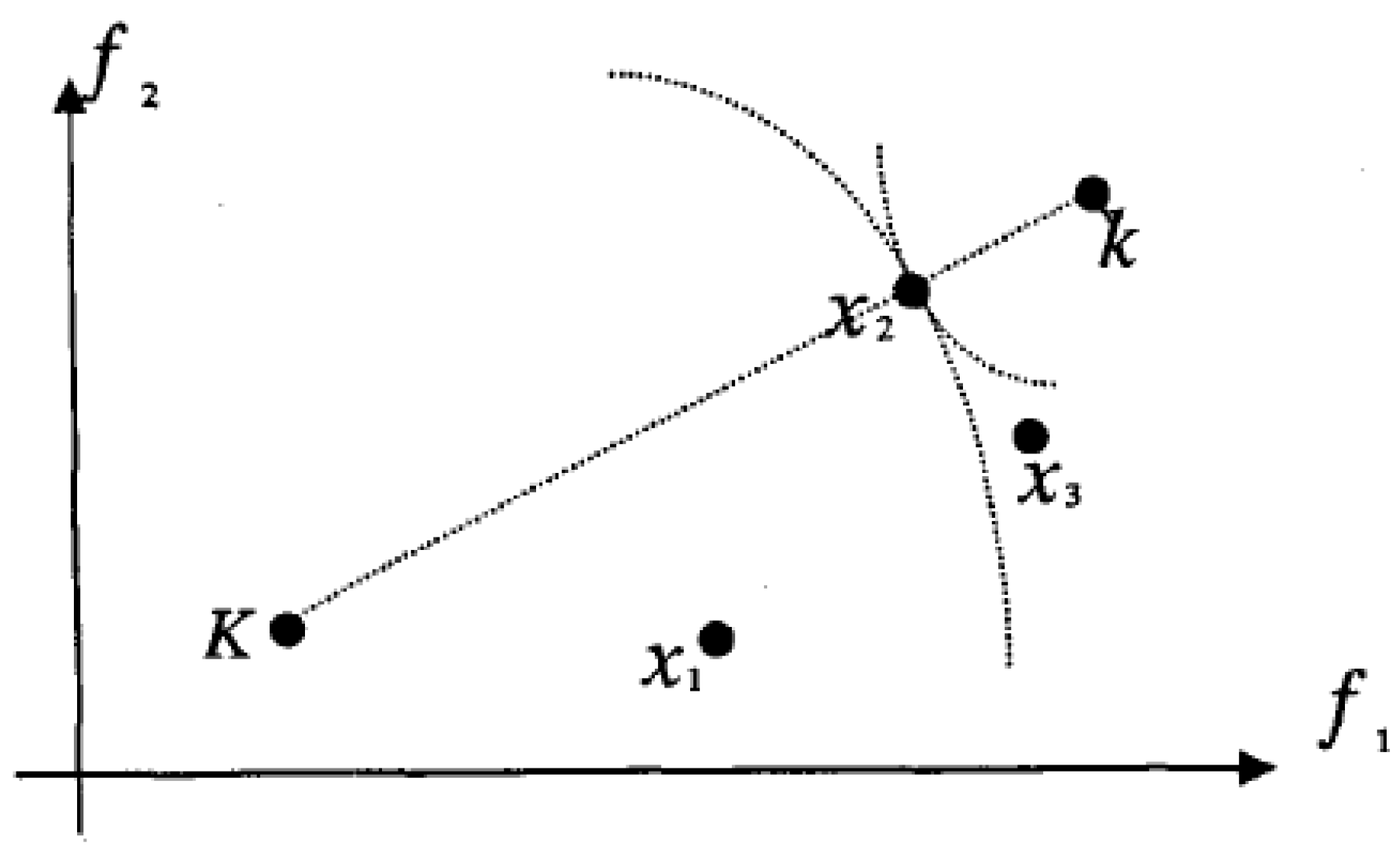
2. Multi-Objective Decision-Making Model
3. Materials and Methods
3.1. Experimental Materials
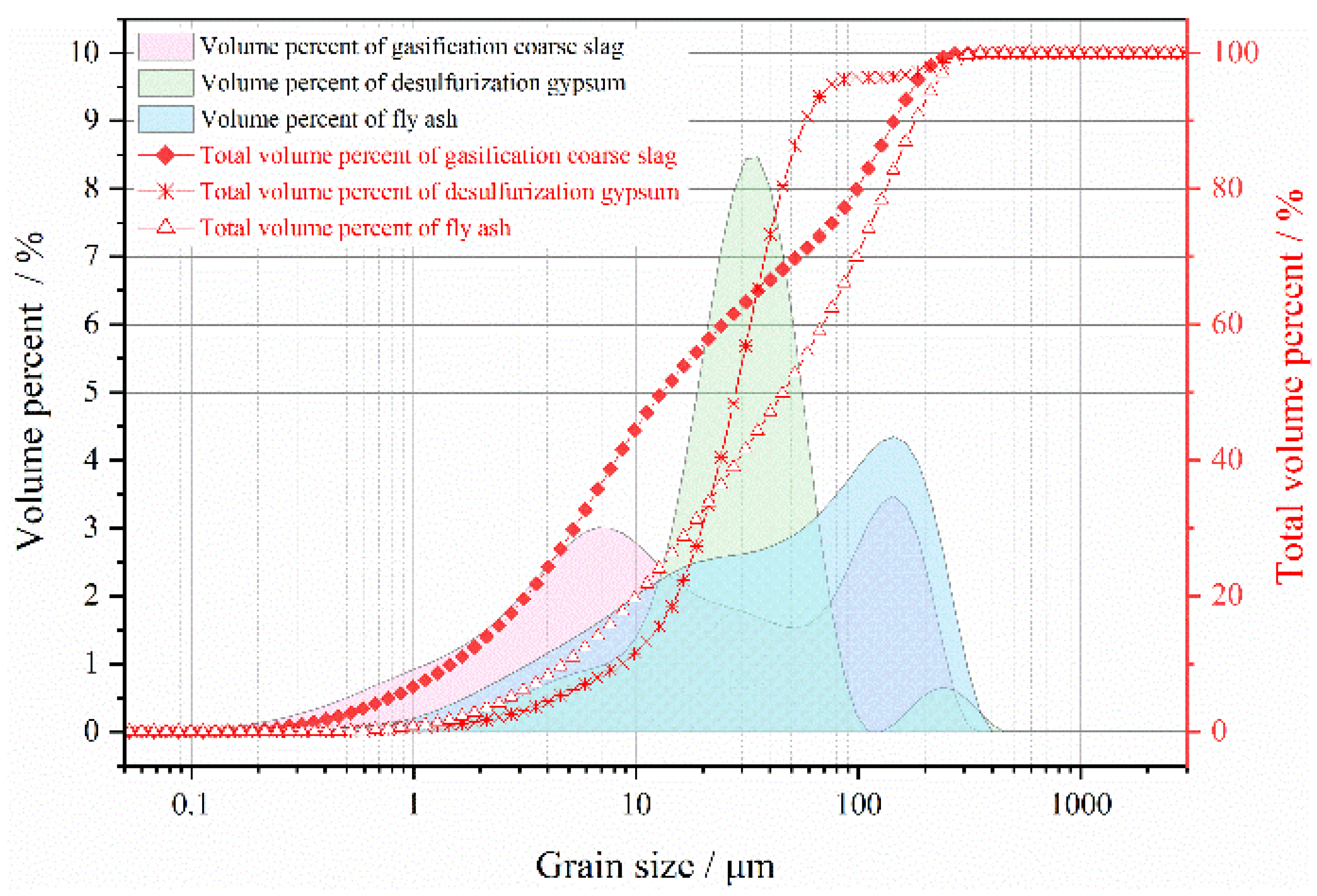
3.1.1. FA
3.1.2. GCS
3.1.3. FGD Gypsum
3.1.4. CG
3.1.5. OPC
3.2. Solid Waste Mix Proportion Scheme
3.2.1. Slump-Flow and Bleeding Rate Test
3.2.2. Strength Test
4. Experimental Result
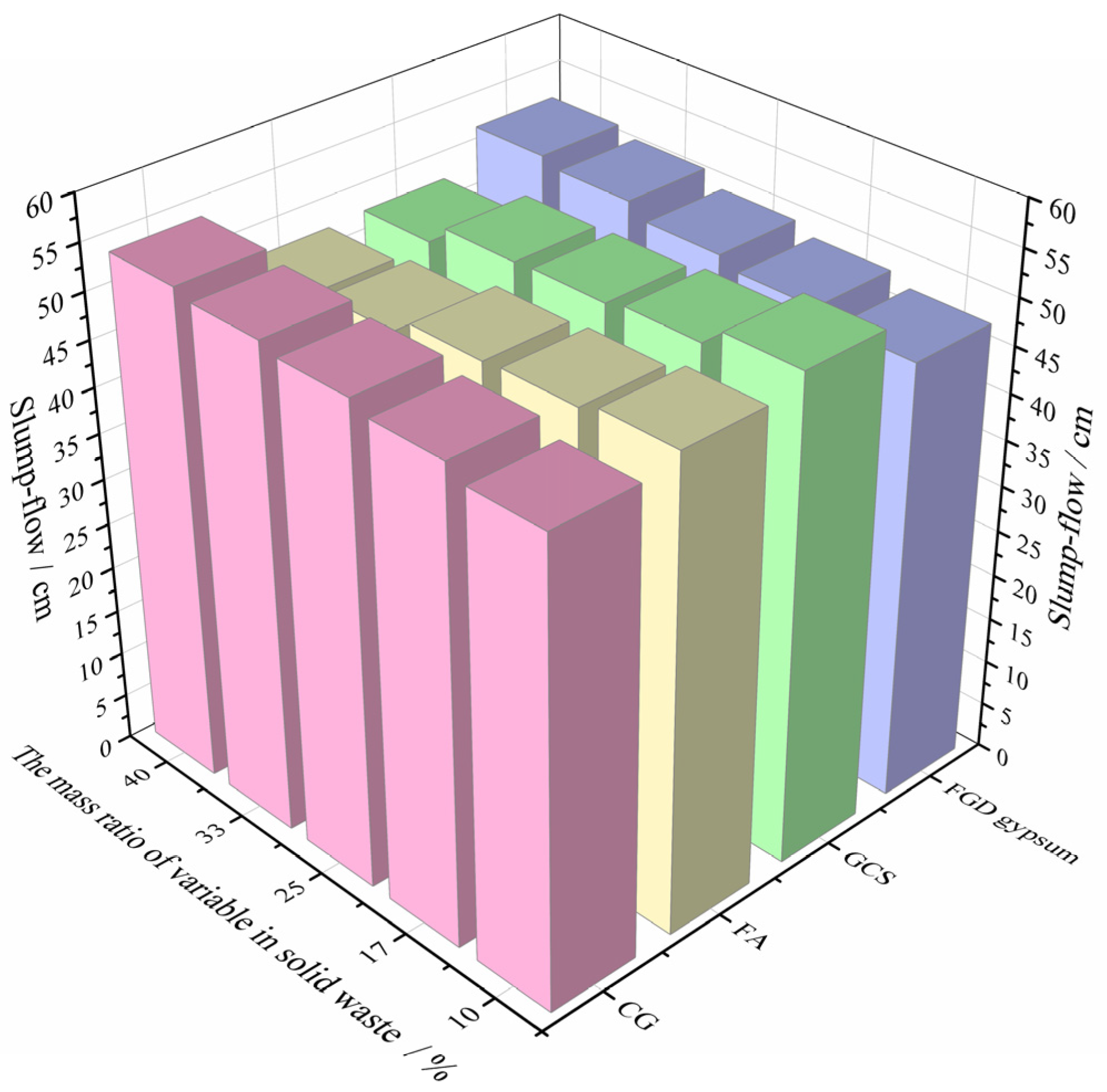
4.1. Slump-Flow
4.2. Bleeding Rate
4.3. Early Strength
4.4. Reasonable Proportion of Solid Wastes
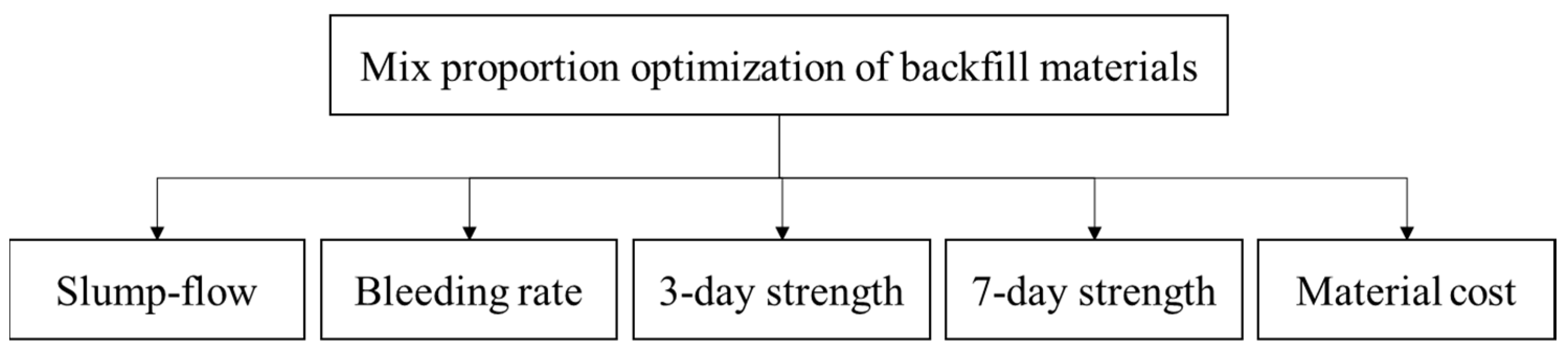
5. Mix Proportion of Backfill Material
Experimental Scheme
6. Experimental Result
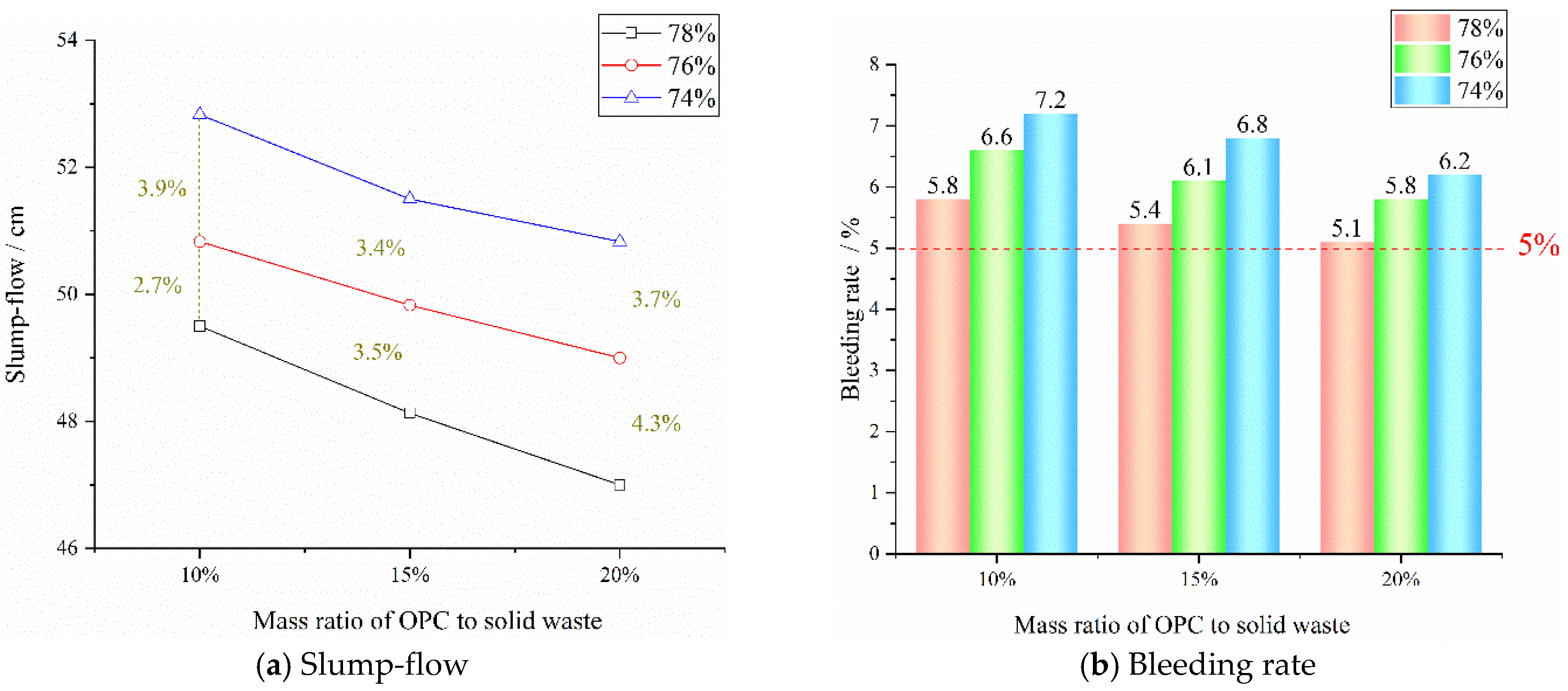
6.1. Slump-Flow and Bleeding Rate
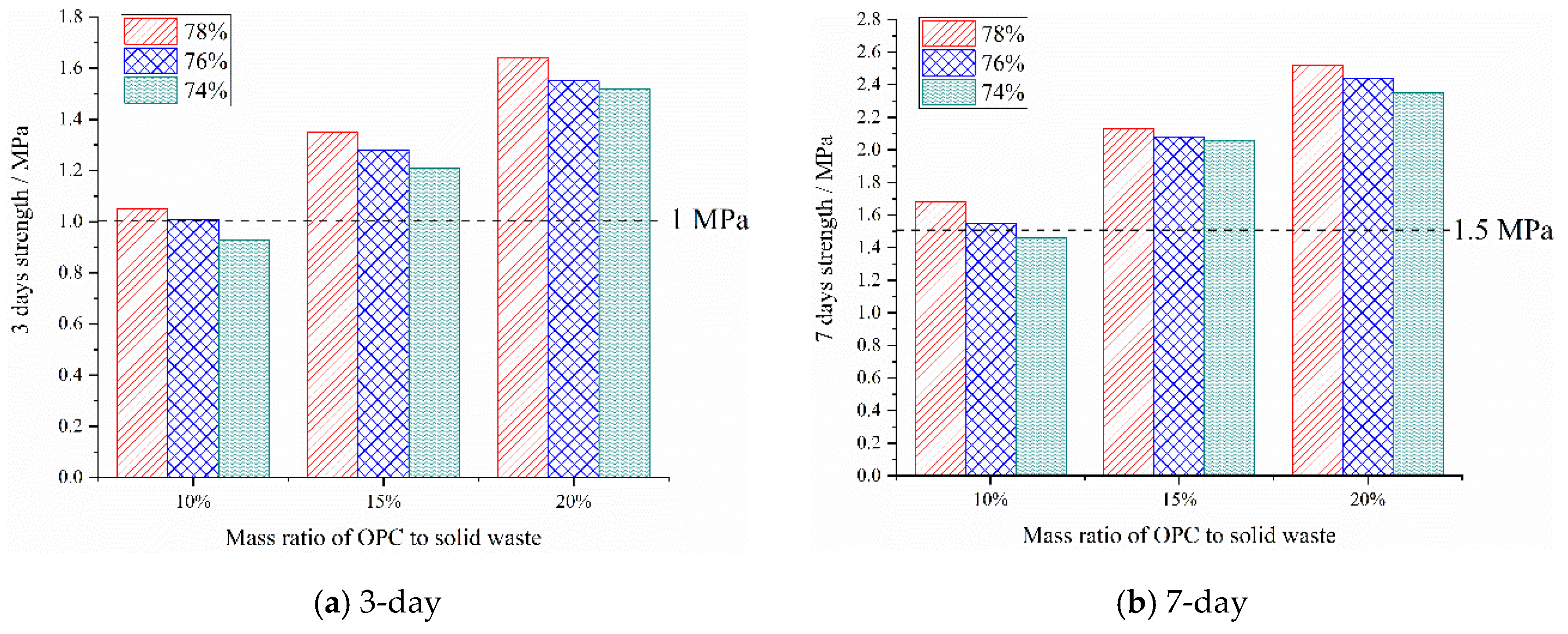
6.2. Early Strength
6.3. Mix Proportion Optimization
7. Performance of Backfill with Optimal Mix Proportion
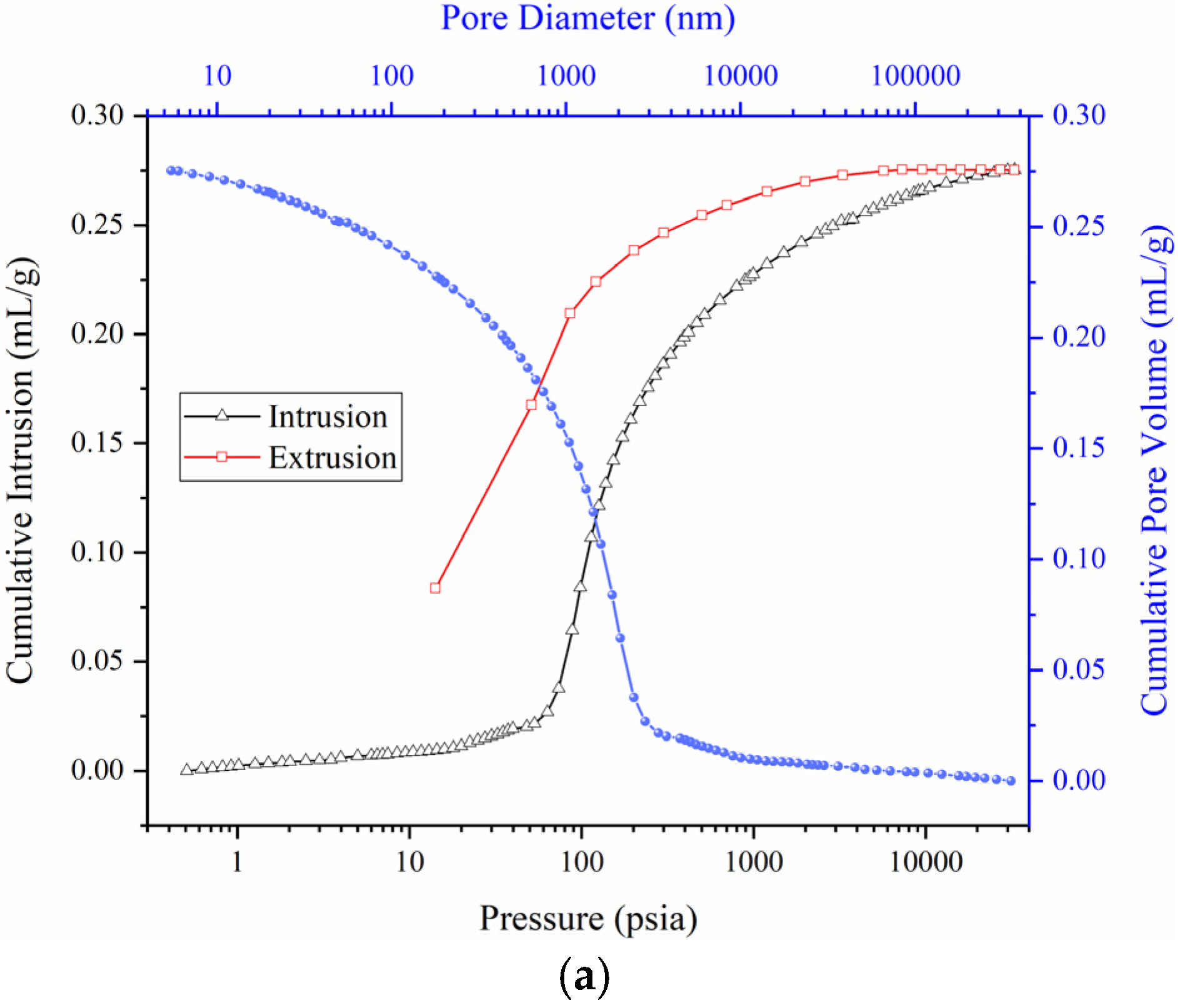
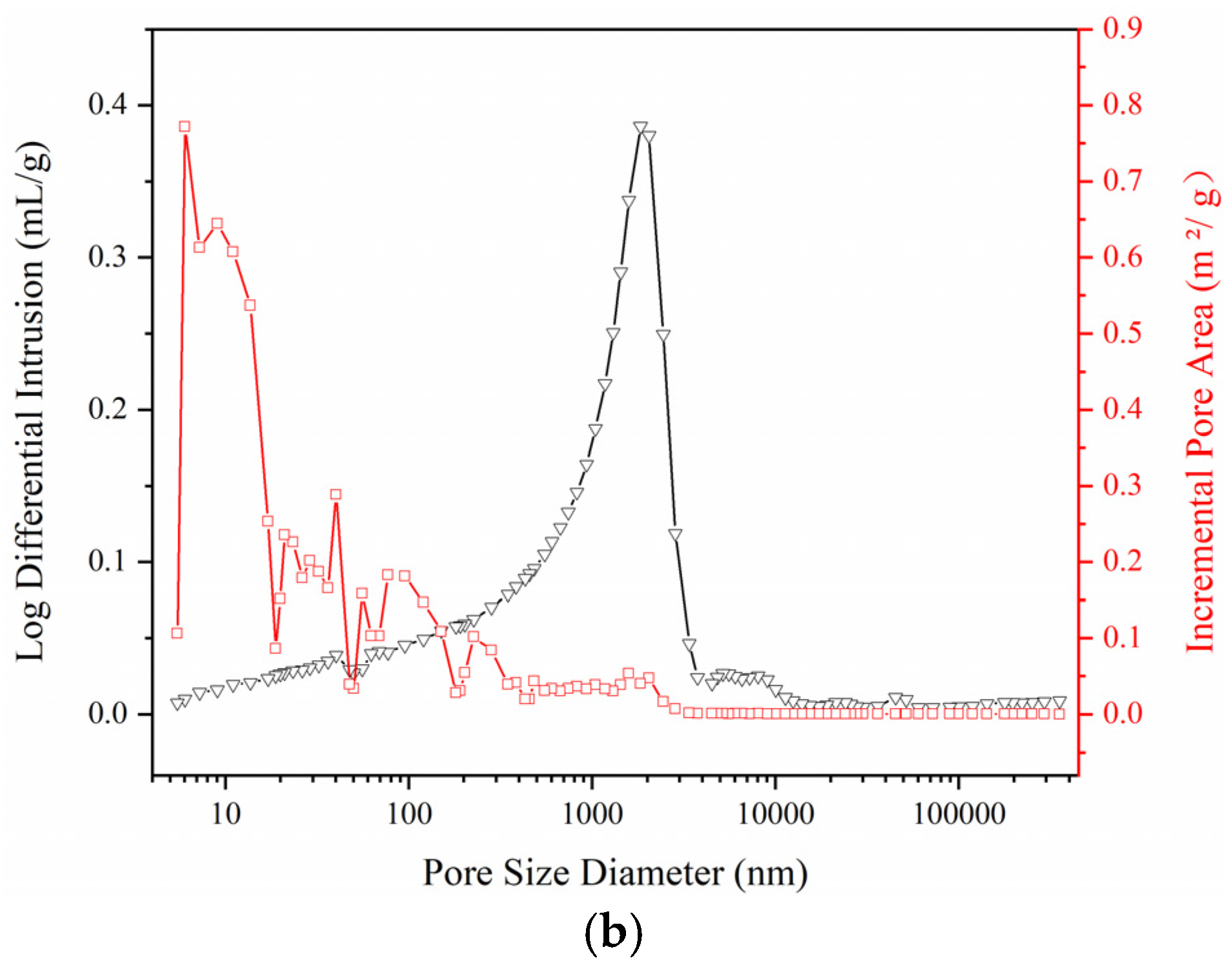
7.1. Pore Structure
7.2. Micromorphology and Composition
8. Discussion
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Peng, S.P.; Bi, Y.L. Strategic consideration and core technology about environmental ecological restoration in coal mine areas in the Yellow River basin of China. J. China Coal Soc. 2020, 45, 1211–1221. [Google Scholar]
- Niu, G.C.; Zhai, J.; Yong, L. Discussion on the utilization of industrial solid waste resources in Ningdong Energy And Chemical Base. China-Arab States Sci. Technol. Forum 2020, 1, 97–103. [Google Scholar]
- Yang, K.; Zhao, X.; Wei, Z.; Zhang, J. Development overview of paste backfill technology in China’s coal mines: A review. Environ. Sci. Pollut. Res. 2021, 28, 67957–67969. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.L.; Wang, W.F.; Bian, Z.F. Prospects of resource utilization and disposal of coal-based solid wastes in Xinjiang. Coal Sci. Technol. 2021, 49, 319–330. [Google Scholar]
- Yang, K.; Wei, Z.; Zhao, X.; Zhang, J.; Ji, J. Theory and technology of green filling mining of solid waste underground in coal power base of yellow river basin. J. China Coal Soc. 2021, 46, 925–935. [Google Scholar]
- Liu, J.G.; Li, X.W.; He, T. Application status and prospect of backfill mining in Chinese coal mines. J. China Coal Soc. 2020, 45, 141–150. [Google Scholar]
- Chang, Q.L.; Chen, J.H.; Zhou, H.Q.; Bai, J.B. Implementation of Paste Backfill Mining Technology in Chinese Coal Mines. Sci. World J. 2014, 2014, 821025. [Google Scholar] [CrossRef] [Green Version]
- Yin, S.H.; Shao, Y.J.; Wu, A.X.; Wang, H.J.; Liu, X.H.; Wang, Y. A systematic review of paste technology in metal mines for cleaner production in China. J. Clean. Prod. 2020, 247, 119590. [Google Scholar] [CrossRef]
- Cui, L.; Fall, M. Mathematical modelling of cemented tailings backfill: A review. Int. J. Min. Reclam. Environ. 2019, 33, 389–408. [Google Scholar] [CrossRef]
- Lan, W.; Wu, A.; Wang, Y. Experimental Study on Factors Affecting the Filling Performance of Composite Condensate Expansion Materials. Adv. Eng. Sci. 2019, 51, 192–198. [Google Scholar]
- Wu, H.; Zhao, G.; Chen, Y. Multi-objective optimization for mix proportioning of mine filling materials. J. Harbin Inst. Technol. 2017, 49, 101–108. [Google Scholar]
- Fall, M.; Benzaazoua, M.; Saa, E.G. Mix proportioning of underground cemented tailings backfill. Tunn. Undergr. Space Technol. 2008, 23, 80–90. [Google Scholar] [CrossRef]
- Zhang, J.Q.; Yang, K.; He, X.; Wei, Z.; Zhao, X.Y.; Fang, J.J. Experimental Study on Strength Development and Engineering Performance of Coal-Based Solid Waste Paste Filling Material. Metals 2022, 12, 1155. [Google Scholar] [CrossRef]
- Li, X.B.; Zhou, Y.N.; Zhu, Q.Q.; Zhou, S.T.; Min, C.D.; Shi, Y. Slurry Preparation Effects on the Cemented Phosphogypsum Backfill through an Orthogonal Experiment. Minerals 2019, 9, 13. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Wu, A.X.; Zhang, L.F.; Jin, F.; Liu, X.H. Investigating the Effect of Solid Components on Yield Stress for Cemented Paste Backfill via Uniform Design. Adv. Mater. Sci. Eng. 2018, 2018, 3839174. [Google Scholar] [CrossRef] [Green Version]
- Wei, Z.; Yang, K.; He, X.; Zhang, J.Q.; Hu, G.C. Experimental Study on the Optimization of Coal-Based Solid Waste Filling Slurry Ratio Based on the Response Surface Method. Materials 2022, 15, 5318. [Google Scholar] [CrossRef]
- Tang, Y.; Zhang, L.; Lv, H. Study on proportion optimization of coal-based solid wastes filling materials. J. Min. Sci. Technol. 2019, 4, 327–336. [Google Scholar]
- Zhao, X.; Yang, K.; He, X.; Wei, Z.; Zhang, J. Study on proportioning experiment and performance of solid waste for underground backfilling. Mater. Today Commun. 2022, 32, 103863. [Google Scholar] [CrossRef]
- Fu, Z.; Qiao, D.; Guo, Z.; Xie, J.; Huang, F.; Wang, J. Experimental research on mixture proportion and strength of cemented hydraulic fill with waste rock and eolian sand based on RSM-BBD. J. China Coal Soc. 2018, 43, 694–703. [Google Scholar]
- Liu, S.; Wang, F.; Li, G.; Liu, G.; Wang, J.; Qi, Z. Optimization of mixture ratio and microstructure influence mechanisn of composite filling slurry based on response surface method. Acta Mater. Compos. Sin. 2021, 38, 2724–2736. [Google Scholar]
- Liu, L. Research on Proportion Optimization and Flow Characteristic of Backfill Paste in Mine Sites; Central South University: Changsha, China, 2013. [Google Scholar]
- Huang, Y.; Rao, Y.; Liu, J.; Zhang, X. Filling ratio prediction with neural network and genetic algorithm. Nonferrous Met. Sci. Eng. 2016, 7, 76–80. [Google Scholar]
- Feng, F.S.; Li, L.R.; Zhang, J.Q.; Yang, Z.; Chi, X.L. Strength Prediction of Coal-Based Solid Waste Filler Based on BP Neural Network. Front. Mater. 2021, 8, 767031. [Google Scholar] [CrossRef]
- Li, X.; Liu, Z. On Mechanics of high consolidated tailings backfill and cement-tailing ratios optimi- zation with game tree. J. Saf. Environ. 2004, 4, 87–90. [Google Scholar]
- Shi, J.; Meng, X.; Dong, Y.; Chen, Z.; Sun, Y. Study on performance optimization of paste filling material for controlling surface subsidence. J. Saf. Sci. Technol. 2017, 13, 143–144. [Google Scholar]
- Wen, Z.; Gao, Q.; Wang, Y.; Yang, X. Development of composite cementitious material and optimization of slurry proportion based on fuzzy comprehensive evaluation. Chin. J. Nonferrous Met. 2020, 30, 698–707. [Google Scholar]
- Zindani, D.; Maity, S.R.; Bhowmik, S. Decision making tools for optimal material selection: A review. J. Cent. South Univ. 2020, 27, 629–673. [Google Scholar] [CrossRef]
- Brauers, W.K.M.; Zavadskas, E.K.; Peldschus, F.; Turskis, Z. Multi-objective decision-making for road design. Transport 2008, 23, 183–193. [Google Scholar] [CrossRef]
- Gao, F.; Wang, Q.; Peng, X.; Kaiming, A. Orthogonal optimization test of backfill mix ratio based on index satisfaction. J. Fuzhou Univ. (Nat. Sci. Ed.) 2015, 43, 422–427. [Google Scholar]
- Deng, X.; Li, J.; Zeng, H.; Chen, J.; Zhao, J. Research on computation methods of ahp wight vector and its applications. Math. Pract. Theory 2012, 42, 93–100. [Google Scholar]
- Saaty, T.L. How to make a decision: The analytic hierarchy process. Eur. J. Oper. Res. 1990, 48, 9–26. [Google Scholar] [CrossRef]
- Qiu, J.P.; Guo, Z.B.; Yang, L.; Jiang, H.Q.; Zhao, Y.L. Effect of tailings fineness on flow, strength, ultrasonic and microstructure characteristics of cemented paste backfill. Constr. Build. Mater. 2020, 263, 120645. [Google Scholar] [CrossRef]
- Saak, A.W.; Jennings, H.M.; Shah, S.P. A generalized approach for the determination of yield stress by slump and slump flow. Cem. Concr. Res. 2004, 34, 363–371. [Google Scholar] [CrossRef]
- Wei, H.B.; Xiao, B.L.; Gao, Q. Flow Properties Analysis and Identification of a Fly Ash-Waste Rock Mixed Backfilling Slurry. Minerals 2021, 11, 576. [Google Scholar] [CrossRef]
- Hodot, B.B. Coal and Gas Outburst; Song, S.Z.; Wang, Y.A., Translators; China Coal Industry Press: Beijing, China, 2022; pp. 20–35. [Google Scholar]




| Variable Factor | Mass Concentration | FA:GCS:FGD Gypsum:G | Mass Ratio of OPC to Solid Waste |
|---|---|---|---|
| FA | 78% | 10%:30%:30%:30% | 2% |
| 17%:27.7%:27.7%:27.7% | |||
| 25%:25%:25%:25% | |||
| 33%:22.3%:22.3%:22.3% | |||
| 40%:20%:20%:20% | |||
| GCS | 78% | 30%:10%:30%:30% | 2% |
| 27.7%:17%:27.7%:27.7% | |||
| 25%:25%:25%:25% | |||
| 22.3%:33%:22.3%:22.3% | |||
| 20%:40%:20%:20% | |||
| FGD gypsum | 78% | 30%:30%:10%:30% | 2% |
| 27.7%:27.7%:17%:27.7% | |||
| 25%:25%:25%:25% | |||
| 22.3%:22.3%:33%:22.3% | |||
| 20%:20%:40%:20% | |||
| CG | 78% | 30%:30%:30%:10% | 2% |
| 27.7%:27.7%:27.7%:17% | |||
| 25%:25%:25%:25% | |||
| 22.3%:22.3%:22.3%:33% | |||
| 20%:20%:20%:40% |
| No. | FA:GCS:FGD Gypsum:CG | Slump-Flow/cm | Bleeding Rate/% | 3-Day Strength/MPa | 7-Day Strength/MPa |
|---|---|---|---|---|---|
| A1 | 10%:30%:30%:30% | 51.4 | 5.5 | 0.12 | 0.16 |
| A2 | 17%:27.7%:27.7%:27.7% | 50.5 | 5.1 | 0.13 | 0.17 |
| A3 | 20%:40%:20%:20% | 47 | 5.5 | 0.14 | 0.19 |
| A4 | 22.3%:22.3%:33%:22.3% | 51.4 | 5.4 | 0.13 | 0.18 |
| A5 | 20%:20%:40%:20% | 52.2 | 5.8 | 0.13 | 0.17 |
| A6 | 25%:25%:25%:25% | 52.5 | 5.3 | 0.15 | 0.22 |
| A7 | 22.3%:22.3%:22.3%:33% | 53.33 | 5.8 | 0.14 | 0.19 |
| A8 | 20%:20%:20%:40% | 54 | 6.4 | 0.13 | 0.17 |
| No. | Mass Concentration | FA:GCS:FGD Gypsum:CG | Mass Ratio of OPC to Solid Waste |
|---|---|---|---|
| 1 | 78% | 25%:25%:25%:25% | 10% |
| 2 | 78% | 25%:25%:25%:25% | 15% |
| 3 | 78% | 25%:25%:25%:25% | 20% |
| 4 | 76% | 25%:25%:25%:25% | 10% |
| 5 | 76% | 25%:25%:25%:25% | 15% |
| 6 | 76% | 25%:25%:25%:25% | 20% |
| 7 | 74% | 25%:25%:25%:25% | 10% |
| 8 | 74% | 25%:25%:25%:25% | 15% |
| 9 | 74% | 25%:25%:25%:25% | 20% |
| Index | Slump-Flow/cm | Bleeding Rate/% | 3-Day Strength/MPa | 7-Day Strength/MPa | Cost/CNY |
|---|---|---|---|---|---|
| Weight | 0.1 | 0.05 | 0.2 | 0.15 | 0.5 |
| 1 | 49.5 | 5.8 | 1.05 | 1.68 | 43 |
| 2 | 48.13 | 5.4 | 1.35 | 2.13 | 64 |
| 3 | 47 | 5.1 | 1.64 | 2.52 | 85 |
| 4 | 50.83 | 6.6 | 1.01 | 1.55 | 45 |
| 5 | 49.83 | 6.1 | 1.28 | 2.08 | 66 |
| 6 | 49 | 5.8 | 1.55 | 2.44 | 87 |
| 7 | 51.5 | 6.8 | 1.21 | 2.06 | 68 |
| 8 | 50.83 | 6.2 | 1.52 | 2.35 | 89 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Yang, K.; He, X.; Wei, Z.; Yu, X.; Zhang, J. Study on Mix Proportion Optimization and Microstructure of Coal-Based Solid Waste (CSW) Backfill Material Based on Multi-Objective Decision-Making Model. Materials 2022, 15, 8464. https://doi.org/10.3390/ma15238464
Zhao X, Yang K, He X, Wei Z, Yu X, Zhang J. Study on Mix Proportion Optimization and Microstructure of Coal-Based Solid Waste (CSW) Backfill Material Based on Multi-Objective Decision-Making Model. Materials. 2022; 15(23):8464. https://doi.org/10.3390/ma15238464
Chicago/Turabian StyleZhao, Xinyuan, Ke Yang, Xiang He, Zhen Wei, Xiang Yu, and Jiqiang Zhang. 2022. "Study on Mix Proportion Optimization and Microstructure of Coal-Based Solid Waste (CSW) Backfill Material Based on Multi-Objective Decision-Making Model" Materials 15, no. 23: 8464. https://doi.org/10.3390/ma15238464








