An Evaluation Index of Fracability for Reservoir Rocks Based on Fracture Process Zone
Abstract
:1. Introduction
- (1)
- Based on mineral composition (e.g., [5]), especially the weight or volume proportion of hard minerals such as quartz: a positive correlation seems to exist between the brittleness and mineral contents of rocks. However, such indices do not consider many other factors that also contribute to brittleness, such as grain size and loading conditions.
- (2)
- (3)
- Based on strength: for example, one such index is the ratio of tensile and compressive strengths [9]. Such indices are easily measured, but they lack a physical correlation to brittleness and cracking propagation mechanisms. Thus, these indices may return similar values for various types of rocks with different levels of brittleness.
- (4)
- Based on characteristics of the stress–strain curve such as the relative stress drop, post-peak modulus, and various combinations [10,11]: these indices characterize rock brittleness well and are widely used in predicting the rockburst proneness. However, high brittleness does not consistently represent strong fracability because brittle rock can also act as a barrier to hydraulic fracturing [12].
- (1)
- Has a firm physical basis;
- (2)
- Consider the heterogeneity of rock material;
- (3)
- Be convenient to measure;
- (4)
- Characterize the effects of loading conditions.
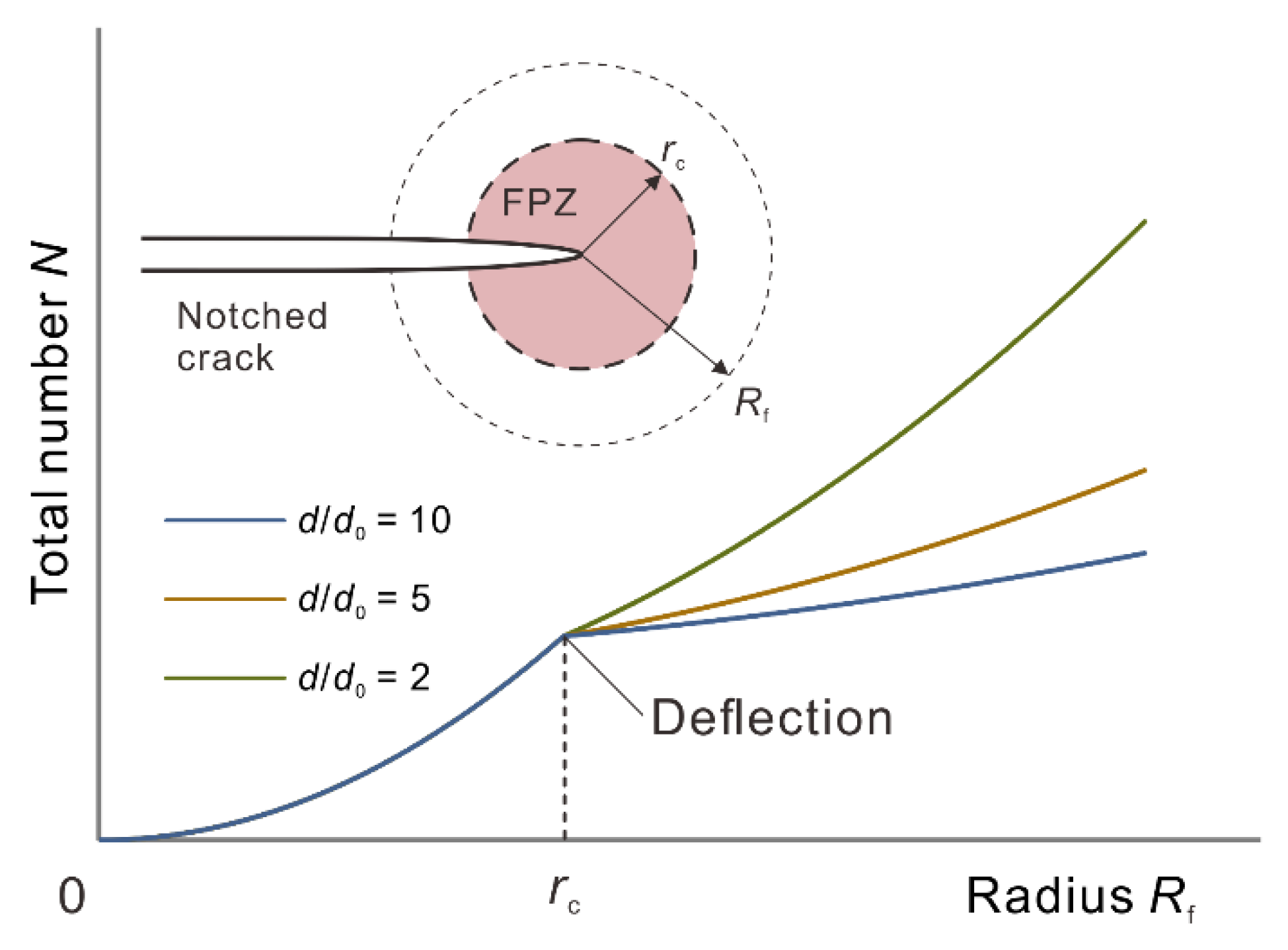
2. Fracture Process Zone and Crack Tolerance
3. Experiments
3.1. Specimens
3.2. Experimental Methodology
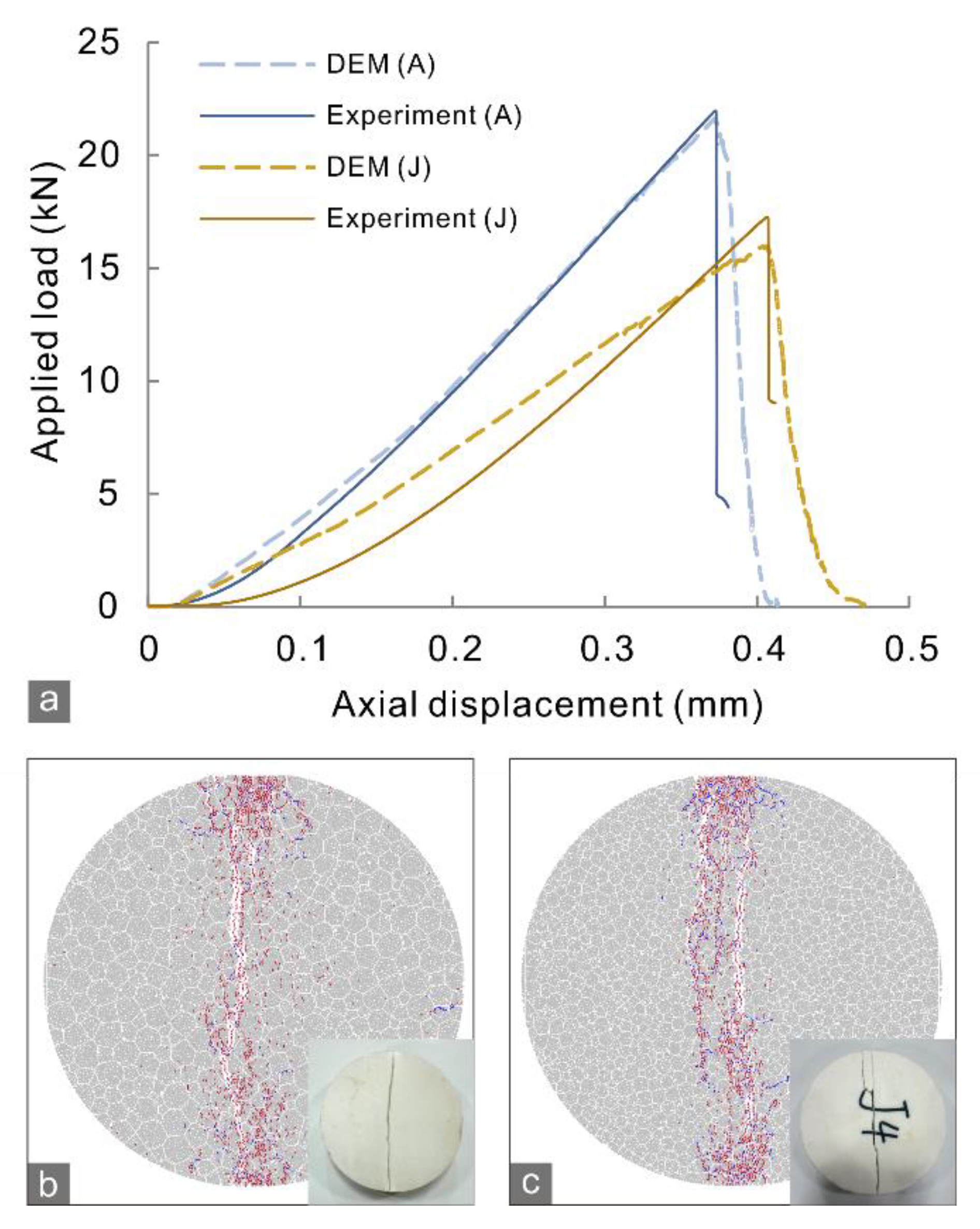
3.3. Experimental Results
4. Numerical Analysis with the Discrete Element Method
4.1. Particle Flow Code
4.2. Model Setup and Parameter Calibration
4.3. Simulation Results
5. Discussion
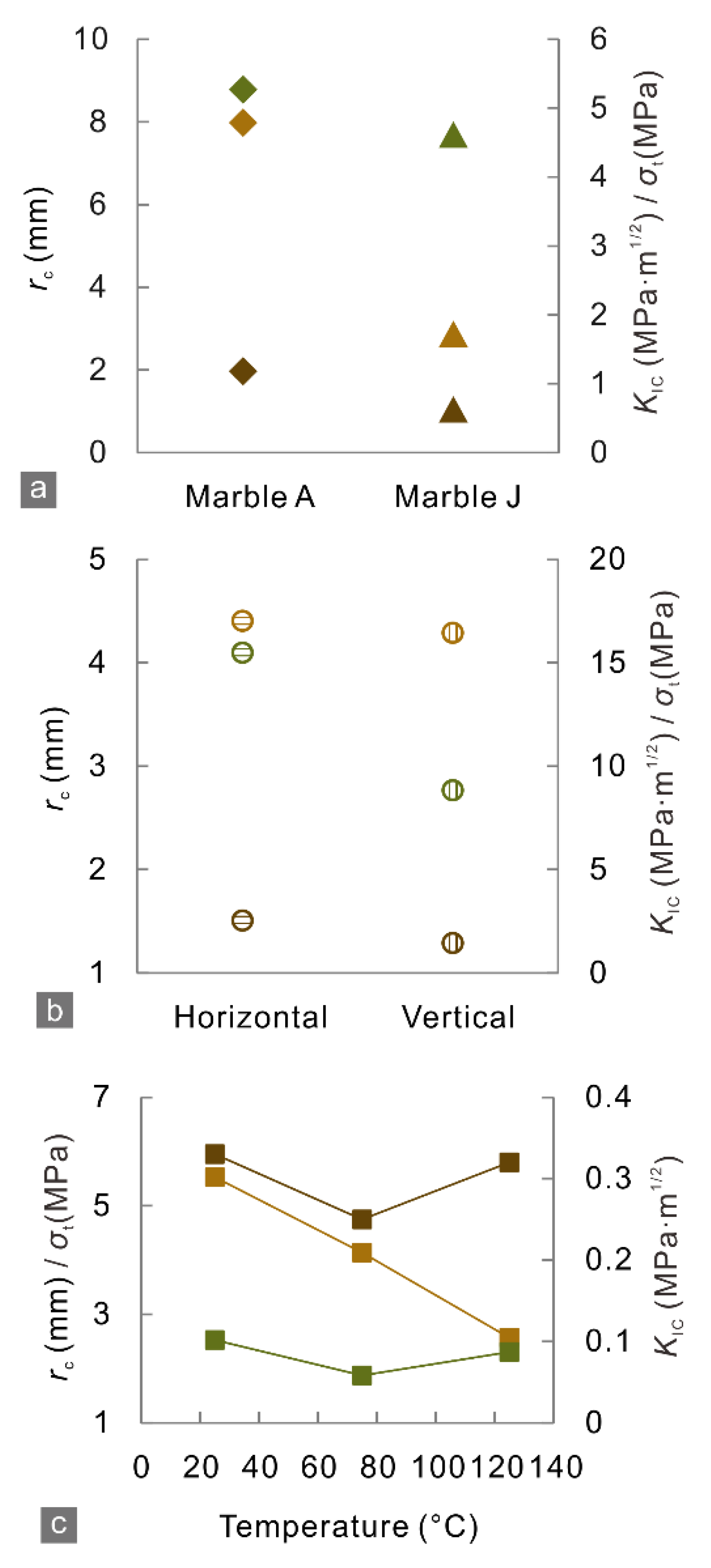
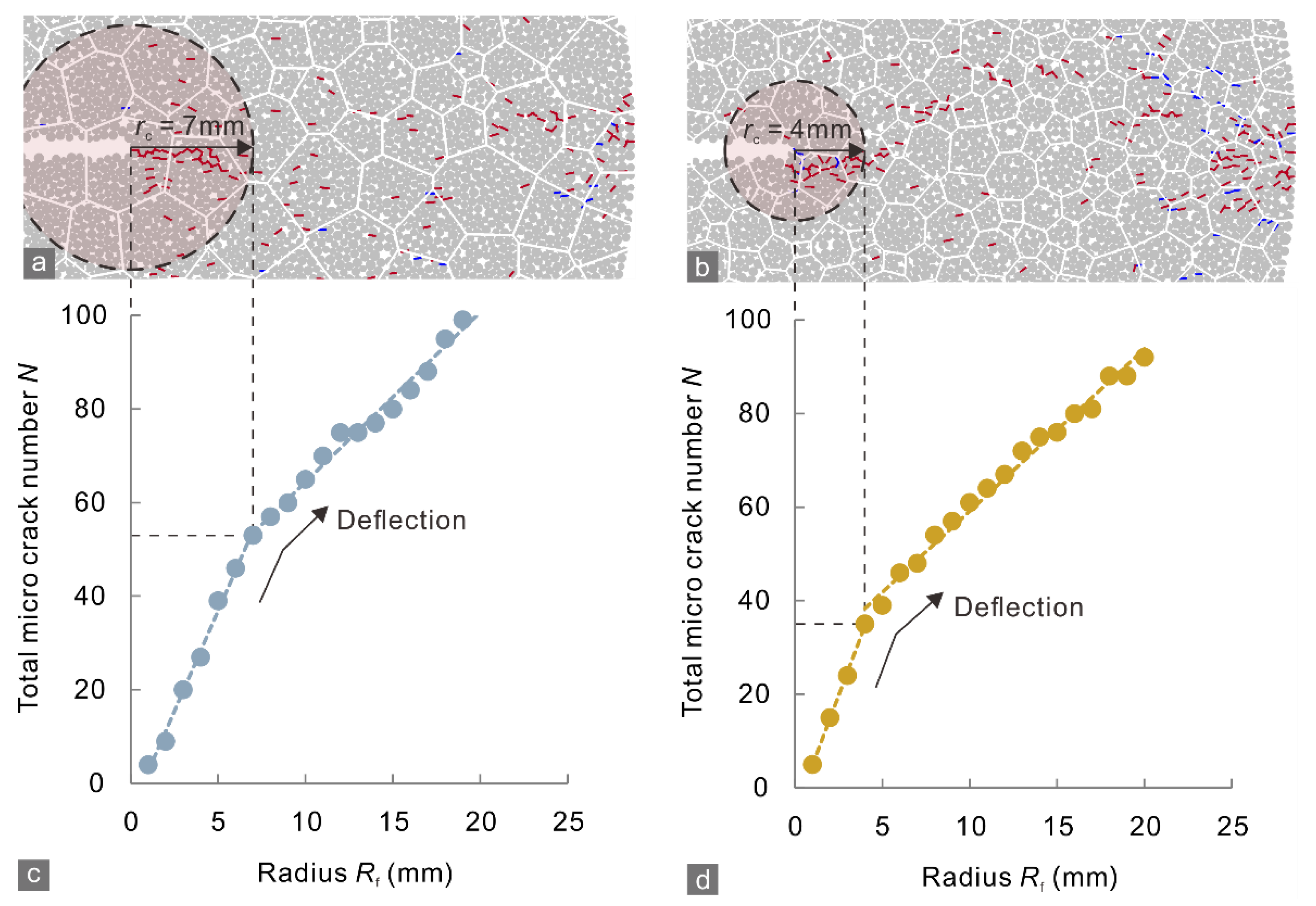
5.1. Effect of Grain Size on Crack Tolerance
5.2. Effects of the Bedding Orientation and Environmental Temperature
5.3. Implications in Hydraulic Fracturing
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| List of symbols | |
| a0 | Initial chevron notched crack length |
| a1 | Final chevron notched crack length |
| ASTM | American Society of Testing Materials |
| B | Thickness of CCNBD specimen |
| B′ | Thickness of BD specimen |
| BD | Brazilian disk |
| CCNBD | Cracked chevron notched Brazilian disk |
| d | Average micro-crack density inside FPZ |
| D | Diameter of CCNBD specimen |
| D′ | Diameter of BD specimen |
| d0 | Average micro-crack density outside FPZ |
| DEM | Discrete element method |
| FPZ | Fracture process zone |
| GBM | Grain-based model |
| ISRM | International Society for Rock Mechanics |
| KI | Tensile stress intensity factor |
| KIC | Tensile fracture toughness |
| N | Total micro-crack number |
| PFC | Particle flow code |
| Pmax | Peak applied axial load in CCNBD test |
| P′max | Peak applied axial load in BD test |
| R | Radius of CCNBD specimen |
| r | Polar radius |
| rc | Radius of circular FPZ |
| Rf | Radius of circular statistical range |
| Rs | Saw radius |
| u | Geometric constants |
| v | Geometric constants |
| XRD | X-ray diffraction |
| Y*min | Critical dimensionless stress intensity |
| Greek symbols | |
| α0 | Dimensionless parameter |
| α1 | Dimensionless parameter |
| αB | Dimensionless parameter |
| θ | Polar angle |
| σ1 | Maximum principal stress |
| σ2 | Intermediate principal stress |
| σt | Tensile strength |
References
- Mullen, M.J.; Enderlin, M.B. Fracability index—More than rock properties. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 8–10 October 2012; pp. 1–10. [Google Scholar]
- Wang, S.; Li, X.; Yao, J.; Gong, F.; Li, X.; Du, K.; Tao, M.; Huang, L.; Du, S. Experimental investigation of rock breakage by a conical pick and its application to non-explosive mechanized mining in deep hard rock. Int. J. Rock Mech. Min. Sci. 2019, 122, 104063. [Google Scholar] [CrossRef]
- Meng, F.; Wong, L.N.Y.; Zhou, H. Rock brittleness indices and their applications to different fields of rock engineering: A review. J. Rock Mech. Geotech. Eng. 2021, 13, 221–247. [Google Scholar] [CrossRef]
- Zhang, D.; Ranjith, P.G.; Perera, M.S.A. The brittleness indices used in rock mechanics and their application in shale hydraulic fracturing: A review. J. Pet. Sci. Eng. 2016, 143, 158–170. [Google Scholar] [CrossRef]
- Jarvie, D.M.; Hill, R.J.; Ruble, T.E.; Pollastro, R.M. Unconventional shale-gas systems: The Mississippian Barnett Shale of north-central Texas as one model for thermogenic shale-gas assessment. AAPG Bull. 2007, 91, 475–499. [Google Scholar] [CrossRef]
- Rickman, R.; Mullen, M.J.; Petre, J.E.; Grieser, W.V.; Kundert, D. A practical use of shale petrophysics for stimulation design optimization: All shale plays are not clones of the Barnett shale. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 21–24 September 2008; pp. 1–9. [Google Scholar]
- Bai, M. Why are brittleness and fracability not equivalent in designing hydraulic fracturing in tight shale gas reservoirs. Petroleum 2016, 2, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Nasehi, M.J.; Mortazavi, A. Effects of in-situ stress regime and intact rock strength parameters on the hydraulic fracturing. J. Pet. Sci. Eng. 2013, 108, 211–221. [Google Scholar] [CrossRef]
- Hucka, V.; Das, B. Brittleness determination of rocks by different methods. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1974, 11, 389–392. [Google Scholar] [CrossRef]
- Meng, F.; Zhou, H.; Zhang, C.; Xu, R.; Lu, J. Evaluation methodology of brittleness of rock based on post-peak stress–strain curves. Rock Mech. Rock Eng. 2015, 48, 1787–1805. [Google Scholar] [CrossRef]
- Xia, Y.; Zhou, H.; Zhang, C.; He, S.; Gao, Y.; Wang, P. The evaluation of rock brittleness and its application: A review study. Eur. J. Environ. Civ. Eng. 2022, 26, 239–279. [Google Scholar] [CrossRef]
- Jin, X.; Shah, S.N.; Roegiers, J.-C.; Zhang, B. Fracability evaluation in shale reservoirs—An integrated petrophysics and geomechanics approach. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 4–6 February 2014; pp. 1–14. [Google Scholar]
- Wang, S.; Sun, L.; Li, X.; Zhou, J.; Du, K.; Wang, S.; Khandelwal, M. Experimental investigation and theoretical analysis of indentations on cuboid hard rock using a conical pick under uniaxial lateral stress. Geomech. Geophys. Geo Energ. Geo Resour. 2022, 8, 34. [Google Scholar] [CrossRef]
- Atkinson, B.K. Fracture Mechanics of Rock; Academic Press: London, UK, 1987. [Google Scholar]
- Lawn, B.R.; Wilshaw, T.R. Fracture of Brittle Solids; Cambridge University Press: New York, NY, USA, 1975. [Google Scholar]
- Saleur, H.; Sammis, C.G.; Sornette, D. Discrete scale invariance, complex fractal dimensions, and log-periodic fluctuations in seismicity. J. Geophys. Res. Solid Earth 1996, 101, 17661–17677. [Google Scholar] [CrossRef]
- Ghamgosar, M.; Bahaaddini, M.; Erarslan, N.; Williams, D.J. A new experimental approach to quantify microfractures in the Fracture Process Zone (FPZ) under various loading conditions. Eng. Geol. 2021, 283, 106024. [Google Scholar] [CrossRef]
- Ghamgosar, M.; Erarslan, N.; Williams, D.J. Experimental investigation of fracture process zone in rocks damaged under cyclic loadings. Exp. Mech 2017, 57, 97–113. [Google Scholar] [CrossRef]
- Guha Roy, D.; Singh, T.N.; Kodikara, J. Influence of joint anisotropy on the fracturing behavior of a sedimentary rock. Eng. Geol. 2017, 228, 224–237. [Google Scholar] [CrossRef]
- Zietlow, W.K.; Labuz, J.F. Measurement of the intrinsic process zone in rock using acoustic emission. Int. J. Rock Mech. Min. Sci. 1998, 35, 291–299. [Google Scholar] [CrossRef]
- Erarslan, N. Microstructural investigation of subcritical crack propagation and Fracture Process Zone (FPZ) by the reduction of rock fracture toughness under cyclic loading. Eng. Geol. 2016, 208, 181–190. [Google Scholar] [CrossRef]
- Han, Z.; Zhang, L.; Azzam, R.; Zhou, J.; Wang, S. A statistical index indicating the degree and mechanical effects of grain size heterogeneity in rocks. Eng. Geol. 2021, 293, 106292. [Google Scholar] [CrossRef]
- Fowell, R.J.; Xu, C.; Dowd, P.A. An update on the fracture toughness testing methods related to the cracked chevron-notched Brazilian disk (CCNBD) specimen. Pure Appl. Geophys. 2006, 163, 1047–1057. [Google Scholar] [CrossRef]
- American Society of Testing Materials. Standard Test Method for Splitting Tensile Strength of Intact Rock Core Specimens; American Society of Testing Materials: West Conshohocken, PA, USA, 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Wong, L.N.Y.; Einstein, H.H. Crack coalescence in molded gypsum and Carrara marble: Part 2—Microscopic observations and interpretation. Rock Mech. Rock Eng. 2009, 42, 513–545. [Google Scholar] [CrossRef]
- Wang, H. Experimental Study of Shale Rock Mechanical Properties and Volume Fracturing. Ph.D. Thesis, University of Chinese Academy of Sciences, Beijing, China, 2015. [Google Scholar]
- Chen, H.; Niu, J.; Zhai, M. Characteristics of the fracture process zone for reservoir rock with various heterogeneity. Energies 2022, 15, 8332. [Google Scholar] [CrossRef]
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Potyondy, D.O. A grain-based model for rock: Approaching the true microstructure. In Proceedings of the Rock Mechanics in the Nordic Countries 2010, Kongsberg, Norway, 9–12 June 2010; pp. 225–234. [Google Scholar]
- Itasca Consulting Group Inc. PFC2D—Particle Flow Code in 2 Dimensions; Itasca Consulting Group Inc: Minneapolis, MN, USA, 2019. [Google Scholar]
- Pierce, M.; Cundall, P.; Potyondy, D.; Ivars, D.M. A synthetic rock mass model for jointed rock. In Proceedings of the 1st Canada—U.S. Rock Mechanics Symposium, Vancouver, BC, Canada, 27–31 May 2007. [Google Scholar]
- Whitney, D.L.; Broz, M.; Cook, R.F. Hardness, toughness, and modulus of some common metamorphic minerals. Am. Miner. 2007, 92, 281–288. [Google Scholar] [CrossRef]
- Wang, S.; Zhou, J.; Zhang, L.; Han, Z.; Zhang, F. Parameter studies on the mineral boundary strength influencing the fracturing of the crystalline rock based on a novel Grain-Based Model. Eng. Fract. Mech. 2021, 241, 107388. [Google Scholar] [CrossRef]
- Zhou, J.; Lan, H.; Zhang, L.; Yang, D.; Song, J.; Wang, S. Novel grain-based model for simulation of brittle failure of Alxa porphyritic granite. Eng. Geol. 2019, 251, 100–114. [Google Scholar] [CrossRef]
- Moore, D.E.; Lockner, D.A. The role of microcracking in shear-fracture propagation in granite. J. Struct. Geol. 1995, 17, 95–114. [Google Scholar] [CrossRef]
- Janssen, C.; Wagner, F.; Zang, A.; Dresen, G. Fracture process zone in granite: A microstructural analysis. Int. J. Earth. Sci. 2001, 90, 46–59. [Google Scholar] [CrossRef]
- Eberhardt, E.; Stimpson, B.; Stead, D. Effects of grain size on the initiation and propagation thresholds of stress-induced brittle fractures. Rock Mech. Rock Eng. 1999, 32, 81–99. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, X.; Sun, W. A review of laboratory studies and theoretical analysis for the interaction mode between induced hydraulic fractures and pre-existing fractures. J. Nat. Gas. Sci. Eng. 2021, 86, 103719. [Google Scholar] [CrossRef]
- Lin, C.; He, J.; Li, X.; Wan, X.; Zheng, B. An experimental investigation into the effects of the anisotropy of shale on hydraulic fracture propagation. Rock Mech. Rock Eng. 2017, 50, 543–554. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, Y.; Wang, C.; Liu, Q. Hydraulic fracturing characteristics and evaluation of fracturing effectiveness under different anisotropic angles and injection rates: An experimental investigation in absence of confining pressure. J. Nat. Gas. Sci. Eng. 2022, 97, 104343. [Google Scholar] [CrossRef]
- Sha, S.; Rong, G.; Tan, J.; He, R.; Li, B. Tensile strength and brittleness of sandstone and granite after high-temperature treatment: A review. Arab. J. Geosci. 2020, 13, 598. [Google Scholar] [CrossRef]
- Zhang, W.; Sun, Q.; Hao, S.; Geng, J.; Lv, C. Experimental study on the variation of physical and mechanical properties of rock after high temperature treatment. Appl. Eng. 2016, 98, 1297–1304. [Google Scholar] [CrossRef]
- Sirdesai, N.N.; Mahanta, B.; Ranjith, P.G.; Singh, T.N. Effects of thermal treatment on physico-morphological properties of Indian fine-grained sandstone. Bull. Eng. Geol. Env. 2019, 78, 883–897. [Google Scholar] [CrossRef]
- Zuo, J.; Zhou, H.; Xie, H. Fracture characteristics of sandstone under thermal effects. Eng. Mech. 2008, 25, 124–130. [Google Scholar]
- Niu, J. Research on the Fracture Mechanics Index of Rock Fracability Evaluation. Ph.D. Thesis, University of Chinese Academy of Sciences, Beijing, China, 2015. [Google Scholar]
- Chen, B.; Barboza, B.R.; Sun, Y.; Bai, J.; Thomas, H.R.; Dutko, M.; Cottrell, M.; Li, C. A review of hydraulic fracturing simulation. Arch. Comput. Method E. 2022, 29, 1–58. [Google Scholar] [CrossRef]
- Liu, P.; Ju, Y.; Gao, F.; Ranjith, P.G.; Zhang, Q. CT identification and fractal characterization of 3-D propagation and distribution of hydrofracturing cracks in low-permeability heterogeneous rocks. J. Geophys. Res. Sol. Ea. 2018, 123, 2156–2173. [Google Scholar] [CrossRef]










| Microscopy Observation | Qualitative Description | Average Size (mm) | Grain Size Distribution |
|---|---|---|---|
 | Medium-coarse grains | 3.4 | 3–5 mm: 70% 1–3 mm: 30% |
 | Medium grains | 1.5 | 1–2 mm |
 | Fine grains | <0.1 | / |
 | Coarse grains | 2 | 1–3 mm |
| Elements | Microscale Parameters | Marble A | Marble J |
|---|---|---|---|
| Particles | Density (kg/m3) | 2690 | 2690 |
| Effective modulus (GPa) | 70 | 70 | |
| Normal to shear stiffness ratio | 1.5 | 1.5 | |
| Friction coefficient | 0.6 | 0.6 | |
| Soft-bonded intra-grain contact | Effective modulus (GPa) | 15.0 | 10.0 |
| Normal to shear stiffness ratio | 2.0 | 2.0 | |
| Friction coefficient | 0.6 | 0.6 | |
| Tensile strength (MPa) | 28.0 | 18.0 | |
| Cohesion (MPa) | 112.0 | 72.0 | |
| Friction angle (°) | 45 | 45 | |
| Softening factor | 0.1 | 0.1 | |
| Softening tensile strength factor | 0.7 | 0.7 | |
| Smooth-joint inter-grain contact | Tensile strength coefficient | 0.3 | 0.3 |
| Cohesion coefficient | 0.8 | 0.8 | |
| Friction angle coefficient | 0.6 | 0.6 | |
| Friction adjustment coefficient | 0.5 | 0.5 | |
| Normal stiffness coefficient | 0.8 | 0.8 | |
| Shear stiffness coefficient | 0.15 | 0.15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Niu, J.; Zhai, M. An Evaluation Index of Fracability for Reservoir Rocks Based on Fracture Process Zone. Materials 2022, 15, 8485. https://doi.org/10.3390/ma15238485
Chen H, Niu J, Zhai M. An Evaluation Index of Fracability for Reservoir Rocks Based on Fracture Process Zone. Materials. 2022; 15(23):8485. https://doi.org/10.3390/ma15238485
Chicago/Turabian StyleChen, Hongran, Jingrui Niu, and Mengyang Zhai. 2022. "An Evaluation Index of Fracability for Reservoir Rocks Based on Fracture Process Zone" Materials 15, no. 23: 8485. https://doi.org/10.3390/ma15238485





