Buckling Behavior of Sandwich Cylindrical Shells Covered by Functionally Graded Coatings with Clamped Boundary Conditions under Hydrostatic Pressure
Abstract
:1. Introduction
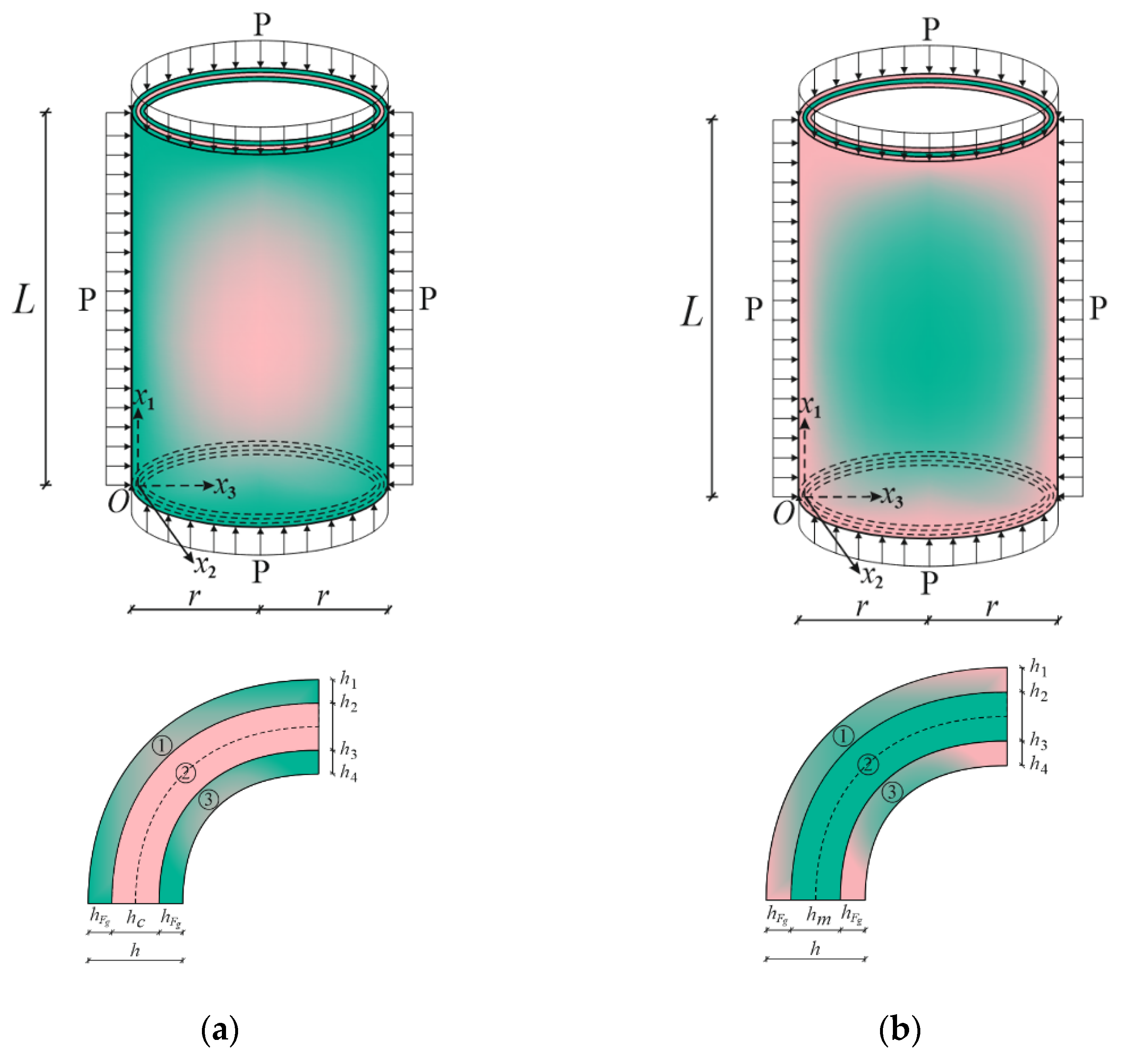
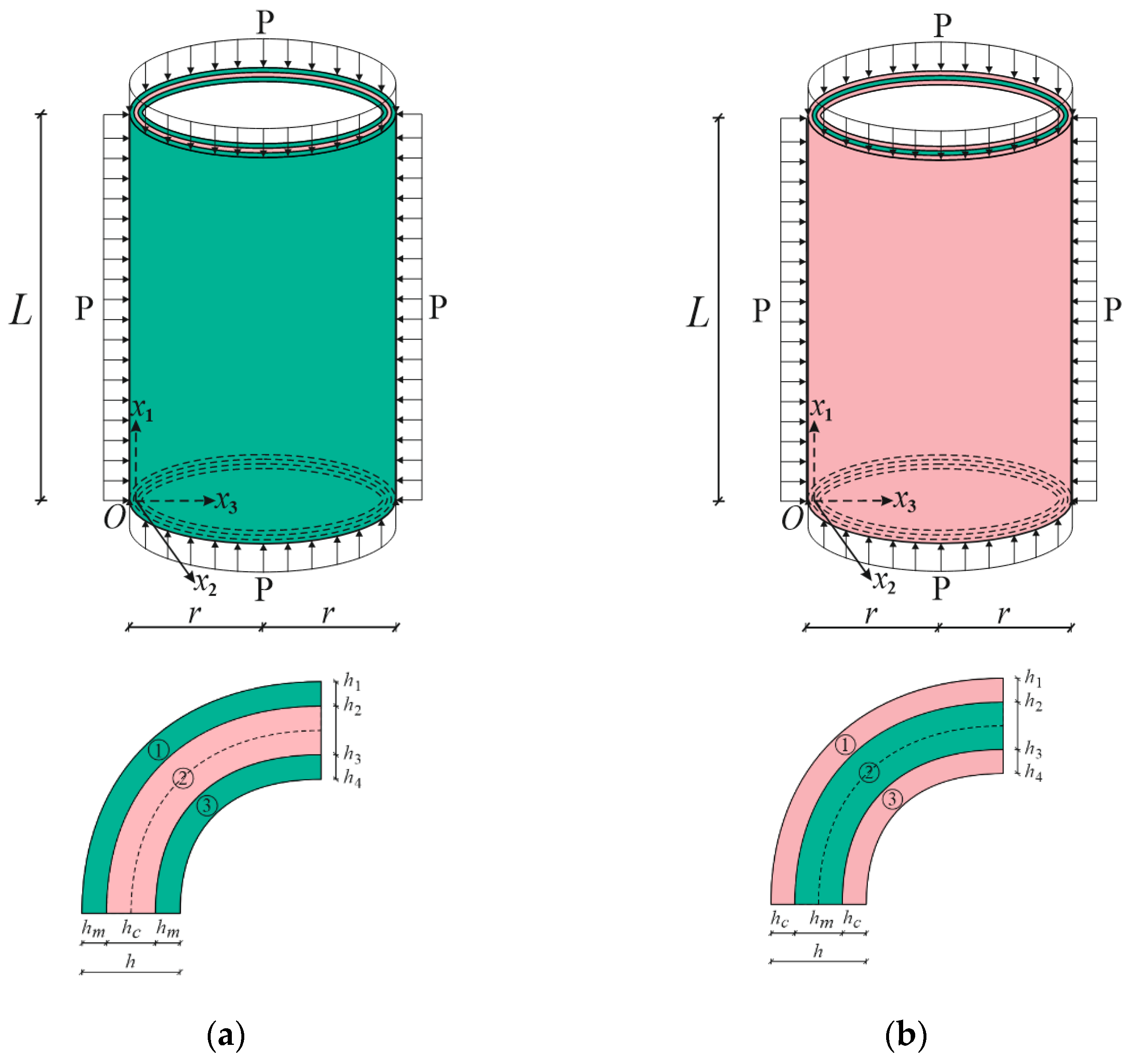
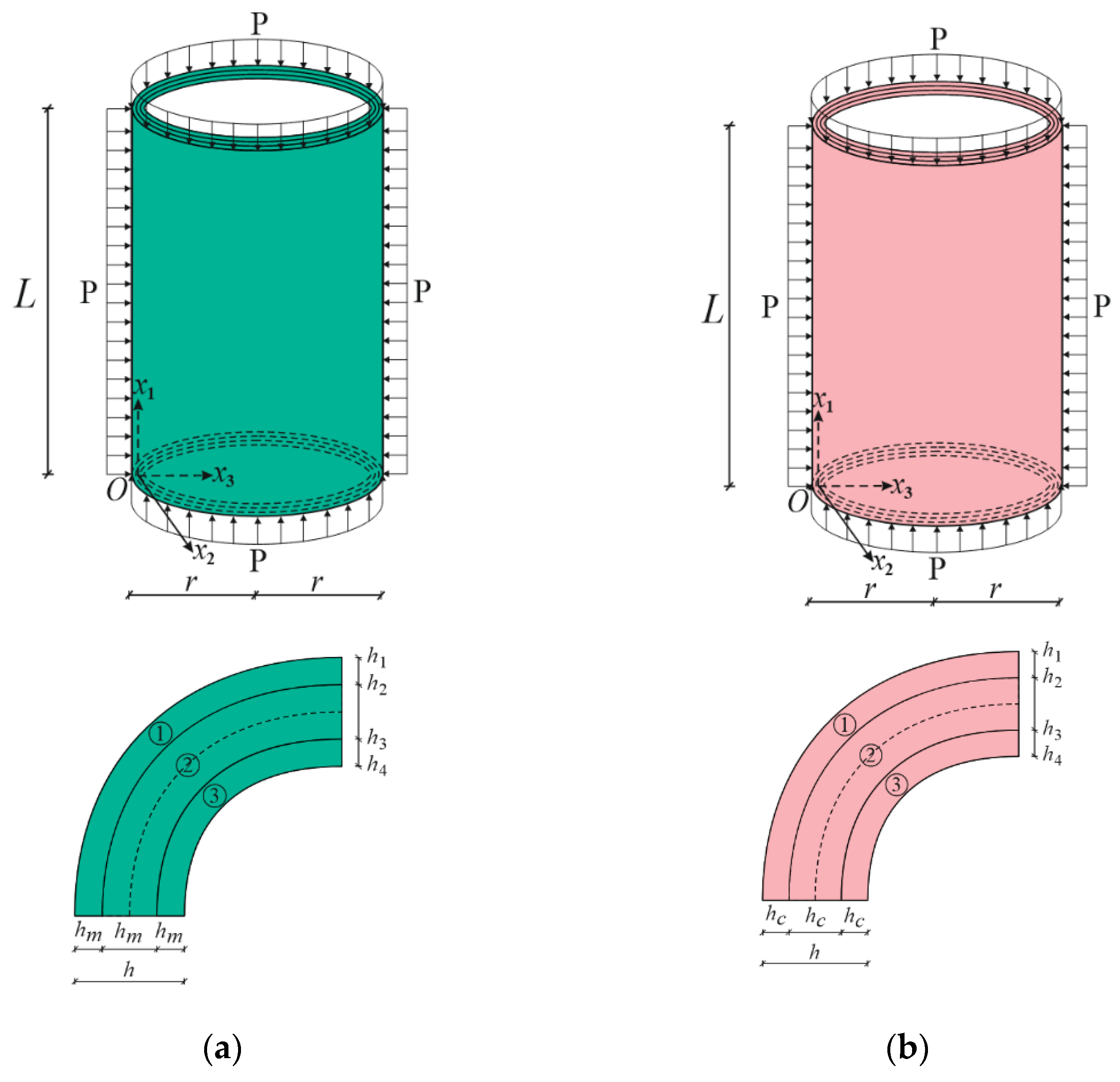
2. Material and Geometric Model of Problem
3. Basic Relations and Equations
4. Solution Procedure
5. Numerical Results and Discussion
5.1. Comparison
5.2. Novel Applications
6. Conclusions
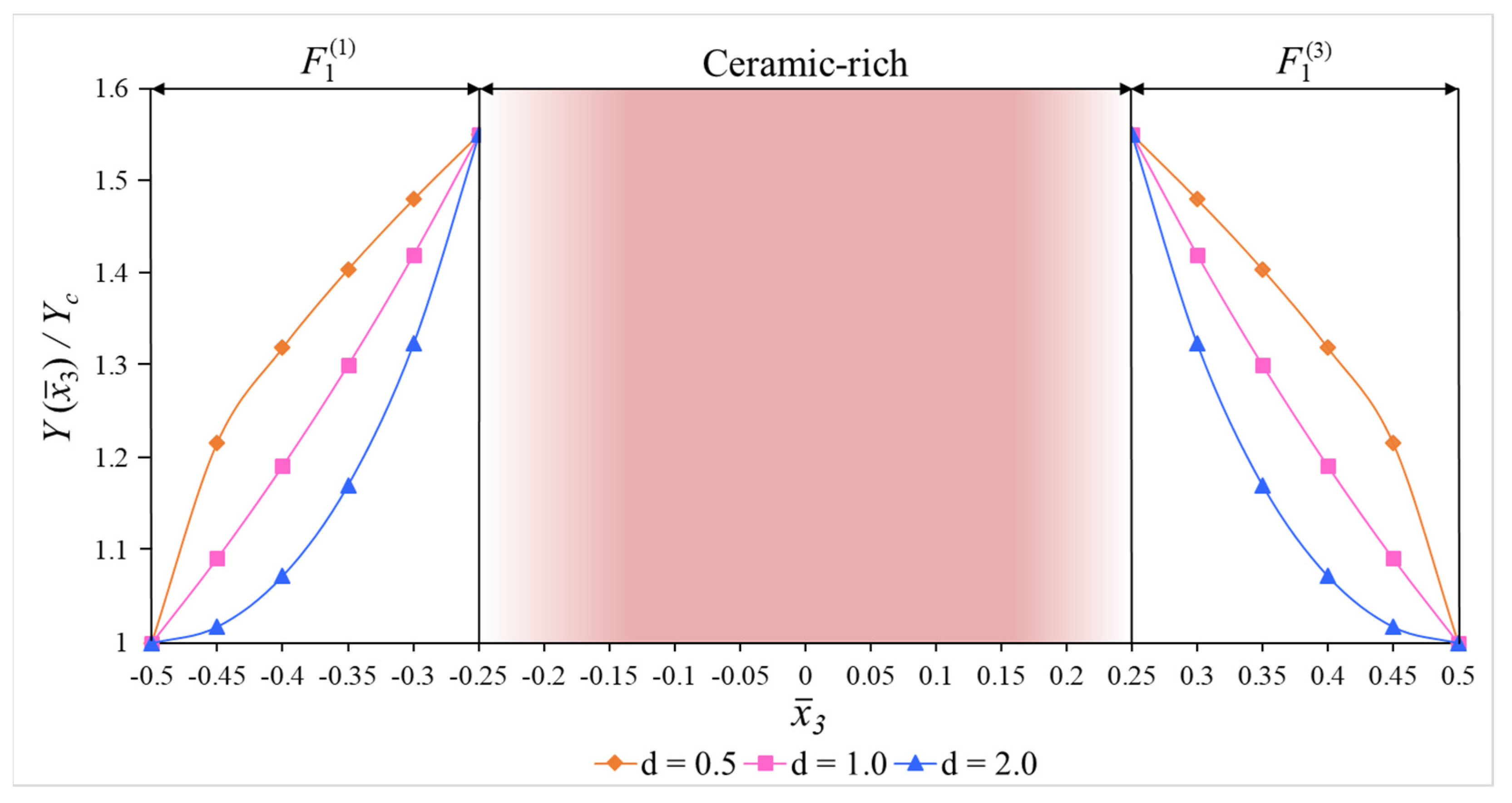
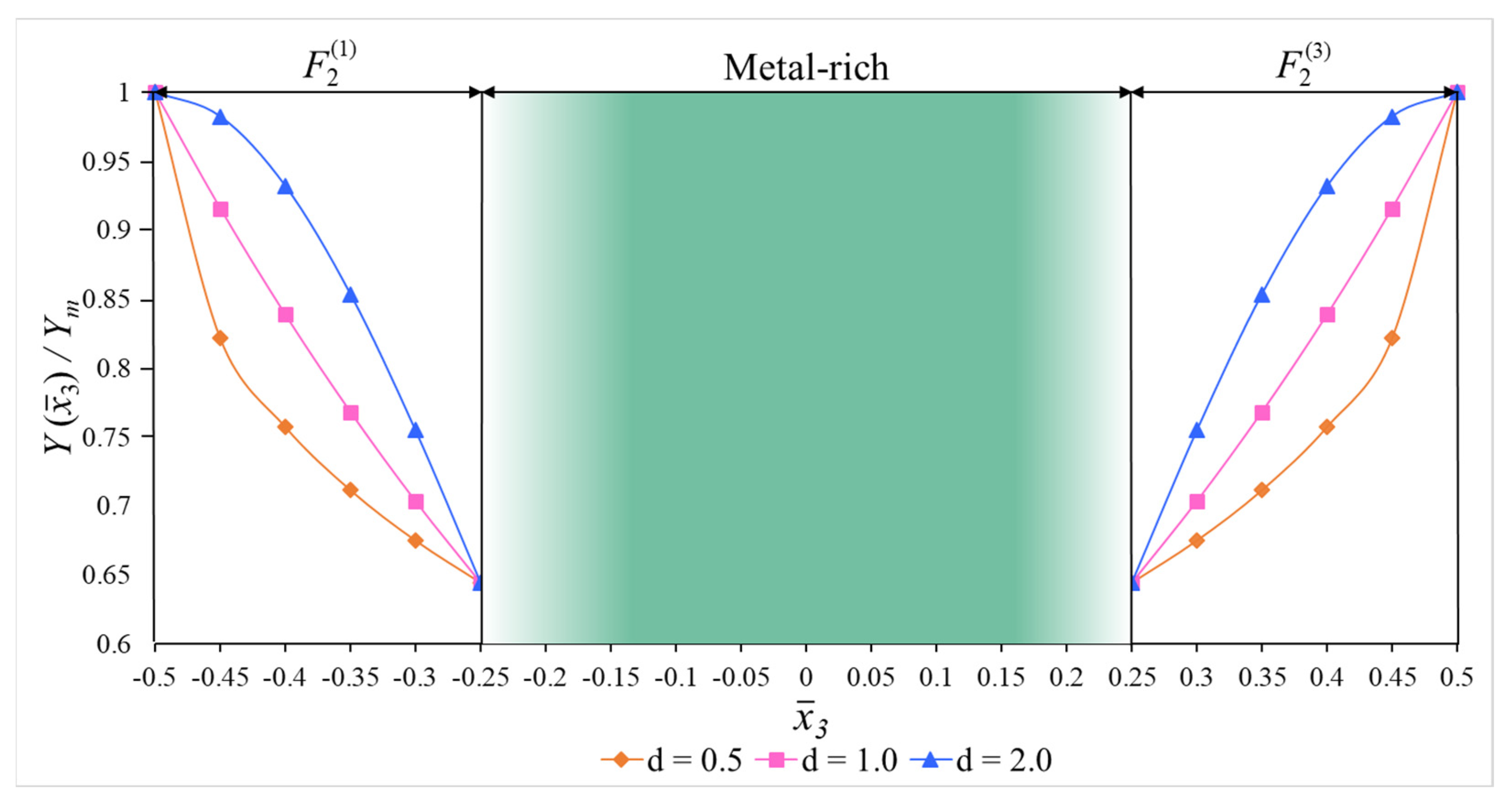
- The and values for the cylindrical shells covered by the FG1 and FG2 coatings decrease, while the number of circumferential waves increases depending on the increase in the .
- As the of the FG1- and FG2-coated sandwich cylinders are compared with the metal- and ceramic-coated homogeneous sandwich cylinders in the framework of the FOST, the influence of the FG1 and FG2 coatings on the dimensionless hydrostatic buckling pressure decreases as the increases.
- As the FG1 and FG2-coated sandwich shells are compared with pure ceramic and pure metal cylindrical shells in the framework of the ST, the effect of the FG1 and FG2 coatings on the increases as the increases.
- The most significant effect of the transverse shear strains on the DHBP of the FG1- and FG2-coated sandwich cylindrical shells occurs in the shell covered by the FG2 coating at = 20.
- The magnitudes of and for the FG1 sandwich cylindrical shells decrease, while they increase for the FG2 sandwich cylindrical shells, as the volume fraction index increases.
- When FG1- and FG2-coated shells are compared with the pure ceramic and pure metal single-layer cylinders, respectively, the effect of the FG1 coating on the decreases, whereas the influence of the FG2 coating on the increases, as the increases.
- The most significant effect of the transverse shear strains on the DHBP occurs in FG2-coated sandwich shell at = 2.
- As the FG1- and FG2-coated sandwich cylinders are compared with the pure ceramic and metal single-layer cylinders, the influence of FG1 and FG2 coatings on the decreases as the increases.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Vinson, J.R. Sandwich structures. Appl. Mech. Rev. 2001, 54, 201–214. [Google Scholar] [CrossRef]
- Garg, A.; Belarbi, M.O.; Chalak, H.D.; Chakrabarti, A. A review of the analysis of sandwich FGM structures. Compos. Struct. 2021, 258, 113427. [Google Scholar] [CrossRef]
- Koizumi, M. The concept of FGM ceramic transactions. Ceram. Trans. Funct. Grad. Mater. 1993, 34, 3–10. [Google Scholar]
- Miyamoto, Y. Functionally Graded Materials: Design, Processing and Applications; Kluwer Academic: Dordrecht/London/Boston, UK, 1999. [Google Scholar]
- Li, Y.; Jian, S.; Min, Z. Application of ceramics metal functionally graded materials on green automobiles. Key Eng. Mater. 2005, 280, 1925–1928. [Google Scholar]
- Udupa, G.; Shrikantha, S.R.; Gangadharan, K.V. Future applications of carbon nanotube reinforced functionally graded composite materials. In Proceedings of the IEEE-International Conference on Advances in Engineering, Science and Management (ICAESM-2012), Nagapattinam, India, 30–31 March 2012; pp. 399–404. [Google Scholar]
- Gupta, N.; Prasad, V.V.B.; Madhu, V.; Basu, B. Ballistic studies on TiB2-Ti functionally graded armor ceramics. Def. Sci. J. 2012, 62, 382–389. [Google Scholar] [CrossRef]
- Gayen, D.; Tiwari, R.; Chakraborty, D. Static and dynamic analyses of cracked functionally graded structural components: A review. Compos. Part B Eng. 2019, 173, 106982. [Google Scholar] [CrossRef]
- Saleh, B.; Jiang, J.; Fathi, R.; Al-hababi, T.; Xu, Q.; Wang, L.; Song, D.; Ma, A. 30 Years of functionally graded materials: An overview of manufacturing methods, Applications and Future Challenges. Compos. Part B Eng. 2020, 201, 108376. [Google Scholar] [CrossRef]
- Zenkour, A.M. A comprehensive analysis of functionally graded sandwich plates: Part 2–buckling and free vibration. Int. J. Solid Struct. 2005, 42, 5243–5258. [Google Scholar] [CrossRef]
- Sofiyev, A.H. The vibration and buckling of sandwich cylindrical shells covered by different coatings subjected to the hydrostatic pressure. Compos. Struct. 2014, 117, 124–134. [Google Scholar] [CrossRef]
- Dung, D.V.; Hoa, L.K.; Thuyet, B.T.; Nga, N.T. Buckling analysis of functionally graded material (FGM) sandwich truncated conical shells reinforced by FGM stiffeners filled inside by elastic foundations. Appl. Math. Mech.-Eng. Edit. 2016, 37, 879–902. [Google Scholar] [CrossRef]
- Alibeigloo, A. Thermo elasticity solution of sandwich circular plate with functionally graded core using generalized differential quadrature method. Compos. Struct. 2016, 136, 229–240. [Google Scholar] [CrossRef]
- Sofiyev, A.H. The stability analysis of shear deformable FGM sandwich conical shells under the axial load. Compos. Struct. 2017, 176, 803–811. [Google Scholar] [CrossRef]
- Moita, J.S.; Araújo, A.J.; Correia, V.F.; Soares, C.M.M.; Herskovits, J. Active-passive damping in functionally graded sandwich plate/shell structures. Compos. Struct. 2018, 202, 324–332. [Google Scholar] [CrossRef]
- Hao, Y.X.; Cao, Z.; Zhang, W.; Chen, J.; Yao, M.H. Stability analysis for geometric nonlinear functionally graded sandwich shallow shell using a new developed displacement field. Compos. Struct. 2019, 210, 202–216. [Google Scholar] [CrossRef]
- Nguyen, H.N.; Tan, T.C.; Luat, D.T.; Phan, V.D.; Thom, D.V.; Minh, P.V. Research on the buckling behavior of functionally graded plates with stiffeners based on the third-order shear deformation theory. Materials 2019, 12, 1262. [Google Scholar] [CrossRef] [Green Version]
- Karroubi, R.; Irani-Rahaghi, M. Rotating sandwich cylindrical shells with an FGM core and two FGPM layers: Free vibration analysis. Appl. Math. Mech.-Eng. Edit. 2019, 40, 563–578. [Google Scholar] [CrossRef]
- Sofiyev, A.H. The buckling and vibration analysis of coating-FGM-substrate conical shells under hydrostatic pressure with mixed boundary conditions. Compos. Struct. 2019, 209, 686–693. [Google Scholar] [CrossRef]
- Garbowski, T.; Gajewski, T.; Grabski, J.K. Torsional and transversal stiffness of orthotropic sandwich panels. Materials 2020, 13, 5016. [Google Scholar] [CrossRef]
- Karakoti, A.; Pandey, S.; Kar, V.R. Free vibration response of P-FGM and S-FGM sandwich shell panels: A comparison. Int. Conf. Aspects Mater. Sci. Eng. Mater. Today-Proceed. 2020, 28, 1701–1705. [Google Scholar] [CrossRef]
- Hung, V.T.; Dong, D.T.; Phuong, N.T.; Ly, L.N.; Minh, T.Q.; Trung, N.T.; Hoa, V.; Nam, V.H. Nonlinear buckling behavior of spiral corrugated sandwich FGM cylindrical shells surrounded by an elastic medium. Materials 2020, 13, 1984. [Google Scholar] [CrossRef]
- Burlayenko, V.N.; Sadowski, T.; Altenbach, H. Efficient free vibration analysis of FGM sandwich flat panels with conventional shell elements. Mech. Adv. Mater. Struct. 2021, 29, 3709–3726. [Google Scholar] [CrossRef]
- Zhang, S.Q.; Huang, Z.T.; Zhao, Y.F.; Ying, S.S.; Ma, S.Y. Static and dynamic analyses of FGPM cylindrical shells with quadratic thermal gradient distribution. Compos. Struct. 2021, 277, 114658. [Google Scholar] [CrossRef]
- Thai, D.N.; Minh, P.V.; Hoang, C.P.; Duc, T.T.; Cam, N.N.T.; Thi, D.N. Bending of symmetric sandwich FGMs beams with shear connectors. Math Prob. Eng. 2021, 2021, 7596300. [Google Scholar] [CrossRef]
- Dung, N.T.; Minh, P.V.; Hung, H.M.; Tien, D.M. The third-order shear deformation theory for modeling the static bending and dynamic responses of piezoelectric bidirectional functionally graded plates. Adv. Mater. Sci. Eng. 2021, 2021, 5520240. [Google Scholar] [CrossRef]
- Duc, N.D.; Vuong, P.M. Nonlinear vibration response of shear deformable FGM sandwich toroidal shell segments. Meccanica 2022, 57, 1083–1103. [Google Scholar]
- Shinde, B.M.; Sayyad, A.S. A new higher order shear and normal deformation theory for FGM sandwich shells. Compos. Struct. 2022, 280, 114865. [Google Scholar] [CrossRef]
- Ramezani, M.; Rezaiee-Pajand, M.; Tornabene, F. Nonlinear dynamic analysis of FG/SMA/FG sandwich cylindrical shells using HSDT and semi ANS functions. Thin-Wall. Struct. 2022, 171, 108702. [Google Scholar] [CrossRef]
- Chaabani, H.; Mesmoudi, S.; Boutahar, L.; El Bikri, K. Buckling of porous FG sandwich plates subjected to various nonuniform compressions and resting on Winkler Pasternak elastic foundation using a finite element model based on the high-order shear deformation theory. Acta Mech. 2022, 233, 5359–5376. [Google Scholar] [CrossRef]
- Alsebai, F.; Al Mukahal, F.H.H.; Sobhy, M. Semi-analytical solution for thermo-piezoelectric bending of FG porous plates reinforced with graphene platelets. Mathematics 2022, 10, 4104. [Google Scholar] [CrossRef]
- Sofiyev, A.H.; Fantuzzi, N. Analytical solution of stability and vibration problem of clamped cylindrical shells containing functionally graded layers within shear deformation theory. Alexandria Eng. J. 2022; in press. [Google Scholar] [CrossRef]
- Hu, Z.; Zhou, C.; Xinran, Z.; Ni, Z.; Li, R. Free vibration of non-Lévy-type functionally graded doubly curved shallow shells: New analytic solutions. Compos. Struct. 2023, 304, 116389. [Google Scholar] [CrossRef]
- Ambartsumian, S.A. Theory of Anisotropic Plates: Strength, Stability and Vibration; CRC Press: Boca Raton, FL, USA, 1991. [Google Scholar]
- Ambartsumian, S.A. Theory of Anisotropic Shells; NASA, TT F-118: Washington, DC, USA, 1964.
- Shen, H.S. Functionally Graded Materials, Nonlinear Analysis of Plates and Shells; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Sofiyev, A.H. On the vibration and stability of clamped FGM conical shells under external loads. J. Compos. Mater. 2011, 45, 771–788. [Google Scholar] [CrossRef]
- Shen, H.S.; Noda, N. Postbuckling of pressure-loaded FGM hybrid cylindrical shells in thermal environments. Compos. Struct. 2007, 77, 546–560. [Google Scholar] [CrossRef]
- Singer, J.; Baruch, M.; Reichenthal, J. Influence of in plane boundary conditions on the buckling of clamped conical shells. Isr. J. Tech. 1971, 9, 127–139. [Google Scholar]
- Lopatin, A.V.; Morozov, E.V. Buckling of composite cylindrical shells with rigid end disks under hydrostatic pressure. Compos. Struct. 2017, 173, 136–143. [Google Scholar] [CrossRef]
| , (ncr) | |||
|---|---|---|---|
| L/r | Singer et al. [39] CC2 Classic | Singer et al. [39] CC1 | Present Study |
| 0.5 | 27.98 (11) | 26.32 (11) | 27.456 (11) |
| 1 | 12.89 (9) | 11.03 (8) | 11.7789 (9) |
| 2 | 6.52 (7) | 5.026 (7) | 5.759 (7) |
| , (ncr) | |||
|---|---|---|---|
| L | Lopatin and Morozov [40] FEM | Lopatin and Morozov [40] Analytical | Present Study |
| 1 | 2003.1 | 1922.4 | 1885.09 (6) |
| 2 | 1027.2 | 994.4 | 860.14 (4) |
| 3 | 724.8 | 754.9 | 704.82 (4) |
| (ncr) | (ncr) | (ncr) | (ncr) | (ncr) | (ncr) | |
|---|---|---|---|---|---|---|
| M/C/M | FG1/M/FG1 | Ceramic | ||||
| 20 | 1.552 (8) | 1.745 (8) | 1.833 (8) | 1.988 (8) | 2.175 (8) | 2.423 (8) |
| 25 | 0.846 (8) | 0.912 (8) | 0.986 (8) | 1.038 (8) | 1.179 (8) | 1.264 (8) |
| 30 | 0.513 (9) | 0.541 (8) | 0.594 (9) | 0.616 (8) | 0.713 (8) | 0.748 (8) |
| 40 | 0.231 (9) | 0.239 (9) | 0.276 (8) | 0.271 (8) | 0.320 (9) | 0.329 (9) |
| 50 | 0.126 (10) | 0.128 (10) | 0.144 (10) | 0.146 (10) | 0.173 (9) | 0.176 (9) |
| C/M/C | FG2/M/FG2 | Metal | ||||
| 20 | 2.073 (8) | 2.314 (8) | 1.706 (8) | 2.020 (8) | 1.451 (8) | 1.635 (8) |
| 25 | 1.121 (8) | 1.204 (8) | 0.942 (8) | 1.051 (8) | 0.789 (8) | 0.852 (8) |
| 30 | 0.676 (8) | 0.710 (8) | 0.575 (8) | 0.620 (8) | 0.478 (8) | 0.504 (8) |
| 40 | 0.303 (9) | 0.312 (9) | 0.260 (9) | 0.272 (9) | 0.215 (9) | 0.221 (9) |
| 50 | 0.163 (9) | 0.166 (9) | 0.141 (9) | 0.145 (9) | 0.116 (9) | 0.118 (9) |
| (ncr) | (ncr) | (ncr) | (ncr) | (ncr) | (ncr) | |
|---|---|---|---|---|---|---|
| M/C/M | FG1/C/FG1 | Ceramic | ||||
| 2 | 1.222 (10) | 1.377 (10) | 1.446 (10) | 1.569 (10) | 1.717 (10) | 1.915 (10) |
| 4 | 1.320 (10) | 1.483 (10) | 1.532 (10) | 1.655 (10) | ||
| 6 | 1.391 (10) | 1.561 (10) | 1.581 (10) | 1.708 (10) | ||
| 8 | 1.442 (10) | 1.616 (10) | 1.612 (10) | 1.743 (10) | ||
| C/M/C | FG2/M/FG2 | Metal | ||||
| 2 | 1.639 (10) | 1.832 (9) | 1.349 (10) | 1.599 (9) | 1.146 (10) | 1.293 (10) |
| 4 | 1.540 (10) | 1.725 (9) | 1.242 (10) | 1.521 (9) | ||
| 6 | 1.469 (10) | 1.648 (9) | 1.159 (10) | 1.474 (10) | ||
| 8 | 1.418 (10) | 1.592 (9) | 1.081 (10) | 1.442 (10) | ||
| Volume Fraction Index ( ) | FG1/C/FG1 | FG2/M/FG2 | ||
|---|---|---|---|---|
| (ncr) | (ncr) | (ncr) | (ncr) | |
| 0.5 | 1.040 (8) | 1.102 (8) | 0.896 (8) | 0.984 (8) |
| 1 | 0.986 (8) | 1.038 (8) | 0.942 (8) | 1.051 (8) |
| 2 | 0.944 (8) | 0.985 (8) | 0.937 (8) | 1.113 (8) |
| Pure ceramic | Pure metal | |||
| 1.179 (8) | 1.264 (8) | 0.789 (8) | 0.852 (8) | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sofiyev, A.H.; Fantuzzi, N.; Ipek, C.; Tekin, G. Buckling Behavior of Sandwich Cylindrical Shells Covered by Functionally Graded Coatings with Clamped Boundary Conditions under Hydrostatic Pressure. Materials 2022, 15, 8680. https://doi.org/10.3390/ma15238680
Sofiyev AH, Fantuzzi N, Ipek C, Tekin G. Buckling Behavior of Sandwich Cylindrical Shells Covered by Functionally Graded Coatings with Clamped Boundary Conditions under Hydrostatic Pressure. Materials. 2022; 15(23):8680. https://doi.org/10.3390/ma15238680
Chicago/Turabian StyleSofiyev, Abdullah H., Nicholas Fantuzzi, Cengiz Ipek, and Gülçin Tekin. 2022. "Buckling Behavior of Sandwich Cylindrical Shells Covered by Functionally Graded Coatings with Clamped Boundary Conditions under Hydrostatic Pressure" Materials 15, no. 23: 8680. https://doi.org/10.3390/ma15238680
APA StyleSofiyev, A. H., Fantuzzi, N., Ipek, C., & Tekin, G. (2022). Buckling Behavior of Sandwich Cylindrical Shells Covered by Functionally Graded Coatings with Clamped Boundary Conditions under Hydrostatic Pressure. Materials, 15(23), 8680. https://doi.org/10.3390/ma15238680









