Optimization of Pin Position and Angle for Z-Pin-Reinforced Foam Core Sandwich Structures
Abstract
1. Introduction
2. Materials and Methods
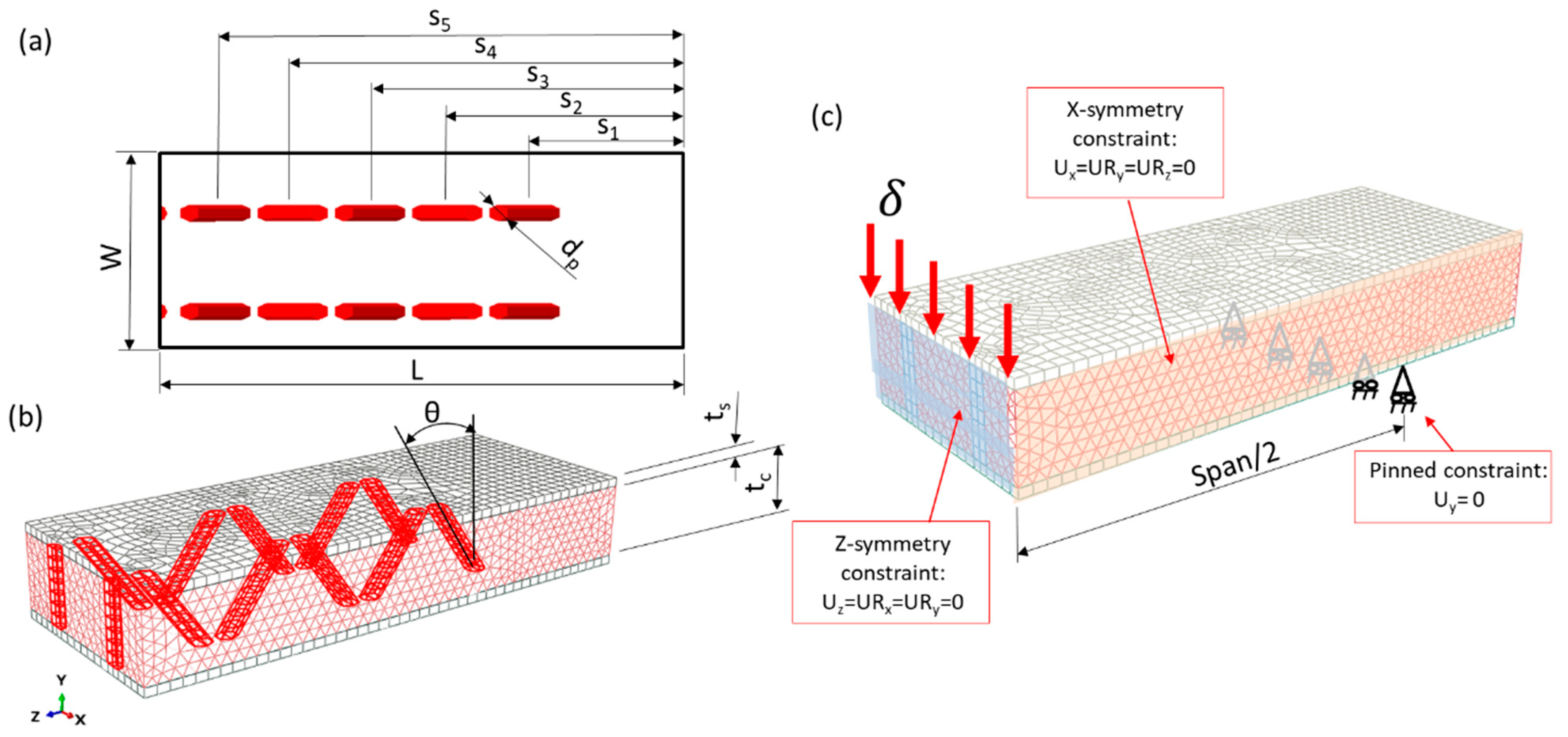
2.1. Optimization Process for Defining Pin Position and Pin Angle
- Optimization of the position of orthogonal Z-pins, which was implemented for 0HD and 0OPT.
- Optimization of both the pin position and pin angle, keeping only one angle for all pins to facilitate the core drilling, which was implemented for AHD and AOPT.
2.2. Numerical Flexural Tests for the Sandwich Structures
2.3. Optimization Problem
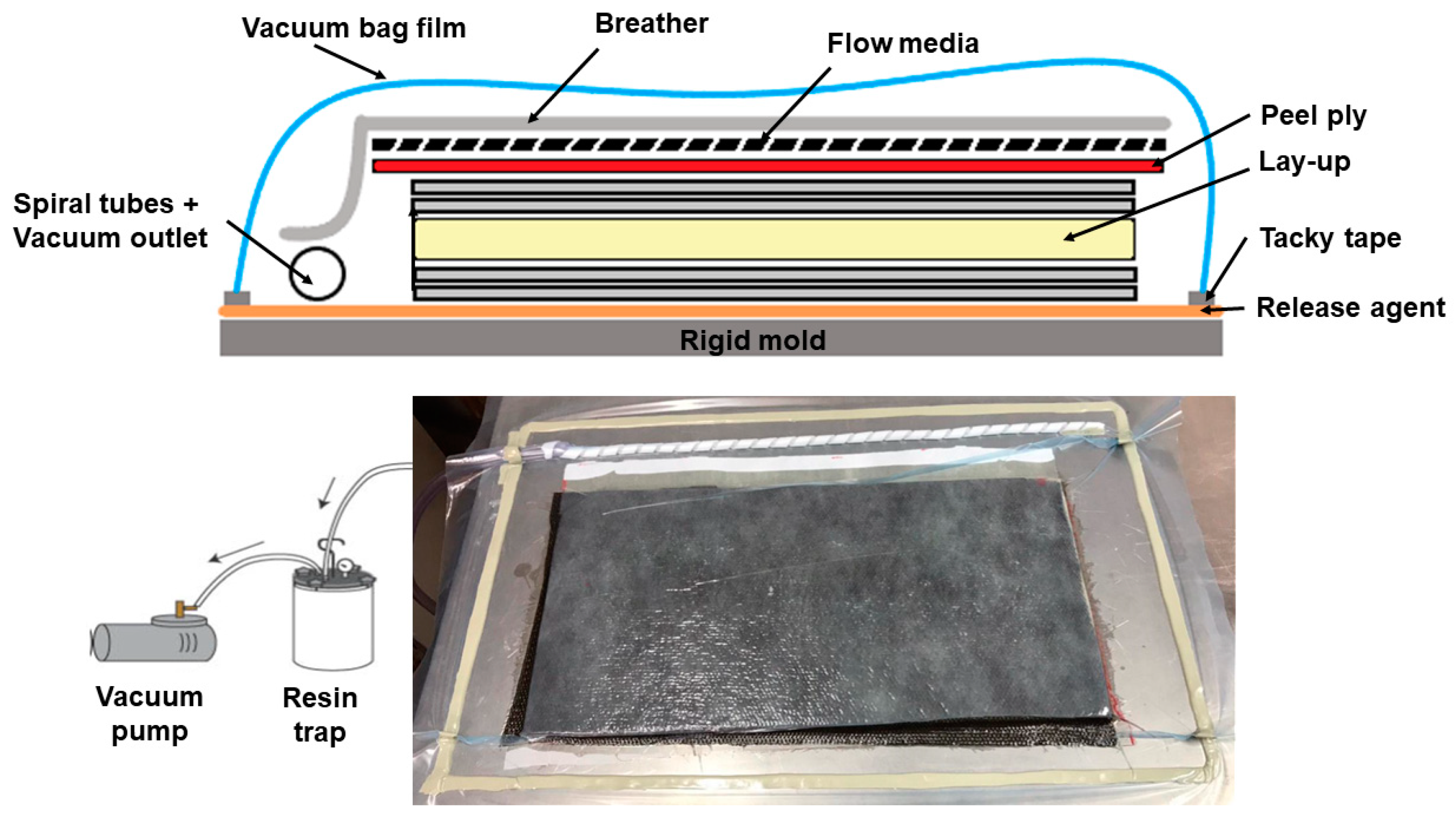
2.4. Manufacture of the Sandwich Structures
2.5. Tensile Tests for the Pins and Skins
2.6. Experimental Flexural Tests for the Sandwich Structures
3. Results and Discussion
3.1. Optimization Process for Defining Pin Position and Pin Angle
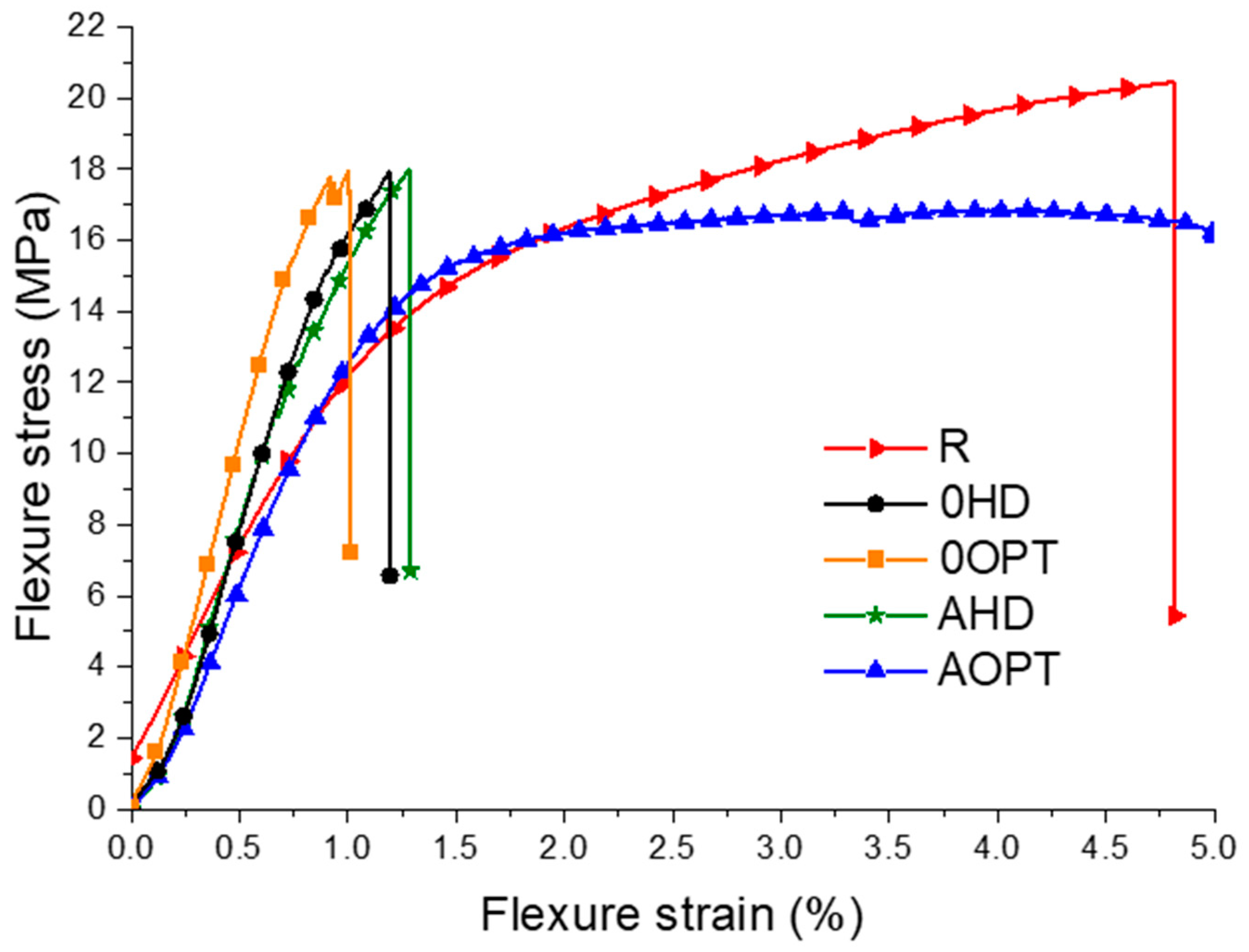
3.2. Experimental Flexural Tests for the Sandwich Structures
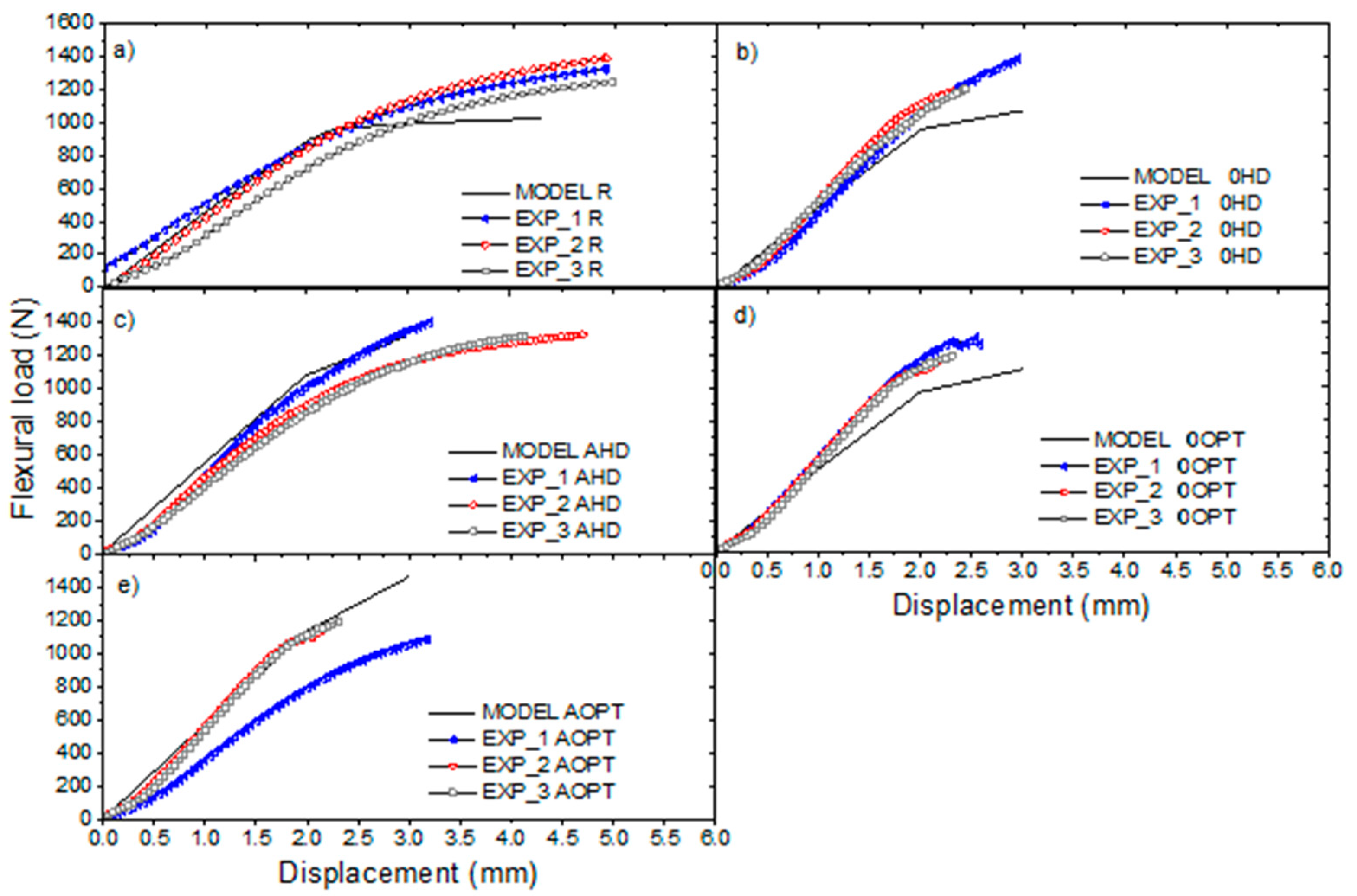
3.3. Numerical Flexural Tests for the Sandwich Structures
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- He, W.; Wu, J.; Yao, L.; Wang, C.; Zhang, H.; Liu, H. Numerical Investigation of Dynamic Response and Failure Mechanisms for Composite Lattice Sandwich Structure under Different Slamming Loads. Appl. Compos. Mater. 2021, 28, 1477–1509. [Google Scholar] [CrossRef]
- Kerche, E.F.; Caldas, B.G.S.; Carvalho, R.F.; Amico, S.C. Mechanical response of sisal/glass fabrics reinforced polyester–polyethylene terephthalate foam core sandwich panels. J. Sandw. Struct. Mater. 2022, 24, 6. [Google Scholar] [CrossRef]
- Delucis, R.D.A.; Tonatto, M.L.P.; Trindade, R.S.; Amico, S.C. In situ L-RTM manufacturing of sandwich panels with PET foam core reinforced by polymeric pins. J. Sandw. Struct. Mater. 2019, 23, 241–254. [Google Scholar] [CrossRef]
- May-Pat, A.; Avilés, F.; Aguilar, J. Mechanical properties of sandwich panels with perforated foam cores. J. Sandw. Struct. Mater. 2010, 13, 427–444. [Google Scholar] [CrossRef]
- Yalkin, H.E.; Icten, B.M.; Alpyildiz, T. Tensile and compressive performances of foam core sandwich composites with various core modifications. J. Sandw. Struct. Mater. 2016, 19, 49–65. [Google Scholar] [CrossRef]
- Grünewald, J.; Orth, T.; Parlevliet, P.; Altstädt, V. Modified foam cores for full thermoplastic composite sandwich structures. J. Sandw. Struct. Mater. 2017, 21, 1150–1166. [Google Scholar] [CrossRef]
- Nanayakkara, A.; Feih, S.; Mouritz, A.P. Experimental impact damage study of a z-pinned foam core sandwich composite. J. Sandw. Struct. Mater. 2012, 14, 469–486. [Google Scholar] [CrossRef]
- Mitra, N. A methodology for improving shear performance of marine grade sandwich composites: Sandwich composite panel with shear key. Compos. Struct. 2010, 92, 1065–1072. [Google Scholar] [CrossRef]
- Garay, A.C.; Souza, J.A.; Amico, S. Evaluation of mechanical properties of sandwich structures with polyethylene terephthalate and polyvinyl chloride core. J. Sandw. Struct. Mater. 2016, 18, 229–241. [Google Scholar] [CrossRef]
- Mallick, P.K. Fiber Reinforced Composites—Materials, Manufacturing and Design; CRC Press: Boca Raton, FL, USA, 2007; Volume 1. [Google Scholar]
- Du, L.; Jiao, G. Indentation study of Z-pin reinforced polymer foam core sandwich structures. Compos. Part A Appl. Sci. Manuf. 2009, 40, 822–829. [Google Scholar] [CrossRef]
- de Oliveira, L.; Tonatto, M.L.P.; Coura, G.L.C.; Freire, R.T.S.; Panzera, T.H.; Scarpa, F. Experimental and numerical assessment of sustainable bamboo core sandwich panels under low-velocity impact. Constr. Build. Mater. 2021, 292, 123437. [Google Scholar] [CrossRef]
- Xie, H.; Shen, C.; Fang, H.; Han, J.; Cai, W. Flexural property evaluation of web reinforced GFRP-PET foam sandwich panel: Experimental study and numerical simulation. Compos. Part B Eng. 2022, 234, 109725. [Google Scholar] [CrossRef]
- Lan, X.; Wu, G.; Huang, G. In-plane compression response of foam filled re-entrant auxetic structure. Appl. Compos. Mater. 2022, 29, 2245–2263. [Google Scholar] [CrossRef]
- Liu, T.; Deng, Z.C.; Lu, T.J. Analytical modeling and finite element simulation of the plastic collapse of sandwich beams with pin-reinforced foam cores. Int. J. Solids Struct. 2008, 45, 5127–5151. [Google Scholar] [CrossRef][Green Version]
- Dang, X.D.; Shi, S.J.; Jiang, J.S.; Xiao, J. Finite Element Analysis of X-Cor Sandwich’s Shear Modulus. Adv. Mater. Res. 2011, 328–330, 1113–1117. [Google Scholar] [CrossRef]
- Haldar, S.; Caputo, D.; Buesking, K.; Bruck, H.A. Flexural behavior of singly curved X-Cor® sandwich composite structures: Experiment and finite element modeling. Compos. Struct. 2015, 129, 70–79. [Google Scholar] [CrossRef]
- Caliri, M.F.; Ferreira, A.J.; Tita, V. A review on plate and shell theories for laminated and sandwich structures highlighting the Finite Element Method. Compos. Struct. 2016, 156, 63–77. [Google Scholar] [CrossRef]
- Fminsearch, Version 9.9.0.123456, Optimization Algorithm; Mathworks: Natick, MA, USA. Available online: https://www.mathworks.com/help/matlab/ref/fminsearch.html (accessed on 20 December 2022).
- Divinycell PET ACW P80 Datasheet; Barracuda Advanced Composites: Rio De Janeiro, Brazil, 2017.
- Composite Materials Handbook: Polymer Matrix Composites Materials Properties MIL-HDBK-1; U.S. Department of Defense: Philadelphia, AR, USA, 2002.
- Selver, E.; Kaya, G. Flexural properties of sandwich composite laminates reinforced with glass and carbon Z-pins. J. Compos. Mater. 2018, 53, 1347–1359. [Google Scholar] [CrossRef]
- Djama, K.; Michel, L.; Ferrier, E.; Gabor, A. Numerical modelling of a truss core sandwich panel: Influence of the connectors’ geometry and mechanical parameters on the mechanical response. Compos. Struct. 2020, 245, 112335. [Google Scholar] [CrossRef]






| Configuration | Nomenclature | Pin Diameter (mm) |
|---|---|---|
| No pins—reference | R | 3.2 |
| Pins oriented 0° throw the thickness and homogeneous distributed | 0HD | |
| Pins oriented 0° throw the thickness and the distance between pins optimized | 0OPT | |
| Pins with optimized angle orientation throw the thickness and homogeneously distributed | AHD | |
| Pins with optimized angle orientation and distance throw the thickness | AOPT |
| Material | Property | Symbol | Value |
|---|---|---|---|
| GFRP skin | Longitudinal elastic modulus * | E11 (MPa) | 10,500 |
| Transverse elastic modulus * | E22 (MPa) | 10,500 | |
| Poisson’s ratio * | ν12 | 0.3 | |
| In-plane shear modulus * | G12 (MPa) | 4038 | |
| PET foam | Elastic modulus ** | E (MPa) | 60 |
| Poisson’s ratio ** | νel | 0.35 | |
| Compressive yield stress ratio ** | K | 1.6656 | |
| Plastic Poisson’s ratio ** | νpl | 0.04 |
| Configuration | S1 * | S2 * | S3 * | S4 * | S5 * | θ (°) | Ef (GPa) | |
|---|---|---|---|---|---|---|---|---|
| R | - | - | - | - | - | - | 1.124 | 1.43 |
| 0HD | 9.00 | 27.2 | 45.40 | 63.60 | 81.80 | 0 | 1.452 | 1.54 |
| 0OPT | 35.75 | 51.00 | 59.65 | 66.30 | 73.98 | 0 | 1.566 | 1.55 |
| AHD | 9.00 | 27.20 | 45.40 | 63.60 | 81.80 | 35.5 | 2.364 | 1.73 |
| AOPT | 30.60 | 45.26 | 59.93 | 74.58 | 89.24 | 36.2 | 2.963 | 1.82 |
| Configuration | Ef (GPa) * | Fsult (MPa) * | Apparent Density (kg/m3) * | Specific Strength (kPa·m3/kg3) |
|---|---|---|---|---|
| R | 1.3 ± 0.11 A | 20.3 ± 0.47 B | 482.3 ± 19.5 A | 41.9 ± 2.4 |
| 0HD | 1.8 ± 0.21 B | 18.2 ± 1.62 A | 542.4 ± 28.2 B | 33.5 ± 5.7 |
| 0OPT | 2.4 ± 0.06 C | 17.2 ± 0.77 A | 540.8 ± 18.9 B | 31.8 ± 4.0 |
| AHD | 1.9 ± 0.18 B | 17.5 ± 0.61 A | 475.9 ± 15.3 A | 36.7 ± 3.9 |
| AOPT | 1.2 ± 0.14 A | 17.2 ± 1.04 A | 470.7 ± 21.0 A | 36.5 ± 4.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kerche, E.F.; Kairytė, A.; Członka, S.; da Silva, A.A.X.; Tonatto, M.L.P.; Bresolin, F.L.; Delucis, R.d.A.; Amico, S.C. Optimization of Pin Position and Angle for Z-Pin-Reinforced Foam Core Sandwich Structures. Materials 2023, 16, 352. https://doi.org/10.3390/ma16010352
Kerche EF, Kairytė A, Członka S, da Silva AAX, Tonatto MLP, Bresolin FL, Delucis RdA, Amico SC. Optimization of Pin Position and Angle for Z-Pin-Reinforced Foam Core Sandwich Structures. Materials. 2023; 16(1):352. https://doi.org/10.3390/ma16010352
Chicago/Turabian StyleKerche, Eduardo Fischer, Agnė Kairytė, Sylwia Członka, Amanda Albertin Xavier da Silva, Maikson Luiz Passaia Tonatto, Francisco Luiz Bresolin, Rafael de Avila Delucis, and Sandro Campos Amico. 2023. "Optimization of Pin Position and Angle for Z-Pin-Reinforced Foam Core Sandwich Structures" Materials 16, no. 1: 352. https://doi.org/10.3390/ma16010352
APA StyleKerche, E. F., Kairytė, A., Członka, S., da Silva, A. A. X., Tonatto, M. L. P., Bresolin, F. L., Delucis, R. d. A., & Amico, S. C. (2023). Optimization of Pin Position and Angle for Z-Pin-Reinforced Foam Core Sandwich Structures. Materials, 16(1), 352. https://doi.org/10.3390/ma16010352







