Reconstruction of Composite Stiffness Matrix with Array-Guided Wave-Based Genetic Algorithm
Abstract
1. Introduction
2. Materials and Methods
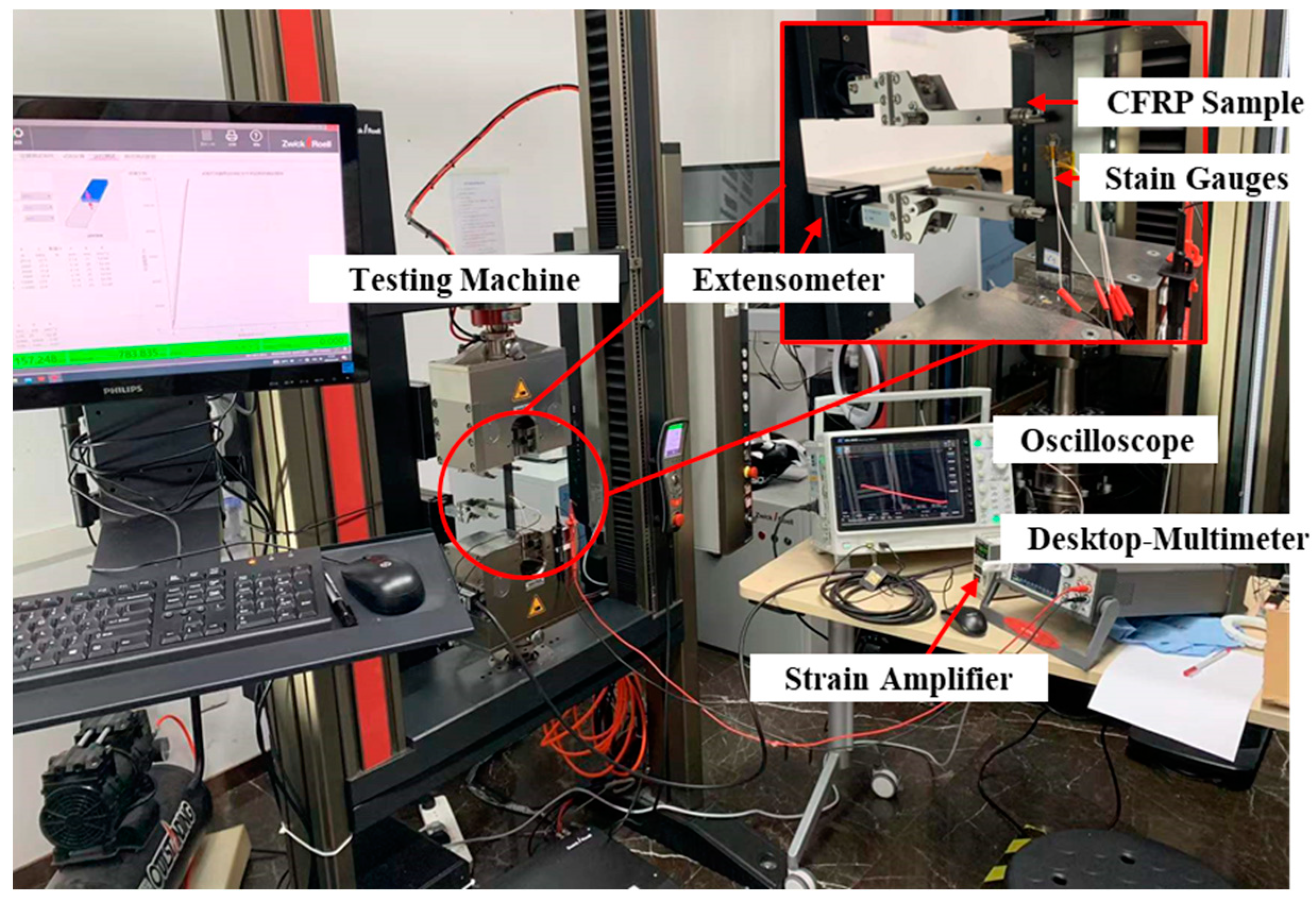
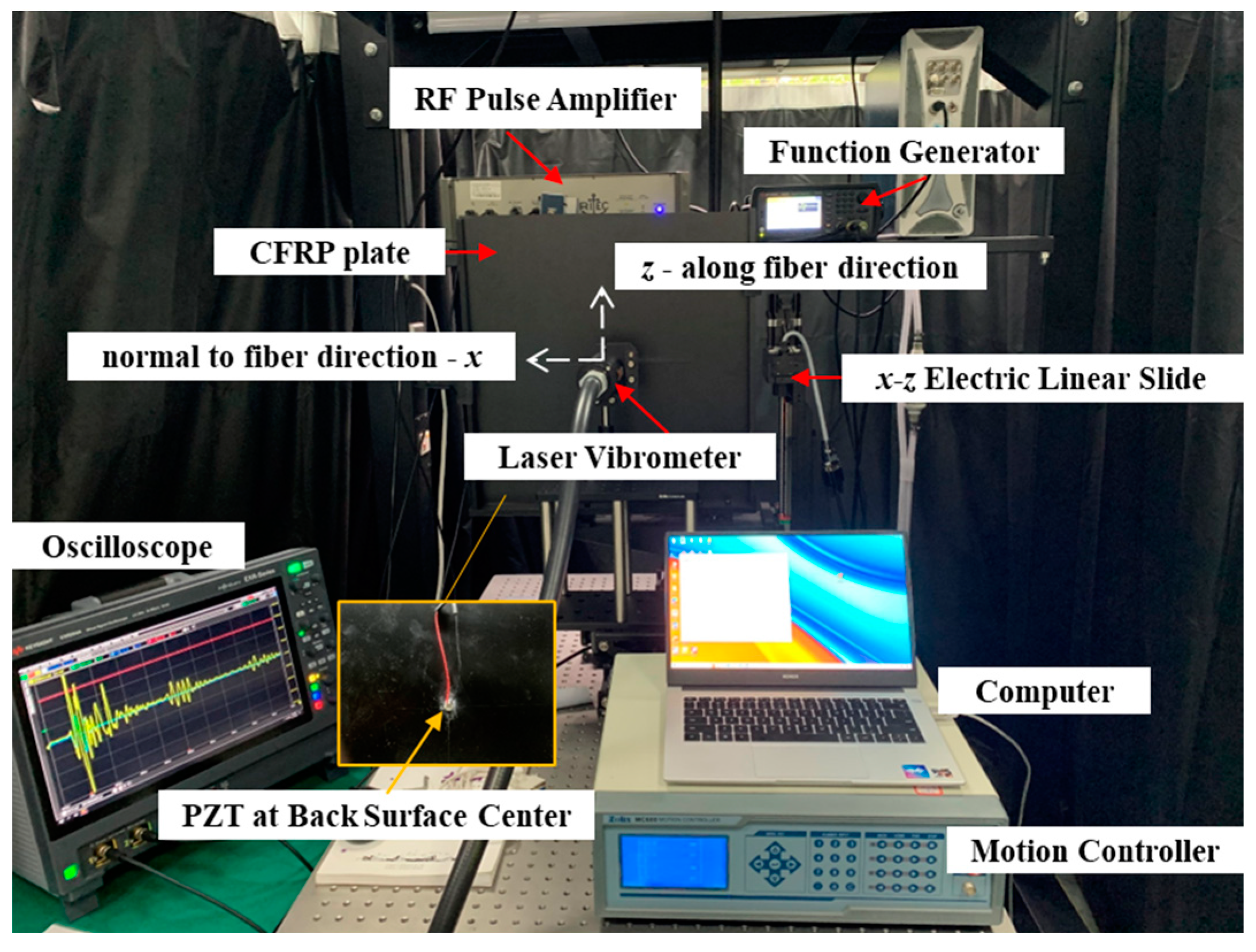
2.1. Experimental Setup
2.1.1. Static Tensile Loading
2.1.2. Longitudinal Wave Testing
2.1.3. Guided Wave Testing
2.2. Methods
2.2.1. Derivation of Material Parameters with Tensile Loading
- (1)
- Young’s modulus along the fiber direction ;where , , and denote the longitudinal stress, strain, and loading force with the sample cut along the fiber direction, and is the cross-sectional area.
- (2)
- Young’s modulus normal to the fiber direction ;where , , and denote the longitudinal stress, strain, and loading force with the sample cut normal to the fiber direction.
- (3)
- Poisson’s ratio ;where and denote the transverse and longitudinal strains with loading to the sample along the fiber direction.
- (4)
- Shear modulus ;The Young’s modulus of the sample cut along 45° to the direction is related to , , , and as follows:thus can be calculated provided the known , , , and .
2.2.2. Derivation of Material Parameter with Longitudinal Wave
- Poisson’s ratio ;The longitudinal wave testing was performed to measure the last parameter , as illustrated in Figure 2. The average velocity of the longitudinal wave is measured experimentally aswhere is the measured thickness and is the time of flight of the pulse-echo. The measurement is performed at five random locations with . The velocity is related to and aswherevia which can be derived.
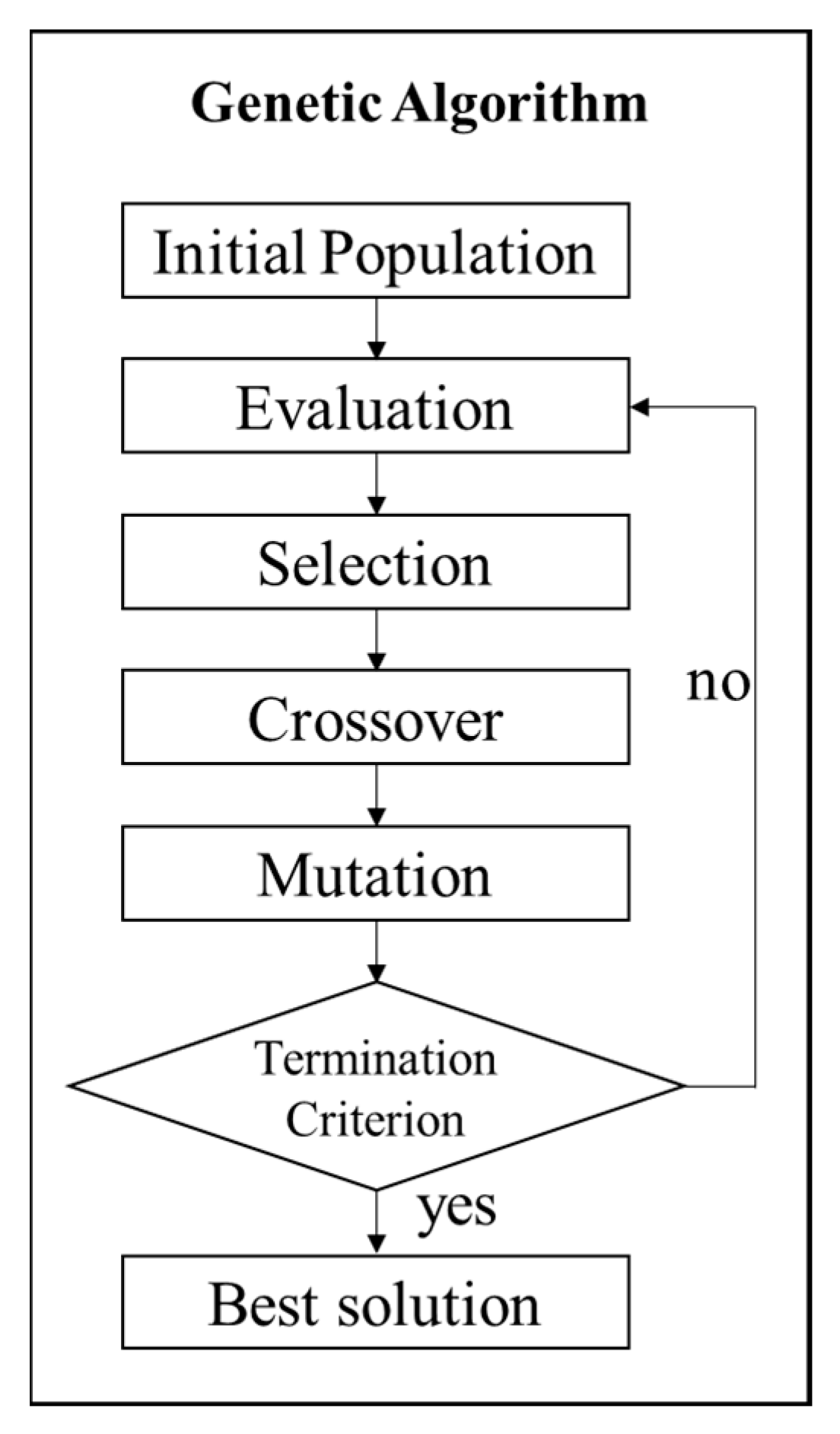
2.2.3. Derivation of Material Parameters with GW-Based GA
3. Results
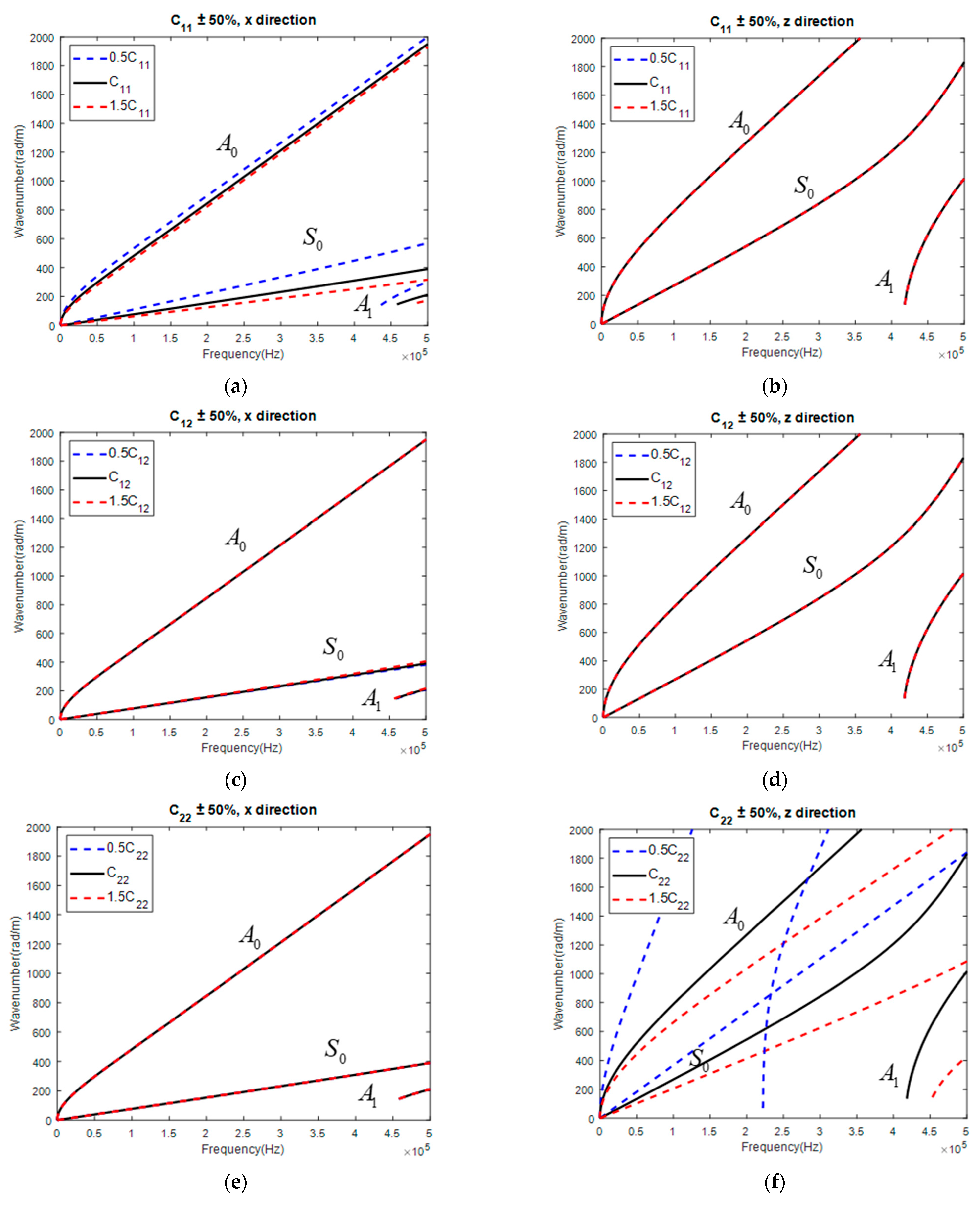
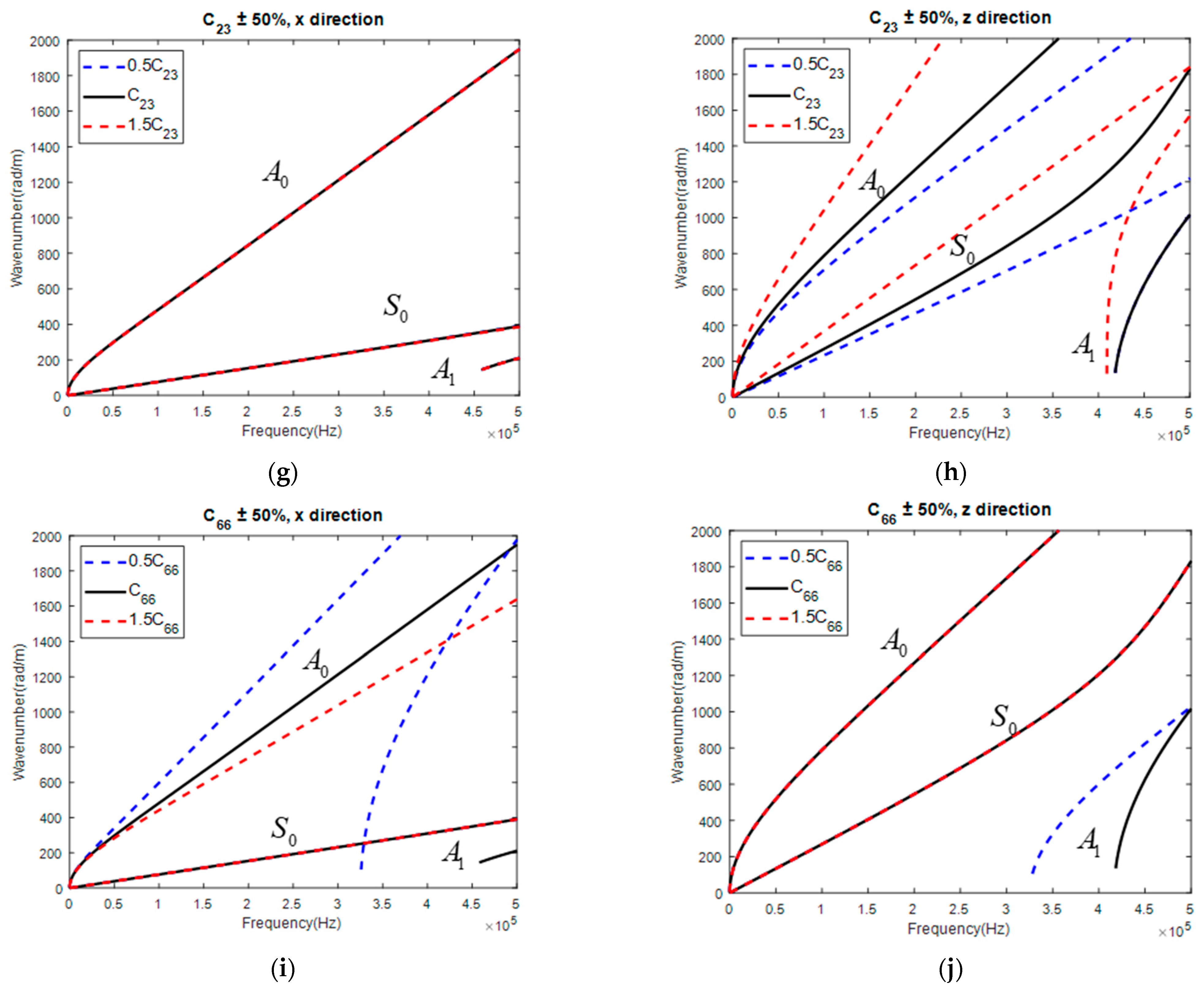
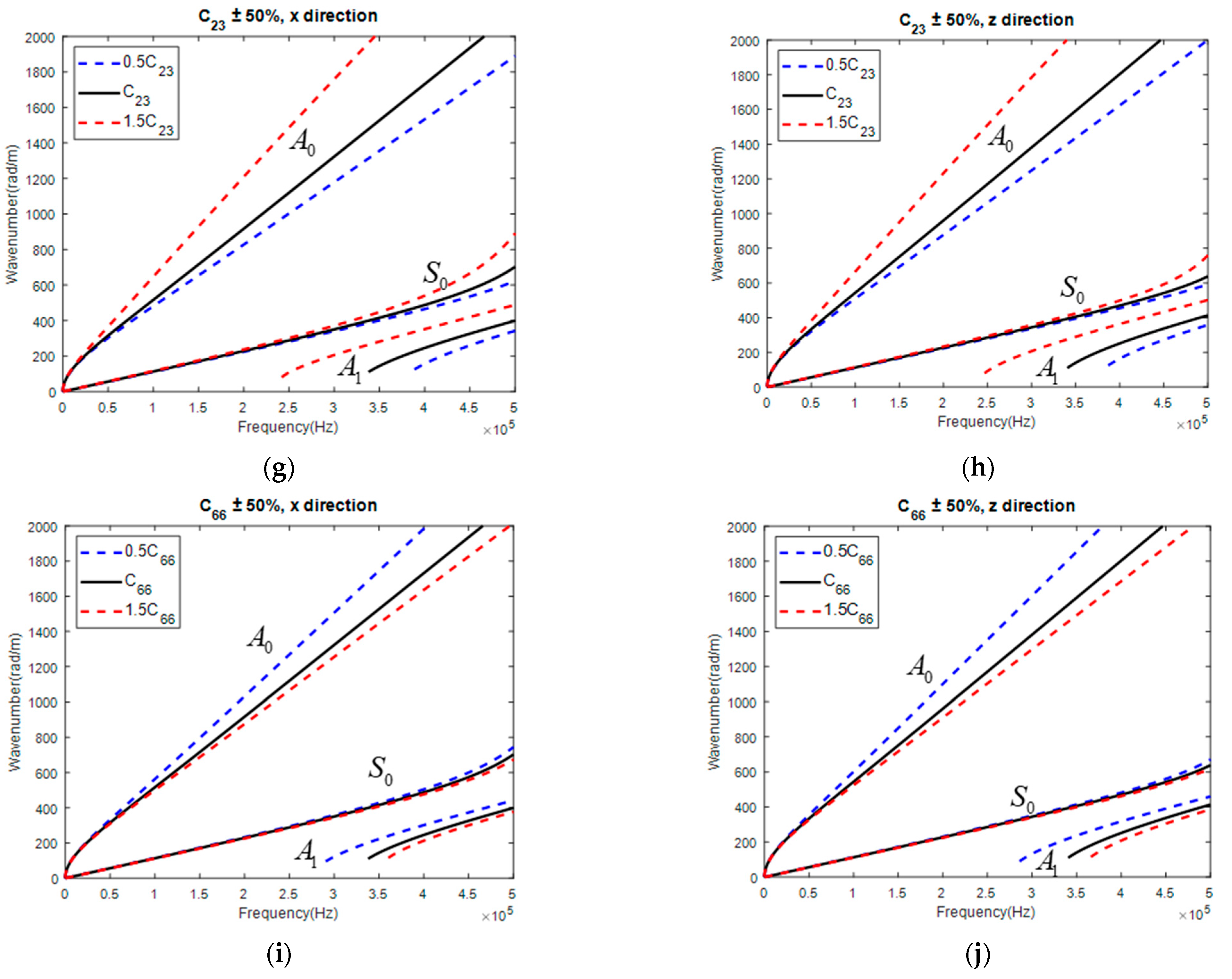
3.1. Sensitivity Analysis of Parameter on GW Dispersion Curve
- (1)
- mainly influenced along the fiber direction while independent from the GW normal to the fiber direction.
- (2)
- slightly influenced the GW along the fiber direction while independent from that normal to the fiber direction.
- (3)
- was almost independent of the GW along the fiber direction while largely influencing the GW normal to the fiber direction.
- (4)
- slightly influenced the GW along the fiber direction while largely influencing the GW normal to the fiber direction.
- (5)
- largely influenced the GW along the fiber direction while independent from the GW normal to the fiber direction.
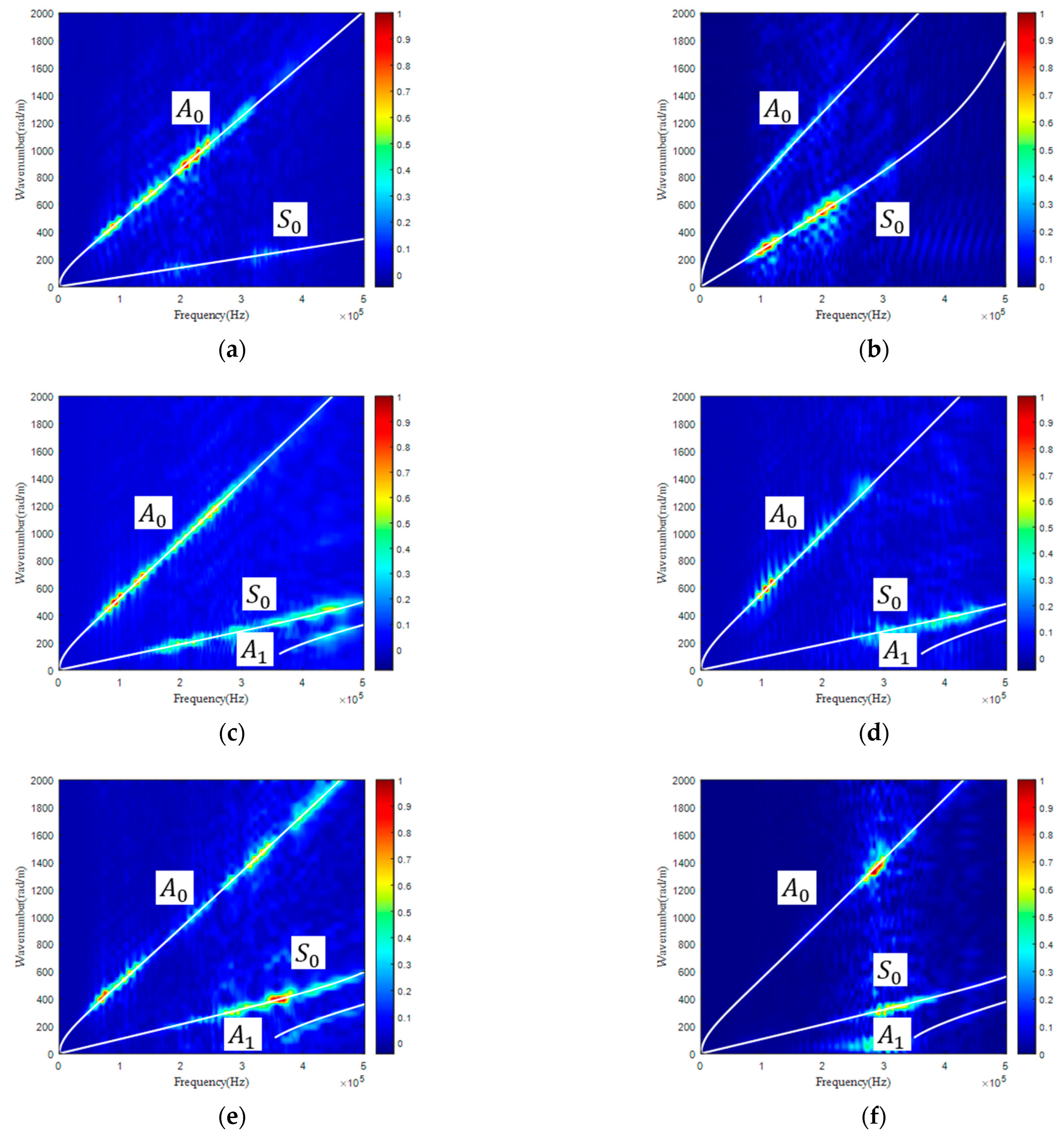
3.2. Reconstruction of Stiffness Matrix of CFRP with GW-Based GA
- (1)
- The maximum deviation percentage of is only 1.42%, which indicates that reconstructed from the GW-based GA is highly accurate and robust.
- (2)
- exerts negligible influence on the GW dispersion curves along both the and directions for CFRPs with the investigated three stacking sequences. Thus, a large maximum deviation of up to 17.5% should be expected.
- (3)
- The maximum deviation percentage of is only 7.80%, which indicates that reconstructed from the GW-based GA is highly accurate and robust. The mean value of the three reconstructed values of with CFRPs of three different stacking sequences is calculated as 10.20 GPa, which is extremely close to the value of 10.28 GPa derived with tensile loading and longitudinal wave. As illustrated in Figure 6f, exerts a significant influence on the GW dispersion curve normal to the fiber direction in unidirectional CFRP. Thus, the reconstructed value of can be highly trusted.
- (4)
- shows a maximum deviation of 23.63%. The reconstructed values from CP and QI are smaller than that from UD, which may be partially attributed to the lower sensitivity of a GW in CP and QI to than that in UD.
- (5)
- (1)
- The deviation percentage of reaches 17.80%, which indicates that the derived from tensile loading is slightly smaller than the value from GW testing. Considering the GW-based GA obtains three values of with only a maximum deviation of 1.42%, the tensile loading may not accurately reconstruct the value of , possibly attributed to the incorrect cutting of the sample for tensile loading, which is further discussed in Section 3.3.1.
- (2)
- The deviation percentage of reaches 61.79%, which can be attributed to the insensitiveness of GW on the change of . This implies that more GW modes at a wider frequency range should be considered to accurately reconstruct the value of .
- (3)
- The deviation percentage of reaches 14.98%, indicating a good match. The one from the longitudinal wave actually measures the stiffness along the thickness direction, while the one from the GW combines the stiffness from both the transverse and thickness directions. This implies that the assumption of transverse isotropy is approximated and satisfied.
- (4)
- The deviation percentage of reaches 10.82%, indicating a good match.
- (5)
- The deviation percentage of reaches 0.53%, indicating an almost exact match.
3.3. Further Refinement of Stiffness Matrix
3.3.1. Refinement of
3.3.2. Refinement of
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| CFRP | carbon fiber reinforced polymer |
| GA | genetic algorithm |
| GW | guided wave |
| SAFE | semi-analytical finite element method |
| 2D-FFT | two-dimensional Fourier transform |
| OF | objective function |
| stress | |
| strain | |
| elastic constants | |
| Young’s modulus | |
| Poisson’s ratio | |
| shear modulus | |
| loading force | |
| cross-sectional area of tensile sample | |
| the measured thickness of tensile sample | |
| theoretically calculated images | |
| experimental images | |
| UD | unidirectional laminate [0]16 |
| CP | cross-ply laminate [0/90]4s |
| QI | quasi-isotropic laminate [0/90/0/90/45/–45/45/–45]s |
References
- Elsheikh, A.H.; Panchal, H.; Shanmugan, S.; Muthuramalingam, T.; El-Kassas, A.M.; Ramesh, B. Recent Progresses in Wood-Plastic Composites: Pre-Processing Treatments, Manufacturing Techniques, Recyclability and Eco-Friendly Assessment. Clean. Eng. Technol. 2022, 8, 100450. [Google Scholar] [CrossRef]
- Elsheikh, A. Bistable Morphing Composites for Energy-Harvesting Applications. Polymers 2022, 14, 1893. [Google Scholar] [CrossRef] [PubMed]
- Abd Elaziz, M.; Elsheikh, A.H.; Oliva, D.; Abualigah, L.; Lu, S.; Ewees, A.A. Advanced Metaheuristic Techniques for Mechanical Design Problems: Review. Arch. Comput. Methods Eng. 2022, 29, 695–716. [Google Scholar] [CrossRef]
- Bulut, M. Mechanical Characterization of Basalt/Epoxy Composite Laminates Containing Graphene Nanopellets. Compos. Part B Eng. 2017, 122, 71–78. [Google Scholar] [CrossRef]
- Padture, N.P. Environmental Degradation of High-Temperature Protective Coatings for Ceramic-Matrix Composites in Gas-Turbine Engines. npj Mater. Degrad. 2019, 3, 11. [Google Scholar] [CrossRef]
- Wang, X.; Gu, Y.; Chen, Y.; Ullah, Z.; Pan, Q.; Zhao, Y. A New Technology for Steel Pipeline Damage Detecting without Removing Cladding. Measurement 2020, 159, 107700. [Google Scholar] [CrossRef]
- Ogierman, W. Inverse Identification of Elastic Properties of Constituents of Discontinuously Reinforced Composites. Materials 2018, 11, 2332. [Google Scholar] [CrossRef]
- ASTM D7291/D7291M-15; Standard Test Method for Through-Thickness “Flatwise” Tensile Strength and Elastic Modulus of a Fiber-Reinforced Polymer Matrix Composite Material. ASTM International: West Conshohocken, PA, USA, 2022.
- Deng, L.; Lei, L.; Lai, S.; Liao, L.; Zhou, Z. Experimental Study on the Axial Tensile Properties of FRP Grid-Reinforced ECC Composites. Materials 2021, 14, 3936. [Google Scholar] [CrossRef]
- Kê, T.S. Development of the Torsion Pendulum and Early Research on Grain Boundary Relaxation and the Cold-Work Internal Friction Peak. J. Alloys Compd. 1994, 211, 7–15. [Google Scholar] [CrossRef]
- Renault, A.; Jaouen, L.; Sgard, F. Characterization of Elastic Parameters of Acoustical Porous Materials from Beam Bending Vibrations. J. Sound Vib. 2011, 330, 1950–1963. [Google Scholar] [CrossRef]
- Paolino, D.S.; Geng, H.; Scattina, A.; Tridello, A.; Cavatorta, M.P.; Belingardi, G. Damaged Composite Laminates: Assessment of Residual Young’s Modulus through the Impulse Excitation Technique. Compos. Part B Eng. 2017, 128, 76–82. [Google Scholar] [CrossRef]
- Xie, M.; Li, F. A Modified Piezoelectric Ultrasonic Composite Oscillator Technique for Simultaneous Measurement of Elastic Moduli and Internal Frictions at Varied Temperature. Rev. Sci. Instrum. 2020, 91, 015110. [Google Scholar] [CrossRef] [PubMed]
- Park, S.H.; Liu, P.; Yi, K.; Choi, G.; Jhang, K.Y.; Sohn, H. Mechanical Properties Estimation of Additively Manufactured Metal Components Using Femtosecond Laser Ultrasonics and Laser Polishing. Int. J. Mach. Tools Manuf. 2021, 166, 103745. [Google Scholar] [CrossRef]
- Wong, V.-K.; Hu, Y.; Tham, Z.W.; Chen, Y.F.; Liu, M.; Lim, K.E.; Park, S.J.; Cui, F.; Zhang, L. Measurement of Elastic Constant Matrix of Carbon Fiber Composites With an Ultrasonic 2D-Array Transducer. IEEE Sens. J. 2022, 22, 5562–5570. [Google Scholar] [CrossRef]
- Cao, H.; Guo, S.; He, Z.; Xie, Y.; Zhang, T.; Feng, W. In Situ Elastic Constant Determination of Unidirectional CFRP Composites via Backwall Reflected Multi-Mode Ultrasonic Bulk Waves Using a Linear Array Probe. Compos. Part B Eng. 2022, 238, 109953. [Google Scholar] [CrossRef]
- Chen, J.; Bai, X.; Yang, K.; Ju, B.F. Simultaneously Measuring Thickness, Density, Velocity and Attenuation of Thin Layers Using V(z, t) Data from Time-Resolved Acoustic Microscopy. Ultrasonics 2015, 56, 505–511. [Google Scholar] [CrossRef]
- Lasn, K.; Echtermeyer, A.T.; Klauson, A.; Chati, F.; Décultot, D. Comparison of Laminate Stiffness as Measured by Three Experimental Methods. Polym. Test. 2015, 44, 143–152. [Google Scholar] [CrossRef]
- Castaings, M.; Hosten, B.; Kundu, T. Inversion of Ultrasonic, Plane-Wave Transmission Data in Composite Plates to Infer Viscoelastic Material Properties. NDT E Int. 2000, 33, 377–392. [Google Scholar] [CrossRef]
- Liu, M.; Wang, K.; Lissenden, C.J.; Wang, Q.; Zhang, Q.; Long, R.; Su, Z.; Cui, F. Characterizing Hypervelocity Impact (HVI)-Induced Pitting Damage Using Active Guided Ultrasonic Waves: From Linear to Nonlinear. Materials 2017, 10, 547. [Google Scholar] [CrossRef]
- Yu, X.; Fan, Z.; Castaings, M.; Biateau, C. Feature Guided Wave Inspection of Bond Line Defects between a Stiffener and a Composite Plate. NDT E Int. 2017, 89, 44–55. [Google Scholar] [CrossRef]
- Vishnuvardhan, J.; Krishnamurthy, C.V.; Balasubramaniam, K. Genetic Algorithm Based Reconstruction of the Elastic Moduli of Orthotropic Plates Using an Ultrasonic Guided Wave Single-Transmitter-Multiple-Receiver SHM Array. Smart Mater. Struct. 2007, 16, 1639–1650. [Google Scholar] [CrossRef]
- Zhao, J.; Qiu, J.; Ji, H. Reconstruction of the Nine Stiffness Coefficients of Composites Using a Laser Generation Based Imaging Method. Compos. Sci. Technol. 2016, 126, 27–34. [Google Scholar] [CrossRef]
- Glushkov, E.; Glushkova, N.; Eremin, A. Efficient Mathematical Representations for Computing the Forced Wave Dynamics of Anisotropic Laminated Composites. CEAS Aeronaut. J. 2013, 4, 11–19. [Google Scholar] [CrossRef]
- Foiret, J.; Minonzio, J.-G.; Chappard, C.; Talmant, M.; Laugier, P. Combined Estimation of Thickness and Velocities Using Ultrasound Guided Waves: A Pioneering Study on in Vitro Cortical Bone Samples. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2014, 61, 1478–1488. [Google Scholar] [CrossRef] [PubMed]
- Eremin, A.A.; Glushkov, E.V.; Glushkova, N.V.; Lammering, R. Evaluation of Effective Elastic Properties of Layered Composite Fiber-Reinforced Plastic Plates by Piezoelectrically Induced Guided Waves and Laser Doppler Vibrometry. Compos. Struct. 2015, 125, 449–458. [Google Scholar] [CrossRef]
- Golub, M.V.; Doroshenko, O.V.; Arsenov, M.A.; Eremin, A.A.; Gu, Y.; Bareiko, I.A. Improved Unsupervised Learning Method for Material-Properties Identification Based on Mode Separation of Ultrasonic Guided Waves. Computation 2022, 10, 93. [Google Scholar] [CrossRef]
- Okumura, S.; Nguyen, V.-H.; Taki, H.; Haïat, G.; Naili, S.; Sato, T. Rapid High-Resolution Wavenumber Extraction from Ultrasonic Guided Waves Using Adaptive Array Signal Processing. Appl. Sci. 2018, 8, 652. [Google Scholar] [CrossRef]
- Yan, L.; Cunfu, H.; Guorong, S.; Bin, W.; Chung, C.-H.; Lee, Y.-C. Elastic Properties Inversion of an Isotropic Plate by Hybrid Particle Swarm-Based-Simulated Annealing Optimization Technique from Leaky Lamb Wave Measurements Using Acoustic Microscopy. J. Nondestruct. Eval. 2014, 33, 651–662. [Google Scholar] [CrossRef]
- Hu, Y.; Cui, F.; Li, F.; Tu, X.; Zeng, L. Sparse Wavenumber Analysis of Guided Wave Based on Hybrid Lasso Regression in Composite Laminates. Struct. Heal. Monit. 2022, 21, 1367–1378. [Google Scholar] [CrossRef]
- Bochud, N.; Laurent, J.; Bruno, F.; Royer, D.; Prada, C. Towards Real-Time Assessment of Anisotropic Plate Properties Using Elastic Guided Waves. J. Acoust. Soc. Am. 2018, 143, 1138–1147. [Google Scholar] [CrossRef]
- Liu, M.; Li, L.; Zhang, Y.; Chen, G.; Cui, F. Dispersion of Guided Waves in Complex Waveguides: A Hybrid Modeling Technique Combining Gauss-Lobatto-Legendre Node Collation and Semi-Analytical Finite Element Method. Int. J. Appl. Mech. 2022. [Google Scholar] [CrossRef]







| Cutting Direction | Size (mm) | Maximum Load (kN) | Resistance of Strain Gauge (Ω) |
|---|---|---|---|
| 0° 45° 90° | 250 × 25 | 2 for 0° 1.5 for 45° 1 for 90° | 350 |
| No. | Stacking Sequence | Thickness (mm) | Density (kg/m3) |
|---|---|---|---|
| 1 | [0]16 | 2.05 | 1507.2 |
| 2 | [0/90]4s | 2.17 | 1490.5 |
| 3 | [0/90/0/90/45/–45/45/–45]s | 2.27 | 1480.1 |
| CFRP Size (mm) | Piezoelectric Wafer | Excitation Central Frequency (kHz) | Array Spacing (mm) | Point Number |
|---|---|---|---|---|
| 500 × 500 | , 0.48 thick | 400 | 1 | 128 |
| 99.55 GPa | 9.305 GPa | 0.3231 | 4.009 GPa | 0.4389 |
| 103.1 GPa | 5.549 GPa | 11.82 GPa | 5.352 GPa | 4.009 GPa |
| Ply Stacking | Resolution | ||||||
|---|---|---|---|---|---|---|---|
| Value (GPa) | UD | 251 × 251 | 121.10 | 2.08 | 9.33 | 3.67 | 4.23 |
| 501 × 501 | 125.42 | 3.43 | 10.28 | 4.83 | 4.03 | ||
| 1001 × 1001 | 129.79 | 2.87 | 8.94 | 3.22 | 4.13 | ||
| 2001 × 2001 | 110.50 | 6.13 | 9.96 | 4.56 | 4.23 | ||
| CP | 251 × 251 | 129.86 | 5.41 | 8.54 | 2.06 | 3.16 | |
| 501 × 501 | 128.70 | 4.69 | 9.57 | 3.67 | 3.55 | ||
| 1001 × 1001 | 129.18 | 6.05 | 9.96 | 3.56 | 3.26 | ||
| 2001 × 2001 | 126.78 | 5.73 | 11.54 | 4.94 | 3.16 | ||
| QI | 251 × 251 | 125.42 | 2.63 | 11.30 | 3.89 | 3.06 | |
| 501 × 501 | 126.58 | 3.90 | 10.75 | 3.22 | 3.06 | ||
| 1001 × 1001 | 128.63 | 2.63 | 9.33 | 3.67 | 4.22 | ||
| 2001 × 2001 | 127.95 | 4.22 | 12.32 | 4.83 | 3.06 | ||
| Maximumdeviation (%) | 251 × 251 | 3.50 | 60.38 | 16.21 | 35.76 | 21.44 | |
| 501 × 501 | 1.42 | 17.05 | 7.80 | 23.63 | 13.63 | ||
| 1001 × 1001 | 2.93 | 21.82 | 14.24 | 38.66 | 20.93 | ||
| 2001 × 2001 | 2.67 | 26.11 | 9.79 | 40.75 | 15.69 |
| Value | |||||
|---|---|---|---|---|---|
| (%) | 17.80 | 61.79 | 14.98 | 10.82 | 0.53 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Zhang, Y.; Li, L.; Chen, G.; Cui, F. Reconstruction of Composite Stiffness Matrix with Array-Guided Wave-Based Genetic Algorithm. Materials 2022, 15, 8715. https://doi.org/10.3390/ma15248715
Liu M, Zhang Y, Li L, Chen G, Cui F. Reconstruction of Composite Stiffness Matrix with Array-Guided Wave-Based Genetic Algorithm. Materials. 2022; 15(24):8715. https://doi.org/10.3390/ma15248715
Chicago/Turabian StyleLiu, Menglong, Yaohui Zhang, Lun Li, Gongfa Chen, and Fangsen Cui. 2022. "Reconstruction of Composite Stiffness Matrix with Array-Guided Wave-Based Genetic Algorithm" Materials 15, no. 24: 8715. https://doi.org/10.3390/ma15248715
APA StyleLiu, M., Zhang, Y., Li, L., Chen, G., & Cui, F. (2022). Reconstruction of Composite Stiffness Matrix with Array-Guided Wave-Based Genetic Algorithm. Materials, 15(24), 8715. https://doi.org/10.3390/ma15248715








