Effect of Grain Size on the Plastic Deformation Behaviors of a Fe-18Mn-1.3Al-0.6C Austenitic Steel
Abstract
1. Introduction
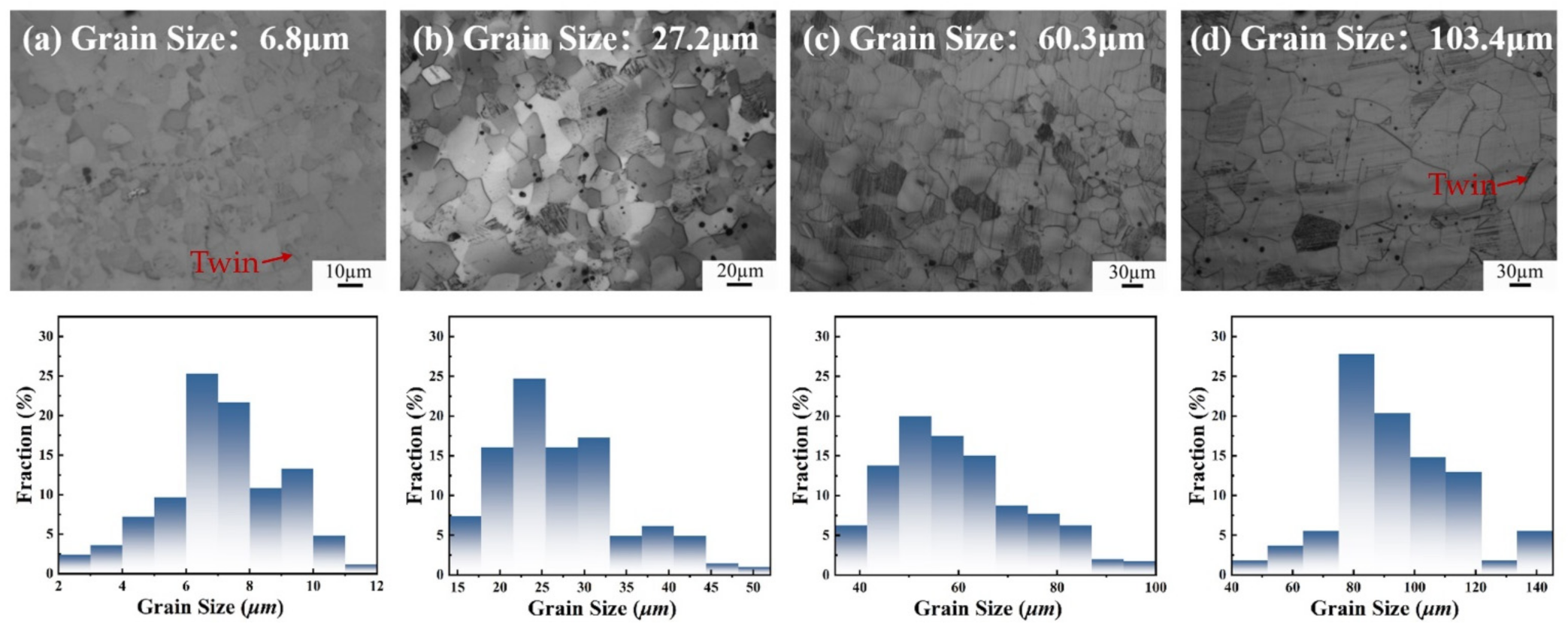
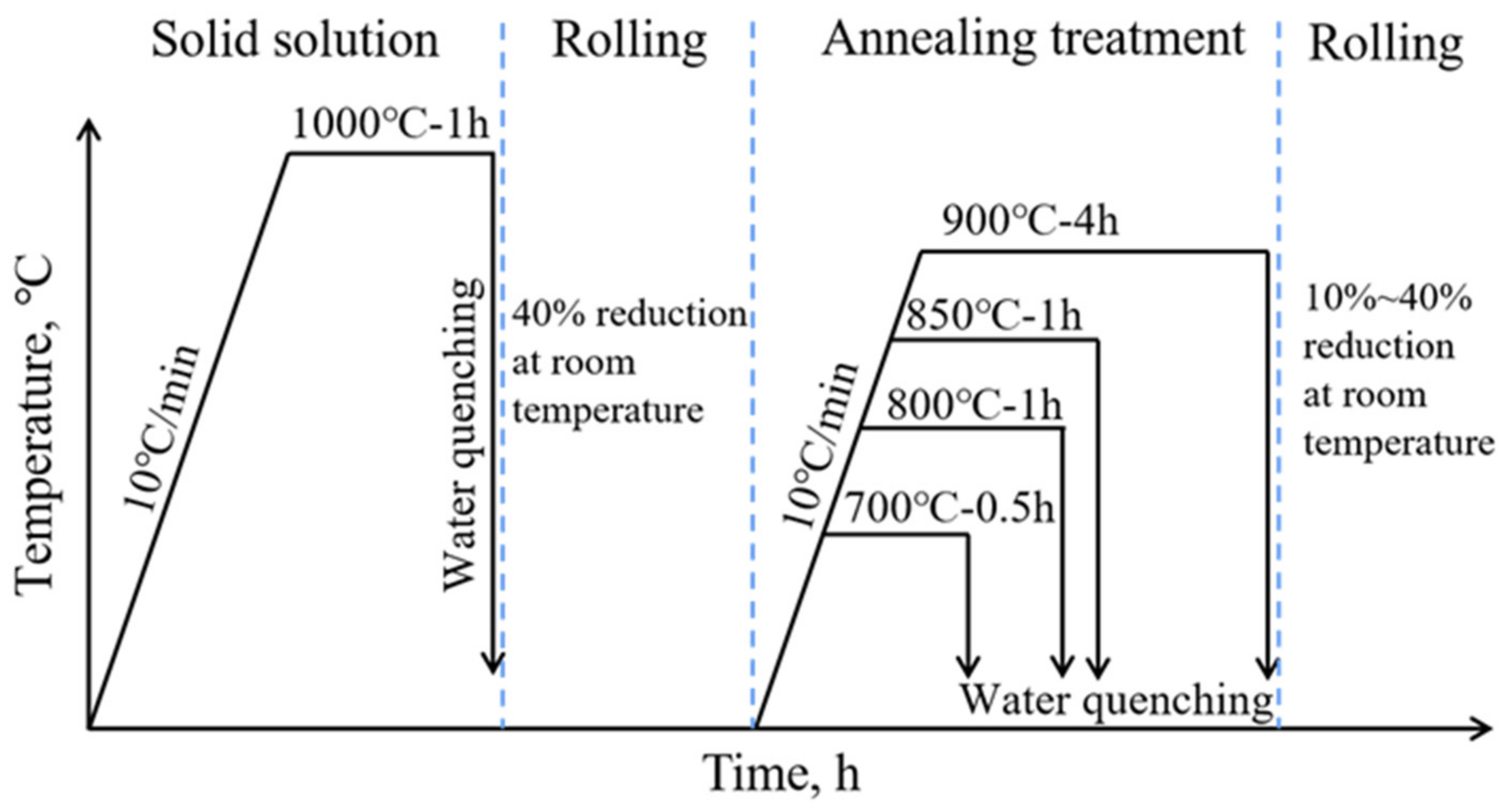
2. Experimental Procedures
3. Results and Discussion
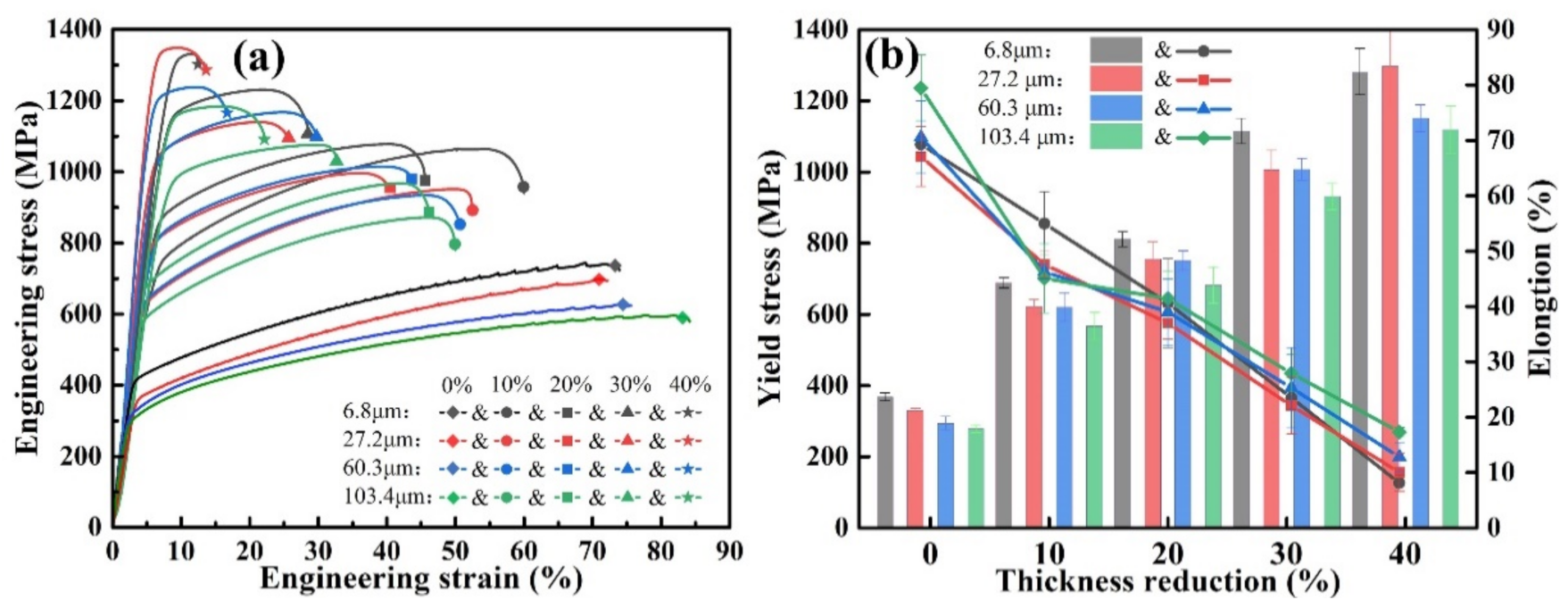
3.1. Tensile Properties
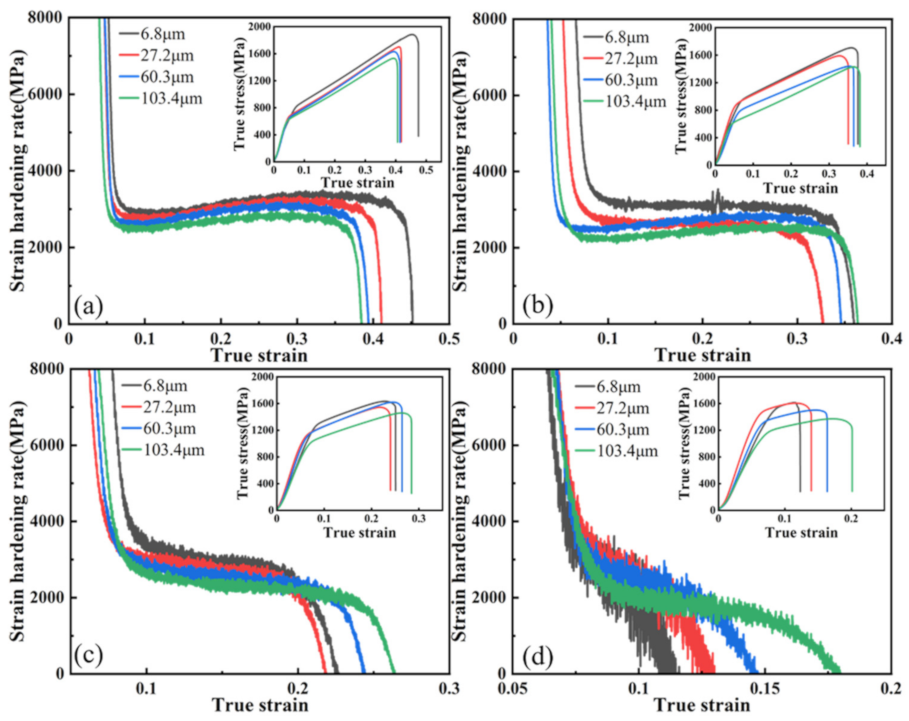
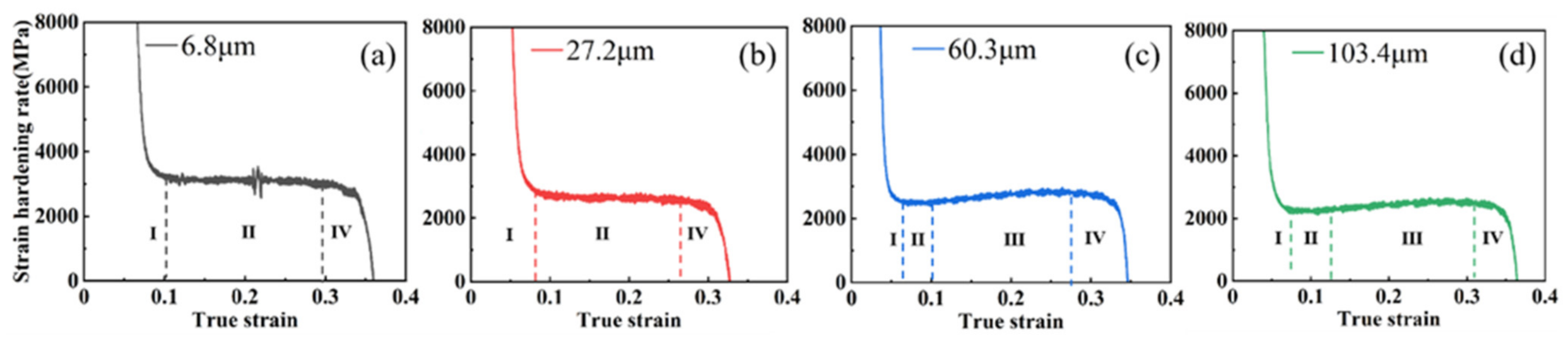
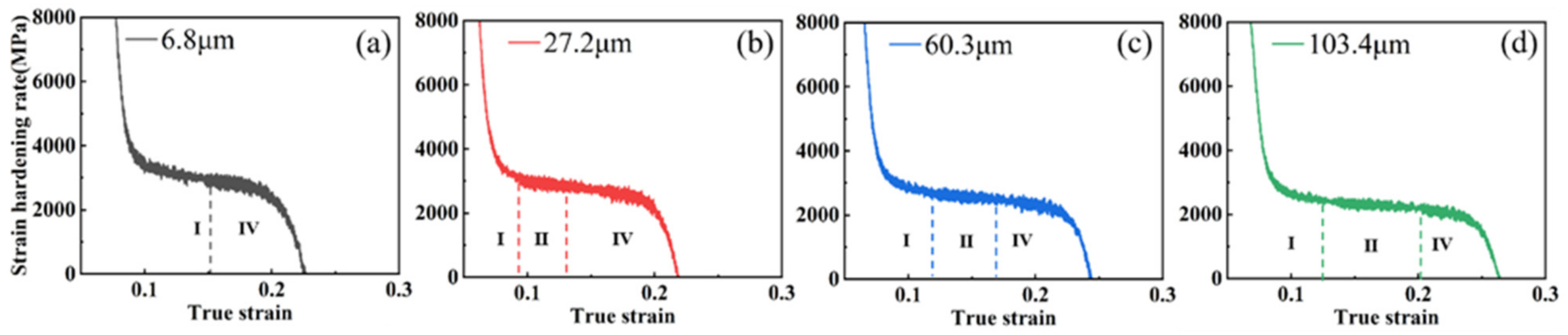
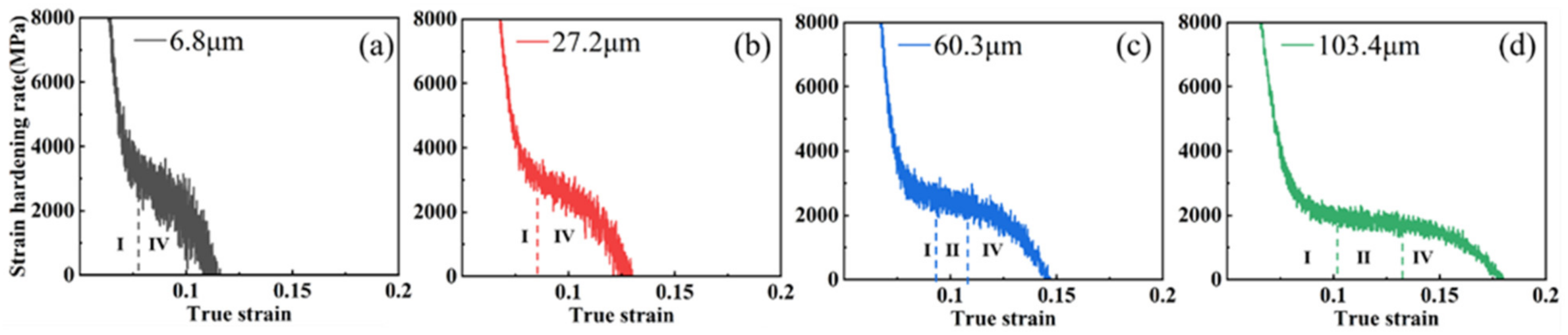
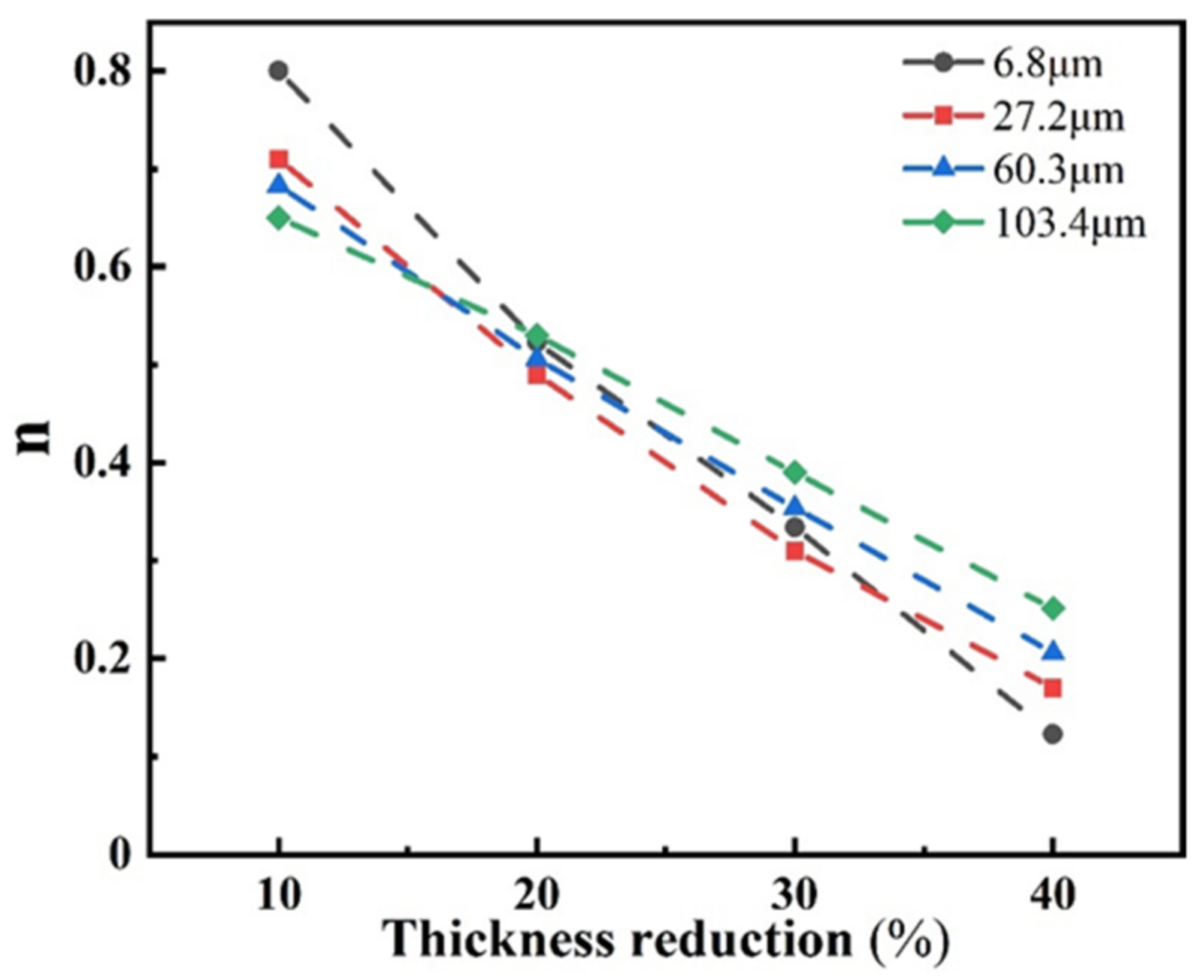
3.2. Effect of Grain Size on Work-Hardening Behavior
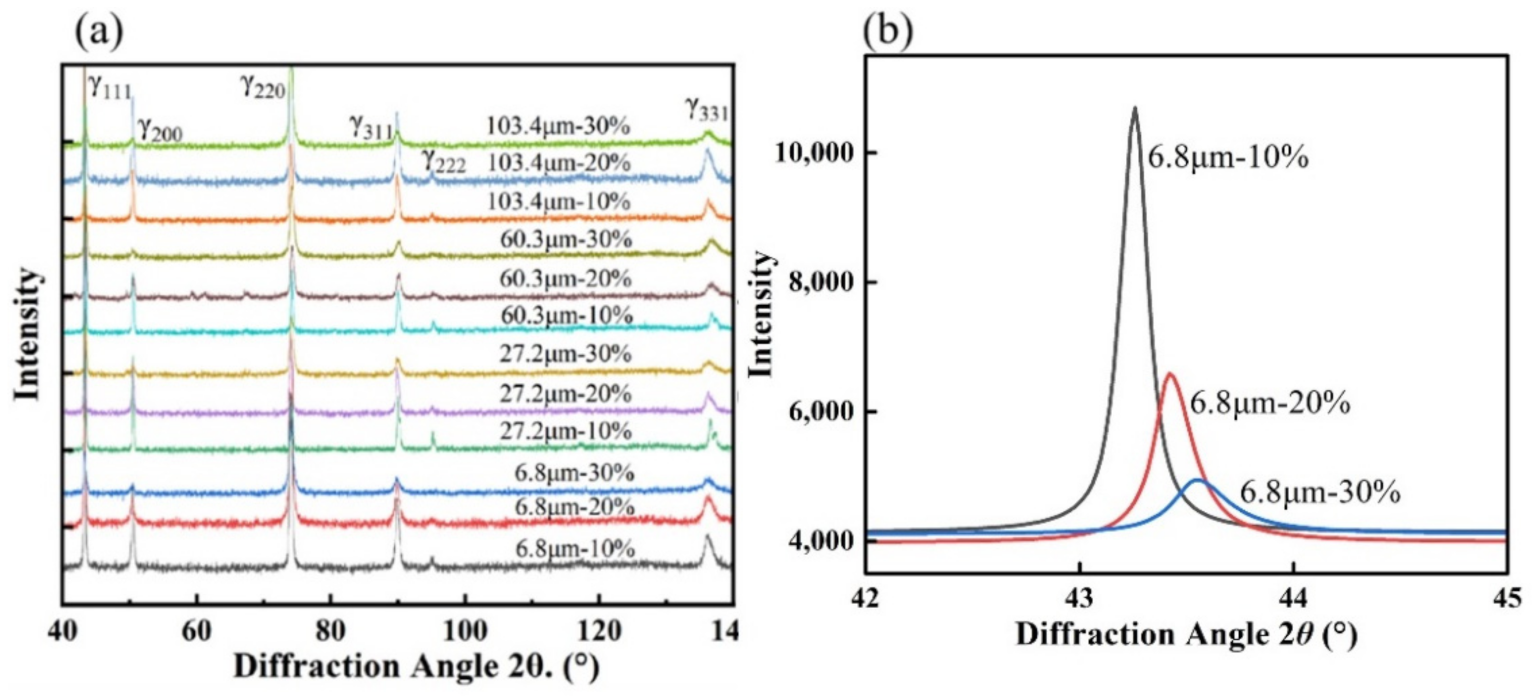
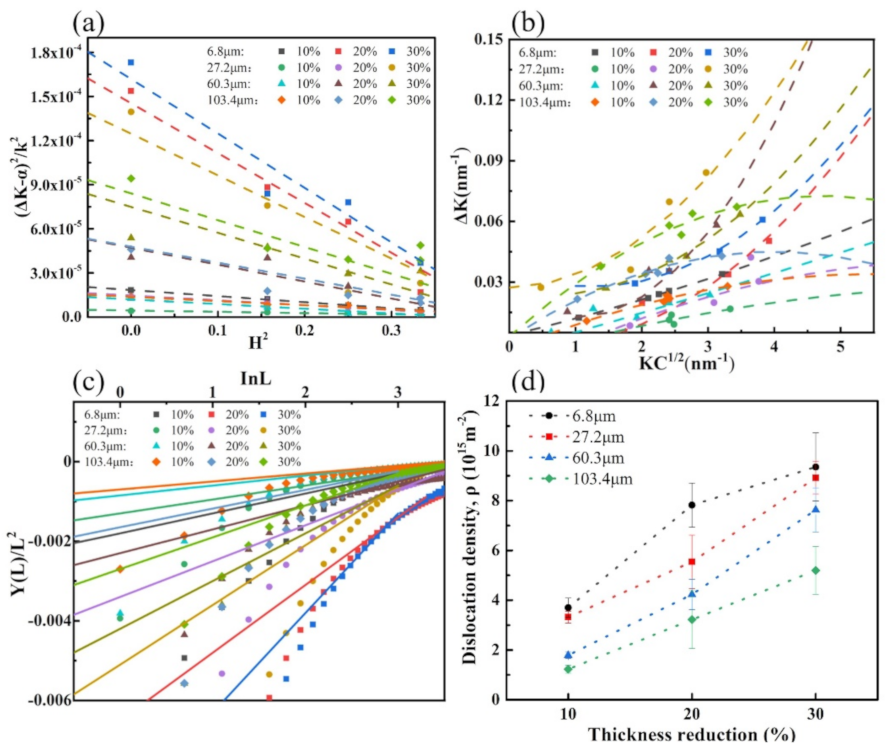
3.3. XRD Analysis and Dislocation Density Calculation
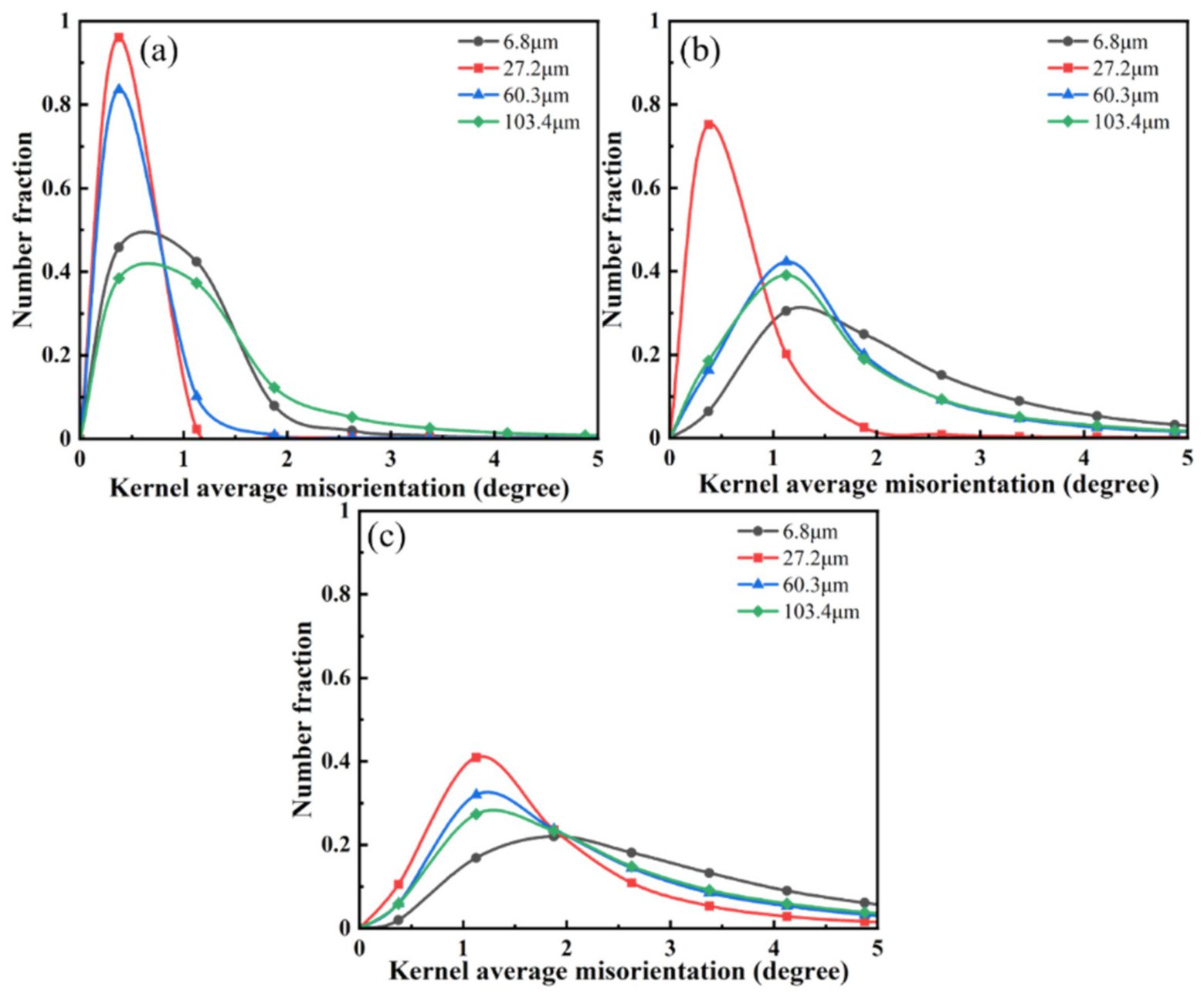
3.4. Microstructural Characteristics of Deformed Steels
4. Conclusions
- The tensile test results showed that the plasticity of the annealed samples decreased with the increase in grain size with a less than 10% rolling reduction. However, with the increase in rolling reduction, the plasticity of the small-sized grain samples decreased rapidly, and the sample with an average grain size of 6.8 μm had only a 13.1% elongation at a 40% reduction. The plasticity of the sample with an average grain size of 103.4 μm still achieved a 22.3% elongation at a 40% reduction.
- By combining XRD analysis for dislocation density calculation and electron backscatter diffraction observation, it could be concluded that a larger grain size could slow down the dislocation proliferation. Since the critical nucleation stress of mechanical twinning decreased with increasing grain size, large grain size samples could effectively promote twinning generation and growth in plastic strain, producing an obvious TWIP effect. The contribution of continuous dislocation strengthening and twinning led to a longer plateau period in the work-hardening rate curve and increased the work-hardening index and work-hardening ability.
- The KAM maps and their distribution analysis showed that in the samples with an average grain size of 6.8 μm, the strain was always concentrated at the grain boundaries, and a small number of strains accumulated at the twin boundaries due to the generation of twins at a high reduction. In the three samples with larger grain sizes, the strain was uniformly distributed at the grain boundaries and twin boundaries inside the grains due to the extensive generation and proliferation of twins, which effectively relieved the stress concentration at the grain boundaries and improved plasticity.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fu, B.; Fu, L.; Liu, S.; Wang, H.R.; Shan, A. High Strength-ductility Nano-structured High Manganese Steel Produced by Cryogenic Asymmetry-Rolling. J. Mater. Sci. Technol. 2017, 34, 695–699. [Google Scholar] [CrossRef]
- Lu, K.; Lu, L.; Suresh, S. Strengthening Materials by Engineering Coherent Internal Boundaries at the Nanoscale. Science 2009, 324, 349–352. [Google Scholar] [CrossRef] [PubMed]
- Bouaziz, O.; Allain, S.; Scott, C.P.; Cugy, P.; Barbier, D. High manganese austenitic twinning induced plasticity steels: A review of the microstructure properties relationships. Curr. Opin. Solid State Mater. Sci. 2011, 15, 141–168. [Google Scholar] [CrossRef]
- De Cooman, B.C.; Estrin, Y.; Kim, S.K. Twinning-induced plasticity (TWIP) steels. Acta Mater. 2018, 142, 283–362. [Google Scholar] [CrossRef]
- Idrissi, H.; Renard, K.; Ryelandt, L.; Schryvers, D.; Jacques, P.J. On the mechanism of twin formation in Fe–Mn–C TWIP steels. Acta Mater. 2010, 58, 2464–2476. [Google Scholar] [CrossRef]
- Li, Y.Z.; Liang, Z.Y.; Huang, M.X. Strengthening contributions of dislocations and twins in warm-rolled TWIP steels. Int. J. Plast. 2022, 150, 103198. [Google Scholar] [CrossRef]
- Renault, C.; Churyumov, A.Y.; Pozdniakov, A.V.; Churyumova, T.A. Microstructure and hot deformation behavior of FeMnAlCMo steel. J. Mater. Res. Technol. 2020, 9, 4440–4449. [Google Scholar] [CrossRef]
- Hutchinson, B.; Ridley, N. On dislocation accumulation and work hardening in Hadfield steel. Scr. Mater. 2006, 55, 299–302. [Google Scholar] [CrossRef]
- Schulz, C. Effect of low nitrogen content on work hardening and microstructural evolution in Hadfield steel. Mater. Charact. 2009, 60, 971–979. [Google Scholar]
- Karaman, I.; Sehitoglu, H.; Gall, K.; Chumlyakov, Y.I.; Maier, H.J. Deformation of single crystal Hadfield steel by twinning and slip. Acta Mater. 2015, 48, 1345–1359. [Google Scholar] [CrossRef]
- El-Danaf, E.; Kalidindi, S.R.; Doherty, R.D. Influence of deformation path on the strain hardening behavior and micro-structure evolution in low SFE FCC metals. Int. J. Plast. 2001, 17, 1245–1265. [Google Scholar] [CrossRef]
- Jin, H.C.; Jeon, J.B.; Chang, Y.W. Work-hardening and ductility enhancement mechanism of cold rolled multiphase TRIP steels. Met. Mater. Int. 2010, 16, 533–541. [Google Scholar]
- Xie, Q.G.; Yan, Z.R.; Yu, D.J.; An, K.; Yan, X.C.; Yin, S.; Gillham, B.; Wu, X.L.; Yang, P.; Zhao, Z.Z.; et al. Crystallographic orientation and spatially resolved damage for polycrystalline deformation of a high manganese steel. Acta Mater. 2022, 226, 117628. [Google Scholar] [CrossRef]
- Lee, S.I.; Lee, S.Y.; Han, J.; Hwang, B. Deformation behavior and tensile properties of an austenitic Fe-24Mn-4Cr-0.5C high-manganese steel. Effect of grain size. Mater. Sci. Eng. A 2019, 742, 334–343. [Google Scholar] [CrossRef]
- Ueji, R.; Tsuchida, N.; Terada, D.; Tsuji, N.; Tanaka, Y.; Takemura, A.; Kunishige, K. Tensile properties and twinning behavior of high manganese austenitic steel with fine-grained structure. Scr. Mater. 2008, 59, 963–966. [Google Scholar] [CrossRef]
- Gutierrez-Urrutia, I.; Raabe, D. Grain size effect on strain hardening in twinning-induced plasticity steels. Scr. Mater. 2012, 66, 992–996. [Google Scholar] [CrossRef]
- Tang, J.; He, S.D.; Mo, Y.; Jiang, F.L.; Fu, D.F.; Teng, J.; Zhang, H. Revealing the cryogenic-temperature toughness and de-formation mechanisms in high manganese austenitic steels. Mater. Charact. 2022, 190, 112024. [Google Scholar] [CrossRef]
- Churyumov, A.Y.; Kazakova, A.A.; Pozdniakov, A.V.; Churyumova, T.A.; Prosviryakov, A.S. Investigation of Hot Defor-mation Behavior and Microstructure Evolution of Lightweight Fe-35Mn-10Al-1C Steel. Metals 2022, 12, 831. [Google Scholar] [CrossRef]
- Ungar, T.; Borbely, A. The effect of dislocation contrast on X-ray line broadening: A new approach to line profile analysis. Appl. Phys. Lett. 1996, 69, 3173–3175. [Google Scholar] [CrossRef]
- Ungár, T.; Stoica, A.D.; Tichy, G.; Wang, X.L. Orientation-dependent evolution of the dislocation density in grain popula-tions with different crystallographic orientations relative to the tensile axis in a polycrystalline aggregate of stainless steel. Acta Materialia 2014, 66, 251–261. [Google Scholar] [CrossRef]
- Ribárik, G.; Gubicza, J.; Ungár, T. Correlation between strength and microstructure of ball-milled Al–Mg alloys determined by X-ray diffraction. Mater. Sci. Eng. A 2004, 387–389, 343–347. [Google Scholar] [CrossRef]
- Paolo, S.; Matteo, L. Fourier modelling of the anisotropic line broadening of X-ray diffraction profiles due to line and plane lattice defects. J. Appl. Crystallogr. 1999, 32, 671–682. [Google Scholar]
- Jiang, F.; Masumura, T.; Hirata, K.; Tsuchiyama, T.; Takaki, S. A new diffraction line profile breadth analysis approach for evaluating plastic lattice strain anisotropy in cold-worked nickel under various strain paths. Int. J. Plast. 2019, 112, 89–107. [Google Scholar] [CrossRef]
- Jiang, F.; Hirata, K.; Masumura, T.; Tsuchiyama, T.; Takaki, S. Effect of the Surface Layer Strained by Mechanical Grinding on X-ray Diffraction Analysis. ISIJ Int. 2018, 58, 376–378. [Google Scholar] [CrossRef]
- Wang, H.Z.; Yang, P.; Mao, W.M.; Lu, F.Y. Effect of hot deformation of austenite on martensitic transformation in high manganese steel. J. Alloys Compd. 2013, 558, 26–33. [Google Scholar] [CrossRef]
- Gutierrez-Urrutia, I.; Raabe, D. Dislocation and twin substructure evolution during strain hardening of an Fe–22 wt.% Mn–0.6 wt.% C TWIP steel observed by electron channeling contrast imaging. Acta Mater. 2011, 59, 6449–6462. [Google Scholar] [CrossRef]
- Mahato, B.; Shee, S.K.; Sahu, T.; Chowdhury, S.G.; Sahu, P.; Porter, D.A.; Karjalainen, L.P. An effective stacking fault energy viewpoint on the formation of extended defects and their contribution to strain hardening in a Fe–Mn–Si–Al twinning-induced plasticity steel. Acta Mater. 2015, 86, 69–79. [Google Scholar] [CrossRef]
- Rahman, K.M.; Vorontsov, V.A.; Dye, D. The effect of grain size on the twin initiation stress in a TWIP steel. Acta Mater. 2015, 89, 247–257. [Google Scholar] [CrossRef]
- Lebedkina, T.A.; Lebyodkin, M.A.; Chateau, J.P.; Jacques, A.; Allain, S. On the mechanism of unstable plastic flow in an austenitic FeMnC TWIP steel. Mater. Sci. Eng. A 2009, 519, 147–154. [Google Scholar] [CrossRef]
- Hollomon, J.H. Tensile Deformation. Met. Technol. 1945, 12, 268–290. [Google Scholar]
- Warren, B.E. X-Ray Studies of Deformed Metals. Prog. Met. Phys. 1959, 8, 147–202. [Google Scholar] [CrossRef]
- Liu, S.; Ge, Y.; Liu, H.; Liu, J.; Feng, Y.; Chen, C.; Zhang, F. Tensile Properties and Microstructure Evolutions of Low-Density Duplex Fe–12Mn–7Al–0.2C–0.6Si Steel. Materials 2022, 15, 2498. [Google Scholar] [CrossRef] [PubMed]
- Cai, W.; Wang, C.H.; Sun, C.Y.; Qian, L.Y.; Fu, M.W. Microstructure evolution and fracture behaviour of TWIP steel under dynamic loading. Mater. Sci. Eng. A 2022, 851, 143657. [Google Scholar] [CrossRef]
- Meyers, M.A.; Vhringer, O.; Lubarda, V.A. The onset of twinning in metals: A constitutive description. Acta Mater. 2001, 49, 4025–4039. [Google Scholar] [CrossRef]
- Chaudhuri, A.; Sarkar, A.; Suwas, S. Investigation of stress-strain response, microstructure and texture of hot deformed pure molybdenum. Int. J. Refract. Met. Hard Mater. 2018, 73, 168–182. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, Z.; He, S.; Tang, J.; Fu, D.; Teng, J.; Jiang, F. Effect of Grain Size on the Plastic Deformation Behaviors of a Fe-18Mn-1.3Al-0.6C Austenitic Steel. Materials 2022, 15, 8717. https://doi.org/10.3390/ma15248717
Cui Z, He S, Tang J, Fu D, Teng J, Jiang F. Effect of Grain Size on the Plastic Deformation Behaviors of a Fe-18Mn-1.3Al-0.6C Austenitic Steel. Materials. 2022; 15(24):8717. https://doi.org/10.3390/ma15248717
Chicago/Turabian StyleCui, Ziyi, Shudong He, Jie Tang, Dingfa Fu, Jie Teng, and Fulin Jiang. 2022. "Effect of Grain Size on the Plastic Deformation Behaviors of a Fe-18Mn-1.3Al-0.6C Austenitic Steel" Materials 15, no. 24: 8717. https://doi.org/10.3390/ma15248717
APA StyleCui, Z., He, S., Tang, J., Fu, D., Teng, J., & Jiang, F. (2022). Effect of Grain Size on the Plastic Deformation Behaviors of a Fe-18Mn-1.3Al-0.6C Austenitic Steel. Materials, 15(24), 8717. https://doi.org/10.3390/ma15248717






