Band Gap Opening in Borophene/GaN and Borophene/ZnO Van der Waals Heterostructures Using Axial Deformation: First-Principles Study
Abstract
:1. Introduction
2. Calculation Details
3. Results
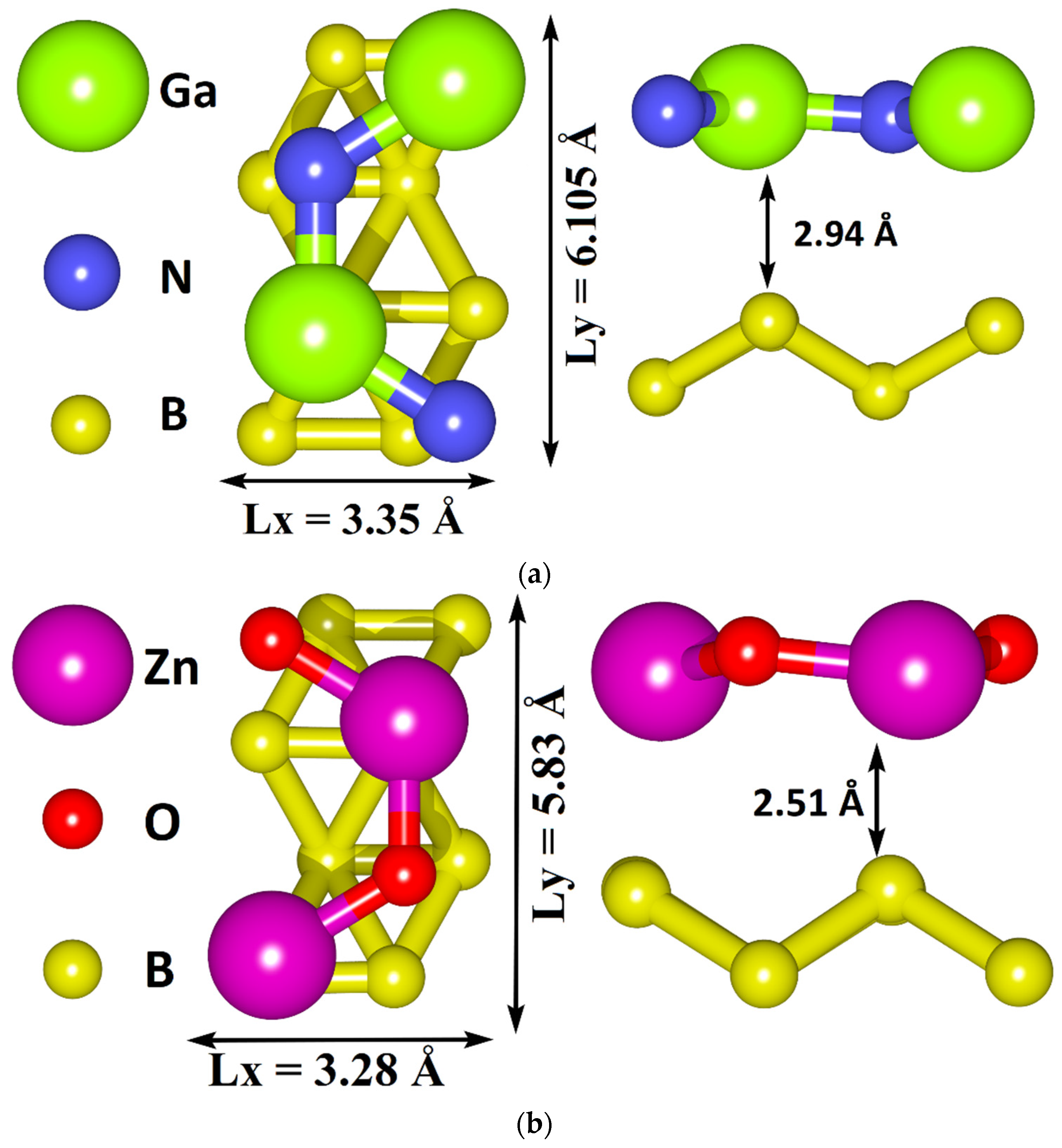
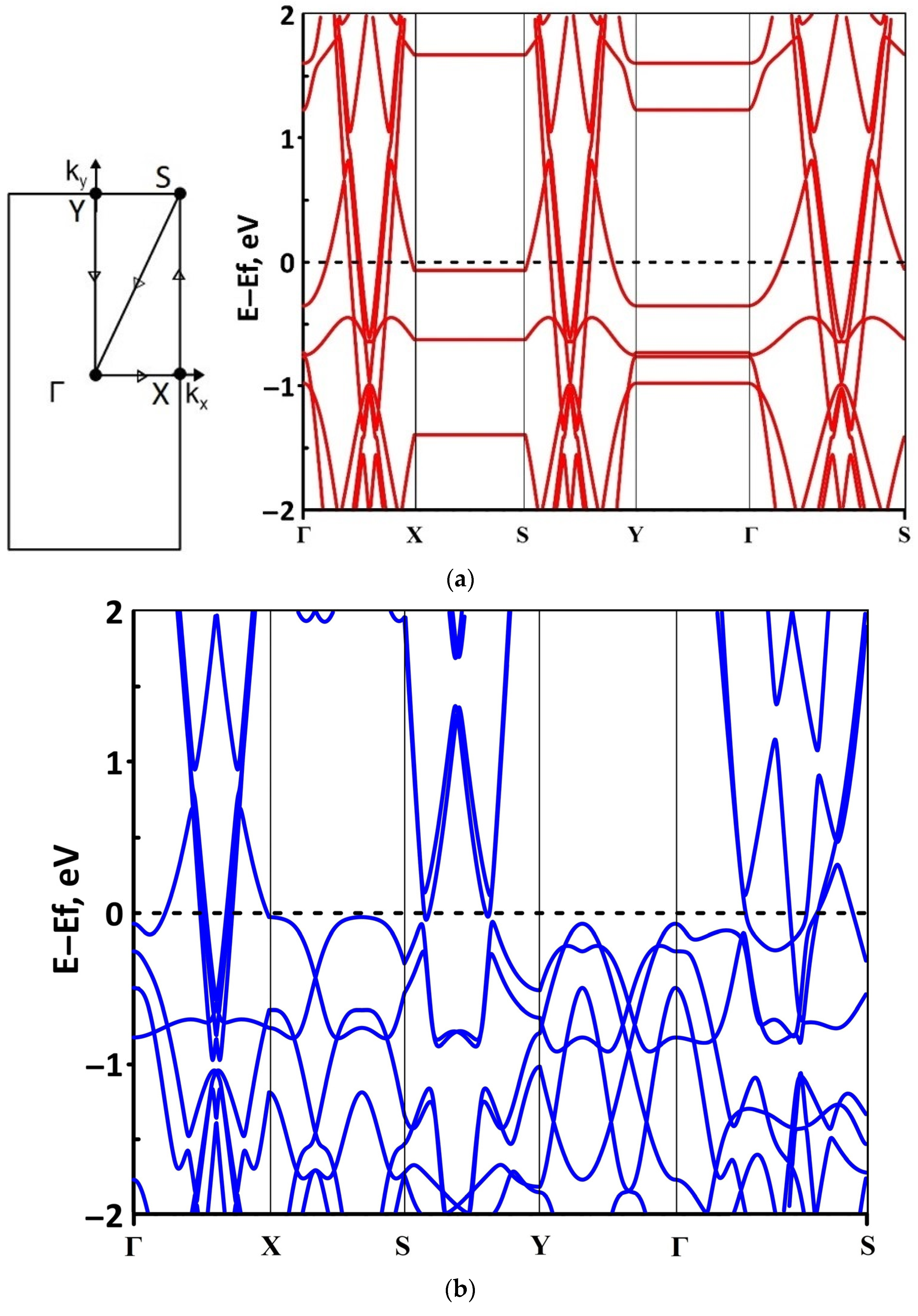
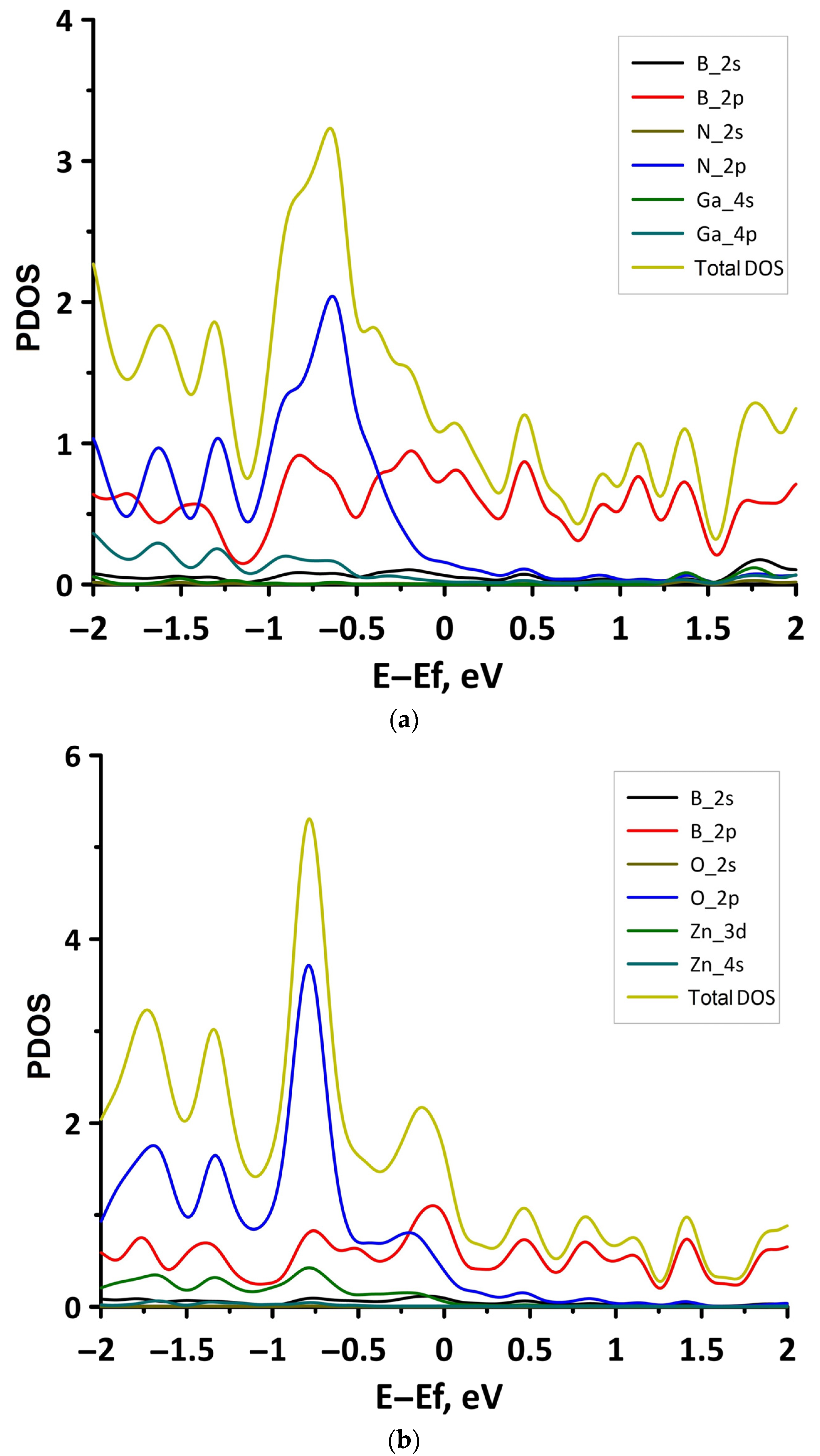
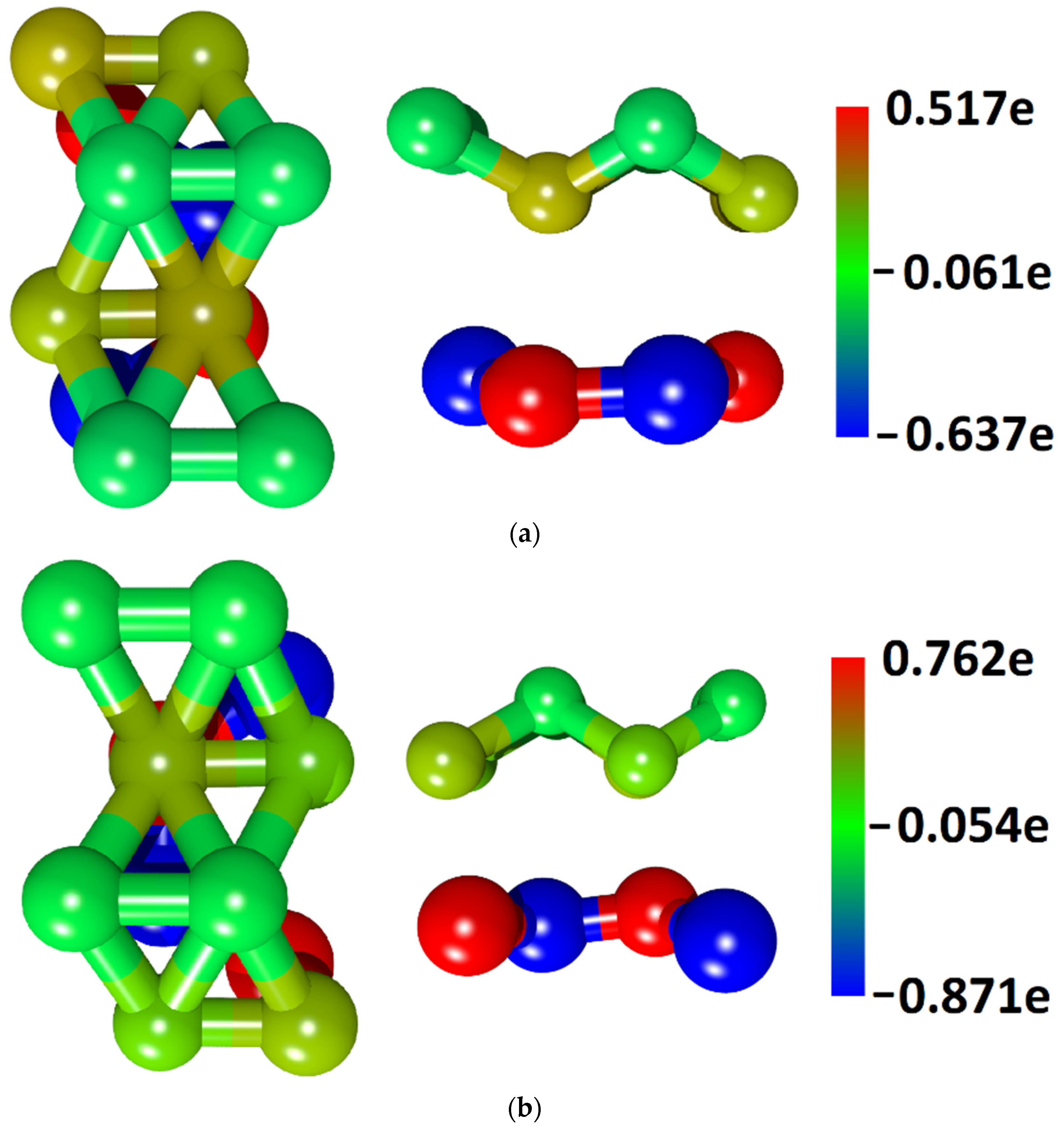
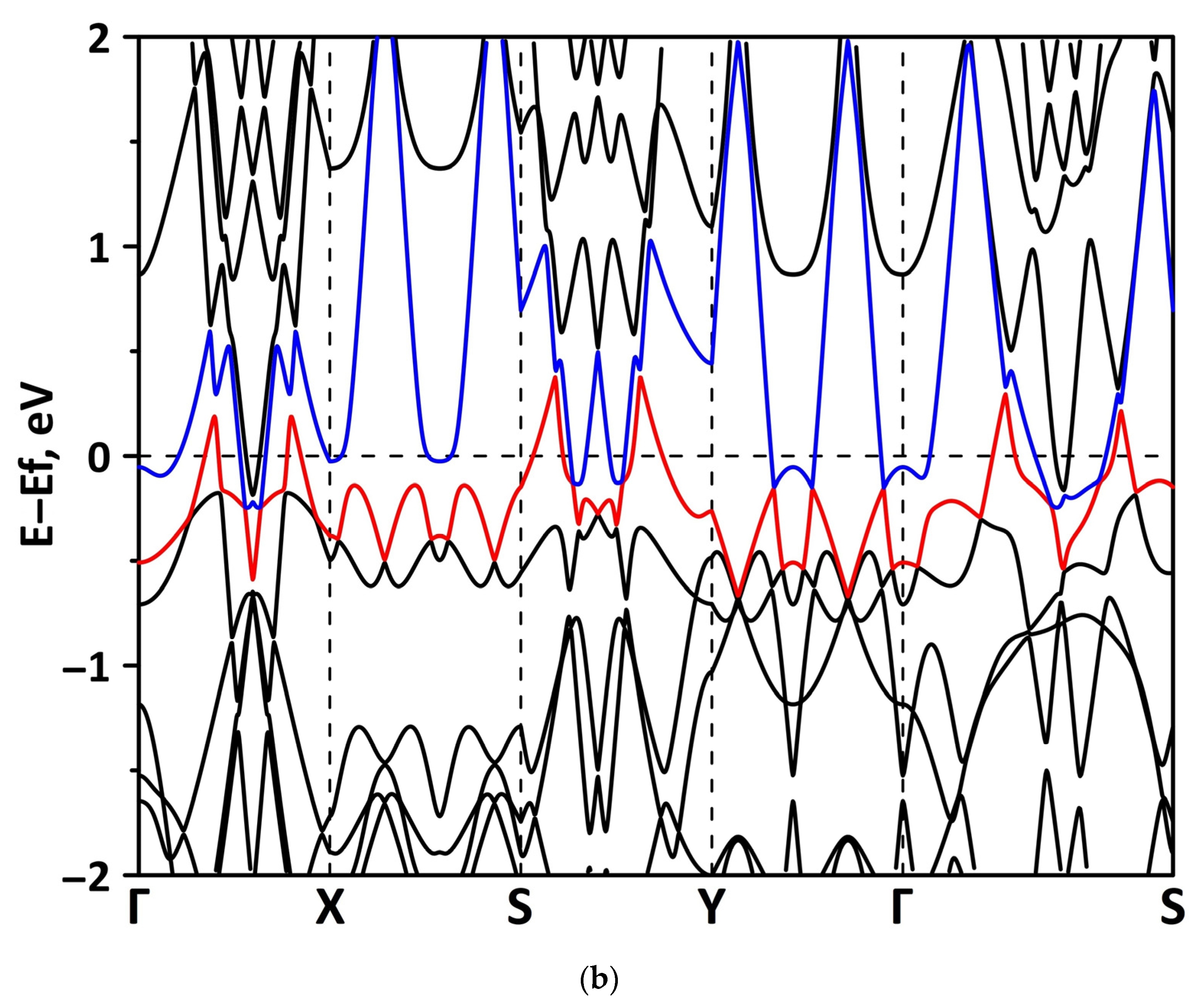
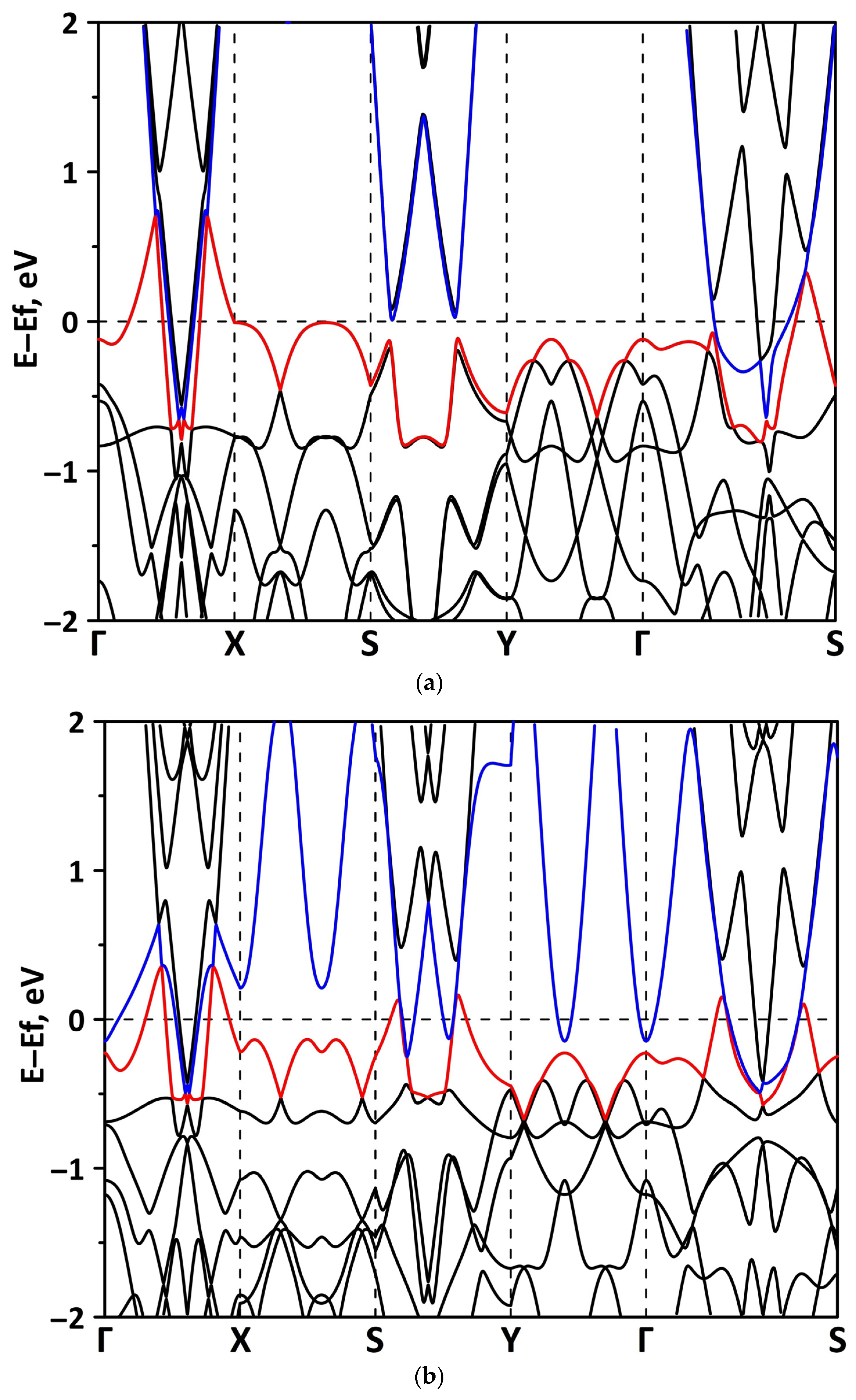
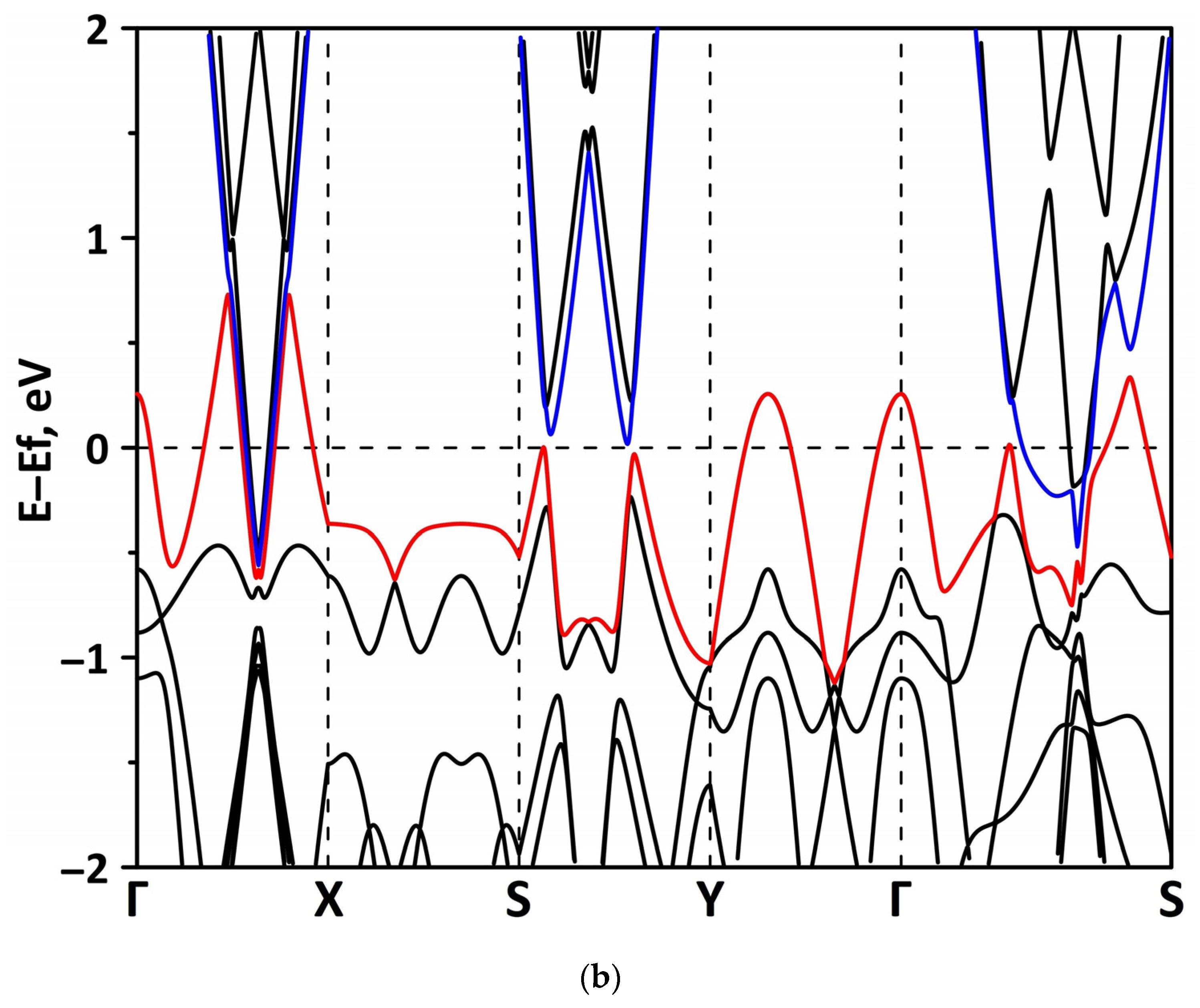
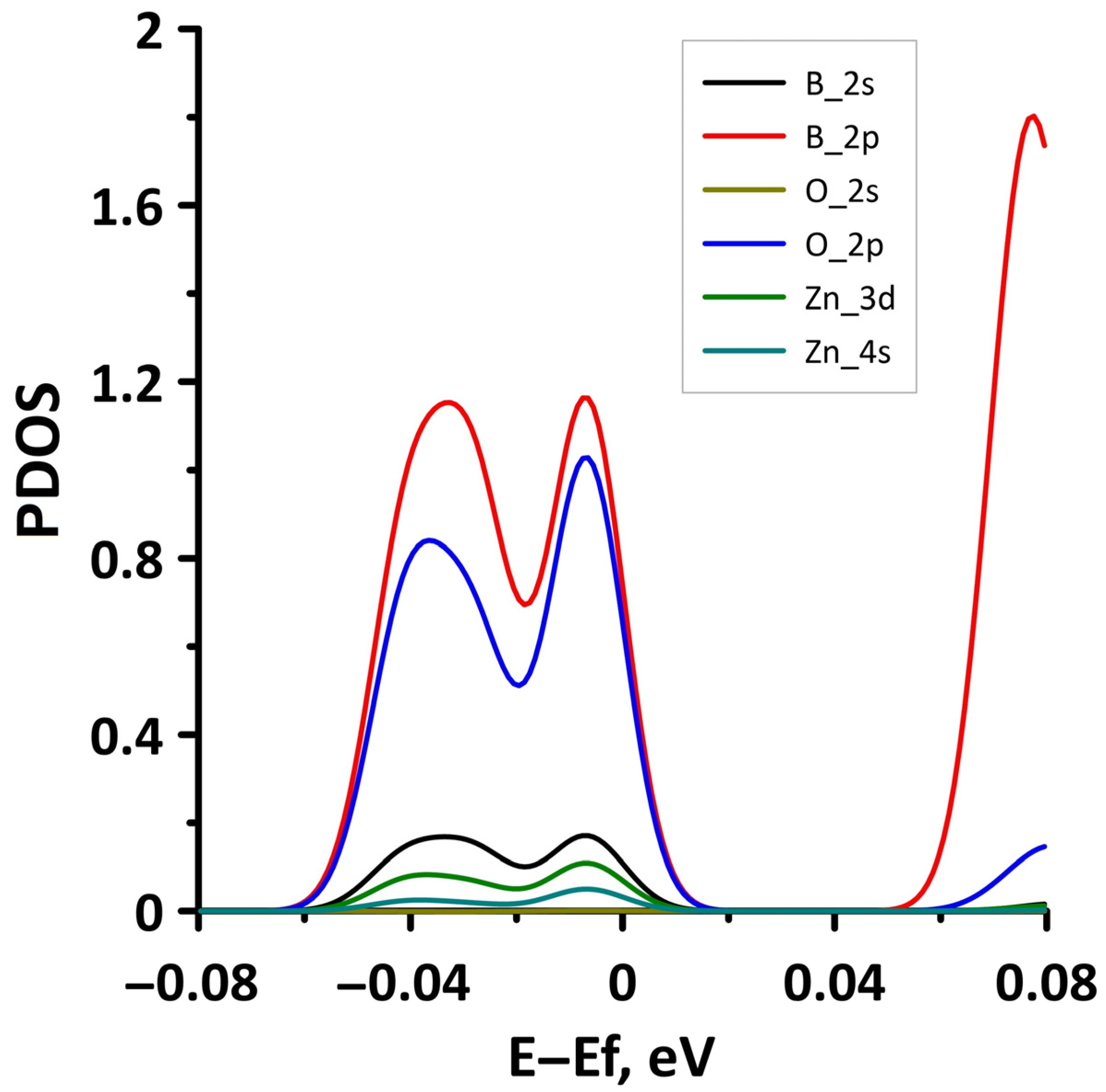
3.1. Atomic and Electronic Structure of Undeformed Borophene/GaN and Borophene/ZnO Van der Waals Heterostructures
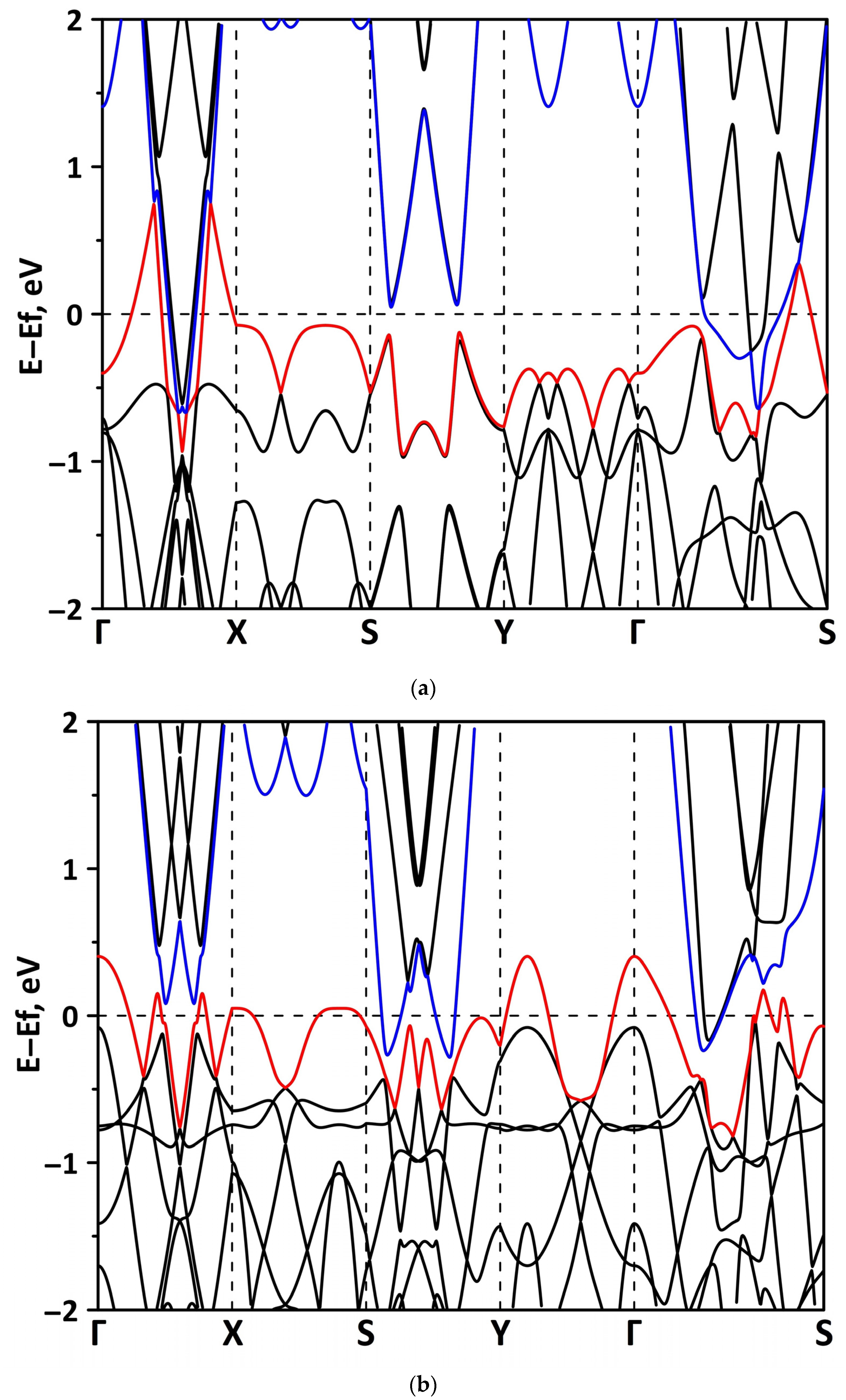
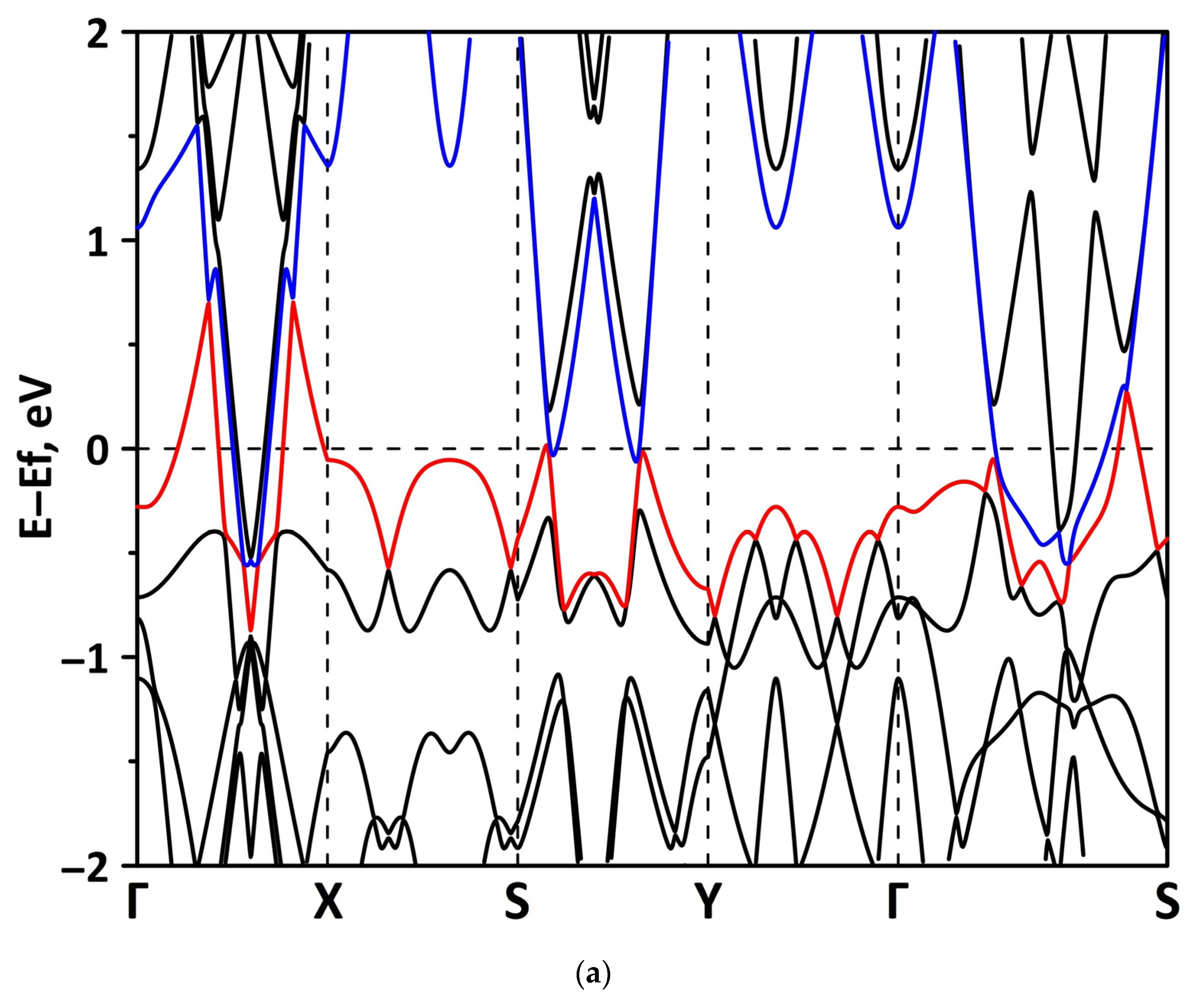
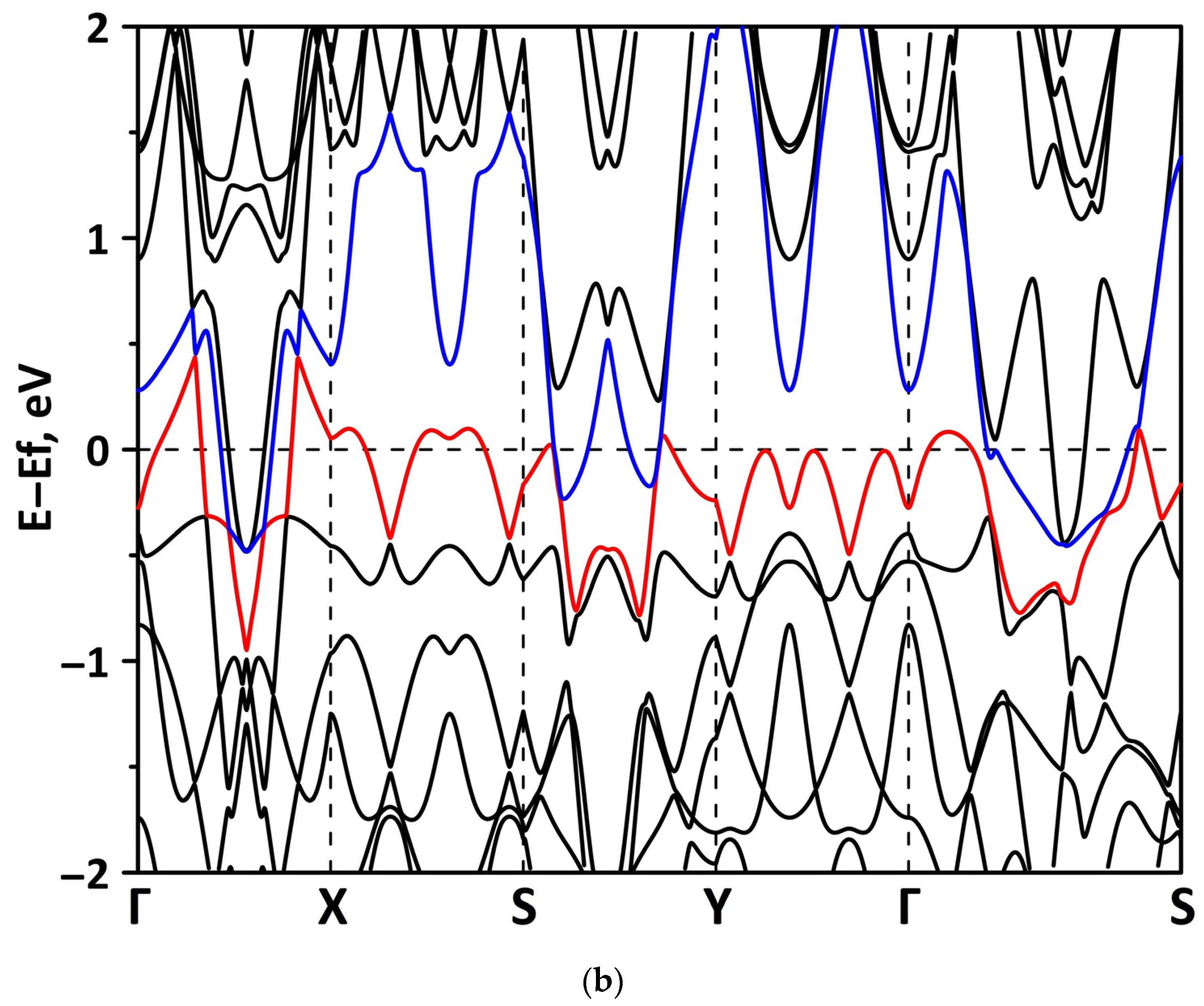
3.2. Effect of Stretching/Compression on the Electronic Structure of Borophene/GaN and Borophene/ZnO Van der Waals Heterostructures
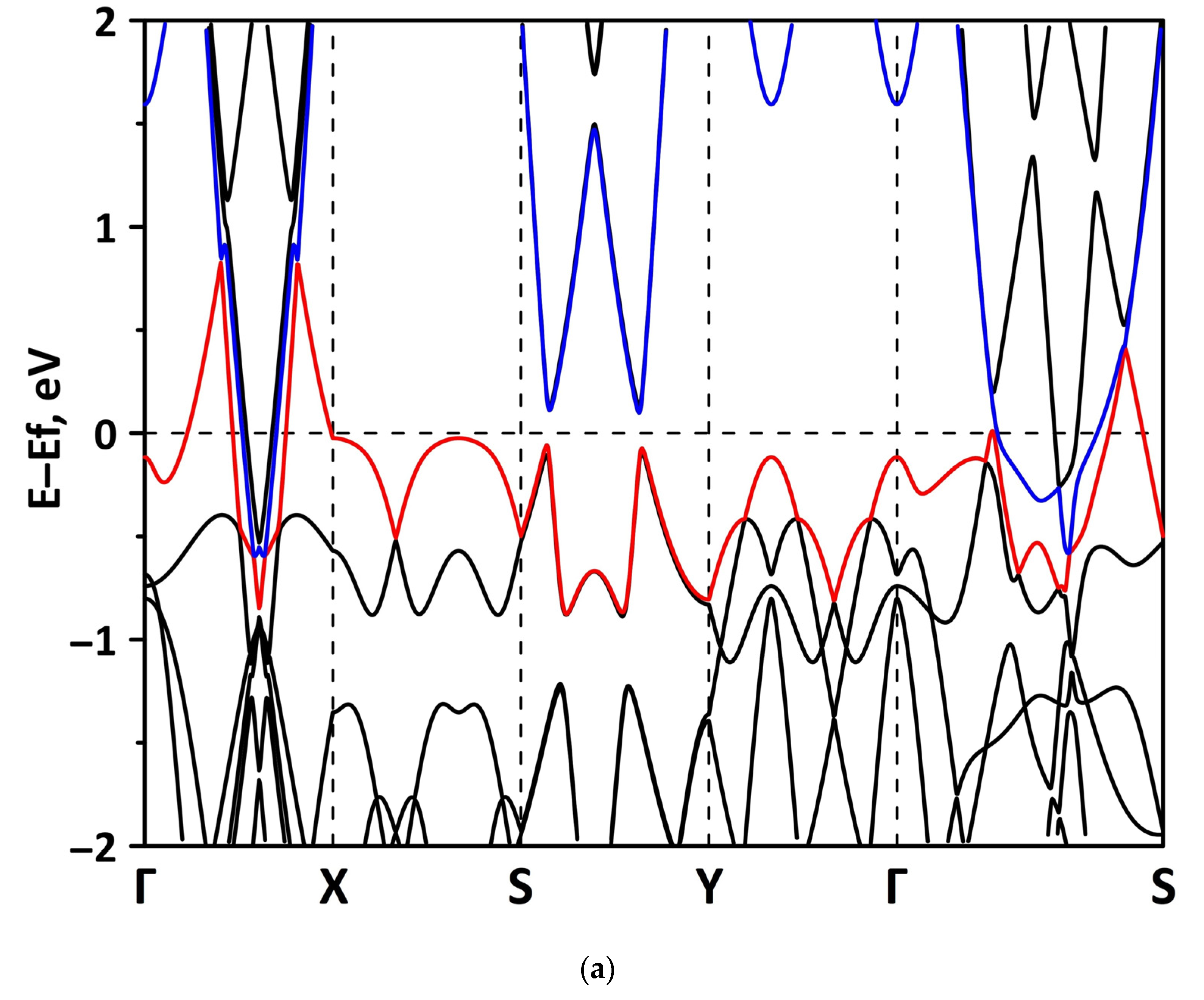
3.2.1. Uniaxial Deformation
3.2.2. Biaxial Deformation
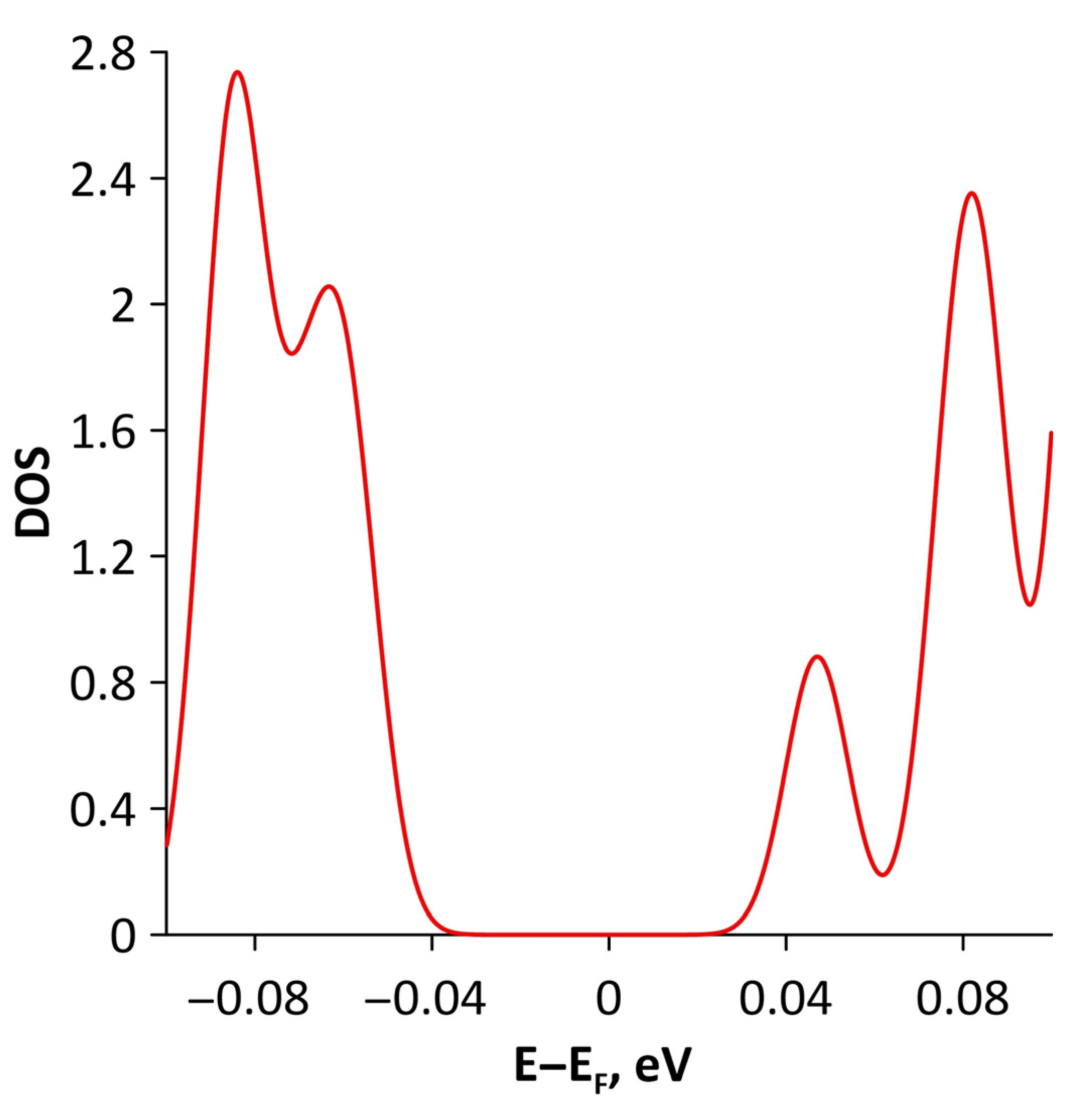
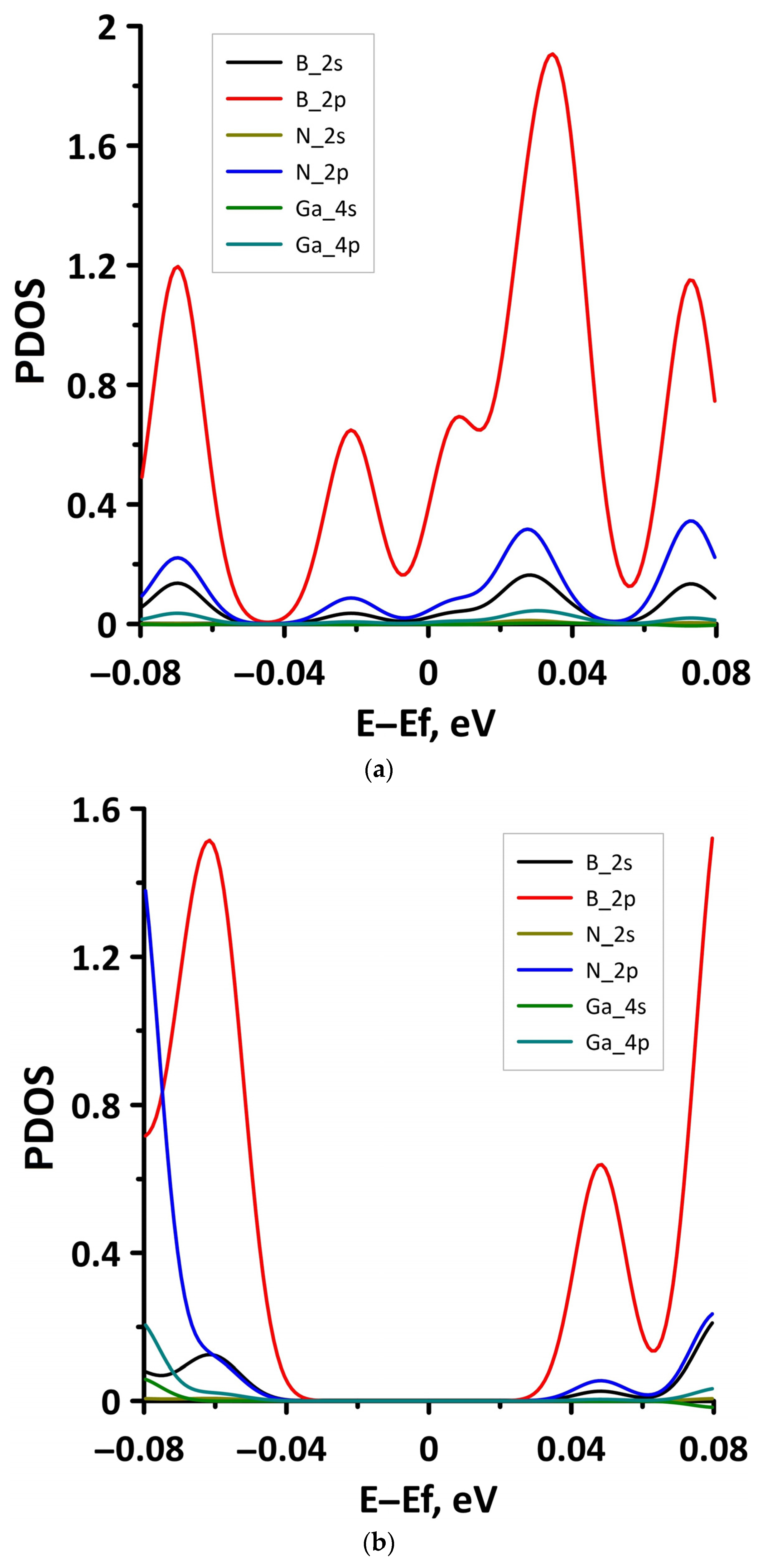
4. Discussion
- (1)
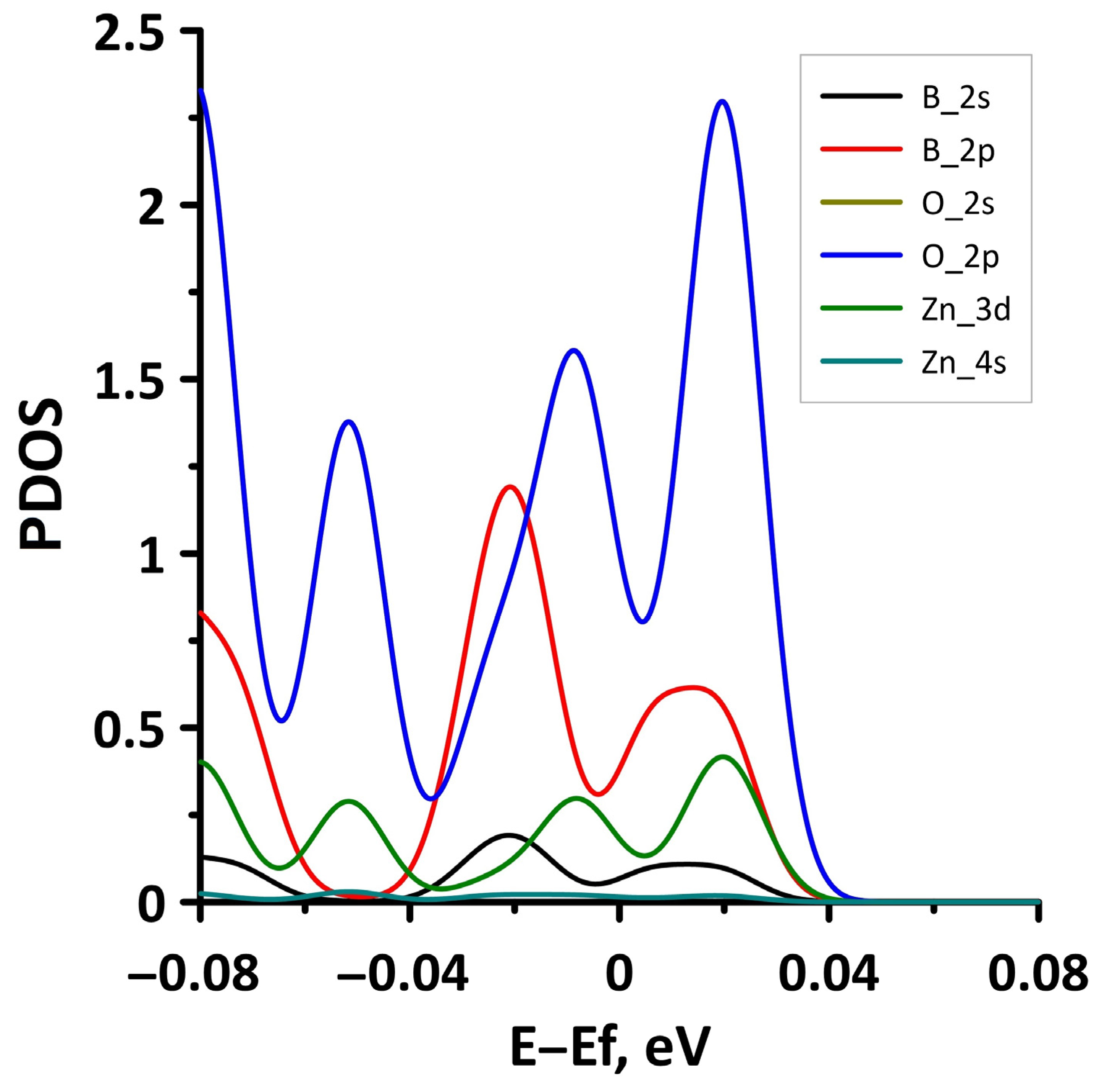
- The different distances along the Z axis between the borophene and GaN/ZnO monolayers in van der Waals heterostructure supercells: the distance between the borophene and GaN was 2.91 Å, the distance between the borophene and ZnO was 2.51 Å. At shorter distances, the interaction between the layers in heterostructure will be more noticeable and, therefore, will lead to more noticeable changes in the properties of the heterostructure as compared to the properties of its constituent monolayers. This is also indicated by difference in the calculated binding energies for the heterostructure supercells. Due to the shorter distance between borophene and ZnO, the binding energy of the borophene/ZnO heterostructure (−0.80 meV) will be greater than the binding energy of the borophene/GaN heterostructure (−0.50 meV). In addition, a shorter distance between borophene and ZnO causes more noticeable changes in the atomic structure of the ZnO monolayer in the borophene/ZnO heterostructure as compared to changes in the atomic structure of the GaN monolayer in the borophene/ZnO heterostructure. In particular, the dihedral angles of the GaN and ZnO monolayers differ greatly: for GaN, it is negative and amounts to −7.21, while for ZnO, it is positive and amounts to 19.18.
- (2)
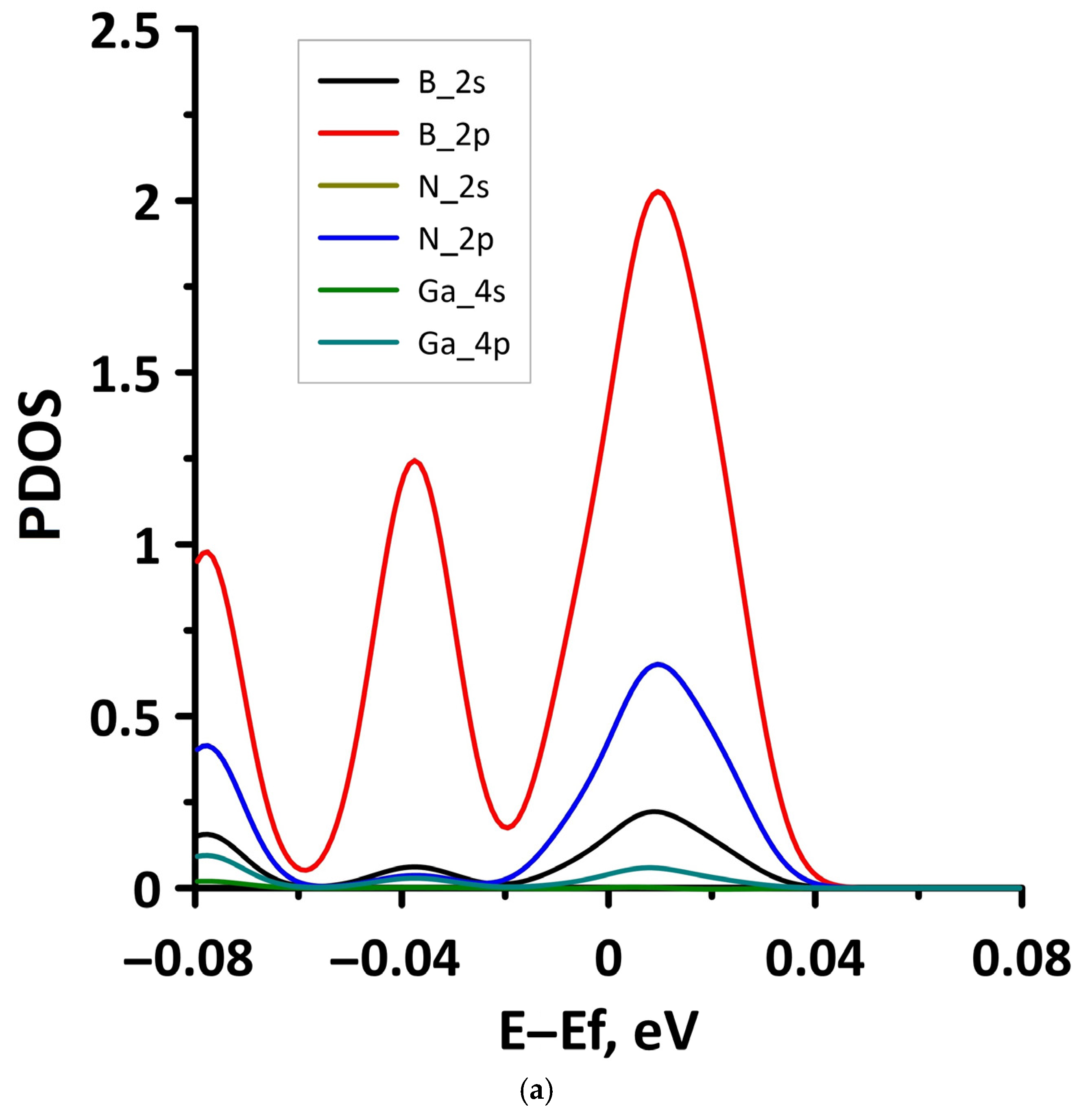
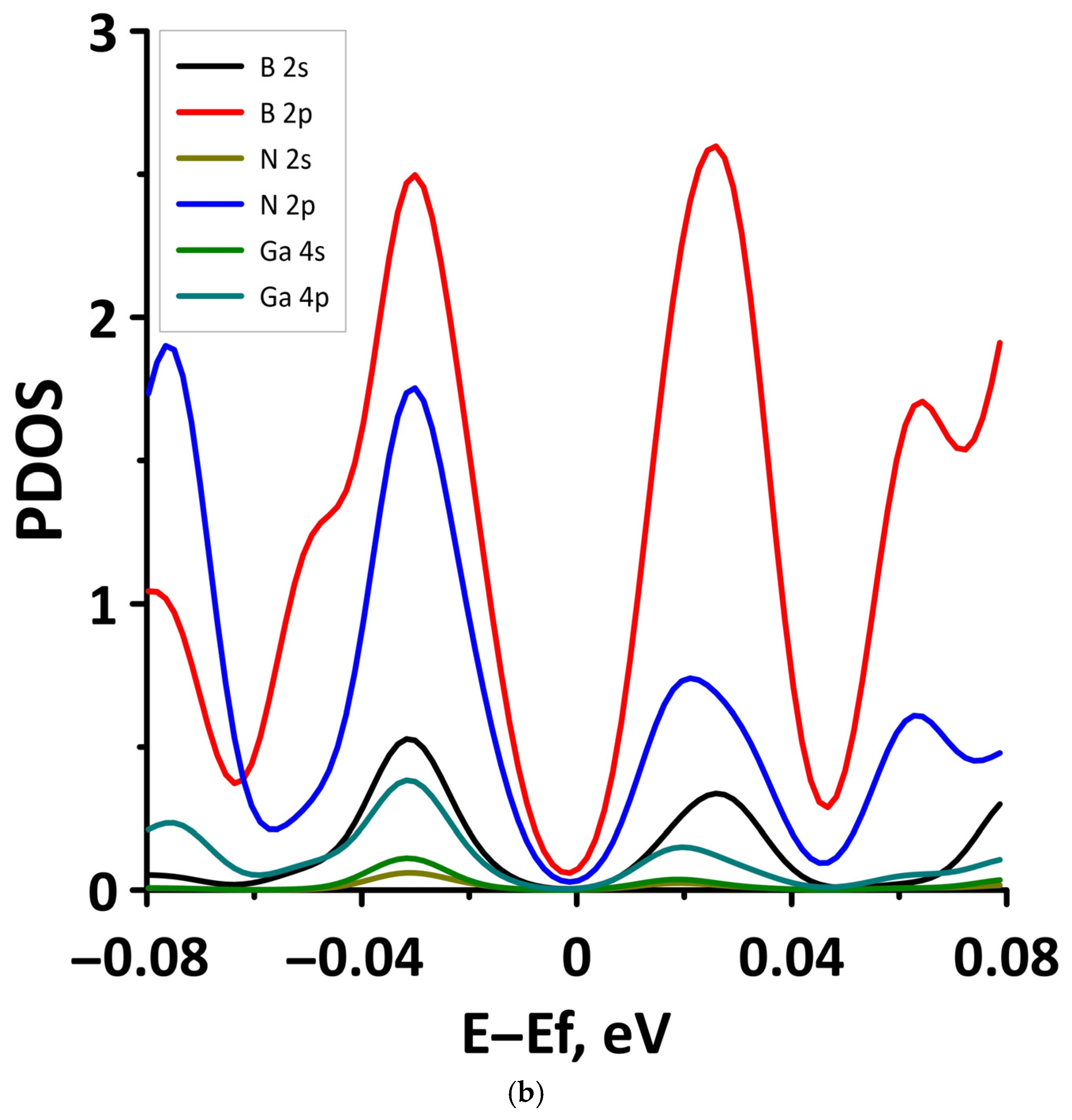
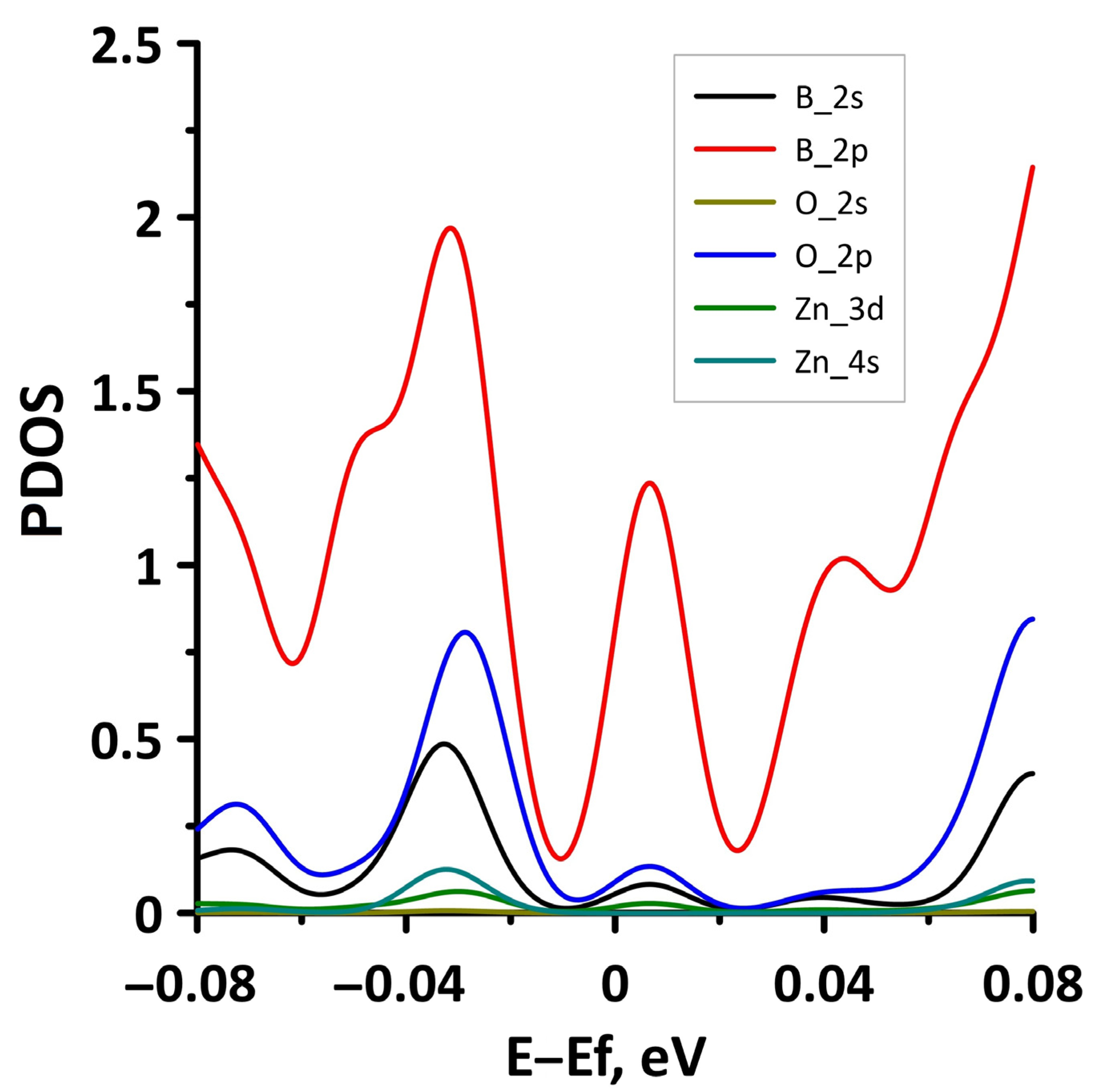
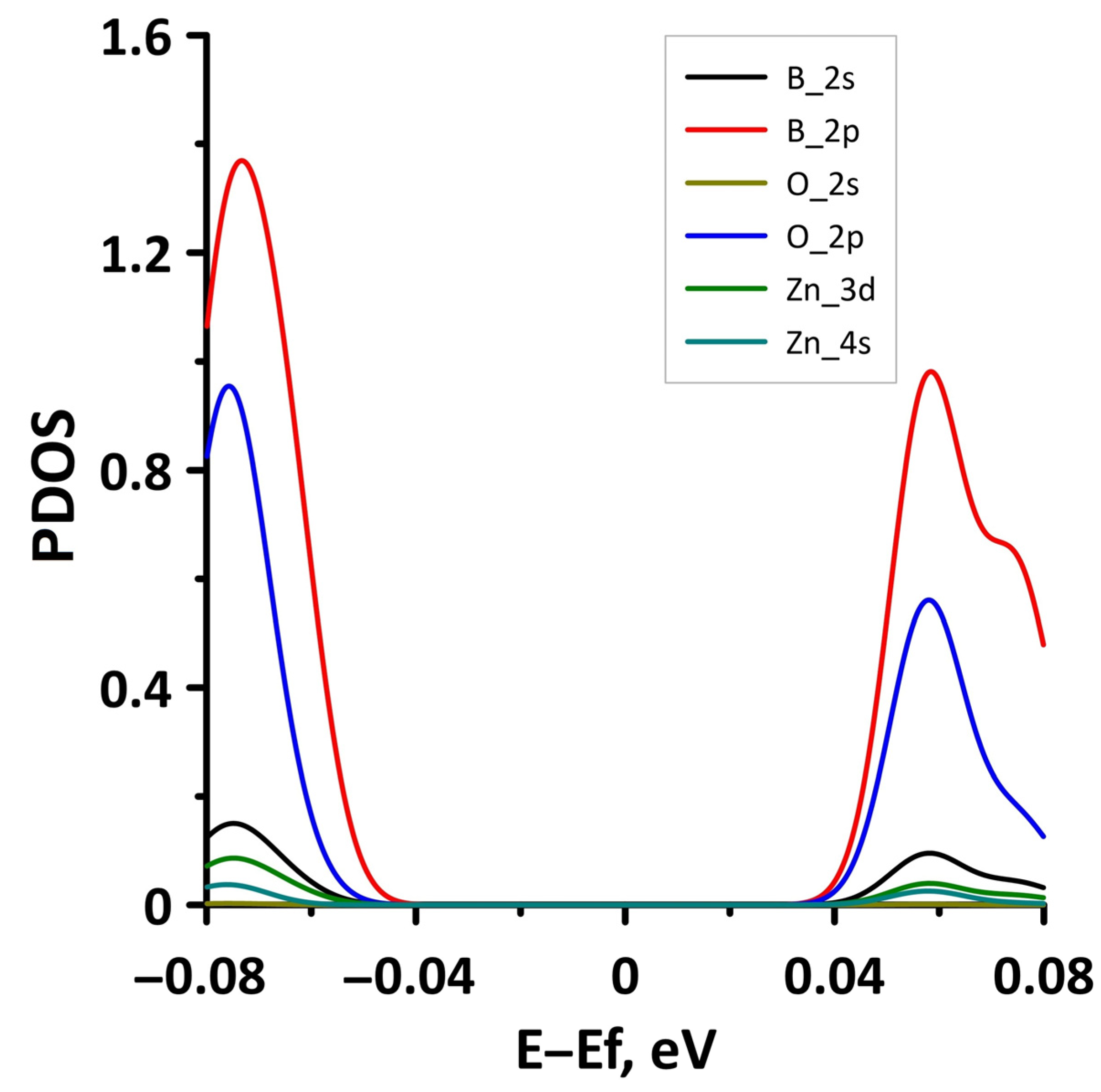
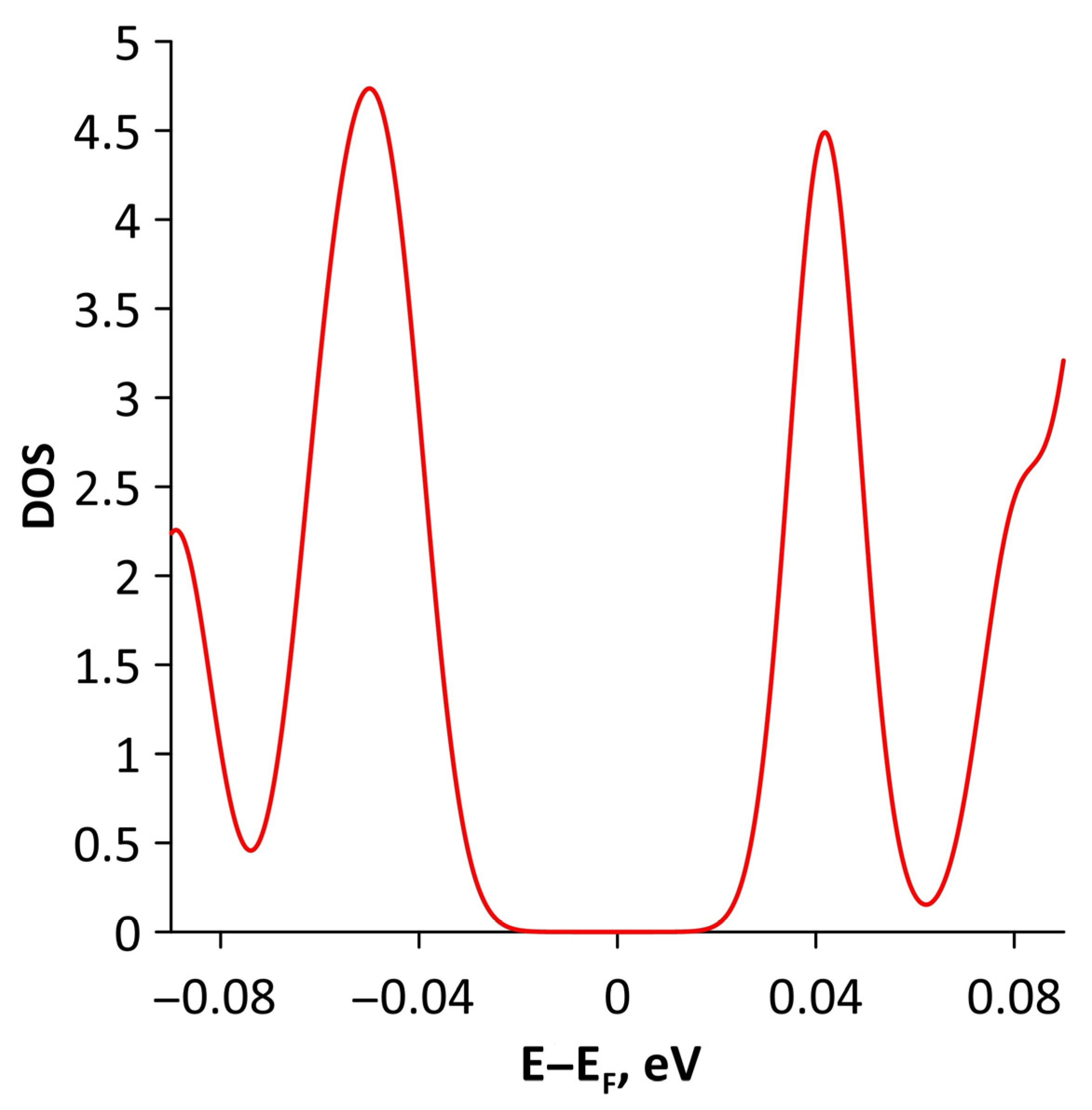
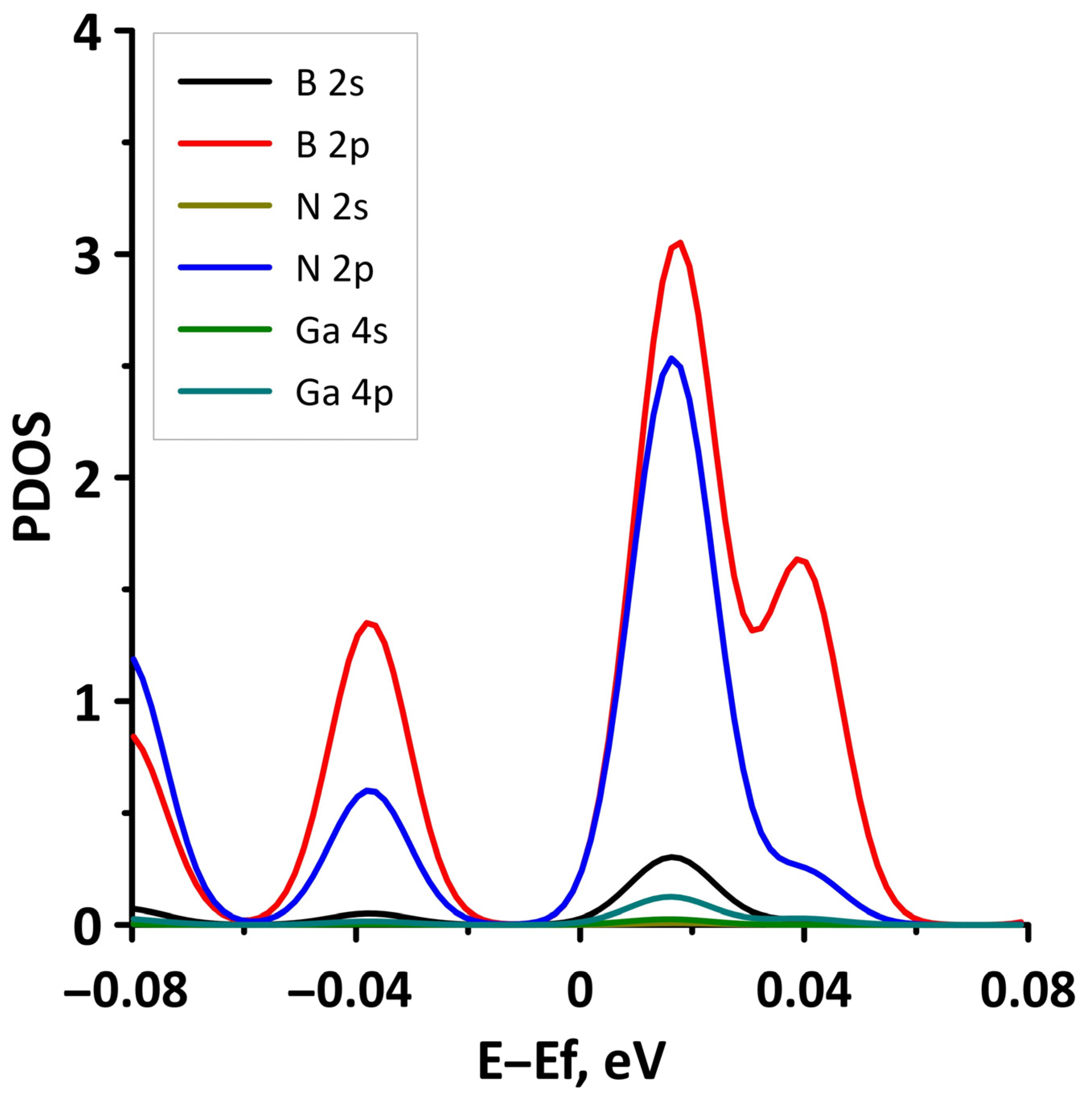
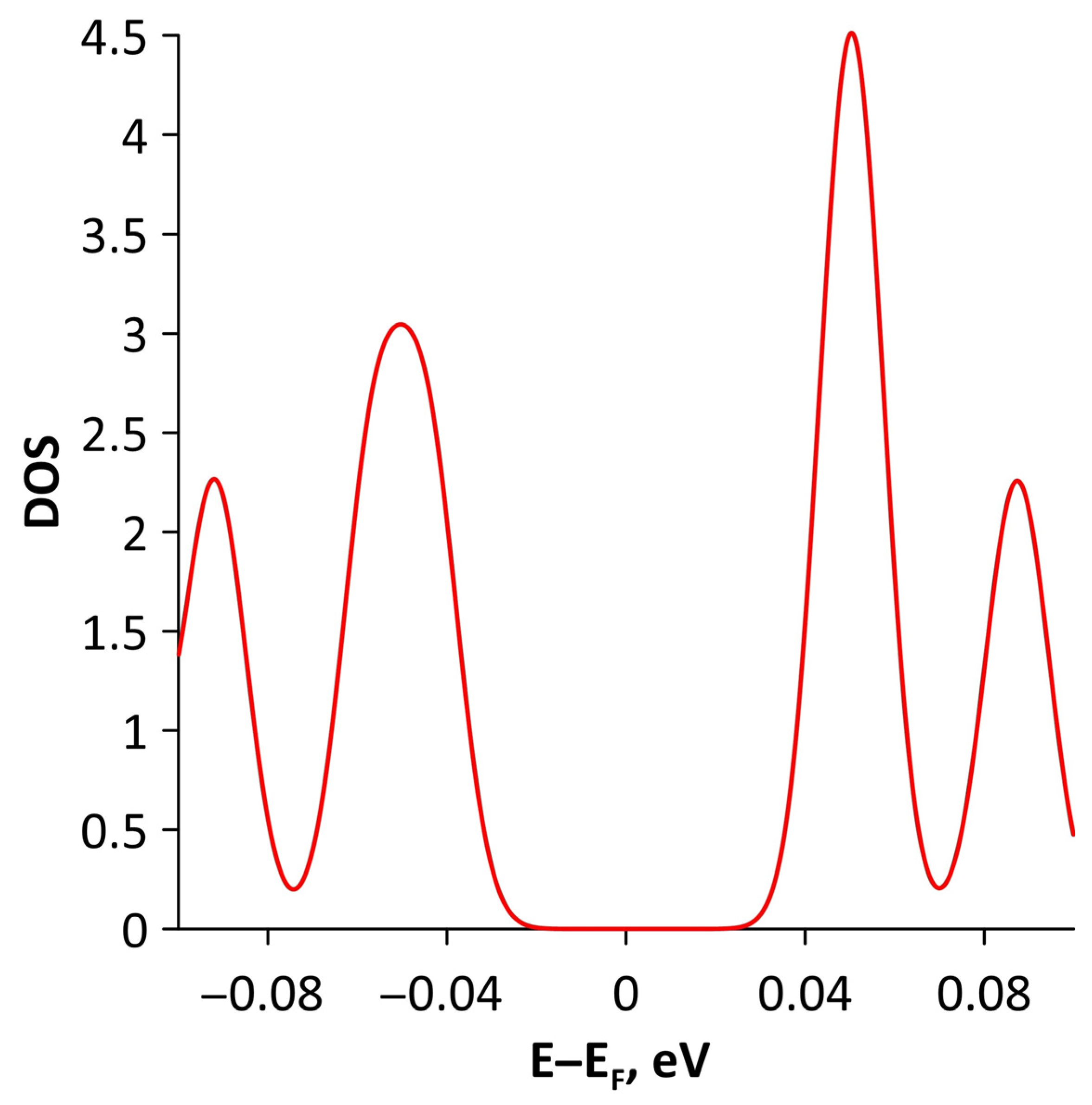
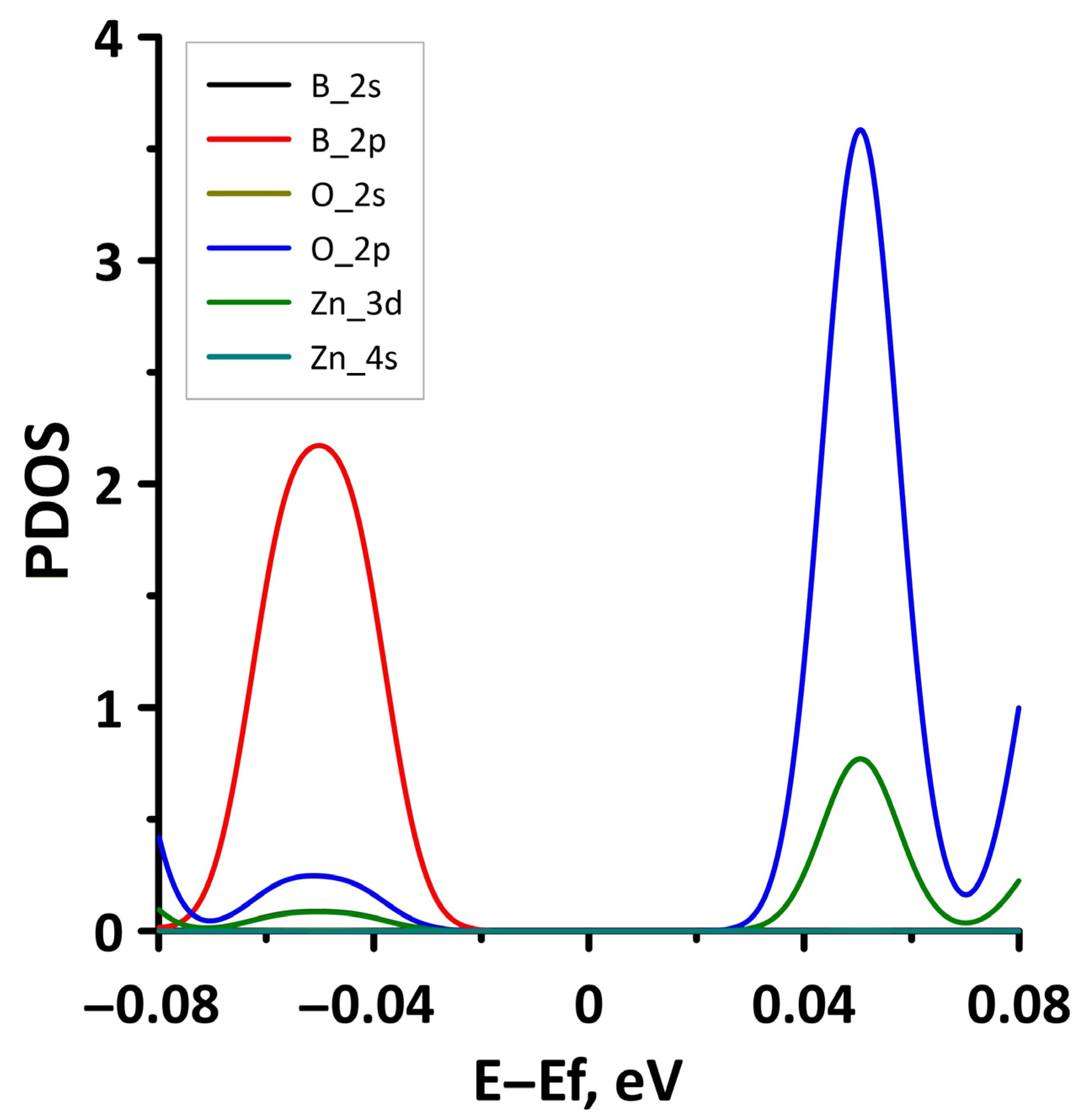
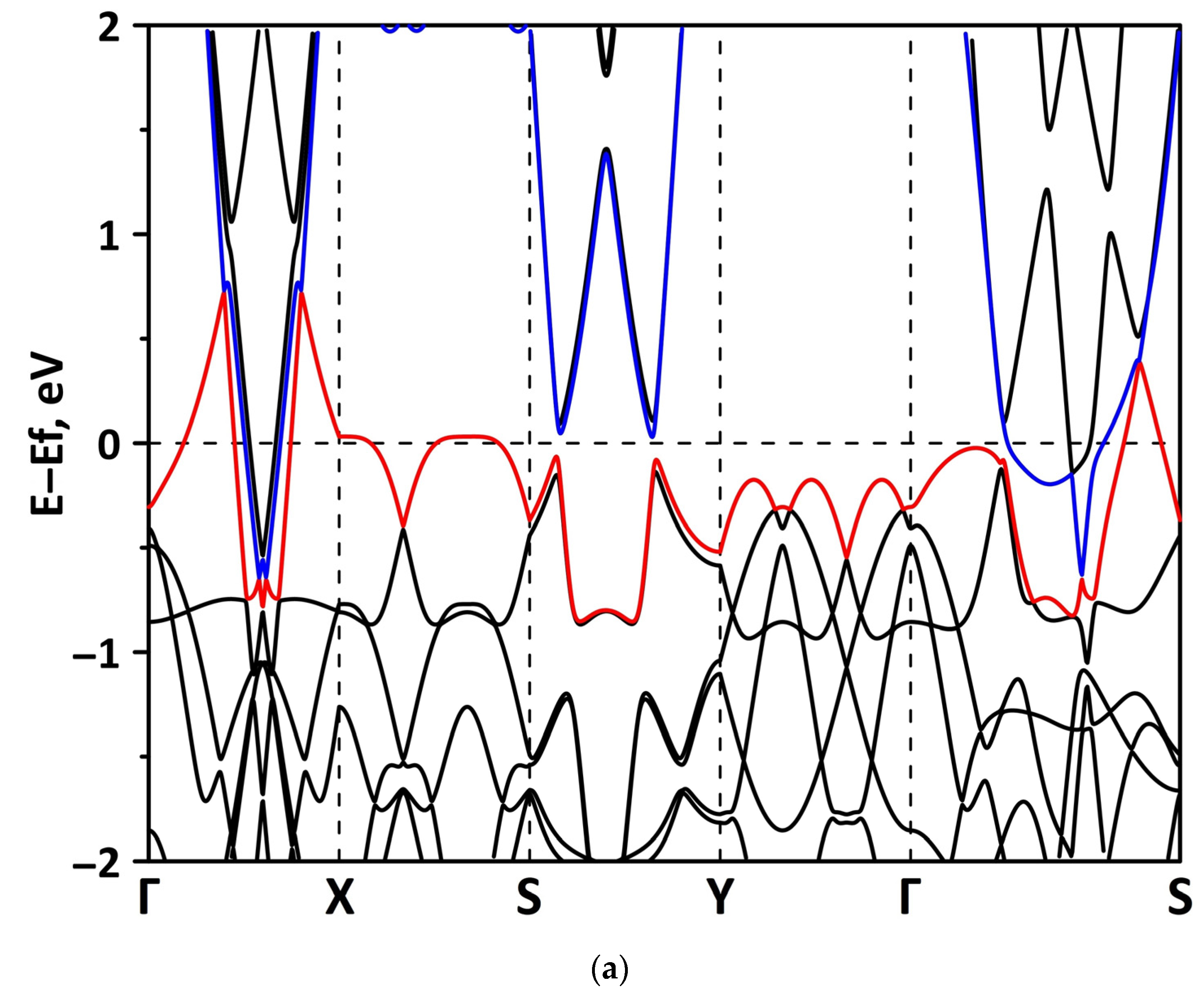
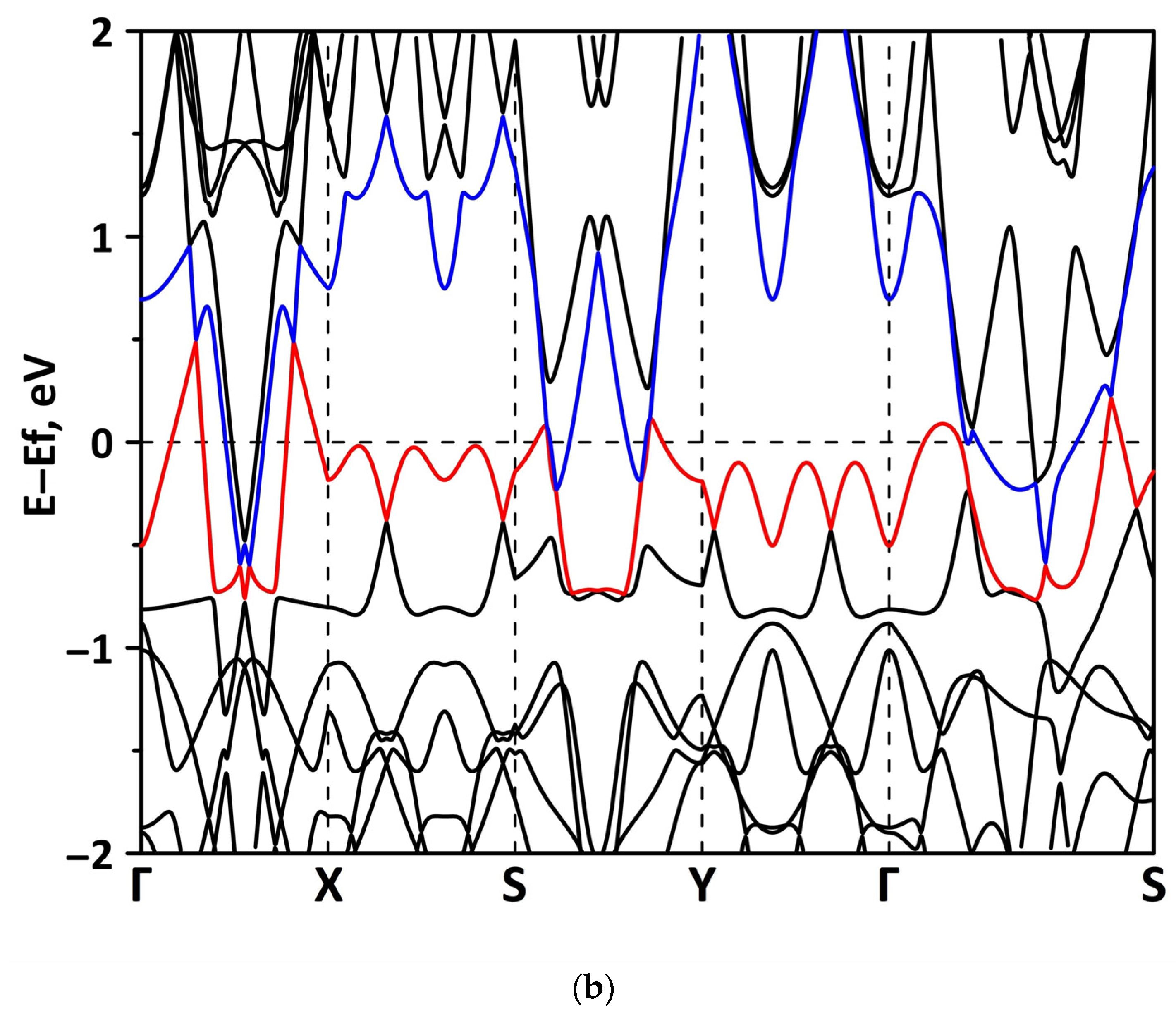
- The differences in the features of the band structure of graphene-like GaN and graphene-like ZnO monolayers. The band structure of graphene-like GaN has an indirect band gap, while graphene-like ZnO has a direct band gap [38,39]. In addition, based on DFT calculations using GGA-PBE approximation, Xia et al. found that the VBM and CBM of graphene-like ZnO are located at the center of the Brillouin zone (Γ point), while the VBM of graphene-like GaN is located at the K point of the Brillouin zone [40]. The authors attribute this difference to the insufficient hybridization of the 4p-orbitals of Ga atoms and 2p-orbitals of the N atoms at the Γ point of the Brillouin zone, which follows from the lower PDOS peaks near the VBM for graphene-like GaN. Finally, according to both known calculated data and experimental data, the size of the band gap for graphene-like GaN and graphene-like ZnO also differs [41,42,43,44,45].
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Geim, A.K.; Grigorieva, I.V. Van der Waals heterostructures. Nature 2013, 499, 419–425. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Novoselov, K.S.; Mishchenko, A.; Carvalho, A.; Castro Neto, A.H. 2D materials and van der Waals heterostructures. Science 2016, 353, aac9439. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yao, J.; Yanga, G. Van der Waals heterostructures based on 2D layered materials: Fabrication, characterization, and application in photodetection. J. Appl. Phys. 2022, 131, 161101. [Google Scholar] [CrossRef]
- Britnell, L.; Gorbachev, R.V.; Jalil, R.; Belle, B.D.; Schedin, F.; Mishchenko, A.; Georgiou, T.; Katsnelson, M.I.; Eaves, L.; Morozov, S.V.; et al. Field-effect tunneling transistor based on vertical graphene heterostructures. Science 2012, 335, 947–950. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.C.; Li, Z.; Shi, L.; Cronin, S.B. Thermoelectric transport across graphene/hexagonal boron nitride/graphene heterostructures. Nano Res. 2015, 8, 666–672. [Google Scholar] [CrossRef]
- Ekuma, C.E.; Najmaei, S. Graphene/ZnO van der Waals Stacks for Thermal Management. ACS Appl. Nano Mater. 2020, 3, 7136–7142. [Google Scholar] [CrossRef]
- Choi, W.; Choudhary, N.; Han, G.H.; Park, J.; Akinwande, D.; Lee, Y.H. Recent development of two-dimensional transition metal dichalcogenides and their applications. Mater. Today 2017, 20, 116–130. [Google Scholar] [CrossRef]
- Hong, X.; Kim, J.; Shi, S.; Zhang, Y.; Jin, C.; Sun, Y.; Tongay, S.; Wu, J.; Zhang, Y.; Wang, F. Ultrafast charge transfer in atomically thin MoS2/WS2 heterostructures. Nat. Nanotech. 2014, 9, 682–686. [Google Scholar] [CrossRef] [Green Version]
- Kang, Z.; Ma, Y.; Tan, X.; Zhu, M.; Zheng, Z.; Liu, N.; Li, L.; Zou, Z.; Jiang, X.; Zhai, T.; et al. MXene–Silicon Van Der Waals Heterostructures for High-Speed Self-Driven Photodetectors. Adv. Electron. Mater. 2017, 3, 1700165. [Google Scholar] [CrossRef]
- Kong, X.; Liu, Q.; Zhang, C.; Peng, Z.; Chen, Q. Elemental two-dimensional nanosheets beyond graphene. Chem. Soc. Rev. 2017, 46, 2127–2157. [Google Scholar] [CrossRef]
- Liu, Y.; Weiss, N.O.; Duan, X.; Cheng, H.-C.; Huang, Y.; Duan, X. Van der Waals heterostructures and devices. Nat. Rev. Mater. 2016, 1, 16042. [Google Scholar] [CrossRef]
- Zhou, X.; Hu, X.; Yu, J.; Liu, S.; Shu, Z.; Zhang, Q.; Li, H.; Ma, Y.; Xu, H.; Zhai, T. 2D Layered Material-Based van der Waals Heterostructures for Optoelectronics. Adv. Funct. Mater. 2018, 28, 1706587. [Google Scholar] [CrossRef]
- Liang, S.; Cheng, B.; Cui, X.; Miao, F. Van der Waals Heterostructures for High-Performance Device Applications: Challenges and Opportunities. Adv. Mater. 2019, 32, 1903800. [Google Scholar] [CrossRef] [Green Version]
- Mannix, A.J.; Zhou, X.-F.; Kiraly, B.; Wood, J.D.; Alducin, D.; Myers, B.D.; Liu, X.; Fisher, B.L.; Santiago, U.; Guest, J.R.; et al. Synthesis of borophenes: Anisotropic, two-dimensional boron polymorphs. Science 2015, 350, 1513–1516. [Google Scholar] [CrossRef] [Green Version]
- Cuxart, M.G.; Seufert, K.; Chesnyak, V.; Waqas, W.A.; Robert, A.; Bocquet, M.L.; Duesberg, G.S.; Sachdev, H.; Auwärter, W. Borophenes made easy. Sci. Adv. 2021, 7, eabk1490. [Google Scholar] [CrossRef]
- Kaneti, Y.V.; Benu, D.P.; Xu, X.; Yuliarto, B.; Yamauchi, Y.; Golberg, D. Borophene: Two-dimensional Boron Monolayer: Synthesis, Properties, and Potential Applications. Chem. Rev. 2022, 122, 1000–1051. [Google Scholar] [CrossRef]
- Liu, X.; Hersam, M.C. Borophene-graphene heterostructures. Sci. Adv. 2019, 5, eaax6444. [Google Scholar] [CrossRef] [Green Version]
- Hou, C.; Tai, G.; Liu, B.; Wu, Z.; Yin, Y. Borophene-graphene heterostructure: Preparation and ultrasensitive humidity sensing. Nano Res. 2021, 14, 2337–2344. [Google Scholar] [CrossRef]
- Yu, J.; Zhou, M.; Yang, M.; Yang, Q.; Zhang, Z.; Zhang, Y. High-Performance Borophene/Graphene Heterostructure Anode of Lithium-Ion Batteries Achieved via Controlled Interlayer Spacing. ACS Appl. Energy Mater. 2020, 3, 11699–11705. [Google Scholar] [CrossRef]
- Kochaev, A.; Katin, K.; Maslov, M.; Singh, S. Covalent and van der Waals interactions in a vertical heterostructure composed of boron and carbon. Phys. Rev. B 2022, 105, 235444. [Google Scholar] [CrossRef]
- Vishwakarma, K.; Rani, S.; Chahal, S.; Lu, C.-Y.; Ray, S.J.; Yang, C.-S.; Kumar, P. Quantum-coupled borophene-based heterolayers for excitonic and molecular sensing applications. Phys. Chem. Chem. Phys. 2022, 24, 12816–12826. [Google Scholar] [CrossRef] [PubMed]
- Shen, J.; Yang, Z.; Wang, Y.; Xu, L.-C.; Liu, R.; Liu, X. Organic Gas Sensing Performance of the Borophene van der Waals Heterostructure. J. Phys. Chem. C 2021, 125, 427–435. [Google Scholar] [CrossRef]
- Katoch, N.; Kumar, A.; Sharma, R.; Ahluwalia, P.K.; Kumar, J. Strain Tunable Schottky Barriers and Tunneling Characteristics of Borophene/MX2 van der Waals Heterostructures. Phys. E Low Dimens. Syst. Nanostruct. 2020, 120, 113842. [Google Scholar] [CrossRef]
- Jing, S.; Chen, W.; Pan, J.; Li, W.; Bian, B.; Liao, B.; Wang, G. Electronic properties of Borophene/InSe van der Waals heterostructures. Mater. Sci. Semicond. Process. 2022, 146, 106673. [Google Scholar] [CrossRef]
- Jiang, J.W.; Wang, X.C.; Song, Y.; Mi, W.B. Tunable Schottky Barrier and Electronic Properties in Borophene/g-C2N van der Waals Heterostructures. Appl. Surf. Sci. 2018, 440, 42–46. [Google Scholar] [CrossRef]
- Kakanakova-Gueorguieva, A.; Giannazzo, F.; Nicotra, G.; Cora, I.; Gueorguiev, G.K.; Persson, P.O.A.; Pecz, B. Material proposal for 2D indium oxide. Appl. Surf. Sci. 2021, 548, 149275. [Google Scholar] [CrossRef]
- Eblagon, K.M.; Rey-Raap, N.; Figueiredo, J.L.; Pereira, M.F.R. Relationships between texture, surface chemistry and performance of N-doped carbon xerogels in the oxygen reduction reaction. Appl. Surf. Sci. 2021, 548, 149242. [Google Scholar] [CrossRef]
- Zhang, Z.; Penev, E.S.; Yakobson, B.I. Two-dimensional boron: Structures, properties and applications. Chem. Soc. Rev. 2017, 46, 6746–6763. [Google Scholar] [CrossRef]
- Deng, Z.; Wang, X.; Cui, J. Effect of interfacial defects on the electronic properties of graphene/g-GaN heterostructures. RSC Adv. 2019, 9, 13418–13423. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Gong, M. ZnO/graphene heterostructure nanohybrids for optoelectronics and sensors. J. Appl. Phys. 2021, 130, 070905. [Google Scholar] [CrossRef]
- Soler, J.M.; Artacho, E.; Gale, J.D.; García, A.; Junquera, J.; Ordejón, P.; Sánchez-Portal, D. The SIESTA method for ab-initio order-N materials simulation. J. Phys. Condens. Matter 2002, 14, 2745–2779. [Google Scholar]
- The SIESTA Group. Available online: Departments.icmab.es/leem/siesta/ (accessed on 10 December 2021).
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671–6687. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-type Density Functional Constructed with a Long-Range Dispersion Correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Pulay, P. Convergence acceleration of iterative sequences. The case of SCF iteration. Chem. Phys. Lett. 1980, 73, 393–398. [Google Scholar] [CrossRef]
- Slepchenkov, M.M.; Kolosov, D.A.; Glukhova, O.E. Novel Van Der Waals Heterostructures Based on Borophene, Graphene-like GaN and ZnO for Nanoelectronics: A First Principles Study. Materials 2022, 15, 4084. [Google Scholar] [CrossRef]
- Xiang, H.; Quan, H.; Hu, Y.; Zhao, W.; Xu, B.; Yin, J. Piezoelectricity of Graphene-like Monolayer, ZnO and GaN. J. Inorg. Mater. 2021, 36, 492–496. [Google Scholar] [CrossRef]
- Ren, K.; Yu, J.; Tang, W. Two-dimensional ZnO/BSe van der waals heterostructure used as a promising photocatalyst for water splitting: A DFT study. J. Alloys Compd. 2020, 812, 152049. [Google Scholar] [CrossRef]
- Xia, S.; Diao, Y.; Kan, C. Electronic and optical properties of two-dimensional GaN/ZnO heterojunction tuned by different stacking configurations. J. Colloid Interface Sci. 2022, 607, 913–921. [Google Scholar] [CrossRef]
- Wang, G.; Tang, W.; Geng, L.; Li, Y.; Wang, B.; Chang, J.; Yuan, H. Rotation Tunable Photocatalytic Properties of ZnO/GaN Heterostructures. Phys. Status Solidi B 2019, 257, 1900663. [Google Scholar] [CrossRef]
- Zhang, Y.-H.; Zhang, M.-L.; Zhou, Y.-C.; Zhao, J.-H.; Fang, S.-M.; Li, F. Tunable electronic and magnetic properties of graphene-like ZnO monolayer upon doping and CO adsorption: A first-principles study. J. Mater. Chem. A 2014, 2, 13129–13135. [Google Scholar] [CrossRef]
- Cui, Z.; Wang, X.; Ding, Y.; Li, E.; Bai, K.; Zheng, J.; Liu, T. Adsorption of CO, NH3, NO, and NO2 on pristine and defective g-GaN: Improved gas sensing and functionalization. Appl. Surf. Sci. 2020, 530, 147275. [Google Scholar] [CrossRef]
- Guo, H.; Zhao, Y.; Lu, N.; Kan, E.; Zeng, X.C.; Wu, X.; Yang, J. Tunable Magnetism in a Nonmetal-Substituted ZnO Monolayer: A First-Principles Study. J. Phys. Chem. C 2012, 116, 11336–11342. [Google Scholar] [CrossRef]
- Wang, G.; Dang, S.; Zhao, W.; Li, Y.; Xiao, S.; Zhong, M. Tunable Photocatalytic Properties of GaN-Based Two-Dimensional Heterostructures. Phys. Status Solidi B 2018, 255, 1800133. [Google Scholar] [CrossRef]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Slepchenkov, M.M.; Kolosov, D.A.; Nefedov, I.S.; Glukhova, O.E. Band Gap Opening in Borophene/GaN and Borophene/ZnO Van der Waals Heterostructures Using Axial Deformation: First-Principles Study. Materials 2022, 15, 8921. https://doi.org/10.3390/ma15248921
Slepchenkov MM, Kolosov DA, Nefedov IS, Glukhova OE. Band Gap Opening in Borophene/GaN and Borophene/ZnO Van der Waals Heterostructures Using Axial Deformation: First-Principles Study. Materials. 2022; 15(24):8921. https://doi.org/10.3390/ma15248921
Chicago/Turabian StyleSlepchenkov, Michael M., Dmitry A. Kolosov, Igor S. Nefedov, and Olga E. Glukhova. 2022. "Band Gap Opening in Borophene/GaN and Borophene/ZnO Van der Waals Heterostructures Using Axial Deformation: First-Principles Study" Materials 15, no. 24: 8921. https://doi.org/10.3390/ma15248921
APA StyleSlepchenkov, M. M., Kolosov, D. A., Nefedov, I. S., & Glukhova, O. E. (2022). Band Gap Opening in Borophene/GaN and Borophene/ZnO Van der Waals Heterostructures Using Axial Deformation: First-Principles Study. Materials, 15(24), 8921. https://doi.org/10.3390/ma15248921






