Flexural Strength of Concrete Beam Reinforced with CFRP Bars: A Review
Abstract
:1. Introduction
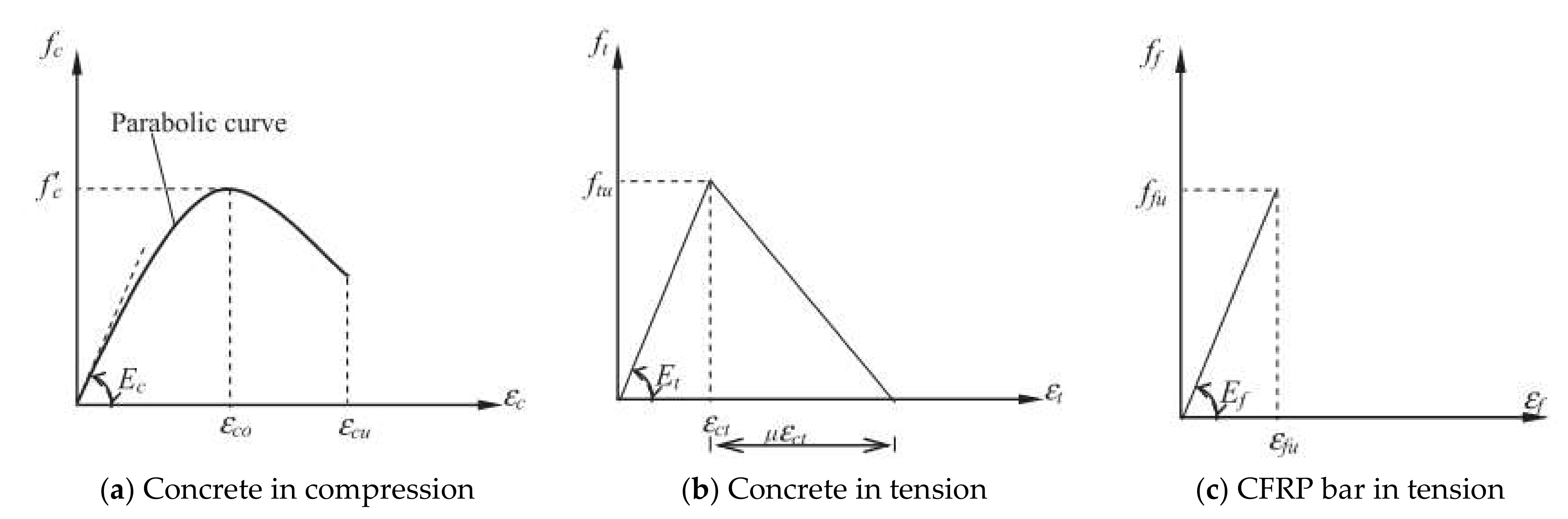
2. Material Properties and Behavior for Concrete and CFRP Bar
3. Flexural Behavior of CFRP RC Beam
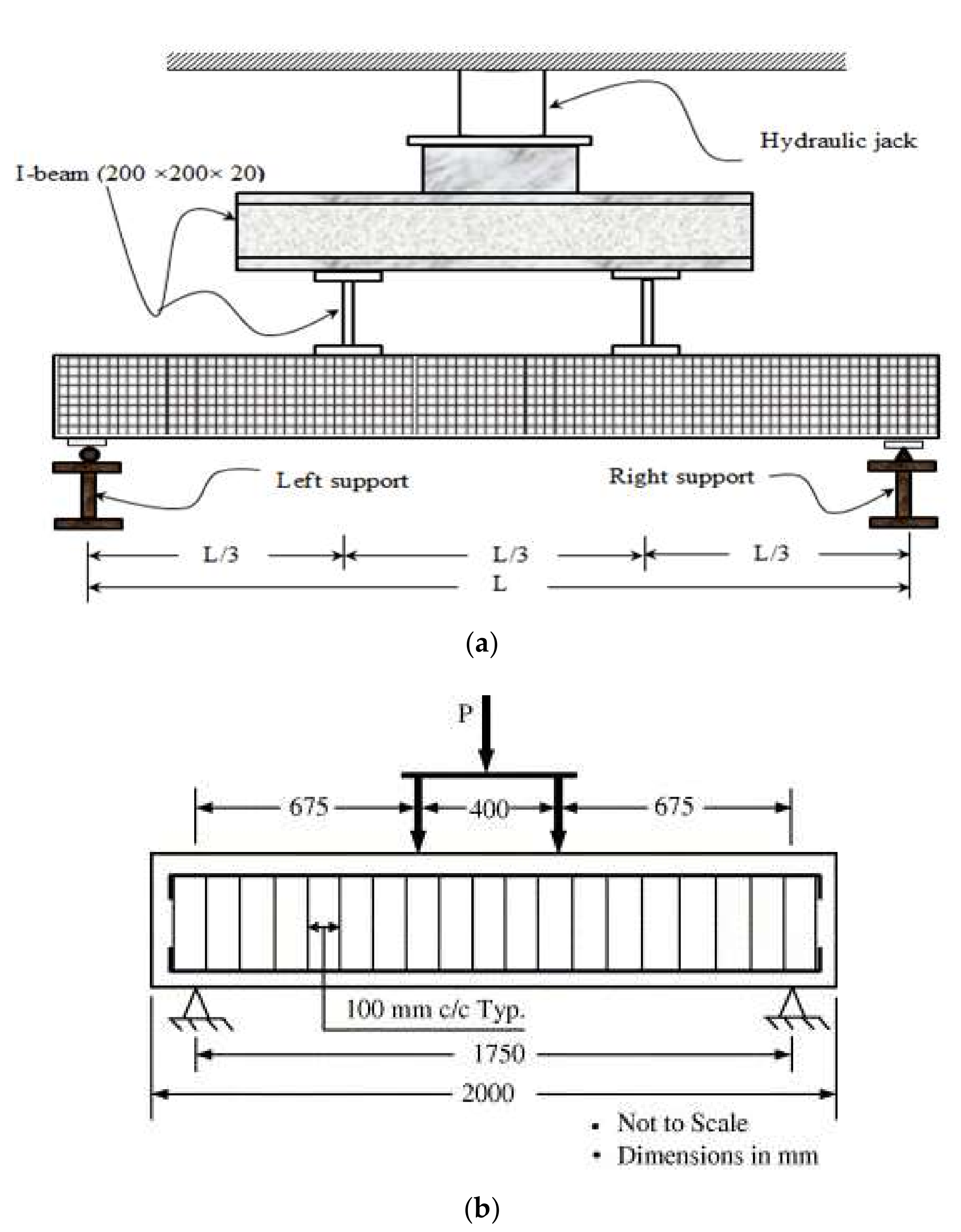
3.1. Beam Specimen and Test Procedures
3.2. Modes of Failure
4. Aspect Behavior of Flexural Strength
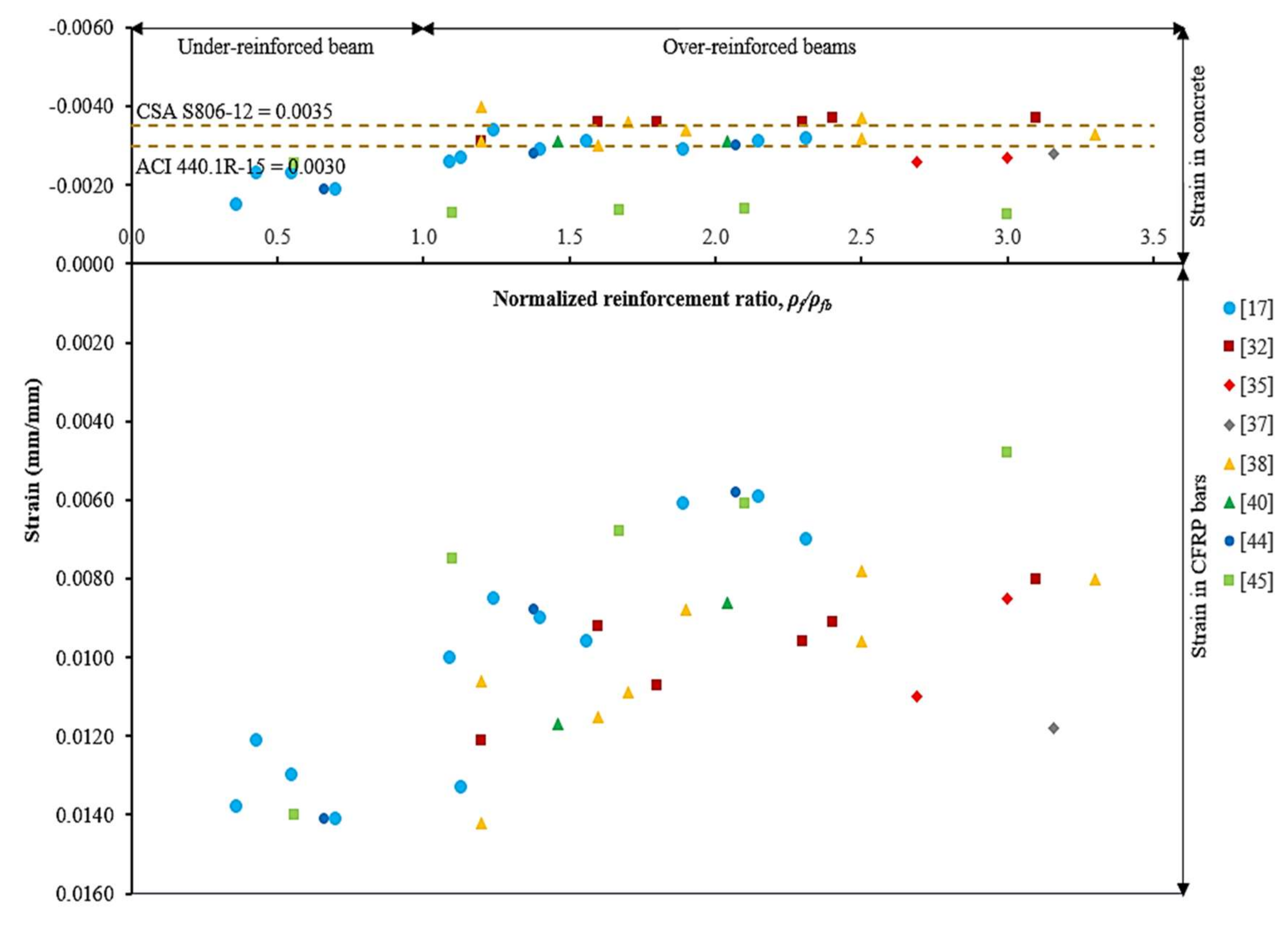
4.1. Concrete Compressive Strain and CFRP Bars Tensile Strain Behavior
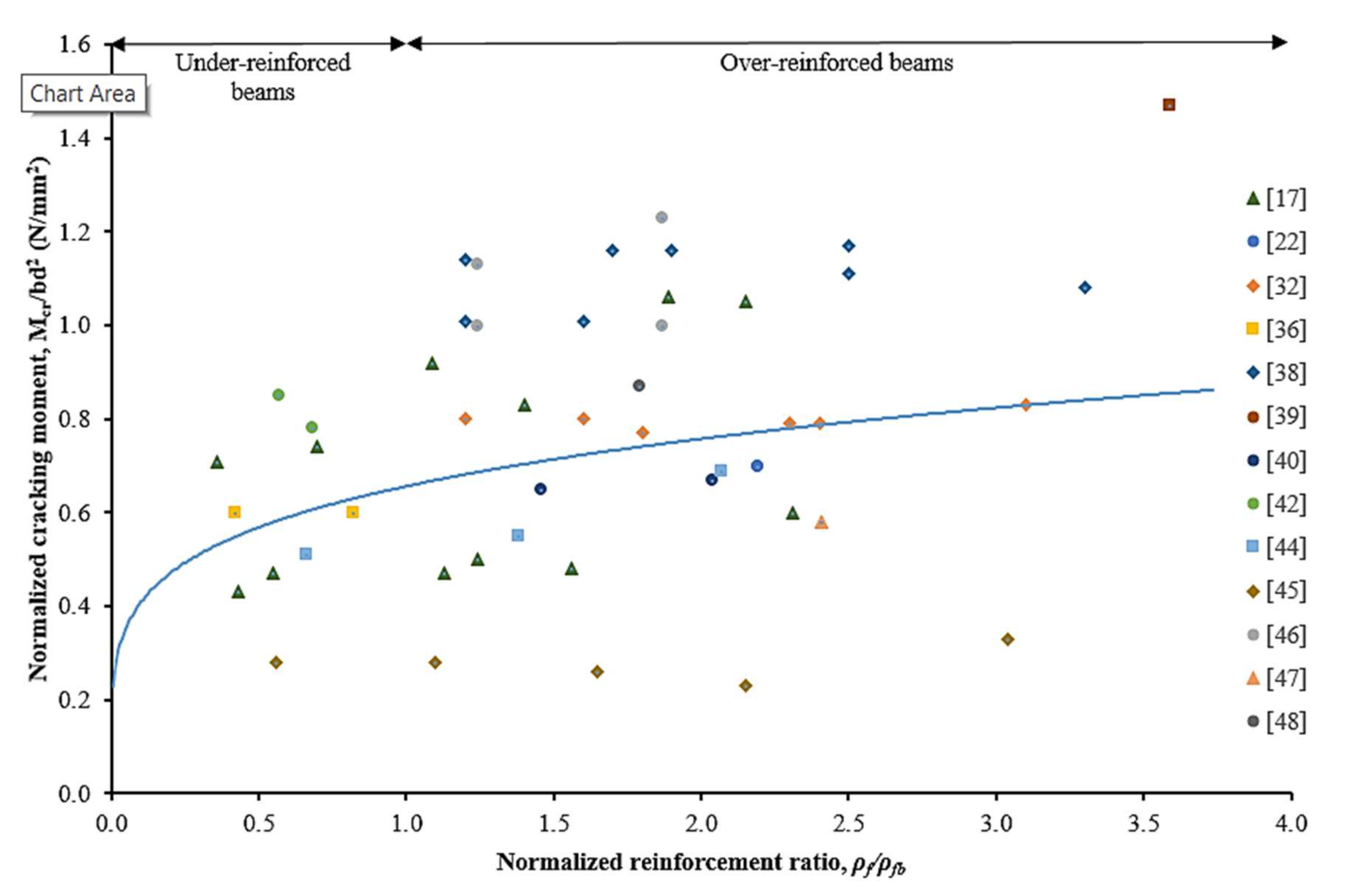
4.2. Effect of Reinforcement Ratio
4.3. Variation of Concrete Compressive Strength
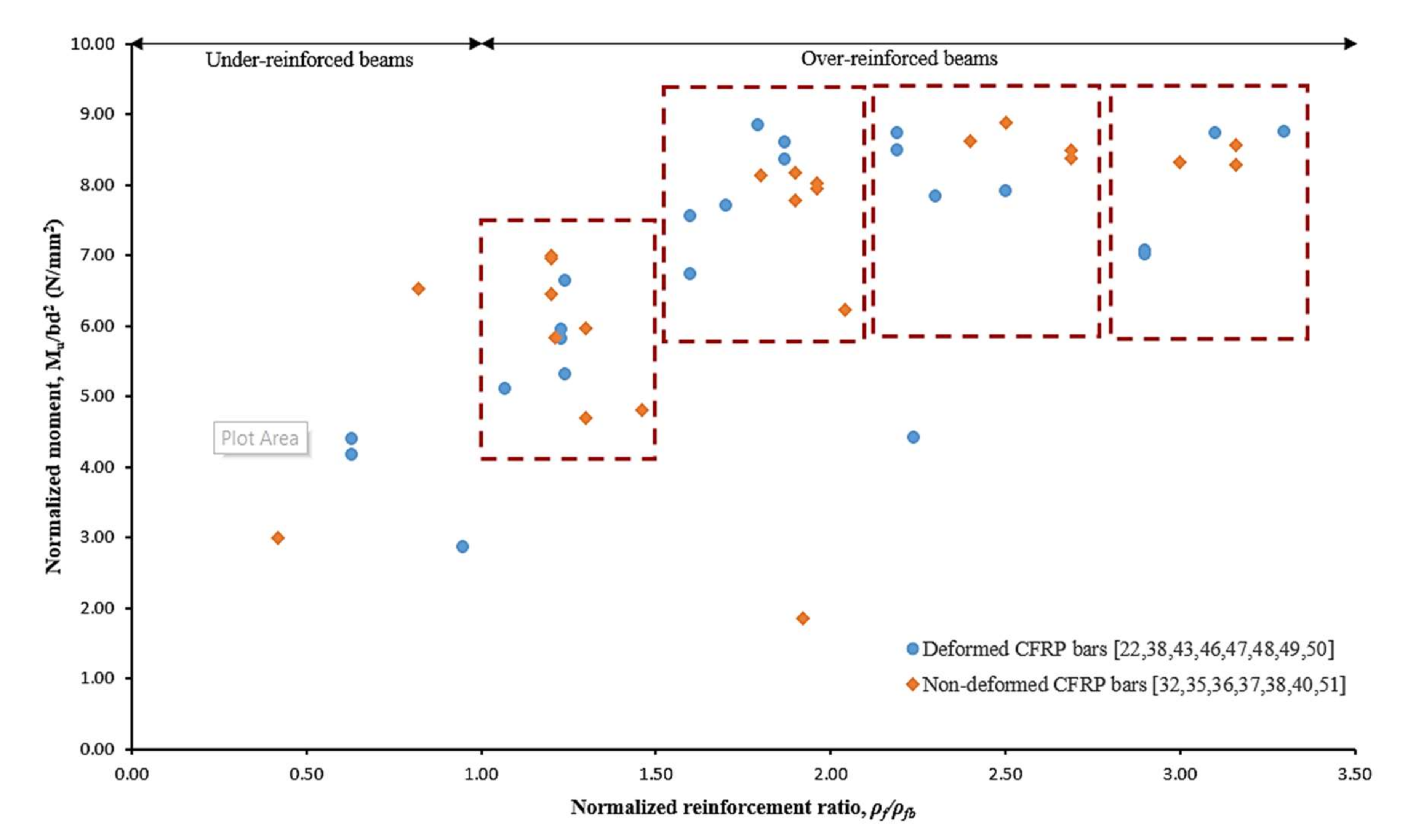
4.4. Variation of CFRP Bars Surface Treatment
4.4.1. Deformed CFRP Bars
4.4.2. Non-Deformed CFRP Bars
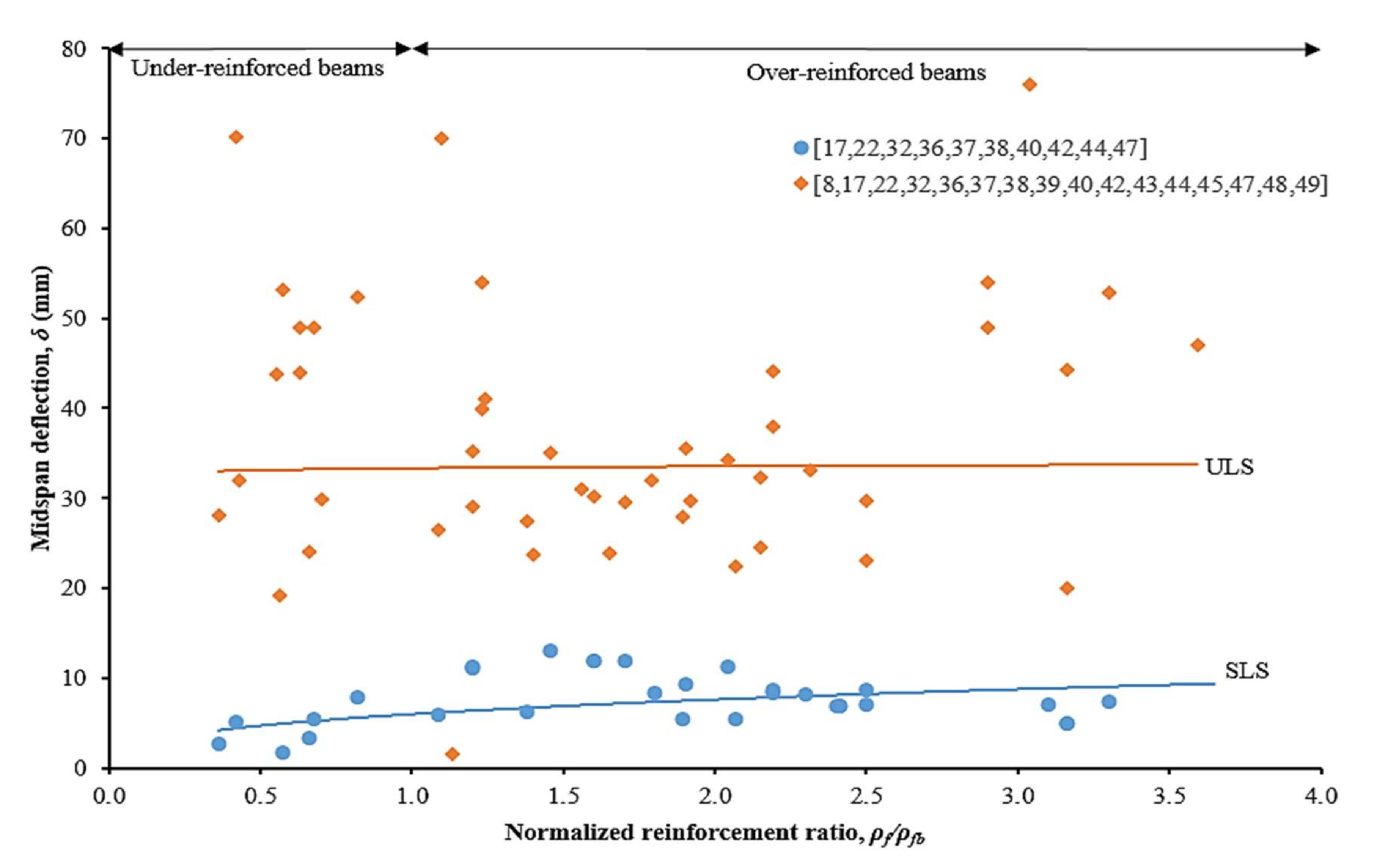
4.5. Deflection Characteristics
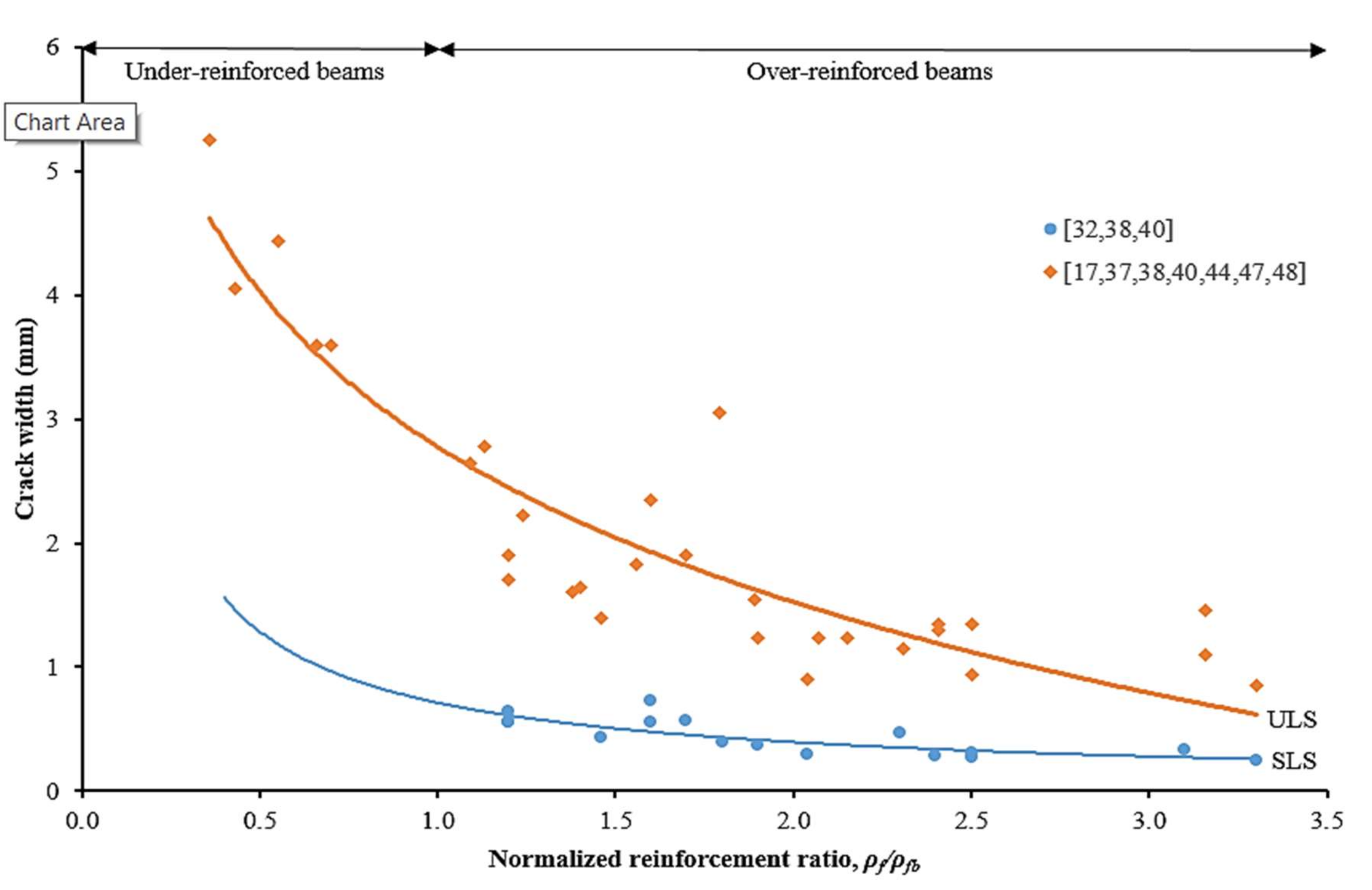
4.6. Crack Width, Crack Spacing and Crack Number
5. Theoretical Prediction of Flexural Moment Capacity
5.1. International Design Provisions
5.2. Proposed Method by Kara and Ashour
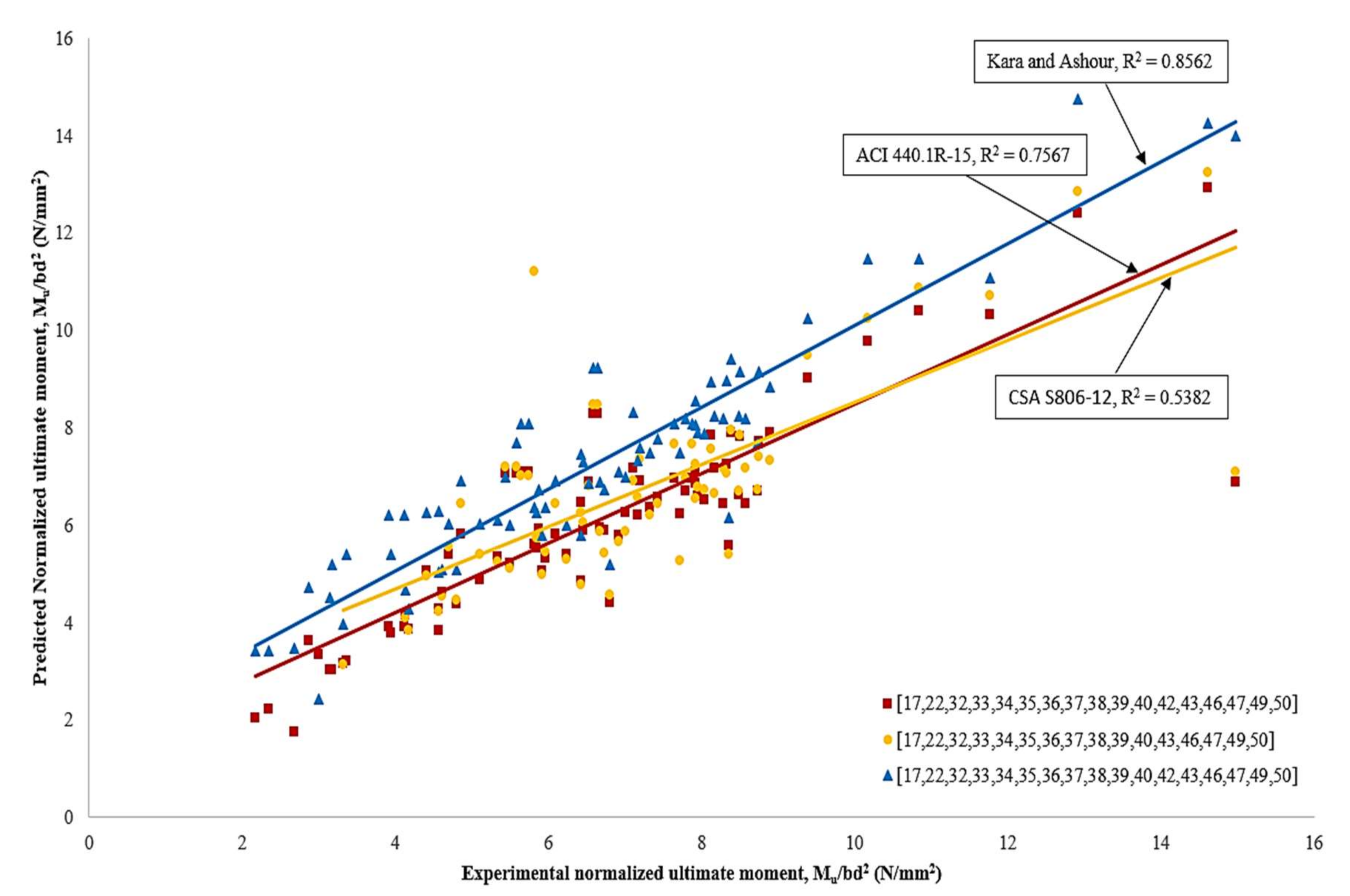
5.3. Comparison between Predicted Ultimate Normalized Moment Capacities against Experimental Values
6. Hotspot Research Topics for Future Investigations
- -
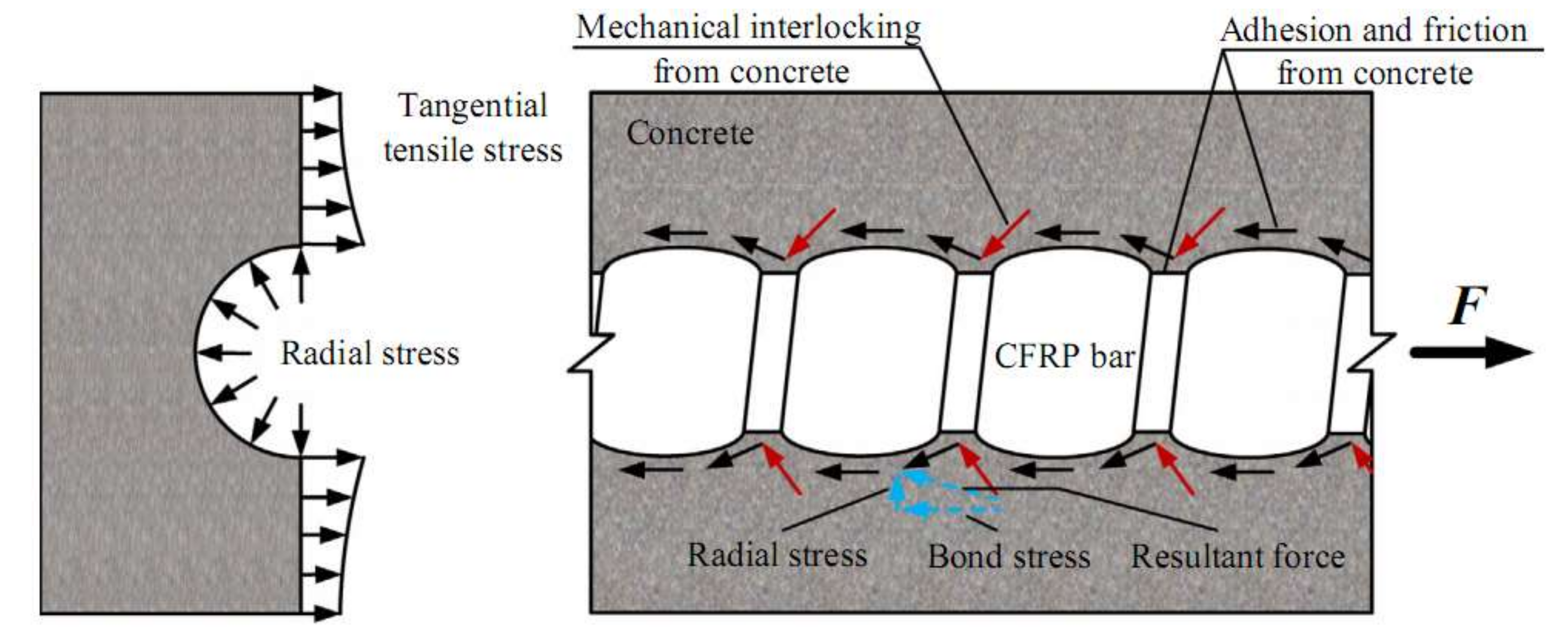
- The bond strength between CFRP bar and concrete: Bond mechanisms between CFRP bar and concrete contribute significant roles in transferring flexural stresses in the tension zone of CFRP RC beams [8]. The sufficient bond strength of CFRP bar to concrete may reduce the crack width and deflection, subsequently increasing the beam stiffness [60]. In the extensive investigation by researchers, they have concluded that CFRP bar’s surface treatment plays enormous roles in affecting various bond strengths [41,58,61,62,63]. Therefore, applying CFRP bar with different surface treatments as flexural reinforcement could have resulted in various bond strengths. Concerning this, extensive investigation on the local bond-slip relationship in CFRP RC beam may become significant to avoid premature slip or de-bond failure of CFRP bars from concrete [42]. Henceforth, perfect bond strength between CFRP bar and concrete is assumed by international guidelines and researchers [5,6,18,19,25,32,40].
- -
- Strength limit state design (under-reinforced CFRP RC beam): It is noteworthy that most CFRP RC beams were designed with an over-reinforced limit state. The compression failure was more desirable due to its less violent than tension failure [7,19]. However, failure of the over-reinforced CFRP RC beam is reliant on the concrete compressive strength itself. The advantages of CFRP bar particularly having high tensile strength may become less significant. The CFRP bar has never reached its ultimate tensile strength for an over-reinforced CFRP RC beam, therefore, it is necessary to consider CFRP RC beams as designed with an under-reinforced limit state. Thorough investigations on the CFRP RC beam behavior at SLS and ULS need to be conducted by taking into account that the large deflection and crack width are within tolerance.
- -
- Application of CFRP bars in geopolymer concrete: Henceforth, few studies have been conducted to investigate the behavior of CFRP bars as flexural reinforcement in geopolymer concrete. The combination of both materials might provide high performance and sustainable structures. A study by Ahmed et al. [17] has discovered the high potential for the application of these materials. Parameters, such as reinforcement ratio and geopolymer compressive strength had affected the flexural strength, deflection, crack numbers, crack width as well as stiffness of the beam specimens. They also noticed the de-bond failure of CFRP bars from the concrete. However, investigation on the shear strength and behavior in future studies might as well contribute to the extending of knowledge.
- -
- Application of CFRP bars in precast concrete beam: Precast concrete structures nowadays are the preferable construction method due to their cost, quality and time effectiveness in completing such projects. The application of CFRP bars as flexural reinforcement in the precast concrete beam may enhance the performance and durability of the beam itself against an aggressive environment. It is important to study the application of CFRP bars in the precast concrete beam due to the following reasons: (i) Construction in the precast industries involve the highest quality control. Handling CFRP bars in the construction operations should be performed in a professional manner to minimize damages to the bars. CFRP bars should be handled, stored and placed accordingly; and, (ii) high strength concrete in the precast beam allows for a better combination of high-strength properties of CFRP bars. In addition, precast concrete beams are non-rectangular in shape and their flexural and shear behavior have yet to be confirmed by experimental results [6].
7. Conclusions
- -
- CFRP RC beam experiences four different types of failure modes. The first one is tension failure for under-reinforced beam, followed by tension-compression and compression failure for over-reinforced beam. In addition, another failure mode that has to be considered is the de-bonding of CFRP bars from surrounding concrete.
- -
- Over 98 rectangular CFRP RC beam specimens were mined from the works of literature and presented a comprehensive overview from the systematic review analysis. Primary factors that affect the flexural strength of CFRP RC beams were identified and quantitatively plotted to fully understand their aspect behaviors. Specifically, a factor such as reinforcement ratio has an enormous impact on the behavior and stiffness of the beam specimens for cracking and ultimate moment capacity. Another primary factor, such as concrete compressive strength had resulted in a different significant impact on CFRP RC beams pertaining to their strength limit state design. Moreover, the CFRP bar’s surface treatment plays a vital role in transferring flexural stress in the CFRP RC beam tension zone. Sufficient bond strength between CFRP bars and concrete contribute to a significant role in achieving the ultimate moment capacity of the CFRP RC beam. The combination of these primary factors has ensured the excellent performances of the CFRP RC beam at both SLS and ULS.
- -
- Predictions on the ultimate flexural moment capacity have been specified in the international design standards and as proposed by Kara and Ashour. They are summarized to ensure a better understanding of their capability. The predictions on the ultimate flexural moment capacity obtained from Kara and Ashour have more accurate results with the experimental values compared to ACI 440.1R-15, CSA S806-12.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Almusallam, A.A. Effect of degree of corrosion on the properties of reinforcing steel bars. Constr. Build. Mater. 2001, 15, 361–368. [Google Scholar] [CrossRef]
- Ndahirwa, D.; Qiao, H.; Mahame, C. Effect of Carbonation, Chloride and Sulphate Attacks on reinforced concrete: A review. Int. J. Civ. Eng. Constr. Estate Manag. 2018, 6, 59–64. [Google Scholar]
- Kumar, S.; Singh, S.; Akhtar, S. Evaluating effect of chloride attack and concrete cover on the probability of corrosion. Front. Struct. Civ. Eng. 2013, 7, 379–390. [Google Scholar] [CrossRef]
- Arockiasamy, M.; Chidambaram, S.; Amer, A.; Shahawy, M. Time-dependent deformations of concrete beams reinforced with CFRP bars. Compos. Part B Eng. 2000, 31, 577–592. [Google Scholar] [CrossRef]
- Kara, I.F.; Ashour, A.F.; Köroğlu, M.A. Flexural behavior of hybrid FRP/steel reinforced concrete beams. Compos. Struct. 2015, 129, 111–121. [Google Scholar] [CrossRef]
- ACI 440. 1R-15. ACI 440.1R-15 Guide for the Design and Construction of Structural Concrete Reinforced with Firber-Reinforced Polymer (FRP) bars. In Guide for the Design and Construction of Structural Concrete Reinforced with Firber-Reinforced Polymer (FRP) Bars (ACI440.1R-15); Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Gravina, R.J.; Smith, S.T. Flexural behaviour of indeterminate concrete beams reinforced with FRP bars. Eng. Struct. 2008, 30, 2370–2380. [Google Scholar] [CrossRef]
- Lin, X.; Zhang, Y.X. Bond-slip behaviour of FRP-reinforced concrete beams. Constr. Build. Mater. 2013, 44, 110–117. [Google Scholar] [CrossRef]
- Bocciarelli, M.; Pisani, M.A. Modified force method for the nonlinear analysis of FRP reinforced concrete beams. Compos. Struct. 2015, 131, 645–653. [Google Scholar] [CrossRef]
- Rami Hamad, J.A.; Megat Johari, M.A.; Haddad, R.H. Mechanical properties and bond characteristics of different fiber reinforced polymer rebars at elevated temperatures. Constr. Build. Mater. 2017, 142, 521–535. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, J.; Chen, W.; Fu, F.; Qian, K. Short term crack width prediction of CFRP bars reinforced coral concrete. Eng. Struct. 2020, 218, 110829. [Google Scholar] [CrossRef]
- Al-Mahmoud, F. Comprehensive Composite Materials II. In Comprehensive Composite Materials II.; Zweben, C.H., Beaumont, P., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; Volume 3, pp. 578–591. ISBN 9780128035818. [Google Scholar]
- Cousin, P.; Hassan, M.; Vijay, P.V.; Robert, M.; Benmokrane, B. Chemical resistance of carbon, basalt, and glass fibers used in FRP reinforcing bars. J. Compos. Mater. 2019, 53, 3651–3670. [Google Scholar] [CrossRef]
- Siddika, A.; Mamun, M.A.A.; Alyousef, R.; Amran, Y.H.M. Strengthening of reinforced concrete beams by using fiber-reinforced polymer composites: A review. J. Build. Eng. 2019, 25, 100798. [Google Scholar] [CrossRef]
- Amran, Y.H.M.; Alyousef, R.; Alabduljabbar, H.; Alaskar, A.; Alrshoudi, F. Properties and water penetration of structural concrete wrapped with CFRP. Results Eng. 2020, 5, 100094. [Google Scholar] [CrossRef]
- Mugahed Amran, Y.H.; Alyousef, R.; Rashid, R.S.M.; Alabduljabbar, H.; Hung, C.C. Properties and applications of FRP in strengthening RC structures: A review. Structures 2018, 16, 208–238. [Google Scholar] [CrossRef]
- Ahmed, H.Q.; Jaf, D.K.; Yaseen, S.A. Flexural strength and failure of geopolymer concrete beams reinforced with carbon fibre-reinforced polymer bars. Constr. Build. Mater. 2020, 231, 117185. [Google Scholar] [CrossRef]
- CSA S806-12, Design and Construction of Building Structures with Fibre-Reinforced; Canadian Standards Association, CSA S806: Toronto, ON, Canada, 2012.
- ISIS Canada-2007. Reinforcing Concrete Structures with Fibre Reinforced Polymers Reinforcing Concrete Structures with Fibre Reinforced Polymers; Canadian Standards Association, CSA S806: Toronto, ON, Canada, 2001; p. 151. [Google Scholar]
- Reichenbach, S.; Preinstorfer, P.; Hammerl, M.; Kromoser, B. A review on embedded fibre-reinforced polymer reinforcement in structural concrete in Europe. Constr. Build. Mater. 2021, 307, 124946. [Google Scholar] [CrossRef]
- El-Zeadani, M.; Raizal Saifulnaz, M.R.; Hejazi, F.; Mugahed Amran, Y.H.; Jaafar, M.S.; Alyousef, R.; Alrshoudi, F. Mechanics-based approach for predicting the short-term deflection of CFRP plated RC beams. Compos. Struct. 2019, 225. [Google Scholar] [CrossRef]
- Rafi, M.M.; Nadjai, A.; Ali, F.; Talamona, D. Aspects of behaviour of CFRP reinforced concrete beams in bending. Constr. Build. Mater. 2008, 22, 277–285. [Google Scholar] [CrossRef]
- El-Zeadani, M.R.; Raizal Saifulnaz, M.R.; Mugahed Amran, Y.H.; Hejazi, F.; Jaafar, M.S.; Alyousef, R.; Alabduljabbar, H. Analytical mechanics solution for measuring the deflection of strengthened RC beams using FRP plates. Case Stud. Constr. Mater. 2019, 11, e00272. [Google Scholar] [CrossRef]
- Barris, C.; Torres, L.; Miàs, C.; Vilanova, I. Design of FRP reinforced concrete beams for serviceability requirements. J. Civ. Eng. Manag. 2012, 18, 843–857. [Google Scholar] [CrossRef]
- Fatih, I.; Ashour, A.F. Flexural performance of FRP reinforced concrete beams. Compos. Struct. 2012, 94, 1616–1625. [Google Scholar] [CrossRef] [Green Version]
- Al-Nini, A.; Nikbakht, E.; Syamsir, A.; Shafiq, N.; Mohammed, B.S.; Al-Fakih, A.; Al-Nini, W.; Amran, Y.H.M. Flexural behavior of double-skin steel tube beams filled with fiber-reinforced cementitious composite and strengthened with CFRP sheets. Materials 2020, 13, 3064. [Google Scholar] [CrossRef] [PubMed]
- Rahim, N.I.; Mohammed, B.S.; Al-Fakih, A.; Wahab, M.M.A.; Liew, M.S.; Anwar, A.; Mugahed Amran, Y.H. Strengthening the structural behavior of web openings in RC deep beam using CFRP. Materials 2020, 13, 2804. [Google Scholar] [CrossRef] [PubMed]
- El-Zeadani, M.; Saifulnaz, M.R.R.; Mugahed Amran, Y.H.; Hejazi, F.; Jaafar, M.S.; Alyousef, R.; Alabduljabbar, H. Flexural strength of FRP plated RC beams using a partial-interaction displacement-based approach. Structures 2019, 22, 405–420. [Google Scholar] [CrossRef]
- El-Zeadani, M.; Rashid, R.S.M.; Amran, M.Y.H.; Swi, M.I. Effect of the plate bondstress-slip property on the flexural strength of FRP Plated RC beams using a displacement-based approach. SN Appl. Sci. 2020, 2, 1–23. [Google Scholar] [CrossRef]
- El-Zeadani, M.; Raizal Saifulnaz, M.R.; Amran, M. Full-range bondstress-slip model for externally bonded FRP plates including a frictional component. Compos. Struct. 2021, 262, 113372. [Google Scholar] [CrossRef]
- Hsu, T.T.C.; Mo, Y.L. Unified Theory of Concrete, 1st ed.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2010; ISBN 9780470688748. [Google Scholar]
- El-salakawy, E.F.; Kassem, C.; Benmokrane, B. Flexural behaviour of concrete beams reinforced with carbon FRP composite bars. In Proceedings of the 4th Structural Specialty Conference of the Canadian Society for Civil Engineering, Montreal, QC, Canada, 5–8 June 2002; pp. 173–190. [Google Scholar]
- Newhook, J.; Ghali, A.; Tadros, G. Cracking and Deformability of Concrete Flexural Sections with Fiber Reinforced Polymer. J. Struct. Eng. 2002, 128, 1195–1201. [Google Scholar] [CrossRef]
- Newhook, J.; Ghali, A.; Tadros, G. Concrete flexural members reinforced with fiber reinforced polymer: Design for cracking and deformability. Can. J. Civ. Eng. 2002, 29, 125–134. [Google Scholar] [CrossRef]
- Thiagarajan, G. Experimental and Analytical Behavior of Carbon Fiber-Based Rods as Flexural Reinforcement. J. Compos. Constr. 2003, 7, 64–72. [Google Scholar] [CrossRef]
- Ashour, A.F.; Family, M. Tests of concrete flanged beams reinforced with CFRP bars. Mag. Concr. Res. 2006, 58, 627–639. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Belarbi, A. Ductility characteristics of fiber-reinforced-concrete beams reinforced with FRP rebars. Constr. Build. Mater. 2011, 25, 2391–2401. [Google Scholar] [CrossRef]
- Kassem, C.; Farghaly, A.S.; Benmokrane, B. Evaluation of Flexural Behavior and Serviceability Performance of Concrete Beams Reinforced with FRP Bars. J. Compos. Constr. 2011, 15, 682–695. [Google Scholar] [CrossRef]
- Sun, Z.Y.; Yang, Y.; Qin, W.H.; Ren, S.T.; Wu, G. Experimental study on flexural behavior of concrete beams reinforced by steel-fiber reinforced polymer composite bars. J. Reinf. Plast. Compos. 2012, 31, 1737–1745. [Google Scholar] [CrossRef]
- Dong, H.; Zhou, W.; Wang, Z. Flexural performance of concrete beams reinforced with FRP bars grouted in corrugated sleeves. Compos. Struct. 2019, 215, 49–59. [Google Scholar] [CrossRef]
- Zhang, B.; Zhu, H.; Wu, G.; Wang, Q.; Li, T. Improvement of bond performance between concrete and CFRP bars with optimized additional aluminum ribs anchorage. Constr. Build. Mater. 2020, 241, 118012. [Google Scholar] [CrossRef]
- Saheed, S.; Amran, Y.M.; El-Zeadani, M.; Aziz, F.N.A.; Fediuk, R.; Alyousef, R.; Alabduljabbar, H. Structural behavior of out-of-plane loaded precast lightweight EPS-foam concrete C-shaped slabs. J. Build. Eng. 2021, 33, 101597. [Google Scholar] [CrossRef]
- Al-Sunna, R.; Pilakoutas, K.; Hajirasouliha, I.; Guadagnini, M. Deflection behaviour of FRP reinforced concrete beams and slabs: An experimental investigation. Compos. Part B Eng. 2012, 43, 2125–2134. [Google Scholar] [CrossRef]
- Ahmed, H.Q.; Jaf, D.K.; Yaseen, S.A. Comparison of the Flexural Performance and Behaviour of Fly-Ash-Based Geopolymer Concrete Beams Reinforced with CFRP and GFRP Bars. Adv. Mater. Sci. Eng. 2020, 2020, 3495276. [Google Scholar] [CrossRef] [Green Version]
- Zaher Elsayed, A.A.; Ahmed, M.M.; Salaheldin, H.; Hassan, M. Behavior of beams reinforced with different types of bars from glass fiber reinforced polymer (GFRP), Carbon fiber Reinforced Polymer (CFRP) and high tensile steel (HTS) Under Static Load. IOSR J. Mech. Civ. Eng. 2015, 12, 66–97. [Google Scholar] [CrossRef]
- Tsiatas, G.; Taggart, D.; Wilson, A.; Nair, A.; Kim, T. Investigation of CFRP Reinforced Concrete Interfacial Load Transfer. In Proceedings of the TRB 2003 Annual Meeting, Washington, DC, USA, 12–16 January 2002. [Google Scholar]
- Wang, L.; Zhang, J.; Huang, C.; Fu, F. Comparative Study of Steel-FRP, FRP and Steel-Reinforced Coral Concrete Beams in Their Flexural Performance. Materials 2020, 13, 97. [Google Scholar] [CrossRef]
- Yang, J.M.; Min, K.H.; Shin, H.O.; Yoon, Y.S. Effect of steel and synthetic fibers on flexural behavior of high-strength concrete beams reinforced with FRP bars. Compos. Part B Eng. 2012, 43, 1077–1086. [Google Scholar] [CrossRef]
- Grace, B.N.F.; Soliman, A.K.; Saleh, K.R. Behavior and Ductility of Simple and Continuous FRP Reinforced Beams. J. Compos. Constr. 1998, 2, 186–194. [Google Scholar] [CrossRef]
- Abdalla, H.A. Evaluation of deflection in concrete members reinforced with fibre reinforced polymer (FRP) bars. Compos. Struct. 2002, 56, 63–71. [Google Scholar] [CrossRef]
- Du, J.; Wang, C.; Qiao, M.; Chang, X.; Chen, H. Flexural behavior of concrete beams reinforced by CFRP bars. 2010 Int. Conf. Mech. Autom. Control Eng. 2010, 2010, 1060–1063. [Google Scholar] [CrossRef]
- Siddika, A.; Shojib, M.H.H.; Hossain, M.M.; Hossain, M.I.; Mamun, M.A.A.; Alyousef, R.; Amran, Y.H.M. Flexural performance of wire mesh and geotextile-strengthened reinforced concrete beam. SN Appl. Sci. 2019, 1, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Pour, S.M.; Alam, M.S.; Milani, A.S. Improved Bond Equations for Fiber-Reinforced Polymer Bars in Concrete. Materials 2016, 2016, 737. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cosenza, E.; Manfredi, G.; Realfonzo, R. Development length of FRP straight rebars. Compos. Part B Eng. 2002, 33, 493–504. [Google Scholar] [CrossRef]
- Hao, Q.; Wang, Y.; He, Z.; Ou, J. Bond strength of glass fiber reinforced polymer ribbed rebars in normal strength concrete. Constr. Build. Mater. 2009, 23, 865–871. [Google Scholar] [CrossRef]
- Baena, M.; Torres, L.; Turon, A.; Barris, C. Experimental study of bond behaviour between concrete and FRP bars using a pull-out test. Compos. Part B Eng. 2009, 40, 784–797. [Google Scholar] [CrossRef]
- Okelo, R.; Yuan, R.L. Bond Strength of Fiber Reinforced Polymer Rebars in Normal Strength Concrete. Constr. Build. Mater. 2005, 9, 203–213. [Google Scholar] [CrossRef]
- Solyom, S.; Balázs, G.L. Bond of FRP bars with different surface characteristics. Constr. Build. Mater. 2020, 264, 119839. [Google Scholar] [CrossRef]
- Rafi, M.M.; Nadjai, A.; Ali, F. Experimental testing of concrete beams reinforced with carbon FRP bars. J. Compos. Mater. 2007, 41, 2657–2673. [Google Scholar] [CrossRef]
- Ceroni, F.; Cosenza, E.; Gaetano, M.; Pecce, M. Durability issues of FRP rebars in reinforced concrete members. Cem. Concr. Compos. 2006, 28, 857–868. [Google Scholar] [CrossRef]
- Lee, J.Y.; Kim, T.Y.; Kim, T.J.; Yi, C.K.; Park, J.S.; You, Y.C.; Park, Y.H. Interfacial bond strength of glass fiber reinforced polymer bars in high-strength concrete. Compos. Part B Eng. 2008, 39, 258–270. [Google Scholar] [CrossRef]
- Antonietta, M.A.; Marianovella Leone, M.P. Bond Performances of FRP Rebars-Reinforced Concrete. J. Mater. Civ. Eng. 2007, 19, 205–213. [Google Scholar] [CrossRef]
- Amnon Katzl Bond to Concrete of FRP Rebars and Tendons. Compos. Constr. 2001, 1, 121–129.




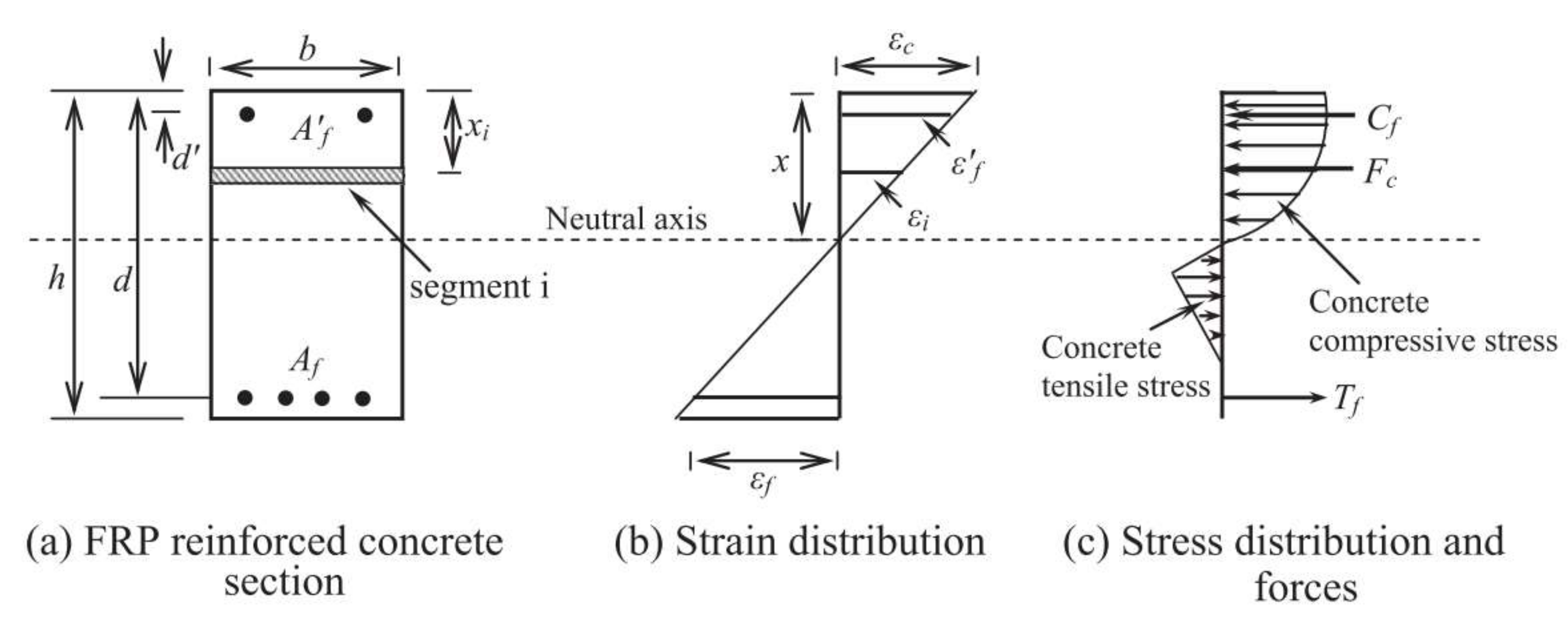
| Compartment | ACI 440.1R-15 [6] | CSA S806-12 [18] | Kara and Ashour [25] |
|---|---|---|---|
| Strain | Strain in concrete and CFRP reinforcement is proportional to the distance from the neutral axis | ||
| Concrete compressive strain | 0.0030 | 0.0035 | 0.0035 |
| Concrete tensile strength | Ignored | Ignored | Accounted |
| Bond strength of CFRP to concrete | Perfect bond | Perfect bond | Perfect bond |
| Strength limit state | Over-reinforced and under-reinforced | Over-reinforced | Over-reinforced and under-reinforced |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bakar, M.B.C.; Muhammad Rashid, R.S.; Amran, M.; Saleh Jaafar, M.; Vatin, N.I.; Fediuk, R. Flexural Strength of Concrete Beam Reinforced with CFRP Bars: A Review. Materials 2022, 15, 1144. https://doi.org/10.3390/ma15031144
Bakar MBC, Muhammad Rashid RS, Amran M, Saleh Jaafar M, Vatin NI, Fediuk R. Flexural Strength of Concrete Beam Reinforced with CFRP Bars: A Review. Materials. 2022; 15(3):1144. https://doi.org/10.3390/ma15031144
Chicago/Turabian StyleBakar, Mohd Basri Che, Raizal Saifulnaz Muhammad Rashid, Mugahed Amran, Mohd Saleh Jaafar, Nikolai Ivanovicn Vatin, and Roman Fediuk. 2022. "Flexural Strength of Concrete Beam Reinforced with CFRP Bars: A Review" Materials 15, no. 3: 1144. https://doi.org/10.3390/ma15031144
APA StyleBakar, M. B. C., Muhammad Rashid, R. S., Amran, M., Saleh Jaafar, M., Vatin, N. I., & Fediuk, R. (2022). Flexural Strength of Concrete Beam Reinforced with CFRP Bars: A Review. Materials, 15(3), 1144. https://doi.org/10.3390/ma15031144