Complete Stress–Strain Relations of Early-Aged Cementitious Grout under Compression: Experimental Study and Constitutive Model
Abstract
:1. Introduction
2. Experimental Program
2.1. Materials
2.2. Testing Methods
3. Test Results and Discussion
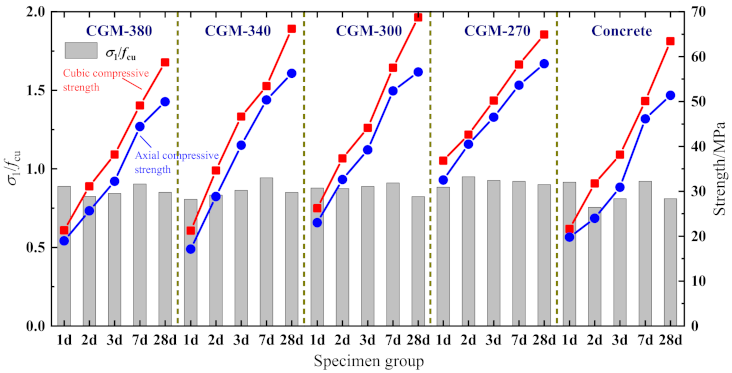
3.1. Cubic Compressive Strength
3.2. Uniaxial Compression Test Results
3.2.1. Failure Modes
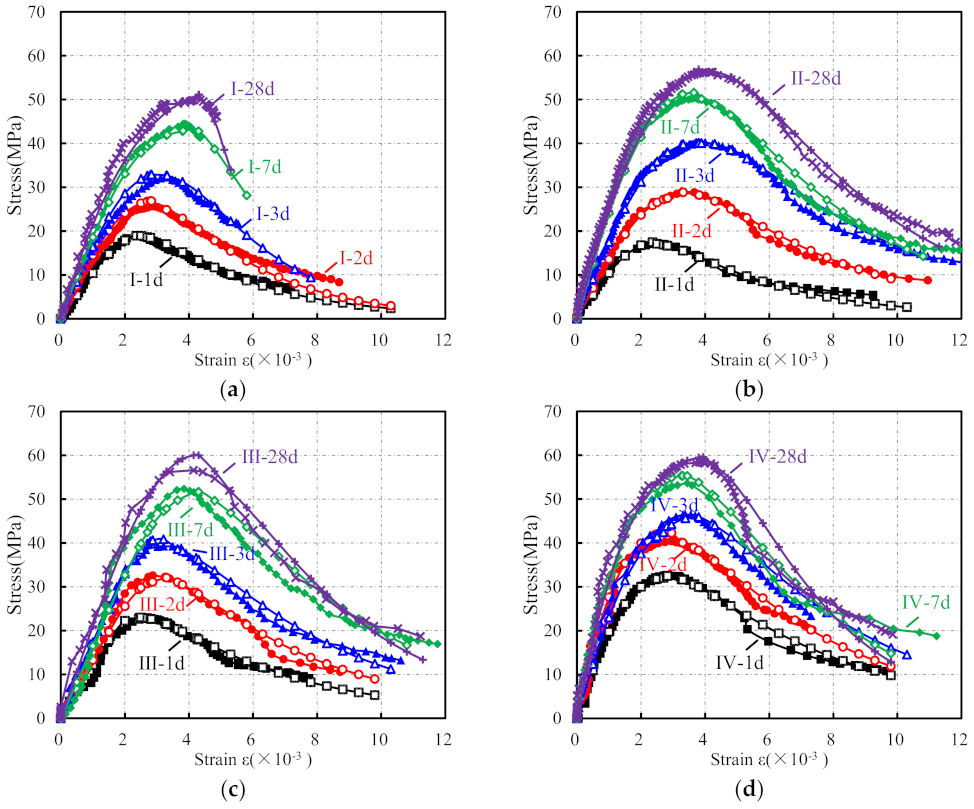
3.2.2. Stress–Strain Curves
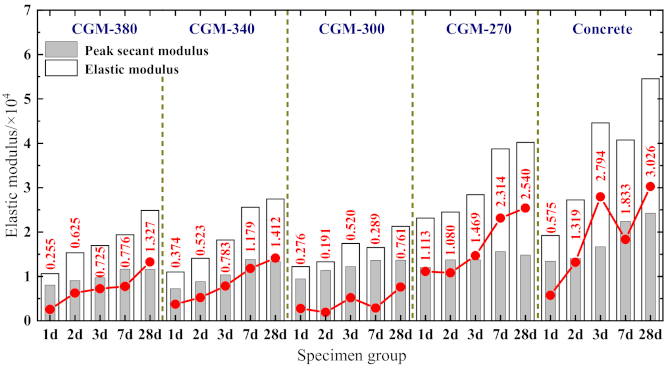
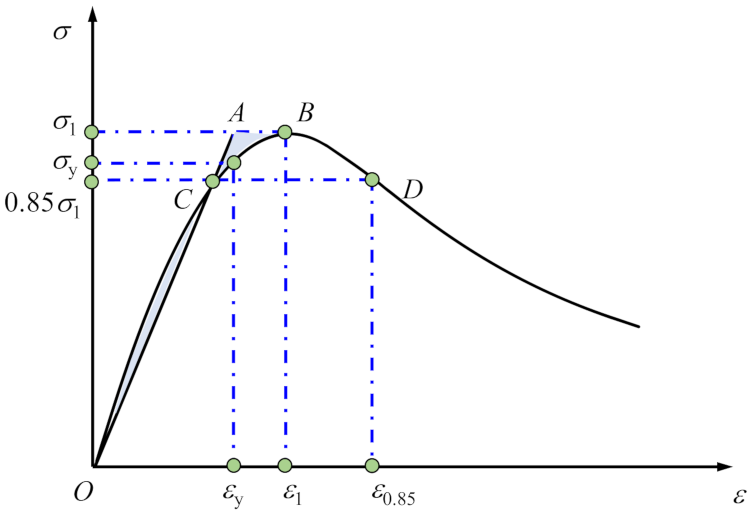
3.2.3. Characteristic Parameters of Stress–Strain Curves
- 1.
- Peak stress σ1
- 2.
- Peak strain ε1
- 3.
- Elastic modulus Ec
- 4.
- Strain ductility coefficient β
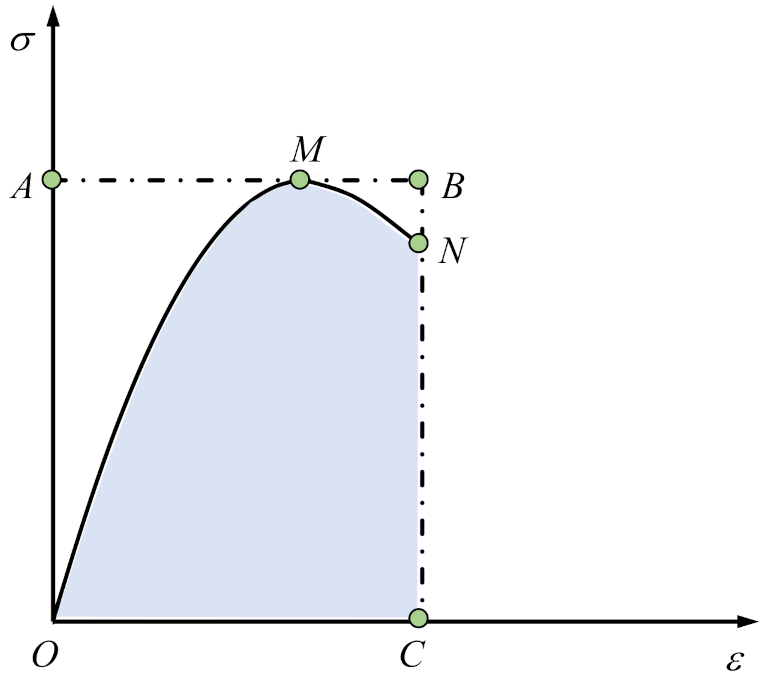
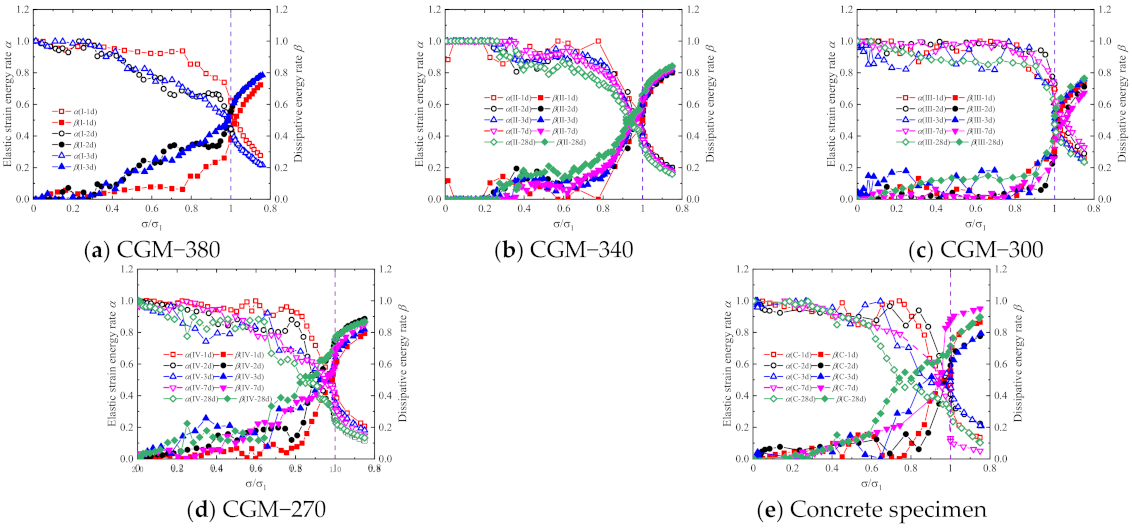
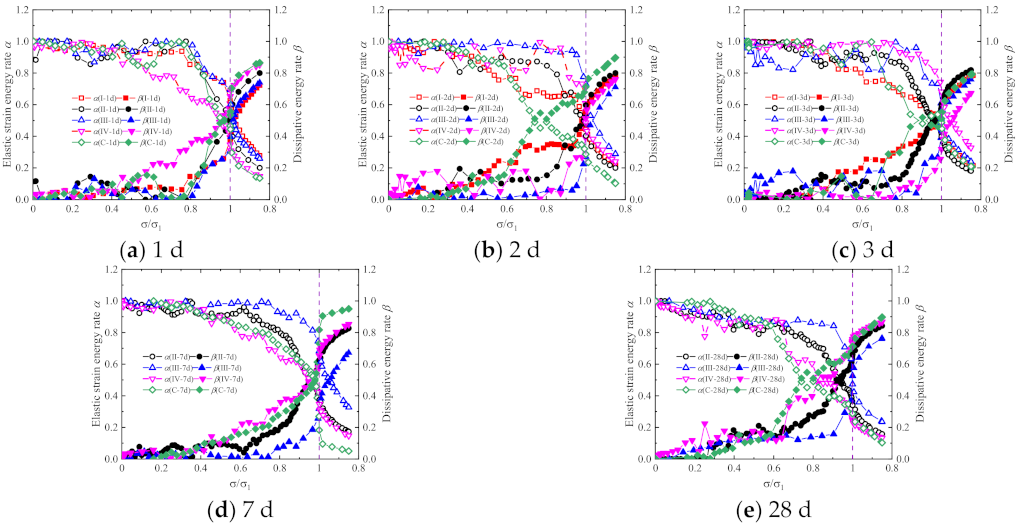
3.2.4. Analysis of Energy Evolution Law
- 1.
- Energy-dissipation coefficient ηe
- 2.
- Energy evolution law
4. Stress–Strain Constitutive Relationships
4.1. Ascending Branches
4.2. Descending Branches
5. Conclusions
- 1.
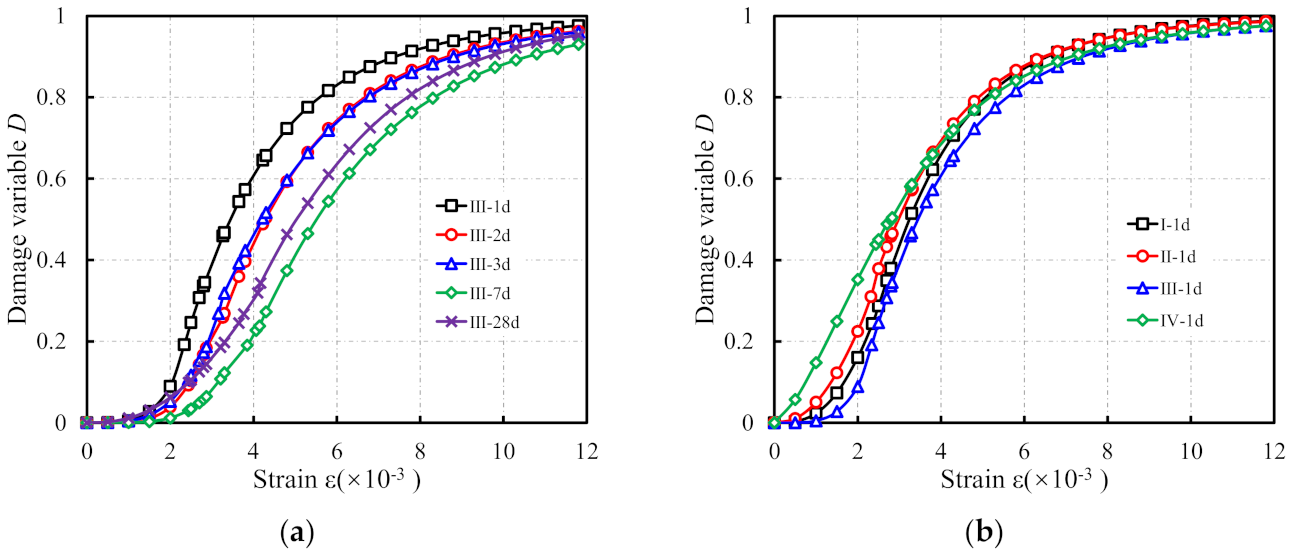
- The prism specimen of cementitious grout experienced four main stages under the uniaxial pressure: elastic deformation, stable crack development, unstable crack development, and descending, and the deformation characteristics of each group are different at each stage. The brittleness characteristics of the specimens were more obvious with the increasing age. For the specimens with ages of 3 d or more, there are fragments breaking out when the specimens are damaged, accompanied by a large cracking sound. Compared with the control specimens, the cementitious grout specimens had relatively short crack-development stages, and had poor integrity after the failure. Moreover, the failure surface of the cementitious grout specimens was flat and smooth.
- 2.
- With an increase in the specimen age, the peak stress, peak strain, ultimate strain, elastic modulus, and peak secant modulus, along with the strain ductility coefficient and energy-dissipation coefficient increased to varying degrees, the brittleness of the specimens became obvious. Comparing the uniaxial compression characteristics of specimens with the same age reveals that the peak stress, peak strain, and ultimate strain of the cementitious grout specimens were greater than that of the concrete specimens; the elastic modulus and peak secant modulus of the specimens were less than that of concrete specimens; and the strain ductility coefficient and energy-dissipation coefficient shows no consistent conclusions with respect to the material type.
- 3.
- The results of the energy evolution analysis show that the elastic strain energy rate decreased while the dissipation energy rate increased with the increasing loading. Moreover, with the increase in age, the decrease rate of the elastic strain rate and the increase rate of the dissipated energy rate gradually decrease. Comparing the energy evolution curves of specimens with different types of cementitious grouts shows that the elastic strain rate and dissipated energy rate of the CGM-270 specimen and the control specimens are greater than that of other specimens, and the decrease rate of the elastic strain rate are less than that of other specimens.
- 4.
- Considering the effects of specimen age on the peak stress, peak strain, and elastic modulus, the calculation models of the peak stress, peak strain, and elastic modulus were established based on the experimental data. Moreover, based on the statistical damage theory, together with the characteristics of cementitious grouts, a statistically stochastic damage constitutive model suitable for early-aged cementitious grouts was established. Good agreement was observed between the calculated curves and the test results, indicating that the proposed stress–strain curve calculation model can accurately describe the deformation characteristics of early-aged cementitious grouts under uniaxial compression.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dou, J.L.; Dou, J.F.; Guo, Y.J. Researching on a new grouting material and its engineering application. Adv. Mater. Res. 2015, 1088, 544–548. [Google Scholar] [CrossRef]
- Shannag, M.J. High-performance cementitious grouts for structural repair. Cem. Concr. Res. 2002, 32, 803–808. [Google Scholar] [CrossRef]
- Liu, J.H.; Song, S.M. Research on self-shrinkage of high performance cement matrix grouting material. J. Wuhan Univ. Technol. 2006, 28, 36–38. (In Chinese) [Google Scholar]
- Li, Q.T.; Liu, L.J.; Huang, Z.H.; Yuan, G.L. Degradation of the elastic modulus of cement-based grouting material with early ages after fire. Constr. Build. Mater. 2018, 187, 510–518. [Google Scholar] [CrossRef]
- Li, Q.T.; Liu, L.J.; Huang, Z.H.; Yuan, G.L. Residual compressive strength of cement-based grouting material with early ages after fire. Constr. Build. Mater. 2017, 138, 316–325. [Google Scholar] [CrossRef]
- Yuan, G.L.; Li, Q.; Li, Q.T.; Zhang, Q. Degradation of compressive strength of high-performance cementitious grouting material after exposure to high temperature. J. Build. Mater. 2014, 17, 470–474. (In Chinese) [Google Scholar]
- Liu, Y.X.; Chi, Y.Y.; Tian, W.; Zhang, J.H. Effect of different expanders on properties of cement-based grouting material. J. Build. Mater. 2021, 1–13. Available online: http://kns.cnki.net/kcms/detail/31.1764.TU.20210514.1112.024.html (accessed on 14 May 2021). (In Chinese).
- Liu, Y.X.; Li, X.G.; Zhang, C.M.; Lv, B.N. Properties of iron tailing sand cement based grouting material. J. Build. Mater. 2019, 22, 538–544. (In Chinese) [Google Scholar]
- Ye, X.; Wu, W.X.; Hou, W.H.; Lei, S.; Zhou, Z. Influence of expander on volume stability of high-strength grouting material. J. Build. Mater. 2018, 21, 950–955. (In Chinese) [Google Scholar]
- Wang, L.X.; Wang, X.S. Experimental study on the performance of high performance cementitious grout. Low Temp. Archit. Technol. 2012, 8, 9–10. (In Chinese) [Google Scholar]
- Wu, Y.; Wang, K.; Yang, X.J.; Wei, B. Experimental study on basic mechanical properties of cementitious grout. Build. Struct. 2014, 44, 95–98. (In Chinese) [Google Scholar]
- Wang, X.S.; Li, S.L.; Wu, Y. Experimental study of mechanical properties and deformability of pisolite grouting material. Ind. Constr. 2008, 9, 82–84. (In Chinese) [Google Scholar]
- Chen, D.C.; Lin, Y.C.; Guo, J.B.; Li, L.R.; Peng, B. Experimental study on testing the early strength of grouting material by rebound method. J. Railw. Sci. Eng. 2020, 17, 66–72. (In Chinese) [Google Scholar]
- Chen, D.C.; Li, L.R.; Peng, B.; Lin, Y.C. Experimental study on influence of different test molds on early compressive strength of grouting materials. J. Hunan Univ. 2021, 48, 73–79. (In Chinese) [Google Scholar]
- Wu, Y.; Yang, X.Q.; Wang, K.; He, T.H. Experimental study on the stress-strain curve of cementitious grout under uniaxial compression. Ind. Constr. 2014, 44, 909–913. (In Chinese) [Google Scholar]
- GB/T 50448–2015. Technical Code for Application of Cementitious Grout; China Architecture and Building Press: Beijing, China, 2015. [Google Scholar]
- Hu, X.P.; Peng, G.; Niu, D.T.; Wu, X.; Zhang, L. Bond behavior between deformed steel bars and cementitious grout. Constr. Build. Mater. 2020, 262, 120810. [Google Scholar] [CrossRef]
- GB/T 50081-2019. Standard for Test Method of Mechanical Properties on Ordinary Concrete; China Architecture and Building Press: Beijing, China, 2019. [Google Scholar]
- CEB-FIP. Model Code for Concrete Structures; CEB Bulletin d’Information; Comite Euro International du Beton: Lausanne, Switzerland, 1993. [Google Scholar]
- Dong, J.J. Development and Properties of High Performance Cementitious Grout for Coupler; Hefei University of Technology: Hefei, China, 2016. (In Chinese) [Google Scholar]
- Wang, F.; Liu, H.Y.; Wang, C.J. Effects of grout age on mechanical behavior of grout sleeve splicing. J. Shandong Univ. Technol. 2020, 34, 74–78. (In Chinese) [Google Scholar]
- GB 50010–2010. Code for Design of Concrete Structures; China Architecture and Building Press: Beijing, China, 2010. [Google Scholar]
- Guo, Z.H. Principle and Analysis of Reinforced Concrete; Tsinghua University Press: Beijing, China, 2003; pp. 15–18. (In Chinese) [Google Scholar]
- Wang, P.T. Stress-strain curves of normal and lightweight concrete in compression. J. Proc. 1978, 75, 603–611. [Google Scholar]
- Xu, M.; Wang, T.; Chen, Z.F. Experimental research on uniaxial compressive stress-strain relationship of recycled concrete after high temperature. J. Build. Struct. 2015, 36, 158–164. (In Chinese) [Google Scholar]
- ACI Committee 209. Prediction of Creep, Shrinkage, and Temperature Effects in Concrete Structures; American Concrete Institute: NewYork, NY, USA, 2008. [Google Scholar]
- Liu, X.H.; Hao, Q.J.; Hu, A.K.; Zheng, Y. Study on determination of uniaxial characteristic stress of coal rock under quasi-static strain rate. Chin. J. Rock Mech. Eng. 2020, 39, 2038–2046. (In Chinese) [Google Scholar]
- Xie, H.P.; Ju, Y.; Li, L.Y. Criteria for strength and structural failure of rocks based on energy dissipation and energy release principles. Chin. J. Rock Mech. Eng. 2005, 24, 2004–2010. (In Chinese) [Google Scholar]
- Chen, Z.P.; Zhou, C.H.; Chen, Y.L.; Huang, J. Mechanical property and strain-stress constitutive relationship of recycled pebble aggregate concrete. J. Basic Sci. Eng. 2014, 22, 763–774. (In Chinese) [Google Scholar]
- Kachanov, M.; Montagut, E. Interaction of a crack with certain microcrack arrays. Eng. Fract. Mech. 1986, 25, 625–636. [Google Scholar] [CrossRef]
- Kandarpa, S.; Kirkner, D.J.; Spencer, B.F. Stochastic damage model for brittle materials subjected to monotonic loading. J. Eng. Mech. 1996, 122, 788–795. [Google Scholar] [CrossRef]
- Lemaitre, J. How to use damage mechanics. Nucl. Eng. Des. 1984, 80, 233–245. [Google Scholar] [CrossRef]
- Li, J.; Ren, X.D. Stochastic damage model for concrete based on energy equivalent strain. Int. J. Solids Struct. 2009, 46, 2407–2419. [Google Scholar] [CrossRef] [Green Version]
- Benallal, A.; Billardon, R.; Lemaitre, J. Failure analysis of structures by continuum damage mechanics. In Fracture 84; Pergamon: Oxford, UK, 1984; pp. 3669–3676. [Google Scholar]
- Wu, Z.; Zhang, C.J. Investigation of rock damage model and its mechanical behaviour. Chin. J. Rock Mech. Eng. 1996, 15, 55–61. (In Chinese) [Google Scholar]
- Liu, X.; Wu, T.; Liu, Y. Stress-strain relationship for plain and fibre-reinforced lightweight aggregate concrete. Constr. Build. Mater. 2019, 225, 256–272. [Google Scholar] [CrossRef]
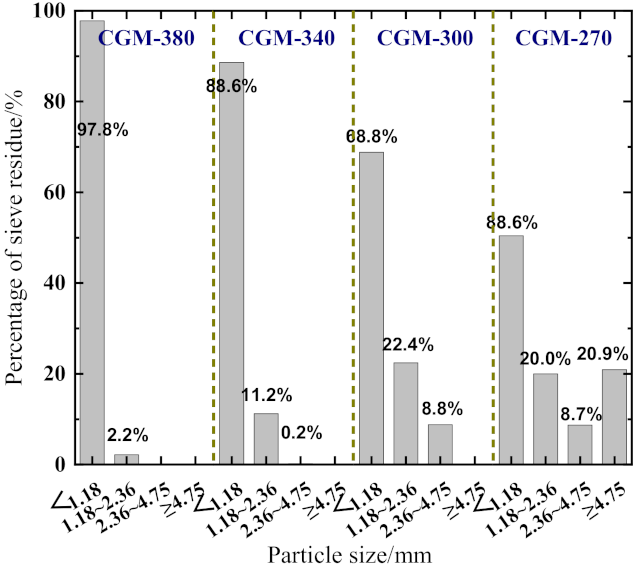
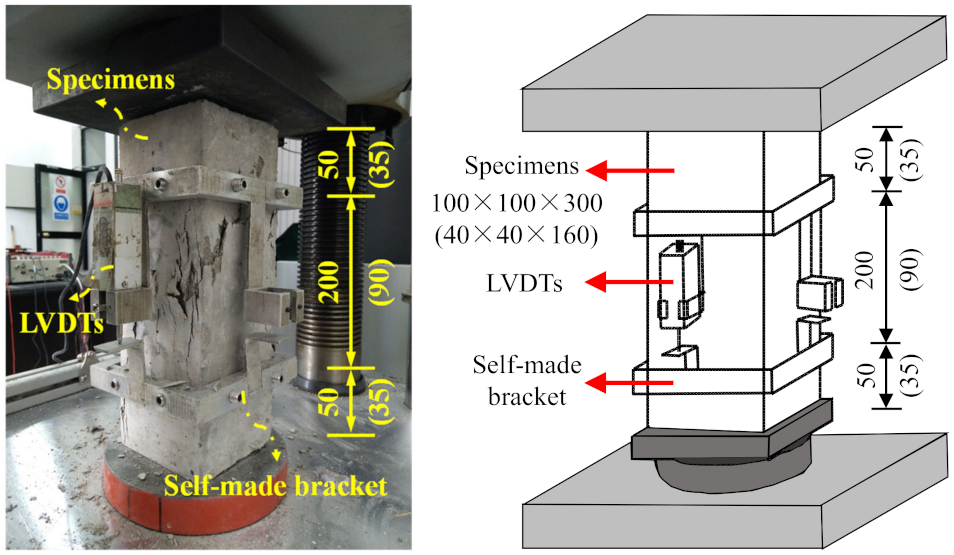
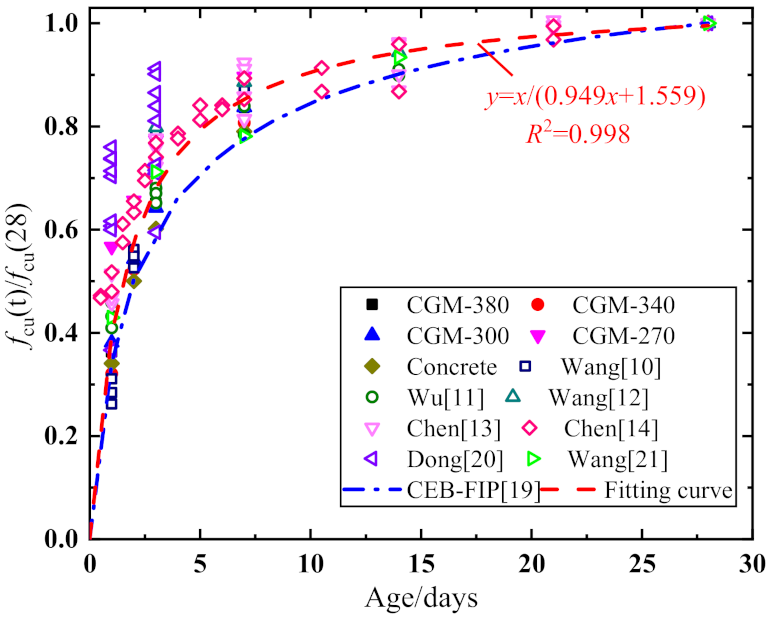

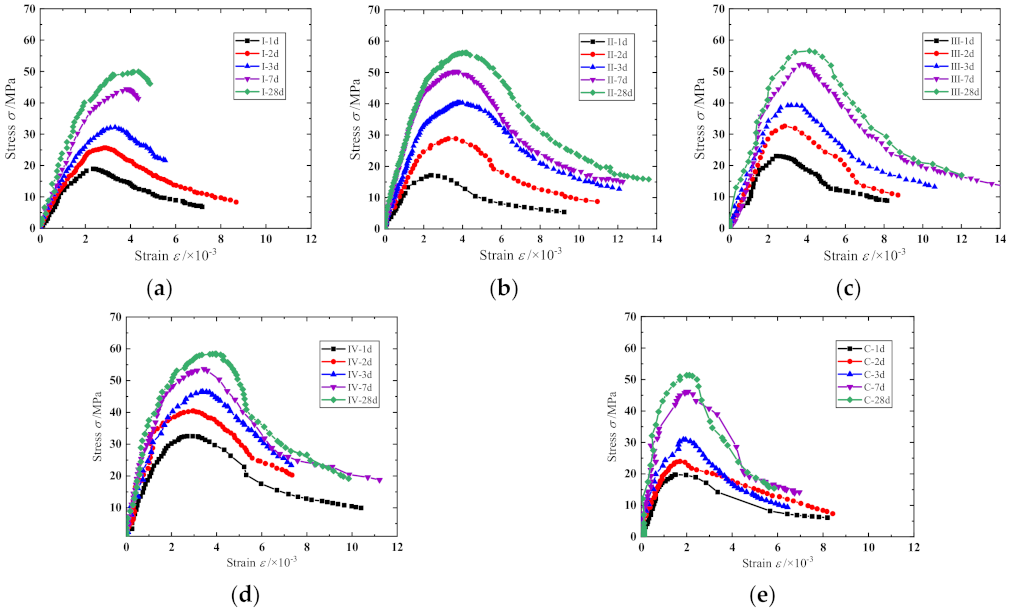




| Indexes | CGM−380 | CGM−340 | CGM−300 | CGM−270 | ||
|---|---|---|---|---|---|---|
| Flow cone fluidity/s | Initial values | Limit values | ≤35 | - | - | - |
| Test results | 33.57 | - | - | - | ||
| 30 min | Limit values | ≤50 | - | - | - | |
| Test results | 49.89 | - | - | - | ||
| Truncated cone fluidity/mm | Initial values | Limit values | - | ≥340 | ≥290 | ≥650 |
| Test results | - | 383 | 342 | 802 | ||
| 30 min | Limit values | - | ≥310 | ≥260 | ≥550 | |
| Test results | - | 356 | 294 | 582 | ||
| Vertical expansion rate/% | 3 h | Limit values | 0.1~3.5 | |||
| Test results | 0.13 | 0.41 | 0.15 | 0.16 | ||
| Discrepancies between 24 h and 3 h | Limit values | 0.02~0.50 | ||||
| Test results | 0.02 | 0.16 | 0.08 | 0.08 | ||
| Compressive strength/MPa | 1 day | Limit values | ≥15 | ≥20 | ||
| Test results | 18.9 | 26.4 | 27.9 | 39.7 | ||
| 3 days | Limit values | ≥30 | ≥40 | |||
| Test results | 34.7 | 42.8 | 48.6 | 47.1 | ||
| 28 days | Limit values | ≥50 | ≥60 | |||
| Test results | 59.3 | 65.7 | 69.1 | 62.6 | ||
| Ingredient/kg∙m−3 | 28 d Compressive Strength/MPa | ||||
|---|---|---|---|---|---|
| Cement | Sand | Crushed Stone | Water | Superplasticizer | |
| 500 | 648 | 1152 | 150 | 2.50 | 63.4 |
| Material Type | p | q | c | |||
|---|---|---|---|---|---|---|
| m1 | n1 | m2 | n2 | m3 | n3 | |
| CGM−380 | −0.535 | 2.877 | 0.603 | 3.668 | −0.146 | 0.722 |
| CGM−340 | −0.304 | 2.299 | 0.475 | 4.028 | −0.040 | 0.761 |
| CGM−300 | −0.599 | 4.972 | 0.775 | 3.530 | −0.066 | 0.811 |
| CGM−270 | −0.136 | 1.441 | 0.138 | 3.569 | −0.092 | 0.831 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, G.; Hu, X.; Niu, D.; Zhong, S. Complete Stress–Strain Relations of Early-Aged Cementitious Grout under Compression: Experimental Study and Constitutive Model. Materials 2022, 15, 1238. https://doi.org/10.3390/ma15031238
Peng G, Hu X, Niu D, Zhong S. Complete Stress–Strain Relations of Early-Aged Cementitious Grout under Compression: Experimental Study and Constitutive Model. Materials. 2022; 15(3):1238. https://doi.org/10.3390/ma15031238
Chicago/Turabian StylePeng, Gang, Xiaopeng Hu, Ditao Niu, and Shuai Zhong. 2022. "Complete Stress–Strain Relations of Early-Aged Cementitious Grout under Compression: Experimental Study and Constitutive Model" Materials 15, no. 3: 1238. https://doi.org/10.3390/ma15031238
APA StylePeng, G., Hu, X., Niu, D., & Zhong, S. (2022). Complete Stress–Strain Relations of Early-Aged Cementitious Grout under Compression: Experimental Study and Constitutive Model. Materials, 15(3), 1238. https://doi.org/10.3390/ma15031238






