Charge Transport Characteristics of Molecular Electronic Junctions Studied by Transition Voltage Spectroscopy
Abstract
:1. Introduction
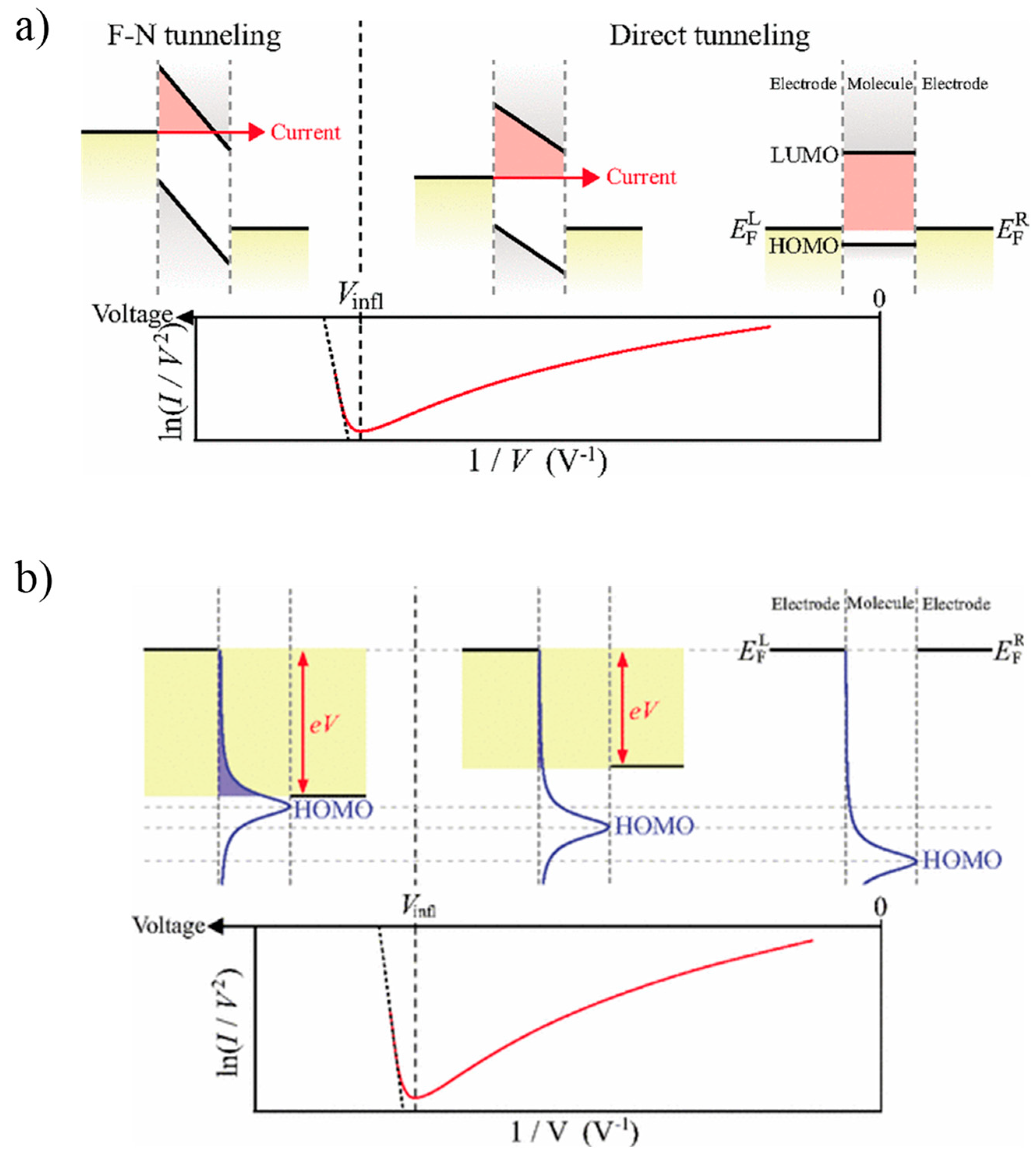
2. Fundamentals of Transition Voltage Spectroscopy
2.1. Initial Tunneling Barrier Conjecture
2.2. Coherent Molecular Transport Model
2.3. Single-Level Model Analysis
3. Applications of Transition Voltage Spectroscopy in Molecular Junctions
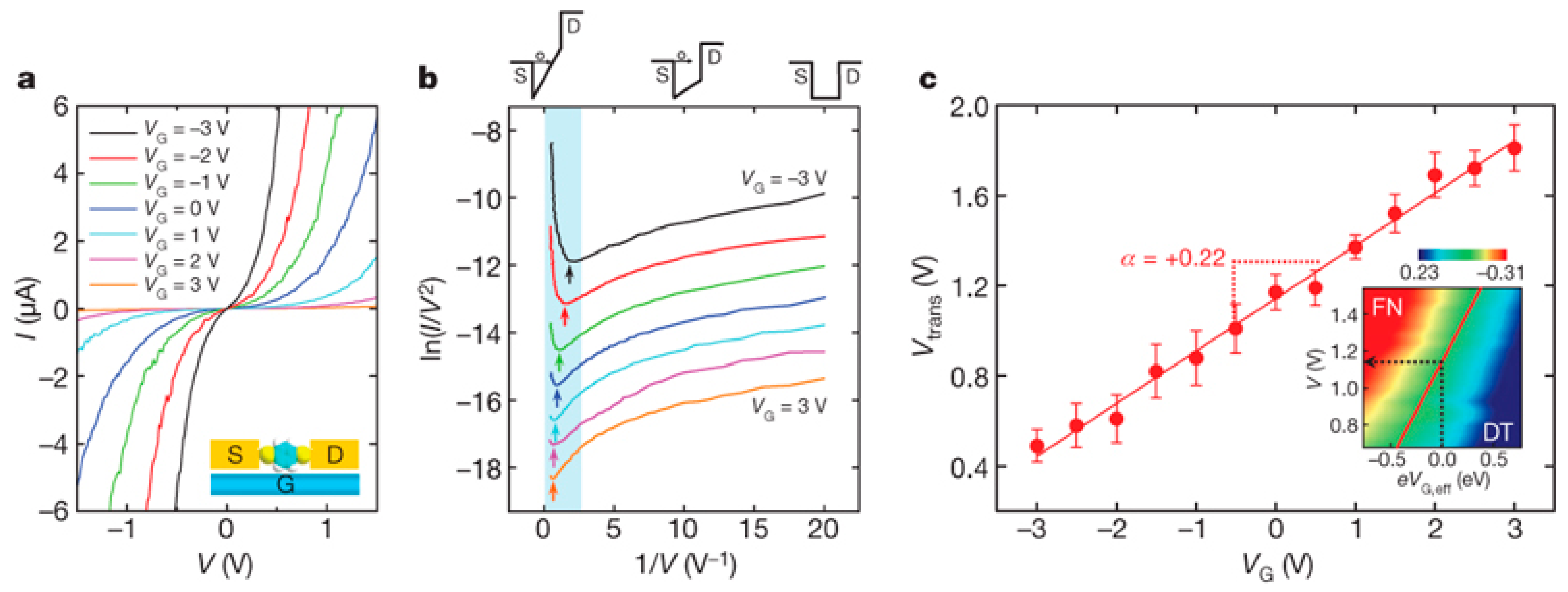
3.1. Molecular Transistor with Three-Terminal Electrodes
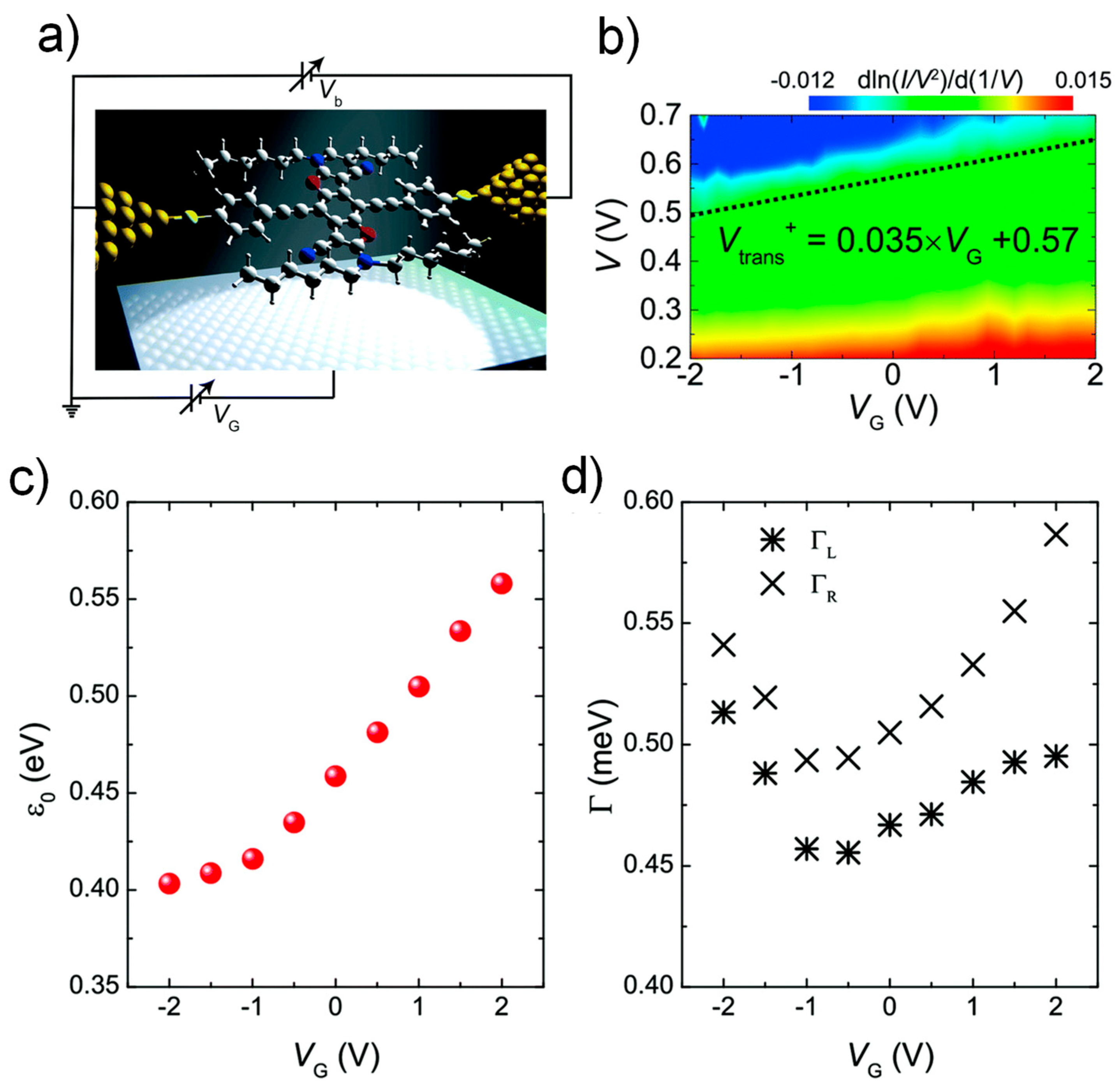
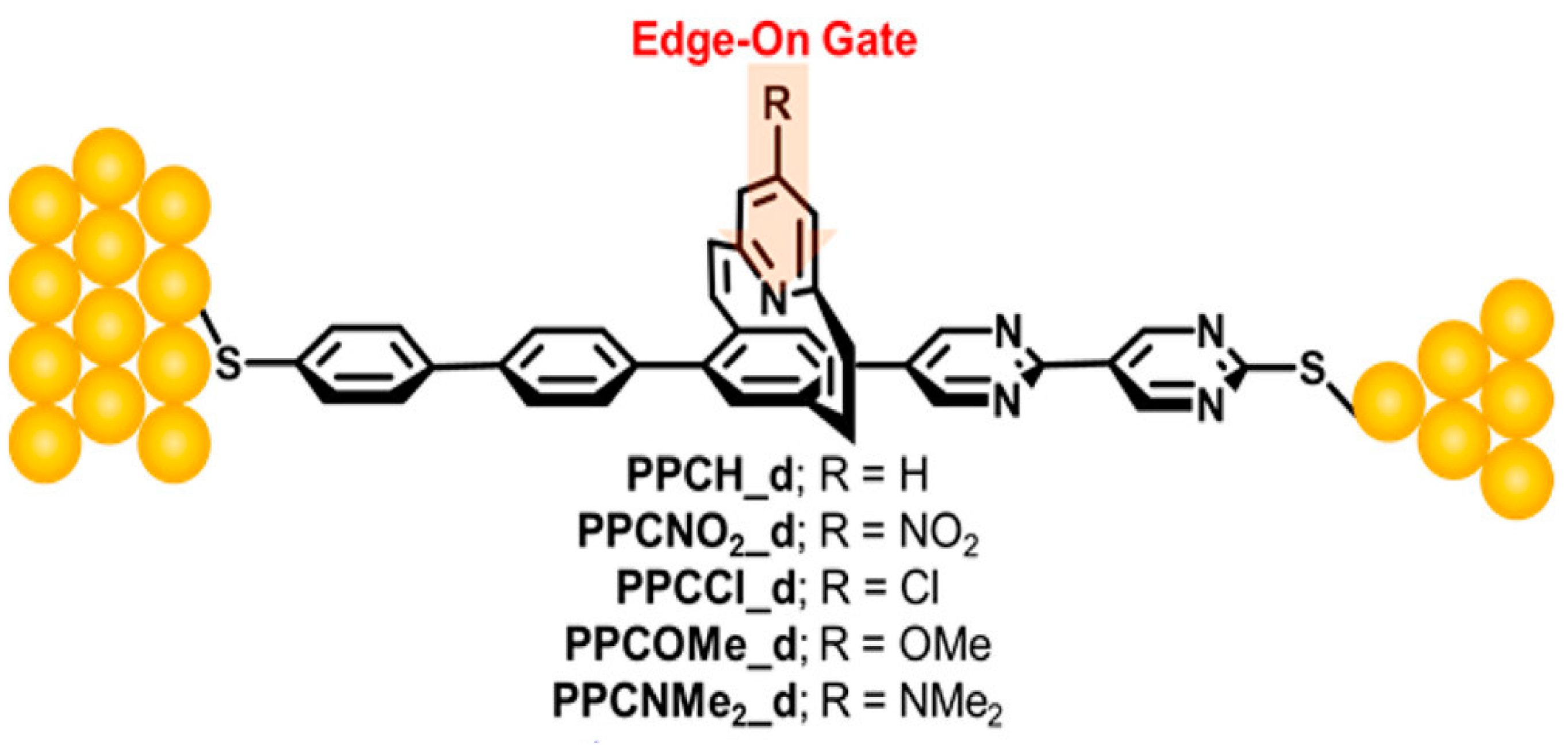
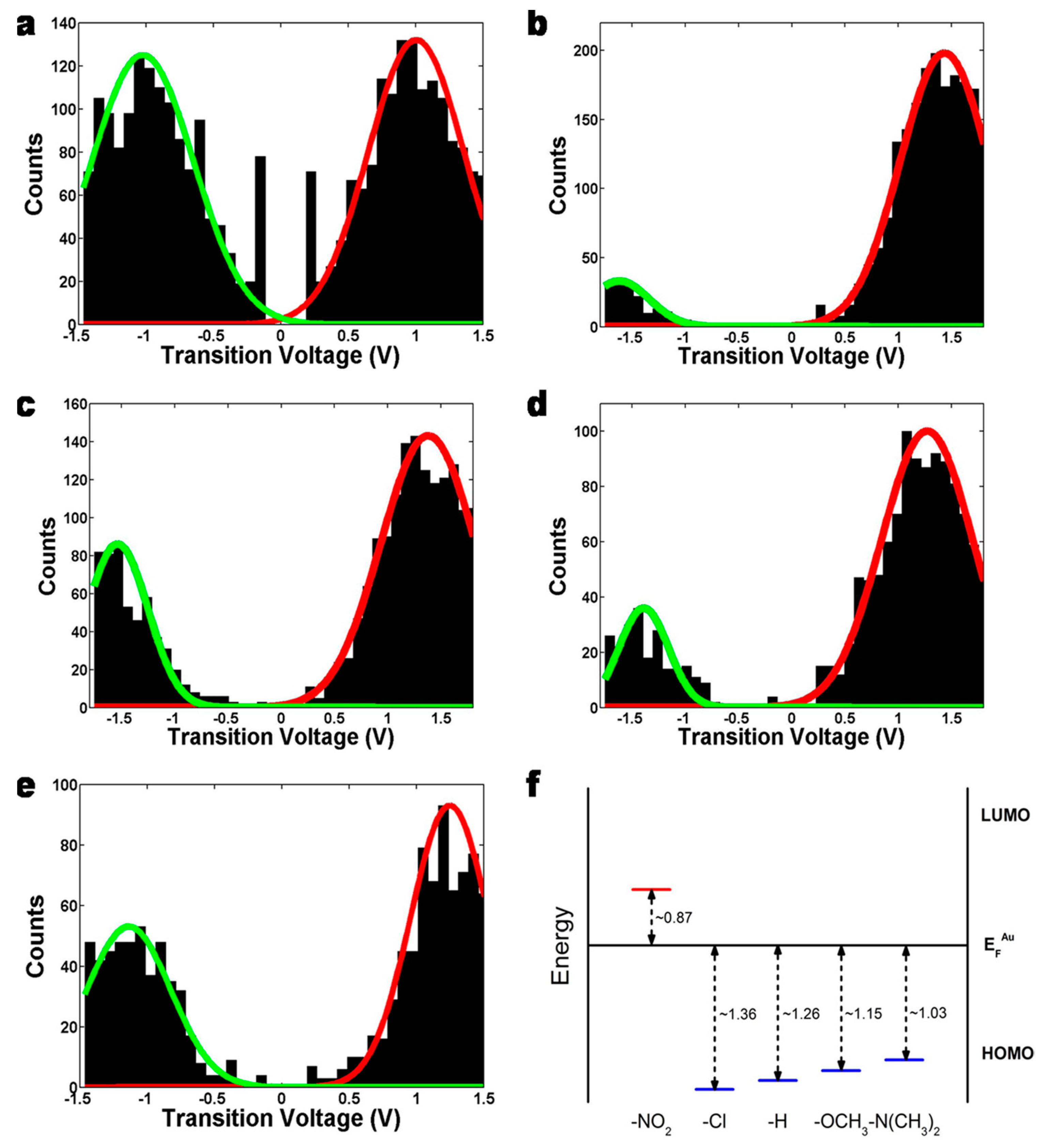
3.2. Chemical Gating of Molecular Junction Using Edge-on Substituents
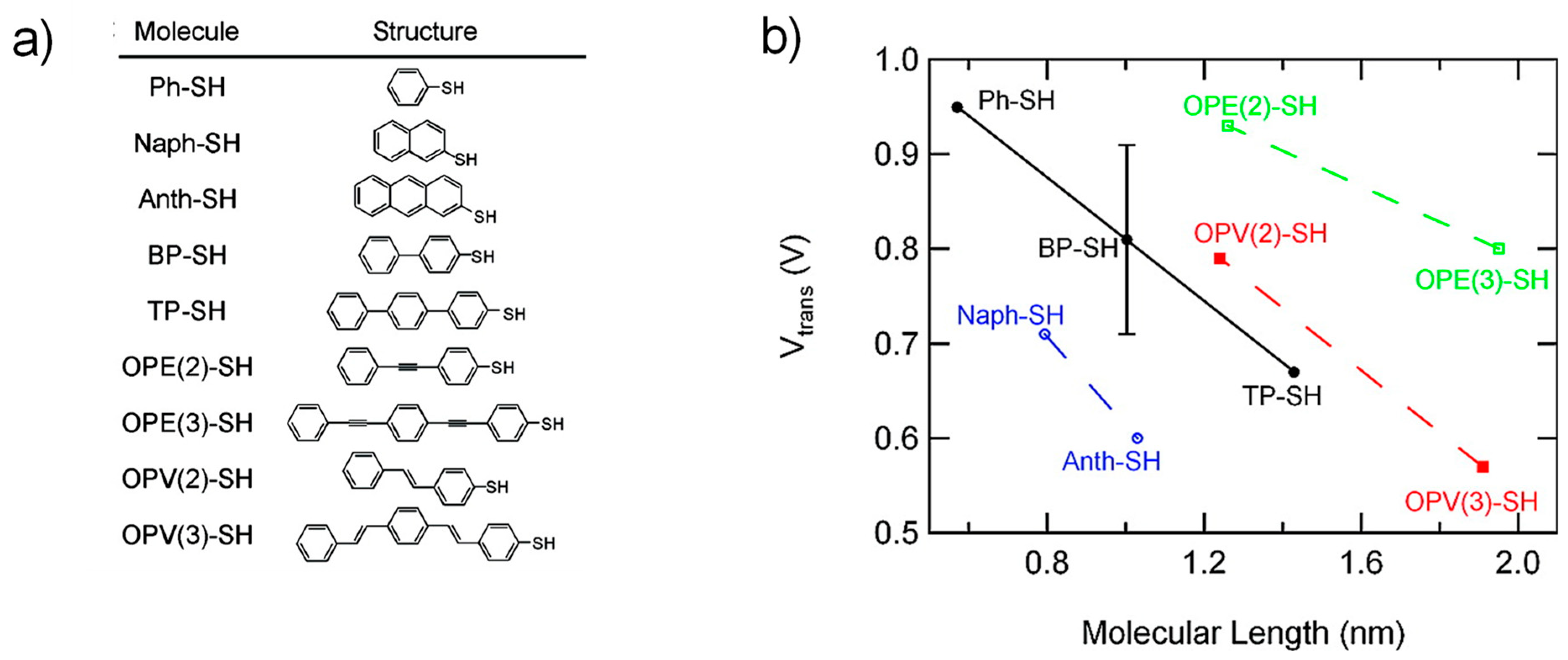
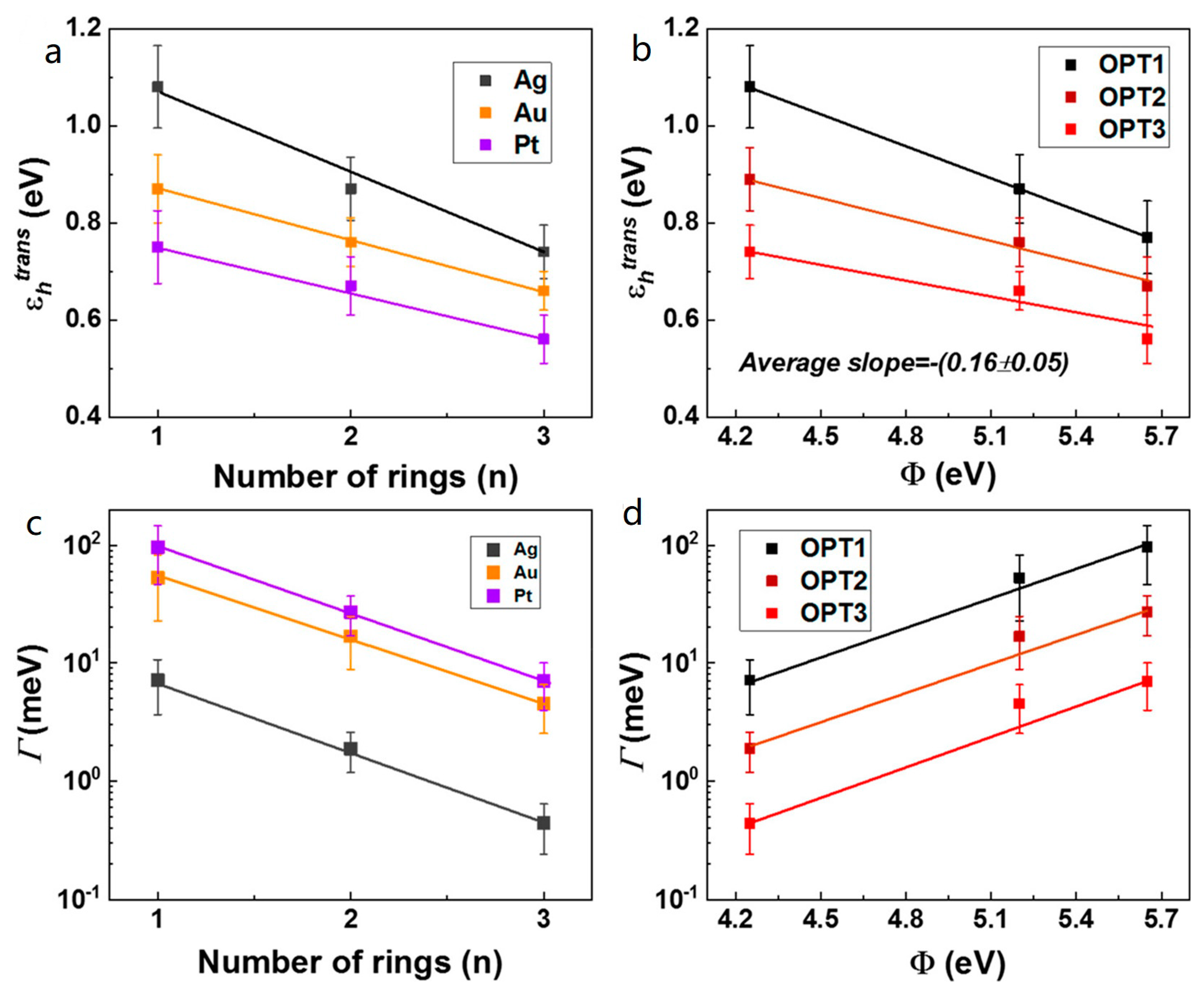
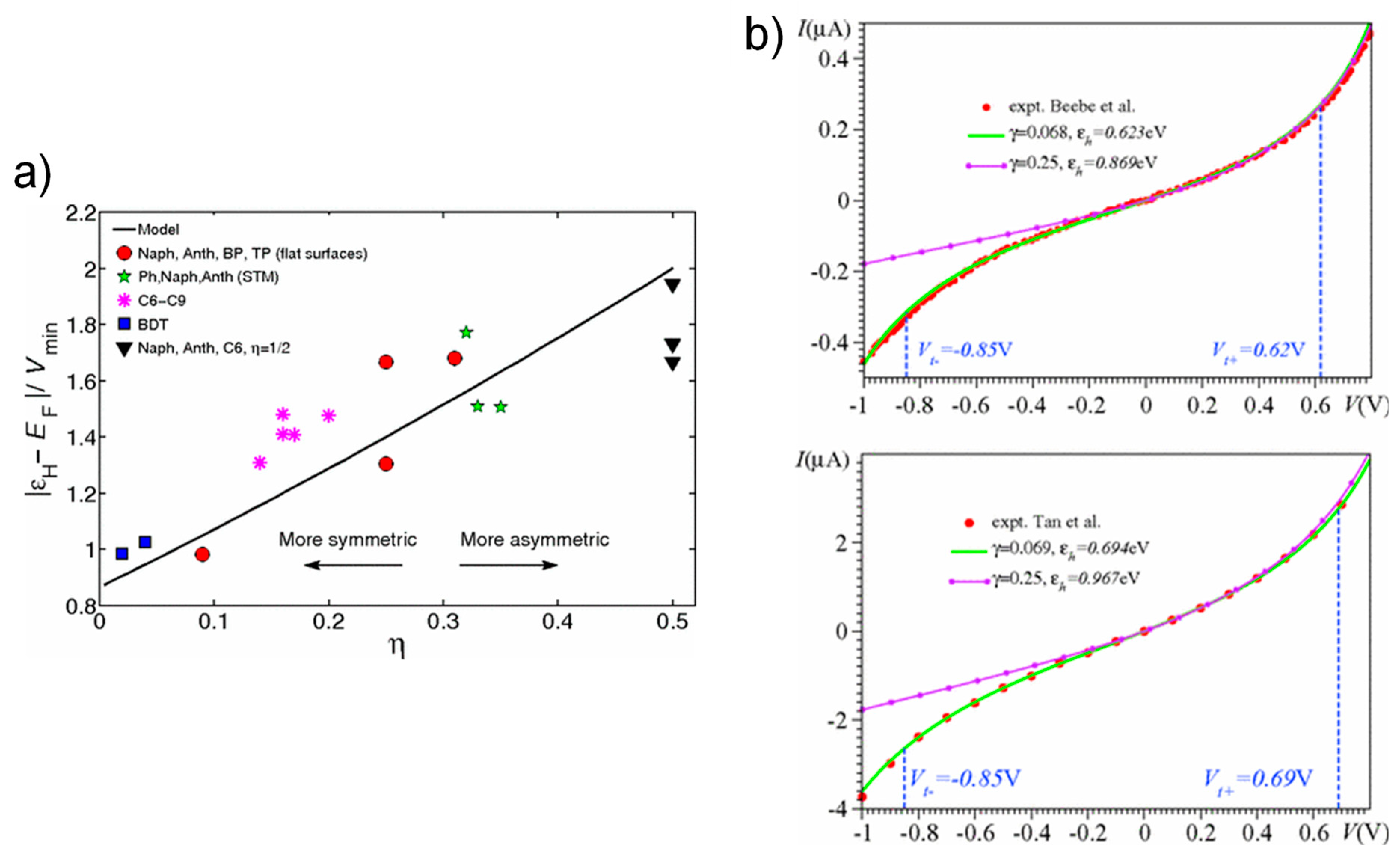
3.3. Dependence of Molecular Length and Electrode Work Function
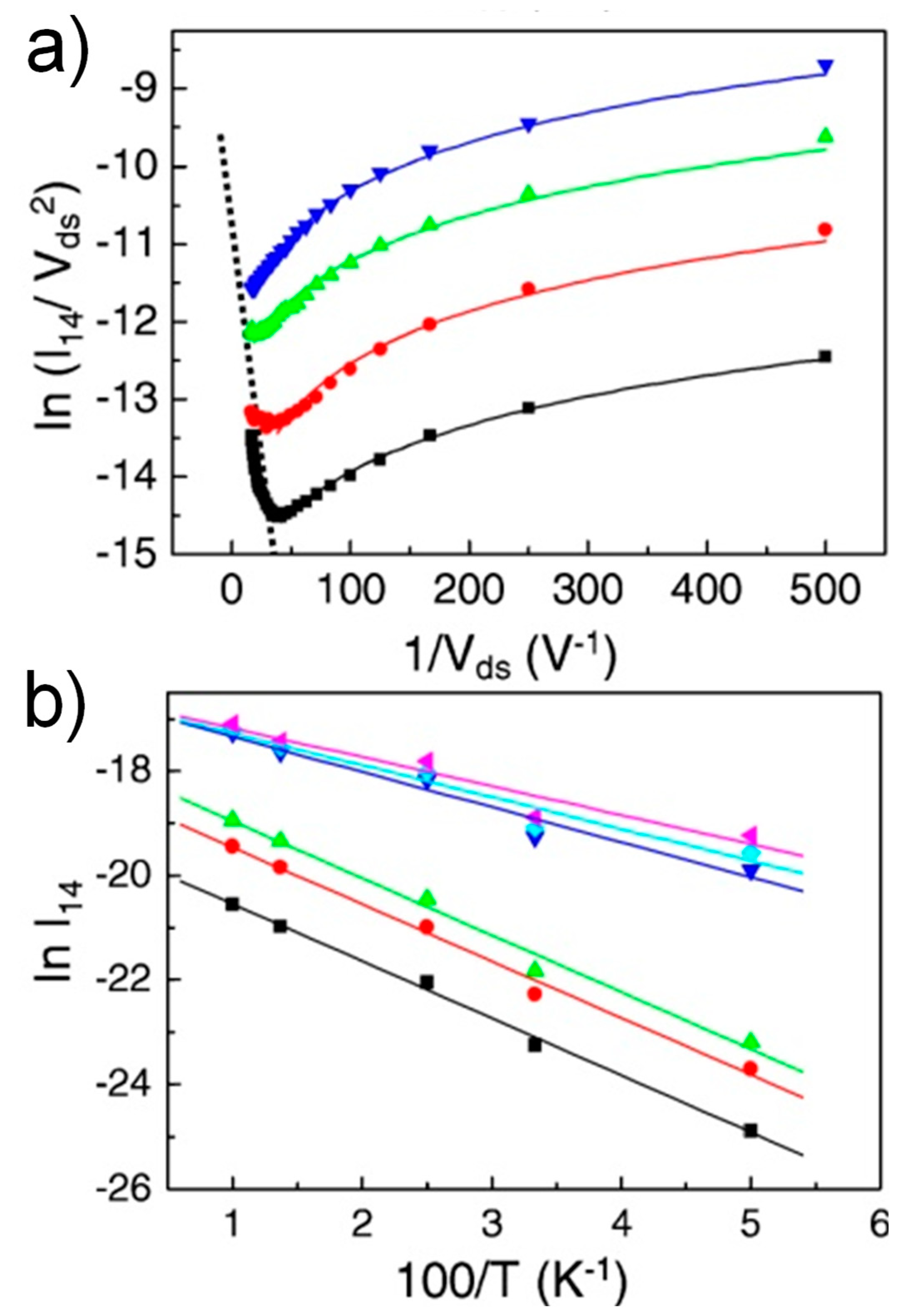
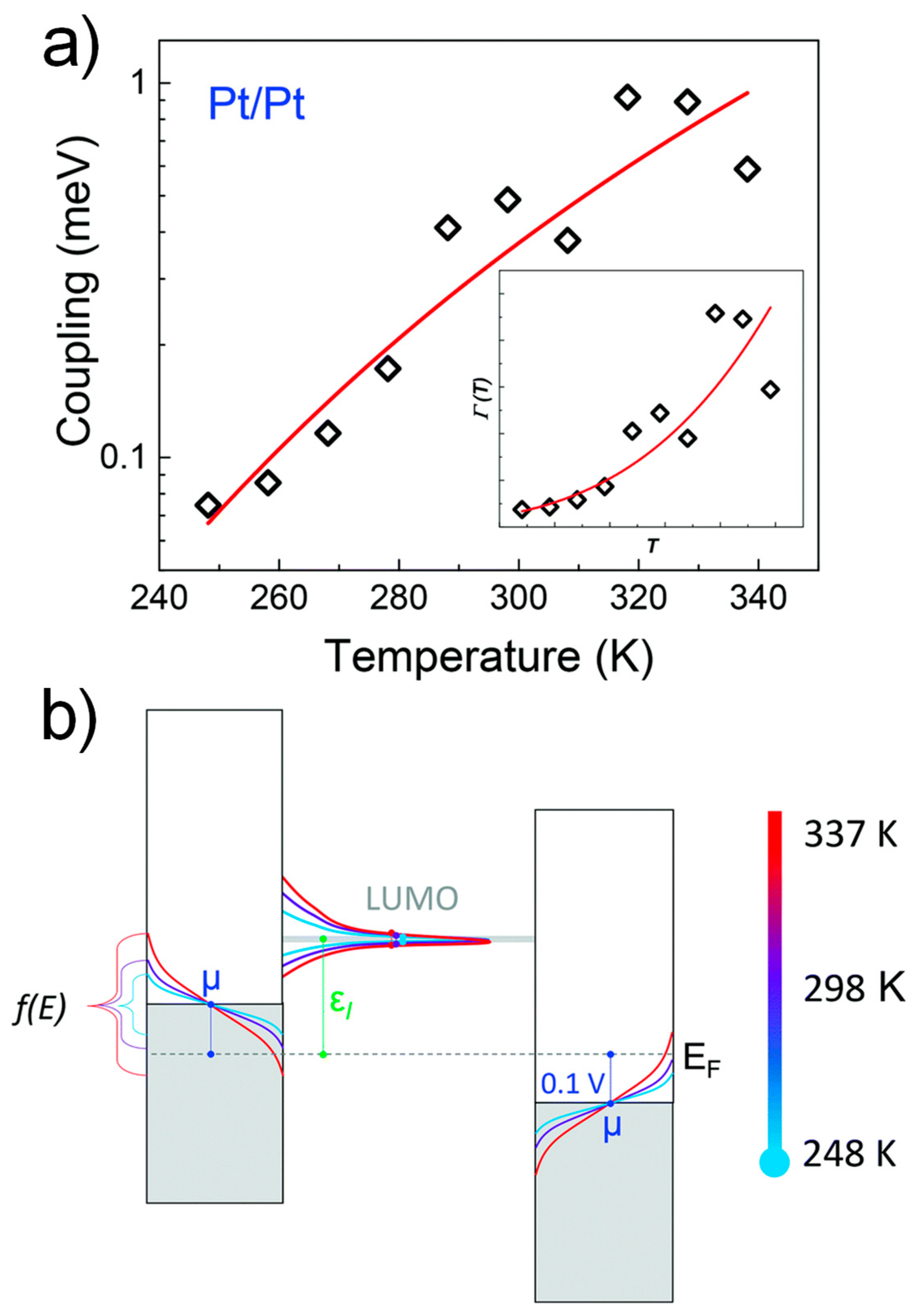
3.4. Temperature Dependence
3.5. Ambipolar Transition Voltage Spectroscopy
3.6. Molecule–Electrode Interface
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xiang, D.; Wang, X.; Jia, C.; Lee, T.; Guo, X. Molecular-Scale Electronics: From Concept to Function. Chem. Rev. 2016, 116, 4318–4440. [Google Scholar] [CrossRef]
- Liu, Y.; Qiu, X.; Soni, S.; Chiechi, R.C. Charge Transport through Molecular Ensembles: Recent Progress in Molecular Electronics. Chem. Phys. Rev. 2021, 2, 021303. [Google Scholar] [CrossRef]
- Chen, H.; Stoddart, J.F. From Molecular to Supramolecular Electronics. Nat. Rev. Mater. 2021, 6, 804–828. [Google Scholar] [CrossRef]
- Song, H.; Reed, M.A.; Lee, T. Single Molecule Electronic Devices. Adv. Mater. 2011, 23, 1583–1608. [Google Scholar] [CrossRef] [PubMed]
- Lörtscher, E. Wiring Molecules into Circuits. Nat. Nanotechnol. 2013, 8, 381–384. [Google Scholar] [CrossRef]
- Perrin, M.L.; Burzurı, E.; van der Zant, H.S.J. Single-Molecule Transistors. Chem. Soc. Rev. 2015, 44, 902–919. [Google Scholar] [CrossRef]
- Ratner, M. A Brief History of Molecular Electronics. Nat. Nanotechnol. 2013, 8, 378–381. [Google Scholar] [CrossRef] [PubMed]
- Aradhya, S.V.; Venkataraman, L. Single-Molecule Junctions beyond Electronic Transport. Nat. Nanotechnol. 2013, 8, 399–410. [Google Scholar] [CrossRef] [PubMed]
- Gehring, P.; Thijssen, J.M.; van der Zant, H.S.J. Single-Molecule Quantum-Transport Phenomena in Break Junctions. Nat. Rev. Phys. 2019, 1, 381–396. [Google Scholar] [CrossRef]
- Cuevas, J.C.; Scheer, E. Molecular Electronics: An Introduction to Theory and Experiment; World Scientific: Singapore, 2009. [Google Scholar]
- Schwarz, F.; Lörtscher, E. Break-Junction for Investigating Transport at the Molecular Scale. J. Phys. Condens. Matter 2014, 26, 474201. [Google Scholar] [CrossRef]
- Nichols, R.J.; Higgins, S.J. Single-Molecule Electronics: Chemical and Analytical Perspectives. Annu. Rev. Anal. Chem. 2015, 8, 389–417. [Google Scholar] [CrossRef] [PubMed]
- Vilan, A.; Aswal, D.; Cahen, D. Large-Area, Ensemble Molecular Electronics: Motivation and Challenges. Chem. Rev. 2017, 117, 4248–4286. [Google Scholar] [CrossRef] [PubMed]
- Joachim, C.; Ratner, M.A. Molecular Electronics: Some Views on Transport Junctions and Beyond. Proc. Natl Acad. Sci. USA 2015, 102, 8801–8808. [Google Scholar] [CrossRef] [Green Version]
- van der Molen, S.J.; Naaman, R.; Scheer, E.; Neaton, J.B.; Nitzan, A.; Natelson, D.; Tao, N.J.; van der Zant, H.S.J.; Mayor, M.; Ruben, M.; et al. Visions for a Molecular Future. Nat. Nanotechnol. 2013, 8, 385–389. [Google Scholar]
- Lambert, C.J. Basic Concepts of Quantum Interference and Electron Transport in Single-Molecule Ectronics. Chem. Soc. Rev. 2015, 44, 875–888. [Google Scholar] [CrossRef]
- Su, T.A.; Neupane, M.; Steigerwald, M.L.; Venkataraman, L.; Nuckolls, C. Chemical Principles of Single-Molecule Electronics. Nat. Rev. Mater. 2016, 1, 16002. [Google Scholar] [CrossRef]
- Xin, N.; Guan, J.; Zhou, C.; Gu, C.; Li, Y.; Ratner, M.A.; Nitzan, A.; Stoddart, J.F.; Guo, X. Concepts in the Design and Engineering of Single-Molecule Electronic Devices. Nat. Rev. Phys. 2019, 1, 211–230. [Google Scholar] [CrossRef]
- Yoshizawa, K. An Orbital Rule for Electron Transport in Molecules. Acc. Chem. Res. 2012, 45, 1612–1621. [Google Scholar] [CrossRef]
- Hybertsen, M.S.; Venkataraman, L. Structure–Property Relationships in Atomic-Scale Junctions: Histograms and Beyond. Acc. Chem. Res. 2016, 49, 452–460. [Google Scholar] [CrossRef]
- Su, T.A.; Li, H.; Klausen, R.S.; Kim, N.T.; Neupane, M.; Leigton, J.L.; Steigerwald, M.L.; Venkataraman, L.; Nuckolls, C. Silane and Germane Molecular Electronics. Acc. Chem. Res. 2017, 50, 1088–1095. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Rudnev, A.V.; Hong, W.; Wandlowski, T. Break Junction under Electrochemical Gating: Testbed for Single-Molecule Electronics. Chem. Soc. Rev. 2015, 44, 889–901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Quek, S.Y.; Kamenetska, M.; Steigerwald, M.L.; Choi, H.J.; Louie, S.G.; Hybertsen, M.S.; Neaton, J.B.; Venkataraman, L. Mechanically Controlled Binary Conductance Switching of a Single-Molecule Junction. Nat. Nanotechnol. 2009, 4, 230–234. [Google Scholar] [CrossRef] [Green Version]
- Jia, C.; Migliore, A.; Xin, N.; Huang, S.; Wang, S.; Chen, H.; Wang, D.; Feng, B.; Liu, Z.; Zhang, G.; et al. Covalently Bonded Single-Molecule Junctions with Stable and Reversible Photoswitched Conductivity. Science 2016, 352, 1443–1445. [Google Scholar] [CrossRef] [PubMed]
- Guo, C.; Chen, X.; Ding, S.-Y.; Mayer, D.; Wang, Q.; Zhao, Z.; Ni, L.; Liu, H.; Lee, T.; Xu, B.; et al. Molecular Orbital Gating Surface-Enhanced Raman Scattering. ACS Nano 2018, 12, 11229–11235. [Google Scholar] [CrossRef]
- Guédon, C.M.; Valkenier, H.; Markussen, T.; Thygesen, K.S.; Hummelen, J.C.; van der Molen, S.J. Observation of Quantum Interference in Molecular Charge Transport. Nat. Nanotechnol. 2012, 7, 305–309. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kamenetska, M.; Koentopp, M.; Whalley, A.C.; Park, Y.S.; Steigerwald, M.L.; Nuckolls, C.; Hybertsen, M.S.; Venkataraman, L. Formation and Evolution of Single-Molecule Junctions. Phys. Rev. Lett. 2009, 102, 126803. [Google Scholar] [CrossRef]
- Parker, S.M.; Smeu, M.; Franco, I.; Ratner, M.A.; Seideman, T. Molecular Junctions: Can Pulling Influence Optical Controllability? Nano Lett. 2014, 14, 4587–4591. [Google Scholar] [CrossRef]
- Van Dyck, C.; Geskin, V.; Cornil, J. Fermi Level Pinning and Orbital Polarization Effects in Molecular Junctions: The Role of Metal Induced Gap States. Adv. Funct. Mater. 2014, 24, 6154–6165. [Google Scholar] [CrossRef]
- Wang, W.; Lee, T.; Reed, M.A. Mechanism of Electron Conduction in Self-Assembled Alkanethiol Monolayer Devices. Phys. Rev. B 2003, 68, 035416. [Google Scholar] [CrossRef]
- Beebe, J.M.; Kim, B.; Gadzuk, J.W.; Frisbie, C.D.; Kushmerick, J.G. Transition from Direct Tunneling to Field Emission in Metal-Molecule-Metal Junctions. Phys. Rev. Lett. 2006, 97, 026801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Beebe, J.M.; Kim, B.; Frisbie, C.D.; Kushmerick, J.G. Measuring Relative Barrier Heights in Molecular Electronic Junctions with Transition Voltage Spectroscopy. ACS Nano 2008, 2, 827–832. [Google Scholar] [CrossRef]
- Wold, D.J.; Frisbie, C.D. Formation of Metal-Molecule-Metal Tunnel Junctions: Microcontacts to Alkanethiol Monolayers with a Conducting AFM Tip. J. Am. Chem. Soc. 2000, 122, 2970–2971. [Google Scholar] [CrossRef]
- Bâldea, I. Ambipolar Transition Voltage Spectroscopy: Analytical Results and Experimental Agreement. Phys. Rev. B 2012, 85, 035442. [Google Scholar] [CrossRef] [Green Version]
- Nose, D.; Dote, K.; Sato, T.; Yamamoto, M.; Ishii, H.; Noguchi, Y. Effects of Interface Electronic Structures on Transition Voltage Spectroscopy of Alkanethiol Molecular Junctions. J. Phys. Chem. C 2015, 119, 12765. [Google Scholar] [CrossRef]
- Tan, A.; Balachandran, J.; Dunietz, B.D.; Jang, S.Y.; Gavini, V.; Reddy, P. Length Dependence of Frontier Orbital Alignment in Aromatic Molecular Junctions. Appl. Phys. Lett. 2012, 101, 243107. [Google Scholar] [CrossRef]
- Nguyen, Q.V.; Xie, Z.; Frisbie, C.D. Quantifying Molecular Structure-Tunneling Conductance Relationships: Oligophenylene Dimethanethiol vs Oligophenylene Dithiol Molecular Junctions. J. Phys. Chem. C 2021, 125, 4292–4298. [Google Scholar] [CrossRef]
- Shin, J.; Gu, K.; Yang, S.; Lee, C.-H.; Lee, T.; Jang, Y.H.; Wang, G. Correlational Effects of the Molecular-Tilt Configuration and the Intermolecular van der Waals Interaction on the Charge Transport in the Molecular Junction. Nano Lett. 2018, 18, 4322–4330. [Google Scholar] [CrossRef]
- Xie, Z.; Bâldea, I.; Nguyen, Q.V.; Frisbie, C.D. Quantitative Analysis of Weak Current Rectification in Molecular Tunnel Junctions Subject to Mechanical Deformation Reveals Two Different Rectification Mechanisms for Oligophenylene Thiols versus Alkane Thiols. Nanoscale 2021, 13, 16755–16768. [Google Scholar] [CrossRef]
- Bâldea, I. Transition Voltage Spectroscopy Reveals Significant Solvent Effects on Molecular Transport and Settles an Important Issue in Bipyridine-Based Junctions. Nanoscale 2013, 5, 9222–9230. [Google Scholar] [CrossRef] [Green Version]
- Xie, Z.; Bâldea, I.; Frisbie, C.D. Energy Level Alignment in Molecular Tunnel Junctions by Transport and Spectroscopy: Self-Consistency for the Case of Alkyl Thiols and Dithiols on Ag, Au, and Pt Electrodes. J. Am. Chem. Soc. 2019, 141, 18182–18192. [Google Scholar] [CrossRef] [PubMed]
- Xie, Z.; Bâldea, I.; Frisbie, C.D. Determination of Energy-Level Alignment in Molecular Tunnel Junctions by Transport and Spectroscopy: Self-Consistency for the Case of Oligophenylene Thiols and Dithiols on Ag, Au, and Pt Electrodes. J. Am. Chem. Soc. 2019, 141, 3670–3681. [Google Scholar] [CrossRef]
- Huisman, E.H.; Trouwborst, M.L.; Bakker, F.L.; de Boer, B.; van Wees, B.J.; van der Molen, S.J. Stabilizing Single Atom Contacts by Molecular Bridge Formation. Nano Lett. 2008, 8, 3381–3385. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, J.; Markussen, T.; and Thygesen, K.S. Quantifying Transition Voltage Spectroscopy of Molecular Junctions: Ab Initio Calculations. Phys. Rev. B 2010, 82, 121412. [Google Scholar] [CrossRef] [Green Version]
- Markussen, T.; Chen, J.; Thygesen, K.S. Improving Transition Voltage Spectroscopy of Molecular Junctions. Phys. Rev. B 2011, 83, 155407. [Google Scholar] [CrossRef] [Green Version]
- Mirjani, F.; Thijssen, J.M.; van der Molen, S.J. Advantages and Limitations of Transition Voltage Spectroscopy: A Theoretical Analysis. Phys. Rev. B 2011, 84, 115402. [Google Scholar] [CrossRef] [Green Version]
- Trouwborst, M.L.; Martin, C.A.; Smit, R.H.M.; Guédon, C.M.; Baart, T.V.; van der Molen, S.J.; van Ruitenbeek, J.M. Transition Voltage Spectroscopy and the Nature of Vacuum Tunneling. Nano Lett. 2011, 11, 614–617. [Google Scholar] [CrossRef] [Green Version]
- Araidai, M.; Tsukada, M. Theoretical Calculations of Electron Transport in Molecular Junctions: Inflection Behavior in Fowler-Nordheim Plot and its Origin. Phys. Rev. B 2010, 81, 235114. [Google Scholar] [CrossRef]
- Simmons, J.G. Generalized Formula for the Electric Tunnel Effect between Similar Electrodes Seperatated by a Thin Insulating Film. J. Appl. Phys. 1963, 34, 1793–1803. [Google Scholar] [CrossRef] [Green Version]
- Song, H.; Kim, Y.; Jeong, H.; Reed, M.A.; Lee, T. Coherent Tunneling Transport in Molecular Junctions. J. Phys. Chem. C 2010, 114, 20431–20435. [Google Scholar] [CrossRef]
- Xie, Z.; Bâldea, I.; Smith, C.E.; Wu, Y.; Frisbie, C.D. Experimental and Theoretical Analysis of Nanotransport in Oligophenylene Dithiol Junctions as a Function of Molecular Length and Contact Work Function. ACS Nano 2015, 9, 8022–8036. [Google Scholar] [CrossRef]
- Smith, C.E.; Xie, Z.; Baldea, I.; Frisbie, C.D. Work Function and Temperature Dependence of Electron Tunneling through an N Type Perylene Diimide Molecular Junction with Isocyanide Surface Linkers. Nanoscale 2018, 10, 964–975. [Google Scholar] [CrossRef] [PubMed]
- Xie, Z.; Bâldea, I.; Oram, S.; Smith, C.E.; Frisbie, C.D. Effect of Heteroatom Substitution on Transport in Alkane Dithiol-Based Molecular Tunnel Junctions: Evidence for Universal Behavior. ACS Nano 2017, 11, 569–578. [Google Scholar] [CrossRef]
- Rodriguez-Gonzalez, S.; Xie, Z.; Galangau, O.; Selvanathan, P.; Norel, L.; Van Dyck, C.; Costuas, K.; Frisbie, C.D.; Rigaut, S.; Cornil, J. HOMO Level Pinning in Molecular Junctions: Joint Theoretical and Experimental Evidence. J. Phys. Chem. Lett. 2018, 9, 2394–2403. [Google Scholar] [CrossRef]
- Zahid, F.; Paulsson, M.; Datta, S. Electrical Conduction through Molecules in Advanced Semiconductors and Organic Nano-Techniques; Morkoc, H., Ed.; Academic Press: New York, NY, USA, 2003; Volume 3. [Google Scholar]
- Ventra, M.D.; Pantelides, S.T.; Lang, N.D. The benzene Molecule as a Molecular Resonant-Tunneling Transistor. Appl. Phys. Lett. 2000, 76, 3448. [Google Scholar] [CrossRef]
- Damle, P.; Rakshit, T.; Paulsson, M.; Datta, S. Current-Voltage Characteristics of Molecular Conductors: Two versus Three Terminal. IEEE Trans. Nanotechnol. 2002, 1, 145–153. [Google Scholar] [CrossRef]
- Lang., D.; Solomon, P.M. Charge Control in a Model Biphenyl Molecular Transistor. Nano Lett. 2005, 5, 921–924. [Google Scholar] [CrossRef] [PubMed]
- Solomon, P.M.; Lang, N.D. The Biphenyl Molecule as a Model Transistor. ACS Nano 2008, 2, 435–440. [Google Scholar] [CrossRef]
- Ghosh, A.W.; Rakshit, T.; Datta, S. Gating of a Molecular Transistor: Electrostatic and Conformational. Nano Lett. 2004, 4, 565–568. [Google Scholar] [CrossRef] [Green Version]
- Song, H.; Kim, Y.; Jang, Y.H.; Jeong, H.; Reed, M.A.; Lee, T. Observation of Molecular Orbital Gating. Nature 2009, 462, 1039–1043. [Google Scholar] [CrossRef]
- Park, H.; Park, J.; Lim, A.K.; Anderson, E.H.; Alivisatos, A.P.; McEuen, P.L. Nanomechanical Oscillations in a Single-C60 Transistor. Nature 2000, 407, 57–60. [Google Scholar] [CrossRef]
- Park, J.; Pasupathy, A.N.; Goldsmith, J.I.; Chang, C.; Yaish, Y.; Petta, J.R.; Rinkoski, M.; Sethna, J.P.; Abruna, H.D.; McEuen, P.L.; et al. Coulomb Blockade and the Kondo Effect in Single-Atom Transistors. Nature 2002, 417, 722–725. [Google Scholar] [CrossRef]
- Xiang, A.; Li, H.; Chen, S.; Liu, S.X.; Decurtins, S.; Bai, M.; Hou, S.; Liao, J. Electronic Transport in Benzodifuran Single-Molecule Transistors. Nanoscale 2015, 7, 7665–7673. [Google Scholar] [CrossRef]
- Lo, W.-Y.; Bi, W.; Li, L.; Jung, I.H.; Yu, L. Edge-on Gating Effect in Molecular Wires. Nano Lett. 2015, 15, 958–962. [Google Scholar] [CrossRef] [PubMed]
- Zhang, N.; Lo, W.-Y.; Cai, Z.; Li, L.; Yu, L. Molecular Rectification Tuned by Through-Space Gating Effect. Nano Lett. 2017, 17, 308–312. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Lo, W.-Y.; Cai, Z.; Zhang, N.; Yu, L. Proton-Triggered Switch Based on a Molecular Transistor with Edge-on Gate. Chem. Sci. 2016, 7, 3137–3141. [Google Scholar] [CrossRef] [Green Version]
- Moreno-García, P.; Gulcur, M.; Manrique, D.Z.; Pope, T.; Hong, W.; Kaliginedi, V.; Huang, C.; Batsanov, A.S.; Bryce, M.R.; Lambert, C.; et al. Single-Molecule Conductance of Functionalized Oligoynes: Length Dependence and Junction Evolution. J. Am. Chem. Soc. 2013, 135, 12228–12240. [Google Scholar] [CrossRef] [Green Version]
- Cao, Y.; Steigerwald, M.L.; Nuckolls, C.; Guo, X. Current Trends in Shrinking the Channel Length of Organic Transistors Down to the Nanoscale. Adv. Mater. 2010, 22, 20–32. [Google Scholar] [CrossRef]
- Luo, L.; Benameur, A.; Brignou, P.; Choi, S.H.; Rigaut, S.; Frisbie, C.D. Length and Temperature Dependent Conduction of Ruthenium-Containing Redox-Active Molecular Wires. J. Phys. Chem. C 2011, 115, 19955–19961. [Google Scholar] [CrossRef]
- Hines, T.; Diez-Perez, I.; Hihath, J.; Liu, H.M.; Wang, Z.S.; Zhao, J.W.; Zhou, G.; Müllen, K.; Tao, N.J. Transition from Tunneling to Hopping in Single Molecular Junctions by Measuring Length and Temperature Dependence. J. Am. Chem. Soc. 2010, 132, 11658–11664. [Google Scholar] [CrossRef]
- Luo, L.; Frisbie, C.D. Length-Dependent Conductance of Conjugated Molecular Wires Synthesized by Stepwise “Click” Chemistry. J. Am. Chem. Soc. 2010, 132, 8854–8855. [Google Scholar] [CrossRef]
- Choi, S.H.; Frisbie, C.D. Enhanced Hopping Conductivity in Low Band Gap Donor-Acceptor Molecular Wires up to 20 nm in Length. J. Am. Chem. Soc. 2010, 132, 16191–16201. [Google Scholar] [CrossRef]
- Zhao, X.T.; Huang, C.C.; Gulcur, M.; Batsanov, A.S.; Baghernejad, M.; Hong, W.J.; Bryce, M.R.; Wandlowski, T. Oligo(Aryleneethynylene)S with Terminal Pyridyl Groups: Synthesis and Length Dependence of the Tunneling-to-Hopping Transition of Single-Molecule Conductances. Chem. Mater. 2013, 25, 4340–4347. [Google Scholar] [CrossRef]
- Lafferentz, L.; Ample, F.; Yu, H.; Hecht, S.; Joachim, C.; Grill, L. Conductance of a Single Conjugated Polymer as a Continuous Function of Its Length. Science 2009, 323, 1193–1197. [Google Scholar] [CrossRef] [Green Version]
- Dell, E.J.; Capozzi, B.; Xia, J.; Venkataraman, L.; Campos, L.M. Molecular Length Dictates the Nature of Charge Carriers in Single-Molecule Junctions of Oxidized Oligothiophenes. Nat. Chem. 2015, 7, 209–214. [Google Scholar] [CrossRef]
- O’Neill, L.; Byrne, H.J. Structure-Property Relationships for Electron-Vibrational Coupling in Conjugated Organic Oligomeric Systems. J. Phys. Chem. B 2005, 109, 12685–12690. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Sepunaru, L.; Amdursky, N.; Cohen, S.R.; Pecht, I.; Sheves, M.; Cahen, D. Temperature and Force Dependence of Nanoscale Electron Transport Via the Cu Protein Azurin. ACS Nano 2012, 6, 10816–10824. [Google Scholar] [CrossRef] [Green Version]
- Di Ventra, M.; Kim, S.G.; Pantelides, S.T.; Lang, N.D. Temperature Effects on the Transport Properties of Molecules. Phys. Rev. Lett. 2001, 86, 288–291. [Google Scholar] [CrossRef] [Green Version]
- Poot, M.; Osorio, E.; O’Neill, K.; Thijssen, J.M.; Vanmaekelbergh, D.; van Walree, C.A.; Jenneskens, L.W.; van der Zant, H.S.J. Temperature Dependence of Three-Terminal Molecular Junctions with Sulfur End-Functionalized Tercyclohexylidenes. Nano Lett. 2006, 6, 1031–1035. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.K.; Yamada, R.; Tanaka, S.; Chang, G.S.; Asai, Y.; Tada, H. Universal Temperature Crossover Behavior of Electrical Conductance in a Single Oligothiophene Molecular Wire. ACS Nano 2012, 6, 5078–5082. [Google Scholar] [CrossRef]
- van Zalinge, H.; Schiffrin, D.J.; Bates, A.D.; Starikov, E.B.; Wenzel, W.; Nichols, R.J. Variable-Temperature Measurements of the Single-Molecule Conductance of Double-Stranded DNA. Angew. Chem. Int. Ed. 2006, 45, 5499–5502. [Google Scholar] [CrossRef]
- Chiu, P.W.; Roth, S. Transition from Direct Tunneling to Field Emission in Carbon Nanotube Intramolecular Junctions. Appl. Phys. Lett. 2008, 92, 042107. [Google Scholar] [CrossRef]
- Medvedev, I.G. Tunnel Current Through a Redox Molecule Coupled to Classical Phonon Modes in the Strong Tunneling Limit. Phys. Rev. B 2007, 76, 125312. [Google Scholar] [CrossRef]
- Wang, G.; Kim, Y.; Na, S.I.; Kahng, Y.H.; Ku, J.; Park, S.; Jang, Y.H.; Kim, D.Y.; Lee, T. Investigation of the Transition Voltage Spectra of Molecular Junctions Considering Frontier Molecular Orbitals and the Asymmetric Coupling Effect. J. Phys. Chem. C 2011, 115, 17979–17985. [Google Scholar] [CrossRef]
- Tan, A.; Sadat, S.; Reddy, P. Measurement of Thermopower and Current-Voltage Characteristics of Molecular Junctions to Identify Orbital Alignment. Appl. Phys. Lett. 2010, 96, 013110. [Google Scholar] [CrossRef]
- Silva Jr, C.B.; da Silva, S.J.S.; Leal, J.F.P.; Pinheiro, F.A.; Del Nero, J. Electronic Transport in Oligo-Para-Phenylene Junctions Attached to Carbon Nanotube Electrodes: Transition-Voltage Spectroscopy and Chirality. Phys. Rev. B 2011, 83, 245444. [Google Scholar] [CrossRef] [Green Version]
- Bennett, N.; Xu, G.; Esdaile, L.J.; Anderson, H.L.; Macdonald, J.E.; Elliott, M. Transition Voltage Spectroscopy of Porphyrin Molecular Wires. Small 2010, 6, 2604–2611. [Google Scholar] [CrossRef]
- Lennartz, M.C.; Atodiresei, N.; Caciuc, V.; Karthäuser, S. Identifying Molecular Orbital Energies by Distance-Dependent Transition Voltage Spectroscopy. J. Phys. Chem. C 2011, 115, 15025–15030. [Google Scholar] [CrossRef]
- Ricœur, G.; Lenfant, S.; Guérin, D.; Vuillaume, D. Molecule/Electrode Interface Energetics in Molecular Junction: A “Transition Voltage Spectroscopy” Study. J. Phys. Chem. C 2012, 116, 20722–20730. [Google Scholar] [CrossRef] [Green Version]
- Sotthewes, K.; Hellenthal, C.; Kumar, A.; Zandvliet, H.J.W. Transition Voltage Spectroscopy of Scanning Tunneling Microscopy Vacuum Junctions. RSC Adv. 2014, 4, 32438–32442. [Google Scholar] [CrossRef] [Green Version]
- Wu, K.; Bai, M.; Sanvito, S.; Hou, S. Origin of the Transition Voltage in Gold–Vacuum–Gold Atomic Junctions. Nanotechnology 2012, 24, 025203. [Google Scholar] [CrossRef]
- Jia, C.; Wang, J.; Yao, C.; Cao, Y.; Zhong, Y.; Liu, Z.; Liu, Z.; Guo, X. Conductance Switching and Mechanisms in Single-Molecule Junctions. Angew. Chem. Int. Edit. 2013, 52, 8666–8670. [Google Scholar] [CrossRef]
- Karthäuser, S. Control of Molecule-Based Transport for Future Molecular Devices. J. Phys. Condens. Matter. 2010, 23, 013001. [Google Scholar] [CrossRef]
- Jia, C.; Guo, X. Molecule–Electrode Interfaces in Molecular Electronic Devices. Chem. Soc. Rev. 2013, 42, 5642–5660. [Google Scholar] [CrossRef] [PubMed]
- Kim, B.; Choi, S.H.; Zhu, X.Y.; Frisbie, C.D. Molecular Tunnel Junctions Based on π-Conjugated Oligoacene Thiols and Dithiols between Ag, Au, and Pt Contacts: Effect of Surface Linking Group and Metal Work Function. J. Am. Chem. Soc. 2011, 133, 19864–19877. [Google Scholar] [CrossRef]
- Guo, S.; Hihath, J.; Díez-Pérez, I.; Tao, N. Measurement and Statistical Analysis of Single-Molecule Current–Voltage Characteristics, Transition Voltage Spectroscopy, and Tunneling Barrier Height. J. Am. Chem. Soc. 2011, 133, 19189–19197. [Google Scholar] [CrossRef] [PubMed]
- Gu, M.W.; Peng, H.H.; Chen, I.W.P.; Chen, C.-H. Tuning Surface d Bands with Bimetallic Electrodes to Facilitate Electron Transport Across Molecular Junctions. Nat. Mater. 2021, 20, 658–664. [Google Scholar] [CrossRef]
- Vilan, A.; Cahen, D.; Kraisler, E. Rethinking Transition Voltage Spectroscopy within a Generic Taylor Expansion View. ACS Nano 2013, 7, 695–706. [Google Scholar] [CrossRef]
- Artés, J.M.; López-Martínez, M.; Giraudet, A.; Díez-Pérez, I.; Sanz, F.; Gorostiza, P. Current–Voltage Characteristics and Transition Voltage Spectroscopy of Individual Redox Proteins. J. Am. Chem. Soc. 2012, 134, 20218–20221. [Google Scholar] [CrossRef] [PubMed]
- Bâldea, I. Revealing Molecular Orbital Gating by Transition Voltage Spectroscopy. Chem. Phys. 2010, 337, 15–20. [Google Scholar]
- Bâldea, I. Interpretation of Stochastic Events in Single-Molecule Measurements of Conductance and Transition Voltage Spectroscopy. J. Am. Chem. Soc. 2012, 134, 7958–7962. [Google Scholar] [CrossRef]
- Shamai, T.; Selzer, Y. Spectroscopy of Molecular Junctions. Chem. Soc. Rev. 2011, 40, 2293–2305. [Google Scholar] [CrossRef] [PubMed]
- Wu, K.; Bai, M.; Sanvito, S.; Hou, S. Transition Voltages of Vacuum-Spaced and Molecular Junctions with Ag and Pt Electrodes. J. Chem. Phys. 2014, 141, 014707. [Google Scholar] [CrossRef] [PubMed] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, Y.; Im, K.; Song, H. Charge Transport Characteristics of Molecular Electronic Junctions Studied by Transition Voltage Spectroscopy. Materials 2022, 15, 774. https://doi.org/10.3390/ma15030774
Kim Y, Im K, Song H. Charge Transport Characteristics of Molecular Electronic Junctions Studied by Transition Voltage Spectroscopy. Materials. 2022; 15(3):774. https://doi.org/10.3390/ma15030774
Chicago/Turabian StyleKim, Youngsang, Kyungjin Im, and Hyunwook Song. 2022. "Charge Transport Characteristics of Molecular Electronic Junctions Studied by Transition Voltage Spectroscopy" Materials 15, no. 3: 774. https://doi.org/10.3390/ma15030774
APA StyleKim, Y., Im, K., & Song, H. (2022). Charge Transport Characteristics of Molecular Electronic Junctions Studied by Transition Voltage Spectroscopy. Materials, 15(3), 774. https://doi.org/10.3390/ma15030774




