The Migration and Deposition Behaviors of Montmorillonite and Kaolinite Particles in a Two-Dimensional Micromodel
Abstract
:1. Introduction
2. Materials and Methods
2.1. Fine Clay Particle Materials
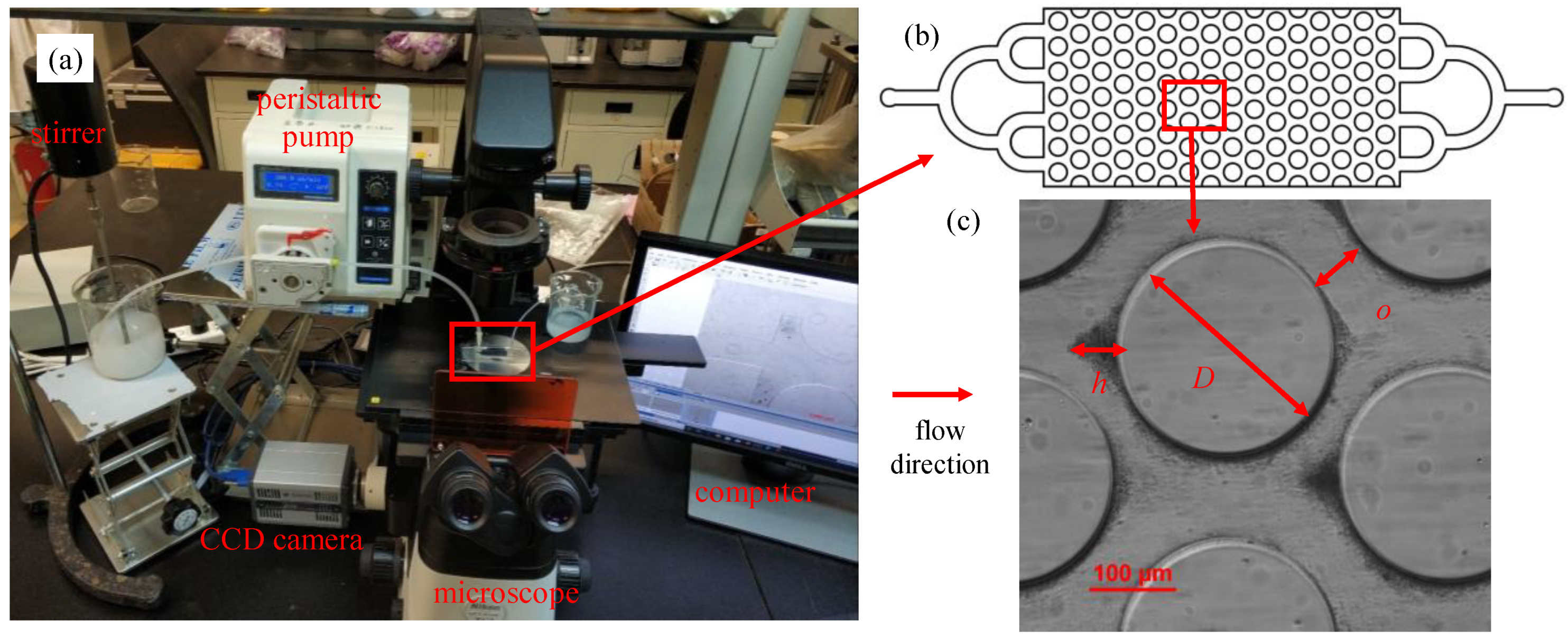
2.2. Micromodels
2.3. Experimental Methods
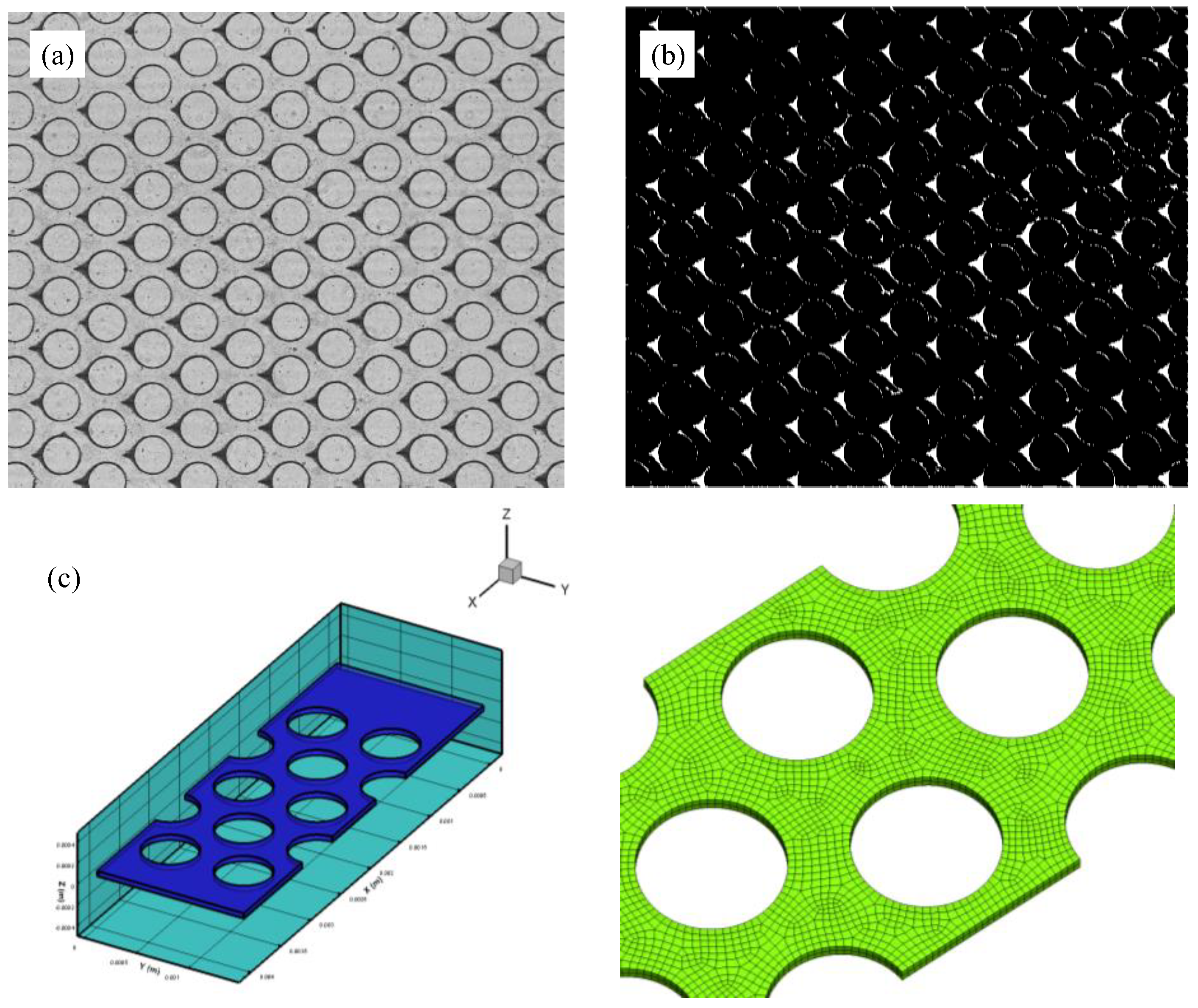
2.4. Image Processing
2.5. Numerical Simulation
3. Results and Discussion
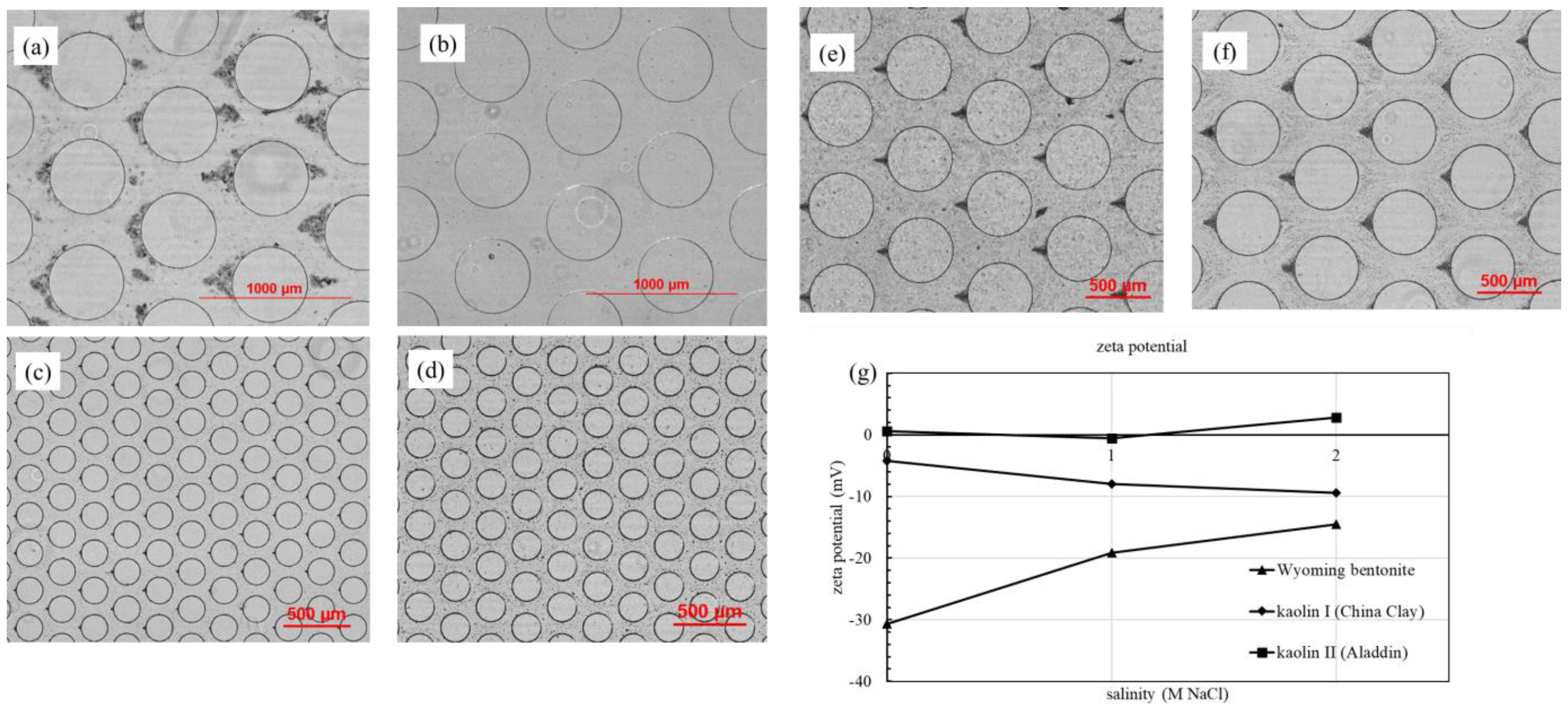
3.1. Effect of Suspension Salinity
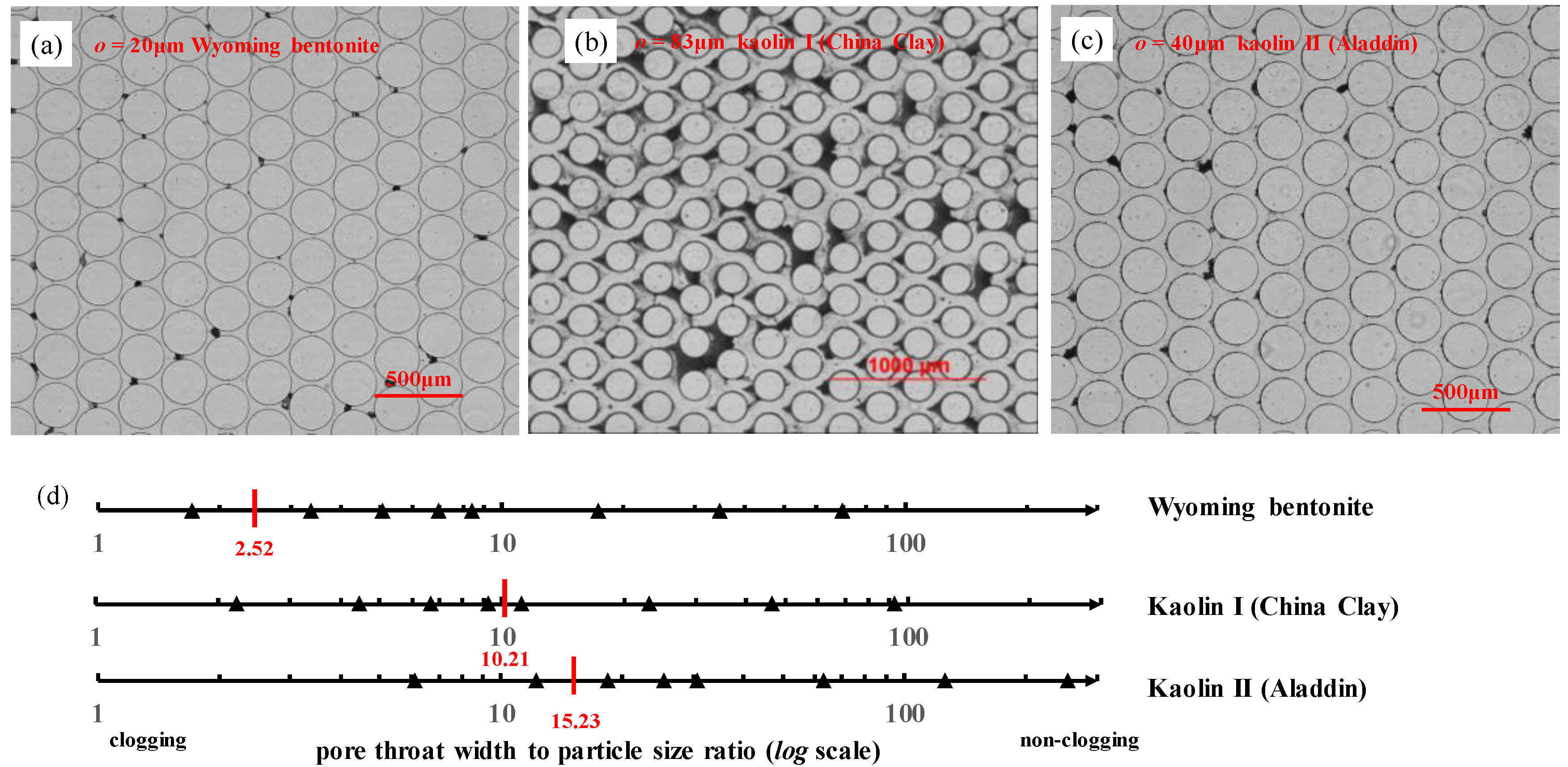
3.2. Particles Clogging at the Pore Throats
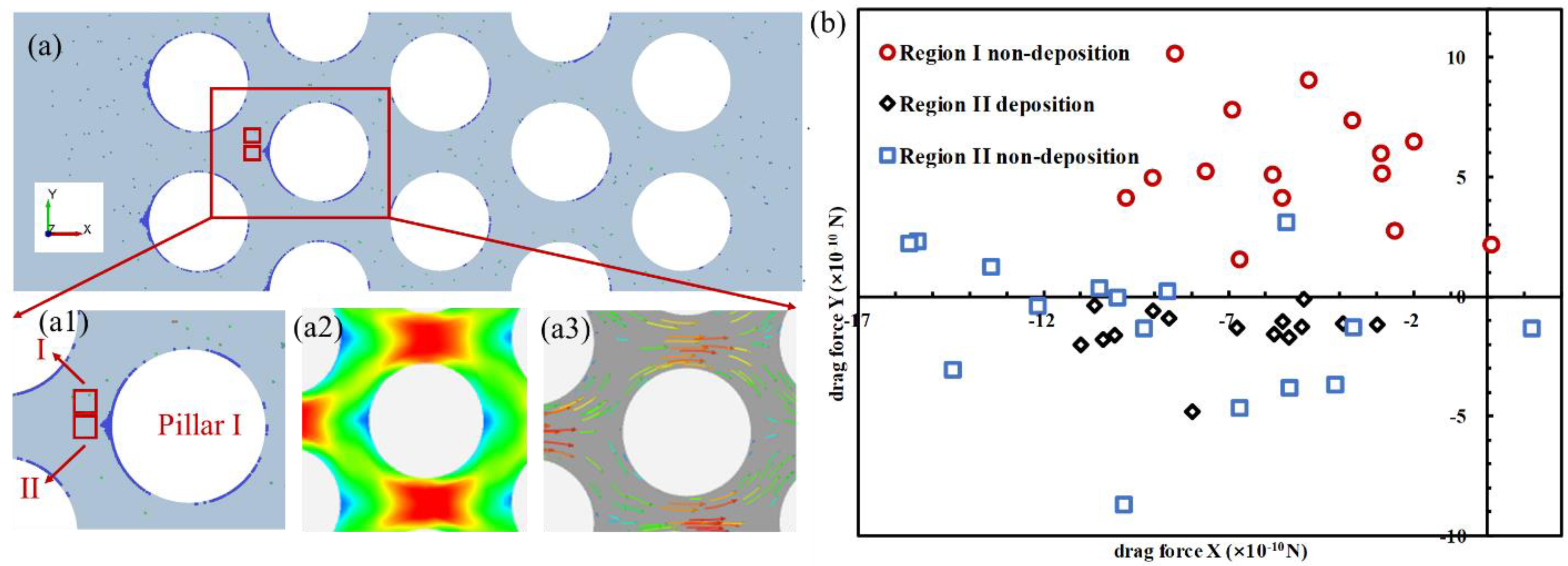
3.3. Particle Deposition Criteria
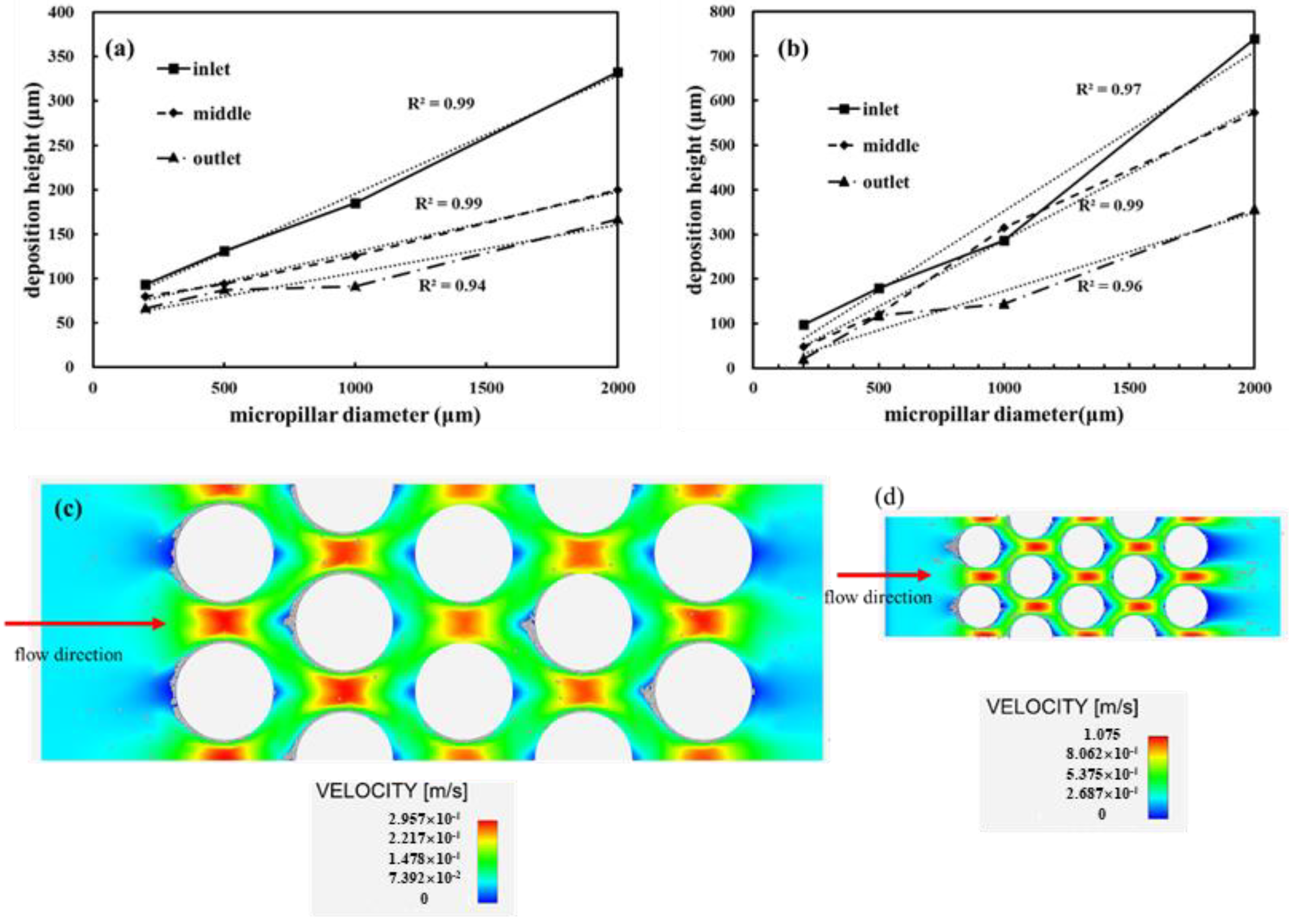
3.4. Effects of Micropillar Diameter on Particle Deposition
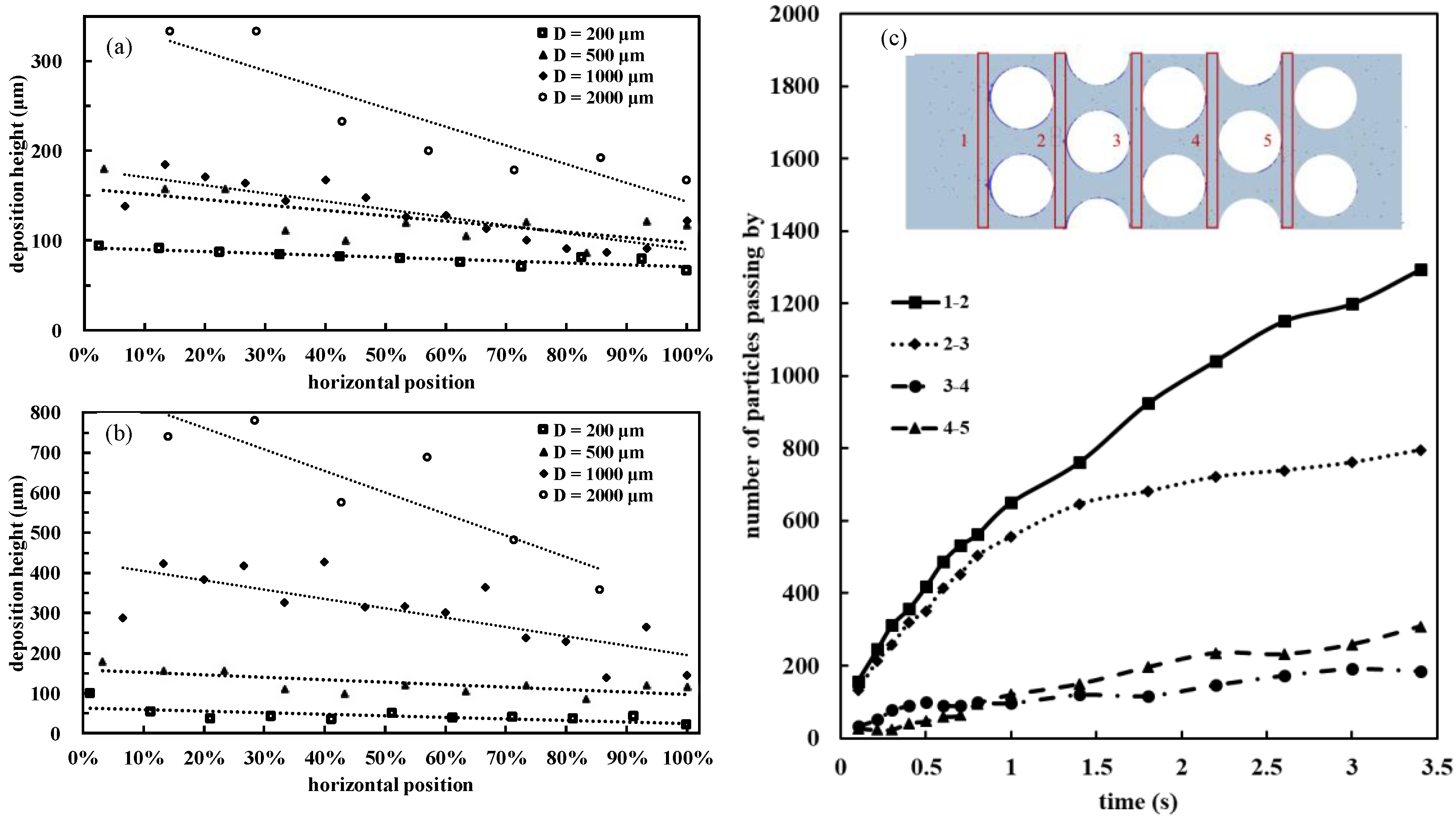
3.5. Deposition Height Decline along the Flow Direction
3.6. Effect of Air–Liquid Two-Phase Flow
3.7. Applicability in Related Engineering Field
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Strutz, T.J.; Hornbruch, G.; Dahmke, A.; Kober, R. Effect of injection velocity and particle concentration on transport of nanoscale zero-valent iron and hydraulic conductivity in saturated porous media. J. Contam. Hydrol. 2016, 191, 54–65. [Google Scholar] [CrossRef]
- Zhou, Z.-L.; Du, X.-M.; Wang, S.-Y.; Cai, X.; Chen, Z. Cement grout transport within sand with fractal characteristics considering filtration. Eur. J. Environ. Civ. Eng. 2019, 23, 1497–1519. [Google Scholar] [CrossRef]
- Sharif, Y.A.; Elkholy, M.; Chaudhry, M.H.; Imran, J. Experimental Study on the Piping Erosion Process in Earthen Embankments. J. Hydraul. Eng. 2015, 141, 04015012. [Google Scholar] [CrossRef]
- Zornberg, J.G.; Bouazza, A.; McCartney, J.S. Geosynthetic capillary barriers: Current state of knowledge. Geosynth. Int. 2010, 17, 273–300. [Google Scholar] [CrossRef] [Green Version]
- Cao, S.C.; Jang, J.; Jung, J.; Waite, W.F.; Collett, T.S.; Kumar, P. 2D micromodel study of clogging behavior of fine-grained particles associated with gas hydrate production in NGHP-02 gas hydrate reservoir sediments. Mar. Pet. Geol. 2018, 108, 714–730. [Google Scholar] [CrossRef]
- Barnaji, M.J.; Pourafshary, P.; Rasaie, M.R. Visual investigation of the effects of clay minerals on enhancement of oil recovery by low salinity water flooding. Fuel 2016, 184, 826–835. [Google Scholar] [CrossRef]
- Song, W.; Kovscek, A. Direct visualization of pore-scale fines migration and formation damage during low-salinity waterflooding. J. Nat. Gas Sci. Eng. 2016, 34, 1276–1283. [Google Scholar] [CrossRef]
- Song, W.; Kovscek, A.R. Functionalization of micromodels with kaolinite for investigation of low salinity oil-recovery processes. Lab Chip 2015, 15, 3314–3325. [Google Scholar] [CrossRef] [PubMed]
- Al-Sarihi, A.; Zeinijahromi, A.; Genolet, L.; Behr, A.; Kowollik, P.; Bedrikovetsky, P. Fines Migration as an EOR Method during Low Salinity Waterflooding. In Proceedings of the SPE Asia Pacific Oil and Gas Conference and Exhibition, Society of Petroleum Engineers, Brisbane, Australia, 20–22 October 2018; p. 14. [Google Scholar]
- Nguyen, P.T.; Zeinijahromi, A.; Bedrikovetsky, P.G. Taking Advantage of Fines Migration Formation Damage for Enhanced Gas Recovery. In Proceedings of the SPE International Symposium and Exhibition on Formation Damage Control, Society of Petroleum Engineers, Lafayette, LA, USA, 15–17 February 2012; p. 21. [Google Scholar]
- Li, N.; Li, J.; Zhao, L.; Luo, Z.; Liu, P.; Guo, Y. Laboratory Testing and Numeric Simulation on Laws of Proppant Transport in Complex Fracture Systems. In Proceedings of the SPE Asia Pacific Hydraulic Fracturing Conference, Society of Petroleum Engineers, Beijing, China, 24–26 August 2016; p. 16. [Google Scholar]
- Pan, L.; Zhang, Y.; Cheng, L.; Lu, Z.; Kang, Y.; He, P.; Dong, B. Migration and distribution of complex fracture proppant in shale reservoir volume fracturing. Nat. Gas Ind. B 2018, 5, 606–615. [Google Scholar] [CrossRef]
- Mangane, P.O.; Gouze, P.; Luquot, L. Permeability impairment of a limestone reservoir triggered by heterogeneous dissolution and particles migration during CO2-rich injection, Geophys. Res. Lett. 2013, 40, 4614–4619. [Google Scholar] [CrossRef]
- Othman, F.; Yu, M.; Kamali, F.; Le-Hussain, F. Fines migration during supercritical CO2 injection in sandstone. J. Nat. Gas Sci. Eng. 2018, 56, 344–357. [Google Scholar] [CrossRef]
- Zhang, X.; Ge, J.; Kamali, F.; Othman, F.; Wang, Y.; Le-Hussain, F. Wettability of Sandstone Rocks and their Mineral Components during CO2 Injection in Aquifers: Implications for Fines Migration. J. Nat. Gas Sci. Eng. 2019, 73, 103050. [Google Scholar] [CrossRef]
- Raychoudhury, T.; Tufenkji, N.; Ghoshal, S. Straining of polyelectrolyte-stabilized nanoscale zero valent iron particles during transport through granular porous media. Water Res. 2014, 50, 80–89. [Google Scholar] [CrossRef] [Green Version]
- Shubair, T.; Eljamal, O.; Khalil, M.E.A.; Matsunaga, N. Multilayer system of nanoscale zero valent iron and Nano-Fe/Cu particles for nitrate removal in porous media. Sep. Purif. Technol. 2018, 193, 242–254. [Google Scholar] [CrossRef]
- Lin, L.; Yan, X.; Liao, X.; Wang, Z. Migration and arsenic adsorption study of starch-modified Fe-Ce oxide on a silicon-based micromodel observation platform. J. Hazard. Mater. 2017, 338, 202–207. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Elliott, D.W.; Zhang, W. Zero-Valent Iron Nanoparticles for Abatement of Environmental Pollutants: Materials and Engineering Aspects. Crit. Rev. Solid State Mater. Sci. 2006, 31, 111–122. [Google Scholar] [CrossRef]
- Diao, Z.-H.; Xu, X.-R.; Jiang, D.; Kong, L.-J.; Sun, Y.-X.; Hu, Y.-X.; Hao, Q.-W.; Chen, H. Bentonite-supported nanoscale zero-valent iron/persulfate system for the simultaneous removal of Cr(VI) and phenol from aqueous solutions. Chem. Eng. J. 2016, 302, 213–222. [Google Scholar] [CrossRef]
- Jin, X.; Chen, Z.; Zhou, R.; Chen, Z. Synthesis of kaolin supported nanoscale zero-valent iron and its degradation mechanism of Direct Fast Black G in aqueous solution. Mater. Res. Bull. 2015, 61, 433–438. [Google Scholar] [CrossRef]
- Liu, Q.; Zhao, B.; Santamarina, J.C. Particle Migration and Clogging in Porous Media: A Convergent Flow Microfluidics Study. J. Geophys. Res. Solid Earth 2019, 124, 9495–9504. [Google Scholar] [CrossRef] [Green Version]
- Khilar, K.C.; Fogler, H.S. Migrations of Fines in Porous Media; Springer: Dordrecht, The Netherlands, 1998. [Google Scholar]
- Oyeneyin, M.B.; Peden, J.M.; Hosseini, A.; Ren, G. Factors to Consider in the Effective Management and Control of Fines Migration in High Permeability Sands. In Proceedings of the SPE European Formation Damage Conference, Society of Petroleum Engineers, The Hague, The Netherlands, 13–14 May 1995; p. 14. [Google Scholar]
- Auset, M.; Keller, A.A. Pore-scale visualization of colloid straining and filtration in saturated porous media using micromodels. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef] [Green Version]
- Mitchell, J.K.; Soga, K. Fundamentals of Soil Behavior, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Shackelford, C.D.; Benson, C.H.; Katsumi, T.; Edil, T.B.; Lin, L. Evaluating the hydraulic conductivity of GCLs permeated with non-standard liquids. Geotext. Geomembr. 2000, 18, 133–161. [Google Scholar] [CrossRef]
- Tansel, B.; Boglaienko, D. Characterization of aggregation and declustering tendency of hydrophobic fine particles in water. Granul. Matter 2019, 21, 34. [Google Scholar] [CrossRef]
- Shang, J.; Flury, M.; Deng, Y. Force measurements between particles and the air-water interface: Implications for particle mobilization in unsaturated porous media. Water Resour. Res. 2009, 45, 6. [Google Scholar] [CrossRef] [Green Version]
- Gao, B.; Steenhuis, T.S.; Zevi, Y.; Morales, V.L.; Nieber, J.L.; Richards, B.K.; McCarthy, J.F.; Parlange, J.-Y. Capillary retention of colloids in unsaturated porous media. Water Resour. Res. 2008, 44, 4. [Google Scholar] [CrossRef] [Green Version]
- Jung, J.W.; Jang, J.; Santamarina, J.C.; Tsouris, C.; Phelps, T.J.; Rawn, C.J. Gas Production from Hydrate-Bearing Sediments: The Role of Fine Particles. Energy Fuels 2012, 26, 480–487. [Google Scholar] [CrossRef]
- Ivanov, I.B.; Kralchevsky, P.A.; Nikolov, A.D. Film and line tension effects on the attachment of particles to an interface: I. Conditions for mechanical equilibrium of fluid and solid particles at a fluid interface. J. Colloid Interface Sci. 1986, 112, 97–107. [Google Scholar] [CrossRef] [Green Version]
- Williams, D.F.; Berg, J.C. The aggregation of colloidal particles at the air—Water interface. J. Colloid Interface Sci. 1992, 152, 218–229. [Google Scholar] [CrossRef] [Green Version]
- Cao, J.; Bate, B.; Bouazza, A.; Deng, W. Measuring Retardation Factors of Cesium133 and Strontium88 Cations Using Column Test. J. Geotech. Geoenvironm. Eng. 2019, 145, 06019009. [Google Scholar] [CrossRef]
- Li, B.; Pu, S.; Mandal, S.; Li, M. Viscosity modification enhanced the migration and distribution of colloidal Mg(OH)(2) in aquifers contaminated by heavy metals. Environ. Int. 2020, 138, 105658. [Google Scholar] [CrossRef]
- Tosco, T.; Petrangeli Papini, M.; Cruz Viggi, C.; Sethi, R. Nanoscale zerovalent iron particles for groundwater remediation: A review. J. Clean. Prod. 2014, 77, 10–21. [Google Scholar] [CrossRef]
- Zou, Y.; Chen, C.; Zhang, L. Simulating Progression of Internal Erosion in Gap-Graded Sandy Gravels Using Coupled CFD-DEM. Int. J. Geomech. 2020, 20, 04019135. [Google Scholar] [CrossRef]
- Zhang, F.; Li, M.; Peng, M.; Chen, C.; Zhang, L. Three-dimensional DEM modeling of the stress-strain behavior for the gap-graded soils subjected to internal erosion. Acta Geotech. 2019, 14, 487–503. [Google Scholar] [CrossRef]
- Hu, R.; Wu, D.-S.; Yang, Z.; Chen, Y.-F. Energy Conversion Reveals Regime Transition of Imbibition in a Rough Fracture. Geophys. Res. Lett. 2018, 45, 8993–9002. [Google Scholar] [CrossRef]
- Wang, Y.; Soga, K.; Dejong, J.T.; Kabla, A.J. A microfluidic chip and its use in characterising the particle-scale behaviour of microbial-induced calcium carbonate precipitation (MICP). Géotechnique 2019, 69, 1086–1094. [Google Scholar] [CrossRef] [Green Version]
- Cao, S.; Bate, B.; Hu, J.; Jung, J. Engineering Behavior and Characteristics of Water-Soluble Polymers: Implication on Soil Remediation and Enhanced Oil Recovery. Sustainability 2016, 8, 205. [Google Scholar] [CrossRef] [Green Version]
- Valdes, J.R.; Santamarina, J.C. Clogging: Bridge formation and vibration-based destabilization. Can. Geotech. J. 2008, 45, 177–184. [Google Scholar] [CrossRef]
- Derjaguin, B.; Landau, L. Theory of the stability of strongly charged lyophobic sols and of the adhesion of strongly charged particles in solutions of electrolytes. Acta Phys. Chmica USSR 1941, 14, 633. [Google Scholar] [CrossRef]
- Verwey, E.J.W.; Overbeek, J.T.G. Theory of the Stability of Lyophobic Colloids. J. Phys. Colloid Chem. 1948, 51, 631–636. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shang, J.Q.; Lo, K.Y.; Quigley, R.M. Quantitative determination of potential distribution in Stern–Gouy double-layer model. Can. Geotech. J. 1994, 31, 624–636. [Google Scholar] [CrossRef]
- Anbari, A.; Chien, H.T.; Datta, S.S.; Deng, W.; Weitz, D.A.; Fan, J. Microfluidic Model Porous Media: Fabrication and Applications. Small 2018, 14, e1703575. [Google Scholar] [CrossRef]
- Cao, S.C.; Jung, J.; Radonjic, M. Application of microfluidic pore models for flow, transport, and reaction in geological porous media: From a single test bed to multifunction real-time analysis tool. Microsyst. Technol. 2019, 25, 4035–4052. [Google Scholar] [CrossRef]
- Jung, J.; Cao, S.C.; Shin, Y.-H.; Al-Raoush, R.I.; Alshibli, K.; Choi, J.-W. A microfluidic pore model to study the migration of fine particles in single-phase and multi-phase flows in porous media. Microsyst. Technol. 2018, 24, 1071–1080. [Google Scholar] [CrossRef]
- Dressaire, E.; Sauret, A. Clogging of microfluidic systems. Soft Matter 2017, 13, 37–48. [Google Scholar] [CrossRef] [PubMed]
- Johnson, K.L.; Kendall, K.; Roberts, A.D.; Tabor, D. Surface energy and the contact of elastic solids. Proc. R. Soc. Lond. A Math. Phys. Sci. 1971, 324, 301–313. [Google Scholar]
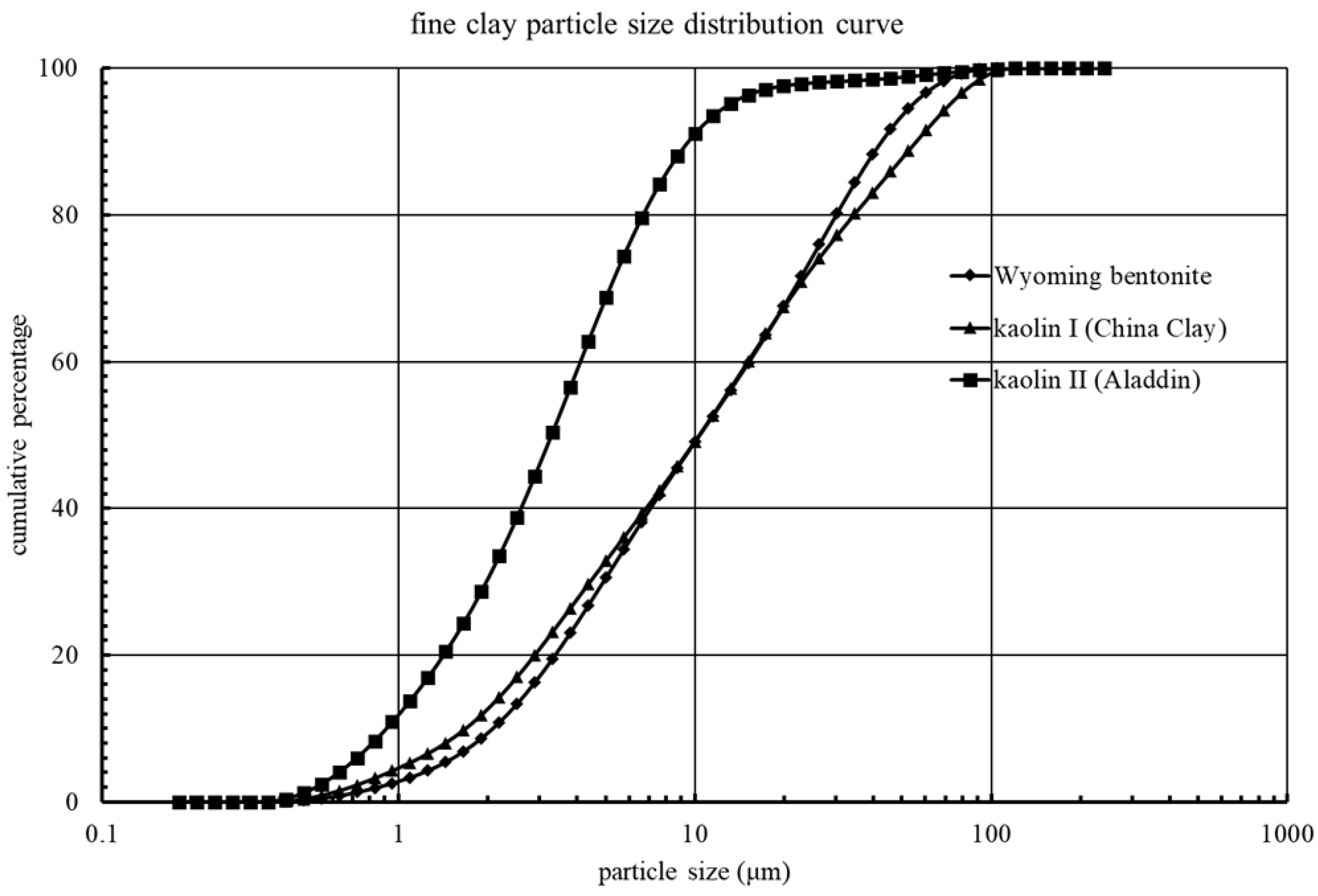

| Clay | Wyoming Bentonite | Kaolin I (China Cay) | Kaolin II (Aladdin) | |
|---|---|---|---|---|
| Carrying Fluid | ||||
| DI water | 1.16 μm | 1.28 μm | 0.92 μm | |
| 1 mol/L NaCl | 4.31 μm | 2.55 μm | 1.35 μm | |
| 2 mol/L NaCl | 4.11 μm | 2.30 μm | 1.05 μm | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bate, B.; Chen, C.; Liu, P.; Zhou, C.; Chen, X.; Nie, S.; Chen, K.; Chen, Y.; Zhang, S. The Migration and Deposition Behaviors of Montmorillonite and Kaolinite Particles in a Two-Dimensional Micromodel. Materials 2022, 15, 855. https://doi.org/10.3390/ma15030855
Bate B, Chen C, Liu P, Zhou C, Chen X, Nie S, Chen K, Chen Y, Zhang S. The Migration and Deposition Behaviors of Montmorillonite and Kaolinite Particles in a Two-Dimensional Micromodel. Materials. 2022; 15(3):855. https://doi.org/10.3390/ma15030855
Chicago/Turabian StyleBate, Bate, Chao Chen, Pengfei Liu, Chen Zhou, Xiao Chen, Shaokai Nie, Kexin Chen, Yunmin Chen, and Shuai Zhang. 2022. "The Migration and Deposition Behaviors of Montmorillonite and Kaolinite Particles in a Two-Dimensional Micromodel" Materials 15, no. 3: 855. https://doi.org/10.3390/ma15030855






