Density Functional Theory Description of Paramagnetic Hexagonal Close-Packed Iron
Abstract
:1. Introduction
2. Methods
3. Results and Discussions
3.1. Equilibrium Properties of hcp Fe
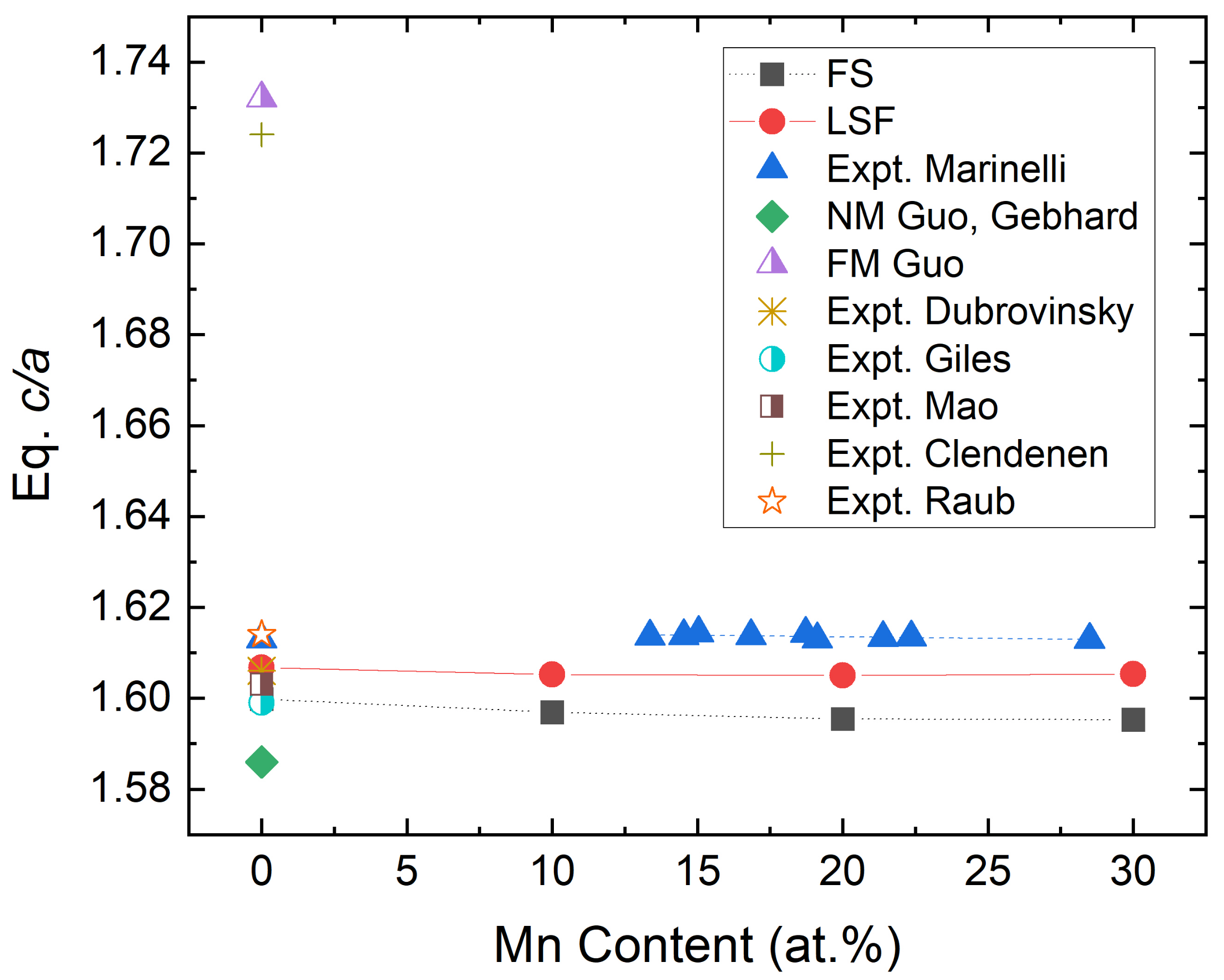
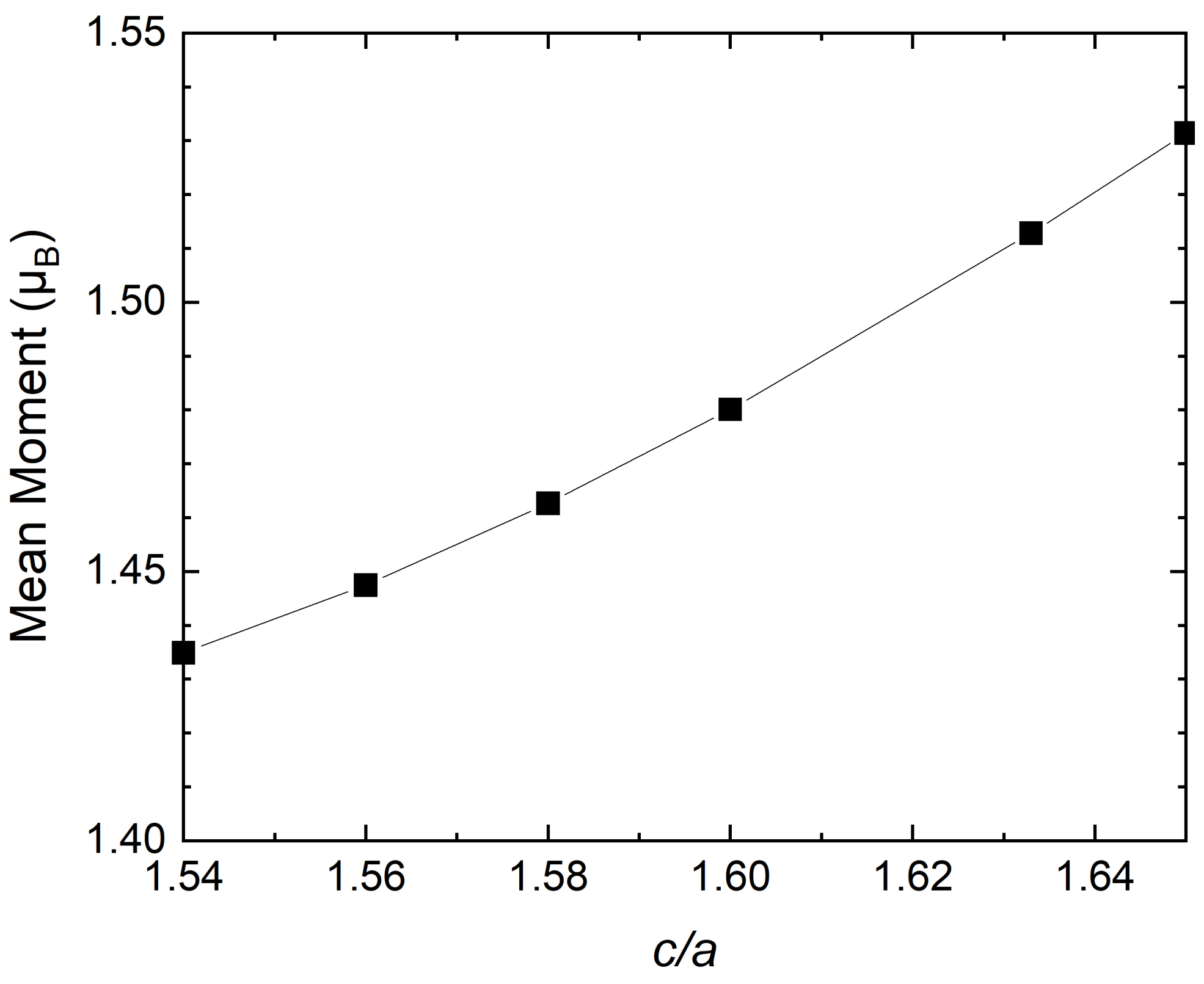
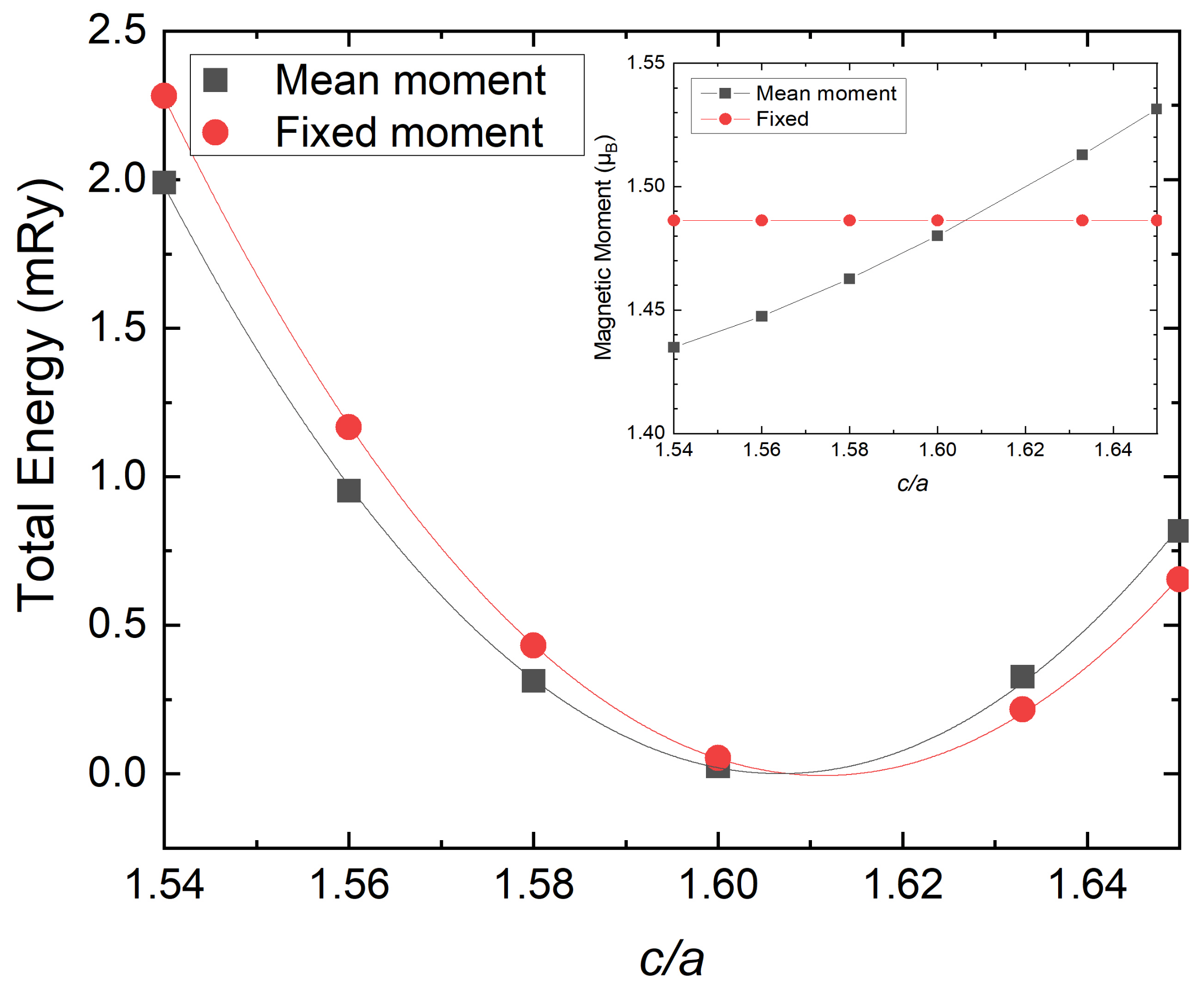
3.2. Magnetic Moments Dependence on
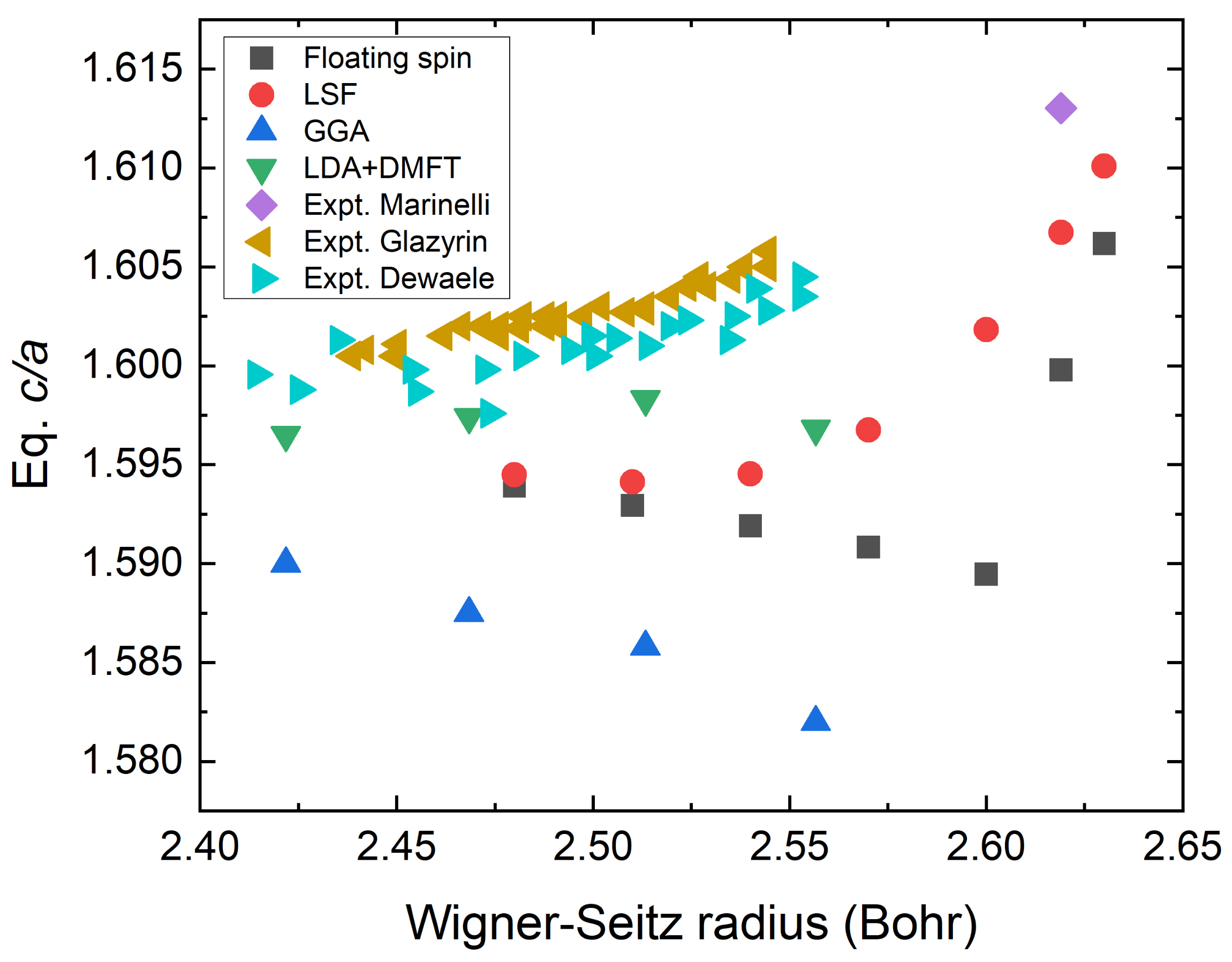
3.3. Dependence on WS Radius
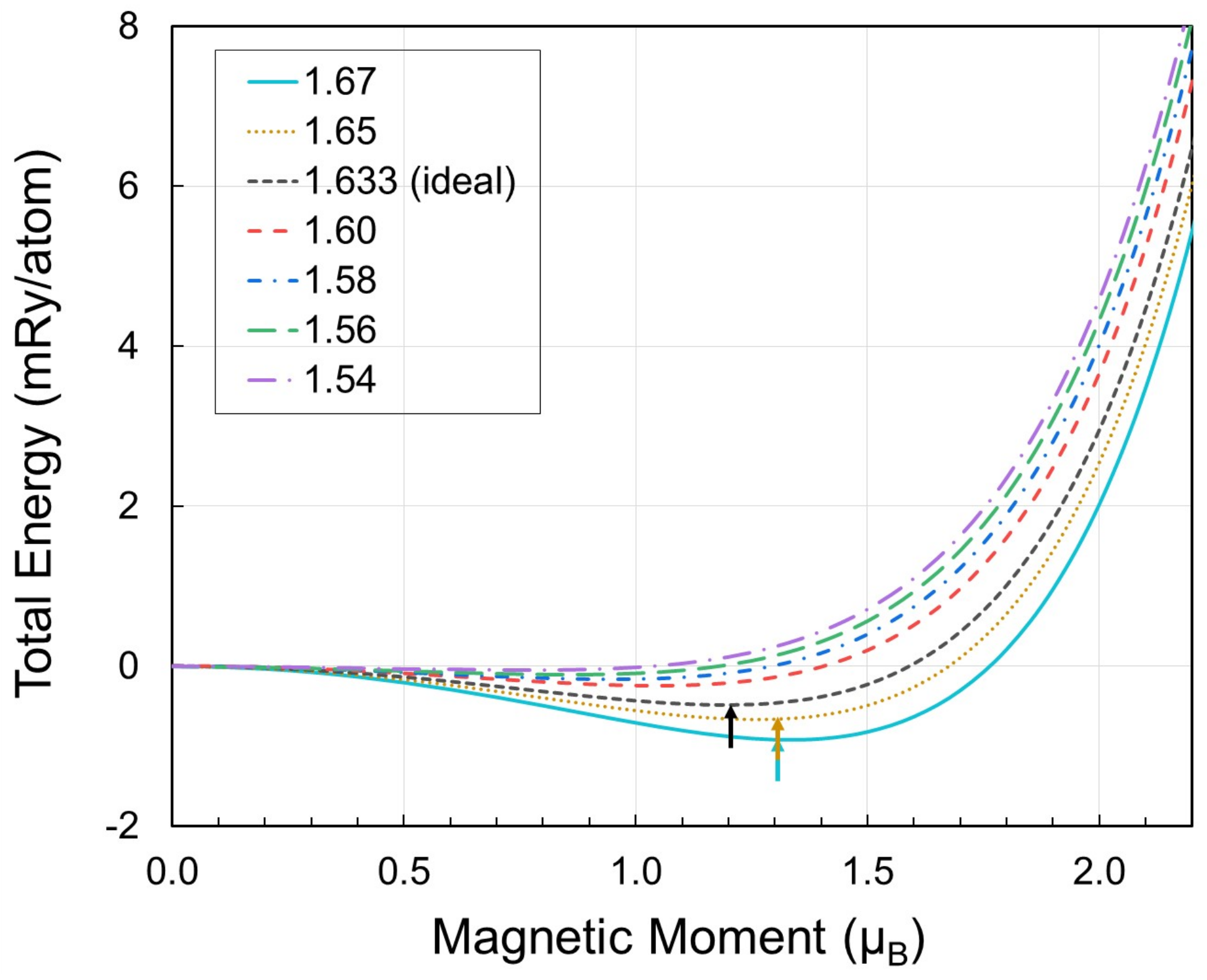
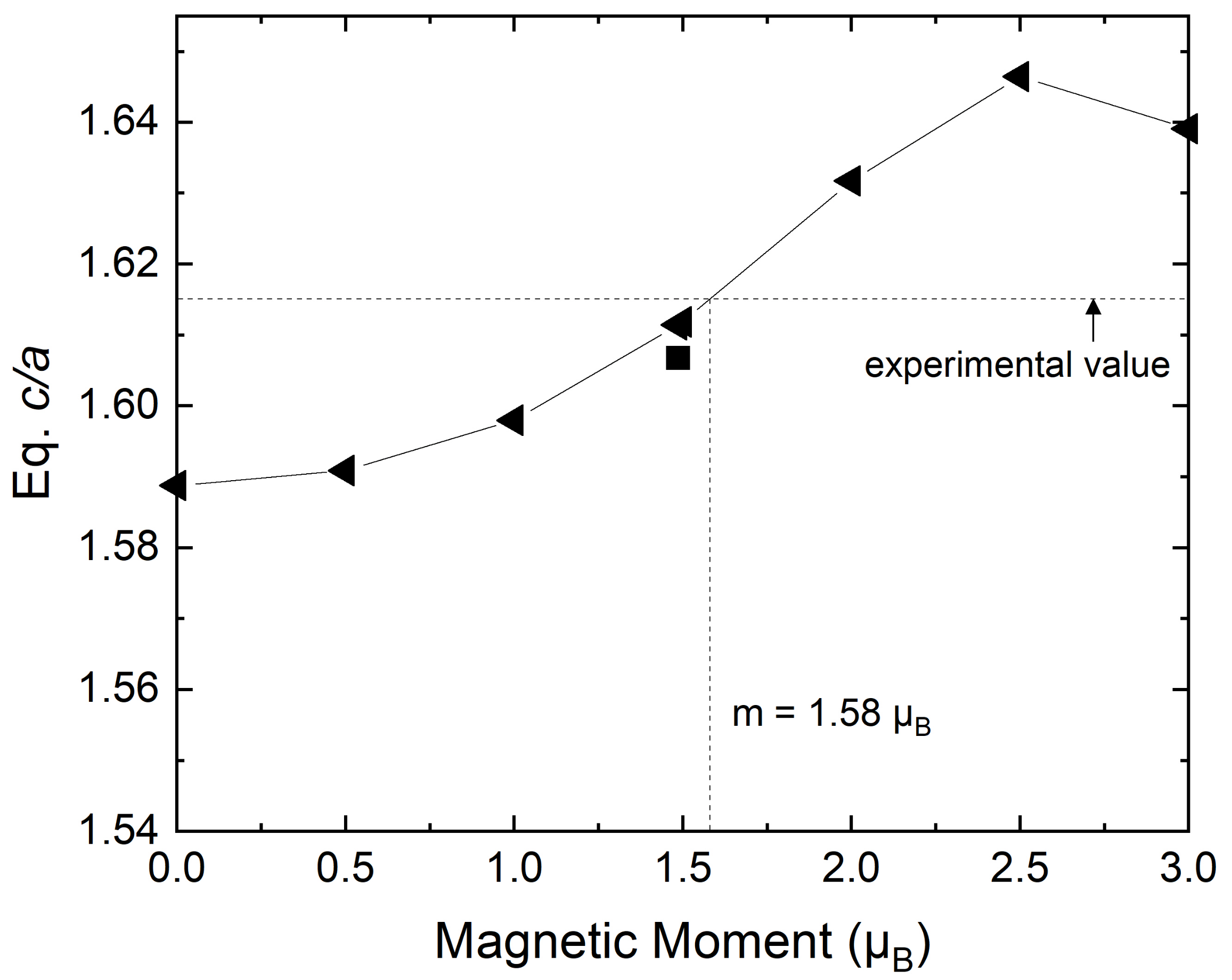
3.4. Effects of Magnetic Moments on
3.5. Other Effects on
3.6. Equation of States of Paramagnetic Fe
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pepperhoff, W.; Acet, M. The structure of iron. In Constitution and Magnetism of Iron and Its Alloys; Springer: Berlin/Heidelberg, Germany, 2001; pp. 1–13. [Google Scholar]
- Takahashi, T.; Bassett, W.A. High-Pressure Polymorph of Iron. Science 1964, 145, 483–486. [Google Scholar] [CrossRef]
- Grimvall, G. Polymorphism of Metals. III. Theory of the Temperature-Pressure Phase Diagram of Iron. Phys. Scr. 1976, 13, 59–64. [Google Scholar] [CrossRef]
- Söderlind, P.; Moriarty, J.; Wills, J. First-principles theory of iron up to earth-core pressures: Structural, vibrational, and elastic properties. Phys. Rev. B 1996, 53, 14063–14072. [Google Scholar] [CrossRef] [PubMed]
- Fei, Y.; Murphy, C.; Shibazaki, Y.; Shahar, A.; Huang, H. Thermal equation of state of hcp-iron: Constraint on the density deficit of Earth’s solid inner core. Geophys. Res. Lett. 2016, 43, 6837–6843. [Google Scholar] [CrossRef] [Green Version]
- Petrillo, C.; Postorino, P.; Orecchini, A.; Sacchetti, F. Search for the elusive magnetic state of hexagonal iron: The antiferromagnetic Fe71Ru29 hcp alloy. J. Mag. Mag. Matter. 2018, 449, 552–557. [Google Scholar] [CrossRef]
- Ritterbex, S.; Tsuchiya, T. Viscosity of hcp iron at Earth’s inner core conditions from density functional theory. Sci. Rep. 2020, 10, 6311. [Google Scholar] [CrossRef] [PubMed]
- Bigdeli, S.; Ehtehsami, H.; Chen, Q.; Mao, H.; Korzhavy, P.; Selleby, M. New description of metastable hcp phase for unaries Fe and Mn: Coupling between first-principles calculations and. Calphad Model. Phys. Status Solidi B 2016, 253, 1830–1836. [Google Scholar] [CrossRef]
- Marinelli, P.; Baruj, A.; Guillermet, A.; Sade, M. Lattice parameters of metastable structures in quenched Fe-Mn alloys. Metallkd 2001, 92, hcp489–hcp493. [Google Scholar]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, 864–871. [Google Scholar] [CrossRef] [Green Version]
- Kohn, W.; Sham, L. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, 1133–1138. [Google Scholar] [CrossRef] [Green Version]
- Bouchet, J.; Mazevet, S.; Morard, G.; Guyot, F.; Musella, R. Ab initio equation of state of iron up to 1500 GPa. Phys. Rev. B 2013, 87, 094102. [Google Scholar] [CrossRef]
- Caspersen, K.; Lew, A.; Ortiz, M.; Carter, E. Importance of Shear in the bcc-to-hcp Transformation in Iron. Phys. Rev. Lett. 2004, 93, 115501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ekman, M.; Sadigh, B.; Einarsdotter, K.; Blaha, P. Ab initio study of the martensitic bcc-hcp transformation in iron. Phys. Rev. B 1998, 58, 5296–5304. [Google Scholar] [CrossRef] [Green Version]
- Friák, M.; Šob, M. Ab initio study of the bcc-hcp transformation in iron. Phys. Rev. B 2008, 77, 174117. [Google Scholar] [CrossRef]
- Lizárraga, R.; Nordström, L.; Eriksson, O.; Wills, J. Noncollinear magnetism in the high-pressure hcp phase of iron. Phys. Rev. B 2008, 78, 064410. [Google Scholar] [CrossRef]
- Miozzi, F.; Matas, J.; Guignot, N.; Badro, J.; Siebert, J.; Fiquet, G. A New Reference for the Thermal Equation of State of Iron. Minerals 2020, 10, 100. [Google Scholar] [CrossRef] [Green Version]
- Moroni, E.; Jarlborg, T. Bcc. and h.c.p. phase competition in Fe. Europhys. Lett. 1996, 33, 223–228. [Google Scholar] [CrossRef]
- Niu, Z.W.; Zeng, Z.Y.; Cai, L.C.; Chen, X.R. Study of the thermodynamic stability of iron at inner core from first-principles theory combined with lattice dynamics. Phys. Earth Planet. Inter. 2015, 248, 12–19. [Google Scholar] [CrossRef]
- Paduani, C.; França, F. Electronic structure of hcp iron. J. Magn. Magn. Mater. 1995, 145, 147–151. [Google Scholar] [CrossRef]
- Ruban, A.; Belonoshko, A.; Skorodumova, N. Impact of magnetism on Fe under Earth’s core conditions. Phys. Rev. B 2013, 87, 014405. [Google Scholar] [CrossRef]
- Sha, X.; Cohen, R. First-principles thermal equation of state and thermoelasticity of hcp Fe at high pressures. Phys. Rev. B 2010, 81, 094105. [Google Scholar] [CrossRef] [Green Version]
- Steinle-Neumann, G.; Stixrude, L.; Cohen, R. First-principles elastic constants for the hcp transition metals Fe, Co, and Re at high pressure. Phys. Rev. B 1999, 60, 791–799. [Google Scholar] [CrossRef] [Green Version]
- Stixrude, L.; Cohen, R.; Singh, D. Iron at high pressure: Linearized-augmented-plane-wave computations in the generalized-gradient approximation. Phys. Rev. B 1994, 50, 6442–6445. [Google Scholar] [CrossRef] [PubMed]
- Wasserman, E.; Stixrude, L.; Cohen, R. Thermal properties of iron at high pressures and temperatures. Phys. Rev. B 1996, 53, 8296–8309. [Google Scholar] [CrossRef] [Green Version]
- Guo, G.; Wang, H. Gradient-Corrected Density Functional Calculation of Elastic Constants of Fe, Co and Ni in bcc, fcc and hcp Structures. Chin. J. Phys. 2000, 38, 949–961. [Google Scholar]
- Gebhardt, T.; Music, D.; Hallstedt, B.; Ekholm, M.; Abrikosov, I.; Vitos, L.; Schneider, J. Ab initio lattice stability of fcc and hcp Fe–Mn random alloys. J. Phys. Condens. Matter. 2010, 22, 295402. [Google Scholar] [CrossRef]
- Dubrovinsky, L.; Saxena, S.; Lazor, P. High-pressure and high-temperature in situ X-ray diffraction study of iron and corundum to 68 GPa using an internally heated diamond anvil cell. Phys. Chem. Miner. 1998, 25, 434–441. [Google Scholar] [CrossRef]
- Giles, P.; Longenbach, M.; Marder, A. High-Pressure α⇆ϵ Martensitic Transformation in Iron. J. Appl. Phys. 1971, 22, 4290. [Google Scholar] [CrossRef]
- Mao, H.; Bassett, W.; Takahashi, T. Effect of Pressure on Crystal Structure and Lattice Parameters of Iron up to 300 kbar. J. Appl. Phys. 1967, 38, 272. [Google Scholar] [CrossRef]
- Clendenen, R.; Drickamer, H. The effect of pressure on the volume and lattice parameters of ruthenium and iron. J. Phys. Chem. Solids 1964, 25, 865. [Google Scholar] [CrossRef]
- Raub, E.; Plate, W. DieEisen-Ruthenium-Legierungen. Z. Metallkd. 1960, 51, 477. [Google Scholar]
- Williamson, D.L.; Bukshpan, S.; Ingalls, R. Search for Magnetic Ordering in hcp Iron. Phys. Rev. B 1972, 6, 4194–4206. [Google Scholar] [CrossRef]
- Cort, G.; Taylor, R.D.; Willis, J.O. Search for magnetism in hcp ϵ-Fe. J. Appl. Phys. 1982, 53, 2064. [Google Scholar] [CrossRef]
- Steinle-Neumann, G.; Stixrude, L.; Cohen, R. Magnetism in dense hexagonal iron. Proc. Natl. Acad. Sci. USA 2004, 101, 33–36. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dong, Z.; Schönecker, S.; Li, W.; Kwon, S.; Vitos, L. Plastic deformation modes in paramagnetic γ-Fe from longitudinal spin fluctuation theory. Inter. J. Plast. 2018, 109, 43–53. [Google Scholar] [CrossRef]
- Nakano, J.; Jacques, P. Effects of the thermodynamic parameters of the hcp phase on the stacking fault energy calculations in the Fe–Mn and Fe–Mn–C systems. Calphad 2010, 34, 167–175. [Google Scholar] [CrossRef]
- Shimizu, K.; Kimura, T.; Furomoto, S.; Takeda, K.; Kontani, K.; Onuki, Y.; Amaya, K. Superconductivity in the non-magnetic state of iron under pressure. Nature 2001, 412, 316–318. [Google Scholar] [CrossRef]
- Jarlborg, T. Ferromagnetic and antiferromagnetic spin fluctuations and superconductivity in the hcp-phase of Fe. Phys. Lett. A 2002, 300, 518–523. [Google Scholar] [CrossRef] [Green Version]
- Mazin, I.; Papaconstantopoulos, D.; Mehl, M. Superconductivity in compressed iron: Role of spin fluctuations. Phys. Rev. B 2002, 65, 100511. [Google Scholar] [CrossRef] [Green Version]
- Pourovskii, L.; Mravlje, J.; Ferrero, M.; Parcollet, O.; Abrikosov, I. Impact of electronic correlations on the equation of state and transport in ϵ-Fe. Phys. Rev. B 2014, 90, 155120. [Google Scholar] [CrossRef] [Green Version]
- Martin, R.M. Electronic Structure: Basic Theory and Practical Methods; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Vitos, L. Computational Quantum Mechanics for Materials Engineers; Springer: London, UK, 2007. [Google Scholar]
- Dong, Z.; Schönecker, S.; Chen, D.; Li, W.; Lu, S.; Vitos, L. Influence of Mn content on the intrinsic energy barriers of paramagnetic FeMn alloys from longitudinal spin fluctuation theory. Int. J. Plast. 2019, 119, 123–139. [Google Scholar] [CrossRef]
- Choi, Y.; Dong, Z.; Li, W.; Schönecker, S.; Kim, H.; Kwon, S.; Vitos, L. Predicting the stacking fault energy of austenitic Fe-Mn-Al (Si) alloys. Mater. Design. 2020, 187, 108392. [Google Scholar] [CrossRef]
- Vitos, L. Total-energy method based on the exact muffin-tin orbitals theory. Phys. Rev. B 2001, 64, 014107. [Google Scholar] [CrossRef]
- Perdew, J.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Levämäki, H.; Punkkinen, M.; Kokko, K.; Vitos, L. Quasi-non-uniform gradient-level exchange-correlation approximation for metals and alloys. Phys. Rev. B 2012, 86, 201104. [Google Scholar] [CrossRef] [Green Version]
- Levämäki, H.; Punkkinen, M.; Kokko, K.; Vitos, L. Flexibility of the quasi-non-uniform exchange-correlation approximation. Phys. Rev. B 2014, 89, 115107. [Google Scholar] [CrossRef] [Green Version]
- Dong, Z.; Li, W.; Schönecker, S.; Lu, S.; Chen, D.; Vitos, L. Thermal spin fluctuation effect on the elastic constants of paramagnetic Fe from first principles. Phys. Rev. B 2015, 92, 224420. [Google Scholar] [CrossRef]
- Pindor, A.; Staunton, J.; Stocks, G.; Winter, H. Disordered local moment state of magnetic transition metals: A self-consistent KKR CPA calculation. J. Phys. F Met. Phys. 1983, 13, 979–989. [Google Scholar] [CrossRef]
- Staunton, J.; Gyorffy, B.; Pindor, A.; Stocks, G.; Winter, H. The disordered local moment picture of itinerant magnetism at finite temperatures. J. Magn. Magn. Mater. 1984, 45, 15–22. [Google Scholar] [CrossRef]
- Soven, P. Coherent-Potential Model of Substitutional Disordered Alloys. Phys. Rev. 1967, 156, 809–813. [Google Scholar] [CrossRef]
- Gyorffy, B. Coherent-Potential Approximation for a Nonoverlapping-Muffin-Tin-Potential Model of Random Substitutional Alloys. Phys. Rev. B 1972, 5, 2382–2384. [Google Scholar] [CrossRef]
- Dong, Z.; Li, W.; Chen, D.; Schönecker, S.; Long, M.; Vitos, L. Longitudinal spin fluctuation contribution to thermal lattice expansion of paramagnetic Fe. Phys. Rev. B 2017, 95, 054426. [Google Scholar] [CrossRef]
- Dong, Z.; Schönecker, S.; Chen, D.; Li, W.; Long, M.; Vitos, L. Elastic properties of paramagnetic austenitic steel at finite temperature: Longitudinal spin fluctuations in multicomponent alloys. Phys. Rev. B 2017, 96, 174415. [Google Scholar] [CrossRef] [Green Version]
- Dong, Z.; Schönecker, S.; Li, W.; Chen, D.; Vitos, L. Thermal spin fluctuations in CoCrFeMnNi high entropy alloy. Sci. Rep. 2018, 8, 12211. [Google Scholar] [CrossRef] [Green Version]
- Debye, P. Zur Theorie der spezifischen Wärmen. Ann. Phys. 1912, 344, 789. [Google Scholar] [CrossRef] [Green Version]
- Ropo, M.; Kokko, K.; Vitos, L. Assessing the Perdew-Burke-Ernzerhof exchange-correlation density functional revised for metallic bulk and surface systems. Phys. Rev. B 2008, 77, 195445. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Lu, S.; Hu, Q.M.; Johansson, B.; Kwon, S.; Grehk, M.; Johnsson, J.; Vitos, L. Generalized stacking fault energy of γ-Fe. Philos. Mag. 2016, 96, 524–541. [Google Scholar] [CrossRef]
- Glazyrin, K.; Pourovskii, L.; Dubrovinsky, L.; Narygina, O.; McCammon, C.; Hewener, B.; Schünemann, V.; Wolny, J.; Muffler, K.; Chumakov, A.; et al. Importance of Correlation Effects in hcp Iron Revealed by a Pressure-Induced Electronic Topological Transition. Phys. Rev. Lett. 2013, 110, 117206. [Google Scholar] [CrossRef]
- Dewaele, A.; Loubeyre, P.; Occelli, F.; Mezouar, M.; Dorogokupets, P.; Torrent, M. Quasihydrostatic Equation of State of Iron above 2 Mbar. Phys. Rev. Lett. 2006, 97, 215504. [Google Scholar] [CrossRef]
- Grimvall, G.; Ebbsjö, I. Polymorphism in Metals I. Vibrational Free Energy. Phys. Scr. 1975, 12, 168–172. [Google Scholar] [CrossRef]
- Grimvall, G. Spin disorder in paramagnetic fcc iron. Phys. Rev. B 1989, 39, 12300–12301. [Google Scholar] [CrossRef]
- Sherman, D. Electronic structure, entropy and the high-pressure stability of bcc iron. AIP Conf. Proc. 1994, 309, 895–898. [Google Scholar]
- Xiang, H.W. Chapter 5—Thermodynamic Properties. In The Corresponding-States Principle and Its Practice; Xiang, H.W., Ed.; Elsevier: Amsterdam, The Netherlands, 2005; pp. 49–148. [Google Scholar] [CrossRef]
- Kimball, C.; Gerber, W.; Arrott, A. Antiferromagnetism in fcc and hcp Iron—Manganese Alloys: Mössbauer. Effect J. Appl. Phys. 1963, 34, 1046–1047. [Google Scholar] [CrossRef]
- Ohno, H.; Mekata, M. Antiferromagnetism in hcp Iron-Manganese Alloys. J. Phys. Soc. Jpn. 1971, 31, 102–108. [Google Scholar] [CrossRef]
- Thakor, V.; Staunton, J.; Poulter, J.; Ostanin, S.; Ginatempo, B.; Bruno, E. Ab initio calculations of incommensurate antiferromagnetic spin fluctuations in hcp iron under pressure. Phys. Rev. B 2003, 67, 180405. [Google Scholar] [CrossRef]
| Wigner–Seitz | a | c | Magnetic | ||
|---|---|---|---|---|---|
| Radius (Bohr) | (Å) | (Å) | Moments | ||
| PBE (0 K) | 2.547 | 1.590 | 2.461 | 3.911 | 0 |
| PBE (300 K) | 2.562 | - | - | - | - |
| PBE (Expt. Vol.) | 2.619 | 1.600 | 2.525 | 4.039 | 1.16 |
| LSF (300 K) | 2.557 | 1.595 | 2.468 | 3.936 | 1.05 |
| LSF (300 K, Expt. Vol.) | 2.619 | 1.607 | 2.521 | 4.051 | 1.49 |
| QNA (0K) | 2.561 | 1.587 | 2.476 | 3.929 | 0 |
| QNA (300 K) | 2.577 | - | - | - | - |
| Expt. (300 K) | 2.619 | 1.613 | 2.517 ± 0.002 | 4.06 ± 0.01 | - |
| B | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| (GPa) | (GPa) | (GPa) | (GPa) | (GPa) | (GPa) | (GPa) | (GPa) | (K) | |
| 1.54 | 879.7 | 146.8 | 138.1 | 190.4 | 92.6 | 385.9 | 386.1 | 92.4 | 610 |
| 1.56 | 924.7 | 151.6 | 134.2 | 193.1 | 90.3 | 398.6 | 396.0 | 92.8 | 614 |
| 1.58 | 975.7 | 156.6 | 129.9 | 193.1 | 84.6 | 409.9 | 403.8 | 90.7 | 617 |
| 1.60 | 1012.7 | 161.5 | 125.9 | 190.8 | 78.3 | 415.8 | 408.5 | 85.6 | 619 |
| 1.633 | 1069.4 | 168.9 | 119.1 | 192.4 | 73.6 | 430.1 | 420.8 | 82.9 | 621 |
| 1.65 | 1099.7 | 173.3 | 115.9 | 194.7 | 72.5 | 439.0 | 429.0 | 82.5 | 623 |
| 1.67 | 1118.1 | 177.3 | 112.2 | 193.1 | 68.9 | 441.6 | 432.6 | 78.0 | 622 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, Y.; Dong, Z.; Li, W.; Lizárraga, R.; Kwon, S.-K.; Vitos, L. Density Functional Theory Description of Paramagnetic Hexagonal Close-Packed Iron. Materials 2022, 15, 1276. https://doi.org/10.3390/ma15041276
Choi Y, Dong Z, Li W, Lizárraga R, Kwon S-K, Vitos L. Density Functional Theory Description of Paramagnetic Hexagonal Close-Packed Iron. Materials. 2022; 15(4):1276. https://doi.org/10.3390/ma15041276
Chicago/Turabian StyleChoi, Youngwon, Zhihua Dong, Wei Li, Raquel Lizárraga, Se-Kyun Kwon, and Levente Vitos. 2022. "Density Functional Theory Description of Paramagnetic Hexagonal Close-Packed Iron" Materials 15, no. 4: 1276. https://doi.org/10.3390/ma15041276
APA StyleChoi, Y., Dong, Z., Li, W., Lizárraga, R., Kwon, S.-K., & Vitos, L. (2022). Density Functional Theory Description of Paramagnetic Hexagonal Close-Packed Iron. Materials, 15(4), 1276. https://doi.org/10.3390/ma15041276






