Numerical and Experimental Study on the Direct Chill Casting of Large-Scale AA2219 Billets via Annular Coupled Electromagnetic Field
Abstract
:1. Introduction
2. Materials and Methods
2.1. Model Formulation
- The melt is incompressible and isotropic;
- The turbulence effects are approximated using the realizable k-ε turbulence model;
- The densities are constant in their respective phases;
- The effect of fluid flow on the components of the electromagnetic field is neglected;
- The Joule heating is not considered in the computation due to its low frequency;
- The displacement current is not considered.
2.1.1. Governing Equation of Electromagnetic Field
2.1.2. Governing Equation
2.2. The Numerical Model
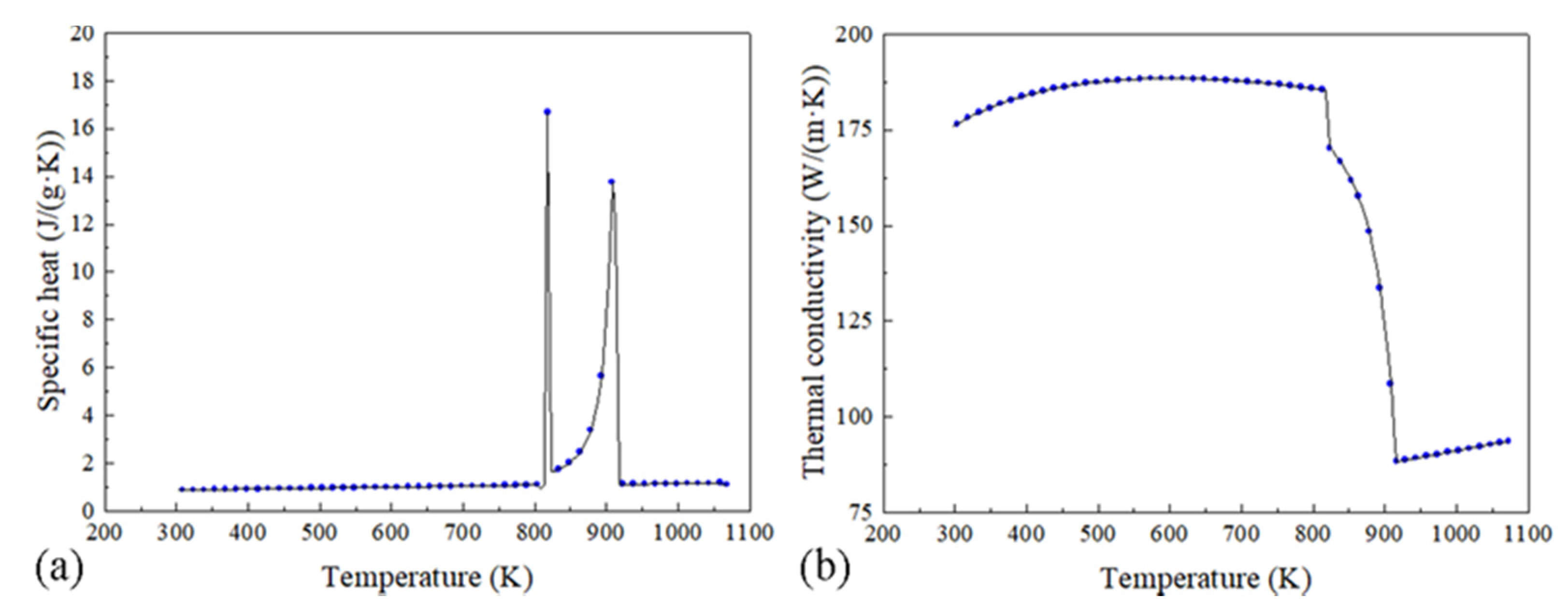
2.3. Material Properties
2.4. Boundary Conditions
2.5. Experimental Method
3. Results
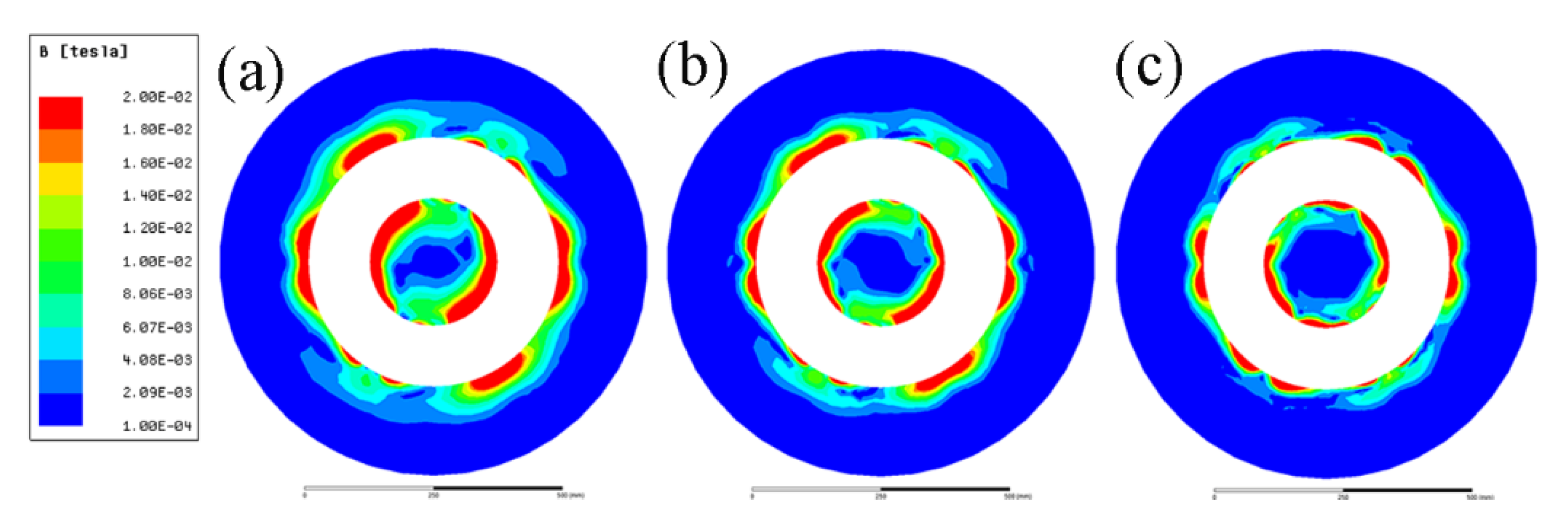
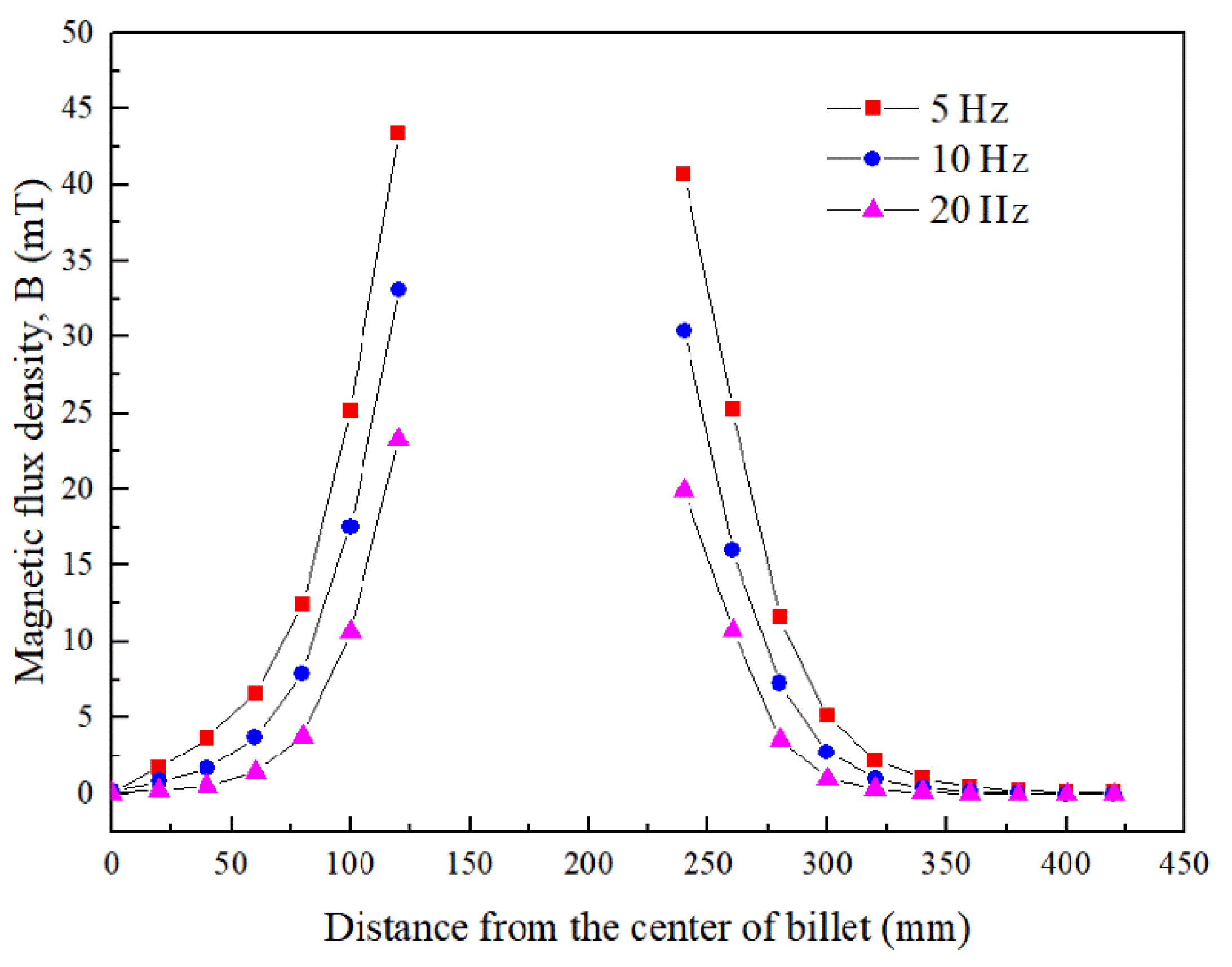
3.1. Electromagnetic Field under ICEMT Process
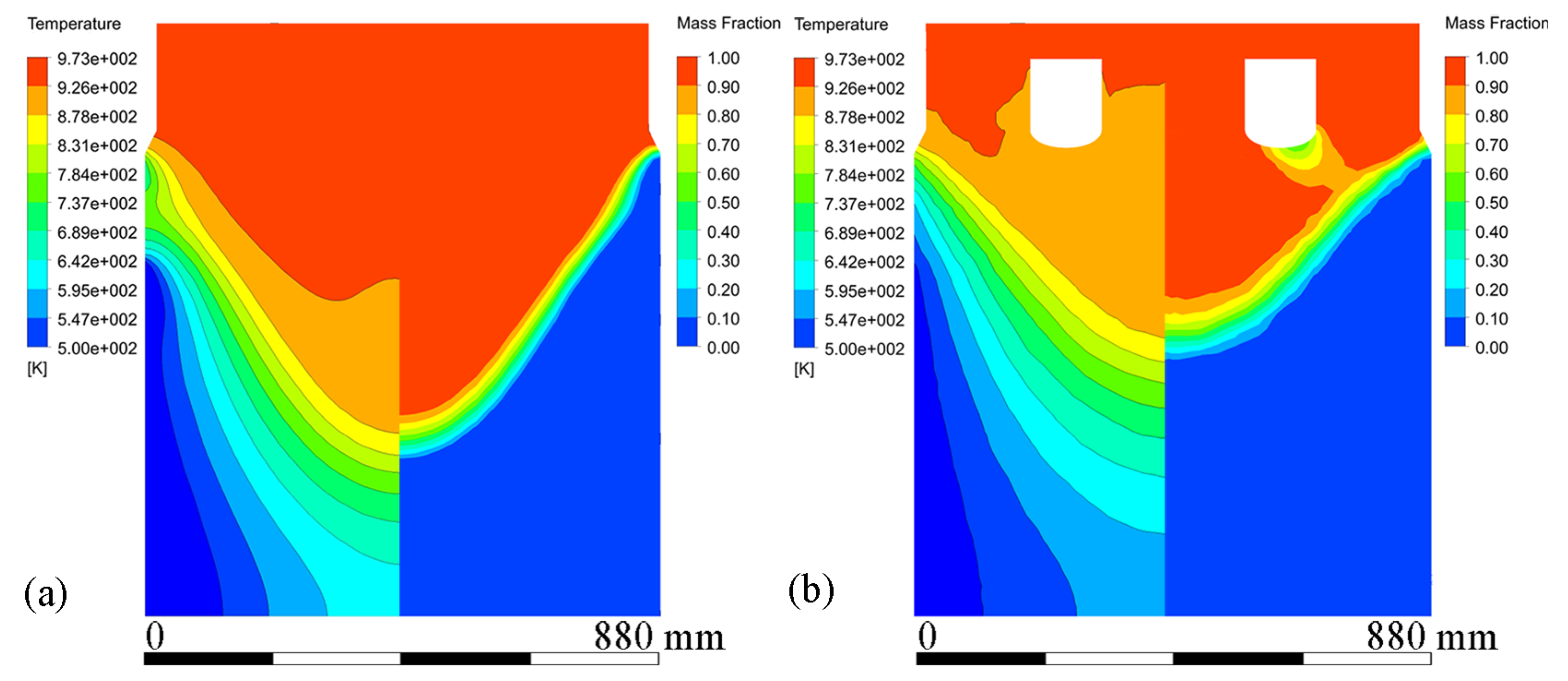
3.2. Melt Flow Pattern and Temperature Fields under ICEMT Process
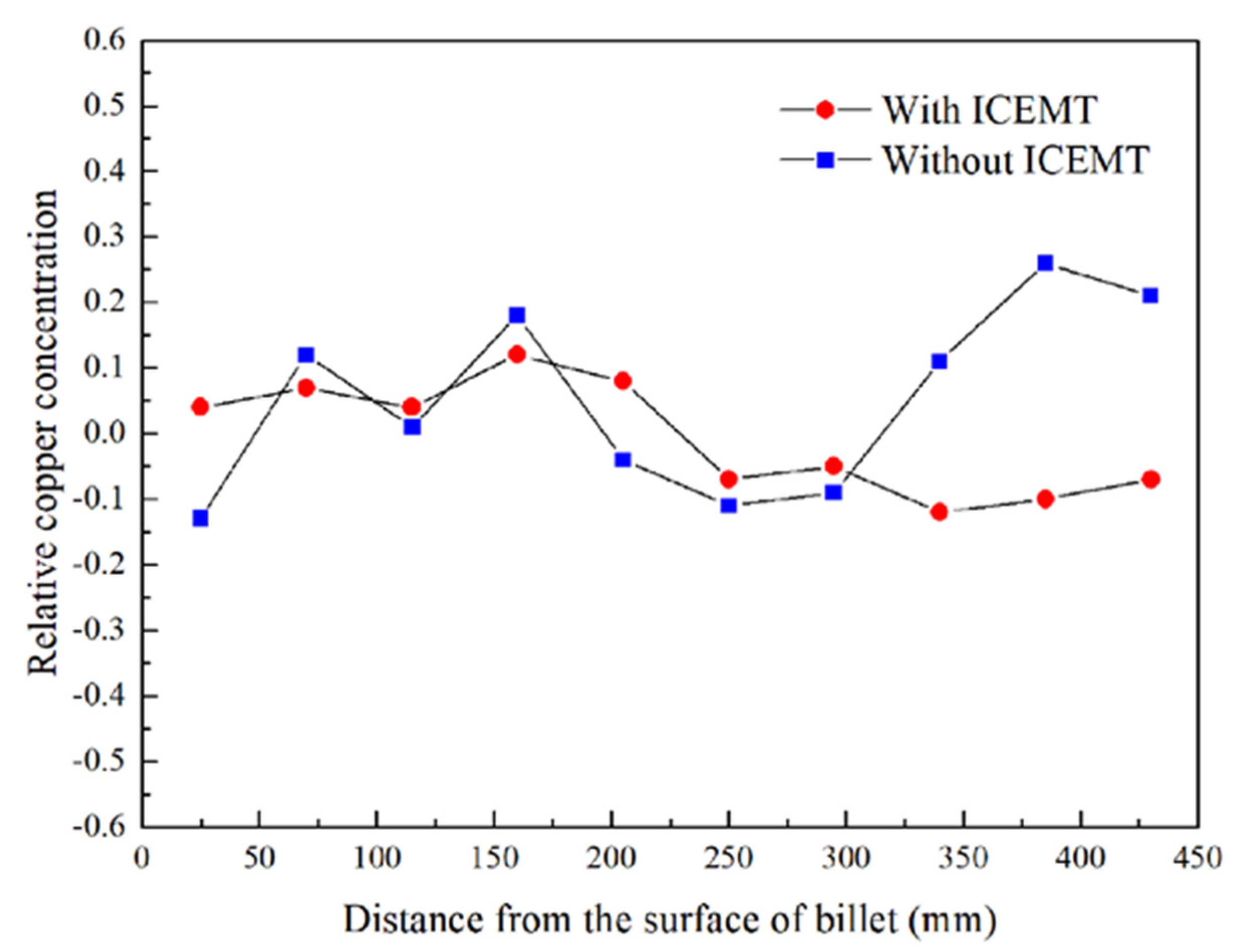
3.3. The Evolution of Microstructure under ICEMT Process
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- An, L.H.; Cai, Y.; Liu, W.; Yuan, S.J.; Zhu, S.Q.; Meng, F.C. Effect of pre-deformation on microstructure and mechanical properties of 2219 aluminum alloy sheet by thermomechanical treatment. Trans. Nonferrous Met. Soc. China 2012, 22, 370–375. [Google Scholar] [CrossRef]
- Jha, A.K.; Murty, S.V.S.N.; Sreekumar, K.; Sinha, P.P. High strain rate deformation and cracking of AA 2219 aluminium alloy welded propellant tank. Eng. Failure Anal. 2009, 16, 2209–2216. [Google Scholar] [CrossRef]
- Nadella, R.; Eskin, D.G.; Du, Q.; Katgerman, L. Macrosegregation in direct-chill casting of aluminium alloys. Prog. Mater. Sci. 2008, 53, 421–480. [Google Scholar] [CrossRef] [Green Version]
- Eskin, D.G.; Du, Q.; Katgerman, L. Scale Rules for Macrosegregation during Direct-Chill Casting of Aluminum Alloys. Metall. Trans. A 2008, 39, 1206–1212. [Google Scholar] [CrossRef]
- Haghayeghi, R.; Ezzatneshan, E.; Bahai, H. Experimental–numerical study of AA5754 microstructural evolution under electromagnetic ultrasonic merged fields. J. Mater. Process. Technol. 2015, 225, 103–109. [Google Scholar] [CrossRef]
- Zhao, Z.H.; Xu, Z.; Wang, G.S.; Zhu, Q.F.; Cui, J.Z. As-cast structure of DC casting 7075 aluminum alloy obtained under dual-frequency electromagnetic field. Int. J. Miner., Metall. Mater. 2014, 21, 150–154. [Google Scholar] [CrossRef]
- Cui, J.Z.; Zhang, Z.Q.; Le, Q.C. DC casting of light alloys under magnetic fields. Trans. Nonferrous Met. Soc. China 2010, 20, 2046–2050. [Google Scholar] [CrossRef]
- Tonry, C.E.H.; Bojarevics, V.; Djambazov, G.; Pericleous, K. Contactless Ultrasonic Treatment in Direct Chill Casting. JOM 2020, 72, 4082–4091. [Google Scholar] [CrossRef]
- Zhong, Z.T.; Li, R.Q.; Li, X.Q.; Chen, P.H. Effect of ultrasonication on the microstructure and macrosegregation of a large 2219 aluminum ingot. Chin. J. Eng. 2017, 39, 1347–1354. [Google Scholar]
- Lu, C.Y.; LI, R.Q.; Zhong, Z.T.; Cao, F.; Li, X.Q. Effects of ultrasonic filed on mirco-defects in large size 2219 aluminum alloy ingot. Tezhong Zhuzao Ji Youse Hejin 2017, 37, 1269–1273. [Google Scholar]
- Liotti, E.; Lui, A.; Vincent, R.; Kumar, S.; Guo, Z.; Connolley, T.; Dolbnya, I.P.; Hart, M.; Arnberg, L.; Mathiesen, R.H.; et al. A synchrotron X-ray radiography study of dendrite fragmentation induced by a pulsed electromagnetic field in an Al–15Cu alloy. Acta Mater. 2014, 70, 228–239. [Google Scholar] [CrossRef]
- Simlandi, S.; Barman, N.; Chattopadhyay, H. Studies on Transport Phenomena during Continuous Casting of an Al-Alloy in Presence of Electromagnetic Stirring. Trans. Indian Inst. Met. 2012, 66, 141–146. [Google Scholar] [CrossRef]
- Zuo, Y.B.; Cui, J.Z.; Mou, D.; Zhu, Q.F.; Wang, X.J.; Li, L. Effect of electromagnetic field on microstructure and macrosegregation of flat ingot of 2524 aluminium alloy. Trans. Nonferrous Met. Soc. China 2014, 24, 2408–2413. [Google Scholar] [CrossRef]
- Vives, C. Electromagnetic refining of aluminum alloys by the CREM process. Metall. Mater. Trans. B 1988, 20, 623–631. [Google Scholar] [CrossRef]
- Zhang, B.; Cui, J.Z.; Lu, G. Effects of low-frequency electromagnetic field on microstructures and macrosegregation of continuous casting 7075 aluminum alloy. Mater. Sci. Eng. A 2003, 355, 325–330. [Google Scholar] [CrossRef]
- Waheed, M.A.; Nzebuka, G.C. Analysis of thermally driven flow pattern formation in aluminium DC casting for different Rayleigh numbers and billet diameters. Therm. Sci. Eng. Prog. 2020, 18, 100536. [Google Scholar] [CrossRef]
- Nzebuka, G.C.; Waheed, M.A. Thermal evolution in the direct chill casting of an Al-4 pct Cu alloy using the low-Reynolds number turbulence model. Int. J. Therm. Sci. 2020, 147, 106152. [Google Scholar] [CrossRef]
- Hatić, V.; Mavrič, B.; Košnik, N.; Šarler, B. Simulation of direct chill casting under the influence of a low-frequency electromagnetic field. Appl. Math. Model. 2018, 54, 170–188. [Google Scholar] [CrossRef]
- Sarler, B.; Dobravec, T.; Glavan, G.; Hatić, V.; Mavrič, B.; Vertnik, R.; Cvahte, P.; Gregor, F.; Jelen, M.; Petrovič, M. Multi-Physics and Multi-Scale Meshless Simulation System for Direct-Chill Casting of Aluminium Alloys. Stroj Vestn-J. Mech. E. 2019, 65, 658–670. [Google Scholar] [CrossRef]
- Wang, H.; Jia, Y.; Le, Q.; Bao, L. Transient numerical simulation of solidification characteristic under differential phase pulsed magnetic field. Comput. Mater. Sci. 2020, 172, 109261. [Google Scholar] [CrossRef]
- Ren, B.; Chen, D.; Wang, H.; Long, M. Numerical Analysis of Coupled Turbulent Flow and Macroscopic Solidification in a Round Bloom Continuous Casting Mold with Electromagnetic Stirring. Steel Res. Int. 2015, 86, 1104–1115. [Google Scholar] [CrossRef]
- Tang, M.O.; Xu, J.; Zhang, Z.F.; Bai, Y.L. Effects of annulus gap on flow and temperature field in electromagnetic direct chill casting process. Trans. Nonferrous Met. Soc. China 2011, 21, 1123–1129. [Google Scholar] [CrossRef]
- Luo, Y.; Zhang, Z. Numerical modeling of annular electromagnetic stirring with intercooling in direct chill casting of 7005 aluminum alloy billet. Prog. Nat. Sci. Mater. Int. 2019, 29, 81–87. [Google Scholar] [CrossRef]
- Luo, Y.; Zhang, Z.; Li, B.; Gao, M.; Qiu, Y.; He, M. Effects of Annular Electromagnetic Stirring Coupled with Intercooling on Grain Refinement and Homogeneity During Direct Chill Casting of Large-Sized 7005 Alloy Billet. JOM 2017, 69, 2640–2643. [Google Scholar] [CrossRef]
- Qiu, Y.; Zhang, Z.; Luo, Y.; Gao, M.; Li, B.; Chen, C. Effect of coupled annular electromagnetic stirring and intercooling on 2219 Al alloy billets. Int. J. Mater. Res. 2018, 5, 469–475. [Google Scholar] [CrossRef]
- Qiu, Y.; Zhang, Z.; Zhao, H. Internal electromagnetic stirring method for preparing a large-sized aluminum alloy billet. Int. J. Mater. Res. 2019, 11, 1083–1086. [Google Scholar] [CrossRef]
- Voller, V.R.; Prakash, C. A fixed grid numerical modelling methodology for convection-diffusion mushy region phase-change problems. Int. J. Heat Mass Transf. 1987, 30, 1709–1719. [Google Scholar] [CrossRef]
- Sengupta, J.; Cockcroft, S.L.; Maijer, D.M.; Wells, M.A.; Larouche, A. On the development of a three-dimensional transient thermal model to predict ingot cooling behavior during the start-up phase of the direct chill-casting process for an AA5182 aluminum alloy ingot. Metall. Mater. B 2004, 35, 523–540. [Google Scholar] [CrossRef]
- Suyitno, W.; Kool, H.; Katgerman, L. Finite element method simulation of mushy zone behavior during direct-chill casting of an Al-4.5 pct Cu alloy. Metall. Mater. A 2004, 35, 2917–2926. [Google Scholar] [CrossRef]
- Eskin, D. Effect of different grain structures on centerline macrosegregation during direct-chill casting. Acta Mater. 2008, 56, 1358–1365. [Google Scholar] [CrossRef] [Green Version]
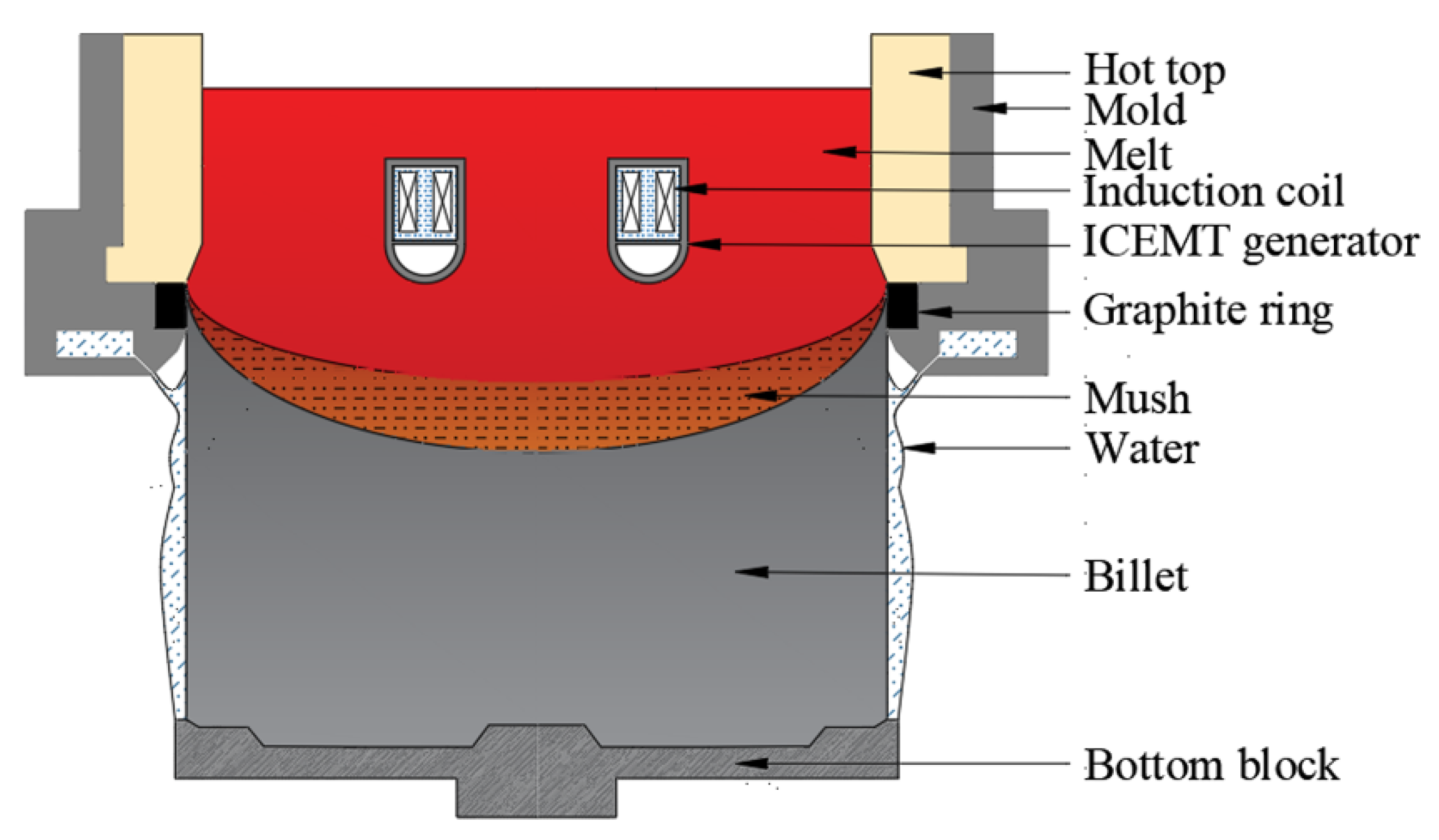
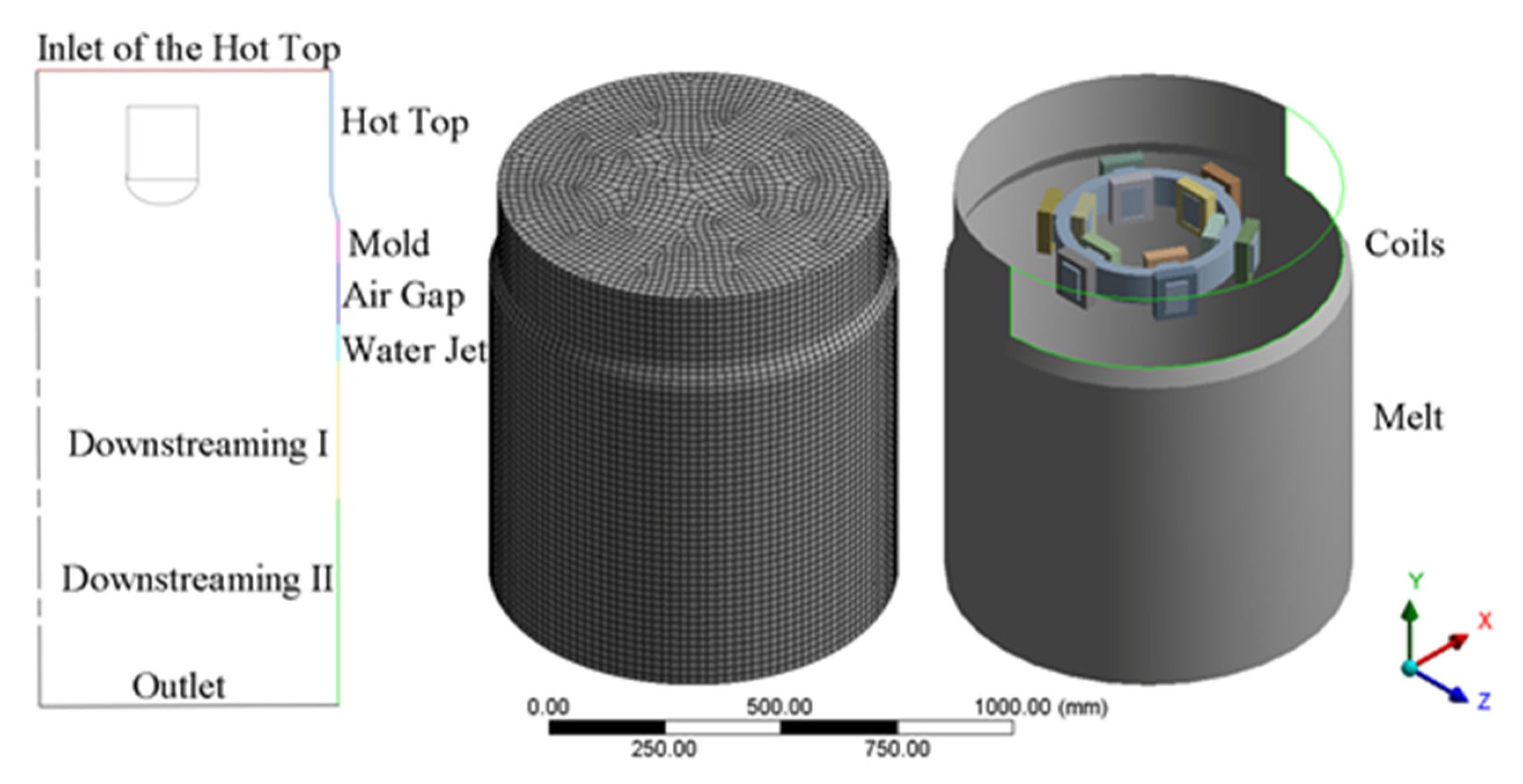


| Geometry Dimensions | Values/mm |
|---|---|
| Hot top | 220 |
| Mold | 60 |
| Air gap | 120 |
| Water jet | 100 |
| DownstreamingI | 200 |
| DownstreamingII | 300 |
| Thermophysical Properties | Values | Unit |
|---|---|---|
| Liquid density | 2520 | kg/m3 |
| Solid density | 2719 | kg/m3 |
| Dynamic viscosity | 1.42 × 10−3 | Pa·s |
| Solidus temperature | 813 | K |
| Liquidus temperature | 916 | K |
| Specific heat | As shown in Figure 3a | J/(g·K) |
| Latent heat | 3.85 × 106 | J/kg |
| Liquid thermal expansion coefficient | 4.4 × 10−5 | 1/K |
| Thermal conductivity | As shown in Figure 3b | W/(m·K) |
| Physical Properties | Al-Alloy | Coils | Yoke | Air |
|---|---|---|---|---|
| Relative permeability | 1 | 1 | 2000 | 1 |
| Relative dielectric | 1 | 1 | 1 | 1 |
| Conductivity (S/m) | 3.8 × 107 | 5.8 × 107 | 2 × 106 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, H.; Zhang, Z.; Bai, Y.; Li, B.; Gao, M. Numerical and Experimental Study on the Direct Chill Casting of Large-Scale AA2219 Billets via Annular Coupled Electromagnetic Field. Materials 2022, 15, 1802. https://doi.org/10.3390/ma15051802
Zhao H, Zhang Z, Bai Y, Li B, Gao M. Numerical and Experimental Study on the Direct Chill Casting of Large-Scale AA2219 Billets via Annular Coupled Electromagnetic Field. Materials. 2022; 15(5):1802. https://doi.org/10.3390/ma15051802
Chicago/Turabian StyleZhao, Haodong, Zhifeng Zhang, Yuelong Bai, Bao Li, and Mingwei Gao. 2022. "Numerical and Experimental Study on the Direct Chill Casting of Large-Scale AA2219 Billets via Annular Coupled Electromagnetic Field" Materials 15, no. 5: 1802. https://doi.org/10.3390/ma15051802
APA StyleZhao, H., Zhang, Z., Bai, Y., Li, B., & Gao, M. (2022). Numerical and Experimental Study on the Direct Chill Casting of Large-Scale AA2219 Billets via Annular Coupled Electromagnetic Field. Materials, 15(5), 1802. https://doi.org/10.3390/ma15051802






