Inverse Design of Materials by Machine Learning
Abstract
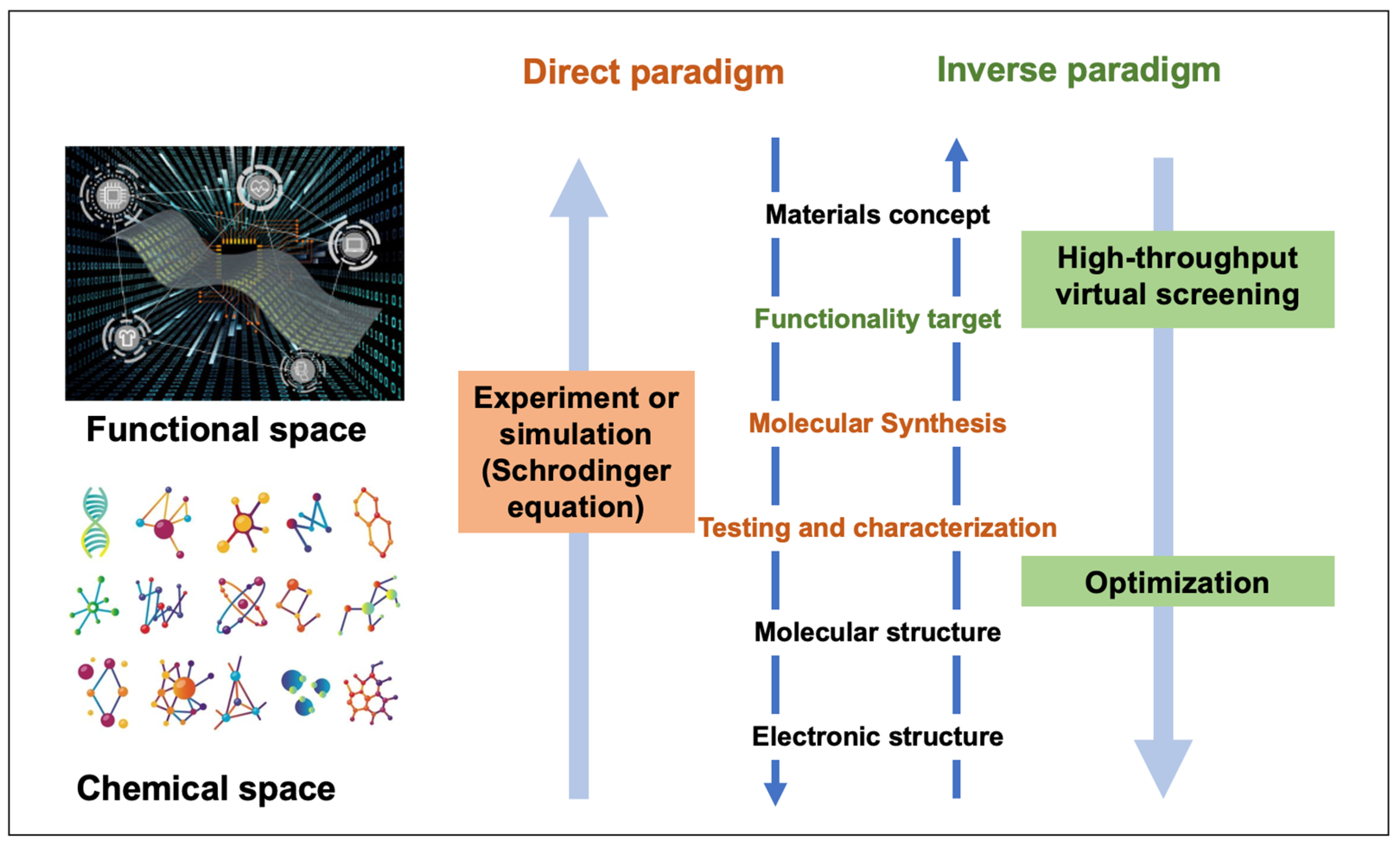
:1. Introduction
2. Inverse Design
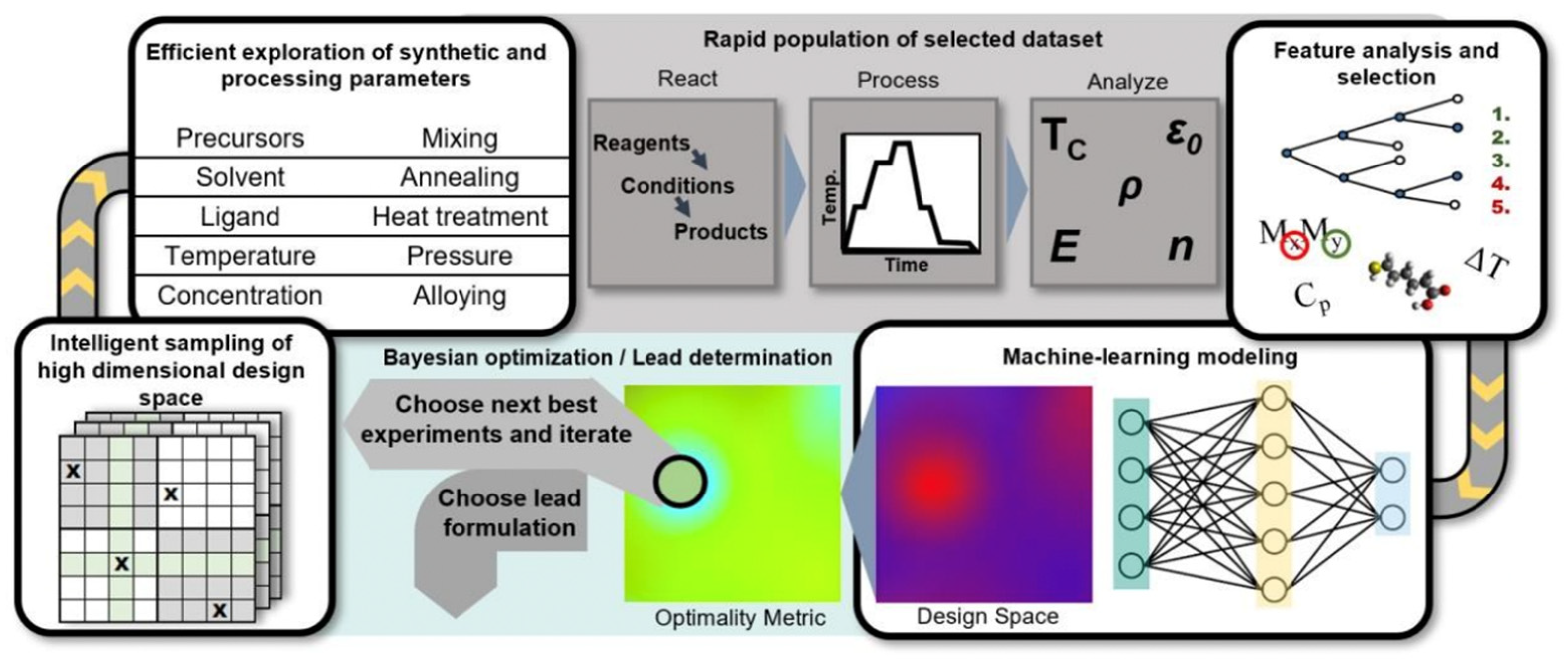
2.1. High Throughput Virtual Screening (HTVS)
2.2. Global Optimization (GO)
2.3. Generative Models (GM)
3. Application in Materials Design
3.1. Polymers
3.2. Photonic
3.3. Inorganic Solid-State Functional Materials
3.4. Porous Materials
3.5. Other Materials
4. Challenges and Opportunities
Author Contributions
Funding
Informed Consent Statement
Conflicts of Interest
References
- Sass, S.L. The Substance of Civilization: Materials and Human History from the Stone Age to the Age of Silicon; Arcade Publishing: New York, NY, USA, 1998. [Google Scholar]
- Headrick, D.R. When Information Came of Age: Technologies of Knowledge in the Age of Reason and Revolution, 1700–1850; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Agrawal, A.; Choudhary, A. Perspective: Materials informatics and big data: Realization of the “fourth paradigm” of science in materials science. APL Mater. 2016, 4, 053208. [Google Scholar] [CrossRef] [Green Version]
- Pople, J.A. Quantum Chemical Models (Nobel Lecture). Angew. Chem. Int. Ed. 1999, 38, 1894–1902. [Google Scholar] [CrossRef]
- Garrity, K.F.; Bennett, J.W.; Rabe, K.M.; Vanderbilt, D. Pseudopotentials for high-throughput DFT calculations. Comput. Mater. Sci. 2014, 81, 446–452. [Google Scholar] [CrossRef] [Green Version]
- Hobart, M.E.; Schiffman, Z.S. Information Ages: Literacy, Numeracy, and the Computer Revolution; JHU Press: Baltimore, MD, USA, 2000. [Google Scholar]
- Mosavi, A.; Vaezipour, A. Reactive Search Optimization; Application to Multiobjective Optimization Problems. Appl. Math. 2012, 3, 1572–1582. [Google Scholar] [CrossRef] [Green Version]
- Rajan, K. Informatics for Materials Science and Engineering: Data-Driven Discovery for Accelerated Experimentation and Application; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]
- Mosavi, A.; Rabczuk, T.; Varkonyi-Koczy, A.R. Reviewing the novel machine learning tools for materials design. In Recent Advances in Technology Research and Education; Advances in Intelligent Systems and Computing; Springer: Cham, Switzerland, 2018; pp. 50–58. [Google Scholar]
- Goh, G.B.; Hodas, N.O.; Vishnu, A. Deep learning for computational chemistry. J. Comput. Chem. 2017, 38, 1291–1307. [Google Scholar] [CrossRef] [Green Version]
- Dam, H.C.; Pham, T.L.; Ho, T.B.; Nguyen, A.T.; Nguyen, V.C. Data mining for materials design: A computational study of single molecule magnet. J. Chem. Phys. 2014, 140, 044101. [Google Scholar] [CrossRef] [PubMed]
- Coley, C.W.; Green, W.H.; Jensen, K.F. Machine Learning in Computer-Aided Synthesis Planning. Acc. Chem. Res. 2018, 51, 1281–1289. [Google Scholar] [CrossRef] [PubMed]
- Kim, E.; Huang, K.; Jegelka, S.; Olivetti, E. Virtual screening of inorganic materials synthesis parameters with deep learning. npj Comput. Mater. 2017, 3, 53. [Google Scholar] [CrossRef]
- Mardt, A.; Pasquali, L.; Wu, H.; Noe, F. VAMPnets for deep learning of molecular kinetics. Nat. Commun. 2018, 9, 5. [Google Scholar] [CrossRef]
- Chen, C.; Lu, Z.; Ciucci, F. Data mining of molecular dynamics data reveals Li diffusion characteristics in garnet Li7La3Zr2O12. Sci. Rep. 2017, 7, 40769. [Google Scholar] [CrossRef] [Green Version]
- Gopnik, A. Making AI More Human. Sci. Am. 2017, 316, 60–65. [Google Scholar] [CrossRef]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef] [PubMed]
- Provost, F.; Kohavi, R. Glossary of terms. J. Mach. Learn. 1998, 30, 271–274. [Google Scholar] [CrossRef]
- Wei, J.; Chu, X.; Sun, X.Y.; Xu, K.; Deng, H.X.; Chen, J.; Wei, Z.; Lei, M. Machine learning in materials science. InfoMat 2019, 1, 338–358. [Google Scholar] [CrossRef]
- Fischer, C.C.; Tibbetts, K.J.; Morgan, D.; Ceder, G. Predicting crystal structure by merging data mining with quantum mechanics. Nat. Mater. 2006, 5, 641–646. [Google Scholar] [CrossRef]
- Takahashi, K.; Tanaka, Y. Material synthesis and design from first principle calculations and machine learning. Comput. Mater. Sci. 2016, 112, 364–367. [Google Scholar] [CrossRef]
- Liu, Y.; Niu, C.; Wang, Z.; Gan, Y.; Zhu, Y.; Sun, S.; Shen, T. Machine learning in materials genome initiative: A review. J. Mater. Sci. Technol. 2020, 57, 113–122. [Google Scholar] [CrossRef]
- Moosavi, S.M.; Jablonka, K.M.; Smit, B. The Role of Machine Learning in the Understanding and Design of Materials. J. Am. Chem. Soc. 2020, 142, 20273–20287. [Google Scholar] [CrossRef] [PubMed]
- Ward, L.; Agrawal, A.; Choudhary, A.; Wolverton, C. A general-purpose machine learning framework for predicting properties of inorganic materials. npj Comput. Mater. 2016, 2, 16028. [Google Scholar] [CrossRef] [Green Version]
- Kim, C.; Batra, R.; Chen, L.; Tran, H.; Ramprasad, R. Polymer design using genetic algorithm and machine learning. Comput. Mater. Sci. 2021, 186, 110067. [Google Scholar] [CrossRef]
- Seko, A.; Hayashi, H.; Nakayama, K.; Takahashi, A.; Tanaka, I. Representation of compounds for machine-learning prediction of physical properties. Phys. Rev. B 2017, 95, 144110. [Google Scholar] [CrossRef] [Green Version]
- Burbidge, R.; Trotter, M.; Buxton, B.; Holden, S. Drug design by machine learning: Support vector machines for pharmaceutical data analysis. Comput. Chem. 2001, 26, 5–14. [Google Scholar] [CrossRef]
- Linares, N.; Silvestre-Albero, A.M.; Serrano, E.; Silvestre-Albero, J.; García-Martínez, J. Mesoporous materials for clean energy technologies. Chem. Soc. Rev. 2014, 43, 7681–7717. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, S.; Shen, Y.; Zhang, Y.; Cui, B.; Xi, S.; Zhang, J.; Xu, L.; Zhu, S.; Chen, Y.; Deng, Y.; et al. Extreme Environmental Thermal Shock Induced Dislocation-Rich Pt Nanoparticles Boosting Hydrogen Evolution Reaction. Adv. Mater. 2021, 34, 2106973. [Google Scholar] [CrossRef]
- Liu, C.; Zhou, W.; Zhang, J.; Chen, Z.; Liu, S.; Zhang, Y.; Yang, J.; Xu, L.; Hu, W.; Chen, Y.; et al. Air-Assisted Transient Synthesis of Metastable Nickel Oxide Boosting Alkaline Fuel Oxidation Reaction. Adv. Energy Mater. 2020, 10, 10. [Google Scholar] [CrossRef]
- Liu, S.; Hu, Z.; Wu, Y.; Zhang, J.; Zhang, Y.; Cui, B.; Liu, C.; Hu, S.; Zhao, N.; Han, X.; et al. Dislocation-Strained IrNi Alloy Nanoparticles Driven by Thermal Shock for the Hydrogen Evolution Reaction. Adv. Mater. 2020, 32, e2006034. [Google Scholar] [CrossRef]
- Wu, H.; Lu, Q.; Zhang, J.; Wang, J.; Han, X.; Zhao, N.; Hu, W.; Li, J.; Chen, Y.; Deng, Y. Thermal Shock-Activated Spontaneous Growing of Nanosheets for Overall Water Splitting. Nanomicro. Lett. 2020, 12, 162. [Google Scholar] [CrossRef]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vettering, W.T. Numerical Recipes in C: The Art of Scientific Computing; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Kuhn, C.; Beratan, D.N. Inverse Strategies for Molecular Design. J. Phys. Chem. 1996, 100, 10595–10599. [Google Scholar] [CrossRef]
- Zunger, A. Inverse design in search of materials with target functionalities. Nat. Rev. Chem. 2018, 2, 0121. [Google Scholar] [CrossRef]
- Sanchez-Lengeling, B.; Aspuru-Guzik, A. Inverse molecular design using machine learning: Generative models for matter engineering. Science 2018, 361, 360–365. [Google Scholar] [CrossRef] [Green Version]
- Peurifoy, J.; Shen, Y.; Jing, L.; Yang, Y.; Cano-Renteria, F.; DeLacy, B.G.; Joannopoulos, J.D.; Tegmark, M.; Soljacic, M. Nanophotonic particle simulation and inverse design using artificial neural networks. Sci. Adv. 2018, 4, eaar4206. [Google Scholar] [CrossRef] [Green Version]
- Patra, T.K.; Loeffler, T.D.; Sankaranarayanan, S. Accelerating copolymer inverse design using monte carlo tree search. Nanoscale 2020, 12, 23653–23662. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.; Yamada, H.; Hayashi, Y.; Zamengo, M.; Yoshida, R. Potentials and challenges of polymer informatics: Exploiting machine learning for polymer design. arXiv 2020, arXiv:2010.07683. [Google Scholar]
- Chen, L.; Zhang, W.; Nie, Z.; Li, S.; Pan, F. Generative models for inverse design of inorganic solid materials. J. Mater. Inform. 2021, 1, 4. [Google Scholar] [CrossRef]
- Sattari, K.; Xie, Y.; Lin, J. Data-driven algorithms for inverse design of polymers. Soft Matter 2021, 17, 7607–7622. [Google Scholar] [CrossRef] [PubMed]
- Pyzer-Knapp, E.O.; Suh, C.; Gómez-Bombarelli, R.; Aguilera-Iparraguirre, J.; Aspuru-Guzik, A. What is high-throughput virtual screening? A perspective from organic materials discovery. Annu. Rev. Mater. Res. 2015, 45, 195–216. [Google Scholar] [CrossRef] [Green Version]
- Jang, J.; Gu, G.H.; Noh, J.; Kim, J.; Jung, Y. Structure-Based Synthesizability Prediction of Crystals Using Partially Supervised Learning. J. Am. Chem. Soc. 2020, 142, 18836–18843. [Google Scholar] [CrossRef] [PubMed]
- Afzal, M.A.F.; Haghighatlari, M.; Ganesh, S.P.; Cheng, C.; Hachmann, J. Accelerated Discovery of High-Refractive-Index Polyimides via First-Principles Molecular Modeling, Virtual High-Throughput Screening, and Data Mining. J. Phys. Chem. C 2019, 123, 14610–14618. [Google Scholar] [CrossRef]
- Scales, J.A.; Smith, M.L.; Fischer, T.L. Global optimization methods for multimodal inverse problems. J. Comput. Phys. 1992, 103, 258–268. [Google Scholar] [CrossRef]
- Harper, E.; Mills, M. Bayesian Optimization of Neural Networks for the Inverse Design of All-Dielectric Metasurfaces; SPIE: Bellingham, WA, USA, 2020; Volume 11469. [Google Scholar]
- Geng, Y.; van Anders, G.; Glotzer, S.C. Predicting colloidal crystals from shapes via inverse design and machine learning. arXiv 2018, arXiv:1801.06219. [Google Scholar]
- Lee, Y.; Choi, G.; Yoon, M.; Kim, C. Genetic Algorithm for Constrained Molecular Inverse Design. arXiv 2021, arXiv:2112.03518. [Google Scholar]
- Odena, A. Semi-supervised learning with generative adversarial networks. arXiv 2016, arXiv:1606.01583. [Google Scholar]
- Kim, K.; Kang, S.; Yoo, J.; Kwon, Y.; Nam, Y.; Lee, D.; Kim, I.; Choi, Y.-S.; Jung, Y.; Kim, S.; et al. Deep-learning-based inverse design model for intelligent discovery of organic molecules. npj Comput. Mater. 2018, 4, 4. [Google Scholar] [CrossRef] [Green Version]
- Ma, W.; Cheng, F.; Xu, Y.; Wen, Q.; Liu, Y. Probabilistic Representation and Inverse Design of Metamaterials Based on a Deep Generative Model with Semi-Supervised Learning Strategy. Adv. Mater. 2019, 31, e1901111. [Google Scholar] [CrossRef] [Green Version]
- Popova, M.; Isayev, O.; Tropsha, A. Deep reinforcement learning for de novo drug design. Sci. Adv. 2018, 4, eaap7885. [Google Scholar] [CrossRef] [Green Version]
- Mishra, M. Encyclopedia of Polymer Applications, 3 Volume Set; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Kumar, J.N.; Li, Q.; Jun, Y. Challenges and opportunities of polymer design with machine learning and high throughput experimentation. MRS Commun. 2019, 9, 537–544. [Google Scholar] [CrossRef] [Green Version]
- Kumar, J.N.; Li, Q.; Tang, K.Y.T.; Buonassisi, T.; Gonzalez-Oyarce, A.L.; Ye, J. Machine learning enables polymer cloud-point engineering via inverse design. npj Comput. Mater. 2019, 5, 537–544. [Google Scholar] [CrossRef] [Green Version]
- Nápoles, G.; Grau, I.; Bello, R. Constricted Particle Swarm Optimization based algorithm for global optimization. Polibits 2012, 5–11. [Google Scholar] [CrossRef]
- Khadilkar, M.R.; Paradiso, S.; Delaney, K.T.; Fredrickson, G.H. Inverse Design of Bulk Morphologies in Multiblock Polymers Using Particle Swarm Optimization. Macromolecules 2017, 50, 6702–6709. [Google Scholar] [CrossRef]
- Hiraide, K.; Hirayama, K.; Endo, K.; Muramatsu, M. Application of deep learning to inverse design of phase separation structure in polymer alloy. Comput. Mater. Sci. 2021, 190, 110278. [Google Scholar] [CrossRef]
- Ramprasad, R.; Batra, R.; Pilania, G.; Mannodi-Kanakkithodi, A.; Kim, C. Machine learning in materials informatics: Recent applications and prospects. npj Comput. Mater. 2017, 3, 54. [Google Scholar] [CrossRef]
- Zhu, M.X.; Deng, T.; Dong, L.; Chen, J.M.; Dang, Z.M. Review of machine learning-driven design of polymer-based dielectrics. IET Nanodielectr. 2021, 1–15. [Google Scholar] [CrossRef]
- Mannodi-Kanakkithodi, A.; Pilania, G.; Huan, T.D.; Lookman, T.; Ramprasad, R. Machine Learning Strategy for Accelerated Design of Polymer Dielectrics. Sci. Rep. 2016, 6, 20952. [Google Scholar] [CrossRef] [Green Version]
- Wu, S.; Lambard, G.; Liu, C.; Yamada, H.; Yoshida, R. iQSPR in XenonPy: A Bayesian Molecular Design Algorithm. Mol. Inf. 2020, 39, e1900107. [Google Scholar] [CrossRef] [Green Version]
- Gurnani, R.; Kamal, D.; Tran, H.; Sahu, H.; Scharm, K.; Ashraf, U.; Ramprasad, R. polyG2G: A Novel Machine Learning Algorithm Applied to the Generative Design of Polymer Dielectrics. Chem. Mater. 2021, 33, 7008–7016. [Google Scholar] [CrossRef]
- Li, C.; Li, Q.; Kaneti, Y.V.; Hou, D.; Yamauchi, Y.; Mai, Y. Self-assembly of block copolymers towards mesoporous materials for energy storage and conversion systems. Chem. Soc. Rev. 2020, 49, 4681–4736. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Zhu, D.; Raju, L.; Cai, W. Tackling Photonic Inverse Design with Machine Learning. Adv. Sci. 2021, 8, 2002923. [Google Scholar] [CrossRef]
- Bendsoe, M.P.; Sigmund, O. Topology Optimization: Theory, Methods, and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Molesky, S.; Lin, Z.; Piggott, A.Y.; Jin, W.; Vucković, J.; Rodriguez, A.W. Inverse design in nanophotonics. Nat. Photonics 2018, 12, 659–670. [Google Scholar] [CrossRef] [Green Version]
- Angeris, G.; Vučković, J.; Boyd, S.P. Computational Bounds for Photonic Design. ACS Photonics 2019, 6, 1232–1239. [Google Scholar] [CrossRef] [Green Version]
- Liu, D.; Tan, Y.; Khoram, E.; Yu, Z. Training Deep Neural Networks for the Inverse Design of Nanophotonic Structures. ACS Photonics 2018, 5, 1365–1369. [Google Scholar] [CrossRef] [Green Version]
- Qu, Y.; Zhu, H.; Shen, Y.; Zhang, J.; Tao, C.; Ghosh, P.; Qiu, M. Inverse design of an integrated-nanophotonics optical neural network. Sci. Bull. 2020, 65, 1177–1183. [Google Scholar] [CrossRef]
- Jensen, J.S.; Sigmund, O. Topology optimization for nano-photonics. Laser Photonics Rev. 2011, 5, 308–321. [Google Scholar] [CrossRef]
- Liu, J.; Gaynor, A.T.; Chen, S.; Kang, Z.; Suresh, K.; Takezawa, A.; Li, L.; Kato, J.; Tang, J.; Wang, C.C.L.; et al. Current and future trends in topology optimization for additive manufacturing. Struct. Multidiscip. Optim. 2018, 57, 2457–2483. [Google Scholar] [CrossRef] [Green Version]
- Long, Y.; Ren, J.; Li, Y.; Chen, H. Inverse design of photonic topological state via machine learning. Appl. Phys. Lett. 2019, 114, 181105. [Google Scholar] [CrossRef]
- Pilozzi, L.; Farrelly, F.A.; Marcucci, G.; Conti, C. Machine learning inverse problem for topological photonics. Commun. Phys. 2018, 1, 57. [Google Scholar] [CrossRef]
- Jiang, J.; Sell, D.; Hoyer, S.; Hickey, J.; Yang, J.; Fan, J.A. Free-form diffractive metagrating design based on generative adversarial networks. ACS Nano 2019, 13, 8872–8878. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Zhu, Z.; Cai, W. Topological encoding method for data-driven photonics inverse design. Opt. Express 2020, 28, 4825–4835. [Google Scholar] [CrossRef] [Green Version]
- Kudyshev, Z.A.; Kildishev, A.V.; Shalaev, V.M.; Boltasseva, A. Machine learning–assisted global optimization of photonic devices. Nanophotonics 2020, 10, 371–383. [Google Scholar] [CrossRef]
- Braham, E.J.; Davidson, R.D.; Al-Hashimi, M.; Arroyave, R.; Banerjee, S. Navigating the design space of inorganic materials synthesis using statistical methods and machine learning. Dalton Trans. 2020, 49, 11480–11488. [Google Scholar] [CrossRef]
- Noh, J.; Gu, G.H.; Kim, S.; Jung, Y. Machine-enabled inverse design of inorganic solid materials: Promises and challenges. Chem. Sci. 2020, 11, 4871–4881. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.; Noh, J.; Gu, G.H.; Aspuru-Guzik, A.; Jung, Y. Generative Adversarial Networks for Crystal Structure Prediction. ACS Cent Sci. 2020, 6, 1412–1420. [Google Scholar] [CrossRef] [PubMed]
- Dan, Y.; Zhao, Y.; Li, X.; Li, S.; Hu, M.; Hu, J. Generative adversarial networks (GAN) based efficient sampling of chemical composition space for inverse design of inorganic materials. npj Comput. Mater. 2020, 6, 84. [Google Scholar] [CrossRef]
- Rosales, A.R.; Wahlers, J.; Limé, E.; Meadows, R.E.; Leslie, K.W.; Savin, R.; Bell, F.; Hansen, E.; Helquist, P.; Munday, R.H.; et al. Rapid virtual screening of enantioselective catalysts using CatVS. Nat. Catal. 2018, 2, 41–45. [Google Scholar] [CrossRef]
- Qin, J.; Chen, Q.; Yang, C.; Huang, Y. Research process on property and application of metal porous materials. J. Alloys Compd. 2016, 654, 39–44. [Google Scholar] [CrossRef]
- Ferey, G. Materials science. The simplicity of complexity–rational design of giant pores. Science 2001, 291, 994–995. [Google Scholar] [CrossRef]
- Kim, B.; Lee, S.; Kim, J. Inverse design of porous materials using artificial neural networks. Sci. Adv. 2020, 6, eaax9324. [Google Scholar] [CrossRef] [Green Version]
- Yao, Z.; Sánchez-Lengeling, B.; Bobbitt, N.S.; Bucior, B.J.; Kumar, S.G.H.; Collins, S.P.; Burns, T.; Woo, T.K.; Farha, O.K.; Snurr, R.Q.; et al. Inverse design of nanoporous crystalline reticular materials with deep generative models. Nat. Mach. Intell. 2021, 3, 76–86. [Google Scholar] [CrossRef]
- Wan, J.; Jiang, J.-W.; Park, H.S. Machine learning-based design of porous graphene with low thermal conductivity. Carbon 2020, 157, 262–269. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, C.; Snoussi, H.; Zhang, G. Machine Learning Approaches for Thermoelectric Materials Research. Adv. Funct. Mater. 2019, 30, 1906041. [Google Scholar] [CrossRef]
- Recatala-Gomez, J.; Suwardi, A.; Nandhakumar, I.; Abutaha, A.; Hippalgaonkar, K. Toward Accelerated Thermoelectric Materials and Process Discovery. ACS Appl. Energy Mater. 2020, 3, 2240–2257. [Google Scholar] [CrossRef]
- Zheng, B.; Yang, J.; Liang, B.; Cheng, J.-C. Inverse design of acoustic metamaterials based on machine learning using a Gauss–Bayesian model. J. Appl. Phys. 2020, 128, 134902. [Google Scholar] [CrossRef]
- Ismail, M.S.; Moghavvemi, M.; Mahlia, T.M.I. Characterization of PV panel and global optimization of its model parameters using genetic algorithm. Energy Convers. Manag. 2013, 73, 10–25. [Google Scholar] [CrossRef]
- Jadrich, R.B.; Lindquist, B.A.; Truskett, T.M. Probabilistic inverse design for self-assembling materials. J. Chem. Phys. 2017, 146, 184103. [Google Scholar] [CrossRef]
- Forte, A.E.; Hanakata, P.Z.; Jin, L.; Zari, E.; Zareei, A.; Fernandes, M.C.; Sumner, L.; Alvarez, J.; Bertoldi, K. Inverse Design of Inflatable Soft Membranes Through Machine Learning. Adv. Funct. Mater. 2022, 2111610. [Google Scholar] [CrossRef]
- Lininger, A.; Hinczewski, M.; Strangi, G. General Inverse Design of Layered Thin-Film Materials with Convolutional Neural Networks. ACS Photonics 2021, 8, 3641–3650. [Google Scholar] [CrossRef]
- Jiang, R.; Da, Y.; Han, X.; Chen, Y.; Deng, Y.; Hu, W. Ultrafast Synthesis for Functional Nanomaterials. Cell Rep. Phys. Sci. 2021, 2, 100302. [Google Scholar] [CrossRef]
- Dou, S.; Xu, J.; Cui, X.; Liu, W.; Zhang, Z.; Deng, Y.; Hu, W.; Chen, Y. High-Temperature Shock Enabled Nanomanufacturing for Energy-Related Applications. Adv. Energy Mater. 2020, 10, 10. [Google Scholar] [CrossRef]
- Genty, G.; Salmela, L.; Dudley, J.M.; Brunner, D.; Kokhanovskiy, A.; Kobtsev, S.; Turitsyn, S.K. Machine learning and applications in ultrafast photonics. Nat. Photonics 2021, 15, 91–101. [Google Scholar] [CrossRef]
- Kitchin, J.R. Machine learning in catalysis. Nat. Catal. 2018, 1, 230–232. [Google Scholar] [CrossRef]







| Materials/Molecules | Methodology | Target | Reference |
|---|---|---|---|
| Acoustic metamaterials | Gauss-Bayesian model | Specific functionalities | [90] |
| Photovoltaic | GA using developed MATLAB code | Voltage-current relation of the PV module. | [91] |
| Organic molecules | RNN | Relation between molecular structures and their material properties | [49] |
| Self-assembling materials | statistical mechanics based approach | Complex microstructures | [92] |
| Soft membranes | Neural network | 3D shapes starting from 2D planar composite membranes | [93] |
| Thin-film materials | Neural networks | Relationships between the metamaterial structure and corresponding ellipsometric and reflectance/transmittance spectra | [94] |
| Colloidal crystals | Alchemical Monte Carlo simulation | Geometric shape structure | [52] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Wang, Y.; Chen, Y. Inverse Design of Materials by Machine Learning. Materials 2022, 15, 1811. https://doi.org/10.3390/ma15051811
Wang J, Wang Y, Chen Y. Inverse Design of Materials by Machine Learning. Materials. 2022; 15(5):1811. https://doi.org/10.3390/ma15051811
Chicago/Turabian StyleWang, Jia, Yingxue Wang, and Yanan Chen. 2022. "Inverse Design of Materials by Machine Learning" Materials 15, no. 5: 1811. https://doi.org/10.3390/ma15051811
APA StyleWang, J., Wang, Y., & Chen, Y. (2022). Inverse Design of Materials by Machine Learning. Materials, 15(5), 1811. https://doi.org/10.3390/ma15051811






