Novel Deployable Panel Structure Integrated with Thick Origami and Morphing Bistable Composite Structures
Abstract
:1. Introduction
2. Design of the Deployable Panel Structure
3. Experimental Test and FE Simulation
3.1. Measurement of the Trigger Force
3.2. Numerical Simulation
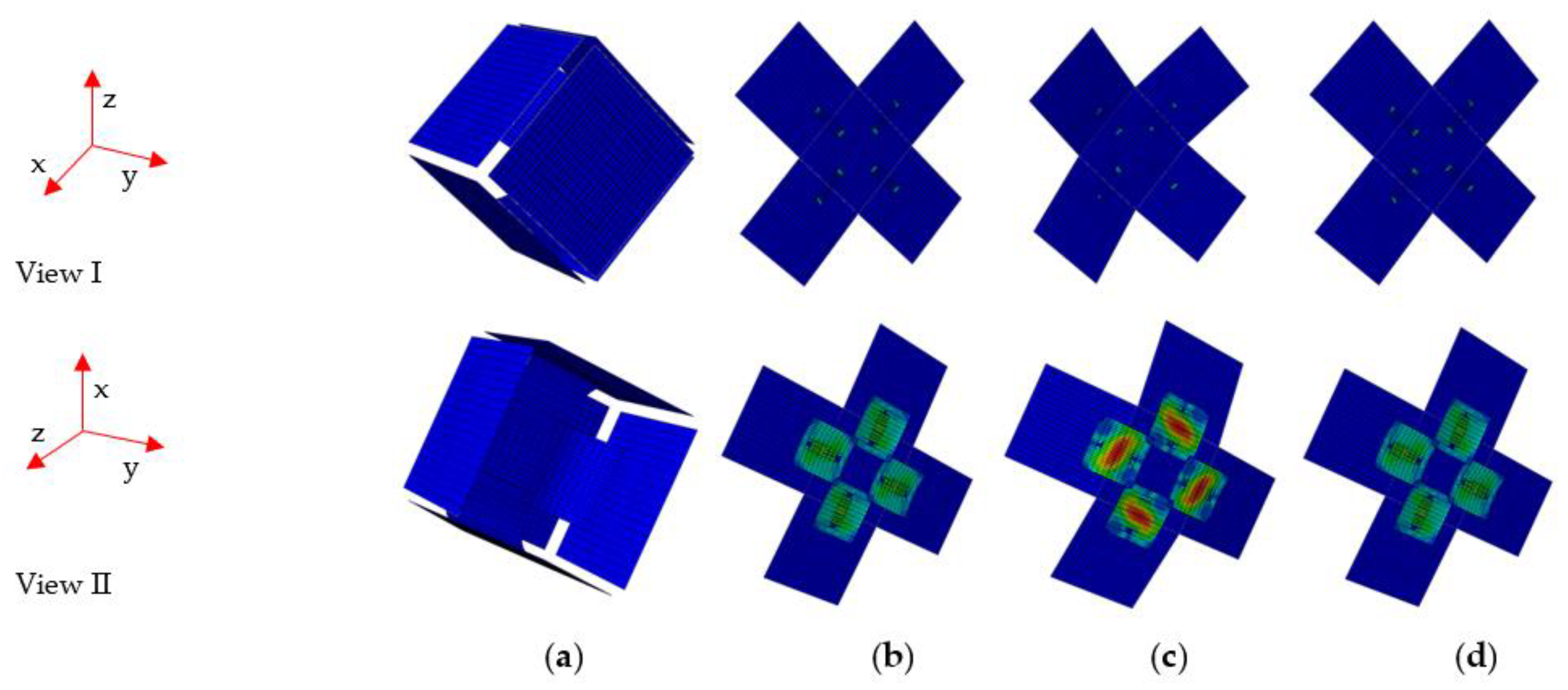
4. Results and Discussion
4.1. Mechanical Properties of the Deployable Panel Model
4.2. Effect of the Distance between Two Junctions Lj
4.3. Effect of the Sidelength of the Deployable Panel Ls
4.4. Effect of the Number of Layers of Bistable CFRP Cylindrical Shells
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Stevenson, A. Oxford Dictionary of English; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Pellegrino, S. Deployable Structures; Springer: Berlin, Germany, 2014; Volume 412. [Google Scholar]
- Hutchinson, R.G.; Wicks, N.; Evans, A.G.; Fleck, N.A.; Hutchinson, J.W. Kagome plate structures for actuation. Int. J. Solids Struct. 2003, 40, 6969–6980. [Google Scholar] [CrossRef]
- Ramrakhyani, D.S.; Lesieutre, G.A.; Frecker, M.; Bharti, S. Aircraft structural morphing using tendon-actuated compliant cellular trusses. J. Aircr. 2005, 42, 1615–1621. [Google Scholar] [CrossRef] [Green Version]
- Fenci, G.E.; Currie, N.G.R. Deployable structures classification: A review. Int. J. Space Struct. 2017, 32, 112–130. [Google Scholar] [CrossRef]
- Zhang, Z.; Pei, K.; Sun, M.; Wu, H.; Wu, H.; Jiang, S.; Zhang, F. Tessellated multistable structures integrated with new transition elements and antisymmetric laminates. Thin-Walled Struct. 2022, 170, 108560. [Google Scholar] [CrossRef]
- Šekularac, N.; Ivanović-Šekularac, J.; Čikić-Tovarović, J. Folded structures in modern architecture. Facta Univ. Ser. Archit. Civ. Eng. 2012, 10, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Lebée, A. From Folds to Structures, a Review. Int. J. Space Struct. 2015, 30, 55–74. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Pei, K.; Wu, H.; Sun, M.; Chai, H.; Wu, H.; Jiang, S. Bistable characteristics of hybrid composite laminates embedded with bimetallic strips. Compos. Sci. Technol. 2021, 212, 108880. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhou, Y.; Shen, H.; Sun, M.; Chai, H.; Wu, H.; Jiang, S. Experimental study of orthogonal bistable laminated composite shell driven by magnetorheological elastomer. Compos. Struct. 2021, 271, 114119. [Google Scholar] [CrossRef]
- Zhong, S.Y.; Zhang, X.; Gill, J.; Fattah, R.; Sun, Y.H. A numerical investigation of the airfoil-gust interaction noise in transonic flows: Acoustic processes. J. Sound Vibr. 2018, 425, 239–256. [Google Scholar] [CrossRef]
- Jeong, D.; Lee, K. Design and analysis of an origami-based three-finger manipulator. Robotica 2018, 36, 261–274. [Google Scholar] [CrossRef] [Green Version]
- Pagano, A.; Yan, T.X.; Chien, B.; Wissa, A.; Tawfick, S. A crawling robot driven by multi-stable origami. Smart Mater. Struct. 2017, 26, 11. [Google Scholar] [CrossRef]
- Daynes, S.; Trask, R.S.; Weaver, P.M. Bio-inspired structural bistability employing elastomeric origami for morphing applications. Smart Mater. Struct. 2014, 23, 125011. [Google Scholar] [CrossRef]
- Liber, M.; Tomov, T.E.; Tsukanov, R.; Berger, Y.; Popov, M.; Khara, D.C.; Nir, E. Study of DNA Origami Dimerization and Dimer Dissociation Dynamics and of the Factors that Limit Dimerization. Small 2018, 14, 1800218. [Google Scholar] [CrossRef] [PubMed]
- Selnihhin, D.; Sparvath, S.M.; Preus, S.; Birkedal, V.; Andersen, E.S. Multifluorophore DNA Origami Beacon as a Biosensing Platform. ACS Nano 2018, 12, 5699–5708. [Google Scholar] [CrossRef] [PubMed]
- Schenk, M.; Guest, S.D. Geometry of Miura-folded metamaterials. Proc. Natl. Acad. Sci. USA 2013, 110, 3276–3281. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yasuda, H.; Yein, T.; Tachi, T.; Miura, K.; Taya, M. Folding behaviour of Tachi-Miura polyhedron bellows. Proc. R. Soc. A Math. Phys. Eng. Sci. 2013, 469, 20130351. [Google Scholar] [CrossRef] [Green Version]
- Fang, H.B.; Li, S.Y.; Ji, H.M.; Wang, K.W. Dynamics of a bistable Miura-origami structure. Phys. Rev. E 2017, 95, 052211. [Google Scholar] [CrossRef] [Green Version]
- Hanna, B.H.; Magleby, S.P.; Lang, R.J.; Howell, L.L. Force-Deflection Modeling for Generalized Origami Waterbomb-Base Mechanisms. J. Appl. Mech. Trans. ASME 2015, 82, 081001. [Google Scholar] [CrossRef]
- Feng, H.J.; Ma, J.Y.; Chen, Y.; You, Z. Twist of Tubular Mechanical Metamaterials Based on Waterbomb Origami. Sci. Rep. 2018, 8, 9522. [Google Scholar] [CrossRef]
- Hanna, B.H.; Lund, J.M.; Lang, R.J.; Magleby, S.P.; Howell, L.L. Waterbomb base: A symmetric single-vertex bistable origami mechanism. Smart Mater. Struct. 2014, 23, 094009. [Google Scholar] [CrossRef]
- Chillara, V.S.C.; Dapino, M.J. Stress-biased laminated composites for smooth folds in origami structures. Mater. Res. Express 2018, 6, 025703. [Google Scholar] [CrossRef]
- Zhang, Z.; Liao, C.; Chai, H.; Ni, X.; Pei, K.; Sun, M.; Wu, H.; Jiang, S. Multi-objective optimization of controllable configurations for bistable laminates using NSGA-II. Compos. Struct. 2021, 226, 113764. [Google Scholar] [CrossRef]
- Chillara, V.S.C.; Dapino, M.J. Stability considerations and actuation requirements in bistable laminated composites. Compos. Struct. 2018, 184, 1062–1070. [Google Scholar] [CrossRef]
- Hu, J.Q.; Lin, S.; Dai, F.H. Pattern Reconfigurable Antenna Based on Morphing Bistable Composite Laminates. IEEE Trans. Antennas Propag. 2017, 65, 2196–2207. [Google Scholar] [CrossRef]
- Zhang, Z.; Ni, X.; Wu, H.; Sun, M.; Bao, G.; Wu, H.; Jiang, S. Pneumatically Actuated Soft Gripper with Bistable Structures. Soft Robot. 2021, 9, 57–71. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Feng, J.; Sun, Q.Z. Lower-order symmetric mechanism modes and bifurcation behavior of deployable bar structures with cyclic symmetry. Int. J. Solids Struct. 2018, 139, 1–14. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, Y.J.; Zhang, T.Q.; Rana, M. Stochastic resonance in an asymmetric bistable system driven by multiplicative and additive Gaussian noise and its application in bearing fault detection. Chin. J. Phys. 2018, 56, 1173–1186. [Google Scholar] [CrossRef]
- Chen, T.; Bilal, O.R.; Shea, K.; Daraio, C. Harnessing bistability for directional propulsion of soft, untethered robots. Proc. Natl. Acad. Sci. USA 2018, 115, 5698–5702. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Li, X.; Yu, X.; Chai, H.; Li, Y.; Wu, H.; Jiang, S. Magnetic actuation bionic robotic gripper with bistable morphing structure. Compos. Struct. 2019, 229, 111422. [Google Scholar] [CrossRef]
- Zhang, H.; Li, C.L.; Liu, G.F.; Zang, X.Z.; Jin, H.Z.; Liu, Y.B.; Zhao, J. Study of human-robot collaboration technologies of bionic robot arm in a surgery. Basic Clin. Pharmacol. Toxicol. 2016, 118, 91. [Google Scholar]
- Sun, Q.Z.; Xing, Y.F. Exact eigensolutions for flutter of two-dimensional symmetric cross-ply composite laminates at high supersonic speeds. Compos. Struct. 2018, 183, 358–370. [Google Scholar] [CrossRef]
- Tawfik, S.A.; Dancila, D.S.; Armanios, E. Planform effects upon the bistable response of cross-ply composite shells. Compos. Pt. A-Appl. Sci. Manuf. 2011, 42, 825–833. [Google Scholar] [CrossRef]
- Kim, I.B.; Song-Hak, U.; Ji, T.H. Determination of local stiffness of a cross-ply composite plate with delaminations and matrix cracks. Compos. Struct. 2018, 196, 127–134. [Google Scholar] [CrossRef]
- Lee, J.G.; Ryu, J.; Kim, S.W.; Koh, J.S.; Cho, K.J.; Cho, M. Effect of initial tool-plate curvature on snap-through load of unsymmetric laminated cross-ply bistable composites. Compos. Struct. 2015, 122, 82–91. [Google Scholar] [CrossRef]
- Zhang, Z.; Pei, K.; Sun, M.; Wu, H.; Yu, X.; Wu, H.; Jiang, S.; Zhang, F. A novel solar tracking model integrated with bistable composite structures and bimetallic strips. Compos. Struct. 2020, 248, 112506. [Google Scholar] [CrossRef]
- Veidt, M.; Ng, C.T. Influence of stacking sequence on scattering characteristics of the fundamental anti-symmetric Lamb wave at through holes in composite laminates. J. Acoust. Soc. Am. 2011, 129, 1280–1287. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Z.; Li, Y.; Yu, X.; Li, X.; Wu, H.; Wu, H.; Jiang, S.; Chai, G. Bistable morphing composite structures: A review. Thin-Walled Struct. 2019, 142, 74–97. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, D.; Jin, Y.; Wang, M.; Mukhopadhyay, T.; You, Z. Modulation of multi-directional auxeticity in hybrid origami metamaterials. Appl. Mater. Today 2020, 20, 100715. [Google Scholar] [CrossRef]











| Longitudinal Modulus E11 (GPa) | Transverse Modulus E22 (GPa) | Shear Modulus in the 1–2 Plane G12 (GPa) | Shear Modulus in the 1–3 Plane G13 (GPa) | Shear Modulus in the 2–3 Plane G23 (GPa) | Poisson Ratio ν12 | Single Layer Thickness t (mm) |
|---|---|---|---|---|---|---|
| 132 | 10.3 | 6.5 | 6.5 | 3.9 | 0.25 | 0.12 |
| Length of the Cylindrical Shell Lc (mm) | Central Angle β (°) | Radius R(mm) | Sidelength of the Deployable Panel Ls (mm) | Thickness of the Deployable Panel h (mm) | Distance between Two Junctions Lj (mm) |
|---|---|---|---|---|---|
| 50 | 90 | 25 | 90 | 3 | 39.25 |
| Distance between Two Junctions Lj (m) | Coverage Area a (m2) | Package Volume v (m3) | Ratio of Coverage Area and Package Volume μ (m−1) |
|---|---|---|---|
| 20 × 10−3 | 405 × 10−4 | 1252 × 10−6 | 32.35 |
| 25 × 10−3 | 405 × 10−4 | 1270 × 10−6 | 31.89 |
| 30 × 10−3 | 405 × 10−4 | 1171 × 10−6 | 34.59 |
| 35 × 10−3 | 405 × 10−4 | 963 × 10−6 | 42.06 |
| 39.5 × 10−3 | 405 × 10−4 | 729 × 10−6 | 55.56 |
| Sidelength of the Deployable Panel Ls (m) | Coverage Area a (m2) | Package Volume v (m3) | Ratio of Coverage Area and Package Volume μ (m−1) |
|---|---|---|---|
| 70 × 10−3 | 245 × 10−4 | 343 × 10−6 | 71.43 |
| 80 × 10−3 | 320 × 10−4 | 512 × 10−6 | 62.50 |
| 90 × 10−3 | 405 × 10−4 | 729 × 10−6 | 55.56 |
| 100 × 10−3 | 500 × 10−4 | 1000 × 10−6 | 50.00 |
| 110 × 10−3 | 605 × 10−4 | 1331 × 10−6 | 45.45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, S.; Sun, M.; Li, Y.; Ma, W.; Zhang, Z. Novel Deployable Panel Structure Integrated with Thick Origami and Morphing Bistable Composite Structures. Materials 2022, 15, 1942. https://doi.org/10.3390/ma15051942
Ding S, Sun M, Li Y, Ma W, Zhang Z. Novel Deployable Panel Structure Integrated with Thick Origami and Morphing Bistable Composite Structures. Materials. 2022; 15(5):1942. https://doi.org/10.3390/ma15051942
Chicago/Turabian StyleDing, Shuyong, Min Sun, Yang Li, Weili Ma, and Zheng Zhang. 2022. "Novel Deployable Panel Structure Integrated with Thick Origami and Morphing Bistable Composite Structures" Materials 15, no. 5: 1942. https://doi.org/10.3390/ma15051942
APA StyleDing, S., Sun, M., Li, Y., Ma, W., & Zhang, Z. (2022). Novel Deployable Panel Structure Integrated with Thick Origami and Morphing Bistable Composite Structures. Materials, 15(5), 1942. https://doi.org/10.3390/ma15051942





