Investigation of the Densification Behavior of Alumina during Spark Plasma Sintering
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. XRD Analysis of Alumina Powder
3.2. Analysis of the Densification Behavior
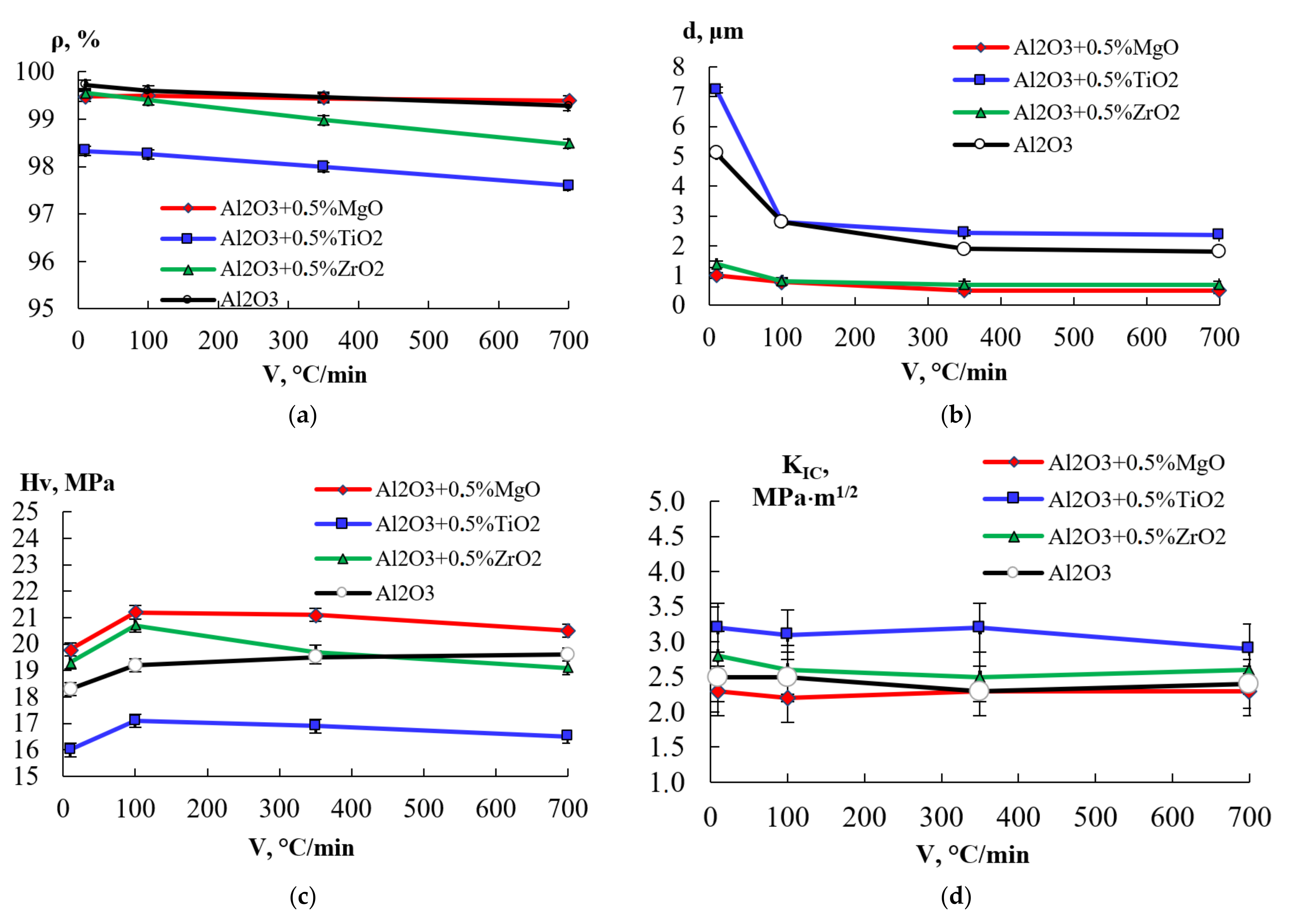
3.3. Study of the Structure and Mechanical Properties of Ceramics
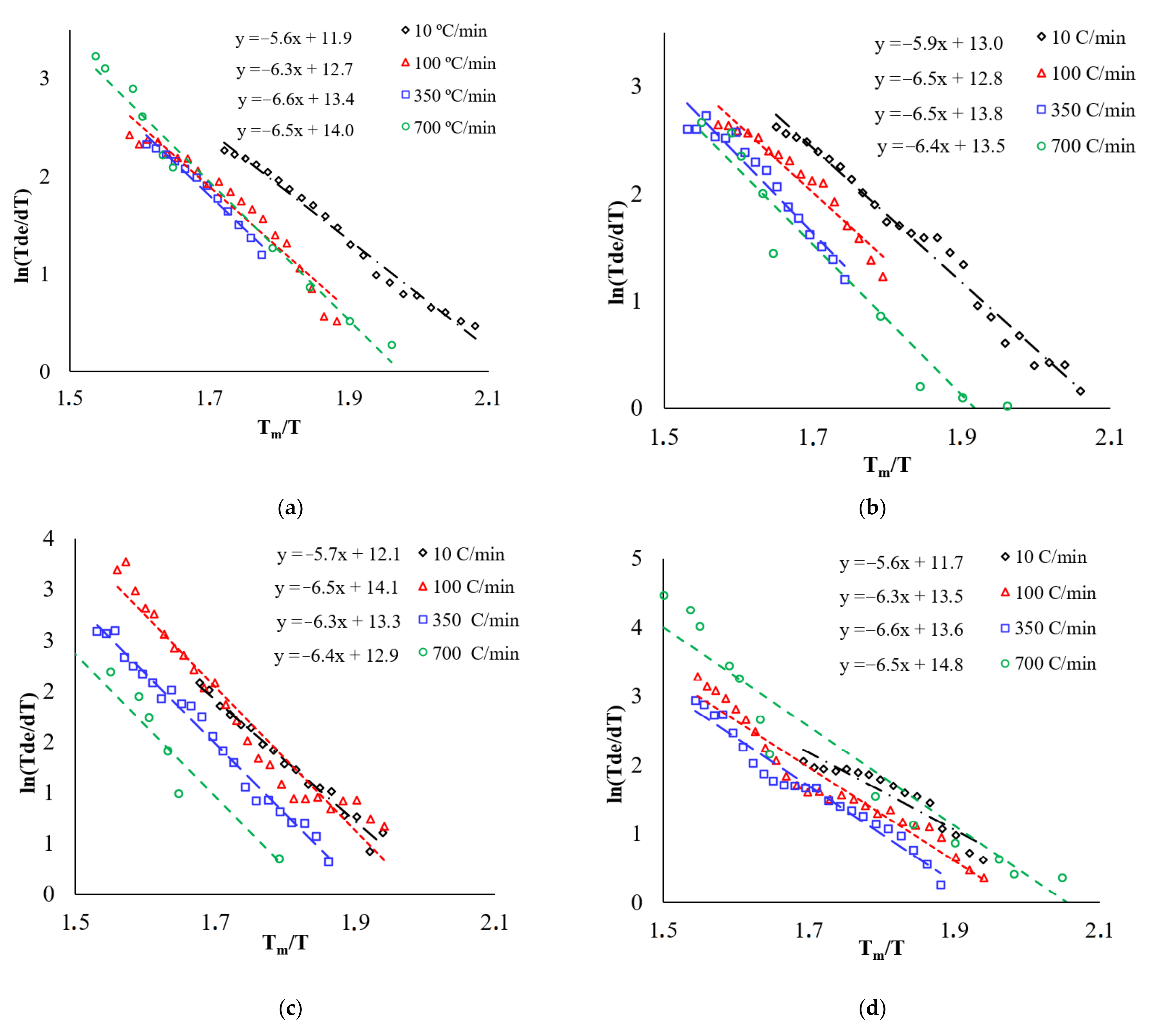
3.4. Analysis of Shrinkage Curves
3.5. First Stage Analysis
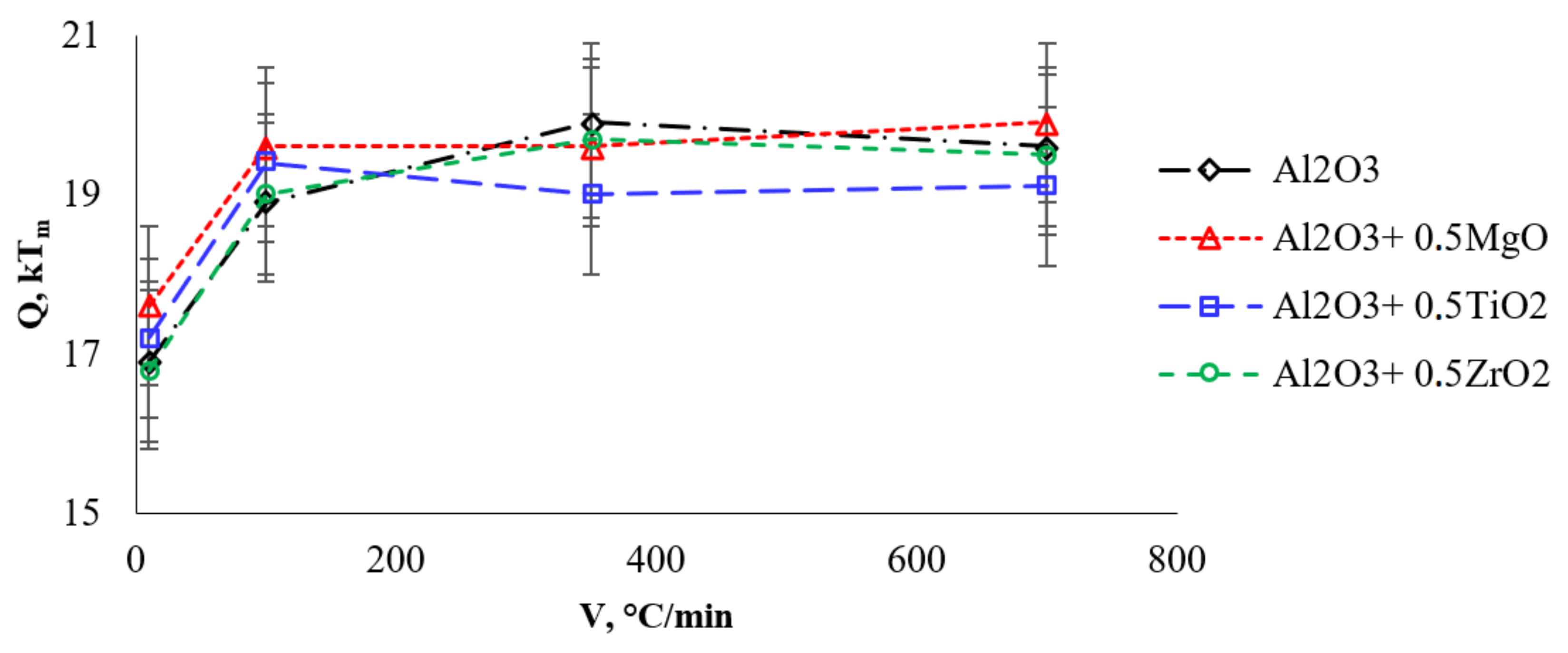
3.6. Second Stage Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Aabbreviations
| Symbol | Description |
| Deformation rate controlled by grain boundary sliding in a material containing particles of the second phase | |
| Constant | |
| Constant | |
| Constant | |
| Grain boundary diffusion coefficient | |
| Pre-exponential coefficient | |
| Volume diffusion coefficient | |
| Pre-exponential coefficient | |
| Hardness | |
| Crack resistance | |
| Initial height of the sintered sample | |
| Activation energies of grain boundary | |
| Slope tangent | |
| Activation energies of volume diffusion | |
| Maximum shrinkage rate | |
| Melting temperature | |
| Temperature at maximum shrinkage | |
| Sintering temperature | |
| Volume fraction of pores | |
| Size of particles of the second phase | |
| Strain rate | |
| Theoretical density | |
| °C | Degrees Celsius |
| Constant | |
| Temperature |
Appendix A




References
- Collection of works International Conference on Synthesis and Consolidation of Powder Materials, SCPM2018 (Russian Federation). 23–26 October 2022. Available online: http://www.ism.ac.ru/events/SCPM-2018/SCPM2018_BookofPapers.pdf (accessed on 14 March 2022).
- Kинетикa электрoимпульснoгo плaзменнoгo спекaния керaмик нa oксидa aлюминия. Ph.D. Thesis, National Research Lobachevsky State University of Nizhni Novgorod, Nizhny Novgorod, Russia, 2022. Available online: https://diss.unn.ru/files/2019/910/diss-Boldin-910.pdf (accessed on 14 March 2022).
- Belmonte, M. Advanced Ceramic Materials for High Temperature Applications. Adv. Eng. Mater. 2009, 8, 693–703. [Google Scholar] [CrossRef] [Green Version]
- Linus, M.; James, B.; Cornelis, K. Two Perspectives on the Evolution and Future of Alumina. Light Met. 2011, 151–155. [Google Scholar] [CrossRef]
- Ruys, A.J. Alumina Ceramics; Woodhead Publishing: Cambridge, UK, 2019; p. 541. [Google Scholar]
- Shackelford, J.F.; Doremus, R.H. Ceramic and Glass Materials; Springer: Berlin, Germany, 2008; p. 209. [Google Scholar]
- Uematsu, K.; Itakura, K.; Uchida, N.; Saito, K.; Miyamoto, A.; Miyashita, T. Hot Isostatic Pressing of Alumina and Examination of the Hot Isostatic Pressing Map. J. Am. Ceram. Soc. 1990, 73, 74–78. [Google Scholar] [CrossRef]
- Bocanegra-Bernal, M.H. Hot Isostatic Pressing (HIP) technology and its applications to metals and ceramics. J. Mater. Sci. 2004, 39, 6399–6420. [Google Scholar] [CrossRef]
- Uskokovic, D.P.; Palmour, H.; Spriggs, R.M. Science of Sintering; Springer: Berlin, Germany, 1989; p. 202. [Google Scholar]
- Rahaman, M.N. Ceramic Processing and Sintering, 2nd ed.; Marcel Dekker, Inc.: New York, NY, USA, 2003; p. 876. [Google Scholar]
- Gurt, J.; Weibel, A.; Estournes, C.; Yang, Q.; Laurent, C.; Peigney, A. Spark plasma sintering of alumina: Study of parameters, formal sintering analysis and hypotheses on the mechanism(s) involved in densification and grain growth. Acta Mater. 2011, 59, 1400–1408. [Google Scholar]
- Shen, Z.; Johnsson, M.; Zhao, Z.; Nygren, M. Spark Plasma Sintering of Alumina. J. Am. Ceram. Soc. 2002, 85, 1921–1927. [Google Scholar] [CrossRef]
- Langer, J.; Hoffmann, M.J.; Guillon, O. Direct comparison between hot pressing and electric field-assisted sintering of submicron alumina. Acta Mater. 2009, 57, 5454–5465. [Google Scholar] [CrossRef]
- Simonenko, T.L.; Kalinina, M.V.; Simonenko, N.P.; Simonenko, E.P.; Glumov, O.V.; Mel’nikova, N.A.; Murin, I.V.; Shichalin, O.O.; Papynov, E.K.; Shilova, O.A.; et al. Synthesis of BaCe0.9xZrxY0.1O3 nanopowders and the study of proton conductors fabricated on their basis by low-temperature spark plasma sintering. Int. J. Hydrogen Energy 2019, 44, 20345–20354. [Google Scholar] [CrossRef]
- Papynov, E.K.; Shichalin, O.O.; Mironenko, A.Y.; Ryakov, A.V.; Manakov, I.V.; Makhrov, P.V.; Buravlev, I.Y.; Tananaev, I.G.; Avramenko, V.A.; Sergienko, V.I. Synthesis of High-Density Pellets of Uranium Dioxide by Spark Plasma Sintering in Dies of Different Types. Radiochemistry 2018, 60, 362–370. [Google Scholar] [CrossRef]
- Papynov, E.K.; Shichalin, O.O.; Medkov, M.A.; Grishchenko, D.N.; Tkachenko, I.A.; Fedorets, A.N.; Pechnikov, V.S.; Golub, A.V.; Buravlev, I.Y.; Tananaev, I.G.; et al. Spark Plasma Sintering of Special-Purpose Functional Ceramics Based on UO2, ZrO2, Fe3O4/α-Fe2O3. Glass Phys. Chem. 2018, 44, 632–640. [Google Scholar] [CrossRef]
- Papynov, E.K.; Portnyagin, A.S.; Modin, E.B.; Mayorov, V.Y.; Shichalin, O.O.; Golikov, A.P.; Pechnikov, V.S.; Gridasova, E.A.; Tananaev, I.G.; Avramenko, V.A. A complex approach to assessing porous structure of structured ceramics obtained by SPS technique. Mater. Charact. 2018, 145, 294–302. [Google Scholar] [CrossRef]
- Mamedov, V. Spark plasma sintering as advanced PM sintering method. Powder Metall. 2002, 45, 322–328. [Google Scholar] [CrossRef]
- Tokita, M. Progress of Spark Plasma Sintering (SPS) Method, Systems, Ceramics Applications and Industrialization. Ceramics 2021, 4, 160–198. [Google Scholar] [CrossRef]
- Ding, H.; Zhao, Z.; Jin, J.; Deng, L.; Gong, P. Densification mechanism of Zr-based bulk metallic glass prepared by two-step spark plasma sintering. J. Alloy. Compd. 2021, 850, 156724. [Google Scholar] [CrossRef]
- Ding, H.; Bao, X.; Jamili-Shirvan, Z.; Jin, J.; Deng, L.; Yao, K.; Gong, P.; Wang, X. Enhancing strength-ductility synergy in an ex situ Zr-based metallic glass composite via nanocrystal formation within high-entropy alloy particles. Mater. Des. 2021, 210, 110108. [Google Scholar] [CrossRef]
- Young, M.K.; Won, T.K.; Young-Wook, K. Development of Al2O3-SiC composite tool for machining application. Ceram. Int. 2004, 30, 2081–2086. [Google Scholar]
- Xu, H.; Zou, J.; Wang, W.; Wang, H.; Ji, W.; Fu, Z. Densification mechanism and microstructure characteristics of nano- and micro- crystalline alumina by high-pressure and low temperature sintering. J. Eur. Ceram. Soc. 2021, 41, 635–645. [Google Scholar] [CrossRef]
- Stuer, M.; Carry, C.P.; Bowen, P.; Zhao, Z. Comparison of apparent activation energies for densification of alumina powders by pulsed electric current sintering (spark plasma sintering) and conventional sintering—toward applications for transparent polycrystalline alumina. J. Mater. Res. 2017, 32, 3309–3318. [Google Scholar] [CrossRef]
- Bernard-Granger, G.; Guizard, C. Spark plasma sintering of a commercially available granulated zirconia powder: I. Sintering path and hypotheses about the mechanism(s) controlling densification. Acta Mater. 2007, 55, 3493–3504. [Google Scholar] [CrossRef]
- Johnson, D.L.; Cutler, I.B. Diffusion Sintering: I, Initial Stage Sintering Models and Their Application to Shrinkage of Powder Compacts. J. Am. Ceram. Soc. 1963, 46, 541–545. [Google Scholar] [CrossRef]
- Johnson, D.L.; Cutler, I.B. Diffusion Sintering: II, Initial Sintering Kinetics of Alumina. J. Am. Ceram. Soc. 1963, 46, 545–550. [Google Scholar] [CrossRef]
- Lakiza, S.M.; Lopato, L.M. Stable and metastable phase relations in the system Alumina-Zirconia-Yttria. J. Am. Ceram. Soc. 1997, 80, 893–902. [Google Scholar] [CrossRef]
- Hallstedt, B. Thermodynamic assessment of the MgO-Al2O3. J. Am. Ceram. Soc. 1992, 75, 1497–1507. [Google Scholar] [CrossRef]
- Kim, I.J.; Gauckler, L.G. Review Formation, Decomposition and Thermal Stability of Al2TiO5 Ceramics. J. Ceram. Sci. Technol. 2012, 3, 49–60. [Google Scholar]
- Chuvildeev, V.N.; Boldin, M.S.; Dyatlova, Y.G.; Rumyantsev, V.I.; Ordanyan, S.S. A comparative study of the hot pressing and spark plasma sintering of Al2O3–ZrO2–Ti(C,N) powders. Inorg. Mater. 2015, 51, 1047–1053. [Google Scholar] [CrossRef]
- Fedosov, S.A.; Pešek, L. Determining Mechanical Properties of Materials by Microindentation: Modern Foreign Methods; Moscow University Press: Moscow, Russia, 2004; p. 100. [Google Scholar]
- Olevsky, E.A.; Kandukuri, S.; Froyen, L. Consolidation enhancement in spark-plasma sintering: Impact of high heating rates. J. Appl. Phys. 2007, 102, 114913. [Google Scholar] [CrossRef]
- Ashby, M.F.; Bahk, S.; Bevk, J.; Turnbull, D. The influence of a dispersion of particles on the sintering of metal powders and wires. Prog. Mater. Sci. 1980, 25, 1–34. [Google Scholar] [CrossRef]
- Ashby, M.F.; Verrall, R.A. Diffusion-Accommodated Flow And Superplasticity. Acta Metall. 1973, 21, 149–163. [Google Scholar] [CrossRef]
- Perevezentsev, V.N.; Rybin, V.V.; Chuvil’deev, V.N. The theory of structural superplasticity-I. The physical nature of the superplasticity phenomenon. Acta Metall. Mater. 1992, 40, 887–894. [Google Scholar] [CrossRef]
- Young, W.S.; Cutler, I.B. Initial sintering with constant rates of heating. J. Am. Ceram. Soc. 1970, 53, 659–663. [Google Scholar] [CrossRef]
- Frost, H.J.; Ashby, M.F. Deformation Mechanism Maps; Elsevier: Amsterdam, The Netherlands, 1982; p. 328. [Google Scholar]
- Evans, A.G.; Langdon, T.G. Structural Ceramics; Pergamon Press: Oxford, UK, 1976; p. 255. [Google Scholar]
- Somiya, S.; Moriyoshi, Y. Sintering Key Papers; Springer: Amsterdam, The Netherlands, 1990; p. 801. [Google Scholar]
- Lartigue-Korinek, S.; Legros, C.; Carry, C.; Herbst, F. Titanium effect on phase transformation and sintering behavior of transition alumina. J. Eur. Ceram. Soc. 2006, 26, 2219–2230. [Google Scholar] [CrossRef]







| Material | Manufacturer | Phase Composition * | Particle Size * |
|---|---|---|---|
| α-Al2O3 | Taimei Chemicals Co., Ltd. (Tokyo, Japan) | α-Al2O3 (rhombohedral) ~ 100% | ~0.2 μm |
| MgO | Alfa Aesar—A Johnson Matthey Company (Kandel, Germany) | MgO (cubic) ~ 100% | ~0.1 μm |
| TiO2 | Institute of Electrophysics, Ural Branch of RAS (Yekaterinburg, Russia) | TiO2 (anatase) ~ 74%, TiO2 (rutile) ~ 26% | ~0.5 μm |
| ZrO2 (3% mol. Y2O3) | Pangea Int., Ltd. (Shanghai, China) | ZrO2 (monoclinic) ~ 58%, ZrO2 (tetragonal) ~ 42% | <0.03 μm |
| System | , °C/min | ρ, % (Δ ± 0.2) | d, μm (Δ ± 0.2) | , GPa (Δ ± 0.5) | , MPa·m1/2 (Δ ± 0.1) |
|---|---|---|---|---|---|
| α-Al2O3 | 10 | 99.7 | 5.1 | 18.3 | 2.5 |
| α-Al2O3 + 0.5%vol. MgO | 99.5 | 1.0 | 19.8 | 2.3 | |
| α-Al2O3 + 0.5%vol. TiO2 | 99.3 | 7.2 | 16.0 | 3.2 | |
| α-Al2O3 + 0.5%vol. ZrO2 | 99.5 | 1.4 | 19.3 | 2.8 | |
| α-Al2O3 | 100 | 99.6 | 2.8 | 19.2 | 2.5 |
| α-Al2O3 + 0.5%vol. MgO | 99.5 | 0.8 | 21.2 | 2.2 | |
| α-Al2O3 + 0.5%vol. TiO2 | 98.3 | 2.8 | 17.1 | 3.1 | |
| α-Al2O3 + 0.5%vol. ZrO2 | 99.4 | 0.8 | 20.7 | 2.6 | |
| α-Al2O3 | 350 | 99.5 | 1.9 | 19.5 | 2.3 |
| α-Al2O3 + 0.5%vol. MgO | 99.4 | 0.5 | 21.1 | 2.3 | |
| α-Al2O3 + 0.5%vol. TiO2 | 98.0 | 2.4 | 16.9 | 3.2 | |
| α-Al2O3 + 0.5%vol. ZrO2 | 98.9 | 0.7 | 19.7 | 2.5 | |
| α-Al2O3 | 700 | 99.3 | 1.8 | 19.6 | 2.4 |
| α-Al2O3 + 0.5%vol. MgO | 99.4 | 0.5 | 20.5 | 2.3 | |
| α-Al2O3 + 0.5%vol. TiO2 | 97.6 | 2.4 | 16.5 | 2.9 | |
| α-Al2O3 + 0.5%vol. ZrO2 | 98.5 | 0.7 | 19.1 | 2.6 |
| System | Heating Rate, °C/min | |||
|---|---|---|---|---|
| 10 | 100 | 350 | 700 | |
| Al2O3 | 16.9 | 18.9 | 19.9 | 19.6 |
| Al2O3 + 0.5%vol. MgO | 17.6 | 19.6 | 19.6 | 19.9 |
| Al2O3 + 0.5%vol. TiO2 | 17.2 | 19.4 | 19.0 | 19.1 |
| Al2O3 + 0.5%vol. ZrO2 | 16.8 | 19.0 | 19.7 | 19.5 |
| System | V, °C/min | |||
|---|---|---|---|---|
| α-Al2O3 | 10 | 2.7·10−3 | 7.0·10−4 | 19.3 |
| α-Al2O3 + 0.5% vol. MgO | 5.7·10−3 | 4.6·10−4 | 19.0 | |
| α-Al2O3 + 0.5% vol. TiO2 | 7.0·10−3 | 7.2·10−4 | 19.9 | |
| α-Al2O3 + 0.5% vol. ZrO2 | 2.8·10−3 | 2.8·10−4 | 20.1 | |
| α-Al2O3 | 100 | 1.4·10−2 | 1.2·10−3 | 19.9 |
| α-Al2O3 + 0.5% vol. MgO | 1.8·10−2 | 1.5·10−3 | 19.3 | |
| α-Al2O3 + 0.5% vol. TiO2 | 1.6·10−2 | 1.6·10−3 | 19.7 | |
| α-Al2O3 + 0.5% vol. ZrO2 | 1.7·10−2 | 1.5·10−3 | 19.6 | |
| α-Al2O3 | 350 | 2.3·10−1 | 1.9·10−3 | 19.8 |
| α-Al2O3 + 0.5% vol. MgO | 5.7·10−1 | 4.7·10−3 | 19.0 | |
| α-Al2O3 + 0.5% vol. TiO2 | 5.1·10−1 | 5.2·10−3 | 19.0 | |
| α-Al2O3 + 0.5% vol. ZrO2 | 6.5·10−1 | 5.6·10−3 | 19.6 | |
| α-Al2O3 | 700 | 1.2·10−1 | 1.0·10−3 | 19.0 |
| α-Al2O3 + 0.5% vol. MgO | 1.2·10−1 | 9.2·10−3 | 19.9 | |
| α-Al2O3 + 0.5% vol. TiO2 | 1.1·10−1 | 1.1·10−3 | 20.3 | |
| α-Al2O3 + 0.5% vol. ZrO2 | 1.2·10−1 | 9.9·10−3 | 19.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boldin, M.S.; Popov, A.A.; Lantsev, E.A.; Nokhrin, A.V.; Chuvil’deev, V.N. Investigation of the Densification Behavior of Alumina during Spark Plasma Sintering. Materials 2022, 15, 2167. https://doi.org/10.3390/ma15062167
Boldin MS, Popov AA, Lantsev EA, Nokhrin AV, Chuvil’deev VN. Investigation of the Densification Behavior of Alumina during Spark Plasma Sintering. Materials. 2022; 15(6):2167. https://doi.org/10.3390/ma15062167
Chicago/Turabian StyleBoldin, Maksim S., Alexander A. Popov, Evgeni A. Lantsev, Aleksey V. Nokhrin, and Vladimir N. Chuvil’deev. 2022. "Investigation of the Densification Behavior of Alumina during Spark Plasma Sintering" Materials 15, no. 6: 2167. https://doi.org/10.3390/ma15062167
APA StyleBoldin, M. S., Popov, A. A., Lantsev, E. A., Nokhrin, A. V., & Chuvil’deev, V. N. (2022). Investigation of the Densification Behavior of Alumina during Spark Plasma Sintering. Materials, 15(6), 2167. https://doi.org/10.3390/ma15062167








