Novel Mixing Relations for Determining the Effective Thermal Conductivity of Open-Cell Foams
Abstract
:1. Introduction
2. Materials and Methods
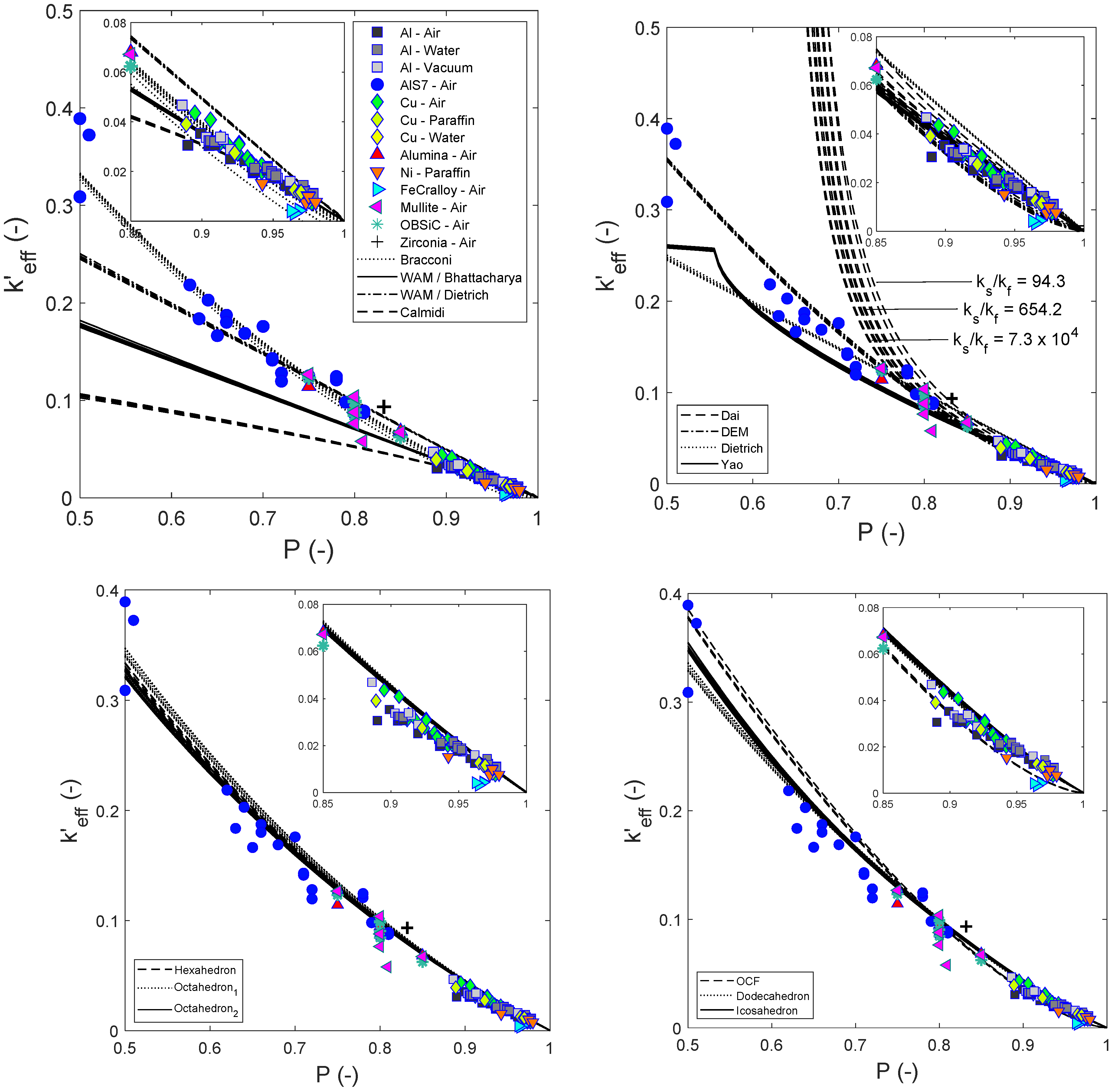
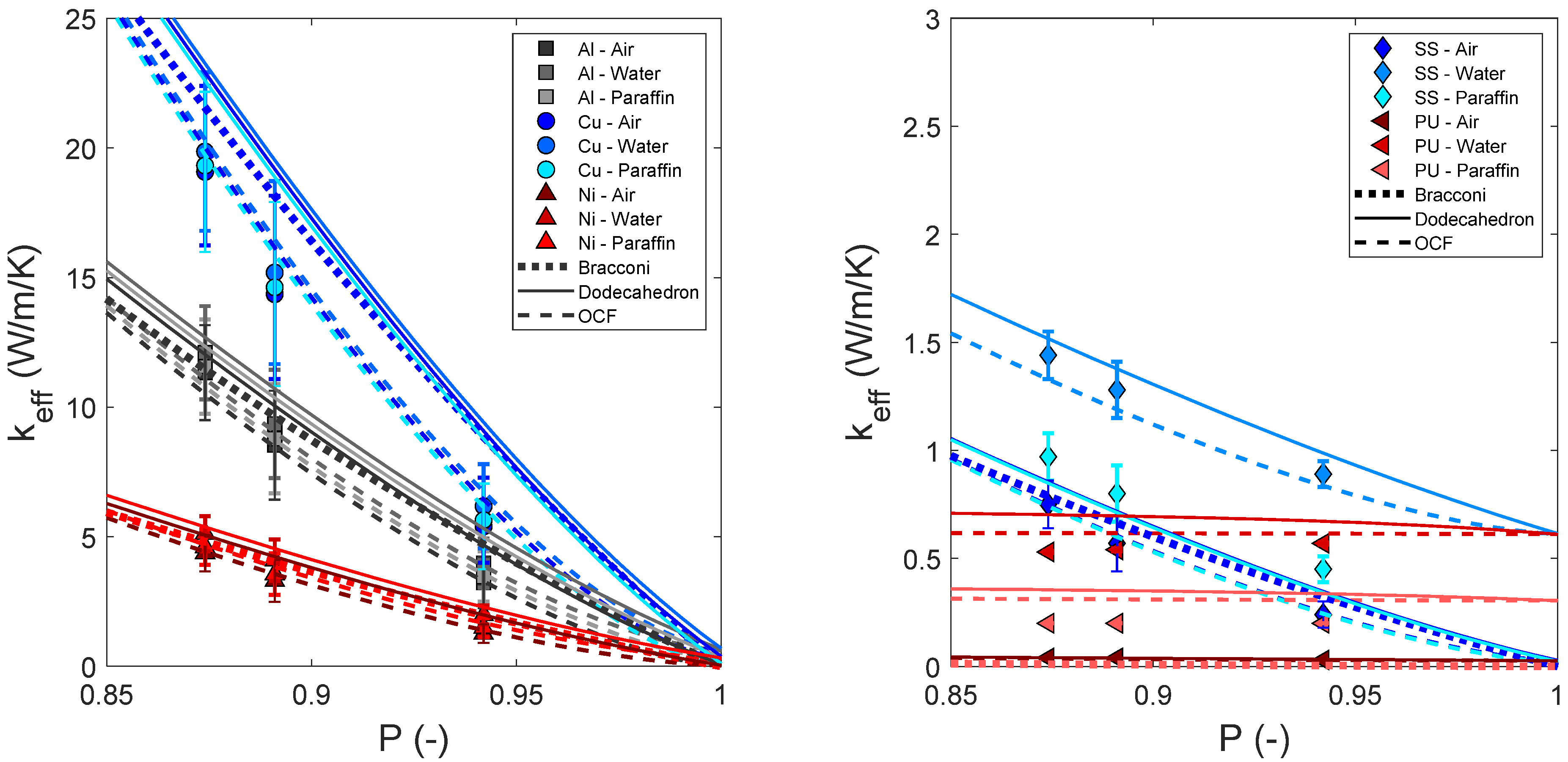
3. Results and Discussion
- For the simulations performed to calculate , the skeleton morphology was reconstructed from µCT-scans of samples with porosities of 0.90 ± 0.01. At this porosity, both experiments and simulations are well estimated by the OCF relation (see Figure 1 and Figure 2). However, 3D erosion and dilation filters [16] were applied for generating models of different porosity, which—depending on the mesh resolution—may produce significant differences compared with the microstructure of real foams.
- The synthetic foam structures generated by August et al. [19] are not morphologically identical despite having the same porosity. Numerically computed and measured experimental values of (as reported by August et al. [19]) only agree if the standard deviation is considered. This indicates that only a few of the synthetic structures are morphologically consistent with real foams.
4. Conclusions
- For foams with porosities ranging from 0.5 to 1.0 and low bulk thermal conductivities of the filling medium, the Bracconi relation [9] is recommended.
- Novel mixing relations are recommended for porosities ranging from 0.5 to 0.9, except for the Platonic relation based on dodecahedrons, which can be applied for porosities from 0.5 to 1.0. In addition, the Platonic relation based on dodecahedrons is recommended over the Bracconi relation for thermal conductivities of the filling medium higher than .
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
List of Abbreviations and Nomenclature
| Abbreviations | Description |
| CT | Computed tomography |
| DEM | Differential effective medium |
| EMA | Effective medium approximation |
| FEM | Finite element method |
| OCF | Open-cell foam |
| PU | Polyurethane |
| RMSE | Root-mean-square error |
| WAM | Weighted arithmetic mean |
| SS | Stainless steel |
| Nomenclature | Description (For dimensionless quantities, units are not indicated) |
| Coefficients of the polynomials for calculating | |
| Geometrical parameter of Yao’s model [11] | |
| Relative permittivity | |
| Dielectric constant | |
| Dielectric loss | |
| Dimensionless foam ligament radius of Dai’s model [10] | |
| Dimensionless cubic node edge length of Dai’s model [10] | |
| Thermal conductivity/ | |
| Dimensionless normalized thermal conductivity | |
| Dimensionless parameter of Yao’s model [11] | |
| Dimensionless correlation parameter of the foam morphology | |
| Real part of | |
| Imaginary part of | |
| Porosity | |
| Thermal resistance on a flux basis/ [10] | |
| Weight parameter [12] | |
| Subscripts | Description |
| A, B, C, D | Unit cell subsection of Dai’s model [10] |
| E, F, G | Layer of unit cell of Yao’s model [11] |
| arithm | Arithmetic |
| eff | Effective |
| f | Filling medium |
| k | Degree of the polynomials for calculating |
| m | Slope value of |
| s | Skeleton |
| 0 | Ordinate-intercept value of |
Appendix A
| Valid Porosity Range | Variable | ||||||
|---|---|---|---|---|---|---|---|
| Hexahedron | |||||||
| 0.058 to 1 | 0.5229 | −0.9951 | 2.4460 | −4.7673 | 3.9566 | −1.1630 | |
| 0.2775 | 4.7271 | −14.1449 | 15.0204 | −6.6742 | 0.7939 | ||
| Octahedron1 | |||||||
| 0.415 to 1 | 0.4008 | 0.6699 | −3.2970 | 3.9169 | −2.2435 | 0.5528 | |
| 2.1613 | −7.0162 | 17.1386 | −28.2326 | 23.5875 | −7.6392 | ||
| Octahedron2 | |||||||
| 0.093 to 1 | 0.6546 | −2.1904 | 6.0160 | −9.7020 | 7.2485 | −2.0266 | |
| 0.3698 | 7.6377 | −26.3063 | 34.1470 | −20.6464 | 4.7987 | ||
| Dodecahedron | |||||||
| 0.078 to 1 | 0.4617 | 0.3546 | −3.9082 | 7.6496 | −7.0236 | 2.4661 | |
| 1.4799 | −10.1720 | 50.1347 | −109.2526 | 103.7717 | −35.9641 | ||
| Icosahedron | |||||||
| 0.267 to 1 | 0.2213 | 4.1649 | −17.8917 | 29.0420 | −21.8497 | 6.3132 | |
| 2.4320 | −21.2239 | 84.7916 | −152.1911 | 124.4845 | −38.2943 | ||
References
- Vasudev, H.; Singh, G.; Bansal, A.; Vardhan, S.; Thakur, L. Microwave heating and its applications in surface engineering: A review. Mater. Res. Express 2019, 6, 102001. [Google Scholar] [CrossRef]
- Pabst, W.; Gregorová, E. Critical Assessment 18: Elastic and thermal properties of porous materials—Rigorous bounds and cross-property relations. Mater. Sci. Technol. 2015, 15, 1801–1808. [Google Scholar] [CrossRef] [Green Version]
- Schwartz, L.M.; Martys, N.; Bentz, D.P.; Garboczi, E.J.; Torquato, S. Cross-property relations and permeability estimation in model porous media. Phys. Rev. E 1993, 6, 4584–4591. [Google Scholar] [CrossRef]
- Kachanov, M.; Sevostianov, I. Chapter 6. Connections between Elastic and Conductive Properties of Heterogeneous Materials. Other Cross-Property Relations. In Micromechanics of Materials, with Applications, 1st ed.; Barber, J.R., Klarbring, A., Eds.; Springer International Publishing: Cham, Switzerland, 2018; Volume 249, pp. 469–548. [Google Scholar] [CrossRef]
- Pietrak, P.; Wisniewski, T.S. A review of models for effective thermal conductivity of composite materials. J. Power Technol. 2014, 95, 14–24. [Google Scholar]
- Krishnan, S.; Murthy, J.Y.; Garimella, S.V. Direct simulation of transport in open-cell metal foams. In Proceedings of the IMECE2005, 2005 ASME International Mechanical Engineering Congress and Exposition, Orlando, FL, USA, 5–11 November 2005; Volume 2005, pp. 597–604. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.H.; Bai, J.X.; Yan, H.B.; Kuang, J.J.; Lu, T.J.; Kim, T. An analytical unit cell model for the effective thermal conductivity of high porosity open-cell metal foams. Transp. Porous Media 2014, 102, 403–426. [Google Scholar] [CrossRef]
- Calmidi, V.V.; Mahajan, R.L. The effective thermal conductivity of high porosity fibrous metal foams. J. Heat Transfer 1999, 121, 466–471. [Google Scholar] [CrossRef]
- Bracconi, M.; Ambrosetti, M.; Maestri, M.; Groppi, G.; Tronconi, E. A fundamental analysis of the influence of the geometrical properties on the effective thermal conductivity of open-cell foams. Chem. Eng. Process.-Process Intensif. 2018, 129, 181–189. [Google Scholar] [CrossRef]
- Dai, Z.; Nawaz, K.; Park, Y.G.; Bock, J.; Jacobi, A.M. Correcting and extending the Boomsma–Poulikakos effective thermal conductivity model for three-dimensional fluid-saturated metal foams. Int. Commun. Heat Mass Transf. 2010, 37, 575–580. [Google Scholar] [CrossRef]
- Yao, Y.; Wu, H.; Liu, Z. A new prediction model for the effective thermal conductivity of high porosity open-cell metal foams. Int. J. Therm. Sci. 2015, 97, 56–67. [Google Scholar] [CrossRef]
- Pabst, W.; Hříbalová, S. Describing the effective conductivity of two-phase and multiphase materials via weighted means of bounds and general power means. JOM 2019, 71, 4005–4014. [Google Scholar] [CrossRef]
- Dietrich, B.; Schell, G.; Bucharsky, E.C.; Oberacker, R.; Hoffmann, M.J.; Schabel, W.; Kind, M.; Martin, H. Determination of the thermal properties of ceramic sponges. Int. J. Heat Mass Transf. 2010, 53, 198–205. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Calmidi, V.; Mahajan, R.L. Thermophysical properties of high porosity metal foams. Int. J. Heat Mass Transf. 2002, 45, 1017–1031. [Google Scholar] [CrossRef]
- Solórzano, E.; Reglero Ruiz, J.; Rodríguez-Pérez, M.; Lehmhus, D.; Wichmann, M.; De Saja, J.A. An experimental study on the thermal conductivity of aluminium foams by using the transient plane source method. Int. J. Heat Mass Transf. 2008, 51, 6259–6267. [Google Scholar] [CrossRef]
- Camacho Hernandez, J.N.; Link, G.; Schubert, M.; Hampel, U. Modeling of the effective permittivity of open-cell ceramic foams inspired by platonic solids. Materials 2021, 14, 7446. [Google Scholar] [CrossRef]
- Iasiello, M.; Savarese, C.; Damian, P.; Bianco, N.; Andreozzi, A.; Chiu, W.; Naso, V. Modeling heat conduction in open-cell metal foams by means of the three-dimensional thermal fin theory. J. Phys. Conf. Ser. 2019, 1224, 12009. [Google Scholar] [CrossRef]
- Sihvola, A.H. Electromagnetic mixing formulas and applications. In IEE Electromagnetic Waves Series: Institution of Electrical Engineers, 1st ed.; Institution of Electrical Engineers: London, UK, 1999; pp. 1–283. ISBN 9780852967720. [Google Scholar]
- August, A.; Reiter, A.; Kneer, A.; Selzer, M.; Nestler, B. Effective thermal conductivity of composite materials based on open cell foams. Heat Mass Transf. Res. J. 2018, 2, 33–45. [Google Scholar] [CrossRef]
- Phanikumar, M.S.; Mahajan, R.L. Non-Darcy natural convection in high porosity metal foams. Int. J. Heat Mass Transf. 2002, 45, 3781–3793. [Google Scholar] [CrossRef]
- Paek, J.W.; Kang, B.H.; Kim, S.Y.; Hyun, J.M. Effective thermal conductivity and permeability of aluminum foam materials. Int. J. Thermophys. 2000, 21, 453–464. [Google Scholar] [CrossRef]
- Boomsma, K.; Poulikakos, D. On the effective thermal conductivity of a three-dimensionally structured fluid-saturated metal foam. Int. J. Heat Mass Transf. 2001, 44, 827–836. [Google Scholar] [CrossRef]
- Schmierer, E.; Razani, A. Self-Consistent open-celled metal foam model for thermal applications. J. Heat Transf. 2006, 128, 194–1203. [Google Scholar] [CrossRef]
- Sadeghi, E.; Hsieh, S.; Bahrami, M. Thermal conductivity and contact resistance of metal foams. J. Phys. D Appl. Phys. 2011, 44, 125406. [Google Scholar] [CrossRef]
- Xiao, X.; Zhang, P.; Li, M. Effective thermal conductivity of open-cell metal foams impregnated with pure paraffin for latent heat storage. Int. J. Therm. Sci. 2014, 81, 94–105. [Google Scholar] [CrossRef]
- Coquard, R.; Rochais, D.; Baillis, D. Experimental investigations of the coupled conductive and radiative heat transfer in metallic/ceramic foams. Int. J. Heat Mass Transf. 2009, 52, 4907–4918. [Google Scholar] [CrossRef]
- Xiao, X.; Zhang, P.; Li, M. Preparation and thermal characterization of paraffin/metal foam composite phase change material. Appl. Energy 2013, 112, 1357–1366. [Google Scholar] [CrossRef]
- Coquard, R.; Loretz, M.; Baillis, D. Conductive heat transfer in metallic/ceramic open-cell foams. Adv. Eng. Mater. 2008, 10, 323–337. [Google Scholar] [CrossRef]
- August, A.; Ettrich, J.; Rölle, M.; Schmid, S.; Berghoff, M.; Selzer, M.; Nestler, B. Prediction of heat conduction in open-cell foams via the diffuse interface representation of the phase-field method. Int. J. Heat Mass Transf. 2015, 84, 800–808. [Google Scholar] [CrossRef]
| Relation | Expression | Remarks |
|---|---|---|
| Bracconi [9] | because it was derived from a correlation for the tortuosity in periodic ordered structures, which is defined by the skeleton structure only. | |
| Weighted arithmetic mean (WAM) [12] | Weighted arithmetic mean of the Wiener bounds using the following: | |
| Calmidi [8] | ||
| Dai [10] | ||
| Differential Effective Medium (DEM) [15] | Known also as the Bruggeman relation, non-symmetric. | |
| Yao [11] | ||
is calculated (implicit method) from as recommended by Yao et al. [11]). |
| Skeleton Material | Filling Medium | ||
|---|---|---|---|
| Aluminum [8] | 218 | Air [11] | 0.0265 |
| Alumina [13] | 25.9 | Paraffin [11] | 0.305 |
| AlSi7 [15] | 167 | Vacuum * [23] | 0.003 |
| Cupper [11] | 401 | Water [11] | 0.613 |
| FeCr-alloy [28] | 16 | ||
| Mullite [13] | 4.4 | ||
| Nickel [25] | 91.4 | ||
| OBSiC [13] | 8.1 | ||
| Stainless steel (SS) [19] | 15 | ||
| Zirconia [28] | 2.5 | ||
| Polyurethane (PU) [19] | 0.2 |
| Skeleton-Fluid | Skeleton-Fluid | ||
|---|---|---|---|
| Al-Air [8,19,20,21,22] | Nickel-Air [19] | ||
| Al-Water [8,19,22] | Nickel-Water [19] | ||
| Al-Paraffin [19] | Nickel-Paraffin [19,27] | ||
| Al-Vacuum [23,24] | Polyurethane-Air [19] | ||
| Alumina-Air [13] | Polyurethane-Water [19] | ||
| AlSi7-Air [15] | Polyurethane-Paraffin [19] | ||
| Cu-Air [11,19] | OBSiC-Air [13] | ||
| Cu-Paraffin [15,22,25] | Stainless steel-Air [19] | ||
| Cu-Water [11,19] | Stainless steel-Water [19] | ||
| FeCr-alloy-Air [26] | Stainless steel-Paraffin [19] | ||
| Mullite-Air [13,26] | Zirconia-Air [26] |
| Relation | RMSE | ||
|---|---|---|---|
| Bracconi | 1.55 | 0.78 | 0.68 |
| Calmidi | 7.80 | 0.98 | 0.81 |
| Dai | 84.05 | 0.80 | 0.73 |
| DEM | 2.10 | 1.77 | 1.72 |
| WAM/Bhattacharya * | 5.38 | 0.68 | 0.58 |
| WAM/Dietrich * | 3.58 | 2.32 | 2.13 |
| Yao | 3.02 | 0.62 | 0.53 |
| Hexahedron | 1.85 | 1.29 | 1.14 |
| Octahedron1 | 1.89 | 1.34 | 1.18 |
| Octahedron2 | 1.90 | 1.32 | 1.18 |
| Dodecahedron | 1.65 | 0.87 | 0.73 |
| Icosahedron | 1.67 | 1.07 | 0.92 |
| OCF | 2.30 | 1.55 | 1.52 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Camacho Hernandez, J.N.; Link, G.; Schubert, M.; Hampel, U. Novel Mixing Relations for Determining the Effective Thermal Conductivity of Open-Cell Foams. Materials 2022, 15, 2168. https://doi.org/10.3390/ma15062168
Camacho Hernandez JN, Link G, Schubert M, Hampel U. Novel Mixing Relations for Determining the Effective Thermal Conductivity of Open-Cell Foams. Materials. 2022; 15(6):2168. https://doi.org/10.3390/ma15062168
Chicago/Turabian StyleCamacho Hernandez, Jesus Nain, Guido Link, Markus Schubert, and Uwe Hampel. 2022. "Novel Mixing Relations for Determining the Effective Thermal Conductivity of Open-Cell Foams" Materials 15, no. 6: 2168. https://doi.org/10.3390/ma15062168






