A Process Parameter Design Method for Improving the Filament Diameter Accuracy of Extrusion 3D Printing
Abstract
:1. Introduction
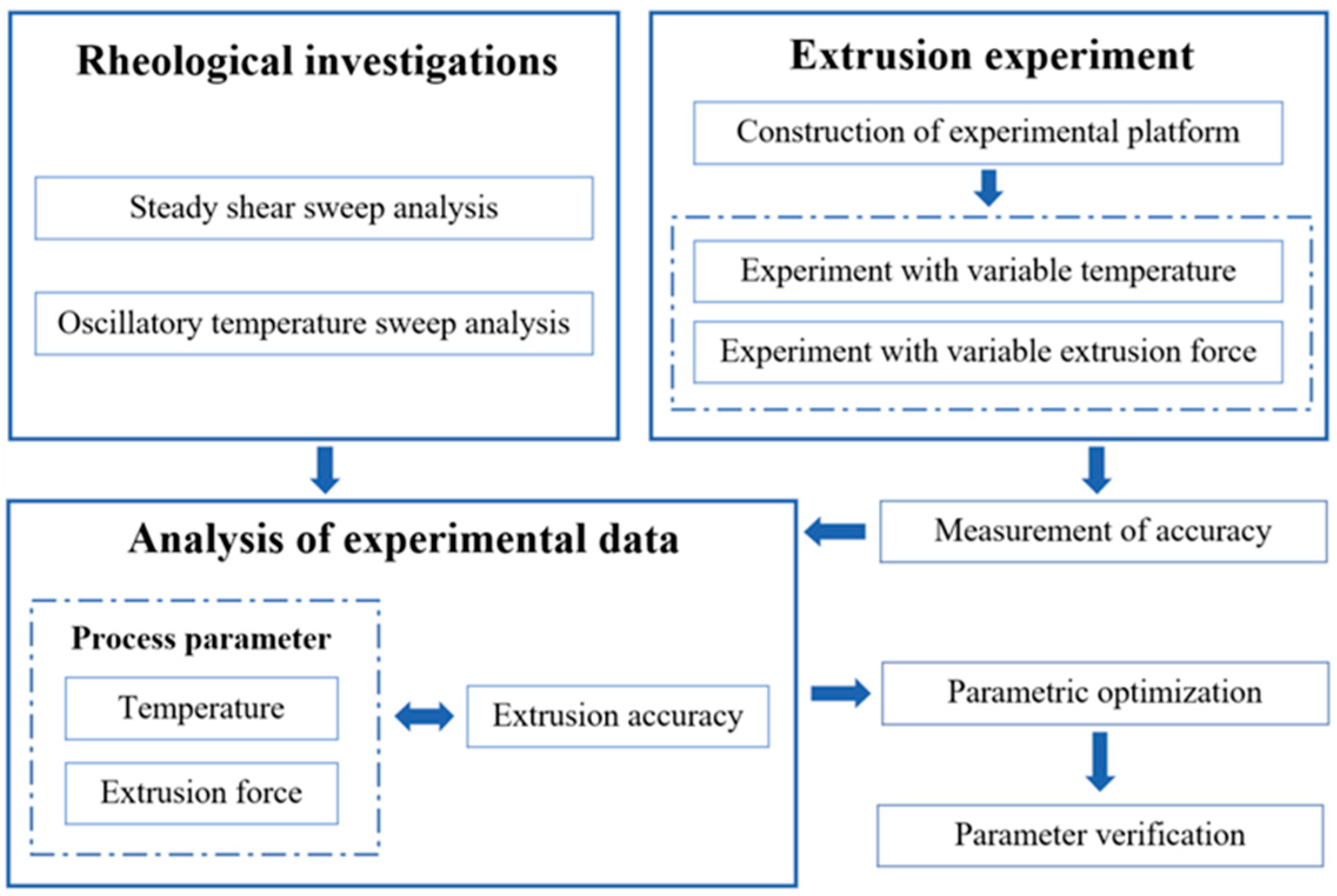
2. An Experiment-Based Process Parameter Design Method
2.1. Rheological Investigation
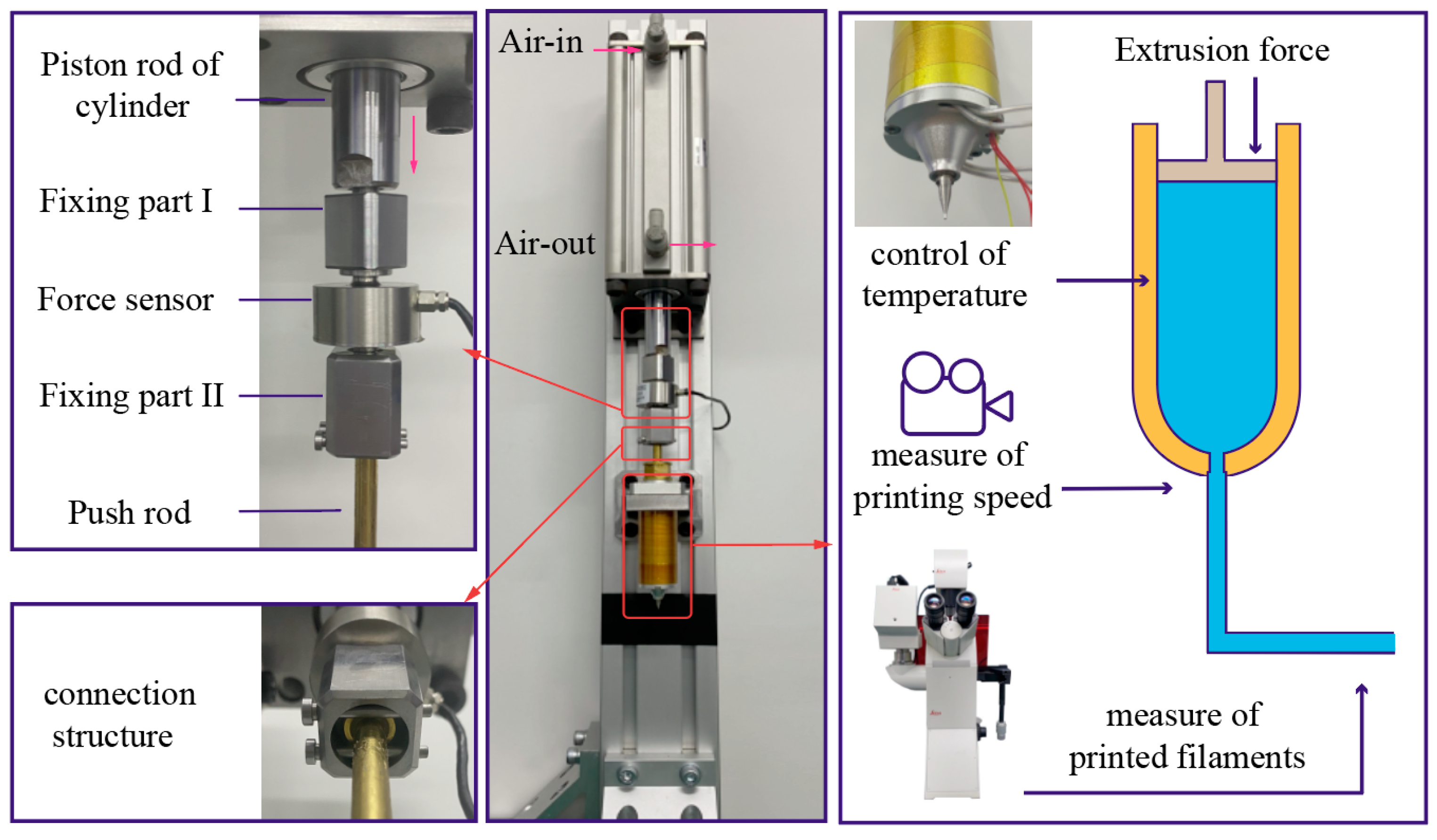
2.2. Extrusion Experiment
2.3. Process Parameter Design
3. Case Study of Process Parameter Design for PLCL
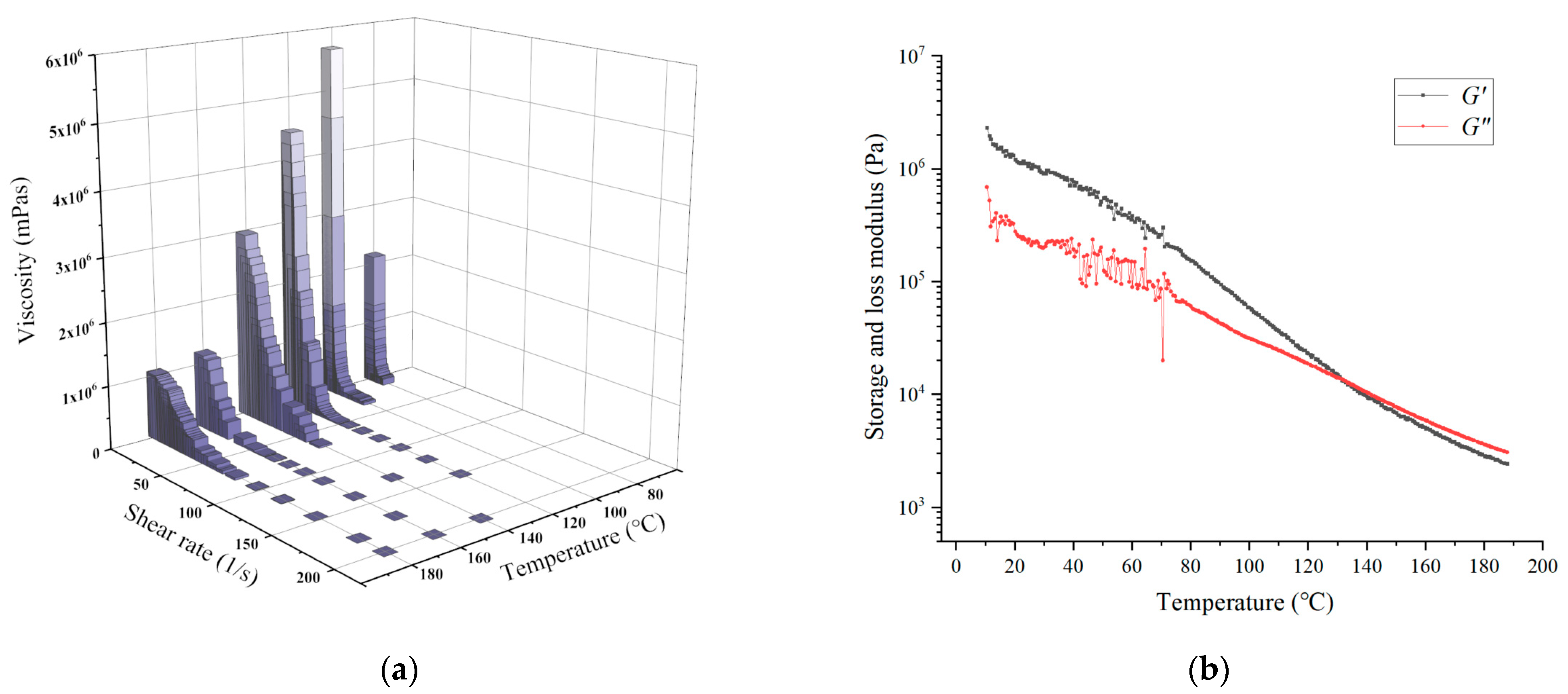
3.1. Rheological Properties of PLCL
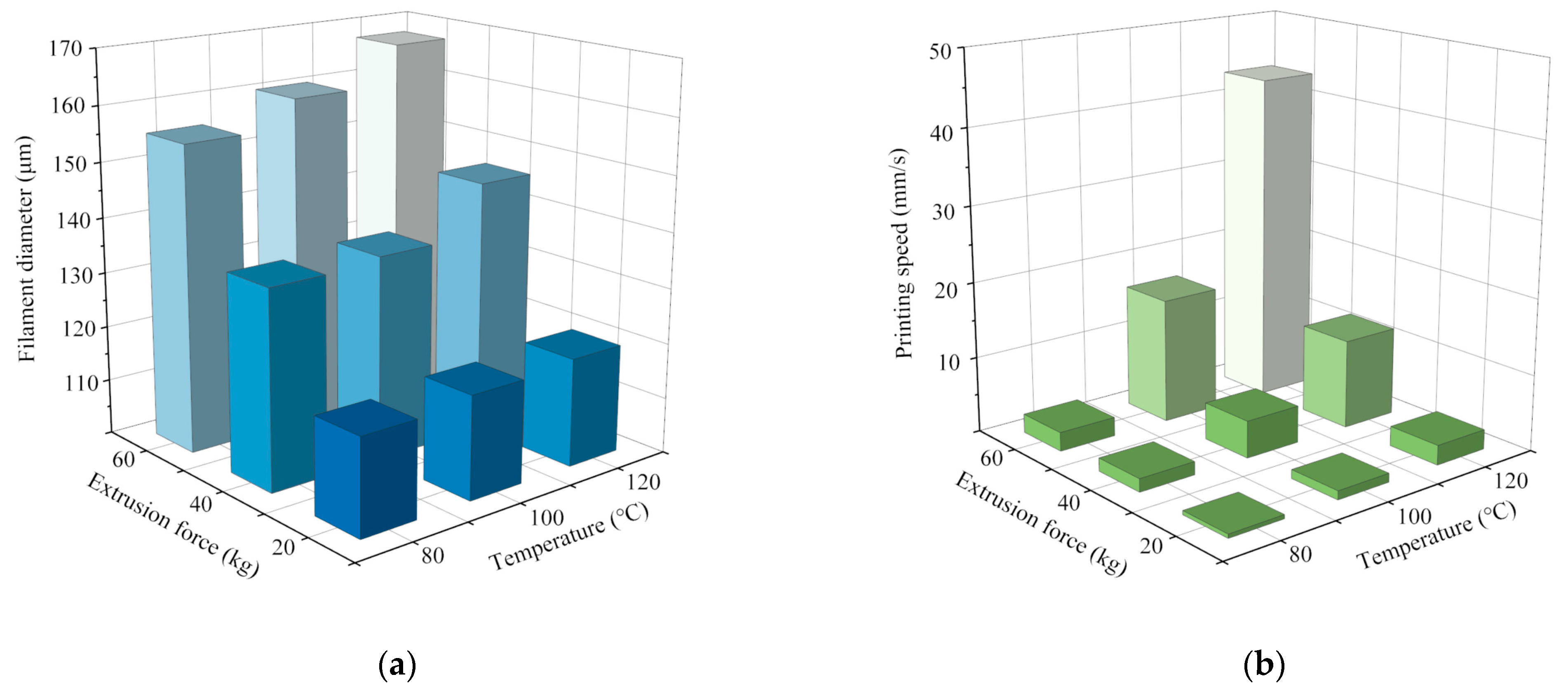
3.2. Influence of Process Parameters on Printing Accuracy
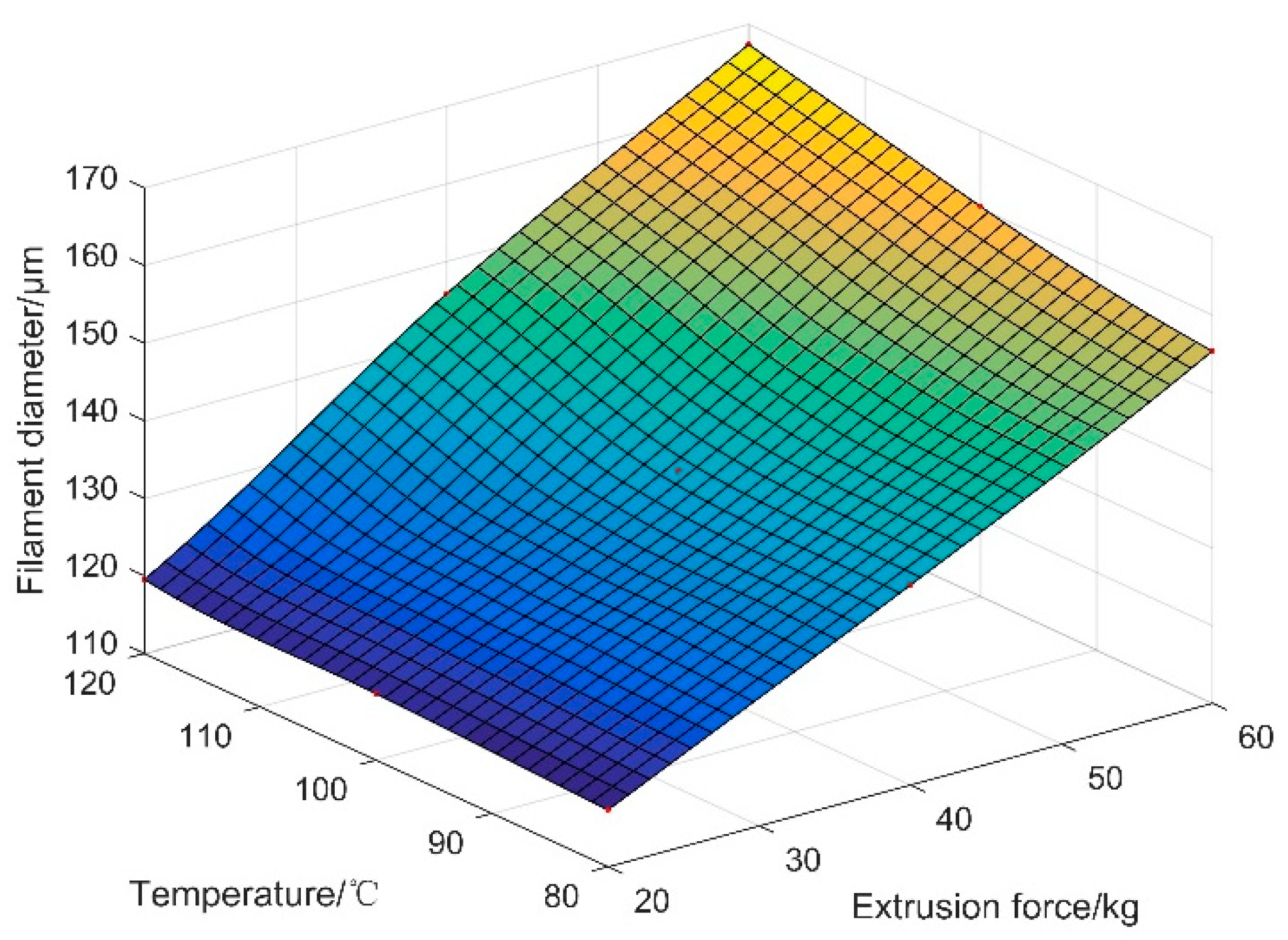
3.3. Design of Process Parameters of PLCL Extrusion 3D Printing
3.4. Experimental Verification
4. Conclusions
- (1)
- To quickly determine the proper process parameters for the desired filament diameters, an experiment-based process parameter design method was proposed to facilitate the process parameter design for extrusion 3D printing;
- (2)
- A novel extrusion 3D printing device was designed to precisely control extrusion force and temperature, by which the relationship between the process parameters and the filament diameter could be obtained efficiently and conveniently;
- (3)
- The process parameter design for PLCL was conducted as a case study of the proposed method. The printable range of the process parameters for PLCL was acquired, and a fitting surface of the experimental data was calculated to facilitate process parameter design.
- (4)
- A group of print trials was conducted, and the deviations between the actual diameters of the printed filaments and the desired diameters were less than 5 μm, which verified the feasibility and reliability of the proposed method.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mironov, V.; Boland, T.; Trusk, T.; Forgacs, G.; Markwald, R.R. Organ Printing: Computer-Aided Jet-Based 3D Tissue Engineering. Trends Biotechnol. 2003, 21, 157–161. [Google Scholar] [CrossRef]
- Daly, A.C.; Prendergast, M.E.; Hughes, A.J.; Burdick, J.A. Bioprinting for the Biologist. Cell 2021, 184, 18–32. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Guo, K.; Zhang, L.; Zhu, H.; Li, S.; Li, S.; Gao, F.; Liu, X.; Gu, Q.; Liu, L.; et al. Valve-Based Consecutive Bioprinting Method for Multimaterial Tissue-Like Constructs with Controllable Interfaces. Biofabrication 2021, 13, 035001. [Google Scholar] [CrossRef] [PubMed]
- Ng, W.L.; Lee, J.M.; Yeong, W.Y.; Win Naing, M. Microvalve-Based Bioprinting—Process, Bio-Inks and Applications. Biomater. Sci. 2017, 5, 632–647. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cheng, E.; Yu, H.; Ahmadi, A.; Cheung, K.C. Investigation of the Hydrodynamic Response of Cells in Drop on Demand Piezoelectric Inkjet Nozzles. Biofabrication 2016, 8, 015008. [Google Scholar] [CrossRef] [PubMed]
- Yamaguchi, S.; Ueno, A.; Akiyama, Y.; Morishima, K. Cell Patterning through Inkjet Printing of One Cell per Droplet. Biofabrication 2012, 4, 045005. [Google Scholar] [CrossRef]
- Tabriz, A.G.; Hermida, M.A.; Leslie, N.R.; Shu, W. Three-Dimensional Bioprinting of Complex Cell Laden Alginate Hydrogel Structures. Biofabrication 2015, 7, 045012. [Google Scholar] [CrossRef]
- Koo, Y.; Kim, G. New strategy for enhancing in situ cell viability of cell-printing process via piezoelectric transducer-assisted three-dimensional printing. Biofabrication 2016, 8, 025010. [Google Scholar] [CrossRef]
- Grigoryan, B.; Paulsen, S.J.; Corbett, D.C.; Sazer, D.W.; Fortin, C.L.; Zaita, A.J.; Greenfield, P.T.; Calafat, N.J.; Gounley, J.P.; Ta, A.H.; et al. Multivascular Networks and Functional Intravascular Topologies within Biocompatible Hydrogels. Science 2019, 364, 458–464. [Google Scholar] [CrossRef]
- Lin, H.; Zhang, D.; Alexander, P.G.; Yang, G.; Tan, J.; Cheng, A.W.; Tuan, R.S. Application of Visible Light-Based Projection Stereolithography for Live Cell-Scaffold Fabrication with Designed Architecture. Biomaterials 2013, 34, 331–339. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.; Lee, H.S.; Chung, J.J.; Kim, S.H.; Park, J.W.; Lee, K.; Jung, Y. Enhanced Regeneration of Vascularized Adipose Tissue with Dual 3D-Printed Elastic Polymer/dECM Hydrogel Complex. Int. J. Mol. Sci. 2021, 22, 2886. [Google Scholar] [CrossRef] [PubMed]
- Park, J.; Lee, S.J.; Jo, H.H.; Lee, J.H.; Kim, W.D.; Lee, J.Y.; Park, S.A. Fabrication and Characterization of 3D-printed Bone-Like B-Tricalcium Phosphate/Polycaprolactone Scaffolds for Dental Tissue Engineering. J. Ind. Eng. Chem. 2017, 46, 175–181. [Google Scholar] [CrossRef]
- Khorsandi, D.; Nodehi, M.; Waqar, T.; Shabani, M.; Kamare, B.; Zare, E.N.; Ersoy, S.; Annabestani, M.; Çelebi, M.F.; Kafadenk, A. Manufacturing of microfluidic sensors utilizing 3d printing technologies: A production system. J. Nanomater. 2021, 2021, 5537074. [Google Scholar] [CrossRef]
- He, Y.; Liu, W.; Guan, L.; Chen, J.; Duan, L.; Jia, Z.; Huang, J.; Li, W.; Liu, J.; Xiong, J.; et al. A 3D-Printed PLCL Scaffold Coated with Collagen Type I and its Biocompatibility. BioMed Res. Int. 2018, 2018, 5147156. [Google Scholar] [CrossRef]
- Merceron, T.K.; Burt, M.; Seol, Y.; Kang, H.; Lee, S.J.; Yoo, J.J.; Atala, A. A 3D Bioprinted Complex Structure for Engineering the Muscle-Tendon Unit. Biofabrication 2015, 7, 035003. [Google Scholar] [CrossRef]
- Kang, H.; Lee, S.J.; Ko, I.K.; Kengla, C.; Yoo, J.J.; Atala, A. A 3D Bioprinting System to Produce Human-Scale Tissue Constructs with Structural Integrity. Nat. Biotechnol. 2016, 34, 312–319. [Google Scholar] [CrossRef]
- Byambaa, B.; Annabi, N.; Yue, K.; Trujillo De Santiago, G.; Alvarez, M.M.; Jia, W.; Kazemzadeh Narbat, M.; Shin, S.R.; Tamayol, A.; Khademhosseini, A. Bioprinted Osteogenic and Vasculogenic Patterns for Engineering 3D Bone Tissue. Adv. Healthc. Mater. 2017, 6, 1700015. [Google Scholar] [CrossRef] [Green Version]
- Ji, S.; Guvendiren, M. Complex 3D Bioprinting Methods. APL Bioeng. 2021, 5, 011508. [Google Scholar] [CrossRef]
- Chang, P.; Li, S.; Sun, Q.; Guo, K.; Wang, H.; Li, S.; Zhang, L.; Xie, Y.; Zheng, X.; Liu, Y. Large Full-Thickness Wounded Skin Regeneration Using 3D-printed Elastic Scaffold with Minimal Functional Unit of Skin. J. Tissue Eng. 2022, 13, 204173142110630. [Google Scholar] [CrossRef]
- Bachtiar, E.O.; Ritter, V.C.; Gall, K. Structure-property relationships in 3D-printed poly(l-lactide-co-ε-caprolactone) degradable polymer. J. Mech. Behav. Biomed. 2021, 121, 104650. [Google Scholar] [CrossRef]
- Duan, R.; Wang, Y.; Zhang, Y.; Wang, Z.; Du, F.; Du, B.; Su, D.; Liu, L.; Li, X.; Zhang, Q. Blending with poly(l-lactic acid) improves the printability of poly(l-lactide-co-caprolactone) and enhances the potential application in cartilage tissue engineering. ACS Omega 2021, 6, 18300–18313. [Google Scholar] [CrossRef] [PubMed]
- Turner, B.N.; Strong, R.; Gold, S.A. A Review of Melt Extrusion Additive Manufacturing Processes: I. Process Design and Modeling. Rapid Prototyp. J. 2014, 20, 192–204. [Google Scholar] [CrossRef]
- Ren, Z.; Huang, X.; Liu, H. A Novel Unified Wall Slip Model for Poiseuille Flow of Polymer Melt in the Circular Tube. Polym. Eng. Sci. 2016, 56, 328–341. [Google Scholar] [CrossRef]
- Hangquan, L.; Dezhen, W.; Zhen, Z. Polymer Physics, 2nd ed.; China Light Inductry Press: Beijing, China, 2020; pp. 239–242. [Google Scholar]
- Zixiong, Z.; Zengnan, D. Viscous Fluid Mechanics, 2nd ed.; Tsinghua University Press: Beijing, China, 2011; pp. 43–46. [Google Scholar]

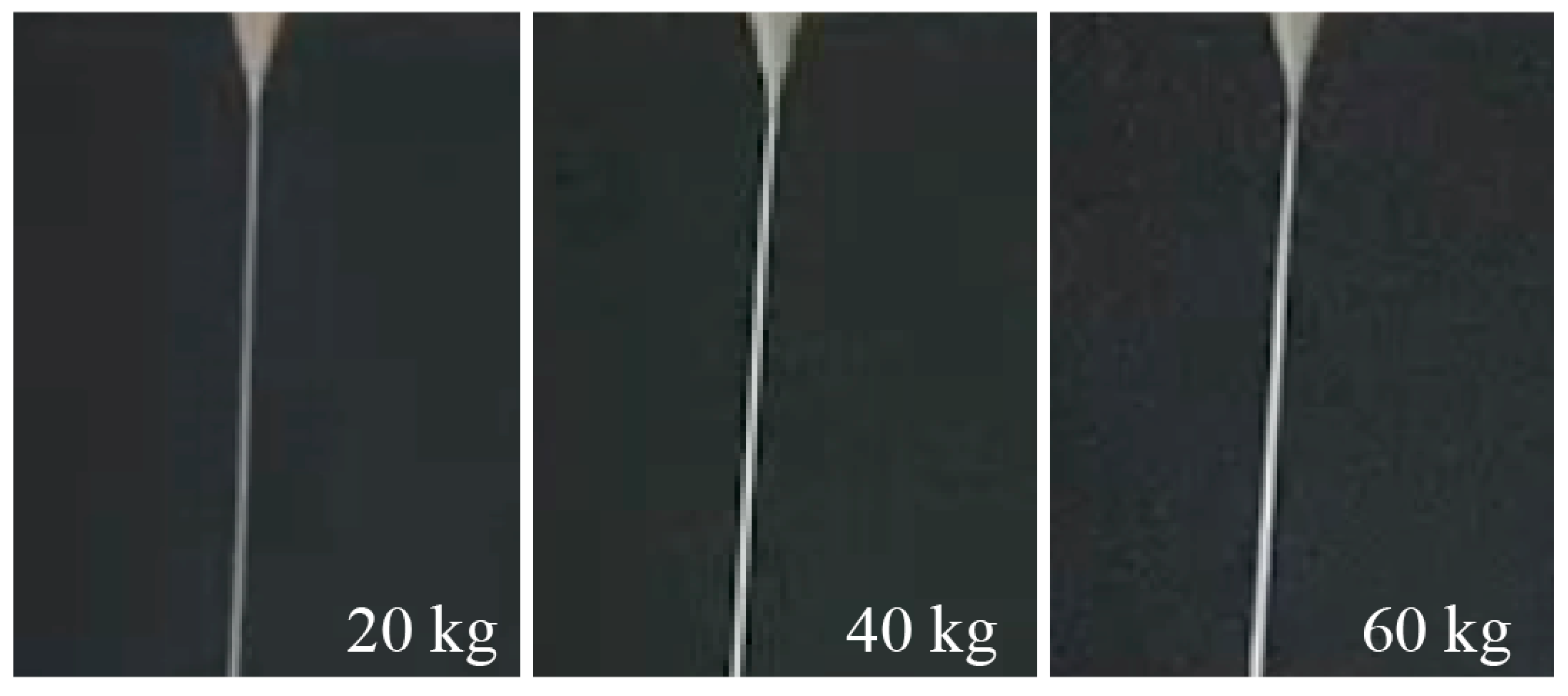
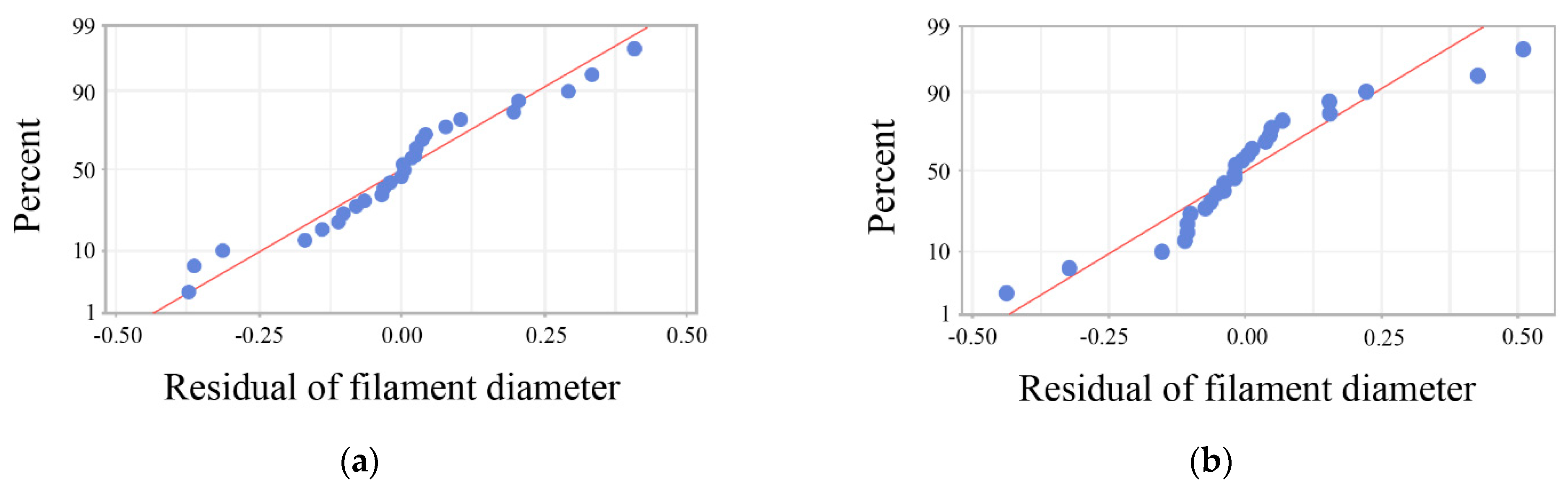

| Reference | Printing Method | Material | Minimum Diameter and Deviation (μm) |
|---|---|---|---|
| [14] | Extrusion 3D printing | PLCL | 244.80 ± 16.71 |
| [19] | 225.24 ± 15.27 | ||
| [20] | 383.81 ± 23.13 | ||
| [21] | 343.79 ± 21.21 |
| Factor | Source | F0.05 | F-Value |
|---|---|---|---|
| Filament diameter | Temperature (°C) | 3.56 | 3065.68 |
| Extrusion force (kg) | 78,988.19 | ||
| 2-way interactions | 2.93 | 483.10 | |
| Printing speed | Temperature (°C) | 3.56 | 14,103.97 |
| Extrusion force (kg) | 17,839.08 | ||
| 2-way interactions | 2.93 | 6303.12 |
| Diameter (μm) | Temperature (°C) | Extrusion Force (kg) |
|---|---|---|
| 120 | 91.0 | 22.2 |
| 130 | 106.4 | 31.2 |
| 140 | 95.4 | 43.8 |
| 150 | 113.2 | 46.7 |
| 160 | 116.2 | 54.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, K.; Gao, Q.; Lu, L.; Zhang, P. A Process Parameter Design Method for Improving the Filament Diameter Accuracy of Extrusion 3D Printing. Materials 2022, 15, 2454. https://doi.org/10.3390/ma15072454
Yu K, Gao Q, Lu L, Zhang P. A Process Parameter Design Method for Improving the Filament Diameter Accuracy of Extrusion 3D Printing. Materials. 2022; 15(7):2454. https://doi.org/10.3390/ma15072454
Chicago/Turabian StyleYu, Kaicheng, Qiang Gao, Lihua Lu, and Peng Zhang. 2022. "A Process Parameter Design Method for Improving the Filament Diameter Accuracy of Extrusion 3D Printing" Materials 15, no. 7: 2454. https://doi.org/10.3390/ma15072454
APA StyleYu, K., Gao, Q., Lu, L., & Zhang, P. (2022). A Process Parameter Design Method for Improving the Filament Diameter Accuracy of Extrusion 3D Printing. Materials, 15(7), 2454. https://doi.org/10.3390/ma15072454







