Fabry-Perot Interference Fiber Acoustic Wave Sensor Based on Laser Welding All-Silica Glass
Abstract
:1. Introduction
2. Structure and Fabrication of Sensor
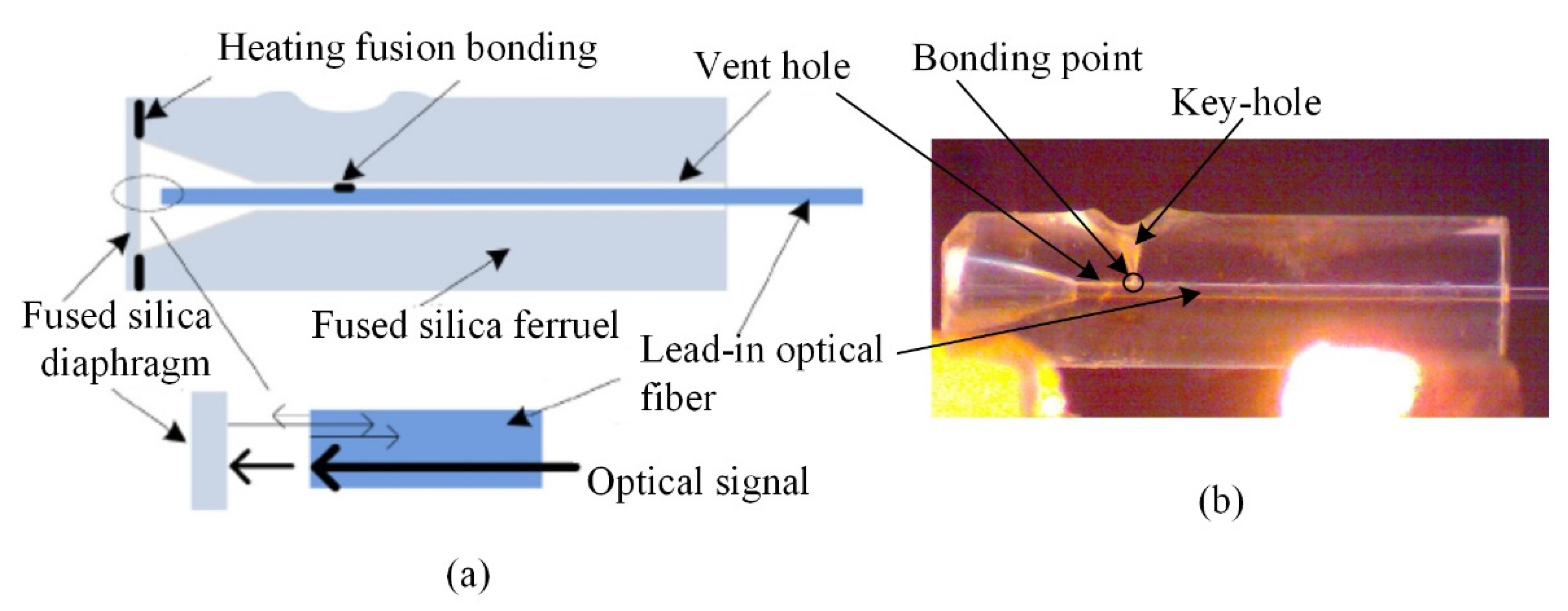
2.1. Structure of the Sensor
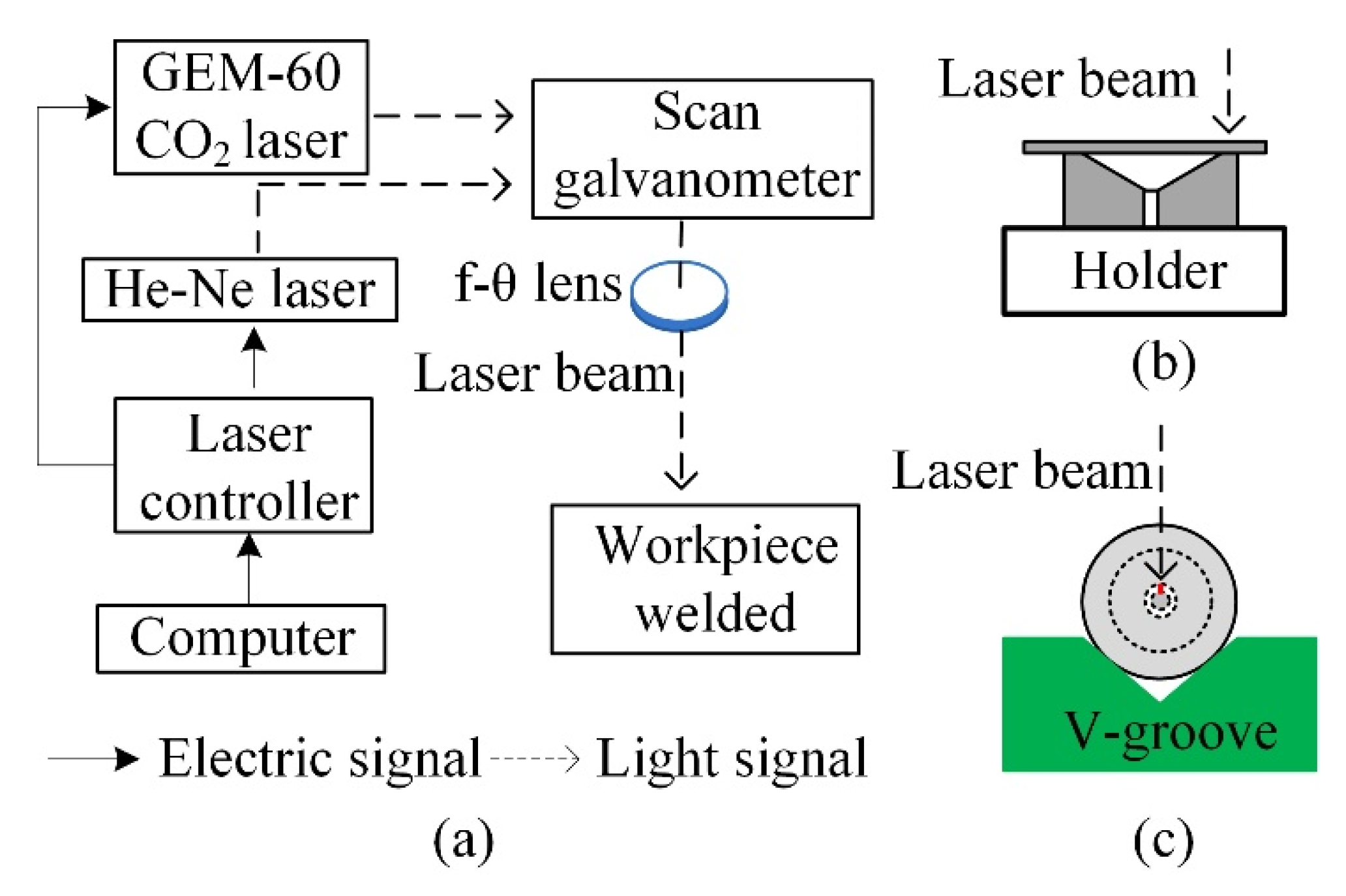
2.2. Fabrication of Sensor
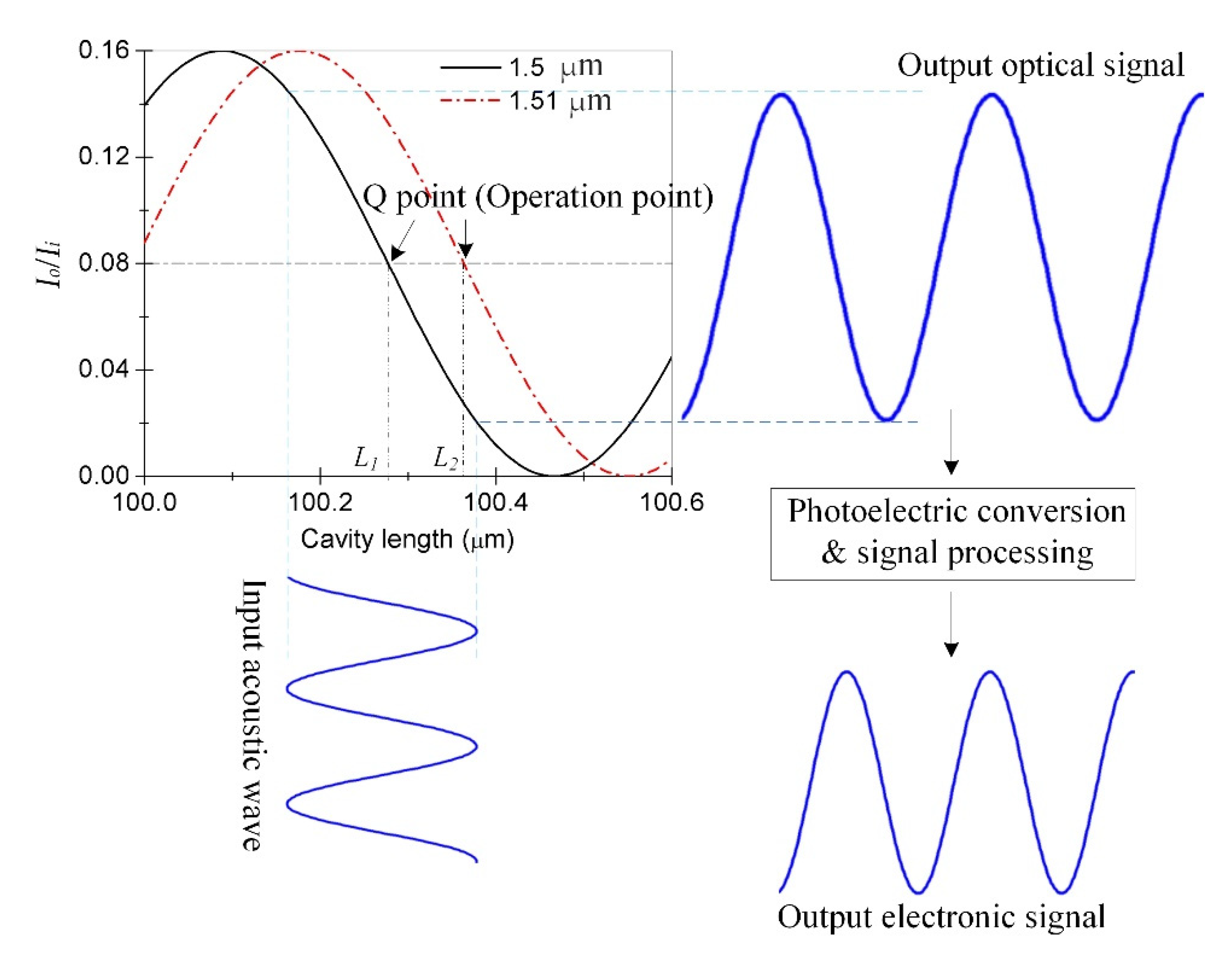
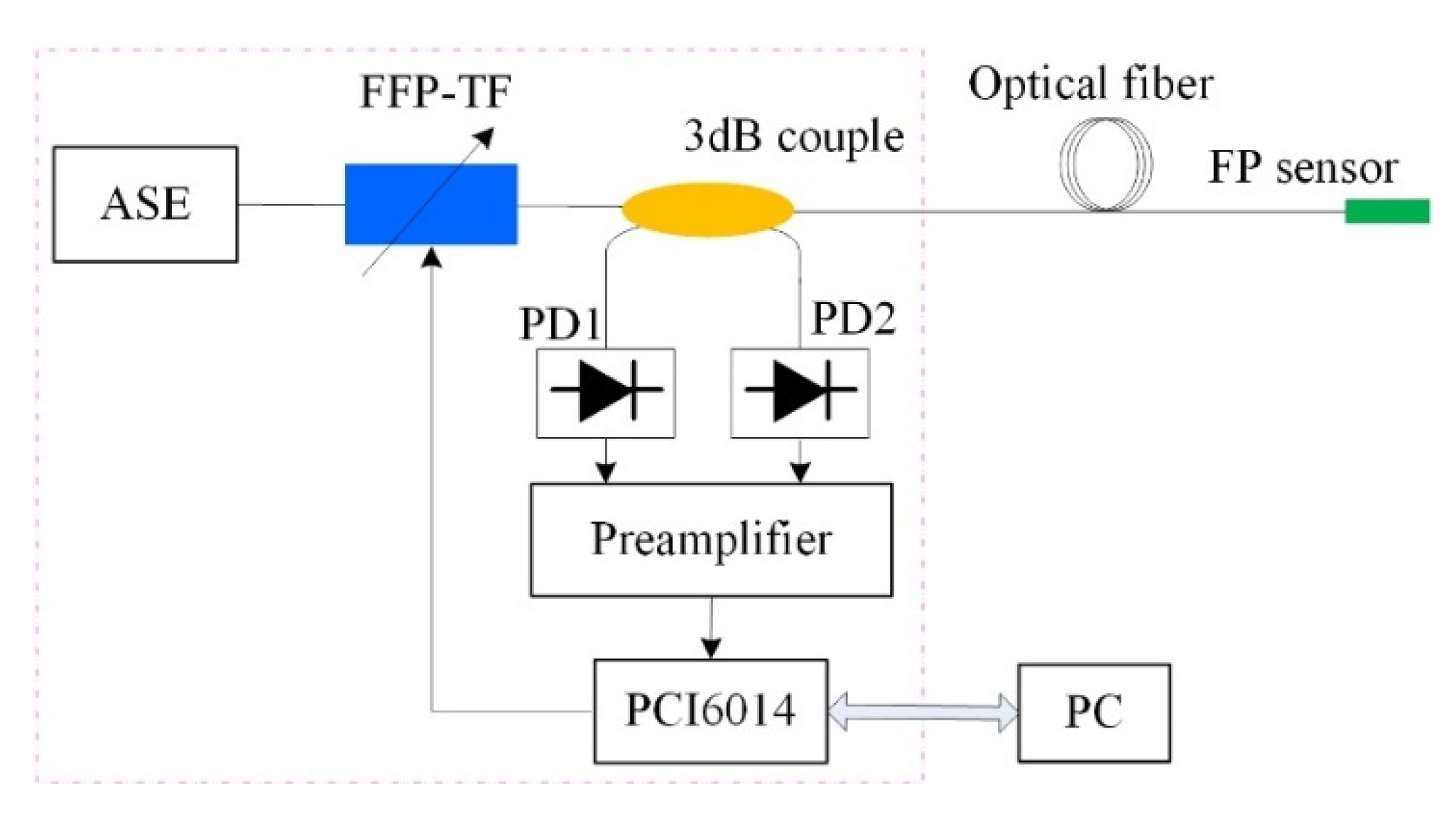
3. Principle and Signal Demodulation of the Sensor
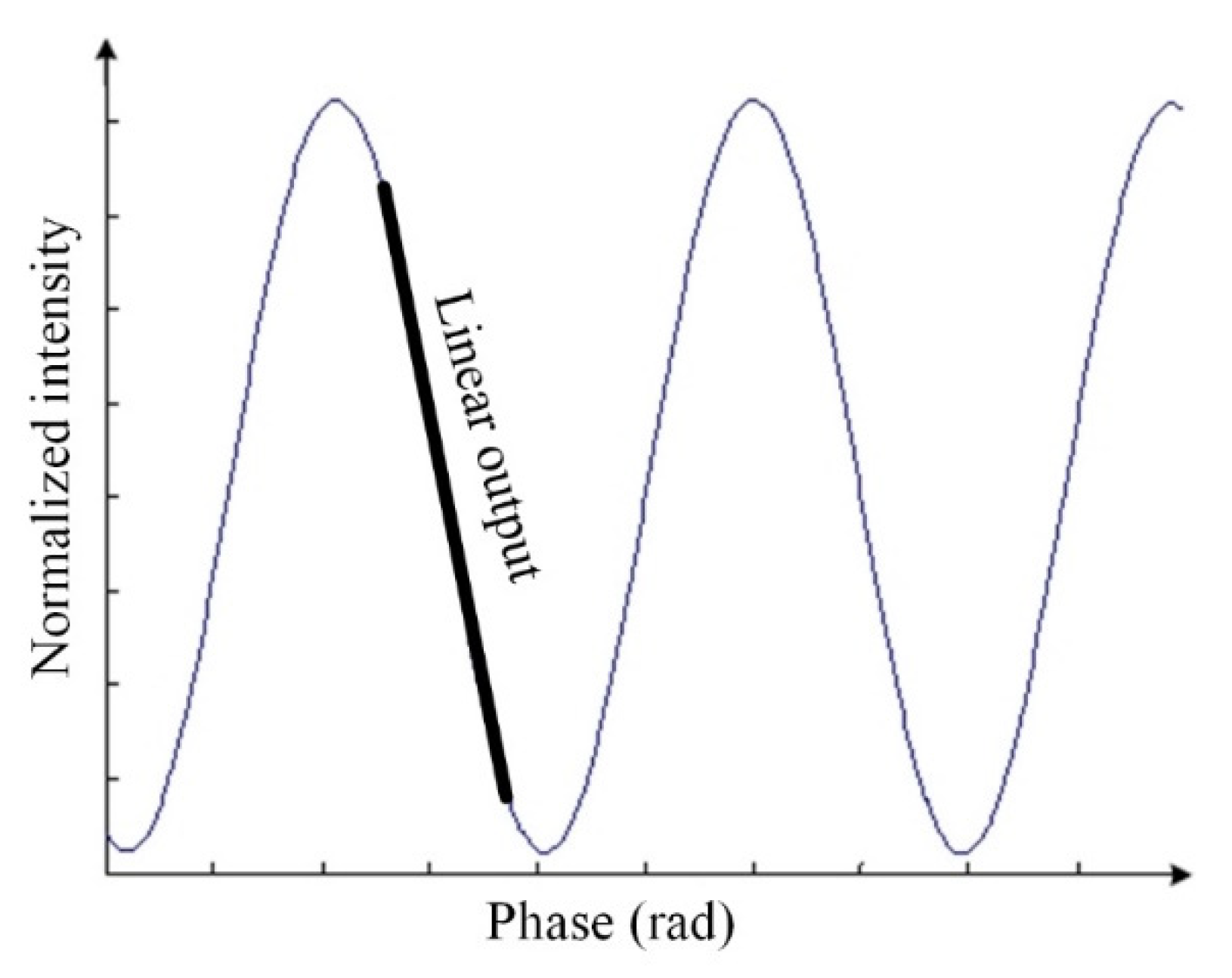
4. Working-Point Stabilization of the Sensor
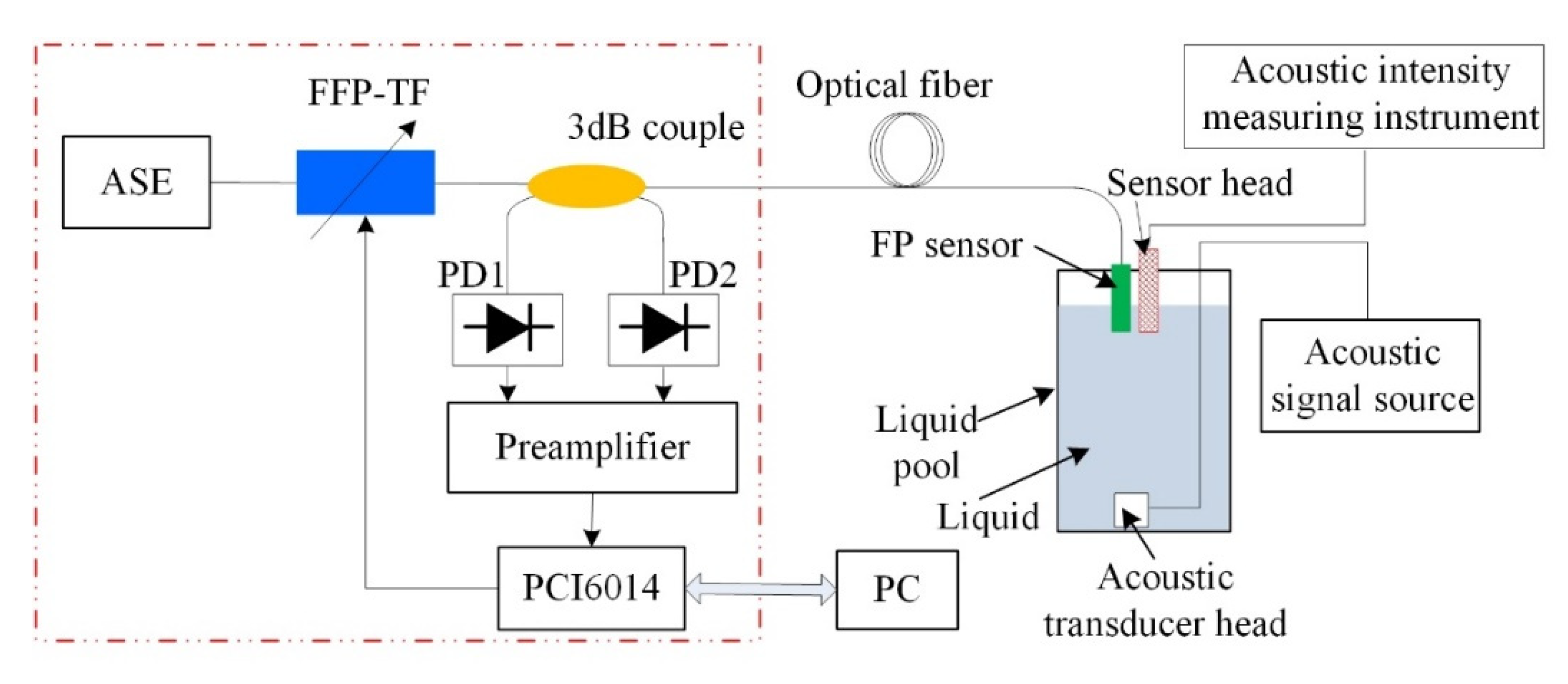
5. Experimental Results and Analysis
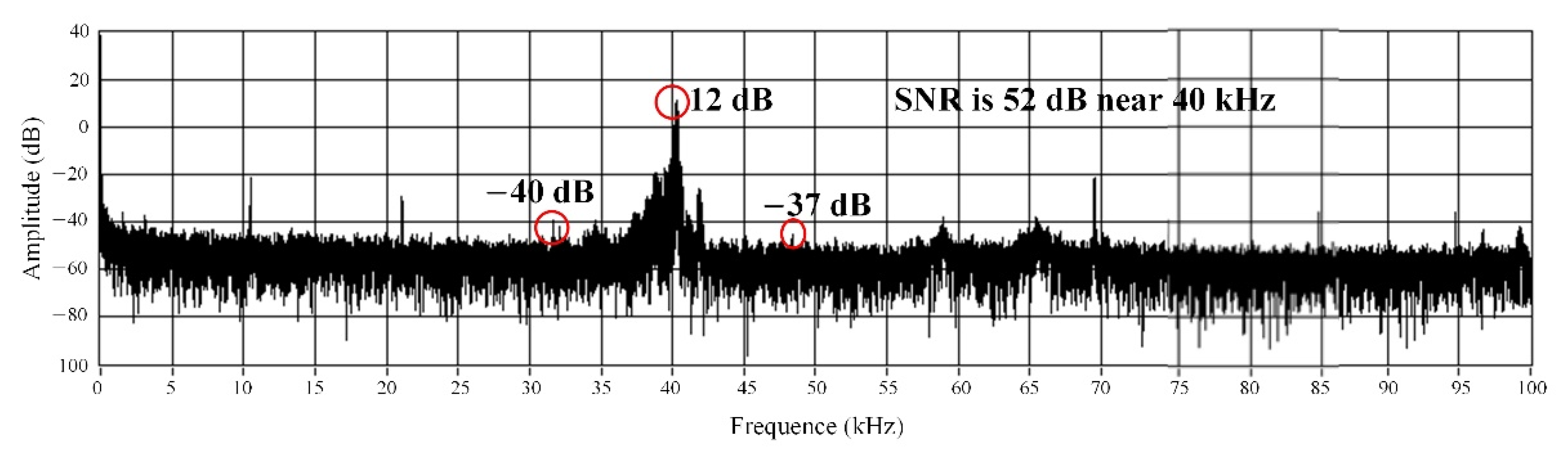
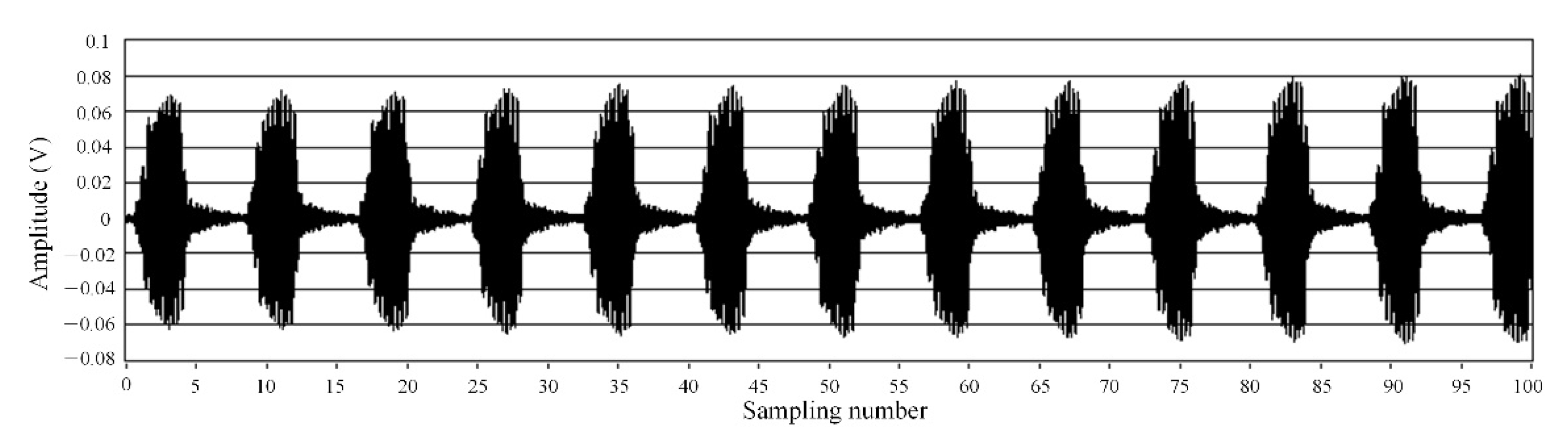
5.1. Acoustic Wave Signal Measurement
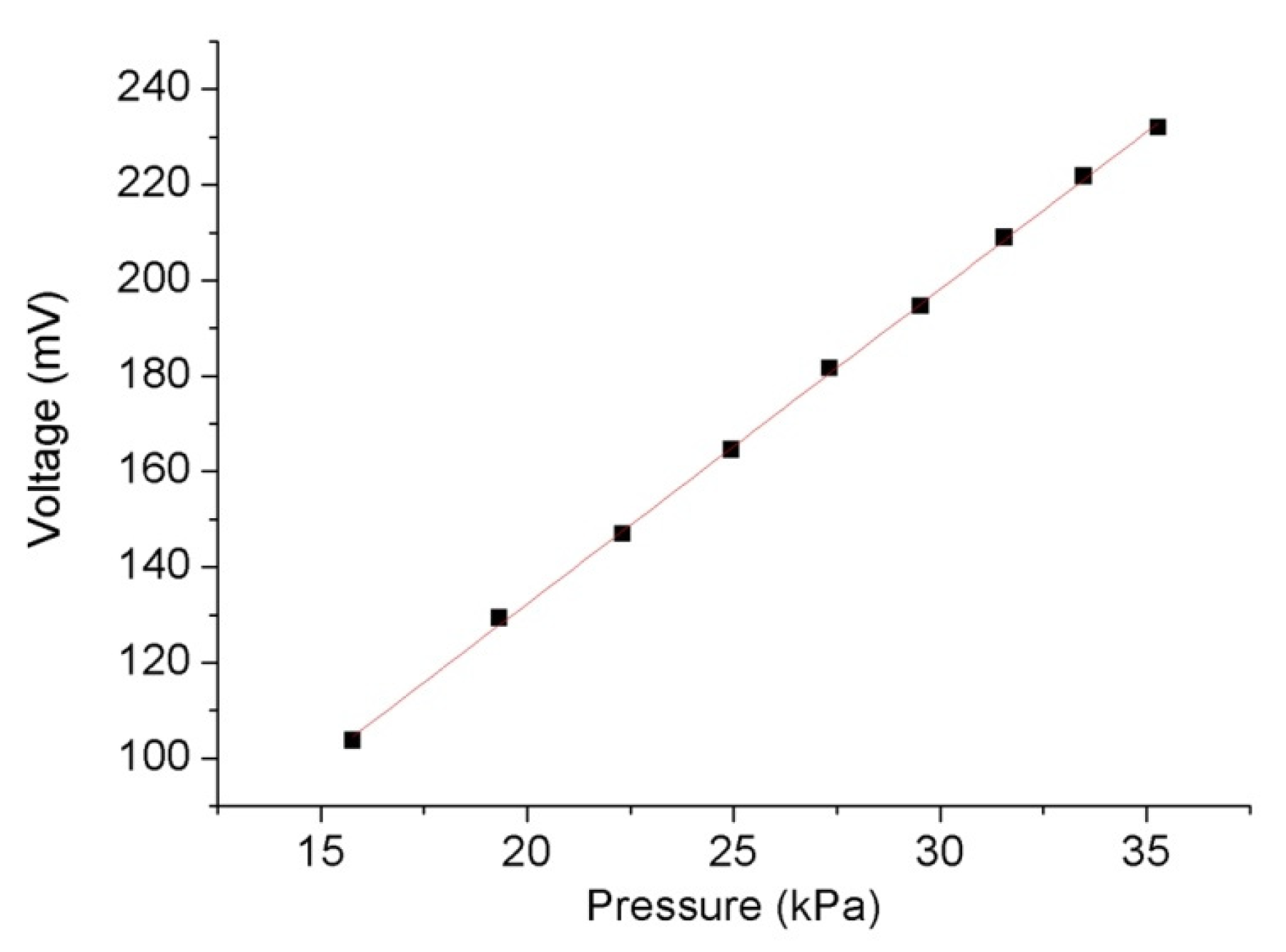
5.2. Sound Pressure Sensitivity of the Sensor
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ye, X.W.; Su, Y.H.; Han, J.P. Structural Health Monitoring of Civil Infrastructure Using Optical Fiber Sensing Technology: A Comprehensive Review. Sci. World J. 2014, 2014, 652329. [Google Scholar] [CrossRef] [Green Version]
- Willberry, J.O.; Papaelias, M.; Franklyn Fernando, G.F. Structural Health Monitoring Using Fibre Optic Acoustic Emission Sensors. Sensors 2020, 20, 6369. [Google Scholar] [CrossRef]
- Ohno, H.; Naruse, H.; Kihara, M.; Shimada, A. Industrial Applications of the BOTDR Optical Fiber Strain Sensor. Opt. Fiber Technol. 2001, 7, 45–64. [Google Scholar] [CrossRef]
- Di Sante, R. Fiber Optic Sensors for Structural Health Monitoring of Aircraft Composite Structures: Recent Advances and Applications. Sensors 2015, 15, 18666–18713. [Google Scholar] [CrossRef]
- Vaiano, P.; Carotenuto, B.; Pisco, M.; Ricciardi, A.; Quero, G.; Consales, M.; Crescitelli, A.; Esposito, E.; Cusano, A. Lab on Fiber Technology for Biological Sensing Applications. Laser Photonics Rev. 2016, 10, 922–961. [Google Scholar] [CrossRef]
- Azil, K.; Ferria, K.; Bouzid, S. Cladless Optical Fiber Sensor Based on Evanescent Wave Absorption for Monitoring Methylene Blue Induced Water Pollution. J. Opt. Soc. Am. B 2020, 37, A253–A258. [Google Scholar] [CrossRef]
- Li, Y.; Dong, B.; Chen, E.Q.; Wang, X.; Zhao, Y. Heart-Rate Monitoring with an Ethyl Alpha-Cyanoacrylate Based Fiber Fabry-Perot Sensor. IEEE J. Sel. Top. Quantum Electron. 2021, 27, 5600206. [Google Scholar] [CrossRef]
- Falcetelli, F.; Martini, A.; Di Sante, R.; Troncossi, M. Strain Modal Testing with Fiber Bragg Gratings for Automotive Applications. Sensors 2022, 22, 946. [Google Scholar] [CrossRef]
- Wachtarczyk, K.; Gąsior, P.; Kaleta, J.; Anuszkiewicz, A.; Bender, M.; Schledjewski, R.; Mergo, P.; Osuch, T. In-Plane Strain Measurement in Composite Structures with Fiber Bragg Grating Written in Side-Hole Elliptical Core Optical Fiber. Materials 2021, 15, 77. [Google Scholar] [CrossRef]
- Jena, J.; Wassin, S.; Bezuidenhout, L.; Doucouré, M.; Gibbon, T. Polarization-Based Optical Fiber Acoustic Waver Sensor for Geological Applications. J. Opt. Soc. Am. B 2020, 37, A147–A153. [Google Scholar] [CrossRef]
- Wang, Z.; Gao, C.F.; Chen, Z.X.; Ren, W.J.; Xie, H.B.; Wang, W. A Novel EFPI Sensor for Ultrasonic Testing of Partial-Discharge in High-Voltage Electrical Equipment. IEEE Access 2021, 7, 163456–163460. [Google Scholar] [CrossRef]
- Wang, Z.T.; Jiang, J.L.; Wang, Z.N.; Xiong, J.; Qiu, Z.; Liu, C.; Rao, Y. Quasi-Distributed Acoustic Sensing with Interleaved Identical Chirped Pulses for Multiplying the Measurement Slew-Rate. Opt. Express 2020, 28, 38465–38479. [Google Scholar] [CrossRef]
- Xing, N.Z.; Jin, S.; Li, Y.T.; Wang, S. Localization of Partial Discharge in Transformer Oil Using Fabry-Perot Optical Fiber Sensor Array. IEEE Trans. Dielectr. Electr. Insul. 2018, 25, 2279–2286. [Google Scholar] [CrossRef]
- Wang, S.C.; Chen, W. A Large-Area and Nanoscale Graphene Oxide Diaphragm-Based Extrinsic Optical Fiber Fabry-Perot Acoustic Waver Sensor Applied for Partial Discharge Detection in Air. Nanomaterials 2020, 10, 2312. [Google Scholar] [CrossRef]
- Lin, M.; Zhao, H.; Xu, M.Z. Fiber FP sensing simulation for PD-induced acoustic emission. High Voltage Eng. 2008, 34, 1027–1031. [Google Scholar]
- Nelson, D.F.; Kleinman, D.A.; Wecht, K.W. Vibration-Induced Modulation of Fiber Guide Transmission. Appl. Phys. Lett. 1977, 30, 94–96. [Google Scholar] [CrossRef]
- Garthe, D. A Optical Fiber Microphone. Sens. Actuators A 1991, 26, 341–345. [Google Scholar] [CrossRef]
- Sirkis, J.S. Optical Fiber Strain Sensing in Engineering Mechanics. Top. Appl. Phys. 2000, 70, 233–273. [Google Scholar] [CrossRef]
- Xu, J.; Wang, X.; Cooper, K.L.; Wang, A. Miniature All-Silica Fiber Optic Pressure and Acoustic Waver Sensors. Opt. Lett. 2005, 30, 3269–3271. [Google Scholar] [CrossRef]
- Han, M.; Wang, X.; Xu, J.; Kristie, L.C.; Wang, A.B. Diaphragm-Based Extrinsic Fabry-Perot Interference Optical Fiber Sensor for Acoustic Wave Detection Under High Background Pressure. Opt. Eng. 2005, 44, 060506. [Google Scholar] [CrossRef]
- Pulliam, W. Micromachined, SiC Fiber Optic Pressure Sensors for High Temperature Aerospace Applications. SPIE 2000, 4202, 21–30. [Google Scholar] [CrossRef]
- Ma, J.; Xuan, H.F.; Ho, H.L.; Jin, W.; Yang, Y.; Fan, S. Fiber-Optic Fabry-Pérot Acoustic Sensor with Multilayer Graphene Diaphragm. IEEE Photonics Technol. Lett. 2013, 25, 932–935. [Google Scholar] [CrossRef]
- Ni, W.J.; Lu, P.; Fu, X.; Zhang, W.; Shum, P.P.; Sun, H.; Yang, C.; Liu, D.; Zhang, J. Ultrathin Graphene Diaphragm-Based Extrinsic Fabry-Perot Interferometer for Ultra-Wideband Fiber Optic Acoustic Sensing. Opt. Express 2018, 26, 20758–20767. [Google Scholar] [CrossRef]
- Gong, Z.; Chen, K.; Zhou, X.; Yang, Y.; Zhao, Z.; Zou, H.; Yu, Q. High-Sensitivity Fabry-Perot Interference Acoustic Waver Sensor for Low-Frequency Acoustic Pressure Detections. J. Lightwave Technol. 2017, 35, 5276–5279. [Google Scholar] [CrossRef]
- Qi, X.G.; Wang, S.; Jiang, J.F.; Liu, K.; Zhang, P.; Li, R.; Liu, T. Flywheel-Like Diaphragm-Based Optical Fiber Fabry-Perot Frequency Tailored Acoustic Waver Sensor. J. Phys. D Appl. Phys. 2020, 53, 415102. [Google Scholar] [CrossRef]
- Zhang, W.; Lu, P.; Ni, W.J.; Xiong, W.; Liu, D.; Zhang, J. Gold-Diaphragm Based Fabry-Perot Ultrasonic Sensor for Partial Discharge Detection and Localization. IEEE Photonics J. 2020, 12, 1–12. [Google Scholar] [CrossRef]
- Xu, J.; Pickrell, G.R.; Wang, X.; Bing, Y.; Wang, A.B. Vacuum-Sealed High Temperature High Bandwidth Fiber Optic Pressure and Acoustic Waver Sensors. SPIE 2005, 5998, 67–72. [Google Scholar] [CrossRef]
- Yu, B.; Kim, D.W.; Deng, J.; Xiao, H.; Wang, A. Fiber Fabry-Perot Sensors for Detection of Partial Discharges in Power Transformers. Appl. Opt. 2003, 42, 3241–3250. [Google Scholar] [CrossRef]
- Wang, W.; Wu, W.; Wu, S.; Li, Y.; Huang, C.; Tian, X.; Fei, X.; Huang, J. Adhesive-Free Bonding Homogenous Fused-Silica Fabry-Perot Optical Fiber Low Pressure Sensor in Harsh Environments by CO2 Laser Welding. Opt. Commun. 2019, 435, 97–101. [Google Scholar] [CrossRef]
- Wang, W.; Wu, N.; Tian, Y.; Niezrecki, C.; Wang, X. Miniature all-silica optical fiber pressure sensor with an ultrathin uniform diaphragm. Opt. Express 2010, 18, 9006–9014. [Google Scholar] [CrossRef]
- Yin, J.; Liu, T.; Jiang, J.; Liu, K.; Wang, S.; Qin, Z.; Zou, S. Batch-Producible Fiber-Optic Fabry-Perot Sensor for Simultaneous Pressure and Temperature Sensing. IEEE Photonics Technol. Lett. 2014, 26, 2070–2073. [Google Scholar] [CrossRef]
- Giovanni, M.D. Flat and Corrugated Diaphragm Design Handbook; Mercel Dekker: New York, NY, USA, 1982. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W. Fabry-Perot Interference Fiber Acoustic Wave Sensor Based on Laser Welding All-Silica Glass. Materials 2022, 15, 2484. https://doi.org/10.3390/ma15072484
Wang W. Fabry-Perot Interference Fiber Acoustic Wave Sensor Based on Laser Welding All-Silica Glass. Materials. 2022; 15(7):2484. https://doi.org/10.3390/ma15072484
Chicago/Turabian StyleWang, Wenhua. 2022. "Fabry-Perot Interference Fiber Acoustic Wave Sensor Based on Laser Welding All-Silica Glass" Materials 15, no. 7: 2484. https://doi.org/10.3390/ma15072484
APA StyleWang, W. (2022). Fabry-Perot Interference Fiber Acoustic Wave Sensor Based on Laser Welding All-Silica Glass. Materials, 15(7), 2484. https://doi.org/10.3390/ma15072484




