Analysis of Multi-Tendon Friction-Based Composite Anchorage Device for CFRP Cables and Its Anchorage Mechanism
Abstract
:1. Introduction
2. Theoretical Analysis of Multi-Tendon Friction-Based Anchorage Devices for CFRP Cables
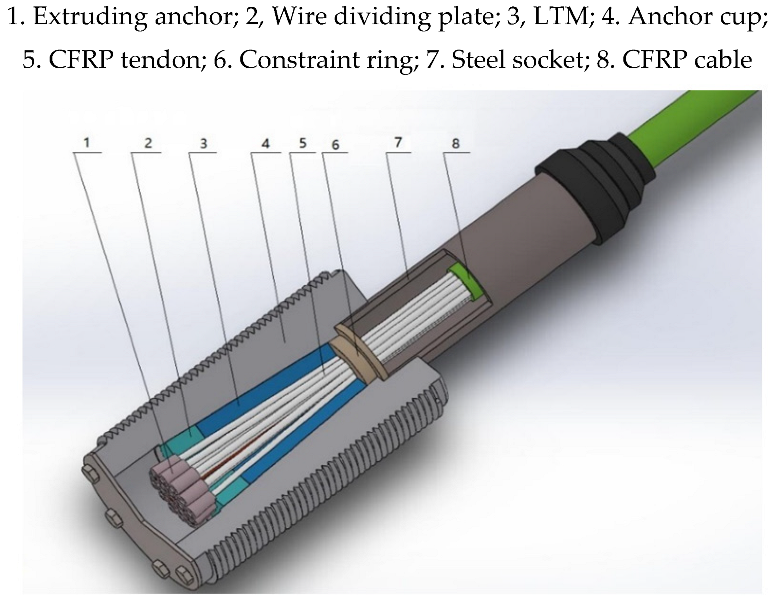
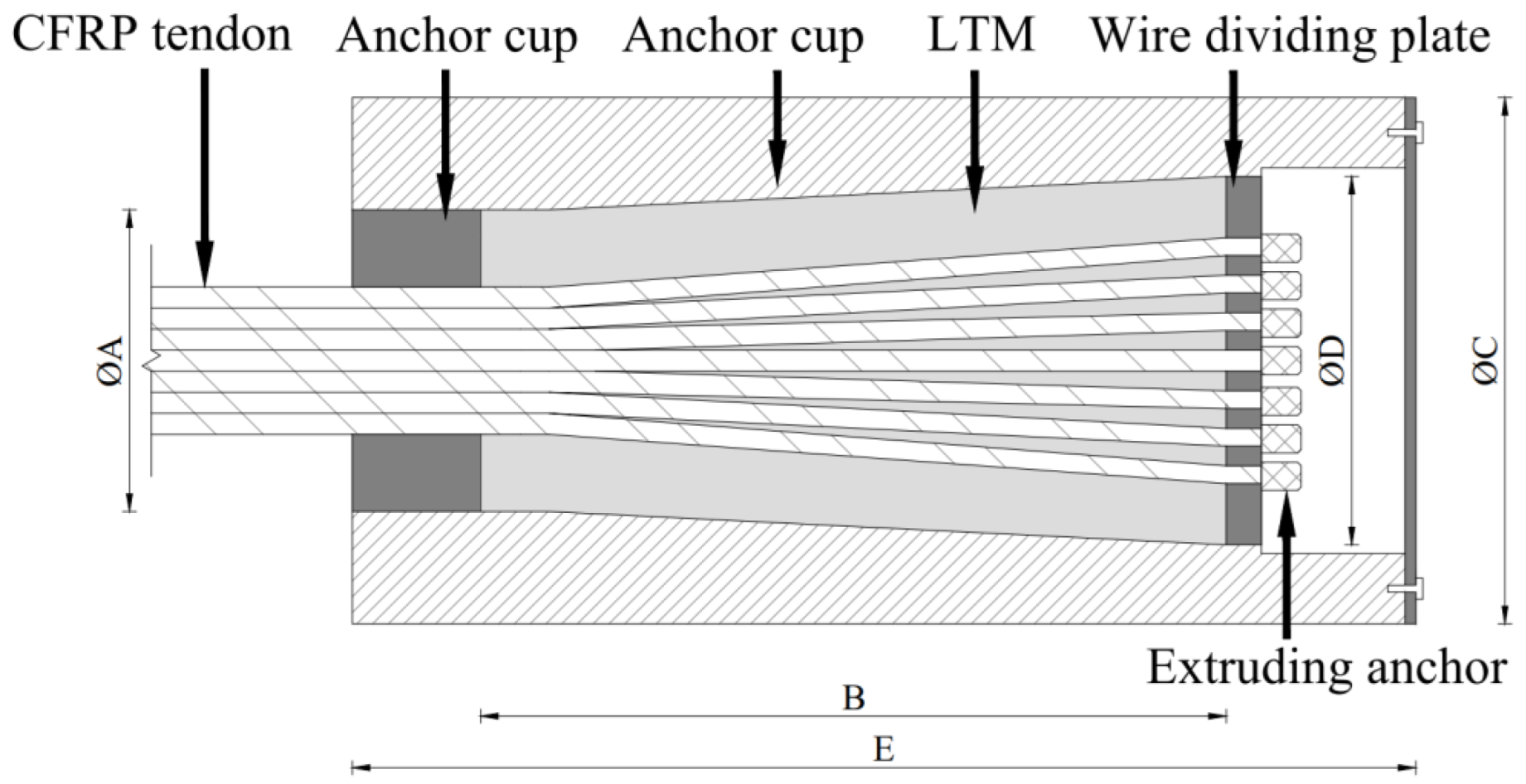
2.1. Overall Scheme of the CFRP Friction-Based Anchorage Device
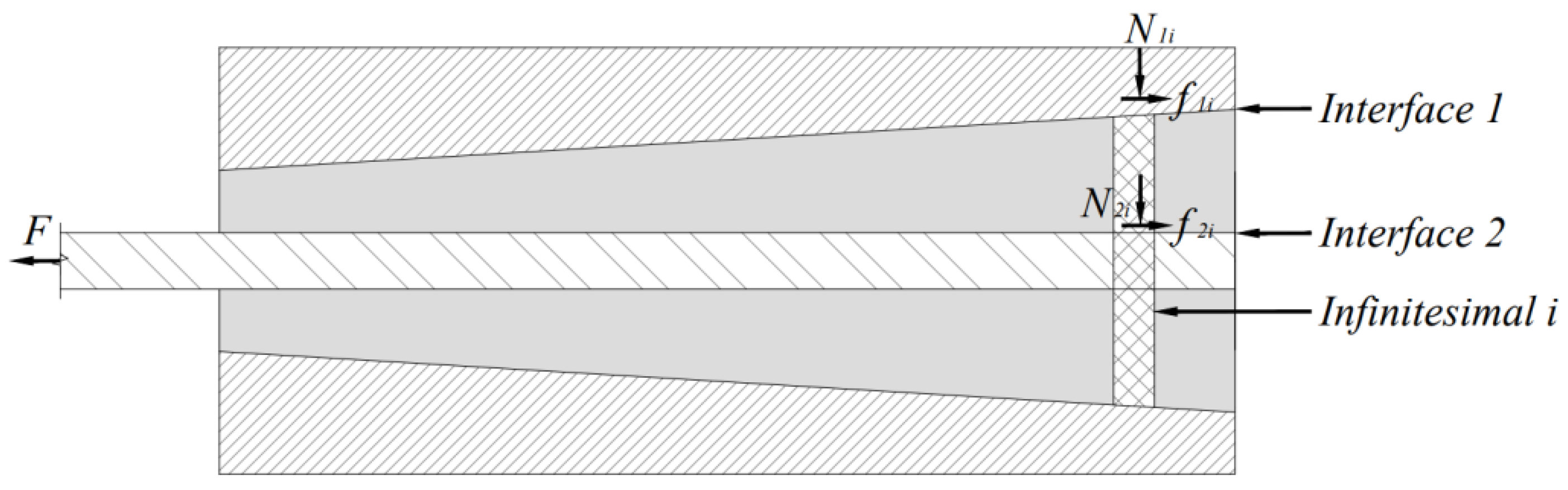
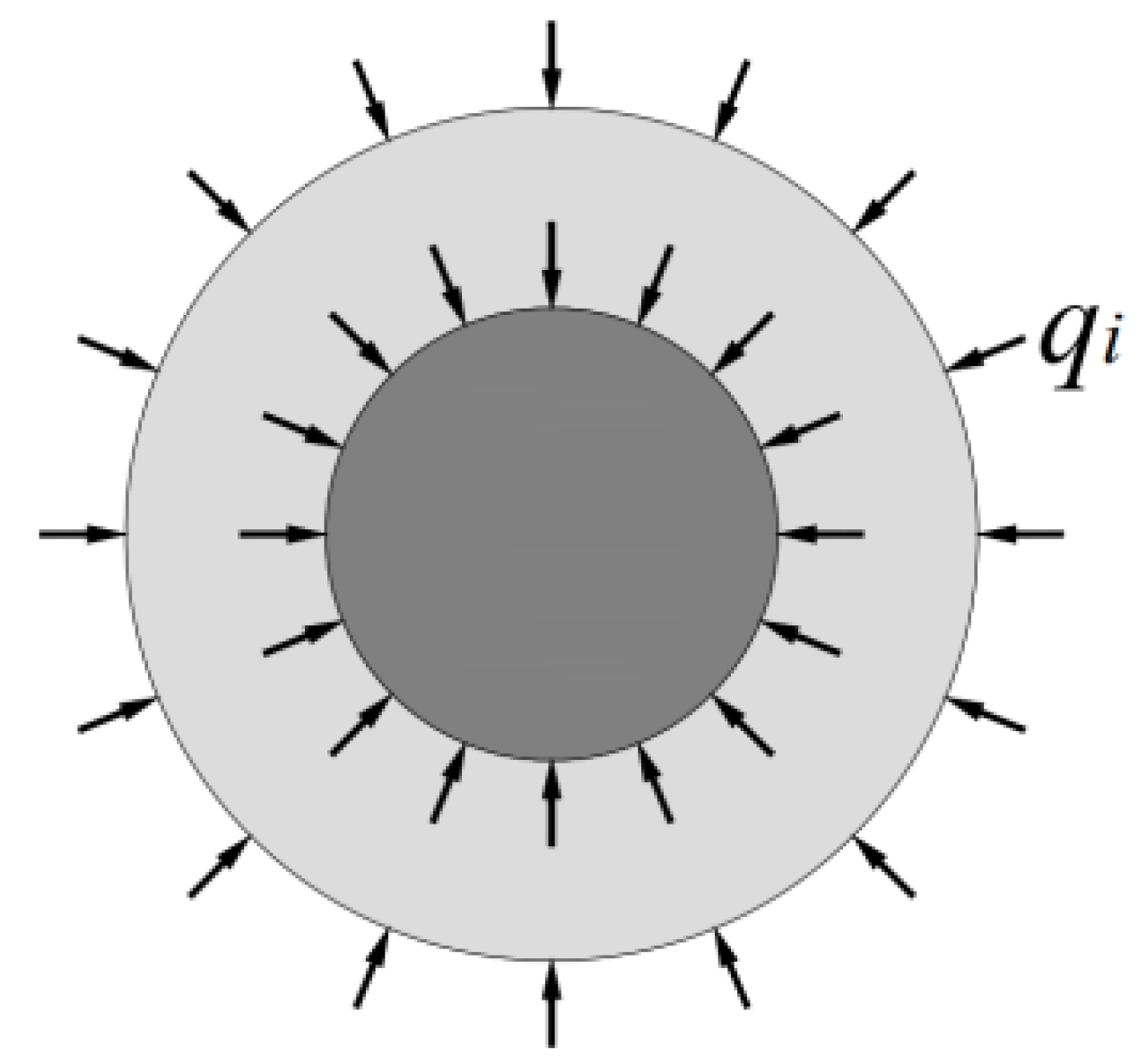
2.2. Anti-Slip Conditions for the CFRP Anchorage Device
2.3. Necessary Conditions for the Non-Failure of the Anchorage Device
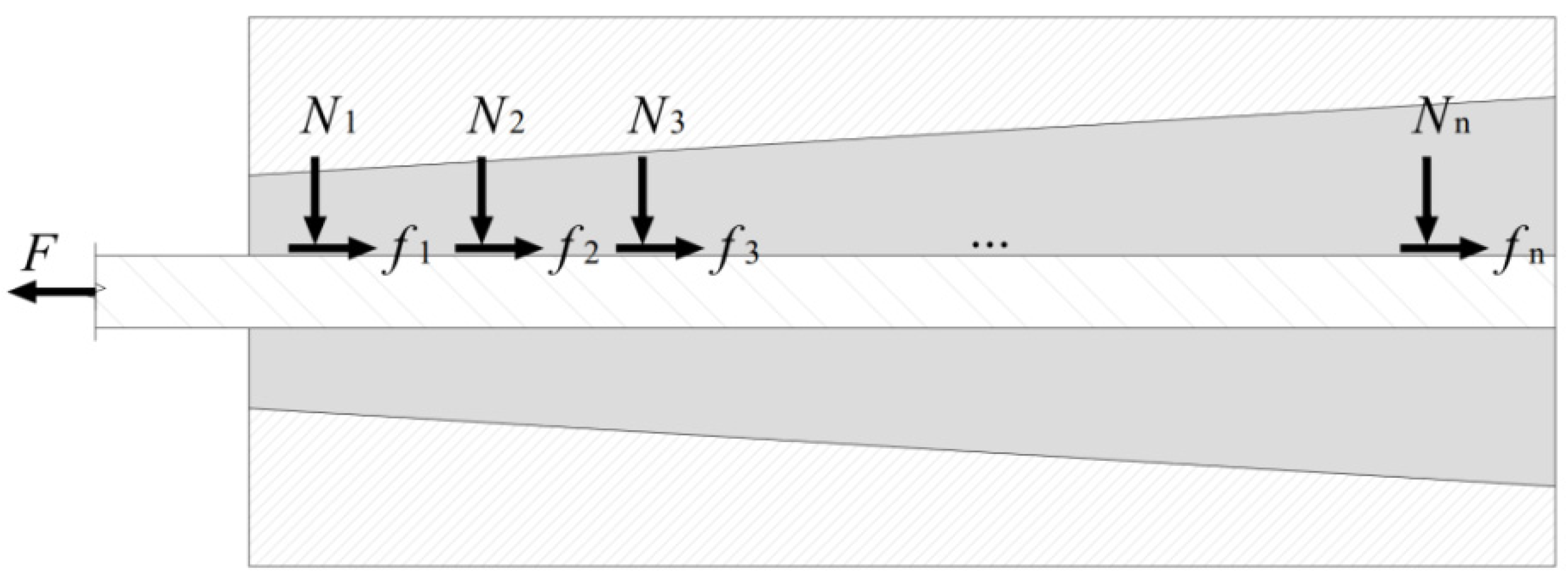
2.4. Stress Adjustment Mechanism in the Anchorage Device
3. Determination of the Dimensional Parameters of the Anchorage Device
- (1)
- Determination of the barrel parameters and LTM materials:
- (2)
- Determination of the inner pore cone angle of the barrel (α) and the diameter of the large end (D):
- (3)
- Determination of the factor l
- (4)
- Trial design of the CFRP composite anchorage device
4. Test Verification of the CFRP Composite Anchorage Device
5. Conclusions
- (1)
- The governing formulas of the anchorage efficiency coefficient ηA, the stress concentration coefficients k1 and k2, the single tendon diameter d, the anchorage length l, the radial stress inhomogeneity coefficient ψ, the dip angle of wedge external conical surface α, and the friction angle β were obtained based on which CFRP tendon anchorage device was designed, and the corresponding minimum anchorage length was determined.
- (2)
- The radial stress inhomogeneity coefficient ψ was proposed to carefully assess the sufficient conditions for the anti-slip failure of the CFRP tendon in the anchorage zone. The CFRP tendon could be prevented from slipping out of the anchorage device when the inner pore size of the barrel reaches the maximum value, and it should be as small as possible.
- (3)
- The CFRP tendon should be gradually compressed tightly from the no-loading end to the load-bearing end; therefore, the stresses in the anchorage device could be reasonably distributed for better anchorage properties.
- (4)
- Two types of CFRP tendon composite anchorage devices were preliminarily designed, and the static load tension tests were carried out under theoretical guidance. The anchorage efficiency coefficients of the designed anchorage devices could be over 90%, peaking at 96.8%, and the failure form of the two devices was divergent destruction, which was rather ideal. As a result, the theoretically designed anchorage device was reasonably verified with experiments.
6. Prospect
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sentry, M.; Bouazza, A.; Al-Mahaidi, R.; Mahawish, A. Durability of Carbon Fibre Reinforced Polymer Strands in Ground Anchors. Environ. Geotech. 2018, 5, 356–370. [Google Scholar] [CrossRef]
- Xin, W.; Wu, Z. Evaluation of FRP and hybrid FRP cables for super long-span cable-stayed bridges. Compos. Struct. 2010, 92, 2582–2590. [Google Scholar]
- Liu, Y.; Zwingmann, B.; Schlaich, M. Carbon Fiber Reinforced Polymer for Cable Structures—A Review. Polymers 2015, 7, 2078–2099. [Google Scholar] [CrossRef] [Green Version]
- Fan, H.; Vassilopoulos, A.P.; Keller, T. Evaluation of grout materials for CFRP ground anchors with strap ends. Constr. Build. Mater. 2017, 145, 196–206. [Google Scholar] [CrossRef]
- Zhu, W.; Sang, R.; Yang, L.; Lei, H. Optimizing the anchoring structure for a super large cable-net structure with improved fatigue resiatance. Adv. Struct. Eng. 2019, 23, 657–669. [Google Scholar] [CrossRef]
- Fan, H.; Vassilopoulos, A.P.; Keller, T. Pull-out behavior of CFRP ground anchors with two-strap ends. Compos. Struct. 2017, 160, 1258–1267. [Google Scholar] [CrossRef]
- Meier, U. Carbon Fiber Reinforced Polymer Cables: Why? Why Not? What If? Arab. J. Sci. Eng. 2012, 37, 399–411. [Google Scholar] [CrossRef] [Green Version]
- Al-Mayah, A.; Soudki, K. Simplified anchor system for CFRP rods. J. Compos. Constr. 2013, 17, 584–590. [Google Scholar] [CrossRef]
- Campbell, T.I.; Keatley, J.P.; Barnes, K.M. Analysis of a Wedge-Type Anchorage System for CFRP Prestressing Tendons. In Extending Performance of Concrete Structures, Proceedings of the International Seminar, Dundee, UK, 7 September 1999; Thomas Telford: London, UK, 1999. [Google Scholar]
- Wanxu, Z.; Lian, S.; Yang, W. Finite Element Analysis and Test of Wedge-type Anchor for Prestressed CFRP Plates. Earthq. Resist. Eng. Retrofit. 2015, 37, 97–101. [Google Scholar]
- Ping, Z.G.; Shizhong, Q. Theoretical and experimental investigation of a new CFRP tendon wedge-anchor. China Civ. Civ. Eng. J. 2011, 44, 67–72. [Google Scholar]
- Bo, F. Study on Anchorage System and Its Long-Term Performance for Large Capacity FRP Cable. Master’s Thesis, Southeast University, Nanjing, China, 2019. [Google Scholar]
- Wang, L.C.; Xu, J.; Han, Q.H. Effects of Cross-Sectional Size and Shape on the Longitudinal Tensile and Anchoring Properties of CFRP Cables. J. Mater. Civ. Eng. 2019, 31, 04019053. [Google Scholar] [CrossRef]
- Xie, G.-H.; Tang, Y.-S.; Wang, C.; Li, S.-Q.; Liu, R.-G. Experimental study on fatigue performance of adhesively bonded anchorage system for CFRP tendons. Compos. Part B Eng. 2018, 150, 47–59. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.; Lee, W.; Jung, W.T.; Chung, W. Bond characteristics of near-surface-mounted anchorage for prestressing. Constr. Build. Mater. 2017, 148, 748–756. [Google Scholar] [CrossRef]
- Mei, K.; Seracino, R.; Lv, Z. An experimental study on bond-type anchorages for carbon fiber-reinforced polymer cables. Constr. Build. Mater. 2016, 106, 584–591. [Google Scholar] [CrossRef]
- Feng, B.; Wang, X.; Wu, Z. Static and Fatigue Behavior of Multitendon CFRP Cables with Integrated Anchorages. J. Compos. Constr. 2019, 23, 04019051. [Google Scholar] [CrossRef]
- Wang, X.; Xu, P.; Wu, Z.; Shi, J. A novel anchor method for multi-tendon FRP cable: Concept and FE study. Compos. Struct. 2015, 120, 552–564. [Google Scholar] [CrossRef]
- Fang, Z.; Zhang, K.; Tu, B. Experimental investigation of a bond-type anchorage system for multiple FRP tendons. Eng. Struct. 2013, 57, 364–373. [Google Scholar] [CrossRef]
- Xie, G.-H.; Yan, P.; Sun, Y.; Feng, Q.-H.; Gedi, A.A. Fatigue performance of anchorage for CFRP tendons affected by water infiltration. Constr. Build. Mater. 2020, 269, 121359. [Google Scholar] [CrossRef]
- Fava, G.; Carvelli, V.; Pisani, M.A. Pisani. Mechanical behaviour modelling of a new anchor system for large diameter GFRP bars. Compos. Part B 2012, 43, 1397–1404. [Google Scholar] [CrossRef]
- Wu, J.Y.; Xian, G.; Li, H. A novel anchorage system for CFRP cable: Experimental and numerical investigation. Compos. Struct. 2018, 194, 555–563. [Google Scholar] [CrossRef]
- Zhang, B.; Benmokrane, B. Design and evaluation of a new bond-type anchorage system for fiber reinforced polymer tendons. Can. J. Civ. Eng. 2004, 31, 14–26. [Google Scholar] [CrossRef]
- Cai, D.S.; Xu, Z.H.; Yin, J.; Liu, R.G.; Liang, G. A numerical investigation on the performance of composite anchors for CFRP tendons. Constr. Build. Mater. 2016, 112, 848–855. [Google Scholar] [CrossRef]
- Xie, G.H.; Yin, J.; Liu, R.G.; Chen, B.; Cai, D.S. Experimental and numerical investigation on the static and dynamic behaviors of cable-stayed bridges with CFRP cables. Compos. Part B Eng. 2016, 111, 235–242. [Google Scholar] [CrossRef]
- Zhu, W.; Jia, K.; Fu, F.; Lan, D.; Qian, K. A New Design of Cable Anchor for Ultra-High Fatigue Stress Cable Net of Largest Telescope in the World. Thin-Walled Struct. 2020, 159, 107280. [Google Scholar] [CrossRef]
- Chen, X.; Sun, X.; Chen, P.; Wang, B.; Gu, J.; Wang, W.; Chai, Y.; Zhao, Y. Rationalized Improvement of Tsai-Wu Failure Criterion Considering Different Failure Modes of Composite Materials. Compos. Struct. 2020, 256, 113120. [Google Scholar] [CrossRef]
- Zhenbang, K. Nonlinear Continuum Mechanics; Shanghai Jiao Tong University Press: Shanghai, China, 2002. [Google Scholar]
- Zongning, H. Determination of Friction Parameters of Carbon Fiber Anchored Structure; Guilin University of Technology: Guilin, China, 2020. [Google Scholar]
- GB/T 14370-2015; Anchorage, Grip and Coupler for Prestressing Tendons; Standards Press of China: Beijing, China, 2015.
- JGJ85—2010; Technical Specification for Application of Anchorage, Grip and Coupler for Prestressing Tendons; China Architecture & Building Press: Beijing, China, 2010.

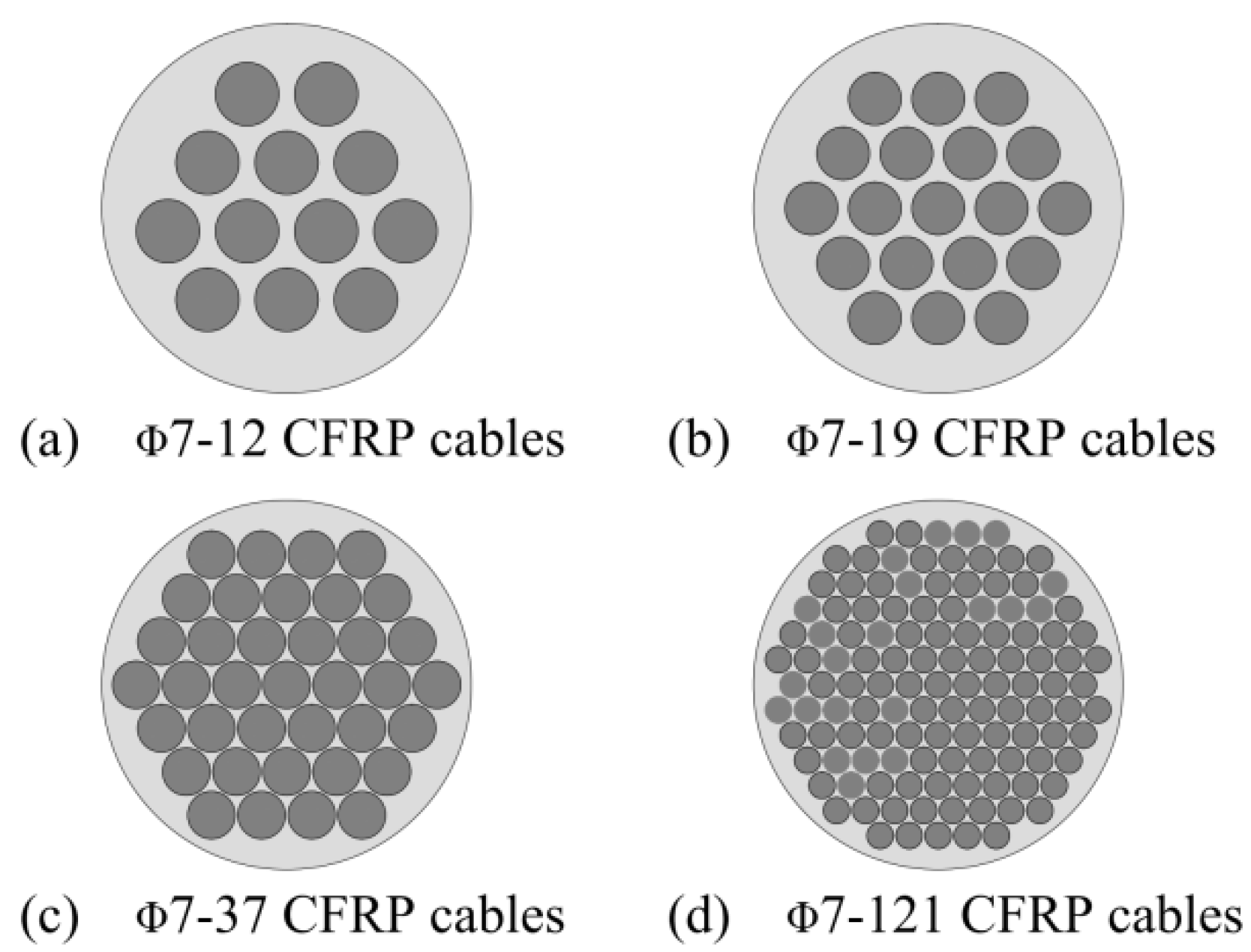



| Quantity of the Φ7CFRP Tendons | Maximum Diameter of the Large End D (mm) | Minimum Effective Anchorage Length l (mm) | ||
|---|---|---|---|---|
| 12 | 0 | 0.8 | 76.27 | 237.93 |
| 19 | 0 | 0.75 | 82.63 | 253.79 |
| 37 | 0.2 | 0.7 | 246.93 | 178.96 |
| 121 | 0.2 | 0.3 | 346.08 | 415.44 |
| Model of Anchorage Devices | Diameter of the Small End ΦA | Effective Anchorage Length B | Diameter of Anchorage Devices ΦC | Diameter of the Large End ΦD | Length of Anchorage Devices E |
|---|---|---|---|---|---|
| Φ7–12 | 42 | 254 | 72 | 53 | 280 |
| Φ7–19 | 68 | 380 | 115 | 74 | 480 |
| Φ7–37 | 86 | 193 | 150 | 105 | 303 |
| Φ7–121 | 126 | 510 | 250 | 180 | 620 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, W.; Chen, H.; Wei, W.; Chen, B.; Chen, X. Analysis of Multi-Tendon Friction-Based Composite Anchorage Device for CFRP Cables and Its Anchorage Mechanism. Materials 2022, 15, 2895. https://doi.org/10.3390/ma15082895
Zhu W, Chen H, Wei W, Chen B, Chen X. Analysis of Multi-Tendon Friction-Based Composite Anchorage Device for CFRP Cables and Its Anchorage Mechanism. Materials. 2022; 15(8):2895. https://doi.org/10.3390/ma15082895
Chicago/Turabian StyleZhu, Wanxu, Hongbin Chen, Wei Wei, Boxuan Chen, and Xuejun Chen. 2022. "Analysis of Multi-Tendon Friction-Based Composite Anchorage Device for CFRP Cables and Its Anchorage Mechanism" Materials 15, no. 8: 2895. https://doi.org/10.3390/ma15082895
APA StyleZhu, W., Chen, H., Wei, W., Chen, B., & Chen, X. (2022). Analysis of Multi-Tendon Friction-Based Composite Anchorage Device for CFRP Cables and Its Anchorage Mechanism. Materials, 15(8), 2895. https://doi.org/10.3390/ma15082895





