Microstructural Evolution and an Improved Dynamic Recrystallization Kinetic Model of a Ni-Cr-Mo Alloy in Hot Deformation
Abstract
:1. Introduction
2. Experimental Material and Procedure
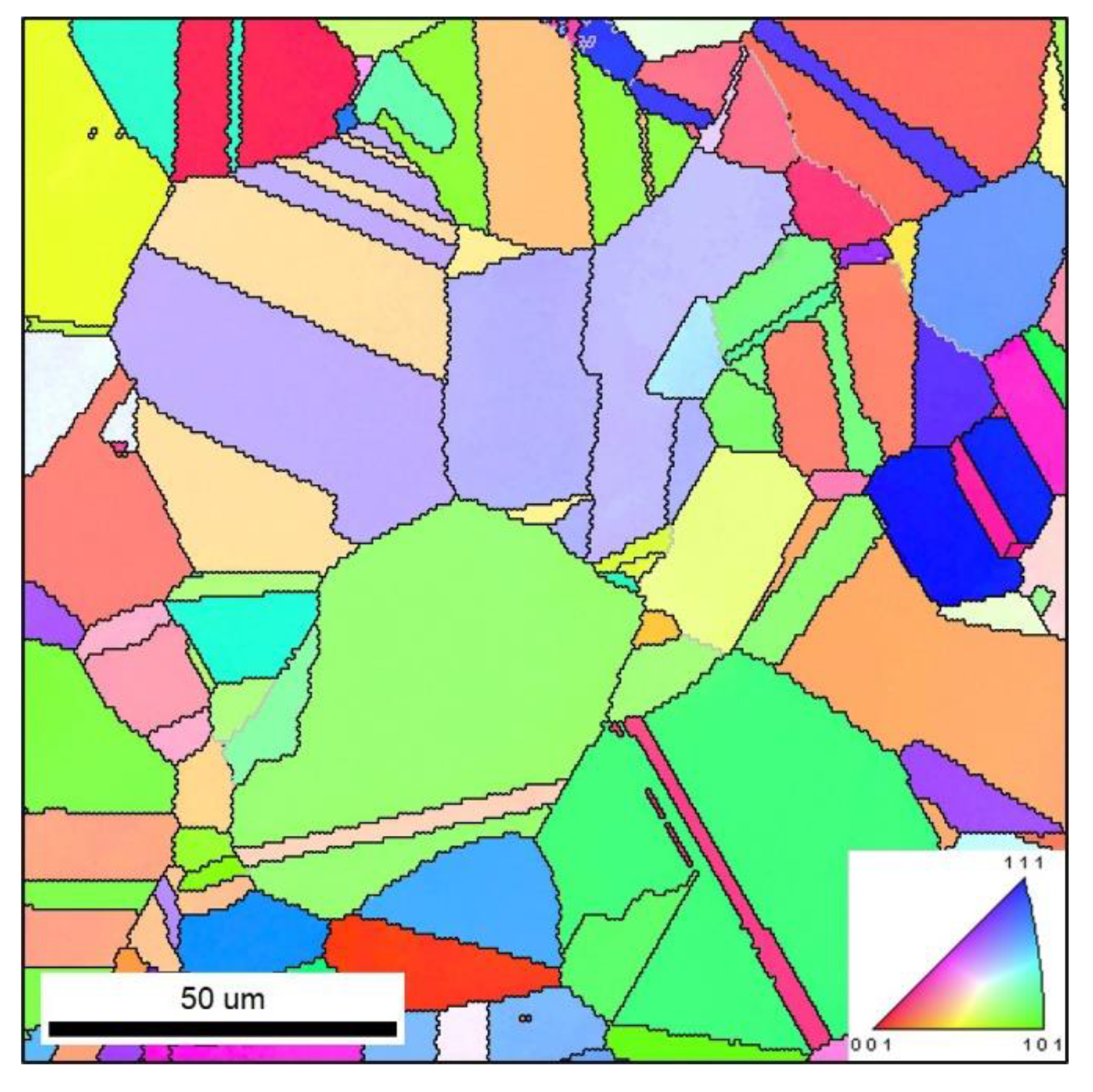
3. Results and Discussion
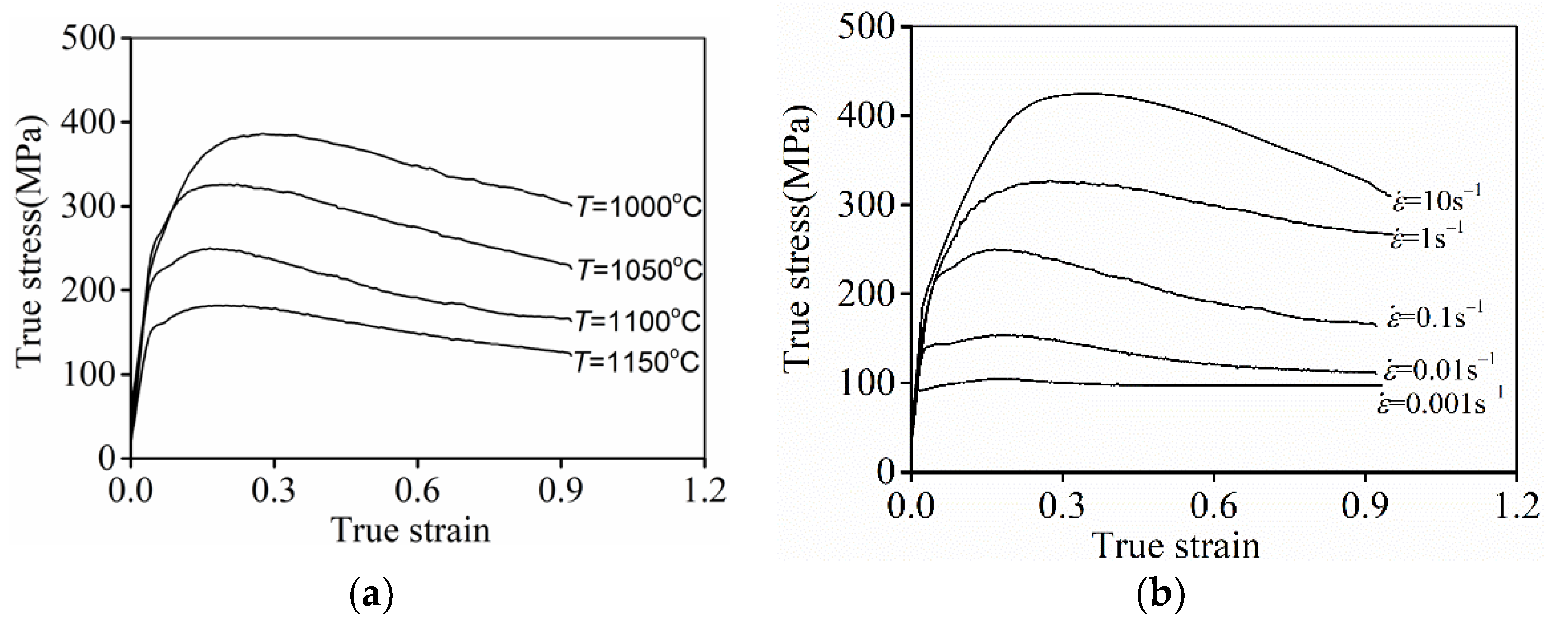
3.1. High-Temperature Compression Characteristics
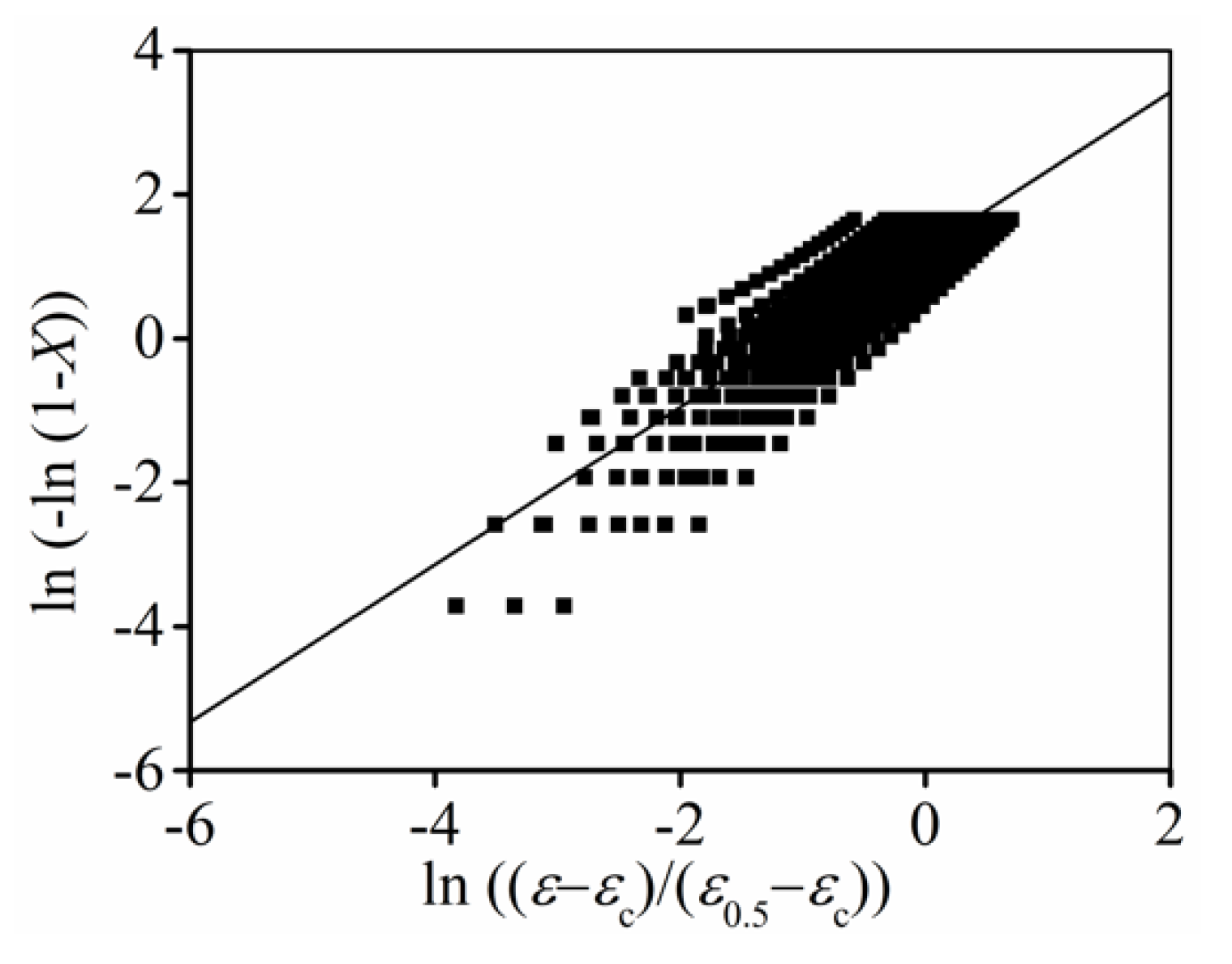
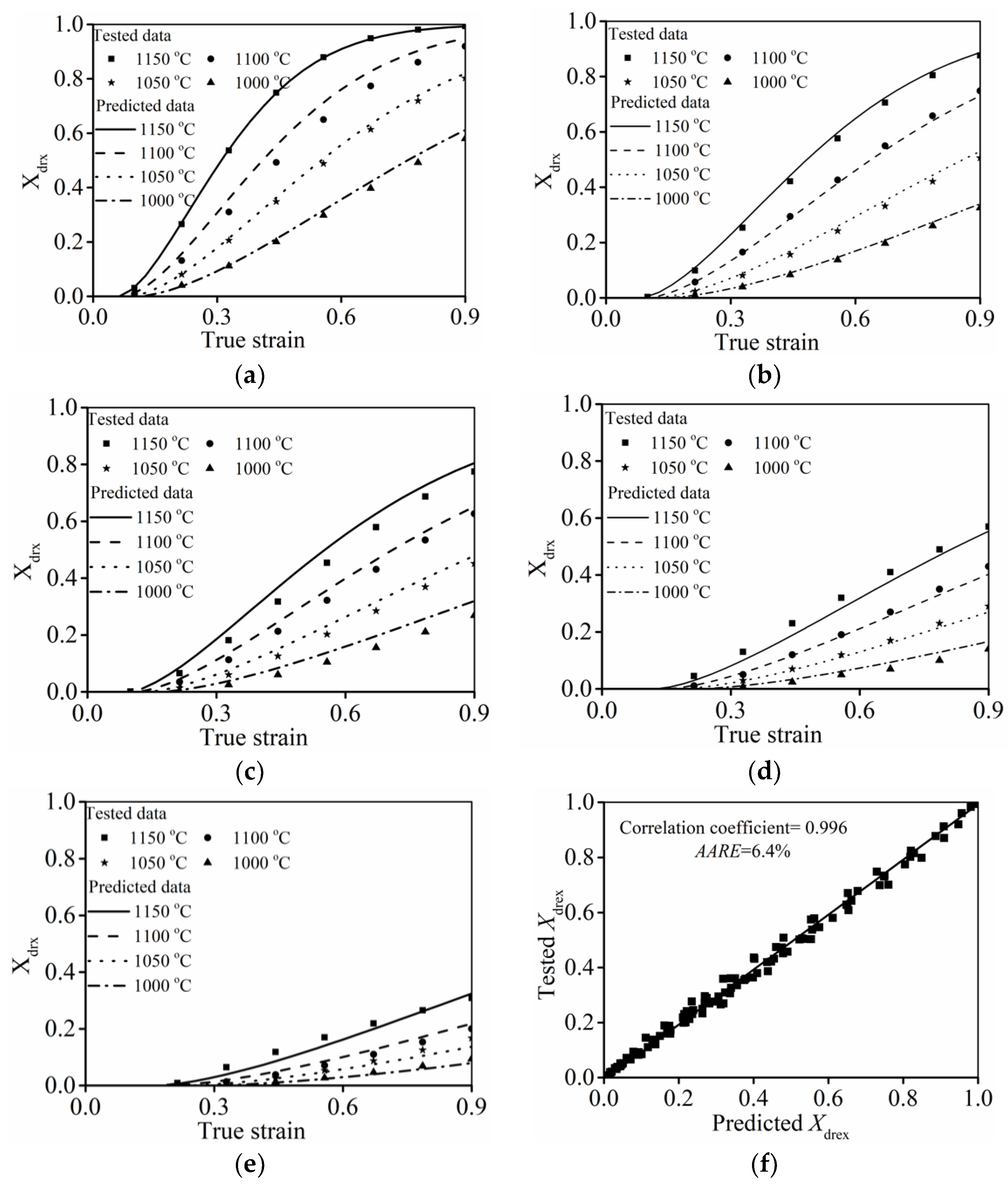
3.2. Classical DRX Kinetics Model
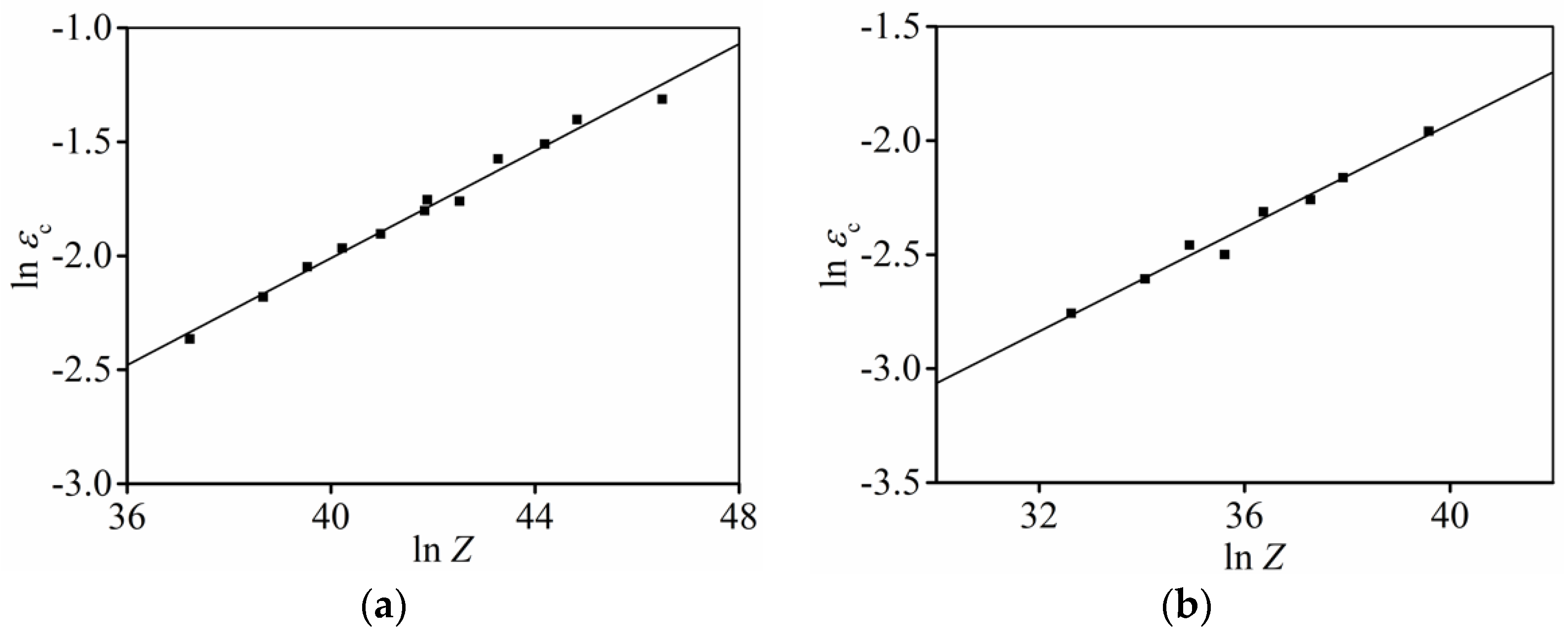
3.2.1. Identification of
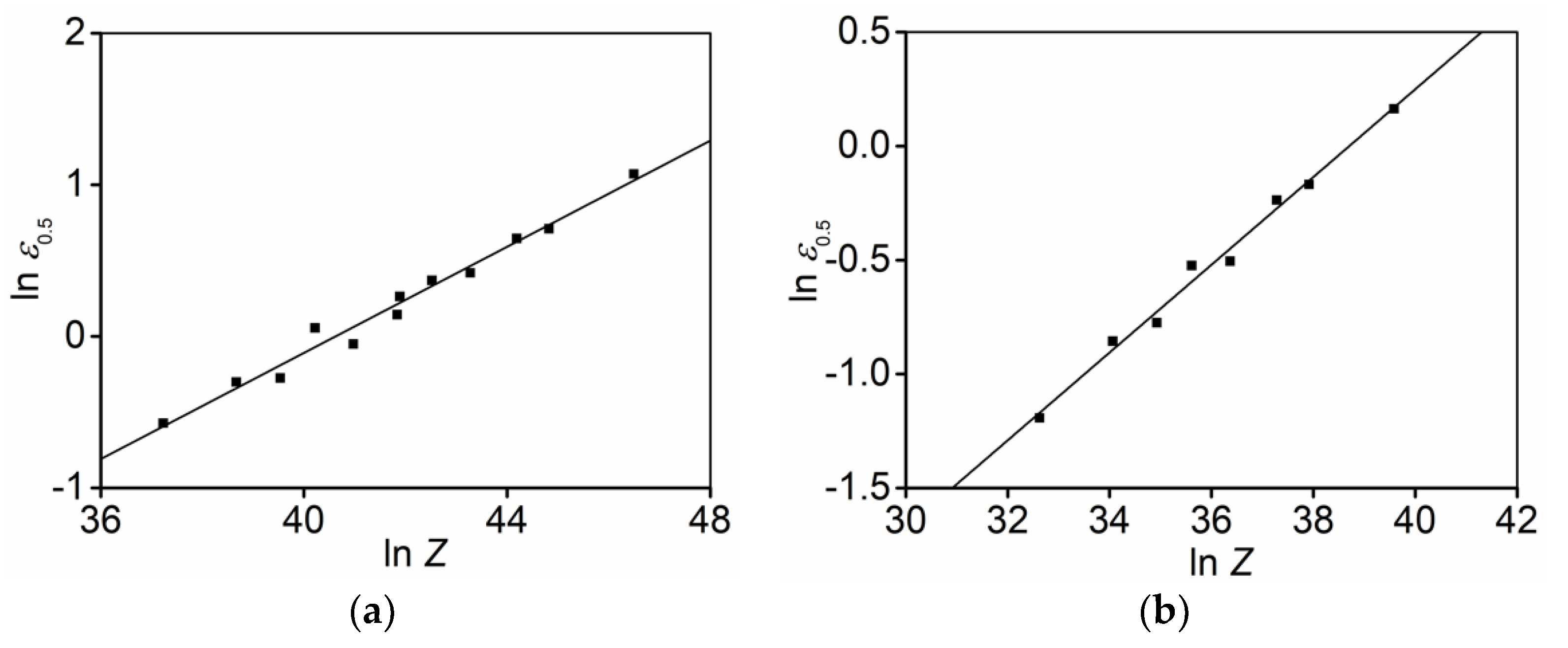
3.2.2. Identification of and
3.2.3. Identification of
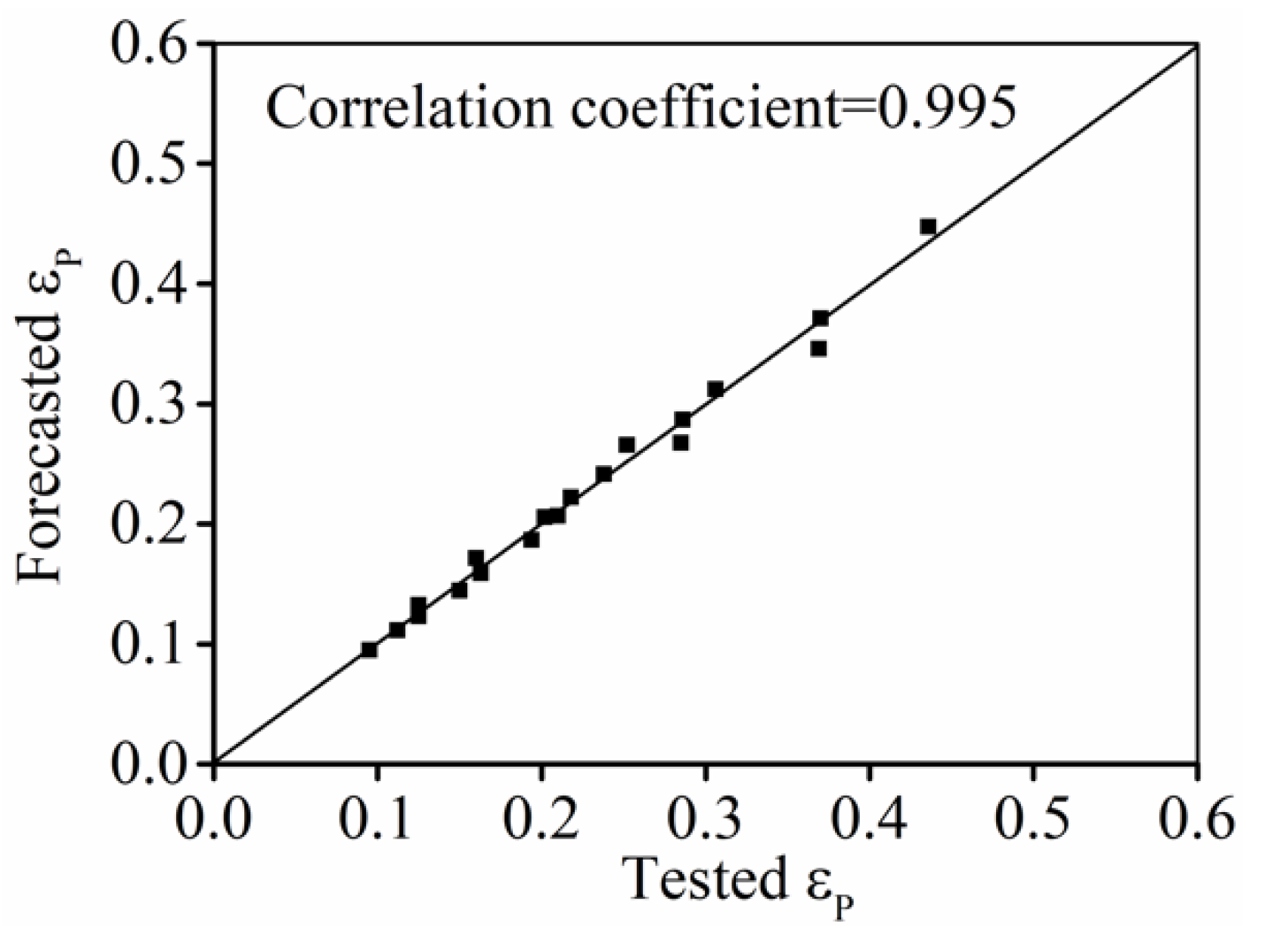
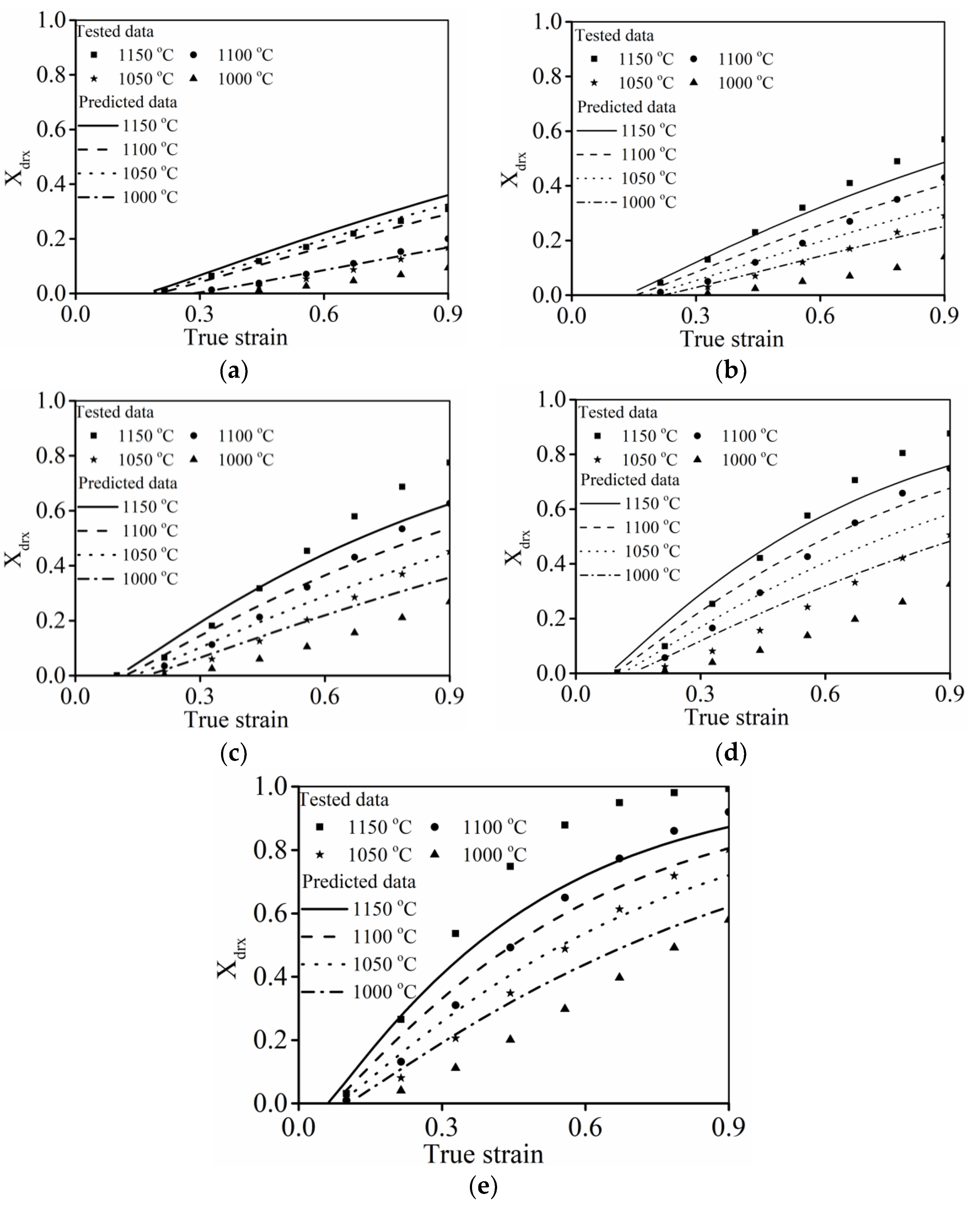
3.2.4. Verification of Classical DRX Kinetic Model
3.3. An Improved DRX Kinetics Model
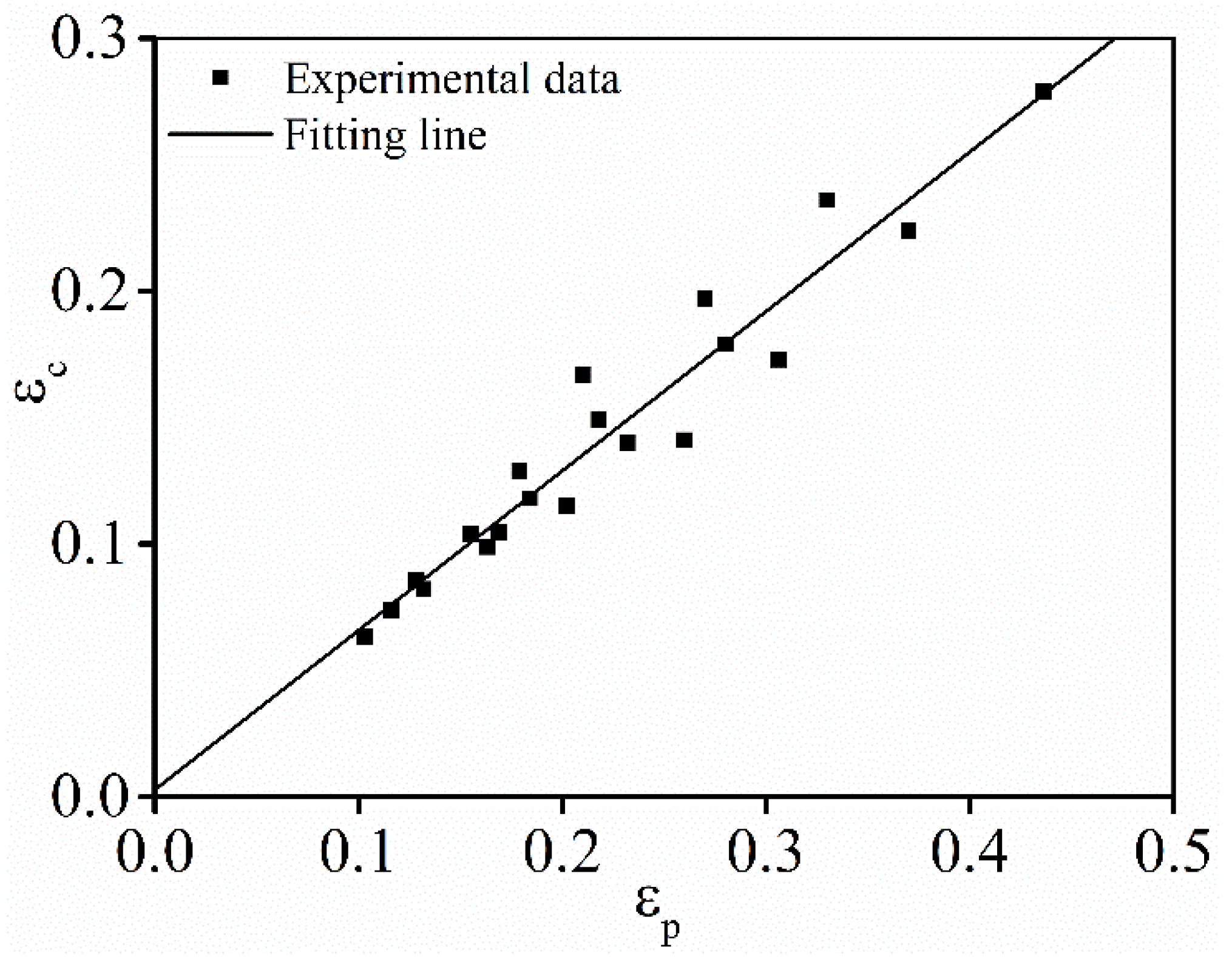
3.3.1. Determination of and
3.3.2. Determination of
3.3.3. Verification of the Improved DRX Kinetic Model
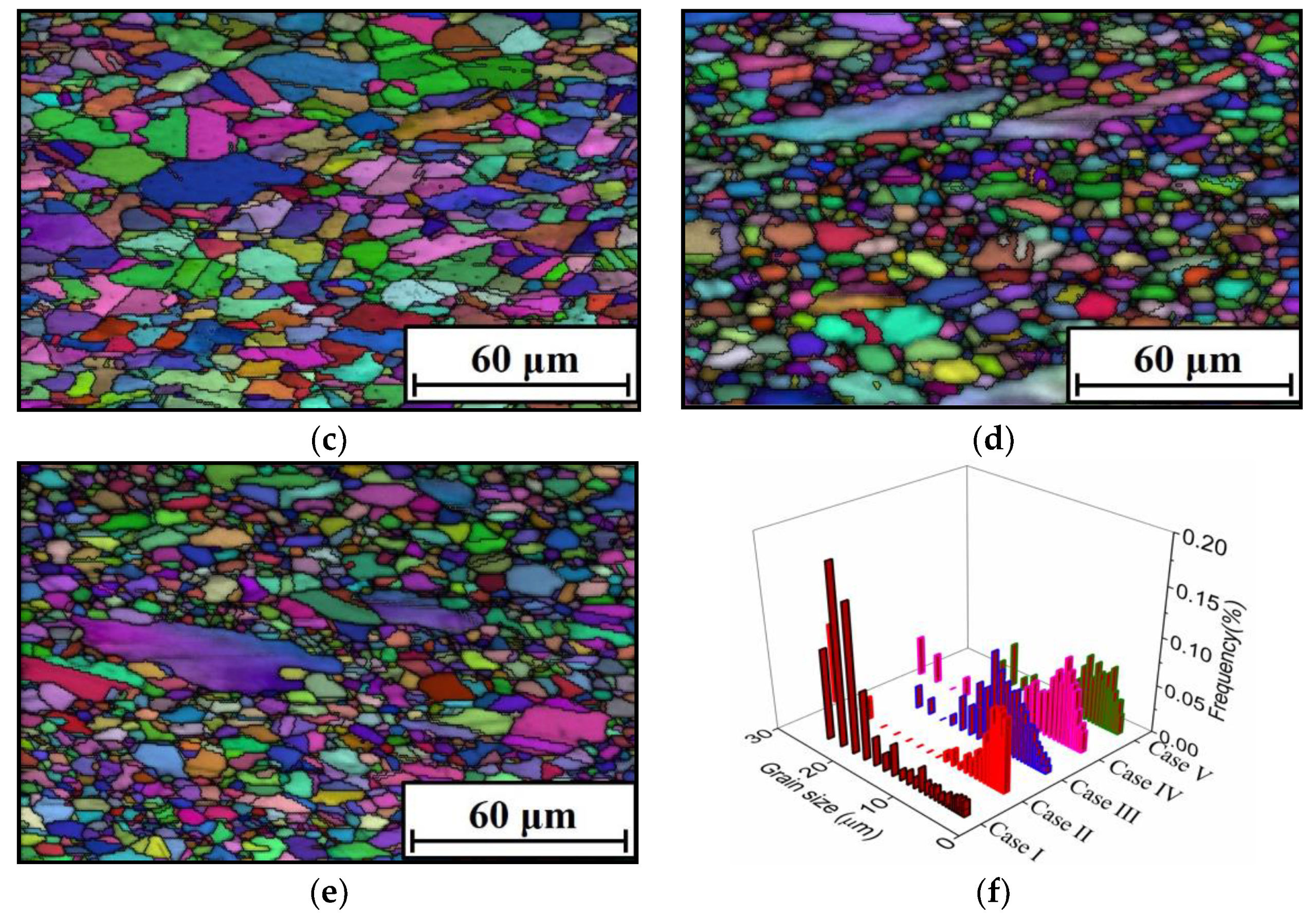
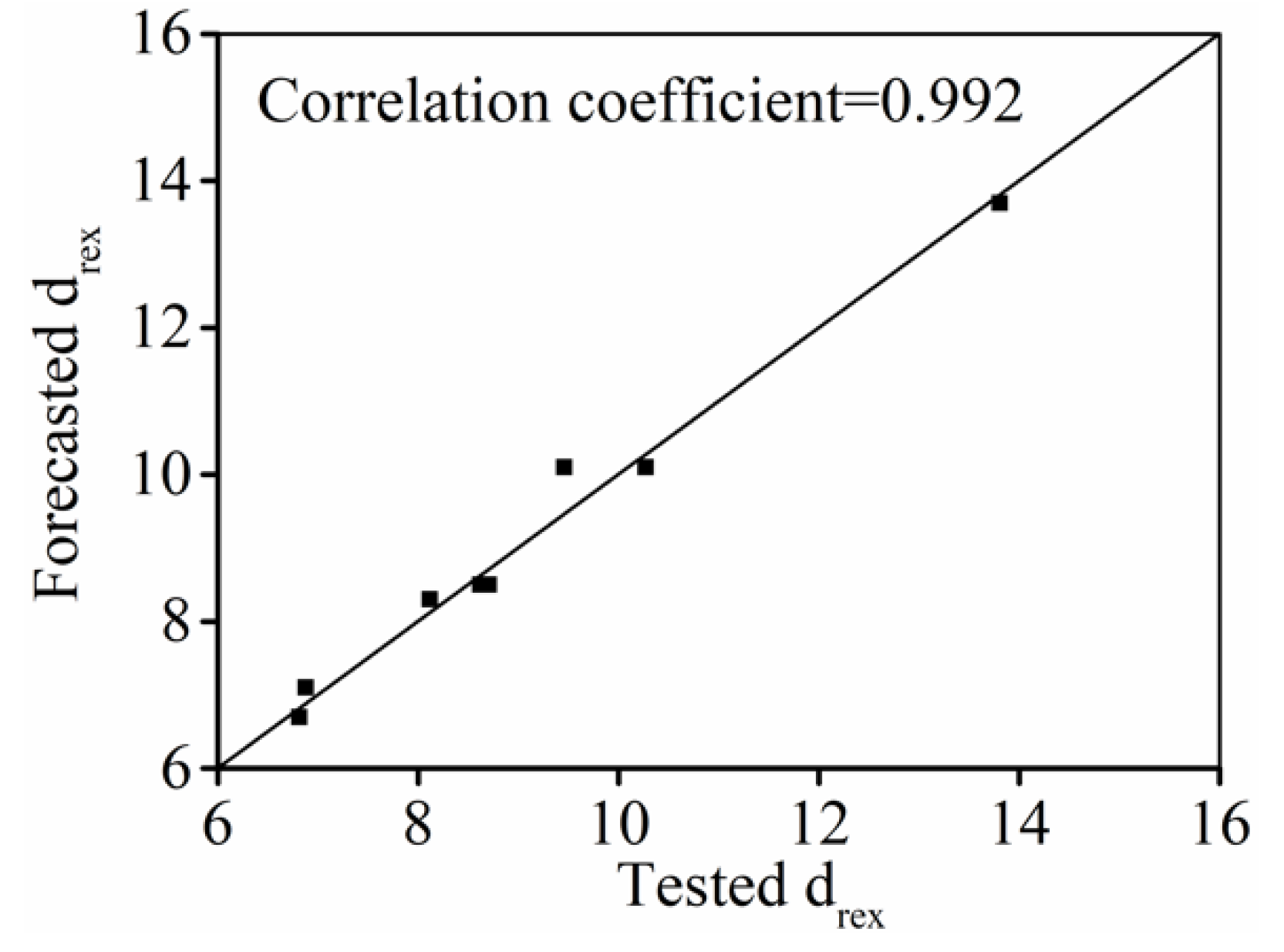
4. Modeling the DRX Grain Size
5. Conclusions
- (1)
- The variations of substructures are closely correlated to forming parameters. The nucleation and interaction of dislocations can be intensified, while the refinement of subgrains/DRX grains is easily limited at high temperatures or low strain rates.
- (2)
- An improved DRX kinetic model that considers the variation characteristics of DRX behavior in the segmented ranges of strain rate is proposed. Good consistency between the forecasted and tested results demonstrates that the established model can strictly elaborate the DRX kinetic features of the researched alloy.
- (3)
- The variation of DRX grains is abruptly affected by forming parameters. At a large strain rate or low temperature, the DRX grain is distinctly refined. The mean size of DRX grains in hot forming is well described as the equation of the forming temperature and strain rate.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, Z.J.; Lin, Y.C.; He, D.G.; Lou, Y.M.; Chen, M.S. A unified dislocation density-based model for an aged polycrystalline Ni-based superalloy considering the coupled effects of complicate deformation mechanisms and initial delta phase. Mater. Sci. Eng. A 2021, 827, 142062. [Google Scholar] [CrossRef]
- Long, J.C.; Xia, Q.X.; Xiao, G.F.; Qin, Y.; Yuan, S. Flow characterization of magnesium alloy ZK61 during hot deformation with improved constitutive equations and using activation energy maps. Int. J. Mech. Sci. 2021, 191, 106069. [Google Scholar] [CrossRef]
- He, X.M.; Yu, Z.Q.; Liu, G.M.; Wang, W.G.; Lai, X.M. Mathematical modeling for high temperature flow behavior of as-cast Ti–45Al–8.5Nb–(W,B,Y) alloy. Mater. Des. 2009, 30, 166–169. [Google Scholar] [CrossRef]
- Xu, W.C.; Jin, X.Z.; Xiong, W.D.; Zeng, X.Q.; Shan, D.B. Study on hot deformation behavior and workability of squeeze-cast 20 vol% SiCw/6061Al composites using processing map. Mater. Charact. 2018, 135, 154–166. [Google Scholar] [CrossRef]
- Wen, D.X.; Yue, T.Y.; Xiong, Y.B.; Wang, K.; Wang, J.K.; Zheng, Z.Z.; Li, J.J. High-temperature tensile characteristics and constitutive models of ultrahigh strength steel. Mater. Sci. Eng. A 2021, 803, 140491. [Google Scholar] [CrossRef]
- Rafiei, M.; Mirzadeh, H.; Malekan, M. Delta processing effects on the creep behavior of a typical Nb-bearing nickel-based superalloy. Vacuum 2021, 184, 109913. [Google Scholar] [CrossRef]
- Wang, G.Q.; Chen, M.S.; Lin, Y.C.; Li, H.B.; Jiang, Y.Q.; Ma, Y.Y.; Peng, C.X.; Cai, J.L.; Chen, Q. Recrystallization nucleation under close-set δ phase in a nickel-based superalloy during annealing. J. Mater. Sci. Technol. 2022, 115, 166–176. [Google Scholar] [CrossRef]
- Eriksson, E.; Colliander, M.H. Dynamic and Post-Dynamic Recrystallization of Haynes 282 below the Secondary Carbide Solvus. Metals 2021, 11, 122. [Google Scholar] [CrossRef]
- Quan, G.Z.; Liu, Q.; Zhao, J.; Xiong, W.; Shi, R.J. Determination of dynamic recrystallization parameter domains of Ni80A superalloy by enhanced processing maps. T. Nonferr. Metal. Soc. 2019, 29, 1449–1464. [Google Scholar]
- Zareian, Z.; Emamy, M.; Malekan, M.; Mirzadeh, H.; Kim, W.J.; Bahmani, A. Tailoring the mechanical properties of Mg-Zn magnesium alloy by calcium addition and hot extrusion process. Mater. Sci. Eng. A 2020, 774, 138929. [Google Scholar] [CrossRef]
- Tang, L.Q.; Jiang, F.L.; Teng, J.; Fu, D.F.; Zhang, H. Strain path dependent evolutions of microstructure and texture in AZ80 magnesium alloy during hot deformation. J. Alloy. Compd. 2019, 806, 292–301. [Google Scholar] [CrossRef]
- Kotkunde, N.; Krishnamurthy, H.N.; Singh, S.K.; Jella, G. Experimental and Numerical Investigations on Hot Deformation Behavior and Processing Maps for ASS 304 and ASS 316. High. Temp. Mater. Process. 2018, 37, 873–888. [Google Scholar] [CrossRef]
- Chen, X.M.; Lin, Y.C.; Li, X.H.; Chen, M.S.; Yuan, W.Q. Investigation on strain dependence of metadynamic recrystallization behaviors of GH4169 superalloy. Vacuum 2018, 149, 1–11. [Google Scholar] [CrossRef]
- Long, J.C.; Zhu, N.Y.; Xia, Q.X.; Cheng, X.Q. A Study of the Dynamic Recrystallization Behavior of Ni-Based Superalloy during Hot Power Spinning Based on Cellular Automaton. Adv. Eng. Mater. 2019, 21, 1801022. [Google Scholar] [CrossRef]
- Kumar, S.; Aashranth, B.; Samantaray, D.; Davinci, M.A.; Borah, U.; Bhaduri, A.K. Investigation on Grain Boundary Character Distribution During Dynamic Recrystallization of Austenitic Stainless Steel During Hot Deformation. Mater. Perform. Charact. 2019, 8, 796–807. [Google Scholar] [CrossRef]
- He, D.G.; Su, G.; Lin, Y.C.; Jiang, Y.Q.; Li, Z.; Chen, Z.J.; Yan, X.T.; Xia, Y.C.; Xie, Y.C. Microstructural Variation and a Physical Mechanism Model for a Ti-55511 Alloy during Double-Stage Hot Deformation with Stepped Strain Rates in the beta Region. Materials 2021, 14, 6371. [Google Scholar] [CrossRef]
- Alone, A.; Chatterjee, R.; Alankar, A. A comparative study of the effect of random and preferred crystallographic orientations on dynamic recrystallization behavior using a cellular automata model. Mater. Today. Commun. 2020, 25, 101200. [Google Scholar] [CrossRef]
- Mozumder, Y.H.; Babu, K.A.; Saha, R.; Sarma, V.S.; Mandal, S. Dynamic microstructural evolution and recrystallization mechanism during hot deformation of intermetallic-hardened duplex lightweight steel. Mater. Sci. Eng. A 2020, 788, 139613. [Google Scholar] [CrossRef]
- Tikhonova, M.; Torganchuk, V.; Brasche, F.; Molodov, D.A.; Belyakov, A.; Kaibyshev, R. Effect of Warm to Hot Rolling on Microstructure, Texture and Mechanical Properties of an Advanced Medium-Mn Steel. Metall. Mater. Trans. A 2019, 50, 4245–4256. [Google Scholar] [CrossRef]
- Zu, G.Q.; Lu, Y.K.; Yan, Y.; Zhang, X.M.; Zhao, J.W.; Du, W.; Ran, X.; Jiang, Z.Y. Effect of Temperature and Strain Rate on the Hot Deformation Behaviour of Ferritic Stainless Steel. Met. Mater. Int. 2020, 26, 248–259. [Google Scholar] [CrossRef]
- Dolzhenko, P.; Tikhonova, M.; Kaibyshev, R.; Belyakov, A. Dynamically Recrystallized Microstructures, Textures, and Tensile Properties of a Hot Worked High-Mn Steel. Metals 2019, 9, 30. [Google Scholar] [CrossRef]
- Xie, B.C.; Zhang, B.Y.; Yu, H.; Yang, H.; Liu, Q.; Ning, Y.Q. Microstructure evolution and underlying mechanisms during the hot deformation of 718Plus superalloy. Mater. Sci. Eng. A 2020, 784, 139334. [Google Scholar] [CrossRef]
- Wang, Q.P.; Zhou, R.F.; Li, Y.K.; Geng, B.Y. Characteristics of dynamic recrystallization in semi-solid CuSn10P1 alloy during hot deformation. Mater. Charact. 2020, 159, 109996. [Google Scholar] [CrossRef]
- Ning, Y.Q.; Fu, M.W.; Yao, W. Recrystallization of the hot isostatic pressed nickel-base superalloy FGH4096. II: Characterization and application. Mater. Sci. Eng. A 2012, 539, 101–106. [Google Scholar] [CrossRef]
- Ji, H.C.; Peng, Z.S.; Huang, X.M.; Wang, B.Y.; Xiao, W.C.; Wang, S.F. Characterization of the Microstructures and Dynamic Recrystallization Behavior of Ti-6Al-4V Titanium Alloy through Experiments and Simulations. J. Mater. Eng. Perform. 2021, 30, 8257–8275. [Google Scholar] [CrossRef]
- Chen, X.M.; Lin, Y.C.; Wen, D.X.; Zhang, J.L.; He, M. Dynamic recrystallization behavior of a typical nickel-based superalloy during hot deformation. Mater. Des. 2014, 57, 568–577. [Google Scholar]
- Chen, F.; Qi, K.; Cui, Z.; Lai, X. Modeling the dynamic recrystallization in austenitic stainless steel using cellular automaton method. Comp. Mater. Sci. 2014, 83, 331–340. [Google Scholar] [CrossRef]
- Lin, Y.C.; He, D.G.; Chen, M.S.; Chen, X.M.; Zhao, C.Y.; Ma, X.; Long, Z.L. EBSD analysis of evolution of dynamic recrystallization grains and δ phase in a nickel-based superalloy during hot compressive deformation. Mater. Des. 2016, 97, 13–24. [Google Scholar] [CrossRef]
- Lin, Y.C.; Wu, X.Y.; Chen, X.M.; Chen, J.; Wen, D.X.; Zhang, J.L.; Li, L.T. EBSD study of a hot deformed nickel-based superalloy. J. Alloy. Compd. 2015, 640, 101–113. [Google Scholar] [CrossRef]
- Wang, M.J.; Sun, C.Y.; Fu, M.W.; Liu, Z.L.; Wang, C.H. Experimental investigations and constitutive modeling of the dynamic recrystallization behavior of Inconel 740 superalloy. Mater. Sci. Eng. A 2020, 793, 139939. [Google Scholar] [CrossRef]
- Li, C.M.; Tan, Y.B.; Zhao, F. Dynamic recrystallization behaviour of H13-mod steel. J. Iron. Steel. Res. Int. 2020, 27, 1073–1086. [Google Scholar] [CrossRef]
- Chen, M.S.; Yuan, W.Q.; Li, H.B.; Zou, Z.H. New insights on the relationship between flow stress softening and dynamic recrystallization behavior of magnesium alloy AZ31B. Mater. Charact. 2019, 147, 173–183. [Google Scholar] [CrossRef]
- Xu, Y.K.; Birnbaum, P.; Pilz, S.; Zhuang, X.C.; Zhao, Z.; Krausel, V. Investigation of constitutive relationship and dynamic recrystallization behavior of 22MnB5 during hot deformation. Results. Phys. 2019, 14, 102426. [Google Scholar] [CrossRef]
- Quan, G.Z.; Shi, R.J.; Zhao, J.; Liu, Q.; Xiong, W.; Qiu, H.M. Modeling of dynamic recrystallization volume fraction evolution for AlCu4SiMg alloy and its application in FEM. T. Nonferr. Metal. Soc. 2019, 29, 1138–1151. [Google Scholar] [CrossRef]
- Momeni, A.; Dehghani, K.; Ebrahimi, G.R. Modeling the initiation of dynamic recrystallization using a dynamic recovery model. J. Alloy. Compd. 2011, 509, 9387–9393. [Google Scholar] [CrossRef]
- Meng, F.X.; Ye, Q.B.; Tian, Y.; Wang, Z.D.; Wu, D. Dynamic Recrystallization Behavior in a Hot Compressed Symmetrical Bulb Flat Steel. J. Mater. Eng. Perform. 2021, 30, 2536–2544. [Google Scholar] [CrossRef]
- Bal, K.S.; Majumdar, J.D.; Choudhury, A.R. Effect of post-weld heat treatment on the tensile strength of laser beam welded Hastelloy C-276 sheets at different heat inputs. J. Manuf. Process. 2019, 37, 578–594. [Google Scholar] [CrossRef]
- Bal, K.S.; Majumdar, J.D.; Choudhury, A.R. Optimization of Melt Zone Area for Electron Beam Welded Hastelloy C-276 Sheet and Study of Corrosion Resistance of the Optimized Melt Zone in 3.5 wt% NaCl Aqueous Solution. Arab. J. Sci. Eng. 2019, 44, 1617–1630. [Google Scholar] [CrossRef]
- Dhananchezian, M. Study the machinability characteristics of Nicked based Hastelloy C-276 under cryogenic cooling. Measurement 2019, 136, 694–702. [Google Scholar] [CrossRef]
- Jaladurgam, N.R.; Kanjarla, A.K. Hot deformation characteristics and microstructure evolution of Hastelloy C-276. Mater. Sci. Eng. A 2018, 712, 240–254. [Google Scholar] [CrossRef]
- Lu, Y.; Liu, J.; Li, X.; Liang, J.; Li, Z.; Wu, G.; Zhou, X. Hot deformation behavior of Hastelly C276 superalloy. Trans. Nonferrous Met. Soc. China 2012, 22, s84–s88. [Google Scholar] [CrossRef]
- Kong, Y.; Chang, P.; Li, Q.; Xie, L.; Zhu, S. Hot deformation characteristics and processing map of nickel-based C276 superalloy. J. Alloy. Compd. 2015, 622, 738–744. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, L.W.; Shen, W.F.; Xu, Q.H.; Cui, Y. The processing map and microstructure evolution of Ni-Cr-Mo-based C276 superalloy during hot compression. J. Alloy. Compd. 2017, 728, 1269–1278. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, L.W.; Shen, W.F.; Li, M.F.; Gu, S.D. Characterization of hot deformation behavior of Hastelloy C-276 using constitutive equation and processing map. J. Mater. Eng. Perform. 2015, 24, 149–157. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, L.W.; Shen, W.F.; Liu, C.R.; Xia, Y.N. The Kinetics of Metadynamic Recrystallization in a Ni-Cr-Mo-Based Superalloy Hastelloy C-276. J. Mater. Eng. Perform. 2016, 25, 545–552. [Google Scholar] [CrossRef]
- Guo, S.; Liu, J.; Du, B.; Liu, S.; Zhang, X.; Li, D. An Investigation on Constitutive Relation and Dynamic Recrystallization of Hastelloy C-276 Alloy During Hot Deformation. J. Mater. Eng. Perform. 2020, 29, 5902–5912. [Google Scholar] [CrossRef]
- Li, B.; Du, Y.; Chu, Z.; Zhou, W.; Yang, X. Research on dynamic recrystallization behavior of Ni-Fe-Cr based alloy. Mater. Charact. 2020, 169, 110653. [Google Scholar] [CrossRef]
- Zhang, C.; Tang, X.L.; Zhang, L.W.; Cui, Y. Cellular automaton modeling of dynamic recrystallization of Ni–Cr–Mo-based C276 superalloy during hot compression. J. Mater. Res. 2019, 34, 3093–3103. [Google Scholar] [CrossRef]
- Chen, Q.; Meng, Y.; Lin, J.Y.; Xiao, H.; Huang, Z.Q.; Sugiyama, S.; Yanagimoto, J. Microstructural evolution of a niobium-microalloyed steel during hot shear deformation and subsequent cooling. J. Mater. Process. Technol. 2022, 300, 117417. [Google Scholar] [CrossRef]




| Elements | C | Si | Cr | Mo | Fe | Co | W | V | P | S | Ni |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Contents | 0.007 | 0.06 | 15.8 | 16.2 | 6.5 | 1.9 | 4.2 | 0.30 | 0.035 | 0.025 | Bal |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, X.; Xia, Y.; He, D.; Lin, Y.C. Microstructural Evolution and an Improved Dynamic Recrystallization Kinetic Model of a Ni-Cr-Mo Alloy in Hot Deformation. Materials 2022, 15, 3161. https://doi.org/10.3390/ma15093161
Yan X, Xia Y, He D, Lin YC. Microstructural Evolution and an Improved Dynamic Recrystallization Kinetic Model of a Ni-Cr-Mo Alloy in Hot Deformation. Materials. 2022; 15(9):3161. https://doi.org/10.3390/ma15093161
Chicago/Turabian StyleYan, Xintao, Yuchi Xia, Daoguang He, and Y. C. Lin. 2022. "Microstructural Evolution and an Improved Dynamic Recrystallization Kinetic Model of a Ni-Cr-Mo Alloy in Hot Deformation" Materials 15, no. 9: 3161. https://doi.org/10.3390/ma15093161
APA StyleYan, X., Xia, Y., He, D., & Lin, Y. C. (2022). Microstructural Evolution and an Improved Dynamic Recrystallization Kinetic Model of a Ni-Cr-Mo Alloy in Hot Deformation. Materials, 15(9), 3161. https://doi.org/10.3390/ma15093161








