Simulation of Lanthanum Purification Using a Finite Element Method
Abstract
:1. Introduction
2. Simulation Model
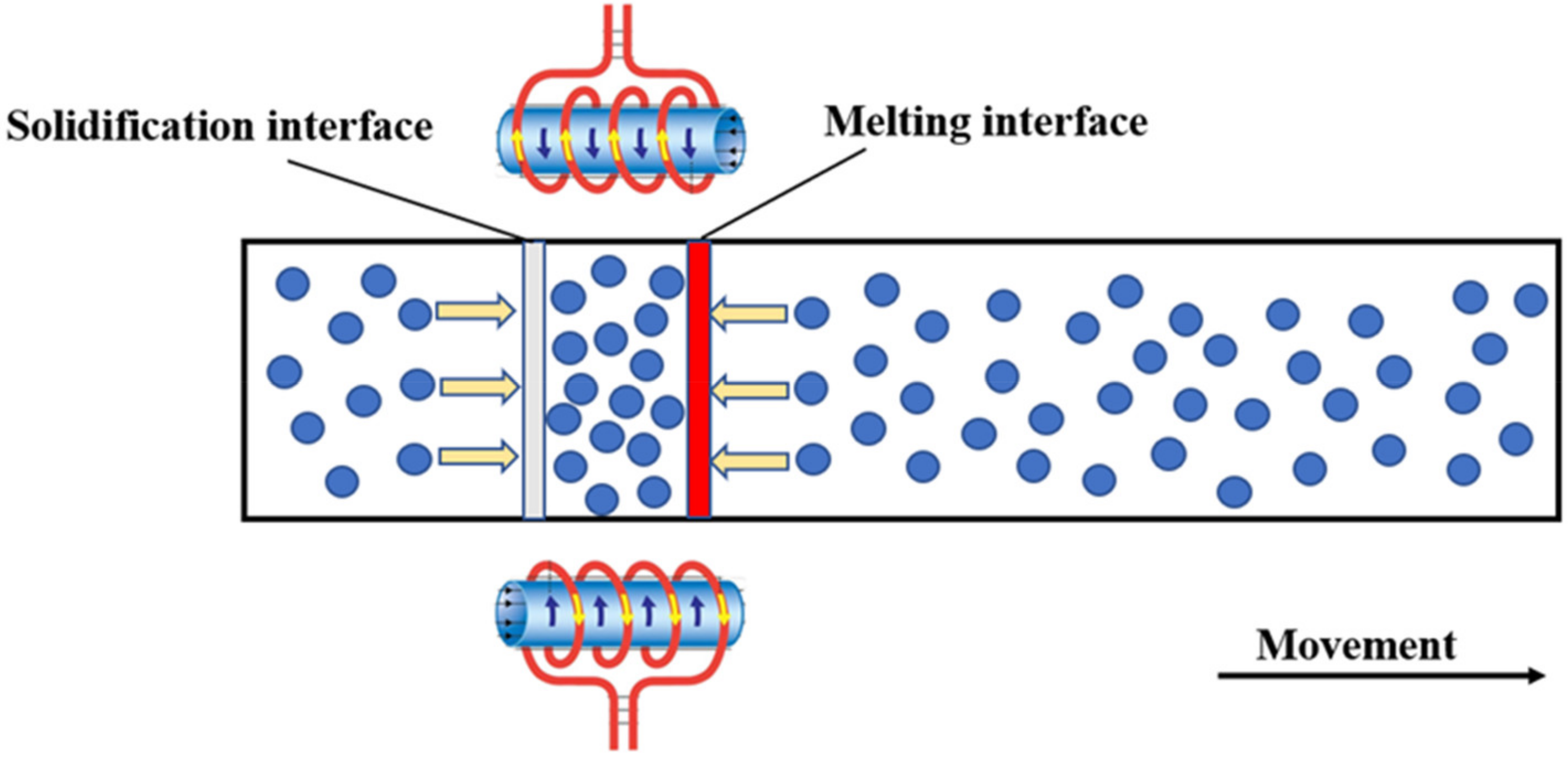
2.1. Reactor Geometry
2.2. Governing Equations
- As current thermal effect produces a significant amount of heart, the temperature change caused by phase transition and the influence of crucible can be neglected after the furnace reaches a stable temperature.
- The whole zone refining process was carried out in vacuum environment. Heat is transferred by conduction and radiation, and the convection is essentially negligible.
- Under the surface tension of the melt, the shape and length of molten zone do not vary over time. The effect of Lorentz force and gravity on the model was ignored.
2.3. Numerical Method
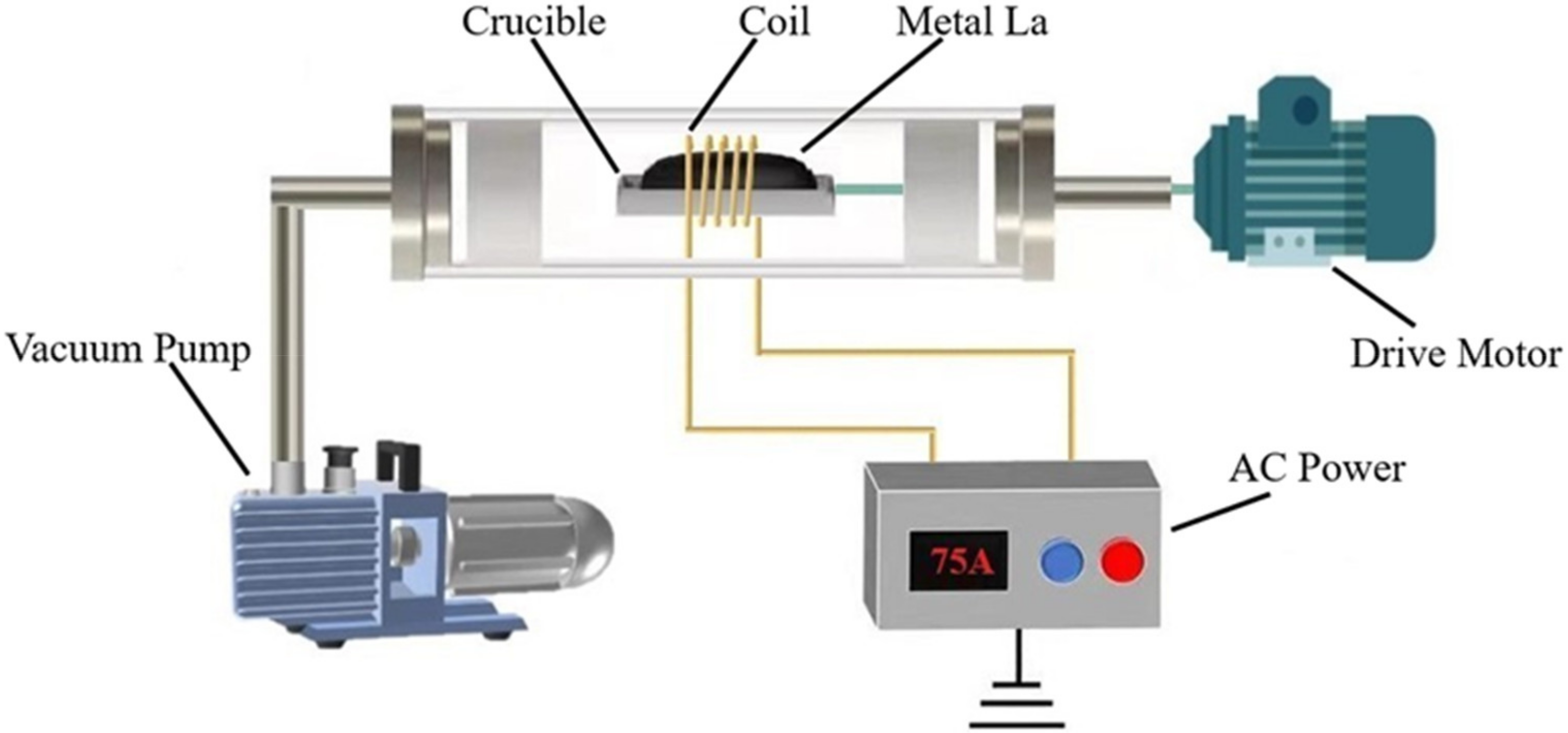
3. Experimental Model
4. Results and Discussion
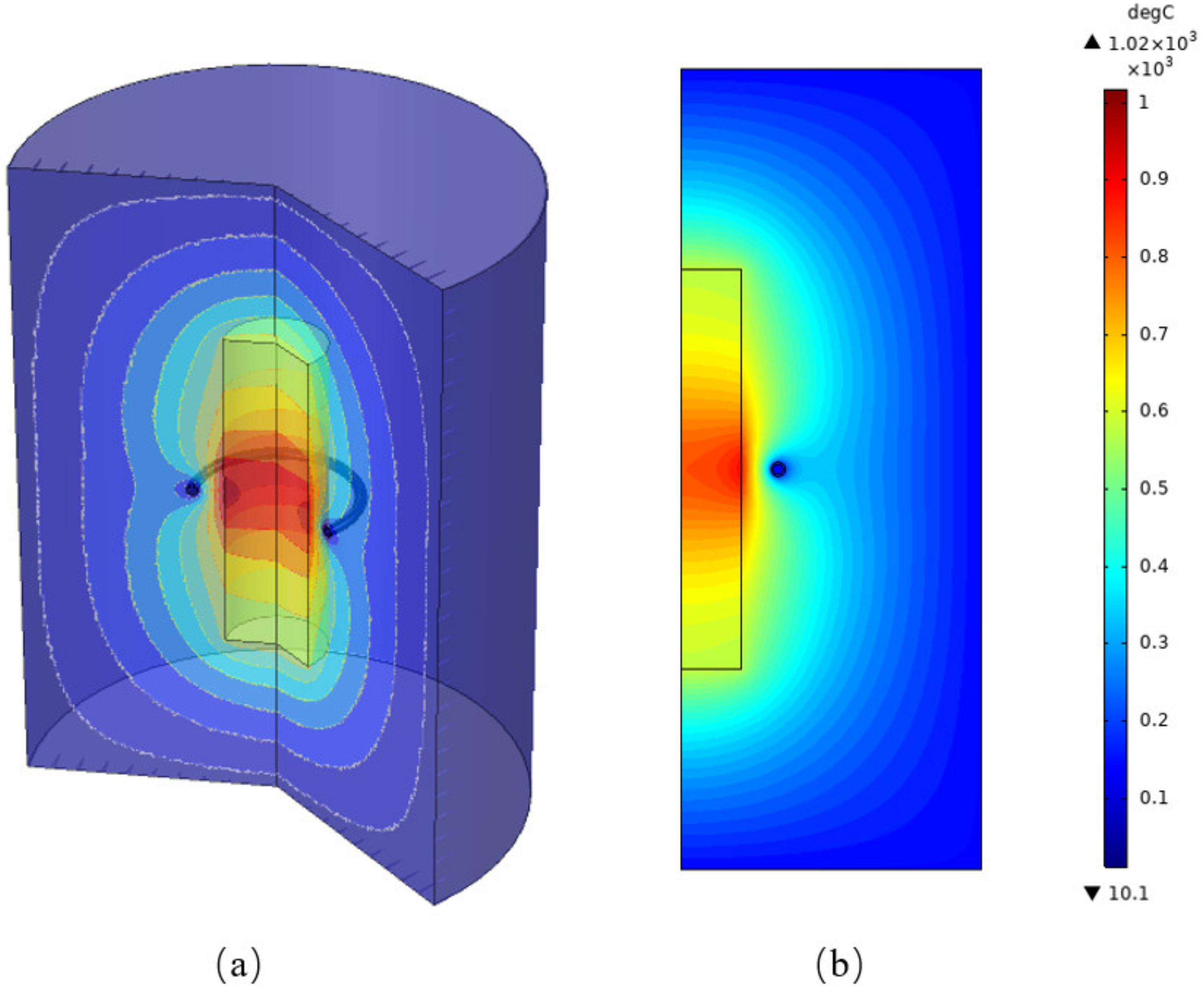
4.1. Simulation Model Validation
4.2. Influence of Frequency on Radial Temperature Distribution
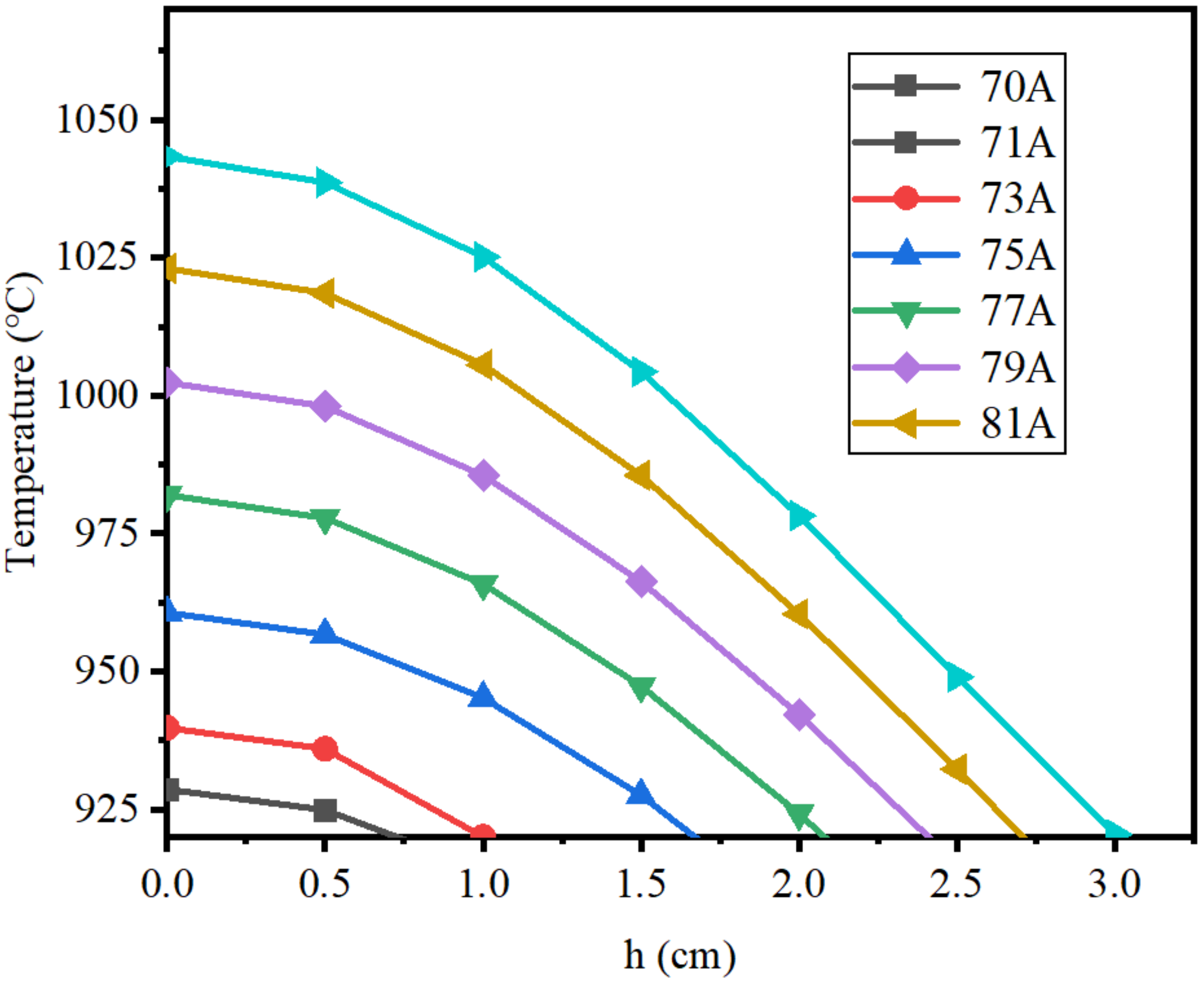
4.3. Influence of Current on Axial Temperature Distribution
4.4. Influences of Frequency and Current on Molten Region Width
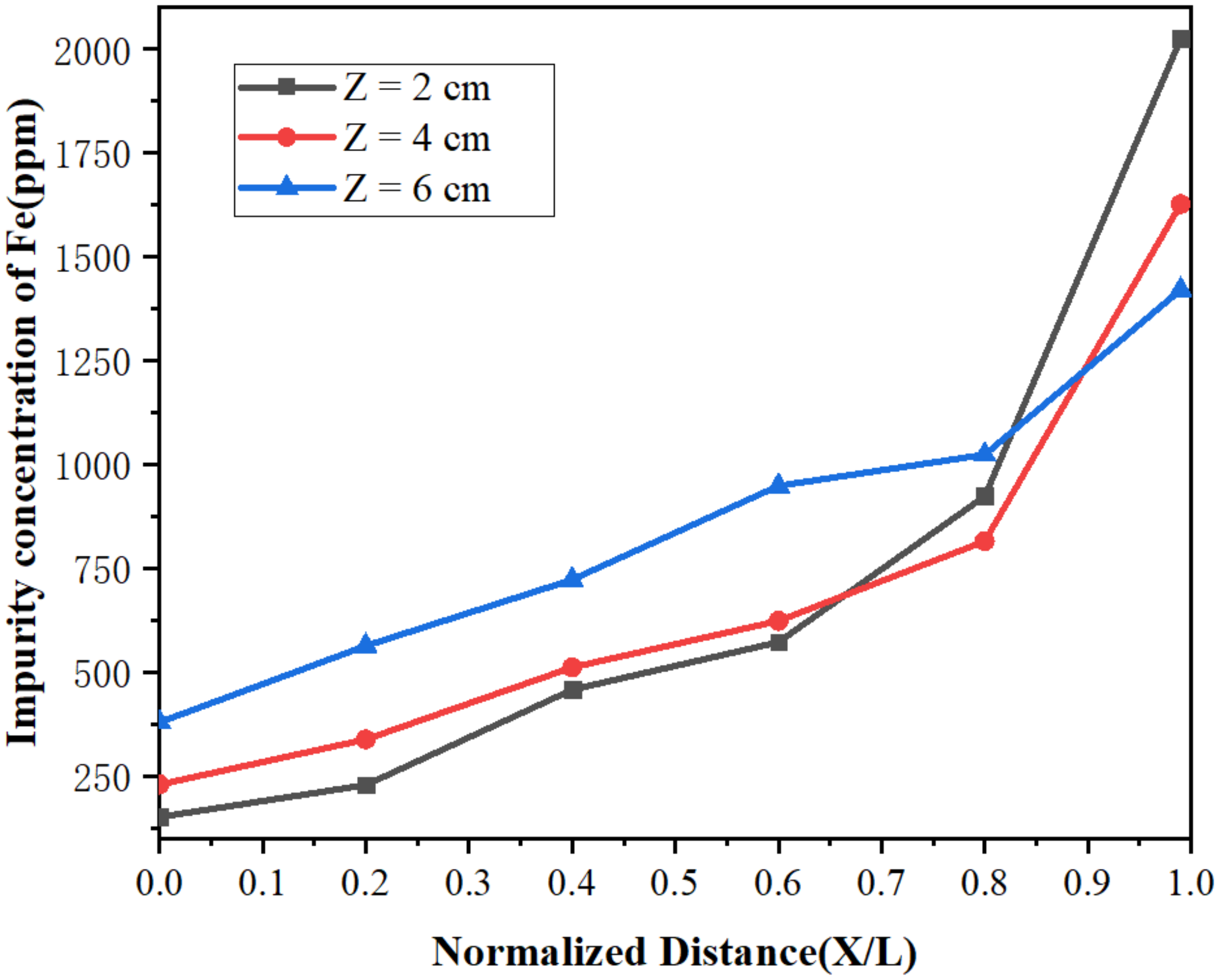
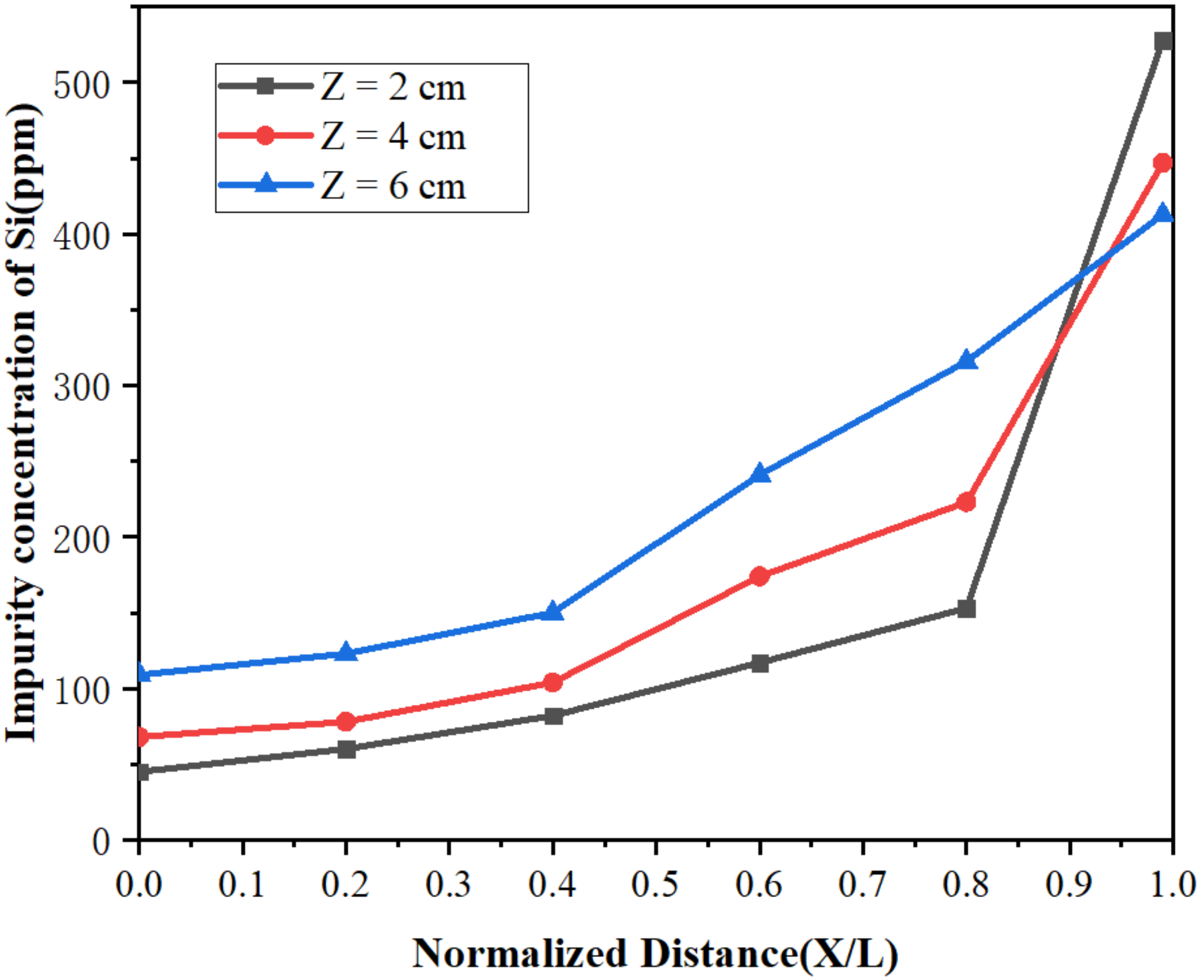
4.5. Influence of the Width of the Molten Region on Impurity Distribution
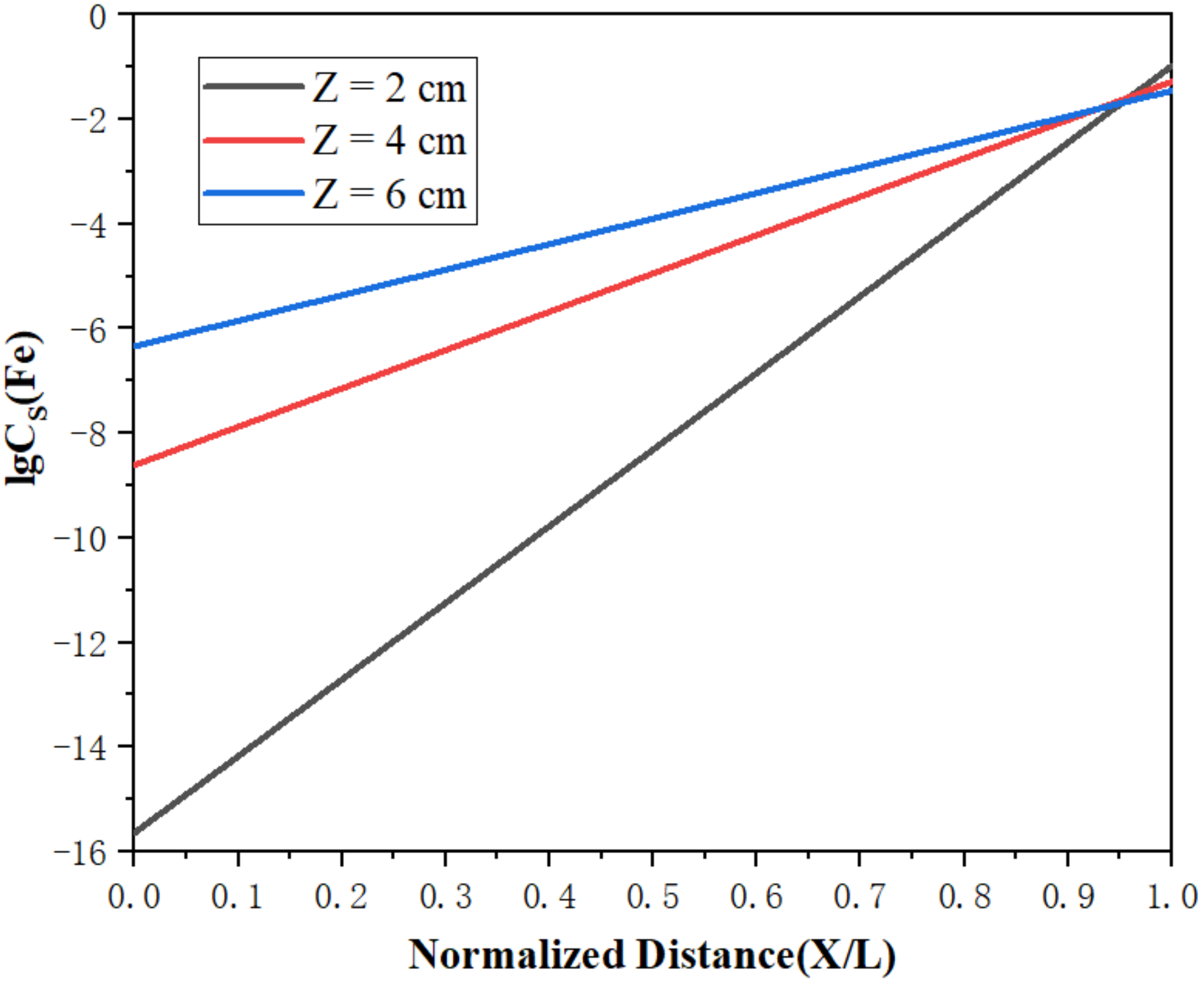
4.6. Effect of Width of Molten Region on Limiting Distribution
5. Conclusions
- We compared the calculation results and the experimental results. The average relative error was 3.64%, which indicates that the simulation model is accurate and reliable.
- The radial temperature distribution of the molten region increased from the center to the surface. With the increase in the frequency, the temperature at the center increased, and the temperature difference between the surface and the center increased gradually.
- With the increase in the width of the molten zone, the impurity concentration increased gradually in the front of the sample, and the purification effect was weakened. After 10 rounds of zone refining and holding the width of molten at 2 cm, the concentrations of Fe and Si at the beginning were 152 and 45 ppm respectively, which are much lower concentrations than those in the raw material, indicating that Fe and Si can be efficiently removed.
- As the width of the molten region decreased, the limiting distributions of impurities also correspondingly decreased, favoring the maximization of purification effect.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Willbold, E.; Gu, X.; Albert, D. Effect of the addition of low rare earth elements (lanthanum, neodymium, cerium) on the biodegradation and biocompatibility of magnesium. Acta Biomater. 2015, 11, 554–562. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Luo, J. A study of the influence of lanthanum rare earth alloy on the structure of cast iron. J. Nanchang Univ. 1989, 7, 974–976. [Google Scholar]
- Tang, J.; Chen, Z.; Yu, X. Rare earth elements (lanthanum, cerium and erbium) doped black oxygen deficient Bi2O3-Bi2O3 as novel photocatalysts enhanced photocatalytic performance. J. Rare Earths 2021, in press. [Google Scholar] [CrossRef]
- Chen, S.Y.; Zhang, X.W.; Li, Z.A. Effect of cold rolling and annealing on the microstructure and texture of erbium metal. Materials 2022, 15, 1370. [Google Scholar] [CrossRef] [PubMed]
- Kato, H.; Asakura, K.; Kudo, A. highly efficient water splitting into H2 and O2 over lanthanum-doped NaTaO3 photocatalysts with high crystallinity and surface nanostructure. J. Am. Chem. Soc. 2003, 125, 3082–3089. [Google Scholar] [CrossRef] [PubMed]
- Wei, Z.; Sun, W.; Liu, S. Lanthanum-dopedα-Ni (OH)(2)1D-2D-3D hierarchical nanostructures for robust bifunctional electro-oxidation. Acta Gran. 2021, 4, 8. [Google Scholar]
- Yang, Z.F. Study on Purification of Metal Lanthanum by Electron Beam Melting. Master’s Thesis, Beijing General Research Institute of Nonferrous Metals, Beijing, China, 2019. [Google Scholar]
- Pang, S.M.; Lu, W.L.; Yang, Z.F.; Zhang, X.W.; Chen, D.H.; Wu, D.G.; Zhou, L.; Miao, R.Y. Mechanism of removing ferrum impurity in lanthanum refined by electron beam melting. J. Rare Earths 2021, 39, 7. [Google Scholar] [CrossRef]
- Wang, H.; Wu, G.; Yan, Z. Synergistic effects of B-In codoping in zone-melted Bi0.48Sb1.52Te3-based thermoelectric. Chem. Eng. J. 2021, 420, 130381. [Google Scholar] [CrossRef]
- Li, M.; Tian, Q.; Wu, M. Numerical simulation analysis on solute redistribution of In–1 wt% Sn alloy during multipass vertical zone refining process. J. Cryst. Growth 2021, 565, 126156. [Google Scholar] [CrossRef]
- Upatov, M.; Koval, Y. Microstructure and mechanical properties of B4C-NbB2-SiC ternary eutectic composites by a crucible-free zone melting method. J. Eur. Ceram. Soc. 2020, 41, 1189–1196. [Google Scholar] [CrossRef]
- Prasad, D.S.; Munirathnam, N.R.; Rao, V. Effect of multi-pass, zone length and translation rate on impurity segregation during zone refining of tellurium. Mater. Lett. 2006, 60, 1875–1879. [Google Scholar] [CrossRef]
- Zhai, X.; Yan, F.U.; Zhang, X. The calculation and determination on distribution coefficient of impurities Fe and Si in Aluminum. Light Met. 2000, 12, 37–39. [Google Scholar]
- Liu, W.S.; Liu, S.H. The latest development of zone melting technology. Rare Met. Cem. Carbides 2013, 41, 66–71. [Google Scholar]
- Liu, J.; Zee, R.H. Growth of molybdenum-based alloy single crystals using electron beam zone melting. J. Cryst. Growth 1996, 163, 259–265. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, J.; Xu, J. Preparation of high-purity tin by zone melting. Russ. J. Non-Ferr. Met. 2020, 61, 9–20. [Google Scholar] [CrossRef]
- Huang, J.; Ren, Q.; Hu, Z. Application of a genetic algorithm to optimize redistribution process in zone refining of cerium. Rare Met. Mater. Eng. 2017, 46, 3633–3638. [Google Scholar]
- Johari, A.; Talebi, A. Stochastic analysis of rainfall-induced slope instability and steady-state seepage flow using random finite-element method. Int. J. Geomech. 2019, 19, 04019085. [Google Scholar] [CrossRef]
- Kostopoulos, V.; Markopoulos, Y.P.; Giannopoulos, G.; Vlachos, D.E. Finite element analysis of impact damage response of composite motorcycle safety helmets. Compos. Part B Eng. 2002, 33, 99–107. [Google Scholar] [CrossRef]
- Cheung, T.; Cheung, N. Application of a genetic algorithm to optimize purification in the zone refining process. Adv. Manuf. Processes 2011, 26, 493–500. [Google Scholar] [CrossRef]
- Tan, Y. Indium Zone-Refining Device and the Analysis of Temperature Field Simulation. Master’s Thesis, Guilin University of Technology, Guilin, China, 2017. [Google Scholar]
- Chen, L.N. Research on Purification of Indium by Oxidation Refining-Zone Refining Combined Method. Master’s Thesis, Guilin University of Technology, Guilin, China, 2021. [Google Scholar]
- Davidson, P.A. An Introduction to Magnetohydrodynamics: High-Frequency Fields: Magnetic Levitation and Induction Heating; Cambridge University Press: Cambridge, UK, 2001; pp. 387–404. [Google Scholar]
- Bermudez, A.; Gomez, D.; Muniz, M.C. Numerical simulation of a thermo-electromagneto-hydrodynamic problem in an induction heating furnace. Appl. Numer. Math. 2009, 59, 2082–2104. [Google Scholar] [CrossRef]
- Narita, T.; Takahashi, N.; Horii, M. Investigation of evolution strategy and optimization of induction heating model. IEEE Trans. Magn. 2002, 36, 1085–1088. [Google Scholar] [CrossRef] [Green Version]
- Hou, Y.Q. Theoretical Analysis and Modeling of Polysilicon Preparation Process by Improved Siemens Method. Ph.D. Thesis, Kunming University of Science and Technology, Kunming, China, 2013. [Google Scholar]
- Ya, D.L.; Gang, X. A CFD model for gas uniform distribution in turbulent flow for the production of titanium pigment in chloride process. Chin. J. Chem. Eng. 2016, 24, 749–756. [Google Scholar]
- Pfann, W.G. Zone Melting, 1st ed.; Literary Licensing, LLC: Whitefish, MT, USA, 1962; pp. 29–76. [Google Scholar]
- Ghosh, K.; Mani, V.N.; Dhar, S. Numerical study and experimental investigation of zone refining in ultra-high purification of gallium and its use in the growth of GaAs epitaxial layers. J. Cryst. Growth 2009, 311, 1521–1528. [Google Scholar] [CrossRef]
- Meier, M. Purification of Cd, Zn and Te for Cd Zn Te Growth. Ph.D. Thesis, Kansas State University, Manhattan, KS, USA, 2009. [Google Scholar]
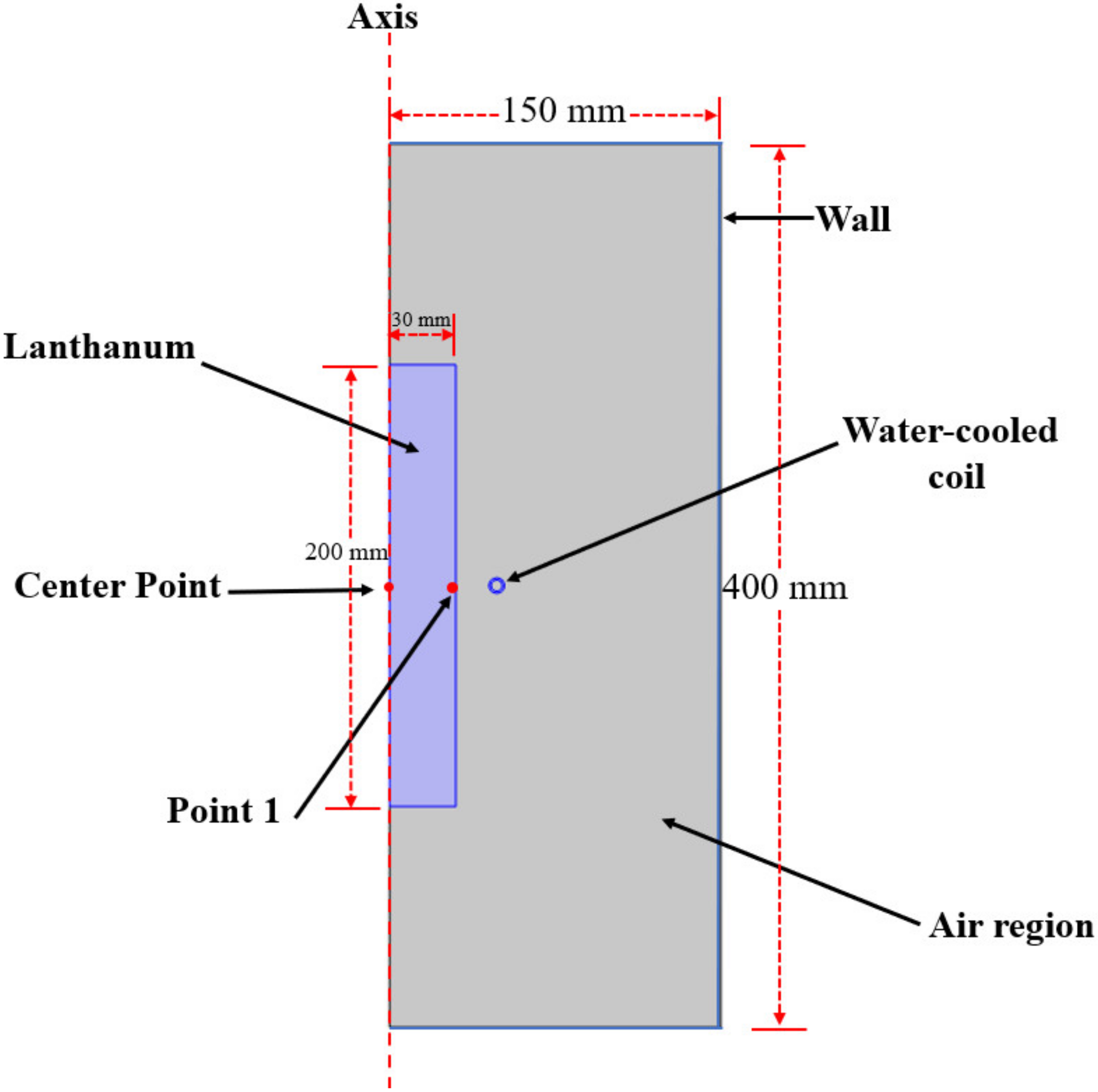






| Region | Items | Data |
|---|---|---|
| Water-cooled coil | Outer diameter | 7 mm |
| Inner diameter | 5 mm | |
| Air region | Width | 150 mm |
| Length | 400 mm | |
| Lanthanum | Width | 30 mm |
| Length | 200 mm | |
| Boundary conditions | Temperature of cooling water | 283 K |
| Temperature of reactor wall | 293 K | |
| Cooling water mass flow rate | 1 kg/min | |
| Emissivity of metal | 0.5 |
| Parameter | Value | Unit |
|---|---|---|
| 1 | H/m | |
| 0.2 | MS/cm | |
| 0.64 | 1 | |
| 0.5 | 1 | |
| 1 | 1 |
| Impurity | Fe | Cu | Cr | Si | Mn |
|---|---|---|---|---|---|
| (ppm) | 787 | 3 | 6 | 345 | 11 |
| Impurity | Zn | Ti | Pr | Ce | Co |
| (ppm) | 33 | 25 | 8 | 3.37 | 2 |
| Width | Fe | Si | ||
|---|---|---|---|---|
| A | B | A | B | |
| Z = 2 cm | 2.25 × 10−16 | 33.79 | 6.94 × 10−20 | 39.55 |
| Z = 4 cm | 2.45 × 10−9 | 16.89 | 1.35 × 10−11 | 19.77 |
| Z = 6 cm | 4.56 × 10−7 | 11.26 | 6.56 × 10−9 | 13.18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, D.; Yu, C.; Wang, Z.; Zhang, X.; Lu, W.; Zhang, D. Simulation of Lanthanum Purification Using a Finite Element Method. Materials 2022, 15, 3183. https://doi.org/10.3390/ma15093183
Chen D, Yu C, Wang Z, Zhang X, Lu W, Zhang D. Simulation of Lanthanum Purification Using a Finite Element Method. Materials. 2022; 15(9):3183. https://doi.org/10.3390/ma15093183
Chicago/Turabian StyleChen, Dehong, Chuang Yu, Zhiqiang Wang, Xiaowei Zhang, Wenli Lu, and Dongwei Zhang. 2022. "Simulation of Lanthanum Purification Using a Finite Element Method" Materials 15, no. 9: 3183. https://doi.org/10.3390/ma15093183
APA StyleChen, D., Yu, C., Wang, Z., Zhang, X., Lu, W., & Zhang, D. (2022). Simulation of Lanthanum Purification Using a Finite Element Method. Materials, 15(9), 3183. https://doi.org/10.3390/ma15093183





