Simulation Analysis and Experimental Study of the Strength of Aluminum Alloy Suspension Structure
Abstract
1. Introduction
2. Structure and Materials
3. Simulation Analysis
4. Experimental Procedure
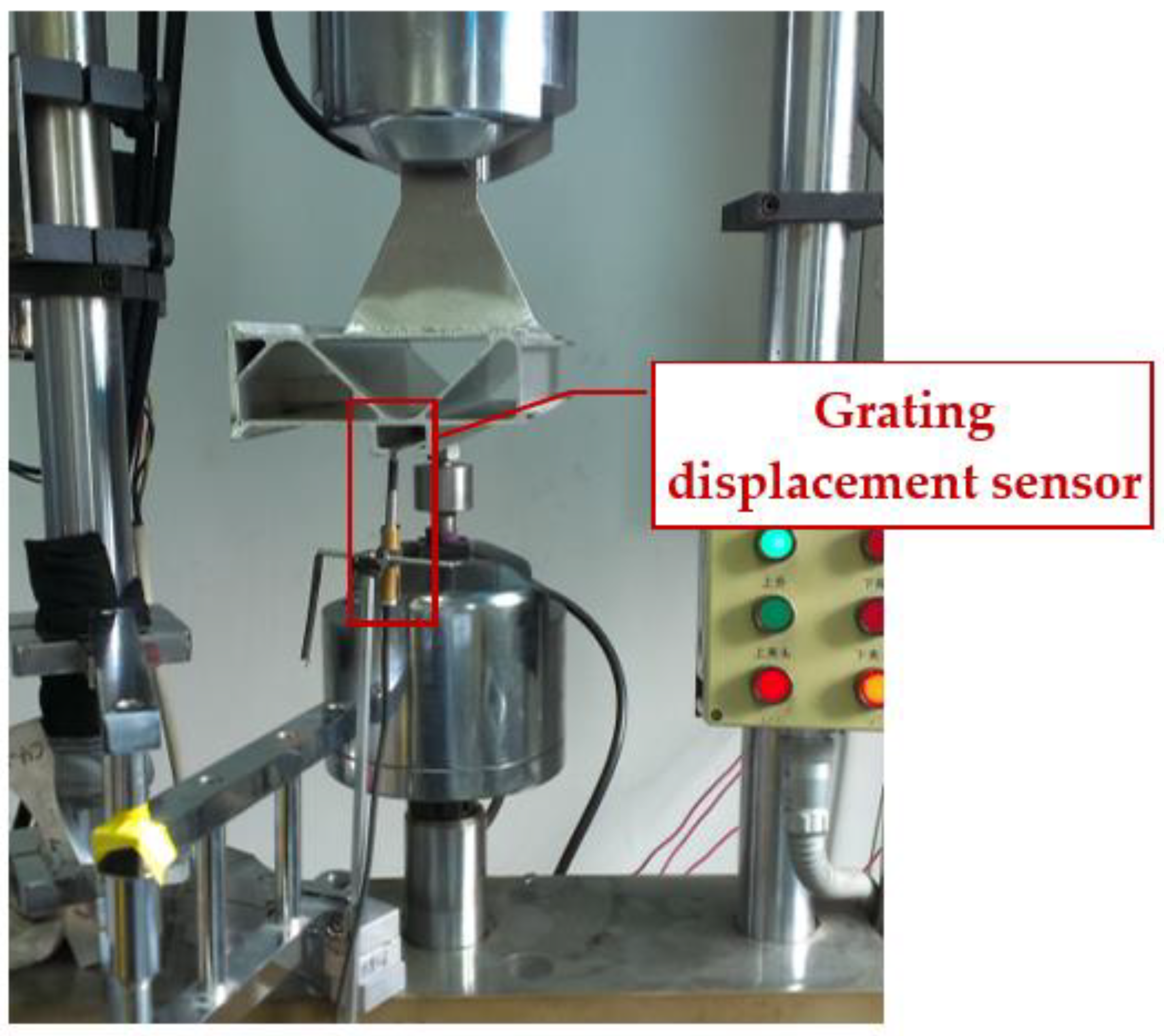
4.1. Static Tensile Test
4.2. Fatigue Performance Test
5. Results and Discussion
6. Conclusions
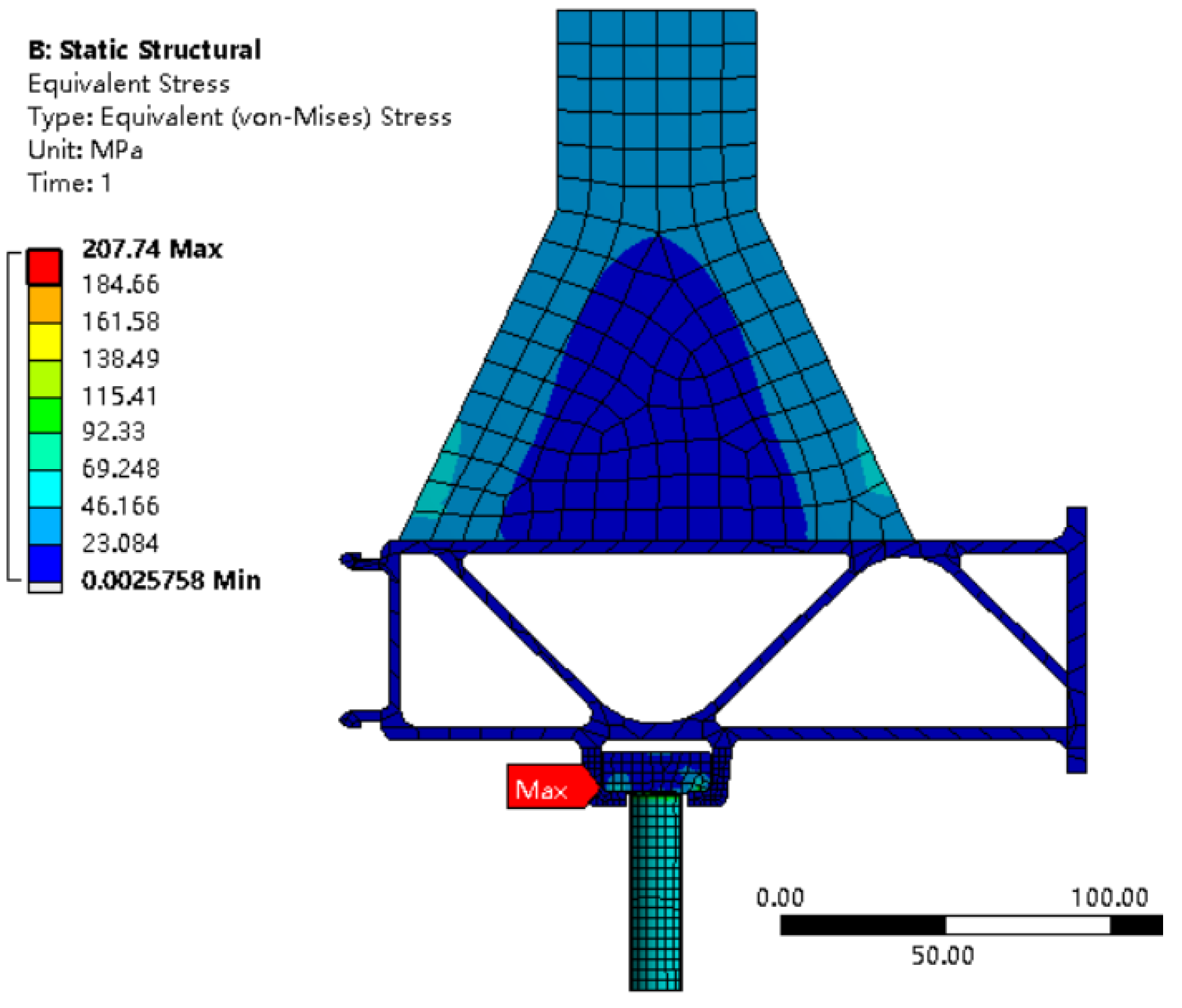
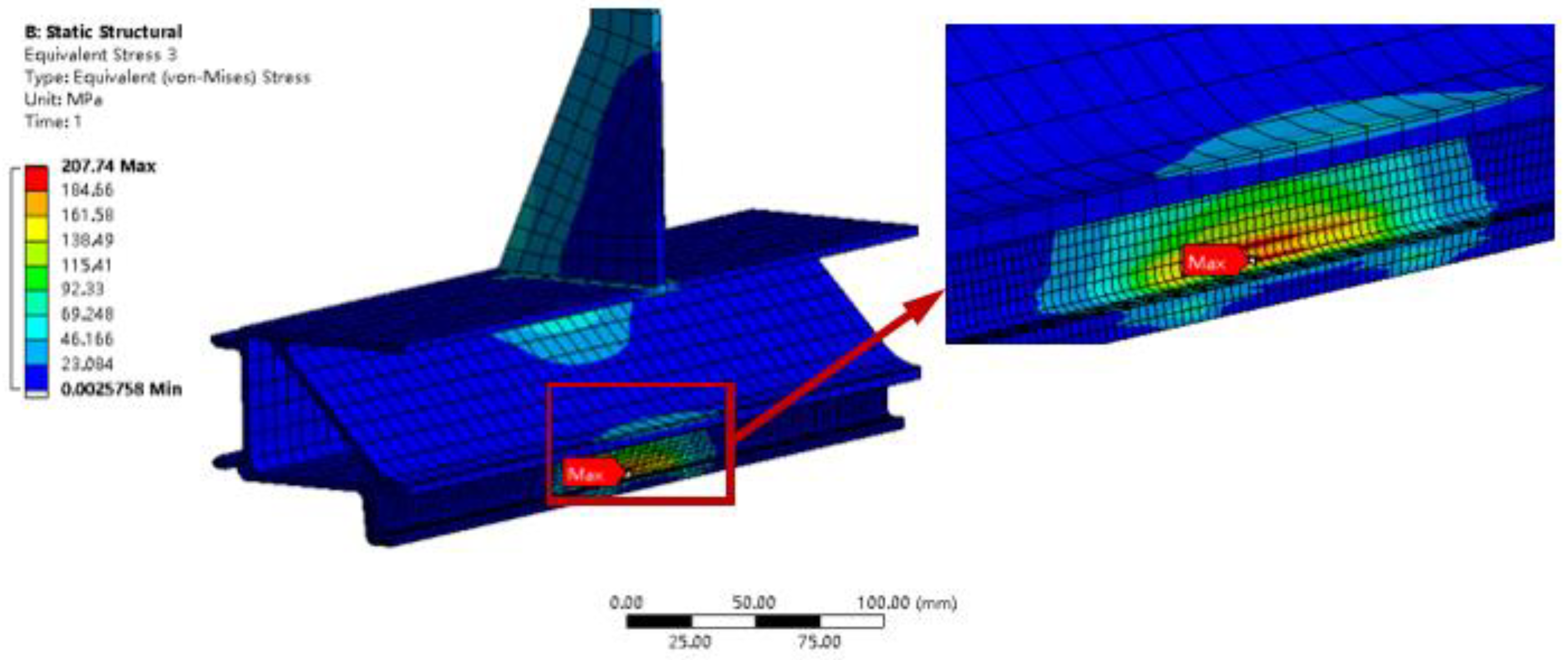
- The maximum stress site of the suspension structure is at the transition round corner of the suspension slot, where there is a stress concentration. When the load level is 11.0 kN, the maximum stress value is 207.74 MPa.
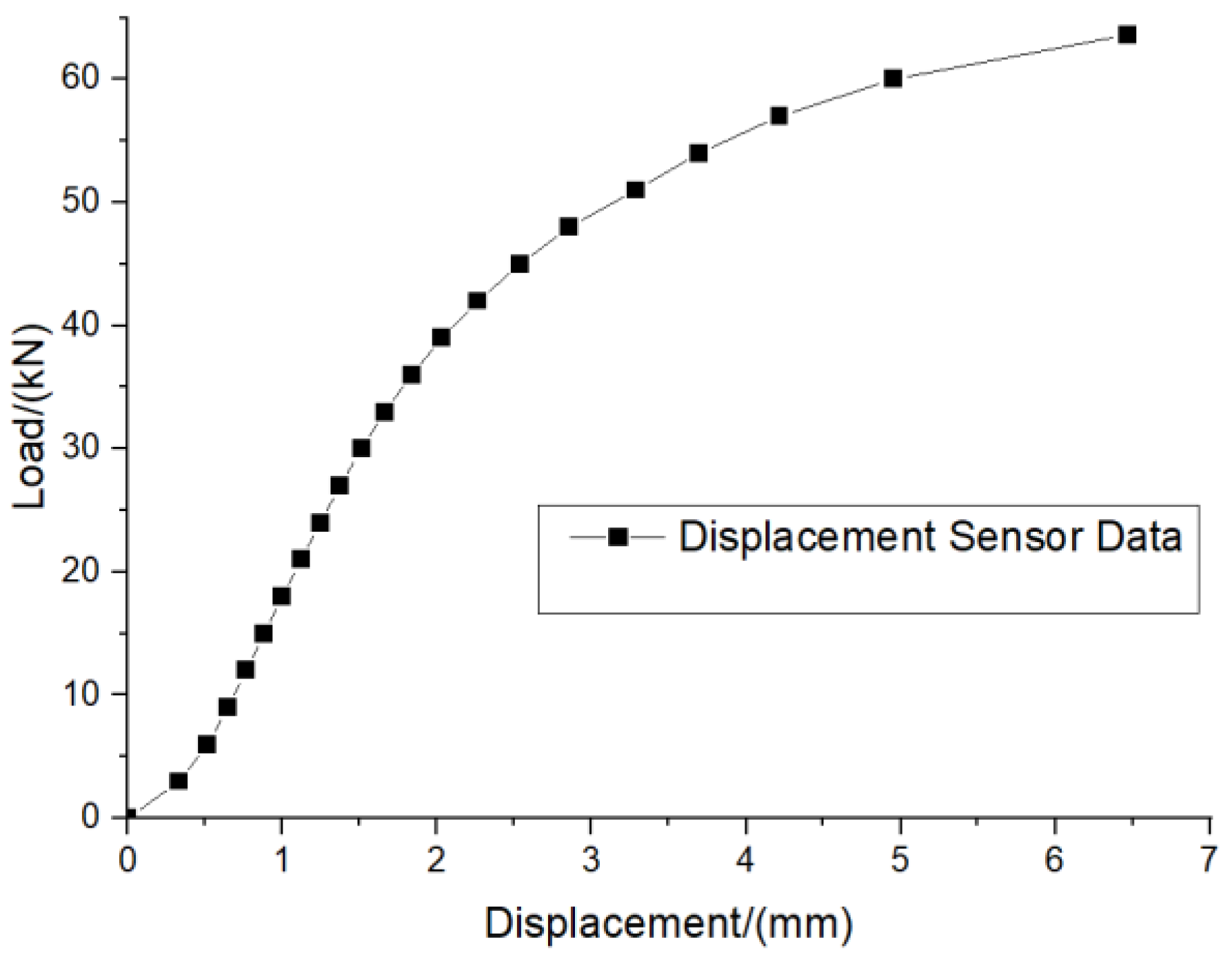
- The tensile test shows that under a large load, the hanging slot will undergo large plastic deformation, the ultimate load-bearing level of the suspension slot is 65 kN, and the static strength can meet the needs of equipment suspension.
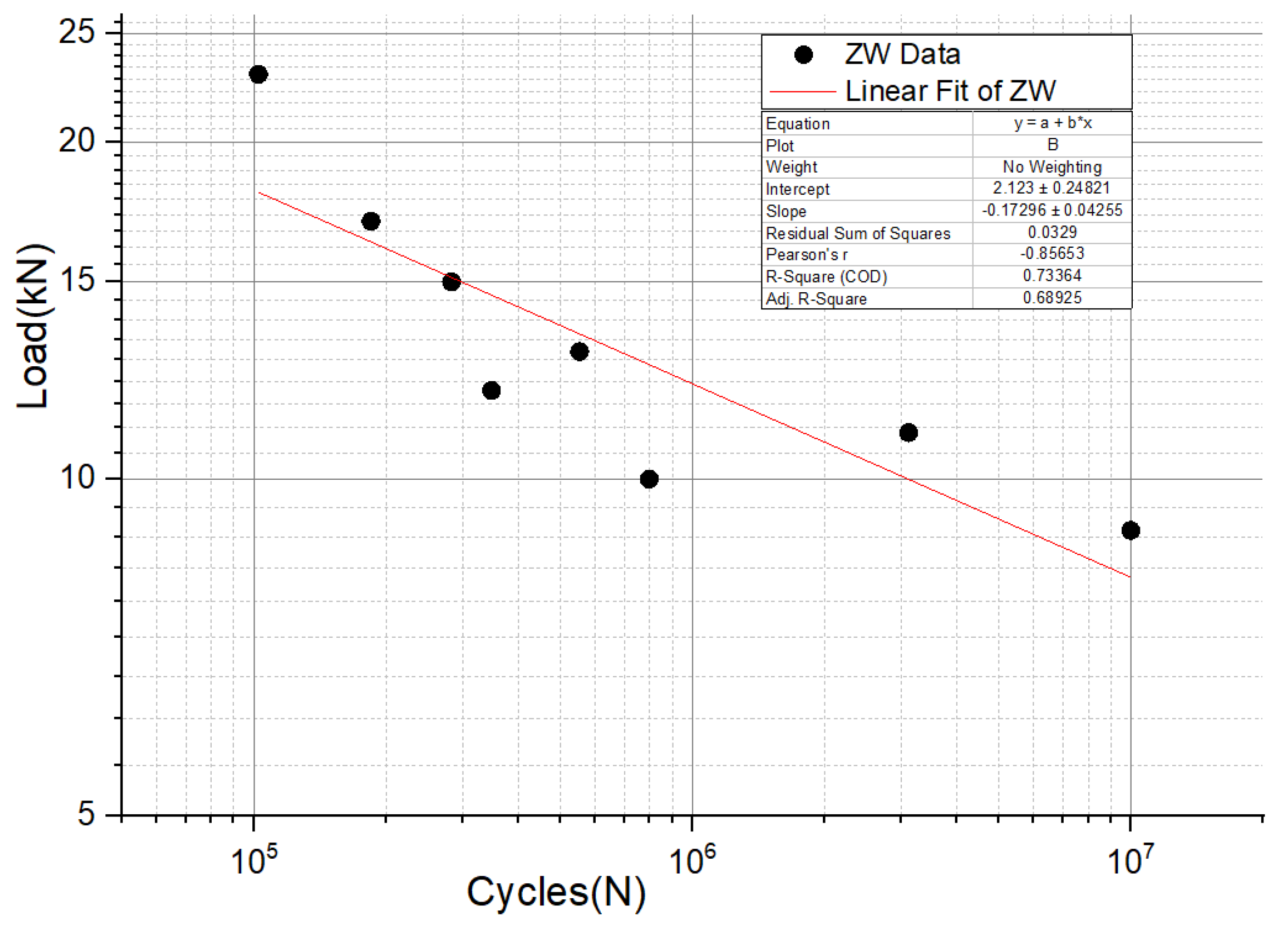
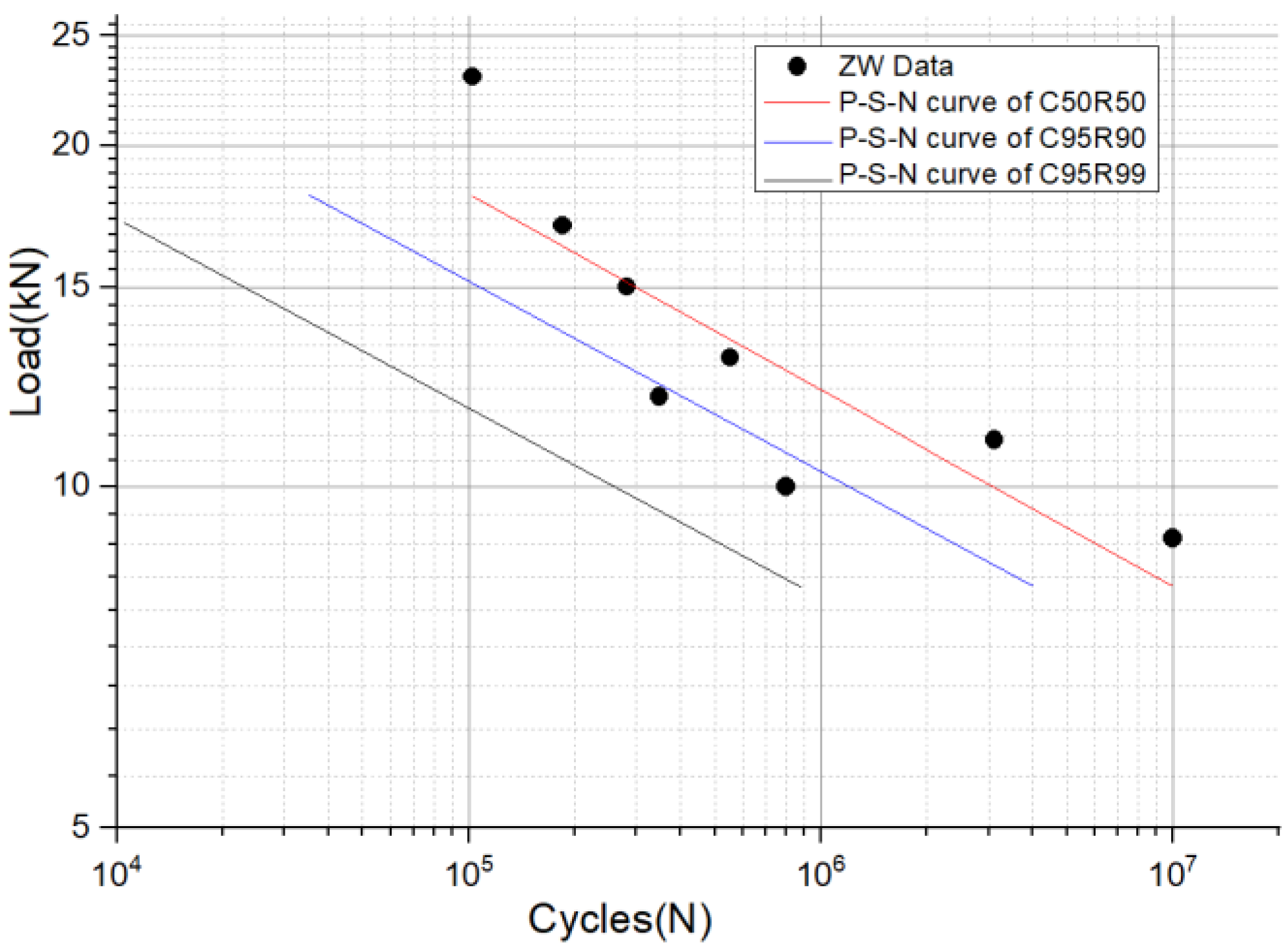
- The median load–life curve obtained by fitting the test data shows that when the load level is 11 kN, the corresponding fatigue life is 1,823,055 cycles. This result has practical significance for the rational arrangement of the number of suspension points.
- The fatigue tests show that the failure site of the structural component is at the transition corner of the suspension slot, which is consistent with the location of the maximum stress from the finite element analysis. The fatigue life of aluminum structures is influenced by many factors and is very sensitive to various defects. As a rule, the fatigue life of structures is highly dispersive. Therefore, a design curve based on a certain level of confidence and reliability, known as a P-S-N curve, should be used when designing the structure, rather than the median S-N curve.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alpu, O. A methodology for evaluating satisfaction with high-speed train services: A case study in Turkey. Transp. Policy 2015, 44, 151–157. [Google Scholar] [CrossRef]
- Chen, H.; Jiang, B. A Review of Fault Detection and Diagnosis for the Traction System in High-Speed Trains. IEEE Trans. Intell. Transp. Syst. 2020, 21, 450–465. [Google Scholar] [CrossRef]
- Li, S.; Yang, L.; Li, K.; Gao, Z. Robust sampled-data cruise control scheduling of high speed train. Transp. Res. Part C Emerg. Technol. 2014, 46, 274–283. [Google Scholar] [CrossRef]
- Wu, Y.; Liao, H.; Tang, Y. Enhanced high-cycle fatigue strength of Al–12Si–4Cu-1.2Mn-T6 cast aluminum alloy at room temperature and 350 C. Mater. Sci. Eng. A 2021, 825, 141917. [Google Scholar] [CrossRef]
- Tomažinčič, D.; Nečemer, B.; Vesenjak, M.; Klemenc, J. Low-cycle fatigue life of thin-plate auxetic cellular structures made from aluminium alloy 7075-T651. Fatigue Fract. Eng. Mater. Struct. 2019, 42, 1022–1036. [Google Scholar] [CrossRef]
- Alexopoulos, N.D.; Examilioti, T.N.; Stergiou, V.; Kourkoulis, S.K. Fatigue and fracture toughness of electron beam welded joints of aluminum alloy 6156 (Al–Mg–Si) for aerospace applications. Fatigue Fract. Eng. Mater. Struct. 2021, 44, 2610–2624. [Google Scholar] [CrossRef]
- Repplinger, C.; Sellen, S.; Kedziora, S.; Zürbes, A.; Maas, S. Analysis of residual stress relaxation of aluminum alloys EN AW 6061/-82 T6 under cyclic loading. Fatigue Fract. Eng. Mater. Struct. 2021, 44, 3023–3041. [Google Scholar] [CrossRef]
- Ponnusamy, P.; Rahman Rashid, R.A.; Masood, S.H.; Ruan, D.; Palanisamy, S. Mechanical Properties of SLM-Printed Aluminium Alloys: A Review. Materials 2020, 13, 4301. [Google Scholar] [CrossRef]
- Xu, L.; Wang, Q.; Zhou, M. Micro-crack initiation and propagation in a high strength aluminum alloy during very high cycle fatigue. Mater. Sci. Eng. A 2018, 715, 404–413. [Google Scholar] [CrossRef]
- Gasem, Z.M.; Ali, S.S. Low-cycle fatigue behavior of powder metallurgy 6061 aluminum alloy reinforced with submicron-scale Al2O3 particles. Mater. Sci. Eng. A 2013, 562, 109–117. [Google Scholar] [CrossRef]
- Sun, W.; Gong, D.; Zhou, J.; Zhao, Y. Influences of Suspended Equipment under Car Body on High-speed Train Ride Quality. Procedia Eng. 2011, 16, 812–817. [Google Scholar] [CrossRef][Green Version]
- Li, B.; Zhou, J.; Gong, D.; You, T. Research on the Influence of Under-Chassis Equipment Parameters and Distribution on Car Body Vibration of High-Speed Railway Vehicle. IEEE Access 2021, 9, 163151–163164. [Google Scholar] [CrossRef]
- Guo, J.; Shi, H.; Li, F.; Wu, P. Field Measurements of Vibration on the Car Body-Suspended Equipment for High-Speed Rail Vehicles. Shock Vib. 2020, 2020, 6041543. [Google Scholar] [CrossRef]
- Zhang, P.; Li, S.; Núñez, A.; Li, Z. Vibration modes and wave propagation of the rail under fastening constraint. Mech. Syst. Signal Process. 2021, 160, 107933. [Google Scholar] [CrossRef]
- Xu, L. On dynamic analysis method for large-scale train–track–substructure interaction. Railw. Eng. Sci. 2022, 30, 162–182. [Google Scholar] [CrossRef]
- Oregui, M.; Man, A.d.; Woldekidan, M.F.; Li, Z.; Dollevoet, R. Obtaining railpad properties via dynamic mechanical analysis. J. Sound Vib. 2016, 363, 460–472. [Google Scholar] [CrossRef]
- Sonsino, C.M.; Breitenberger, M.; Krause, I.; Pötter, K.; Schröder, S.; Jürgens, K. Required Fatigue Strength (RFS) for evaluating of spectrum loaded components by the example of cast-aluminium passenger car wheels. Int. J. Fatigue 2021, 145, 105975. [Google Scholar] [CrossRef]
- Zhou, W.; Chen, L.; Wang, Z.; Ding, S.; Shan, Y. Aerodynamic load spectrum and fatigue behaviour of high-speed train’s equipment cabin. Fatigue Fract. Eng. Mater. Struct. 2019, 42, 2579–2595. [Google Scholar] [CrossRef]
- Lu, Y.; Xiang, P.; Dong, P.; Zhang, X.; Zeng, J. Analysis of the effects of vibration modes on fatigue damage in high-speed train bogie frames. Eng. Fail. Anal. 2018, 89, 222–241. [Google Scholar] [CrossRef]
- Hu, W.; Liu, Z.; Liu, D.; Hai, X. Fatigue failure analysis of high speed train gearbox housings. Eng. Fail. Anal. 2017, 73, 57–71. [Google Scholar] [CrossRef]
- Guo, F.; Wu, S.C.; Liu, J.X.; Zhang, W.; Qin, Q.B.; Yao, Y. Fatigue life assessment of bogie frames in high-speed railway vehicles considering gear meshing. Int. J. Fatigue 2020, 132, 105353. [Google Scholar] [CrossRef]
- Yu, K.; Wang, X.; Peng, W. Robust locating research of welding fixtures for the aluminum alloy sidewall of a high-speed train body. Int. J. Adv. Manuf. Technol. 2022, 122, 3379–3392. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, Y.; Xie, L.; Zhang, Y.; Zhang, K. The effects of pre-cyclic stress on fracture properties and fatigue crack propagation life of 7N01 aluminum alloy. Eng. Fract. Mech. 2018, 191, 1–12. [Google Scholar] [CrossRef]
- Elhadari, H.A.; Patel, H.A.; Chen, D.L.; Kasprzak, W. Tensile and fatigue properties of a cast aluminum alloy with Ti, Zr and V additions. Mater. Sci. Eng. A 2011, 528, 8128–8138. [Google Scholar] [CrossRef]
- Hao, H.; Ye, D.; Chen, C. Strain ratio effects on low-cycle fatigue behavior and deformation microstructure of 2124-T851 aluminum alloy. Mater. Sci. Eng. A 2014, 605, 151–159. [Google Scholar] [CrossRef]
- Hammami, C.; Kammoun, N.; Hentati, H.; Amar, M.B.; Haddar, M. Parametric analysis of the damage characterization tests of aluminum bulk material. J. Mech. Sci. Technol. 2022, 36, 5019–5025. [Google Scholar] [CrossRef]
- Khan, S.; Wilde, F.; Beckmann, F.; Mosler, J. Low cycle fatigue damage mechanism of the lightweight alloy Al2024. Int. J. Fatigue 2012, 38, 92–99. [Google Scholar] [CrossRef]
- Wu, H.; Zhu, H.; Chen, L.; Pan, D.; Fang, Q.; Li, W.; Jin, F.; Fan, H. Engineering failure analyses of aluminum truss-core sandwich panels of portable deployable roadway under tracked loads. Eng. Fail. Anal. 2021, 128, 105655. [Google Scholar] [CrossRef]
- Skejić, D.; Dokšanović, T.; Čudina, I.; Mazzolani, F.M. The Basis for Reliability-Based Mechanical Properties of Structural Aluminium Alloys. Appl. Sci. 2021, 11, 4485. [Google Scholar] [CrossRef]
- Graciano, C.; Loaiza, N.; Casanova, E. Numerical study and design of extruded aluminum beams subjected to concentrated loads. Thin-Walled Struct. 2020, 155, 106917. [Google Scholar] [CrossRef]
- Zhang, C.; Zhao, G.; Guan, Y.; Gao, A.; Wang, L.; Li, P. Virtual tryout and optimization of the extrusion die for an aluminum profile with complex cross-sections. Int. J. Adv. Manuf. Technol. 2014, 78, 927–937. [Google Scholar] [CrossRef]
- Williams, C. A practical method for statistical analysis of strain–life fatigue data. Int. J. Fatigue 2003, 25, 427–436. [Google Scholar] [CrossRef]
- Tridello, A.; Boursier Niutta, C.; Berto, F.; Tedesco, M.M.; Plano, S.; Gabellone, D.; Paolino, D.S. Design against fatigue failures: Lower bound P-S-N curves estimation and influence of runout data. Int. J. Fatigue 2022, 162, 106934. [Google Scholar] [CrossRef]
- Simpson, P.; Cronin, J. Reliability of a Unilateral Horizontal Leg Power Test to Assess Stretch Load Tolerance. Meas. Phys. Educ. Exerc. Sci. 2006, 10, 9. [Google Scholar]
- Li Hongshuang, L.Z. Bootstrap method for confidence lower limit estimation of population percentile and reliability in small number of test sample. Acta Aeronaut. Et Astronaut. Sin. 2006, 27, 6. [Google Scholar]

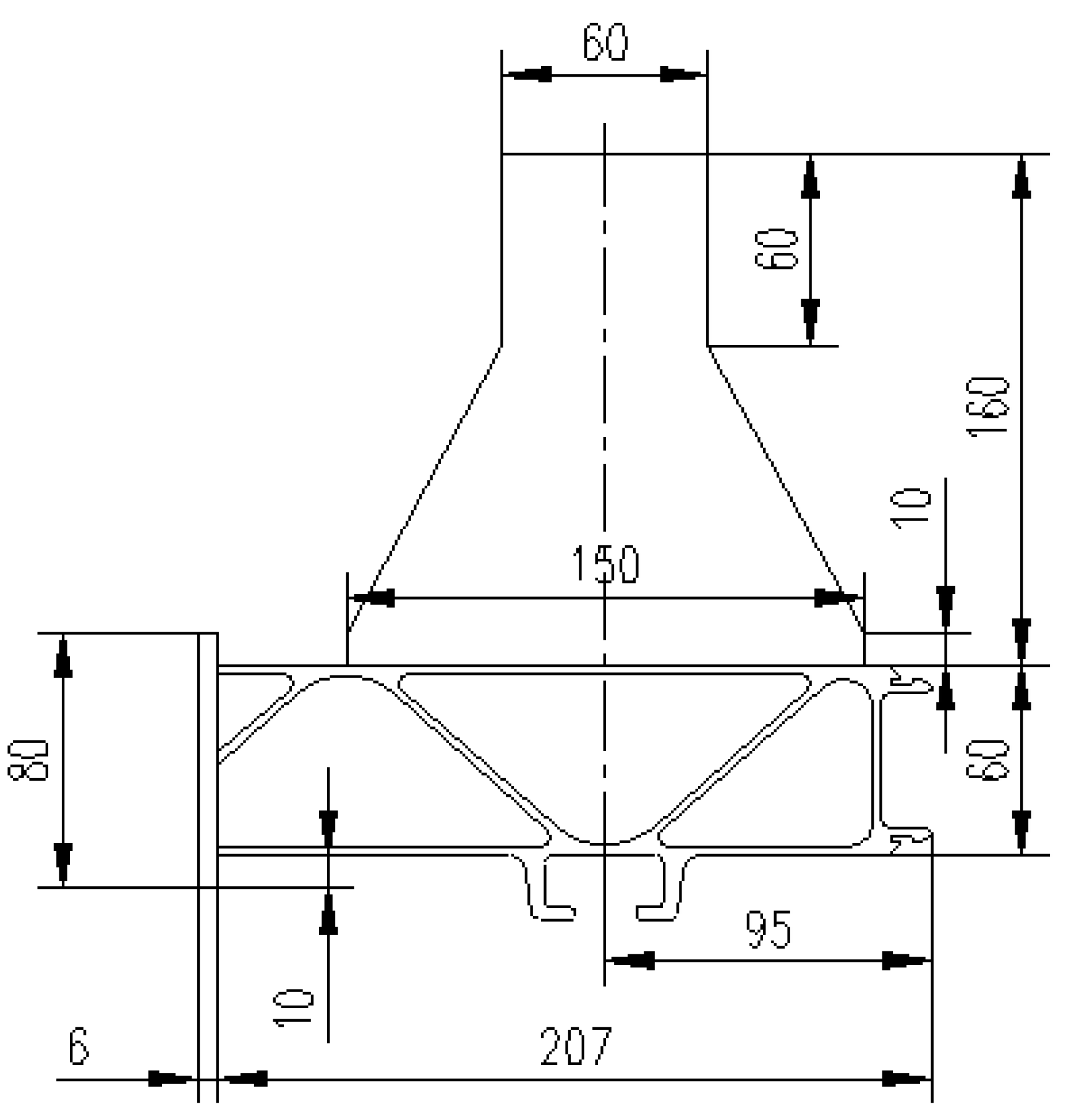
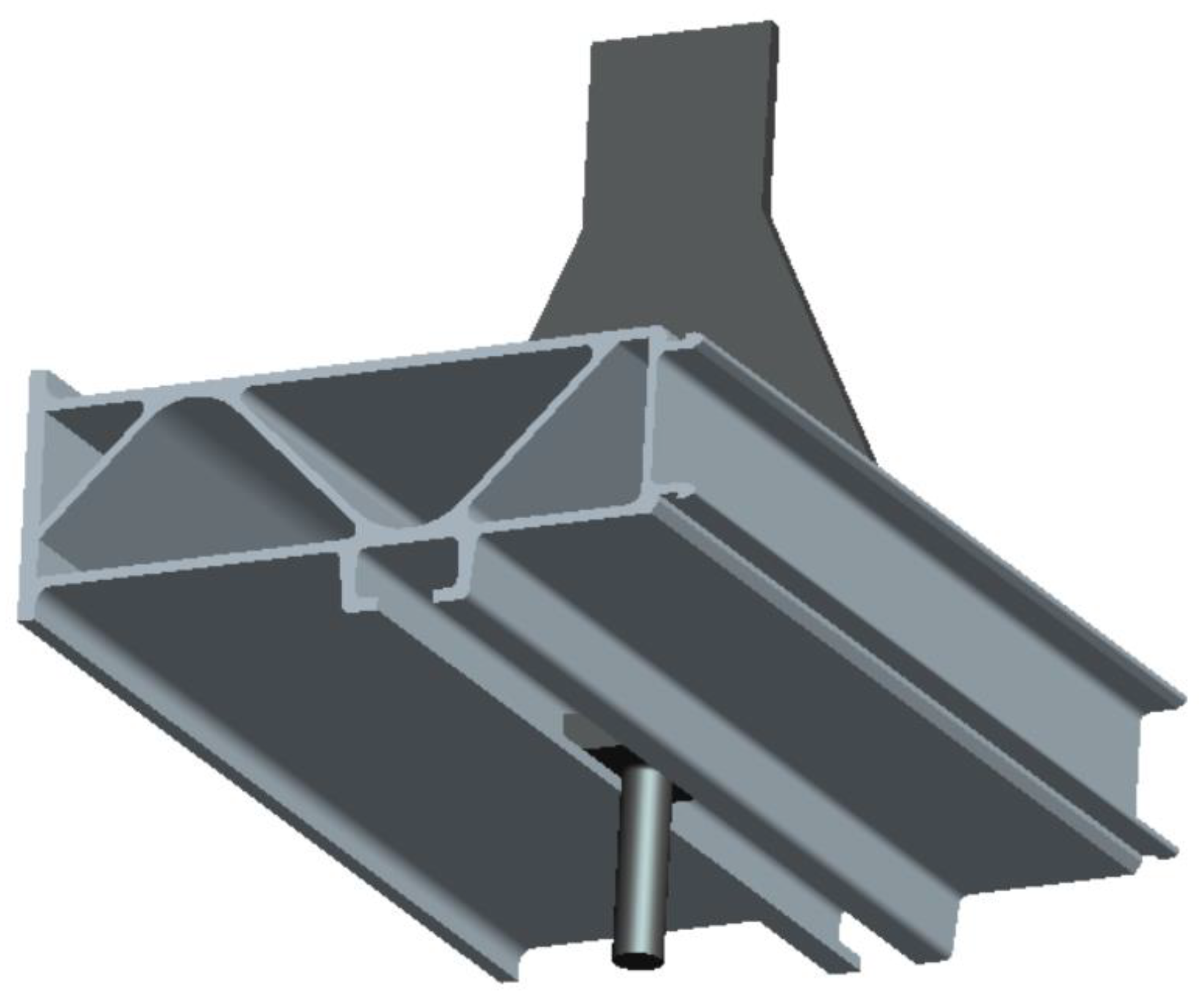
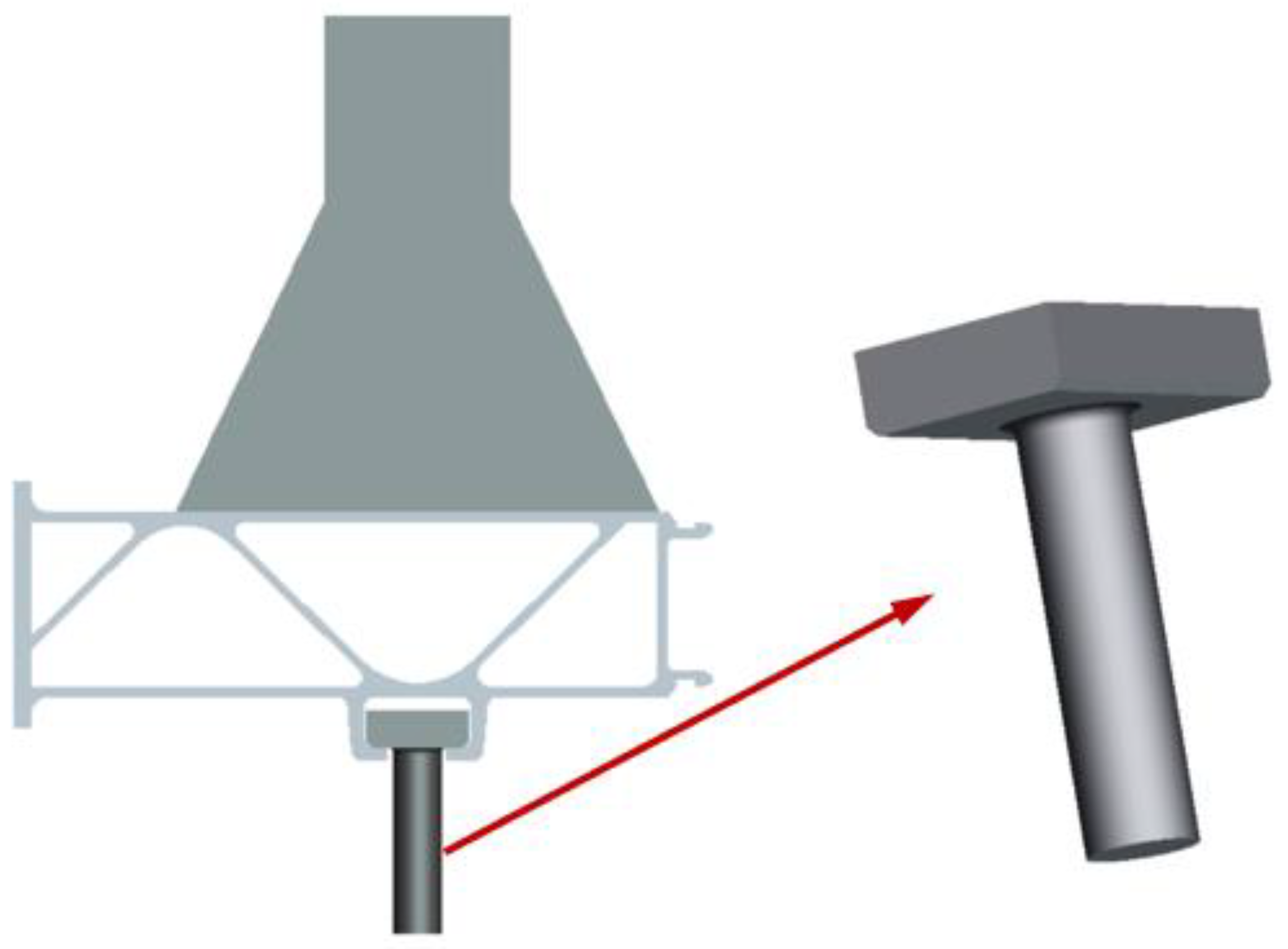





| Material Parameters | Elastic Module (MPa) | Poisson Ratio | Ultimate Tensile Strength (MPa) | Yield Stress (MPa) | Density (t/mm3) |
|---|---|---|---|---|---|
| Value | 70,000 | 0.32 | 255 | 215 | 2.71E-9 |
| Material | Si | Fe | Cu | Mg | Mn | Cr | Zn | Ti | Other | Al |
|---|---|---|---|---|---|---|---|---|---|---|
| 6005A | 0.5 ~ 0.9 | ≤0.35 | ≤0.30 | 0.4 ~ 0.7 | ≤0.50 | ≤0.30 | ≤0.20 | ≤0.10 | ≤0.15 | Balance |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, W.; Wu, N.; Li, H.; Yin, X.; Xie, L. Simulation Analysis and Experimental Study of the Strength of Aluminum Alloy Suspension Structure. Materials 2023, 16, 128. https://doi.org/10.3390/ma16010128
Qian W, Wu N, Li H, Yin X, Xie L. Simulation Analysis and Experimental Study of the Strength of Aluminum Alloy Suspension Structure. Materials. 2023; 16(1):128. https://doi.org/10.3390/ma16010128
Chicago/Turabian StyleQian, Wenxue, Ningxiang Wu, Hao Li, Xiaowei Yin, and Liyang Xie. 2023. "Simulation Analysis and Experimental Study of the Strength of Aluminum Alloy Suspension Structure" Materials 16, no. 1: 128. https://doi.org/10.3390/ma16010128
APA StyleQian, W., Wu, N., Li, H., Yin, X., & Xie, L. (2023). Simulation Analysis and Experimental Study of the Strength of Aluminum Alloy Suspension Structure. Materials, 16(1), 128. https://doi.org/10.3390/ma16010128






