Sub-Surface Analysis of Grinding Burns with Barkhausen Noise Measurements
Abstract
1. Introduction
2. Materials and Methods
2.1. Samples
2.2. Barkhausen Noise Measurements
2.3. Residual Stress Measurements
2.4. Data Pre-Processing
2.5. Data Analysis
- A full model with all the variables was identified.
- F statistics together with p-values were calculated for all model terms.
- The term with the biggest p-value was removed from the model if it was not statistically significant. The α risk for statistical significance was set to 0.05.
- A model without the removed variables was identified and then returned to step 2.
- Steps 2–5 were repeated as long as there were statistically insignificant terms in the model.
3. Results and Discussion
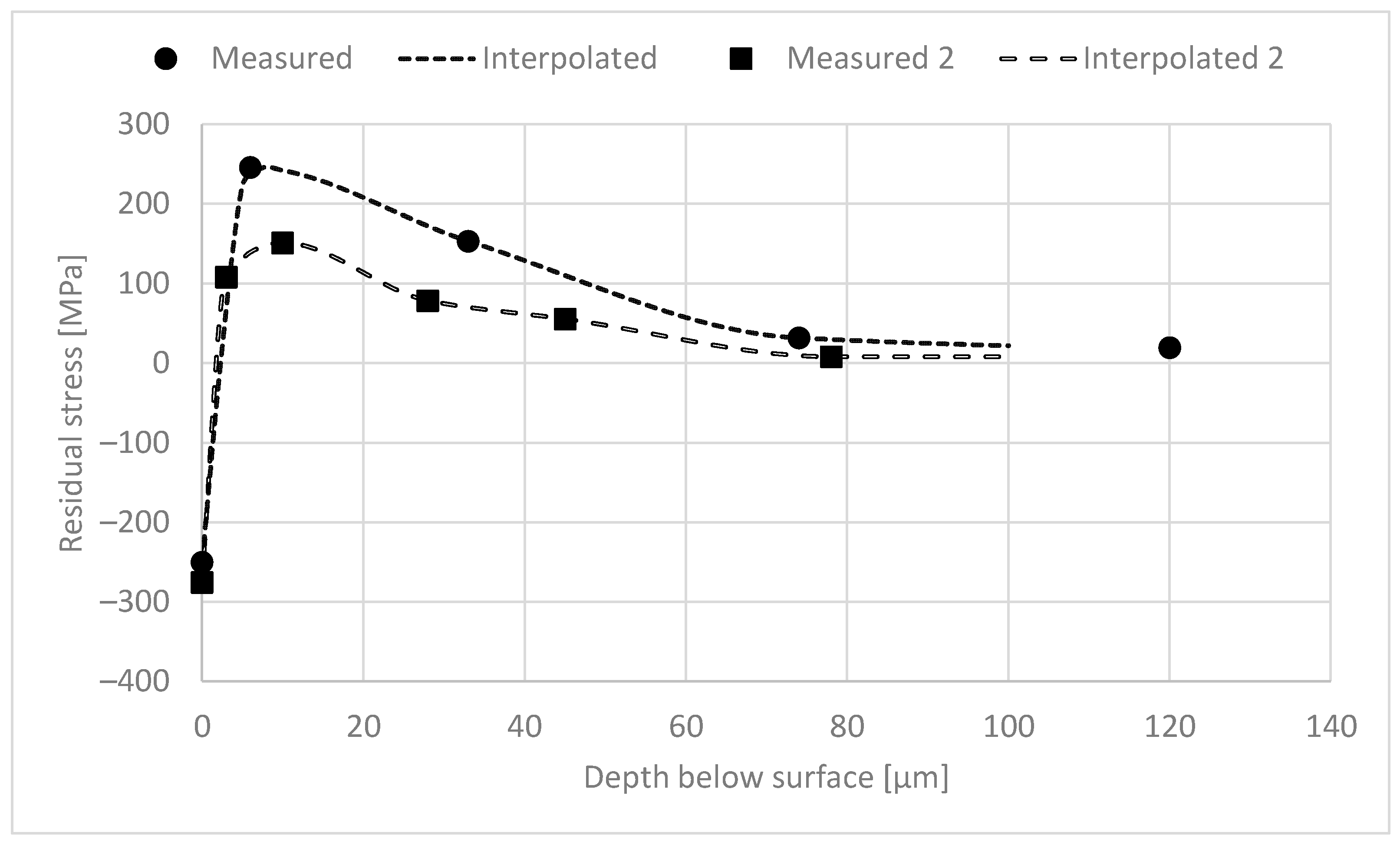
3.1. Analysis of RS as a Function of Depth
3.2. Analysis of XRD FWHM as a Function of Depth
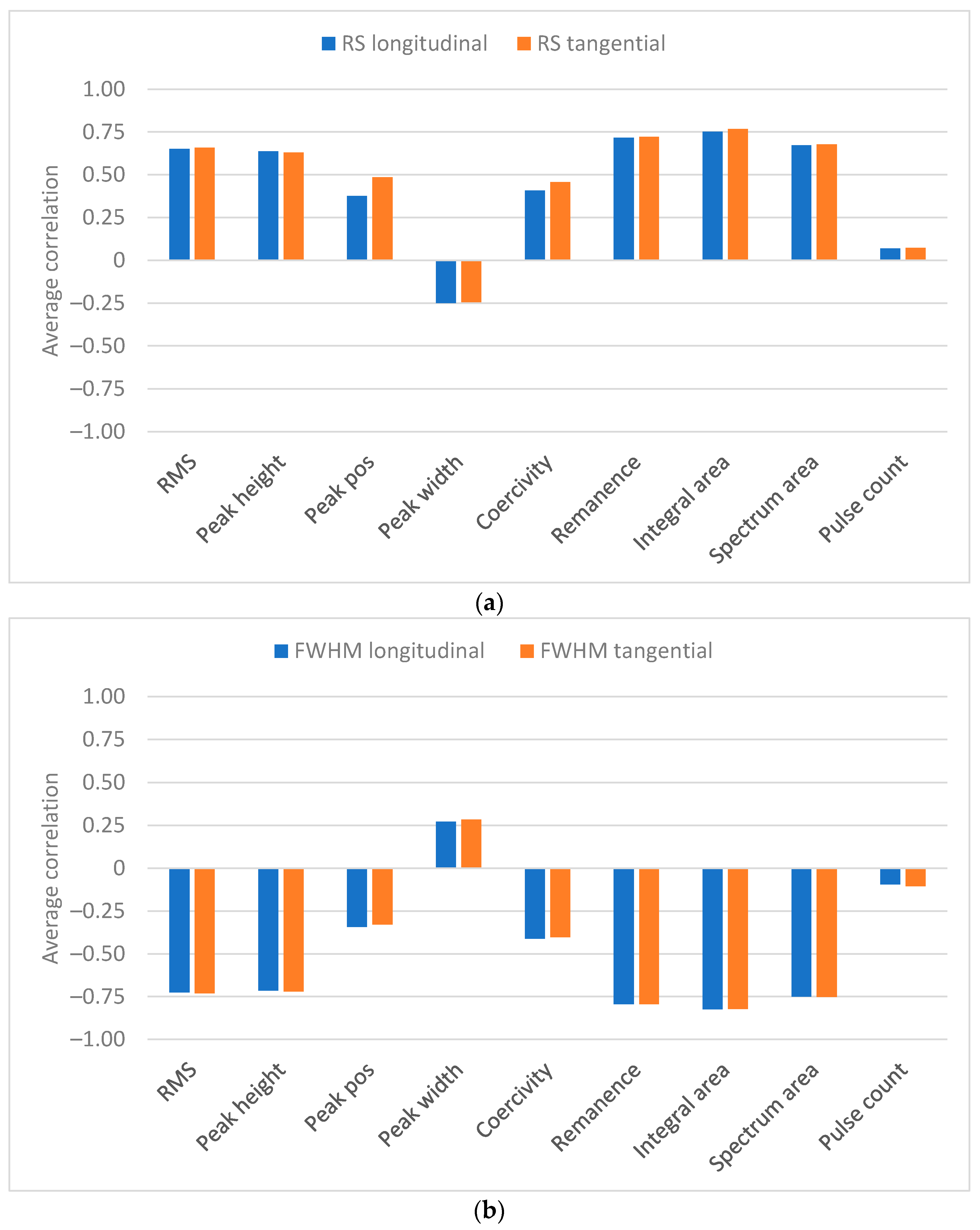
3.3. Analysis of Significant BN Features
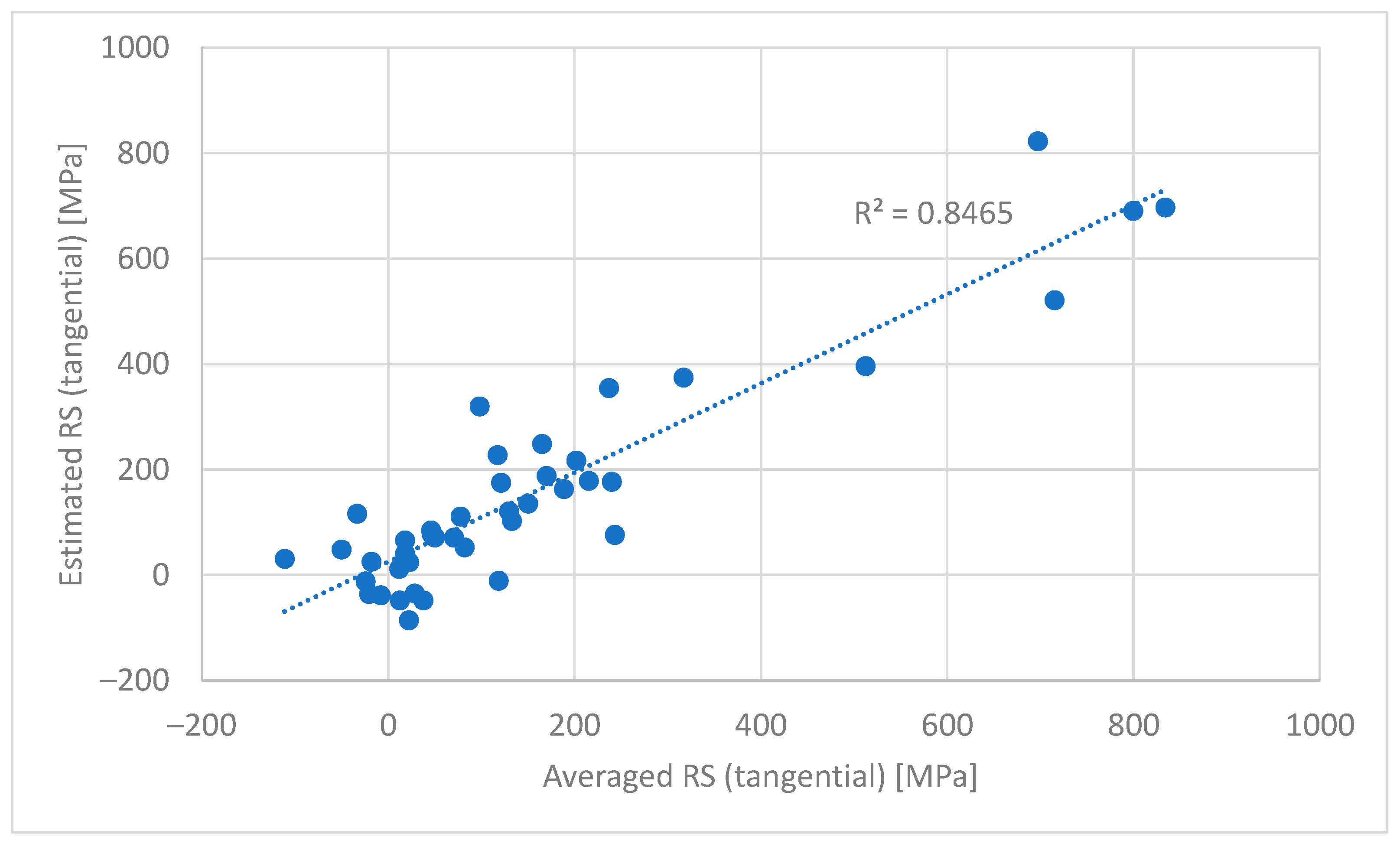
3.4. Estimation of RS in the Sub-Surface Region
4. Conclusions and Further Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Karpuschewski, B.; Inasaki, I. Monitoring systems for grinding processes. In Condition Monitoring and Control for Intelligent Manufacturing; Springer Series in Advanced Manufacturing; Wang, L., Gao, R.X., Eds.; Springer: London, UK, 2006. [Google Scholar]
- Karpuschewski, B.; Beutner, M.; Eckebrecht, J.; Heinzel, J.; Hüsemann, T. Surface integrity aspects in gear manufacturing. Procedia CIRP 2020, 87, 3–12. [Google Scholar] [CrossRef]
- Malkin, S.; Guo, C. Thermal analysis of grinding. Ann. CIRP 2007, 56, 760–782. [Google Scholar] [CrossRef]
- Teixeira, P.H.O.; Rego, R.R.; Pinto, F.W.; Gomes, J.O.; Löpenhas, C. Application of Hall effect for assessing grinding thermal damage. J. Mater. Process. Technol. 2019, 270, 356–364. [Google Scholar] [CrossRef]
- Rowe, B.W. Principles of Modern Grinding Technology; William Andrew Publishing: Norwich, NY, USA, 2009. [Google Scholar]
- Koster, W.P.; Field, M.; Fritz, L.J.; Gatto, L.R.; Kahles, J.F. Surface Integrity of Machined Structural Components; Technical Report AFML-TR-70-11, MMP Project Nr. 721-8; Metcut Research Associates Inc.: Cincinnati, OH, USA, 1970. [Google Scholar]
- Karpuschewski, B.; Bleicher, O.; Beutner, M. Surface integrity inspection on gears using Barkhausen noise analysis. Procedia Eng. 2011, 19, 162–171. [Google Scholar] [CrossRef]
- Sackmann, D.; Heinzel, J.; Karpuschewski, B. An approach for a reliable detection of grinding burn using the Barkhausen noise multi-parameter analysis. Procedia CIRP 2020, 87, 415–419. [Google Scholar] [CrossRef]
- Heinzel, J.; Sackmann, D.; Karpuschewski, B. Micromagnetic analysis of thermally induced influences on surface integrity using the burning limit approach. J. Manuf. Mater. Process 2019, 3, 93. [Google Scholar] [CrossRef]
- Jedamski, R.; Heinzel, J.; Rößler, M.; Epp, J.; Eckebrecht, J.; Gentzen, J.; Putz, M.; Karpuschewski, B. Potential of magnetic Barkhausen noise analysis for in-process monitoring of surface layer properties of steel components in grinding. Tm-Tech. Mess. 2020, 87, 787–798. [Google Scholar] [CrossRef]
- Jedamski, R.; Heinzel, J.; Karpuschewski, B.; Epp, J. In-process measurement of Barkhausen noise for detection of surface integrity during grinding. Appl. Sci. 2022, 12, 4671. [Google Scholar] [CrossRef]
- Stewart, D.M.; Stevens, K.J.; Kaiser, A.B. Magnetic Barkhausen noise analysis of stress in steel. Curr. Appl. Phys. 2004, 4, 308–311. [Google Scholar] [CrossRef]
- Lindgren, M.; Lepistö, T. Estimation of biaxial residual stress in welded steel tubes by Barkhausen noise measurements. Adv. Eng. Mater. 2002, 4, 561–565. [Google Scholar] [CrossRef]
- Kleber, X.; Vincent, A. On the role of residual internal stresses and dislocations on Barkhausen noise in plastically deformed steel. NDT & E Int. 2004, 37, 439–445. [Google Scholar]
- Mierczak, L.; Jiles, D.C.; Fantoni, G. A new method for evaluation of mechanical stress using the reciprocal amplitude of magnetic Barkhausen noise. IEEE Trans. Magn. 2011, 47, 459–465. [Google Scholar] [CrossRef]
- Santa-aho, S.; Vippola, M.; Lepistö, T.; Lindgren, M. Characterisation of case-hardened gear steel by multiparameter Barkhausen noise measurements. Insight 2019, 51, 212–216. [Google Scholar] [CrossRef]
- Santa-aho, S.; Sorsa, A.; Hakanen, M.; Leiviskä, K.; Vippola, M.; Lepistö, T. Barkhausen noise-magnetizing voltage sweep measurement in evaluation of residual stress in hardened components. Meas. Sci. Technol. 2014, 25, 085602. [Google Scholar] [CrossRef]
- SFS-EN 15305:2008; Non-Destructive Testing—Test Method for Residual Stress Analysis by X-ray Diffraction. European Committee for Standardization: Brussels, Belgium, 2008.
- Hauk, V. Structural and Residual Stress Analysis by Nondestructive Methods; Elsevier: Amsterdam, The Netherlands, 1997. [Google Scholar]
- Sackmann, D.; Karpuschewski, B.; Epp, J.; Jedamski, R. Detection of surface damages in ground spur gears by non-destructive micromagnetic methods. Forsch Ing. 2019, 83, 563–570. [Google Scholar] [CrossRef]
- Lu, J. Handbook of Measurement of Residual Stresses; Society for Experimental Mechanics Inc., The Fairmont Press Inc.: Lilburn, GA, USA, 1996. [Google Scholar]
- Vashista, M.; Paul, S. Correlation between full width at half maximum (FWHM) of XRD peak with residual stress on ground surfaces. Philos. Mag. 2012, 92, 4194–4202. [Google Scholar] [CrossRef]
- Lindgren, M.; Lepistö, T. Effect of prestraining on Barkhausen noise vs. stress relation. NDT & E Int. 2001, 34, 37–344. [Google Scholar]
- Jiles, D.C. Dynamics of domain magnetization and the Barkhausen effect. Czechoslov. J. Phys. 2000, 50, 893–924. [Google Scholar] [CrossRef]
- O’Sullivan, D.; Cotterell, M.; Tanner, D.A.; Mészáros, I. Characterisation of ferritic stainless steel by Barkhausen techniques. NDT & E Int. 2004, 37, 489–496. [Google Scholar]
- Moorthy, V.; Vaidyanathan, S.; Laha, K.; Jayakumar, T.; Rao, K.B.S.; Raj, B. Evaluation of microstructures in 2.25Cr-1Mo and 9Cr-1Mo steel weldments using magnetic Barkhausen noise. Mater. Sci. Eng. A 1997, 231, 98–104. [Google Scholar] [CrossRef]
- Davut, K.; Gür, G.H. Monitoring the microstructural changes during tempering of quenched SAE5140 steel by magnetic Barkhausen noise. J. Nondestruct. Eval. 2007, 26, 107–113. [Google Scholar] [CrossRef]
- Cullity, B.D. Introduction to Magnetic Materials; Addison-Wesley Publishing Company: Reading, MA, USA, 1972. [Google Scholar]
- Sorsa, A.; Leiviskä, K.; Santa-aho, S.; Lepistö, T. A data-based modelling scheme for estimating residual stresses from Barkhausen noise measurements. Insight 2012, 54, 278–283. [Google Scholar] [CrossRef]
- Blaow, M.; Evans, J.T.; Shaw, B.A. The effect of microstructure and applied stress on magnetic Barkhausen emission in induction hardened steel. J. Mater. Sci. 2007, 42, 4364–4371. [Google Scholar] [CrossRef]
- Sorsa, A.; Leiviskä, K.; Santa-aho, S.; Lepistö, T. Quantitative prediction of residual stress and hardness in case-hardened steel based on the Barkhausen noise measurement. NDT & E Int. 2012, 46, 100–106. [Google Scholar]
- Tomkowski, R.; Sorsa, A.; Santa-aho, S.; Lundin, P.; Vippola, M. Statistical evaluation of the Barkhausen Noise Testing (BNT) for ground samples. Sensors 2019, 19, 4716. [Google Scholar] [CrossRef]




| Depth below Surface (µm) | BN Features | R2 | RMSE (MPa) |
|---|---|---|---|
| Surface | Peak position, Coercivity, Spectrum area | 0.50 | 139.6 |
| 0–10 | Peak position, Coercivity, Spectrum area | 0.68 | 120.3 |
| 10–20 | Peak position, Coercivity, Integral area | 0.83 | 95.7 |
| 20–30 | RMS value, Peak position, Coercivity, Integral area | 0.85 | 94.2 |
| 30–40 | Peak height, Peak position, Coercivity, Integral area, Spectrum area | 0.84 | 94.7 |
| 40–50 | Peak height, Peak position, Coercivity, Integral area, Spectrum area | 0.82 | 96.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sorsa, A.; Ruusunen, M.; Santa-aho, S.; Vippola, M. Sub-Surface Analysis of Grinding Burns with Barkhausen Noise Measurements. Materials 2023, 16, 159. https://doi.org/10.3390/ma16010159
Sorsa A, Ruusunen M, Santa-aho S, Vippola M. Sub-Surface Analysis of Grinding Burns with Barkhausen Noise Measurements. Materials. 2023; 16(1):159. https://doi.org/10.3390/ma16010159
Chicago/Turabian StyleSorsa, Aki, Mika Ruusunen, Suvi Santa-aho, and Minnamari Vippola. 2023. "Sub-Surface Analysis of Grinding Burns with Barkhausen Noise Measurements" Materials 16, no. 1: 159. https://doi.org/10.3390/ma16010159
APA StyleSorsa, A., Ruusunen, M., Santa-aho, S., & Vippola, M. (2023). Sub-Surface Analysis of Grinding Burns with Barkhausen Noise Measurements. Materials, 16(1), 159. https://doi.org/10.3390/ma16010159







