Metal/Graphene Composites: A Review on the Simulation of Fabrication and Study of Mechanical Properties
Abstract
:1. Introduction
2. Graphene/Metal Composites
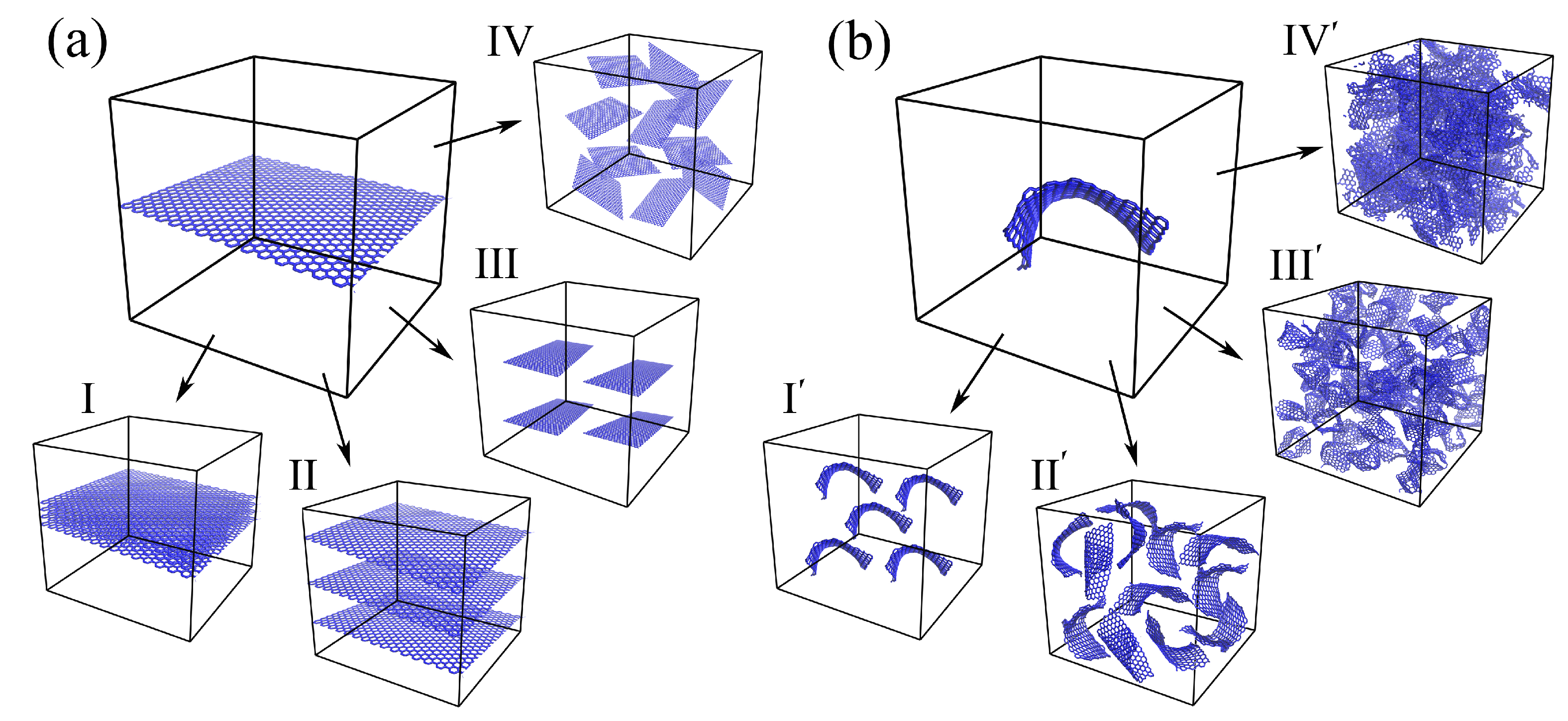
2.1. Morphology of Graphene/Metal Composites
2.2. Interaction between Graphene and Metal
2.3. Mixing of Graphene and Metal Nanoparticles
3. Molecular Dynamics Simulation
3.1. Interatomic Potentials
3.1.1. Lennard–Jones Potential
3.1.2. Morse Potential
3.1.3. Other Potentials
4. Results and Discussion
4.1. Simulation of the Composite Fabrication
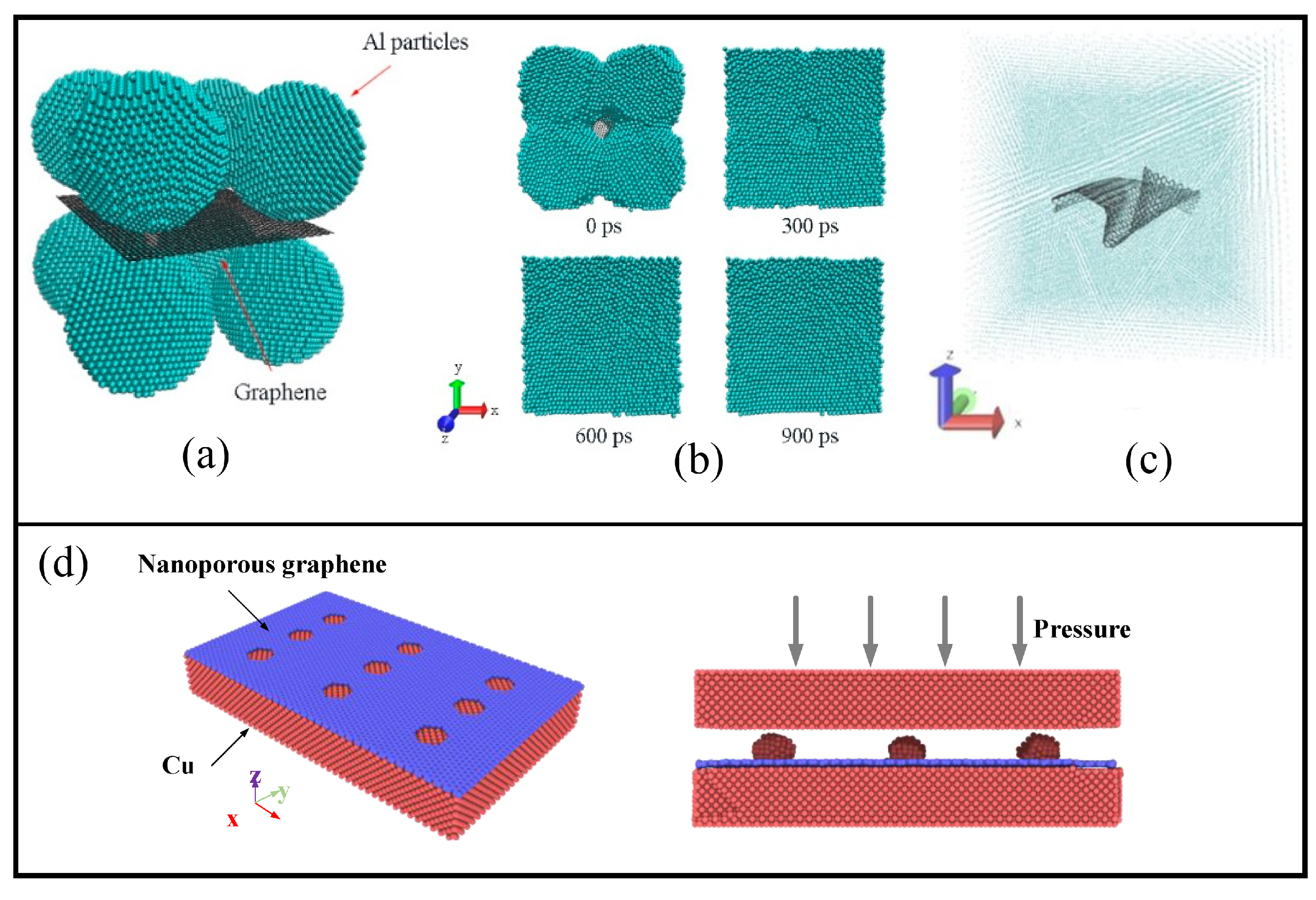
4.1.1. Deposition of Graphene on the Metal Surface
4.1.2. Graphene as the Reinforcement
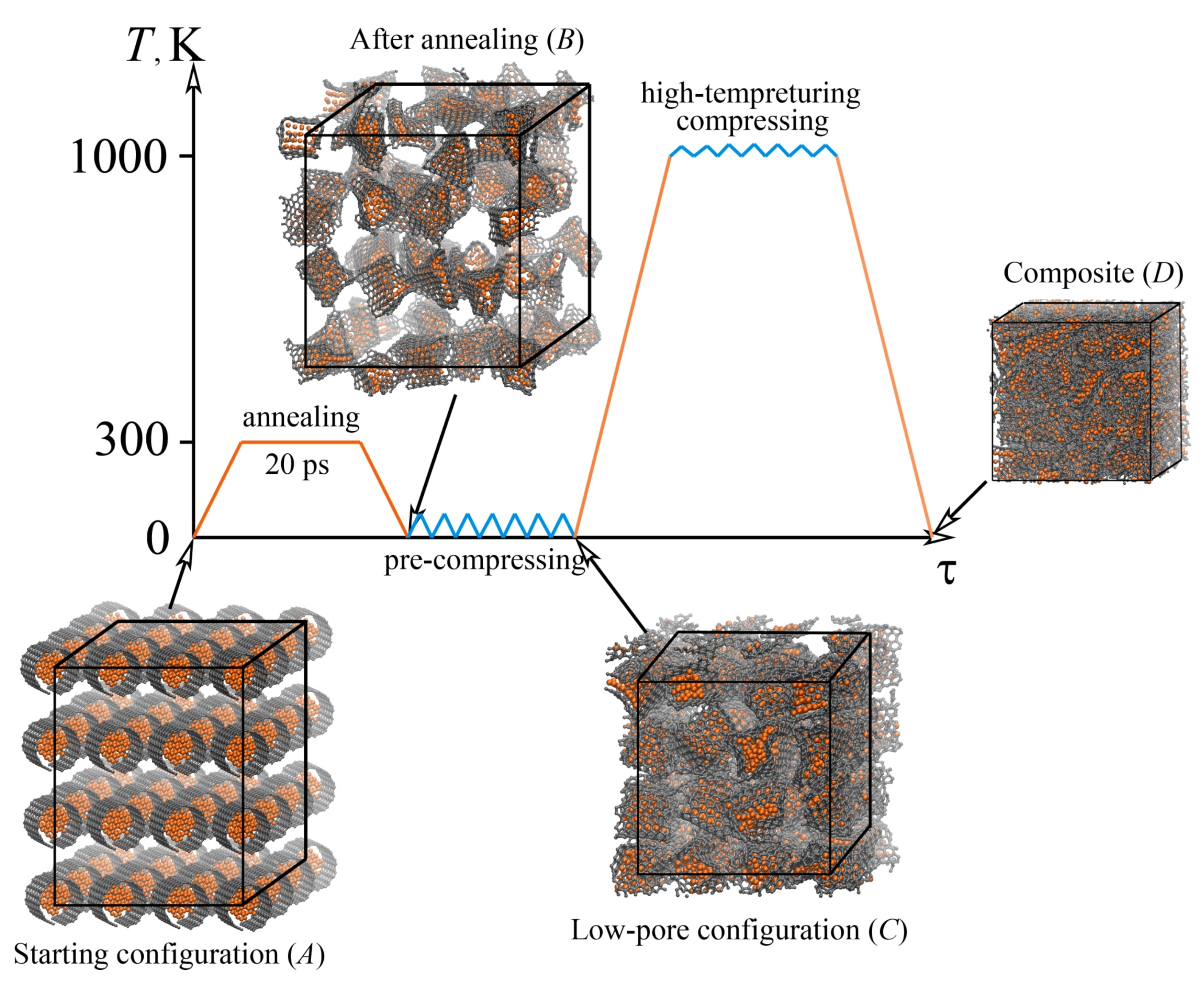
4.1.3. Graphene Network as the Basement for the Composite
4.2. Mechanical Properties
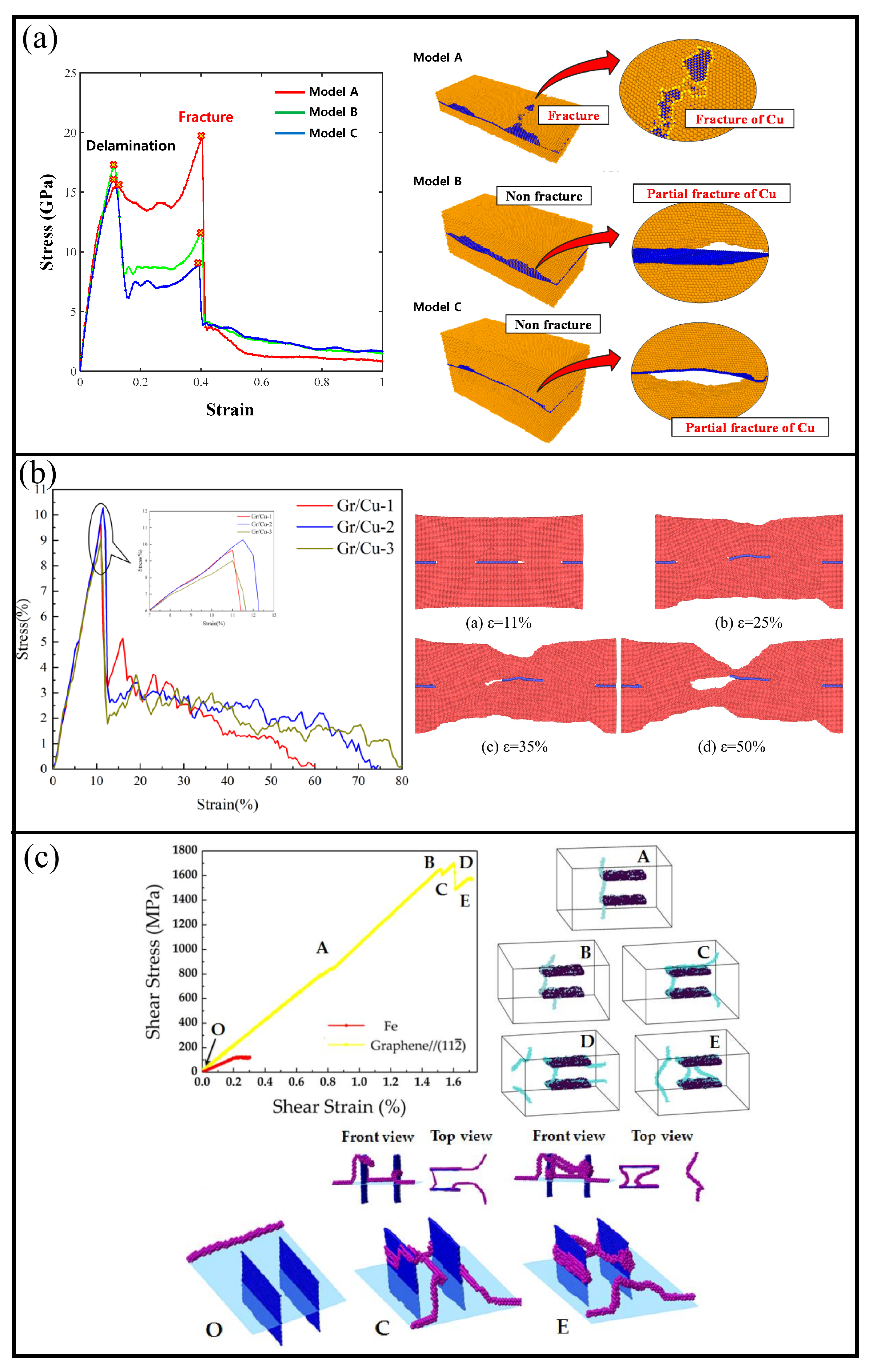
4.2.1. Cu/Graphene Composites
Fe/Graphene Composites
Ni/Graphene Composites
Al/Graphene Composites
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MMCs | metal matrix composites |
| CNTs | carbon nanotubes |
| 2D | two-dimensional |
| 3D | three-dimensional |
| rGO | reduced graphene oxide |
| MD | molecular dynamics |
| CG | crumpled graphene |
| vdW | van der Waals |
| LJ | Lennard–Jones |
| f.c.c. | face-centered cubic |
| h.c.p. | hexagonal close packed |
References
- Ramanathan, A.; Krishnan, P.K.; Muraliraja, R. A review on the production of metal matrix composites through stir casting—Furnace design, properties, challenges, and research opportunities. J. Manuf. Processes 2019, 42, 213–245. [Google Scholar] [CrossRef]
- Bakshi, S.R.; Lahiri, D.; Agarwal, A. Carbon nanotube reinforced metal matrix composites—A review. Int. Mater. Rev. 2010, 55, 41–64. [Google Scholar] [CrossRef]
- Hu, Z.; Tong, G.; Lin, D.; Chen, C.; Guo, H.; Xu, J.; Zhou, L. Graphene-reinforced metal matrix nanocomposites—A review. Mater. Sci. Technol. 2016, 32, 930–953. [Google Scholar] [CrossRef]
- Savina, J.; Raghavendra, B.; Rangappa, D. Experimental investigation on mechanical and tribological behaviour of surfactant coated multi-walled carbon nano tubes reinforced aluminium 6065-silicon metal matrix composite. Lett. Mater. 2021, 11, 73–78. [Google Scholar] [CrossRef]
- Wang, J.; Li, Z.; Fan, G.; Pan, H.; Chen, Z.; Zhang, D. Reinforcement with graphene nanosheets in aluminum matrix composites. Scr. Mater. 2012, 66, 594–597. [Google Scholar] [CrossRef] [Green Version]
- Chu, K.; Jia, C. Enhanced strength in bulk graphene-copper composites. Phys. Status Solidi A 2013, 211, 184–190. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, Q.; Gao, L.; Ma, T.; Qiu, M.; Hu, Y.; Wang, H.; Luo, J. A molecular dynamics study of lubricating mechanism of graphene nanoflakes embedded in Cu-based nanocomposite. Appl. Surf. Sci. 2020, 511, 145620. [Google Scholar] [CrossRef]
- Zhang, C.; Lu, C.; Pei, L.; Li, J.; Wang, R. The wrinkling and buckling of graphene induced by nanotwinned copper matrix: A molecular dynamics study. Nano Mater. Sci. 2021, 3, 95–103. [Google Scholar] [CrossRef]
- Kurapova, O.; Smirnov, I.; Solovyeva, E.; Archakov, I.; Konakov, V. The effect of reduced graphene oxide (rGO) and thermally exfoliated graphite (TEFG) on the mechanical properties of “nickel-graphene” composites. Lett. Mater. 2020, 10, 164–169. [Google Scholar] [CrossRef]
- Yang, M.; Weng, L.; Zhu, H.; Fan, T.; Zhang, D. Simultaneously enhancing the strength, ductility and conductivity of copper matrix composites with graphene nanoribbons. Carbon 2017, 118, 250–260. [Google Scholar] [CrossRef]
- Sangiovanni, D.G.; Faccio, R.; Gueorguiev, G.K.; Kakanakova-Georgieva, A. Discovering atomistic pathways for supply of metal atoms from methyl-based precursors to graphene surface. Phys. Chem. Chem. Phys. 2023, 25, 829–837. [Google Scholar] [CrossRef] [PubMed]
- Song, S.M.; Cho, B.J. Investigation of interaction between graphene and dielectrics. Nanotechnology 2010, 21, 335706. [Google Scholar] [CrossRef] [PubMed]
- Song, X.; Chen, M.; Zhang, J.; Zhang, R.; Zhang, W. Study on Nanoporous Graphene-Based Hybrid Architecture for Surface Bonding. Nanomaterials 2022, 12, 2483. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, N.; Li, W.; Niu, L.; Li, Z. Atomistic Study on the Sintering Process and the Strengthening Mechanism of Al-Graphene System. Materials 2022, 15, 2644. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Guo, Q.; Li, Z.; Fan, G.; Xiong, D.B.; Su, Y.; Zhang, J.; Zhang, D. Enhanced Mechanical Properties of Graphene (Reduced Graphene Oxide)/Aluminum Composites with a Bioinspired Nanolaminated Structure. Nano Lett. 2015, 15, 8077–8083. [Google Scholar] [CrossRef]
- Safina, L.; Baimova, J.; Krylova, K.; Murzaev, R.; Mulyukov, R. Simulation of metal-graphene composites by molecular dynamics: A review. Lett. Mater. 2020, 10, 351–360. [Google Scholar] [CrossRef]
- Safina, L.R.; Krylova, K.A.; Murzaev, R.T.; Baimova, J.A.; Mulyukov, R.R. Crumpled Graphene-Storage Media for Hydrogen and Metal Nanoclusters. Materials 2021, 14, 2098. [Google Scholar] [CrossRef]
- Krylova, K.A.; Safina, L.R.; Murzaev, R.T.; Baimova, J.A.; Mulyukov, R.R. Effect of Nanoparticle Size on the Mechanical Strength of Ni–Graphene Composites. Materials 2021, 14, 3087. [Google Scholar] [CrossRef]
- Krylova, K.A.; Safina, L.R.; Shcherbinin, S.A.; Baimova, J.A. Methodologyfor Molecular Dynamics Simulation of Plastic Deformation of a Nickel/Graphene Composite. Materials 2022, 15, 4038. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, M.; Du, J.; Zhang, W.; Zhou, S.; Ren, W.; Zhou, Q.; Shi, L. Construction of graphene network in Ni matrix composites: A molecular dynamics study of densification process. Carbon 2022, 191, 55–66. [Google Scholar] [CrossRef]
- Kang, J.; Lim, T.; Jeong, M.H.; Suk, J.W. Graphene Papers with Tailored Pore Structures Fabricated from Crumpled Graphene Spheres. Nanomaterials 2019, 9, 815. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, T.; Zhao, J.; Zhang, J.; Zhang, S.; Li, J.; Li, S.; Li, X.; Zhang, J. Nano-Magnesium Silicate Hydroxide/Crumpled Graphene Balls Composites, a Novel Kind of Lubricating Additive with High Performance for Friction and Wear Reduction. Materials 2020, 13, 3669. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Zhang, F.; Yang, X.; Long, G.; Wu, Y.; Zhang, T.; Leng, K.; Huang, Y.; Ma, Y.; Yu, A.; et al. Porous 3D graphene-based bulk materials with exceptional high surface area and excellent conductivity for supercapacitors. Sci. Rep. 2013, 3, 1408. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carraro, F.; Cattelan, M.; Favaro, M.; Calvillo, L. Aerosol Synthesis of N and N-S Doped and Crumpled Graphene Nanostructures. Nanomaterials 2018, 8, 406. [Google Scholar] [CrossRef] [Green Version]
- Jin, Y.; Kulkarni, A.; Kim, H.U.; Hong, S.; Kim, T. Formation of Crumpled Graphene for Flexible Strain Sensor. In Proceedings of the Eurosensors 2017, Paris, France, 3–6 September 2017. [Google Scholar] [CrossRef] [Green Version]
- Krainyukova, N.V. Capturing Gases in Carbon Honeycomb. J. Low Temp. Phys. 2016, 187, 90–104. [Google Scholar] [CrossRef]
- Brodova, I.; Yolshina, L.; Razorenov, S.; Rasposienko, D.; Petrova, A.; Shirinkina, I.; Shorokhov, E.; Muradymov, R.; Garkushin, G.; Savinykh, A. Effect of Grain Size on the Properties of Aluminum Matrix Composites with Graphene. Metals 2022, 12, 1054. [Google Scholar] [CrossRef]
- Qiu, C.; Su, Y.; Yang, J.; Chen, B.; Ouyang, Q.; Zhang, D. Structural modeling and mechanical behaviors of graphene/carbon nanotubes reinforced metal matrix composites via atomic-scale simulations: A review. Compos. Part C Open Access 2021, 4, 100120. [Google Scholar] [CrossRef]
- Elliott, J.A.; Shibuta, Y.; Amara, H.; Bichara, C.; Neyts, E.C. Atomistic modeling of CVD synthesis of carbon nanotubes and graphene. Nanoscale 2013, 5, 6662. [Google Scholar] [CrossRef] [Green Version]
- Wu, Q.; Cai, P.; Long, L. Effect of Content and Size of Reinforcements on the Grain Evolution of Graphene-Reinforced Aluminum Matrix Composites. Nanomaterials 2021, 11, 2550. [Google Scholar] [CrossRef]
- Bi, S.; Liu, Z.; Xiao, B.; Zan, Y.; Wang, D.; Wang, Q.; Ma, Z. Enhancing strength-ductility synergy of carbon nanotube/7055Al composite via a texture design by hot-rolling. Mater. Sci. Eng. A 2021, 806, 140830. [Google Scholar] [CrossRef]
- Dong, S.; Zhou, J.; Hui, D.; Wang, Y.; Zhang, S. Size dependent strengthening mechanisms in carbon nanotube reinforced metal matrix composites. Compos. Part A Appl. Sci. Manuf. 2015, 68, 356–364. [Google Scholar] [CrossRef]
- Batzill, M. The surface science of graphene: Metal interfaces, CVD synthesis, nanoribbons, chemical modifications, and defects. Surf. Sci. Rep. 2012, 67, 83–115. [Google Scholar] [CrossRef]
- Giovannetti, G.; Khomyakov, P.A.; Brocks, G.; Karpan, V.M.; van den Brink, J.; Kelly, P.J. Doping Graphene with Metal Contacts. Phys. Rev. Lett. 2008, 101, 026803. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Buehler, M.J. Interface structure and mechanics between graphene and metal substrates: A first-principles study. J. Phys. Condens. Matter 2010, 22, 485301. [Google Scholar] [CrossRef] [PubMed]
- Choi, W.Y.; Kang, J.W.; Hwang, H.J. Structures of ultrathin copper nanowires encapsulated in carbon nanotubes. Phys. Rev. B 2003, 68, 193405. [Google Scholar] [CrossRef]
- Fang, T.H.; Weng, C.I.; Chang, J.G. Molecular dynamics simulation of nano-lithography process using atomic force microscopy. Surf. Sci. 2002, 501, 138–147. [Google Scholar] [CrossRef]
- He, R.; Zhao, L.; Petrone, N.; Kim, K.S.; Roth, M.; Hone, J.; Kim, P.; Pasupathy, A.; Pinczuk, A. Large Physisorption Strain in Chemical Vapor Deposition of Graphene on Copper Substrates. Nano Lett. 2012, 12, 2408–2413. [Google Scholar] [CrossRef] [Green Version]
- Hong, Y.; Li, L.; Zeng, X.C.; Zhang, J. Tuning thermal contact conductance at graphene–copper interface via surface nanoengineering. Nanoscale 2015, 7, 6286–6294. [Google Scholar] [CrossRef] [Green Version]
- Bardotti, L.; Jensen, P.; Hoareau, A.; Treilleux, M.; Cabaud, B. Experimental Observation of Fast Diffusion of Large Antimony Clusters on Graphite Surfaces. Phys. Rev. Lett. 1995, 74, 4694–4697. [Google Scholar] [CrossRef]
- Karpan, V.M.; Giovannetti, G.; Khomyakov, P.A.; Talanana, M.; Starikov, A.A.; Zwierzycki, M.; van den Brink, J.; Brocks, G.; Kelly, P.J. Graphite and Graphene as Perfect Spin Filters. Phys. Rev. Lett. 2007, 99, 176602. [Google Scholar] [CrossRef] [Green Version]
- Bartolucci, S.F.; Paras, J.; Rafiee, M.A.; Rafiee, J.; Lee, S.; Kapoor, D.; Koratkar, N. Graphene–aluminum nanocomposites. Mater. Sci. Eng. A 2011, 528, 7933–7937. [Google Scholar] [CrossRef]
- Saboori, A.; Pavese, M.; Badini, C.; Fino, P. Microstructure and Thermal Conductivity of Al–Graphene Composites Fabricated by Powder Metallurgy and Hot Rolling Techniques. Acta Metall. Sin. Engl. Lett. 2017, 30, 675–687. [Google Scholar] [CrossRef]
- Chen, F.; Gupta, N.; Behera, R.K.; Rohatgi, P.K. Graphene-Reinforced Aluminum Matrix Composites: A Review of Synthesis Methods and Properties. JOM 2018, 70, 837–845. [Google Scholar] [CrossRef]
- Nieto, A.; Bisht, A.; Lahiri, D.; Zhang, C.; Agarwal, A. Graphene reinforced metal and ceramic matrix composites: A review. Int. Mater. Rev. 2016, 62, 241–302. [Google Scholar] [CrossRef]
- Kim, Y.; Lee, J.; Yeom, M.S.; Shin, J.W.; Kim, H.; Cui, Y.; Kysar, J.W.; Hone, J.; Jung, Y.; Jeon, S.; et al. Strengthening effect of single-atomic-layer graphene in metal–graphene nanolayered composites. Nat. Commun. 2013, 4, 2114. [Google Scholar] [CrossRef] [Green Version]
- Ivanov, V.; Nagy, J.; Lambin, P.; Lucas, A.; Zhang, X.; Zhang, X.; Bernaerts, D.; Tendeloo, G.V.; Amelinckx, S.; Landuyt, J.V. The study of carbon nanotubules produced by catalytic method. Chem. Phys. Lett. 1994, 223, 329–335. [Google Scholar] [CrossRef]
- Hwang, H.J.; Kwon, O.K.; Kang, J.W. Copper nanocluster diffusion in carbon nanotube. Solid State Commun. 2004, 129, 687–690. [Google Scholar] [CrossRef]
- Katin, K.P.; Prudkovskiy, V.S.; Maslov, M.M. Molecular dynamics simulation of nickel-coated graphene bending. Micro Nano Lett. 2018, 13, 160–164. [Google Scholar] [CrossRef]
- Chang, W.; Rajan, S.; Peng, B.; Ren, C.; Sutton, M.; Li, C. Adhesion energy of as-grown graphene on nickel substrates via StereoDIC-based blister experiments. Carbon 2019, 153, 699–706. [Google Scholar] [CrossRef]
- Das, S.; Lahiri, D.; Lee, D.Y.; Agarwal, A.; Choi, W. Measurements of the adhesion energy of graphene to metallic substrates. Carbon 2013, 59, 121–129. [Google Scholar] [CrossRef]
- Yoon, T.; Shin, W.C.; Kim, T.Y.; Mun, J.H.; Kim, T.S.; Cho, B.J. Direct Measurement of Adhesion Energy of Monolayer Graphene As-Grown on Copper and Its Application to Renewable Transfer Process. Nano Lett. 2012, 12, 1448–1452. [Google Scholar] [CrossRef] [PubMed]
- Moseler, M.; Cervantes-Sodi, F.; Hofmann, S.; Csányi, G.; Ferrari, A.C. Dynamic Catalyst Restructuring during Carbon Nanotube Growth. ACS Nano 2010, 4, 7587–7595. [Google Scholar] [CrossRef]
- Montazeri, A.; Panahi, B. MD-based estimates of enhanced load transfer in graphene/metal nanocomposites through Ni coating. Appl. Surf. Sci. 2018, 457, 1072–1080. [Google Scholar] [CrossRef]
- Sheinerman, A. Modeling of structure and interface controlled strength of laminated metal/graphene composites. Mech. Mater. 2021, 158, 103888. [Google Scholar] [CrossRef]
- Biris, A.R.; Lazar, M.D.; Pruneanu, S.; Neamtu, C.; Watanabe, F.; Kannarpady, G.K.; Dervishi, E.; Biris, A.S. Catalytic one-step synthesis of Pt-decorated few-layer graphenes. RSC Adv. 2013, 3, 26391. [Google Scholar] [CrossRef]
- Samantara, A.K.; Mishra, D.K.; Suryawanshi, S.R.; More, M.A.; Thapa, R.; Late, D.J.; Jena, B.K.; Rout, C.S. Facile synthesis of Ag nanowire–rGO composites and their promising field emission performance. RSC Adv. 2015, 5, 41887–41893. [Google Scholar] [CrossRef]
- Huang, X.; Zhao, G.; Wang, X. Fabrication of reduced graphene oxide/metal (Cu, Ni, Co) nanoparticle hybrid composites via a facile thermal reduction method. RSC Adv. 2015, 5, 49973–49978. [Google Scholar] [CrossRef]
- Wei, D.; Liang, J.; Zhu, Y.; Yuan, Z.; Li, N.; Qian, Y. Formation of Graphene-Wrapped Nanocrystals at Room Temperature through the Colloidal Coagulation Effect. Part. Part. Syst. Charact. 2013, 30, 143–147. [Google Scholar] [CrossRef]
- Wang, H.; Cui, L.F.; Yang, Y.; Casalongue, H.S.; Robinson, J.T.; Liang, Y.; Cui, Y.; Dai, H. Mn3O4-Graphene Hybrid as a High-Capacity Anode Material for Lithium Ion Batteries. J. Am. Chem. Soc. 2010, 132, 13978–13980. [Google Scholar] [CrossRef] [PubMed]
- Yuk, J.M.; Park, J.; Ercius, P.; Kim, K.; Hellebusch, D.J.; Crommie, M.F.; Lee, J.Y.; Zettl, A.; Alivisatos, A.P. High-Resolution EM of Colloidal Nanocrystal Growth Using Graphene Liquid Cells. Science 2012, 336, 61–64. [Google Scholar] [CrossRef]
- Jang, H.D.; Kim, S.K.; Chang, H.; Choi, J.W.; Luo, J.; Huang, J. One-Step Synthesis of Pt-Nanoparticles-Laden Graphene Crumples by Aerosol Spray Pyrolysis and Evaluation of Their Electrocatalytic Activity. Aerosol Sci. Technol. 2013, 47, 93–98. [Google Scholar] [CrossRef]
- Tie, X.; Han, Q.; Liang, C.; Li, B.; Zai, J.; Qian, X. Si@SiOx/Graphene Nanosheets Composite: Ball Milling Synthesis and Enhanced Lithium Storage Performance. Front. Mater. 2018, 4, 47. [Google Scholar] [CrossRef] [Green Version]
- Abazari, S.; Shamsipur, A.; Bakhsheshi-Rad, H.R.; Ramakrishna, S.; Berto, F. Graphene Family Nanomaterial Reinforced Magnesium-Based Matrix Composites for Biomedical Application: A Comprehensive Review. Metals 2020, 10, 1002. [Google Scholar] [CrossRef]
- Pragatheeswaran, A.; Ravi, R.; Bakshi, S.R. Microstructural and morphological changes during ball milling of Copper-Silver-Graphite flake mixtures. Adv. Powder Technol. 2019, 30, 2759–2767. [Google Scholar] [CrossRef]
- Shahin, M.; Munir, K.; Wen, C.; Li, Y. Magnesium-based composites reinforced with graphene nanoplatelets as biodegradable implant materials. J. Alloys Compd. 2020, 828, 154461. [Google Scholar] [CrossRef]
- Huang, S.P.; Mainardi, D.S.; Balbuena, P.B. Structure and dynamics of graphite-supported bimetallic nanoclusters. Surf. Sci. 2003, 545, 163–179. [Google Scholar] [CrossRef]
- Stuart, S.J.; Tutein, A.B.; Harrison, J.A. A reactive potential for hydrocarbons with intermolecular interactions. J. Chem. Phys. 2000, 112, 6472–6486. [Google Scholar] [CrossRef] [Green Version]
- Brenner, D.W.; Shenderova, O.A.; Harrison, J.A.; Stuart, S.J.; Ni, B.; Sinnott, S.B. A second-generation reactive empirical bond order (REBO) potential energy expression for hydrocarbons. J. Phys. Condens. Matter 2002, 14, 783–802. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Zhang, Y.; Zhang, Y.; Kitipornchai, S.; Yang, J. Machine learning assisted prediction of mechanical properties of graphene/aluminium nanocomposite based on molecular dynamics simulation. Mater. Des. 2022, 213, 110334. [Google Scholar] [CrossRef]
- Vardanyan, V.H.; Urbassek, H.M. Dislocation interactions during nanoindentation of nickel-graphene nanocomposites. Comput. Mater. Sci. 2019, 170, 109158. [Google Scholar] [CrossRef]
- Agrawal, A.; Gans, J.S.; Goldfarb, A. Exploring the impact of artificial Intelligence: Prediction versus judgment. Inf. Econ. Policy 2019, 47, 1–6. [Google Scholar] [CrossRef]
- Galashev, A.Y.; Katin, K.P.; Maslov, M.M. Morse parameters for the interaction of metals with graphene and silicene. Phys. Lett. A 2019, 383, 252–258. [Google Scholar] [CrossRef]
- Bashirvand, S.; Montazeri, A. New aspects on the metal reinforcement by carbon nanofillers: A molecular dynamics study. Mater. Des. 2016, 91, 306–313. [Google Scholar] [CrossRef]
- Chang, S.W.; Nair, A.K.; Buehler, M.J. Geometry and temperature effects of the interfacial thermal conductance in copper– and nickel–graphene nanocomposites. J. Phys. Condens. Matter 2012, 24, 245301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guo, Y.; Guo, W. Structural transformation of partially confined copper nanowires inside defected carbon nanotubes. Nanotechnology 2006, 17, 4726–4730. [Google Scholar] [CrossRef] [PubMed]
- Arcidiacono, S.; Walther, J.H.; Poulikakos, D.; Passerone, D.; Koumoutsakos, P. Solidification of Gold Nanoparticles in Carbon Nanotubes. Phys. Rev. Lett. 2005, 94, 105502. [Google Scholar] [CrossRef] [Green Version]
- Lewis, L.J.; Jensen, P.; Combe, N.; Barrat, J.L. Diffusion of gold nanoclusters on graphite. Phys. Rev. B 2000, 61, 16084–16090. [Google Scholar] [CrossRef] [Green Version]
- Shuang, F.; Aifantis, K.E. Dislocation-graphene interactions in Cu/graphene composites and the effect of boundary conditions: A molecular dynamics study. Carbon 2021, 172, 50–70. [Google Scholar] [CrossRef]
- Wang, X.; Wang, X.; Wang, Z.; Guo, Y.; Wang, Y. Enhancing mechanism of interfacial metal element on the thermal transport across Cu-graphene interfaces revealed by molecular dynamics simulations. Mater. Today Commun. 2020, 25, 101431. [Google Scholar] [CrossRef]
- Zhang, S.; Huang, P.; Wang, F. Graphene-boundary strengthening mechanism in Cu/graphene nanocomposites: A molecular dynamics simulation. Mater. Des. 2020, 190, 108555. [Google Scholar] [CrossRef]
- Yoon, B.; Luedtke, W.D.; Gao, J.; Landman, U. Diffusion of Gold Clusters on Defective Graphite Surfaces. J. Phys. Chem. B 2003, 107, 5882–5891. [Google Scholar] [CrossRef]
- Luedtke, W.D.; Landman, U. Slip Diffusion and Lévy Flights of an Adsorbed Gold Nanocluster. Phys. Rev. Lett. 1999, 82, 3835–3838. [Google Scholar] [CrossRef] [Green Version]
- Toprak, K.; Bayazitoglu, Y. Numerical modeling of a CNT–Cu coaxial nanowire in a vacuum to determine the thermal conductivity. Int. J. Heat Mass Transf. 2013, 61, 172–175. [Google Scholar] [CrossRef]
- Long, X.; Li, B.; Wang, L.; Huang, J.; Zhu, J.; Luo, S. Shock response of Cu/graphene nanolayered composites. Carbon 2016, 103, 457–463. [Google Scholar] [CrossRef]
- Shang, H.; Wang, W. Shock responses of graphene reinforced composites via molecular dynamics simulations. J. Phys. Conf. Ser. 2014, 500, 112059. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Wang, F.; Wu, H.; Wang, W. Strengthening metal nanolaminates under shock compression through dual effect of strong and weak graphene interface. Appl. Phys. Lett. 2014, 104, 231901. [Google Scholar] [CrossRef]
- Han, Y.; Li, R.; Ge, Y.; Dong, J. Growth of single-walled Ag and Cu nanotubes confined in carbon nanotubes, studied by molecular dynamics simulations. J. Appl. Phys. 2013, 113, 234303. [Google Scholar] [CrossRef]
- Weng, S.; Ning, H.; Fu, T.; Hu, N.; Zhao, Y.; Huang, C.; Peng, X. Molecular dynamics study of strengthening mechanism of nanolaminated graphene/Cu composites under compression. Sci. Rep. 2018, 8, 3089. [Google Scholar] [CrossRef] [Green Version]
- Huang, H.; Tang, X.; Chen, F.; Yang, Y.; Liu, J.; Li, H.; Chen, D. Radiation damage resistance and interface stability of copper–graphene nanolayered composite. J. Nucl. Mater. 2015, 460, 16–22. [Google Scholar] [CrossRef]
- Guo, S.J.; Yang, Q.S.; He, X.; Liew, K. Modeling of interface cracking in copper–graphite composites by MD and CFE method. Compos. Part B Eng. 2014, 58, 586–592. [Google Scholar] [CrossRef]
- Zhang, C.; Lu, C.; Pei, L.; Li, J.; Wang, R. The structural rearrangement with secondary reinforcement in graphene/nanotwinned copper nanocomposites: A molecular dynamics study. Compos. Part B Eng. 2020, 182, 107610. [Google Scholar] [CrossRef]
- Duan, K.; Li, L.; Hu, Y.; Wang, X. Interface mechanical properties of graphene reinforced copper nanocomposites. Mater. Res. Express 2017, 4, 115020. [Google Scholar] [CrossRef]
- He, Y.; Huang, F.; Li, H.; Sui, Y.; Wei, F.; Meng, Q.; Yang, W.; Qi, J. Tensile mechanical properties of nano-layered copper/graphene composite. Phys. E Low-Dimens. Syst. Nanostruct. 2017, 87, 233–236. [Google Scholar] [CrossRef]
- Yan, Y.; Zhou, S.; Liu, S. Atomistic simulation on nanomechanical response of indented graphene/nickel system. Comput. Mater. Sci. 2017, 130, 16–20. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, D.; Lu, Z.; Hu, W. Atomistic simulation on the plastic deformation and fracture of bio-inspired graphene/Ni nanocomposites. Appl. Phys. Lett. 2016, 109, 191909. [Google Scholar] [CrossRef]
- Rezaei, R.; Deng, C.; Tavakoli-Anbaran, H.; Shariati, M. Deformation twinning-mediated pseudoelasticity in metal–graphene nanolayered membrane. Philos. Mag. Lett. 2016, 96, 322–329. [Google Scholar] [CrossRef]
- Zhang, L.; Zhu, Y.; Teng, W.; Xia, T.; Rong, Y.; Li, N.; Ma, H. A molecular dynamics simulation of the graphene growth on Cu(1 1 1) surface. Comput. Mater. Sci. 2017, 130, 10–15. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, Y.; Yang, J.; Kitipornchai, S. Folded graphene reinforced nanocomposites with superior strength and toughness: A molecular dynamics study. J. Mater. Sci. Technol. 2022, 120, 196–204. [Google Scholar] [CrossRef]
- Gan, X.; Hu, W.; Fei, L.; Zhou, N. Atomic mechanism for the transformation of amorphous carbon film to graphene on Cu substrate. Comput. Mater. Sci. 2022, 203, 111145. [Google Scholar] [CrossRef]
- Peng, W.; Sun, K. Interface structures and dislocation nucleation of Cu/graphene interface via molecular dynamic simulations. Materialia 2021, 18, 101131. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, Y.; Yang, J.; Kitipornchai, S. Significantly improved interfacial shear strength in graphene/copper nanocomposite via wrinkles and functionalization: A molecular dynamics study. Carbon 2021, 174, 335–344. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, F.; Huang, P. Enhanced Hall-Petch strengthening in graphene/Cu nanocomposites. J. Mater. Sci. Technol. 2021, 87, 176–183. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, X.; Zhang, Y.; Ren, Q.; Jin, Y.; Zhao, P. Inherent strains in chemical-vapor-deposited bilayer graphene on Cu. Carbon 2021, 184, 109–114. [Google Scholar] [CrossRef]
- Zhang, C.; Godbole, A.; Michal, G.; Lu, C. High shock resistance and self-healing ability of graphene/nanotwinned Cu nanolayered composites. J. Alloys Compd. 2021, 860, 158435. [Google Scholar] [CrossRef]
- Hou, B.; Liu, P.; Wang, A.; Xie, J. Interface optimization strategy for enhancing the mechanical and thermal properties of aligned graphene/Al composite. J. Alloys Compd. 2022, 900, 163555. [Google Scholar] [CrossRef]
- Wang, L.; Jin, J.; Yang, P.; Li, S.; Tang, S.; Zong, Y.; Peng, Q. Effect of interfacial bonding on dislocation strengthening in graphene nanosheet reinforced iron composite: A molecular dynamics study. Comput. Mater. Sci. 2021, 191, 110309. [Google Scholar] [CrossRef]
- Shuang, F.; Aifantis, K.E. modeling dislocation-graphene interactions in a BCC Fe matrix by molecular dynamics simulations and gradient plasticity theory. Appl. Surf. Sci. 2021, 535, 147602. [Google Scholar] [CrossRef]
- Peng, W.; Sun, K. Effects of Cu/graphene interface on the mechanical properties of multilayer Cu/graphene composites. Mech. Mater. 2020, 141, 103270. [Google Scholar] [CrossRef]
- Zhu, J.Q.; Liu, X.; Yang, Q.S. Dislocation-blocking mechanism for the strengthening and toughening of laminated graphene/Al composites. Comput. Mater. Sci. 2019, 160, 72–81. [Google Scholar] [CrossRef]
- Rong, Y.; He, H.; Zhang, L.; Li, N.; Zhu, Y. Molecular dynamics studies on the strengthening mechanism of Al matrix composites reinforced by grapnene nanoplatelets. Comput. Mater. Sci. 2018, 153, 48–56. [Google Scholar] [CrossRef]
- Silvestre, N.; Faria, B.; Lopes, J.N.C. Compressive behavior of CNT-reinforced aluminum composites using molecular dynamics. Compos. Sci. Technol. 2014, 90, 16–24. [Google Scholar] [CrossRef]
- Choi, B.K.; Yoon, G.H.; Lee, S. Molecular dynamics studies of CNT-reinforced aluminum composites under uniaxial tensile loading. Compos. Part B Eng. 2016, 91, 119–125. [Google Scholar] [CrossRef]
- Huang, Y.; Yang, Z.; Lu, Z. Nanoindentation of bio-inspired graphene/nickel nanocomposites: A molecular dynamics simulation. Comput. Mater. Sci. 2021, 186, 109969. [Google Scholar] [CrossRef]
- Yan, Y.; Lei, Y.; Liu, S. Tensile responses of carbon nanotubes-reinforced copper nanocomposites: Molecular dynamics simulation. Comput. Mater. Sci. 2018, 151, 273–277. [Google Scholar] [CrossRef]
- Shibuta, Y.; Maruyama, S. Bond-order potential for transition metal carbide cluster for the growth simulation of a single-walled carbon nanotube. Comput. Mater. Sci. 2007, 39, 842–848. [Google Scholar] [CrossRef]
- Barcaro, G.; Zhu, B.; Hou, M.; Fortunelli, A. Growth of carbon clusters on a Ni(111) surface. Comput. Mater. Sci. 2012, 63, 303–311. [Google Scholar] [CrossRef]
- Wang, X.; Xiao, W.; Wang, J.; Sun, L.; Shi, J.; Guo, H.; Liu, Y.; Wang, L. Enhanced interfacial strength of graphene reinforced aluminum composites via X (Cu, Ni, Ti)-coating: Molecular-dynamics insights. Adv. Powder Technol. 2021, 32, 2585–2590. [Google Scholar] [CrossRef]
- Fang, T.H.; Wu, J.H. Molecular dynamics simulations on nanoindentation mechanisms of multilayered films. Comput. Mater. Sci. 2008, 43, 785–790. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhang, Y.C.; Qi, S.H.; Xiang, Z. Molecular Dynamics Study on the Impact of the Cutting Depth to the Titanium Nanometric Cutting. Appl. Mech. Mater. 2014, 536–537, 1431–1434. [Google Scholar] [CrossRef]
- Gao, F.; Qu, J.; Yao, M. Interfacial thermal resistance between metallic carbon nanotube and Cu substrate. J. Appl. Phys. 2011, 110, 124314. [Google Scholar] [CrossRef] [Green Version]
- Pei, Q.; Lu, C.; Fang, F.; Wu, H. Nanometric cutting of copper: A molecular dynamics study. Comput. Mater. Sci. 2006, 37, 434–441. [Google Scholar] [CrossRef]
- Fang, T.H.; Chang, W.J.; Weng, C.I. Nanoindentation and nanomachining characteristics of gold and platinum thin films. Mater. Sci. Eng. A 2006, 430, 332–340. [Google Scholar] [CrossRef]
- Tsai, P.C.; Jeng, Y.R. Coalescence and epitaxial self-assembly of Cu nanoparticles on graphene surface: A molecular dynamics study. Comput. Mater. Sci. 2019, 156, 104–110. [Google Scholar] [CrossRef]
- Han, R.; Song, H.; Wang, J.; Li, Y. Strengthening mechanism of Al matrix composites reinforced by nickel-coated graphene: Insights from molecular dynamics simulation. Phys. B Condens. Matter 2021, 601, 412620. [Google Scholar] [CrossRef]
- Dixit, S.; Mahata, A.; Mahapatra, D.R.; Kailas, S.V.; Chattopadhyay, K. Multi-layer graphene reinforced aluminum—Manufacturing of high strength composite by friction stir alloying. Compos. Part B Eng. 2018, 136, 63–71. [Google Scholar] [CrossRef]
- Sierra-Suarez, J.A.; Majumdar, S.; McGaughey, A.J.H.; Malen, J.A.; Higgs, C.F. Morse potential-based model for contacting composite rough surfaces: Application to self-assembled monolayer junctions. J. Appl. Phys. 2016, 119, 145306. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Y.; Li, N.; Zhang, L.; Zhang, J.; Niu, L.; Li, W.; Li, S. Atomistic Investigation of the Effects of Different Reinforcements on Al Matrix Composite. Metals 2022, 12, 1252. [Google Scholar] [CrossRef]
- Meng, L.; Sun, Q.; Wang, J.; Ding, F. Molecular Dynamics Simulation of Chemical Vapor Deposition Graphene Growth on Ni (111) Surface. J. Phys. Chem. C 2012, 116, 6097–6102. [Google Scholar] [CrossRef]
- van Duin, A.C.T.; Dasgupta, S.; Lorant, F.; Goddard, W.A. ReaxFF: A Reactive Force Field for Hydrocarbons. J. Phys. Chem. A 2001, 105, 9396–9409. [Google Scholar] [CrossRef]
- Mueller, J.E.; van Duin, A.C.T.; Goddard, W.A. Development and Validation of ReaxFF Reactive Force Field for Hydrocarbon Chemistry Catalyzed by Nickel. J. Phys. Chem. C 2010, 114, 4939–4949. [Google Scholar] [CrossRef]
- Mueller, J.E.; van Duin, A.C.T.; Goddard, W.A. Application of the ReaxFF Reactive Force Field to Reactive Dynamics of Hydrocarbon Chemisorption and Decomposition. J. Phys. Chem. C 2010, 114, 5675–5685. [Google Scholar] [CrossRef] [Green Version]
- Lu, Y.; Yang, X. Molecular simulation of graphene growth by chemical deposition on nickel using polycyclic aromatic hydrocarbons. Carbon 2015, 81, 564–573. [Google Scholar] [CrossRef]
- Hossain, M.J.; Pawar, G.; Liaw, B.; Gering, K.L.; Dufek, E.J.; van Duin, A.C.T. Lithium-electrolyte solvation and reaction in the electrolyte of a lithium ion battery: A ReaxFF reactive force field study. J. Chem. Phys. 2020, 152, 184301. [Google Scholar] [CrossRef] [PubMed]
- Srinivasan, S.G.; van Duin, A.C.T.; Ganesh, P. Development of a ReaxFF Potential for Carbon Condensed Phases and Its Application to the Thermal Fragmentation of a Large Fullerene. J. Phys. Chem. A 2015, 119, 571–580. [Google Scholar] [CrossRef] [PubMed]
- Kowalik, M.; Hossain, M.J.; Lele, A.; Zhu, W.; Banerjee, R.; Granzier-Nakajima, T.; Terrones, M.; Hudson, E.W.; van Duin, A.C.T. Atomistic-Scale Simulations on Graphene Bending Near a Copper Surface. Catalysts 2021, 11, 208. [Google Scholar] [CrossRef]
- Safina, L.L.; Baimova, J.A. Molecular dynamics simulation of fabrication of Ni-graphene composite: Temperature effect. Micro Nano Lett. 2020, 15, 176–180. [Google Scholar] [CrossRef]
- Wei, D.; Song, Y.; Wang, F. A simple molecular mechanics potential for μm scale graphene simulations from the adaptive force matching method. J. Chem. Phys. 2011, 134, 184704. [Google Scholar] [CrossRef]
- Tian, L.X.; Yang, C.L.; Wang, M.S.; Ma, X.G. An Idea to Produce Composite Nanowires with Copper Nanoparticles Filling Into Carbon Nanotubes. J. Comput. Theor. Nanosci. 2011, 8, 2307–2312. [Google Scholar] [CrossRef]
- Liang, T.; Devine, B.; Phillpot, S.R.; Sinnott, S.B. Variable Charge Reactive Potential for Hydrocarbons to Simulate Organic-Copper Interactions. J. Phys. Chem. A 2012, 116, 7976–7991. [Google Scholar] [CrossRef]
- Liang, T.; Shan, T.R.; Cheng, Y.T.; Devine, B.D.; Noordhoek, M.; Li, Y.; Lu, Z.; Phillpot, S.R.; Sinnott, S.B. Classical atomistic simulations of surfaces and heterogeneous interfaces with the charge-optimized many body (COMB) potentials. Mater. Sci. Eng. R Rep. 2013, 74, 255–279. [Google Scholar] [CrossRef]
- Devine, B.; Shan, T.R.; Cheng, Y.T.; McGaughey, A.J.H.; Lee, M.; Phillpot, S.R.; Sinnott, S.B. Atomistic simulations of copper oxidation and Cu/Cu2O interfaces using charge-optimized many-body potentials. Phys. Rev. B 2011, 84, 125308. [Google Scholar] [CrossRef] [Green Version]
- Klaver, T.; Zhu, S.E.; Sluiter, M.; Janssen, G. Molecular dynamics simulation of graphene on Cu (1 0 0) and (1 1 1) surfaces. Carbon 2015, 82, 538–547. [Google Scholar] [CrossRef] [Green Version]
- Verkhovtsev, A.V.; Erofeev, Y.; Solov’yov, A.V. Soft landing of metal clusters on graphite: A molecular dynamics study. Eur. Phys. J. D 2020, 74, 205. [Google Scholar] [CrossRef]
- Xu, Z.; Zhao, G.; Qiu, L.; Zhang, X.; Qiao, G.; Ding, F. Molecular dynamics simulation of graphene sinking during chemical vapor deposition growth on semi-molten Cu substrate. NPJ Comput. Mater. 2020, 6, 14. [Google Scholar] [CrossRef] [Green Version]
- Ayatollahi, M.; Shadlou, S.; Shokrieh, M. Multiscale modeling for mechanical properties of carbon nanotube reinforced nanocomposites subjected to different types of loading. Compos. Struct. 2011, 93, 2250–2259. [Google Scholar] [CrossRef]
- Srivastava, A.K.; Pathak, V.K.; Singh, R.; Dikshit, M.K. Stress–strain behaviour of graphene reinforced aluminum nanocomposite under compressive loading using molecular dynamics. Mater. Today Proc. 2021, 44, 4521–4525. [Google Scholar] [CrossRef]
- Singh, A.; Kumar, D. Effect of temperature on elastic properties of CNT-polyethylene nanocomposite and its interface using MD simulations. J. Mol. Model. 2018, 24, 178. [Google Scholar] [CrossRef] [PubMed]
- Peng, W.; Sun, K.; Abdullah, R.; Zhang, M.; Chen, J.; Shi, J. Strengthening mechanisms of graphene coatings on Cu film under nanoindentation: A molecular dynamics simulation. Appl. Surf. Sci. 2019, 487, 22–31. [Google Scholar] [CrossRef]
- Zhao, Y.; Peng, X.; Fu, T.; Zhu, X.; Hu, N.; Yan, C. Strengthening mechanisms of graphene coated copper under nanoindentation. Comput. Mater. Sci. 2018, 144, 42–49. [Google Scholar] [CrossRef]
- Wang, C.; Song, X.; Shen, X.; Sun, F. Molecular dynamics simulation and experimental investigation of structural transformation and graphitization in diamond during friction. Comput. Mater. Sci. 2020, 184, 109862. [Google Scholar] [CrossRef]
- Zhang, Q.; Diao, D.; Kubo, M. Nanoscratching of multi-layer graphene by molecular dynamics simulations. Tribol. Int. 2015, 88, 85–88. [Google Scholar] [CrossRef]
- Kim, S.M.; Park, W.R.; Kwon, O.H. The Strength and Delamination of Graphene/Cu Composites with Different Cu Thicknesses. Materials 2021, 14, 2983. [Google Scholar] [CrossRef] [PubMed]
- Galashev, A.E.; Elshina, L.A.; Muradymov, R.V. Molecular dynamic study of the mechanism of formation of 2D carbon nanostructures in a solid Al–C nanocomposite grain. Russ. J. Phys. Chem. A 2016, 90, 2444–2448. [Google Scholar] [CrossRef]
- Li, Q.; Qin, Z.; Chen, J.; Xia, D.H.; Deng, Y.; Zhang, Y.; Wu, Z.; Hu, W. Preparation and Mechanical Properties of Layered Cu/Gr Composite Film. Coatings 2021, 11, 502. [Google Scholar] [CrossRef]
- Wang, L.; Jin, J.; Cao, J.; Yang, P.; Peng, Q. Interaction of Edge Dislocations with Graphene Nanosheets in Graphene/Fe Composites. Crystals 2018, 8, 160. [Google Scholar] [CrossRef] [Green Version]
- Safina, L.R.; Krylova, K.A.; Baimova, J.A. Molecular dynamics study of the mechanical properties and deformation behavior of graphene/metal composites. Mater. Today Phys. 2022, 28, 100851. [Google Scholar] [CrossRef]
- Vardanyan, V.H.; Urbassek, H.M. Strength of Graphene-Coated Ni Bi-Crystals: A Molecular Dynamics Nano-Indentation Study. Materials 2020, 13, 1683. [Google Scholar] [CrossRef] [Green Version]
- Chang, S.W.; Nair, A.K.; Buehler, M.J. Nanoindentation study of size effects in nickel–graphene nanocomposites. Philos. Mag. Lett. 2013, 93, 196–203. [Google Scholar] [CrossRef]
- Qiu, Z.; Zhang, Z.; Xiong, Y.; Luo, X.; Li, Z.; Zheng, K.; Hu, W. Size effects of graphene sheets on the strengthening mechanism of Al-graphene composites: A molecular dynamics study. Appl. Surf. Sci. 2022, 596, 153546. [Google Scholar] [CrossRef]
- Pratik, A.; Biswal, S.K.; Haridoss, P. Impact of enhanced interfacial strength on physical, mechanical and tribological properties of copper/reduced graphene oxide composites: Microstructural investigation. Ceram. Int. 2020, 46, 22539–22549. [Google Scholar] [CrossRef]


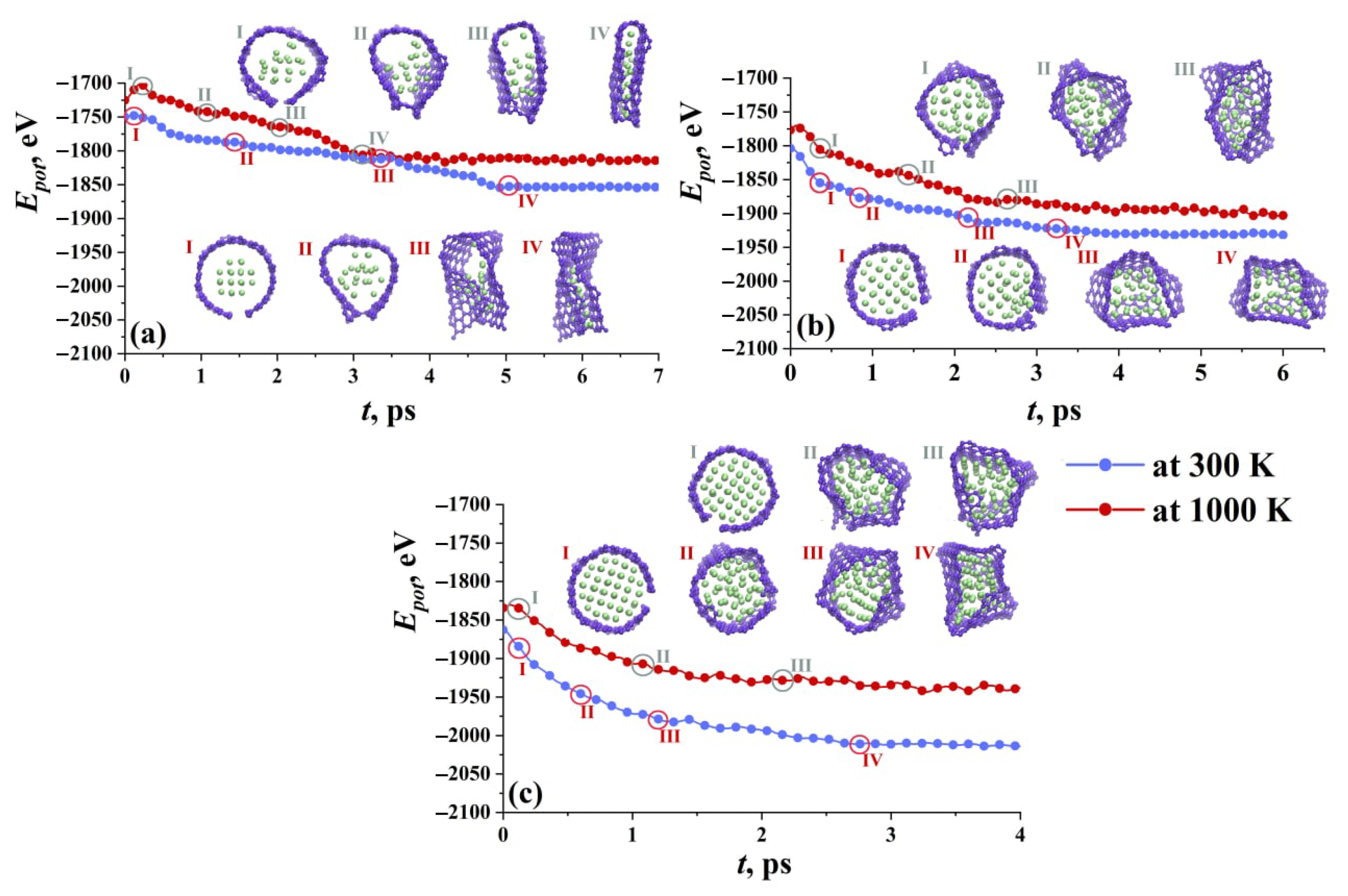
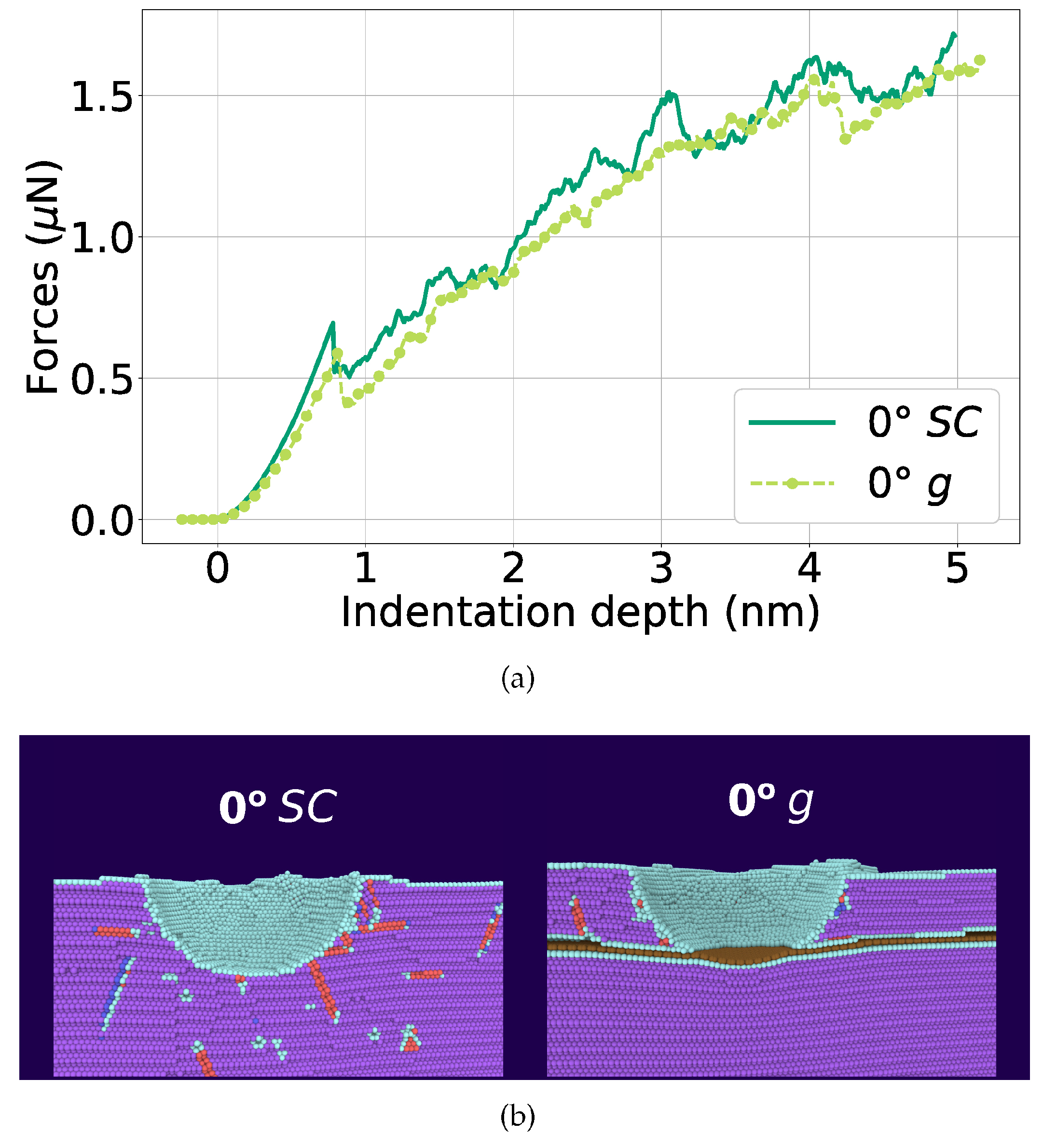
| Metal | Structure | Potential | Studied Properties | Ref. |
|---|---|---|---|---|
| Cu | NC Cu matrix with 1 to 4 Gr (embedded) | LJ | friction, shear resistance | [7] |
| NT Cu, 1 to 4 Gr (embedded) | LJ | tension, compression, shear | [8] | |
| Gr with different boundary conditions (embedded), | LJ | nanoindentation, compression, dislocation dynamics | [108] | |
| NC Cu, Gr, along GBs, from 9.1 vol% to 17.7 vol.% | LJ | tension, dislocation dynamics | [81] | |
| Gr, CNT (embedded) | LJ | tension, temperature dependence on Young’s modulus | [74] | |
| 1 Gr (embedded) | LJ | shock response | [85] | |
| 1 to 6 Gr (embedded) | LJ | radiation damage resistance | [90] | |
| 6 Gr (on the surface) | LJ | surface cracking | [91] | |
| NT Cu, 1 to 5 Gr (embedded) | LJ | tension | [92] | |
| 1 to 5 Gr (embedded) | LJ | solidification of liquid Cu with Gr, tension | [94] | |
| 1-3 Gr, crumpled Gr (embedded) | LJ | tension, Young’s modulus | [99] | |
| 1 Gr (embedded) | LJ | interfaces, dislocation nucleation | [101] | |
| 1 Gr (embedded) | LJ | shear strength, Gr pull-out | [102] | |
| NC Cu, Gr along GBs, from 6.28 vol% to 17.7 vol.% | LJ | tension | [103] | |
| 1 Gr (embedded) | LJ | shock resistance | [105] | |
| 1 to 4 Gt (embedded) | LJ | tension | [109] | |
| 1 to 9 Gr (embedded) | LJ | compression | [89] | |
| 1 Gr (embedded) | LJ | Gr pull-out | [93] | |
| 1 Gr (on the surface) | COMB3 | Gr wrinkling | [143] | |
| 1 to 3 Gr | Finnis and Sinclair | tension | [153] | |
| 1 to 3 Gr, different distribution | LJ | tension | [155] | |
| Ni | 1 to 4 Gr (on the surface) | LJ | nanoindentation | [95] |
| different distribution of Gr | LJ | nanoindentation | [114] | |
| Gr distribution in Ni | LJ | tension | [96] | |
| Gr network | Morse | sintering, tension | [20] | |
| 1 Gr (on the surface) | ReaxFF | bending | [136] | |
| Gr network | Morse | compression, tension | [157] | |
| 1 Gr, on the grain boundary | LJ | indentation | [158] | |
| Cu, Au, Ag | 3 Gr | LJ | tension | [97] |
| Ni, Cu | 1 to 8 Gr | LJ | shock compression | [87] |
| Al | from 1 Gr to 5 vol.%, different orientation | LJ | tension, elastic modulus | [70] |
| 1 Gr (embedded) | LJ | Interface optimization, tension | [106] | |
| 1 to 3 Gr | LJ | compression, dislocation dynamics | [110] | |
| Gr of a different size and chirality | LJ | tension | [111] | |
| 5 Gr (embedded) | LJ | nanoindentation, dislocation dynamics | [160] | |
| 1 Gr (embedded) | Morse | sintering, tension | [128] | |
| 1 Gr, 3 Gr, and Gr with a hole (embedded) | LJ | compression | [147] | |
| Fe | 2 Gr, different orientation (embedded) | LJ | tension, dislocation dynamics | [107] |
| 2 Gr | LJ | dislocation-graphene interaction | [108] | |
| 2 Gr, different orientation (embedded) | embedded atom potential | tension, dislocation dynamics | [156] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baimova, J.A.; Shcherbinin, S.A. Metal/Graphene Composites: A Review on the Simulation of Fabrication and Study of Mechanical Properties. Materials 2023, 16, 202. https://doi.org/10.3390/ma16010202
Baimova JA, Shcherbinin SA. Metal/Graphene Composites: A Review on the Simulation of Fabrication and Study of Mechanical Properties. Materials. 2023; 16(1):202. https://doi.org/10.3390/ma16010202
Chicago/Turabian StyleBaimova, Julia A., and Stepan A. Shcherbinin. 2023. "Metal/Graphene Composites: A Review on the Simulation of Fabrication and Study of Mechanical Properties" Materials 16, no. 1: 202. https://doi.org/10.3390/ma16010202
APA StyleBaimova, J. A., & Shcherbinin, S. A. (2023). Metal/Graphene Composites: A Review on the Simulation of Fabrication and Study of Mechanical Properties. Materials, 16(1), 202. https://doi.org/10.3390/ma16010202







