Analytical Simulation of the Microbubble Collapsing in a Welding Fusion Pool
Abstract
:1. Introduction
2. Theoretical Modelling
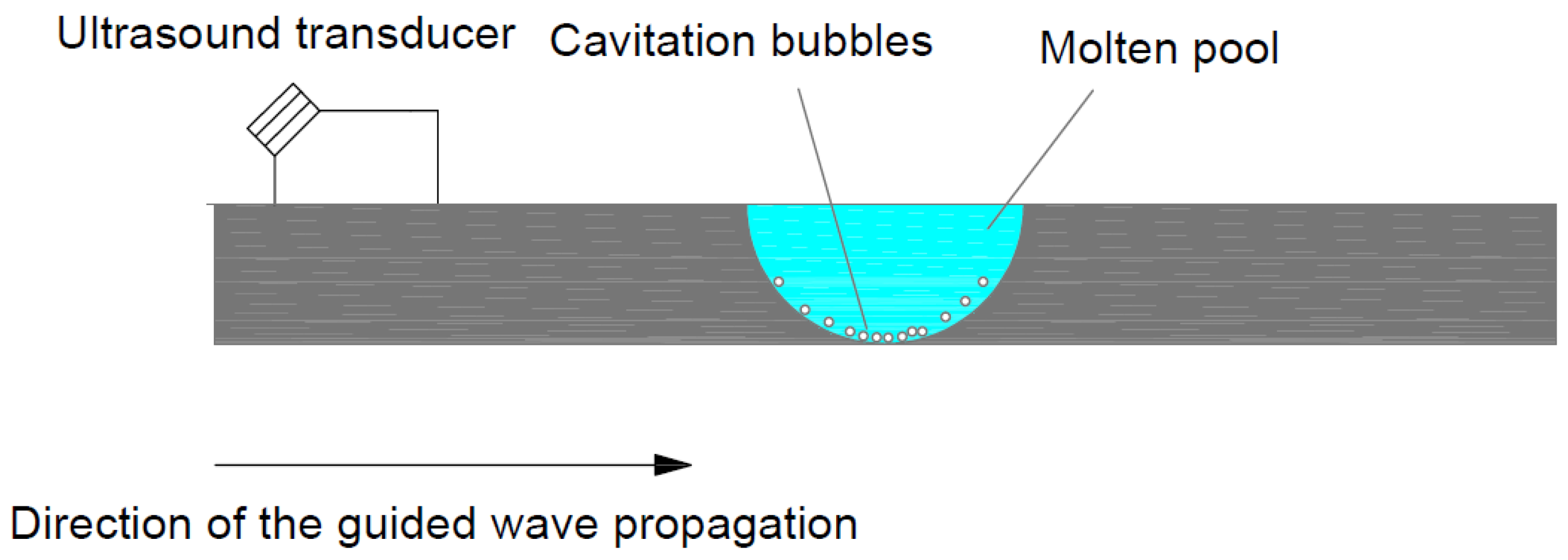
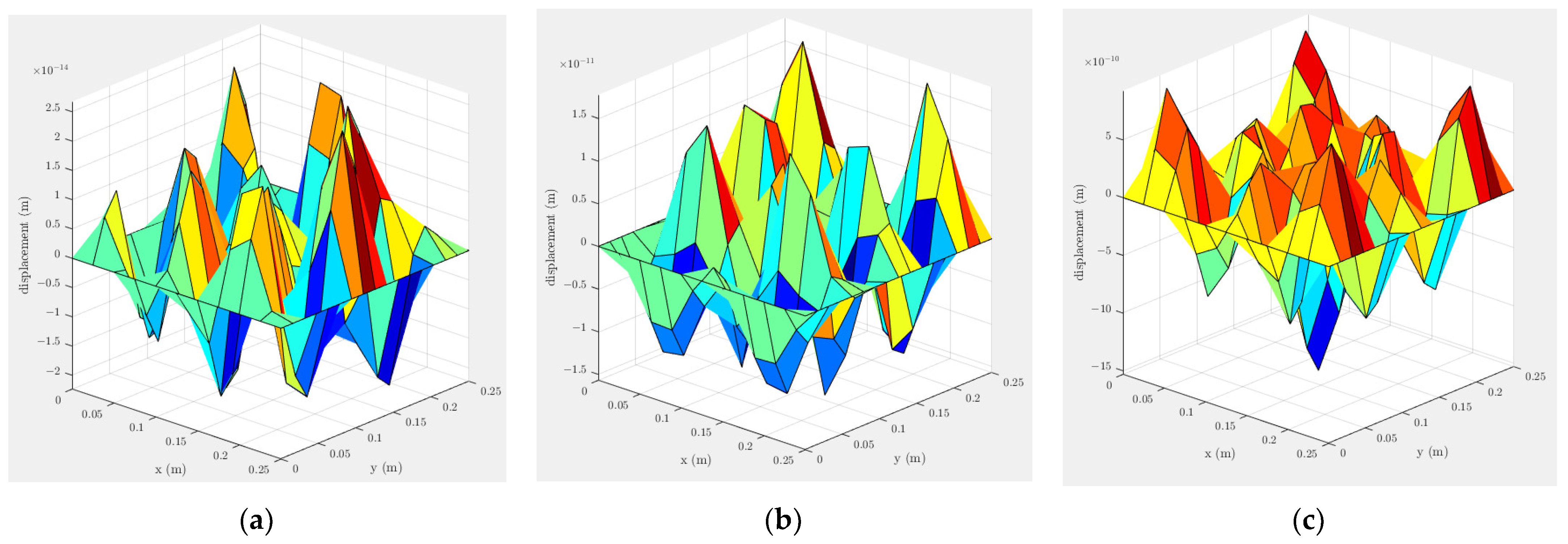
2.1. Ultrasonic Plate Vibration
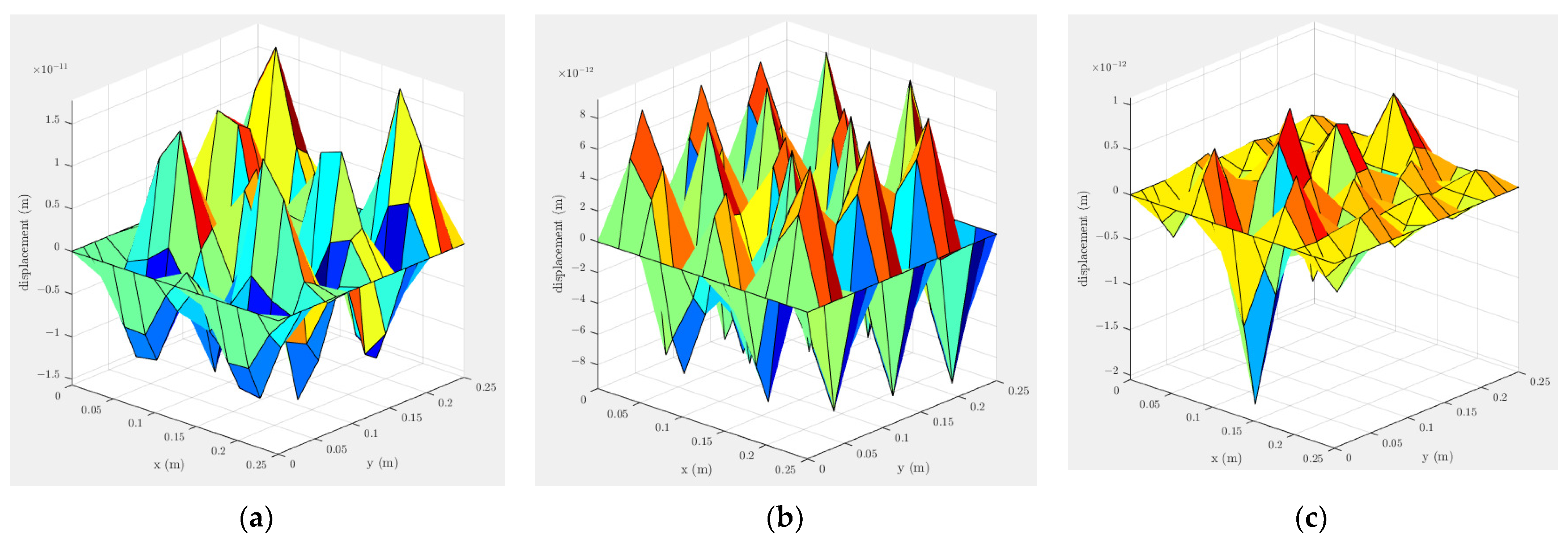
2.2. Coupling of the Plate Vibration and the Fusion Area Pressure
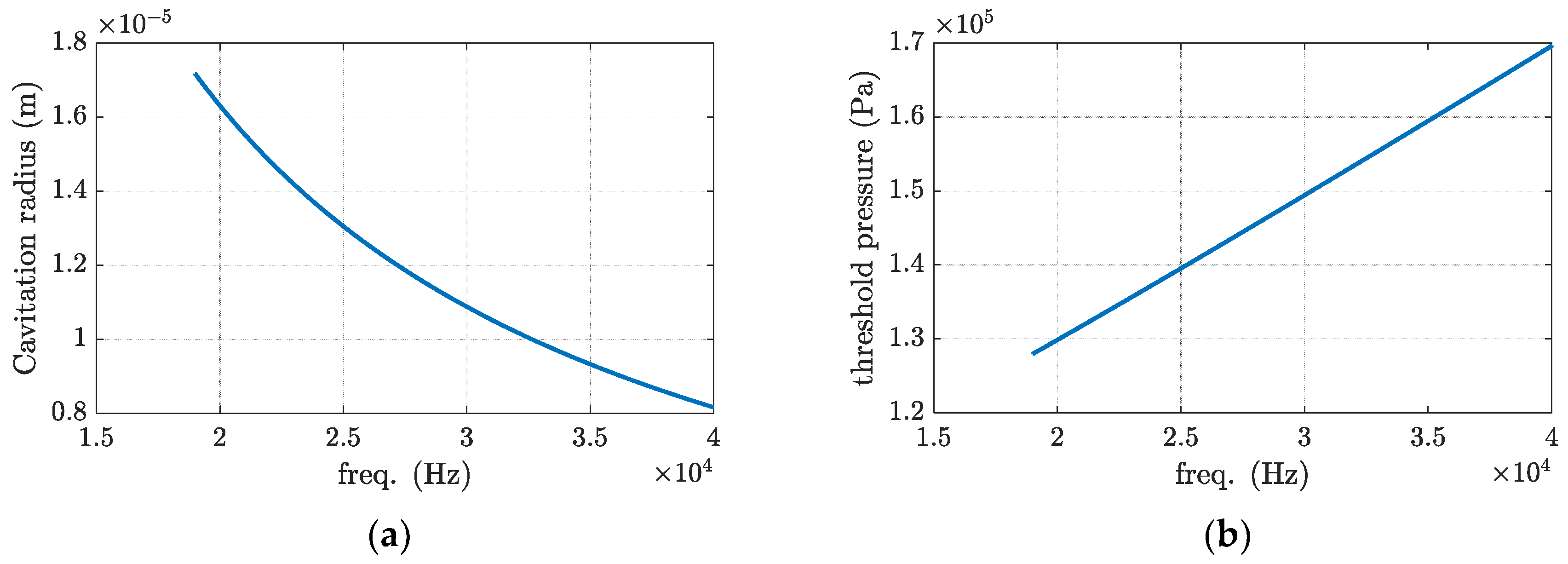
2.3. Cavitation Dynamics
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wei, H.L.; Mazumder, J.; DebRoy, T. Evolution of Solidification Texture during Additive Manufacturing. Sci. Rep. 2015, 5, 16446. [Google Scholar] [CrossRef] [Green Version]
- Franks, J.; Wheatley, G.; Zamani, P.; Masoudi Nejad, R.; Macek, W.; Branco, R.; Samadi, F. Fatigue Life Improvement Using Low Transformation Temperature Weld Material with Measurement of Residual Stress. Int. J. Fatigue 2022, 164, 107137. [Google Scholar] [CrossRef]
- Zwicker, M.F.R.; Moghadam, M.; Zhang, W.; Nielsen, C.V. Automotive Battery Pack Manufacturing—A Review of Battery to Tab Joining. J. Adv. Join. Process. 2020, 1, 100017. [Google Scholar] [CrossRef]
- Favez, D.; Wagniere, J.-D.; Rappaz, M. Au–Fe Alloy Solidification and Solid-State Transformations. Acta Mater. 2010, 58, 1016–1025. [Google Scholar] [CrossRef] [Green Version]
- Ghanbari, H.R.; Shariati, M.; Sanati, E.; Masoudi Nejad, R. Effects of Spot Welded Parameters on Fatigue Behavior of Ferrite-Martensite Dual-Phase Steel and Hybrid Joints. Eng. Fail. Anal. 2022, 134, 106079. [Google Scholar] [CrossRef]
- Mypati, O.; Sahu, S.; Pal, S.K.; Srirangam, P. An Investigation of Mechanical and Electrical Properties of Friction Stir Welded Al and Cu Busbar for Battery Pack Applications. Mater. Chem. Phys. 2022, 287, 126373. [Google Scholar] [CrossRef]
- Li, Y.; Shen, K. The Effect of Melt Vibration on Polystyrene Melt Flowing Behavior during Extrusion. J. Macromol. Sci. Part B 2008, 47, 1228–1235. [Google Scholar] [CrossRef]
- Bast, J.; Hübler, J.; Dommaschk, C. Influence of Vibration during Solidification of Molten Metals on Structure and Casting Properties. Adv. Eng. Mater. 2004, 6, 550–554. [Google Scholar] [CrossRef]
- Nie, K.B.; Wang, X.J.; Wu, K.; Hu, X.S.; Zheng, M.Y.; Xu, L. Microstructure and Tensile Properties of Micro-SiC Particles Reinforced Magnesium Matrix Composites Produced by Semisolid Stirring Assisted Ultrasonic Vibration. Mater. Sci. Eng. A 2011, 528, 8709–8714. [Google Scholar] [CrossRef]
- Huang, Z.; Lucas, M.; Adams, M.J. Influence of Ultrasonics on Upsetting of a Model Paste. Ultrasonics 2002, 40, 43–48. [Google Scholar] [CrossRef] [PubMed]
- Prihandana, G.S.; Mahardika, M.; Hamdi, M.; Wong, Y.S.; Mitsui, K. Effect of Micro-Powder Suspension and Ultrasonic Vibration of Dielectric Fluid in Micro-EDM Processes—Taguchi Approach. Int. J. Mach. Tools Manuf. 2009, 49, 1035–1041. [Google Scholar] [CrossRef]
- Jimma, T.; Kasuga, Y.; Iwaki, N.; Miyazawa, O.; Mori, E.; Ito, K.; Hatano, H. An Application of Ultrasonic Vibration to the Deep Drawing Process. J. Mater. Process. Technol. 1998, 80, 406–412. [Google Scholar] [CrossRef]
- Khavari, M.; Priyadarshi, A.; Hurrell, A.; Pericleous, K.; Eskin, D.; Tzanakis, I. Characterization of Shock Waves in Power Ultrasound. J. Fluid Mech. 2021, 915, R3. [Google Scholar] [CrossRef]
- Eskin, G.I. Ultrasonic Treatment of Light Alloy Melts; CRC Press: Boca Raton, FL, USA, 1998; ISBN 0429075863. [Google Scholar]
- Apfel, R.E.; Holland, C.K. Gauging the Likelihood of Cavitation from Short-Pulse, Low-Duty Cycle Diagnostic Ultrasound. Ultrasound Med. Biol. 1991, 17, 179–185. [Google Scholar] [CrossRef]
- Yasui, K. Influence of Ultrasonic Frequency on Multibubble Sonoluminescence. J. Acoust. Soc. Am. 2002, 112, 1405–1413. [Google Scholar] [CrossRef]
- Brujan, E.A.; Ikeda, T.; Matsumoto, Y. On the Pressure of Cavitation Bubbles. Exp. Fluid Sci. 2008, 32, 1188–1191. [Google Scholar] [CrossRef]
- Sun, Q.J.; Lin, S.B.; Yang, C.L.; Zhao, G.Q. Penetration Increase of AISI 304 Using Ultrasonic Assisted Tungsten Inert Gas Welding. Sci. Technol. Weld. Join. 2009, 14, 765–767. [Google Scholar] [CrossRef]
- Chen, X.; Shen, Z.; Wang, J.; Chen, J.; Lei, Y.; Huang, Q. Effects of an Ultrasonically Excited TIG Arc on CLAM Steel Weld Joints. Int. J. Adv. Manuf. Technol. 2012, 60, 537–544. [Google Scholar] [CrossRef]
- Lan, H.; Gong, X.; Zhang, S.; Wang, L.; Wang, B.; Nie, L. Ultrasonic Vibration Assisted Tungsten Inert Gas Welding of Dissimilar Metals 316L and L415. Int. J. Miner. Metall. Mater. 2020, 27, 943–953. [Google Scholar] [CrossRef]
- Yang, F.; Zhou, J.; Ding, R. Ultrasonic Vibration Assisted Tungsten Inert Gas Welding of Dissimilar Magnesium Alloys. J. Mater. Sci. Technol. 2018, 34, 2240–2245. [Google Scholar] [CrossRef]
- Zhou, S.; Ma, G.; Dongjiang, W.; Chai, D.; Lei, M. Ultrasonic Vibration Assisted Laser Welding of Nickel-Based Alloy and Austenite Stainless Steel. J. Manuf. Process. 2018, 31, 759–767. [Google Scholar] [CrossRef]
- Liu, Z.; Jin, X.; Li, J.; Hao, Z.; Zhang, J. Numerical Simulation and Experimental Analysis on the Deformation and Residual Stress in Trailing Ultrasonic Vibration Assisted Laser Welding. Adv. Eng. Softw. 2022, 172, 103200. [Google Scholar] [CrossRef]
- Liu, J.; Zhu, H.; Li, Z.; Cui, W.; Shi, Y. Effect of Ultrasonic Power on Porosity, Microstructure, Mechanical Properties of the Aluminum Alloy Joint by Ultrasonic Assisted Laser-MIG Hybrid Welding. Opt. Laser Technol. 2019, 119, 105619. [Google Scholar] [CrossRef]
- Lei, Z.; Bi, J.; Li, P.; Guo, T.; Zhao, Y.; Zhang, D. Analysis on Welding Characteristics of Ultrasonic Assisted Laser Welding of AZ31B Magnesium Alloy. Opt. Laser Technol. 2018, 105, 15–22. [Google Scholar] [CrossRef]
- Tarasov, S.Y.; Vorontsov, A.V.; Fortuna, S.V.; Rubtsov, V.E.; Krasnoveikin, V.A.; Kolubaev, E.A. Ultrasonic-Assisted Laser Welding on AISI 321 Stainless Steel. Weld. World 2019, 63, 875–886. [Google Scholar] [CrossRef]
- Teyeb, A.; Silva, J.; Kanfoud, J.; Carr, P.; Gan, T.-H.; Balachandran, W. Improvements in the Microstructure and Mechanical Properties of Aluminium Alloys Using Ultrasonic-Assisted Laser Welding. Metals 2022, 12, 1041. [Google Scholar] [CrossRef]
- Woizeschke, P.; Radel, T.; Nicolay, P.; Vollertsen, F. Laser Deep Penetration Welding of an Aluminum Alloy with Simultaneously Applied Vibrations. Lasers Manuf. Mater. Process. 2017, 4, 1–12. [Google Scholar] [CrossRef]
- Radel, T. Thermal Impacts in Vibration-Assisted Laser Deep Penetration Welding of Aluminum. Phys. Procedia 2017, 89, 131–138. [Google Scholar] [CrossRef]
- Yin, P.; Xu, C.; Pan, Q.; Zhang, W.; Jiang, X. Effect of Different Ultrasonic Power on the Properties of RHA Steel Welded Joints. Materials 2022, 15, 768. [Google Scholar] [CrossRef]
- Wu, J.; Nyborg, W.L. Ultrasound, Cavitation Bubbles and Their Interaction with Cells. Adv. Drug Deliv. Rev. 2008, 60, 1103–1116. [Google Scholar] [CrossRef]
- Prosperetti, A. Vapor Bubbles. Annu. Rev. Fluid Mech. 2017, 49, 221–248. [Google Scholar] [CrossRef]
- Chladni, E.F.F. Entdeckungen Über Die Theorie Des Klanges; Zentralantiquariat der, Breitkopfund Ha¨rtel: Leipzig, Germany, 1787. [Google Scholar]
- Leissa, A.W. Vibration of Plates; Scientific and Technical Information Division, National Aeronautics and Space Administration: Washington, DC, USA, 1969; Volume 160.
- Sung, C.-C.; Chiu, C.-Y. Control of Sound Transmission through Thin Plate. J. Sound Vib. 1998, 218, 605–618. [Google Scholar] [CrossRef]
- Sung, C.-C.; Jan, J.T. The Response of and Sound Power Radiated by a Clamped Rectangular Plate. J. Sound Vib. 1997, 207, 301–317. [Google Scholar] [CrossRef]
- Sung, C.-C.; Jan, C.T. Active Control of Structurally Radiated Sound from Plates. J. Acoust. Soc. Am. 1997, 102, 370–381. [Google Scholar] [CrossRef]
- Vlasov, V.S. Some New Problems on Shells and Thin Structures; Naca Tech: Washington, DC, USA, 1949. [Google Scholar]
- Pinnington, R.J.; Briscoe, A.R. Externally Applied Sensor for Axisymmetric Waves in a Fluid Filled Pipe. J. Sound Vib. 1994, 173, 503–516. [Google Scholar] [CrossRef]
- Louisnard, O.; González-García, J. Acoustic Cavitation. In Ultrasound Technologies for Food and Bioprocessing; Springer: Berlin/Heidelberg, Germany, 2011; pp. 13–64. [Google Scholar]
- Jamshidi, R.; Brenner, G. Dissipation of Ultrasonic Wave Propagation in Bubbly Liquids Considering the Effect of Compressibility to the First Order of Acoustical Mach Number. Ultrasonics 2013, 53, 842–848. [Google Scholar] [CrossRef]
- Brennen, C.E. Cavitation and Bubble Dynamics; Cambridge University Press: Cambridge, UK, 2014; ISBN 1107644763. [Google Scholar]
- Ashokkumar, M. The Characterization of Acoustic Cavitation Bubbles—An Overview. Ultrason Sonochem. 2011, 18, 864–872. [Google Scholar] [CrossRef]
- Chen, C.; Fan, C.; Cai, X.; Lin, S.; Liu, Z.; Fan, Q.; Yang, C. Investigation of Formation and Microstructure of Ti-6Al-4V Weld Bead during Pulse Ultrasound Assisted TIG Welding. J. Manuf. Process. 2019, 46, 241–247. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teyeb, A.; Salimi, M.; El Masri, E.; Balachandran, W.; Gan, T.-H. Analytical Simulation of the Microbubble Collapsing in a Welding Fusion Pool. Materials 2023, 16, 410. https://doi.org/10.3390/ma16010410
Teyeb A, Salimi M, El Masri E, Balachandran W, Gan T-H. Analytical Simulation of the Microbubble Collapsing in a Welding Fusion Pool. Materials. 2023; 16(1):410. https://doi.org/10.3390/ma16010410
Chicago/Turabian StyleTeyeb, Ahmed, Mohamad Salimi, Evelyne El Masri, Wamadeva Balachandran, and Tat-Hean Gan. 2023. "Analytical Simulation of the Microbubble Collapsing in a Welding Fusion Pool" Materials 16, no. 1: 410. https://doi.org/10.3390/ma16010410
APA StyleTeyeb, A., Salimi, M., El Masri, E., Balachandran, W., & Gan, T.-H. (2023). Analytical Simulation of the Microbubble Collapsing in a Welding Fusion Pool. Materials, 16(1), 410. https://doi.org/10.3390/ma16010410







