Composition-Related Dielectric, Ferroelectric and Electrocaloric Properties of Pb5Ge3O11 Single Crystals Modified by Ba Ions
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Dielectric Measurements
3.2. Specific Heat Measurements
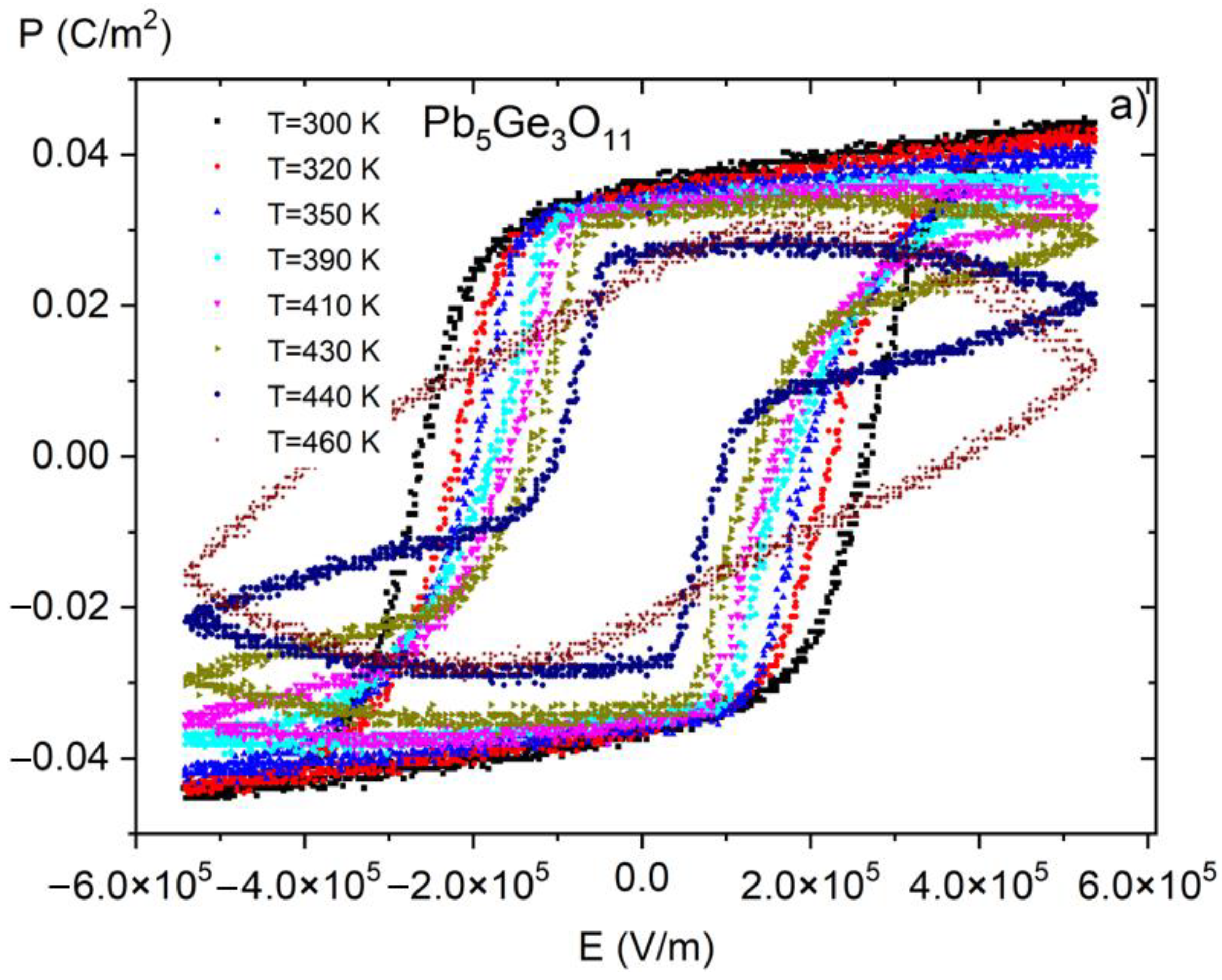
3.3. Polarization Measurements
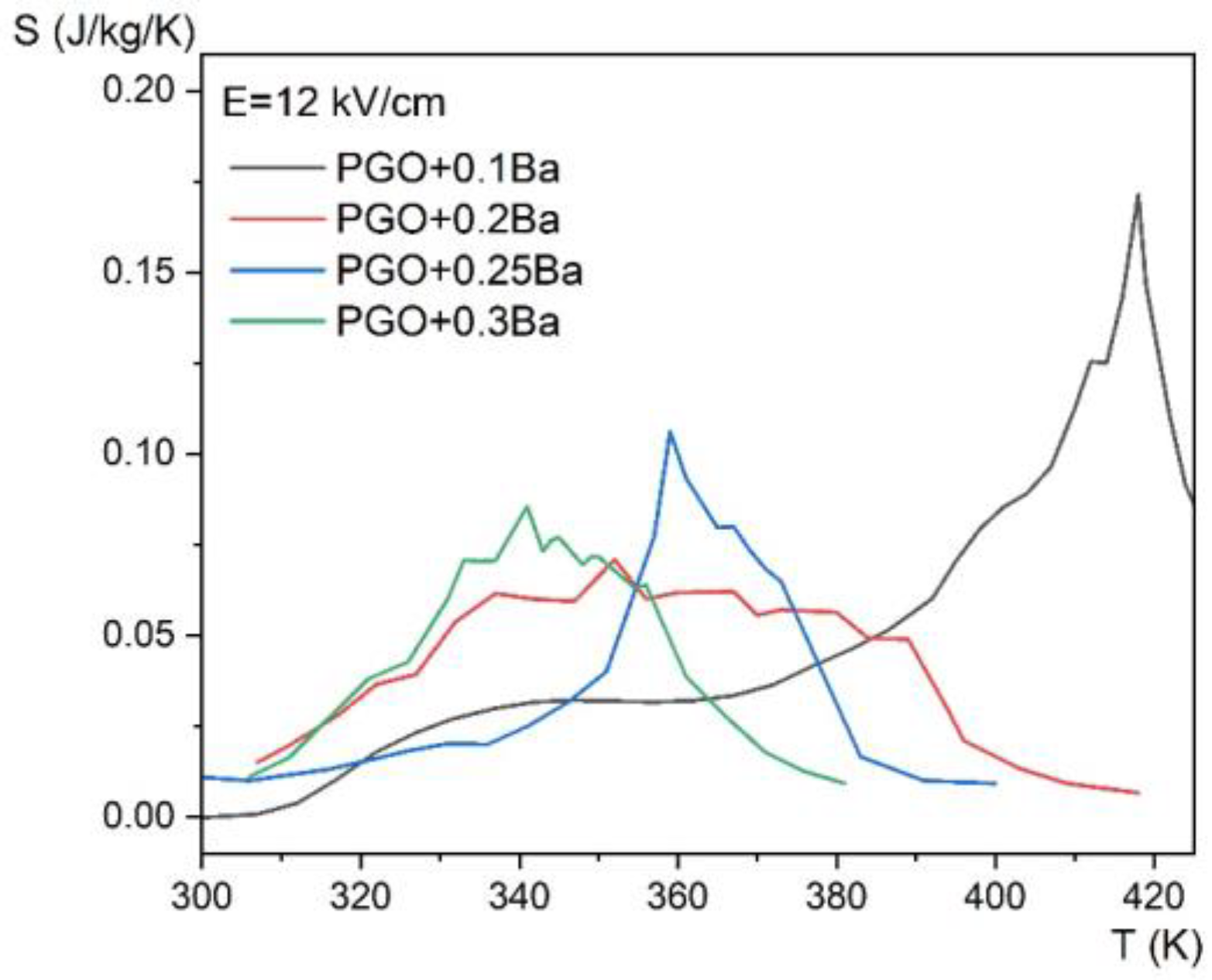
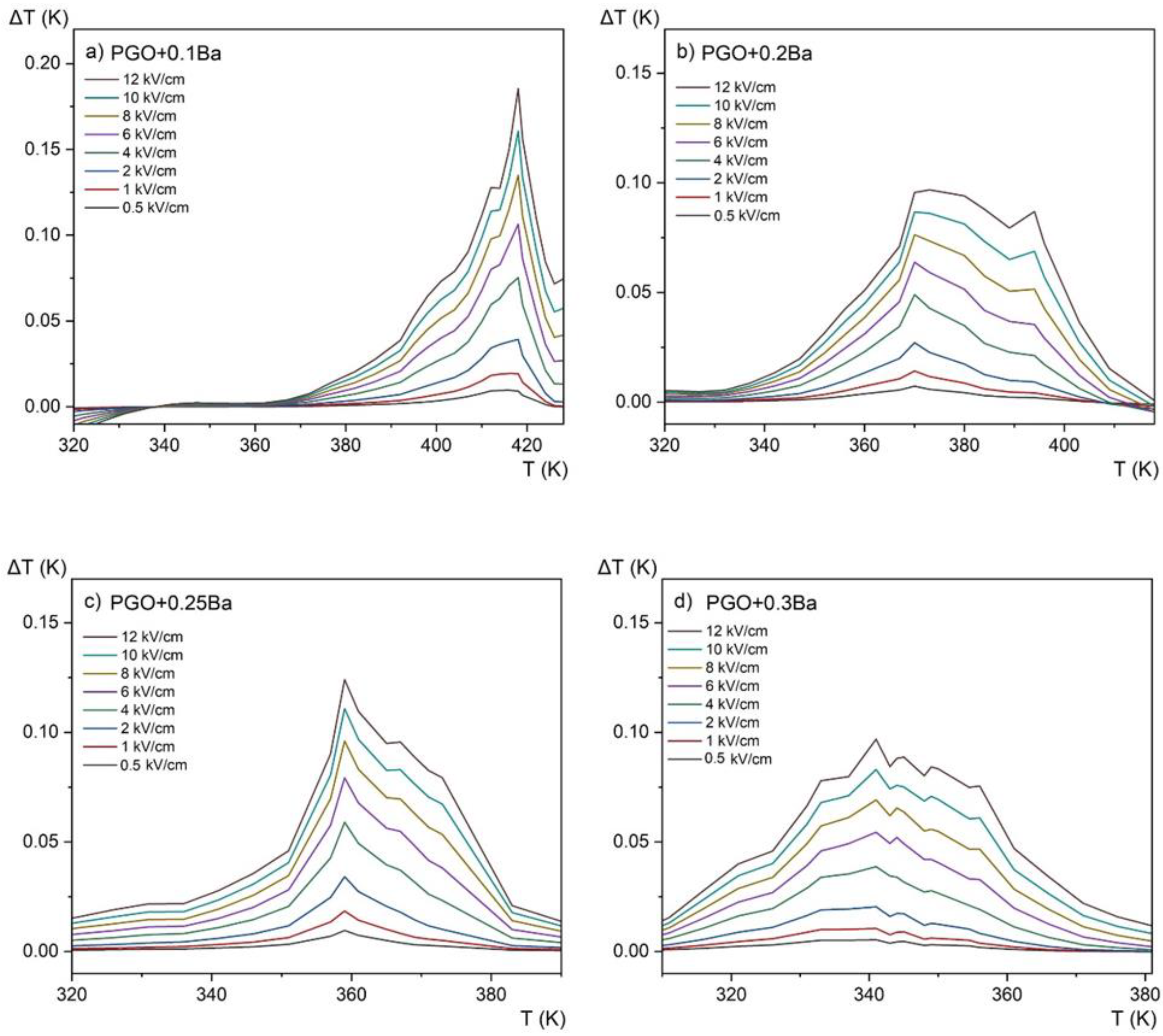
3.4. Electrocaloric Properties
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Landolt-Bornstein New Series. Ferroelectrics and Related Substances: Oxides Groupe III; Springer: Berlin, Germany, 1982; Volume 16a, p. 244. [Google Scholar]
- Iwasaki, H.; Miyazawa, S.; Koizumi, H.; Sugii, K.; Niizeki, N. Ferroelectric and optical properties of Pb5Ge3O11 and its isomorphous compound Pb5Ge2SiO11. J. Appl. Phys. 1972, 43, 4907–4915. [Google Scholar] [CrossRef]
- Ghulghule, G.; Katpatal, A.G. Pyroelectric behaviour of pure and lanthanum-doped lead germanate single crystal. J. Phys. Chem. Solids. 1999, 60, 425–428. [Google Scholar] [CrossRef]
- Iwata, Y.J. Neutron diffraction study of the structure of paraelectric phase of Pb5Ge3O11. Phys. Soc. Japan 1977, 43, 961–967. [Google Scholar] [CrossRef]
- Viennois, R.; Kityk, I.V.; Majchrowski, A.; Zmija, J.; Mierczyk, Z.; Papet, P. Influence of Cr3+ dopants on the enhanced dielectric and nonlinear optical features of pyroelectric Pb5Ge3O11 single crystals. Mater. Chem. Phys. 2018, 213, 461–471. [Google Scholar] [CrossRef]
- Lee, S.D.; Jang, M.S.; Lee, J.H. A study on the elastic and piezoelectric properties of ferroelectric lead germanate single crystals by the ultrasonic pulsed technique. New Phys. 1987, 27, 15–23. [Google Scholar]
- Bachulska, U.; Jankowska-Sumara, I.; Majchrowski, A.; Chrunik, M.; Zasada, D.; Soszyński, A. Thermal and dielectric properties of ferroelectric lead germanate single crystals doped with chromium ions (Pb5Ge3O11:Cr3+). Phase Transit. 2018, 91, 923–931. [Google Scholar] [CrossRef]
- Molak, E.; Talik, M.; Pawełczyk, M.; Adamiec, M.; Koralewski, M. Local disorder influence on electrical phenomena of pure and Ba-doped Pb5Ge3O11 crystals. Phys. Status Solidi (a) 2008, 205, 235–248. [Google Scholar] [CrossRef]
- Miga, S.; Dec, J.; Molak, A.; Koralewski, M. Barium doping-induced polar nanoregions in lead germinate single crystal. Phase Trans. 2008, 81, 1133–1140. [Google Scholar] [CrossRef]
- Jankowska-Sumara, I.; Gwizd, P.; Majchrowski, A.; Soszynski, A. Electrocaloric effect in pure and Cr doped lead germanate single crystals. Mat. Chem Phys. 2020, 242, 122494. [Google Scholar] [CrossRef]
- Zhang, J.; Houa, X.; Zhan, Y.; Tang, G.; Wang, J. Electrocaloric effect in ferroelectric materials: From phase field to first-principles based effective Hamiltonian modeling. Mater. Rep. Energy 2021, 1, 100050. [Google Scholar] [CrossRef]
- Otoničar, M.; Dkhil, B. Electrocalorics hit the top. Nat. Mater. 2020, 19, 9–11. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Scott, J.F.; Dkhil, B. Direct and indirect measurements on electrocaloric effect: Recent developments and perspectives. Appl. Phys. Rev. 2016, 3, 031102. [Google Scholar] [CrossRef] [Green Version]
- Vazhenin, V.A.; Potapov, A.P.; Fokin, A.V.; Shakurov, G.S.; Gorlov, A.D.; Artyomov, M.Y. Trigonal Cr3+ centers in ferroelectric lead germanate. Opt. Mater. 2020, 106, 109855. [Google Scholar] [CrossRef]
- Grosso, G.; Pastori Parravicini, G. Chapter 9 Lattice Dynamics of Crystals Solid State Physics, 2nd ed.; Academic Press: Cambridge, MA, USA, 2014; pp. 391–436. [Google Scholar]
- Watton, R.; Smith, C.; Jons, G.R. Pyroelectric materials: Operation and performance in the pyroelectric camera tube. Ferroelectrics 1976, 14, 719–721. [Google Scholar] [CrossRef]
- Nanda Goswami, M.L.; Choudhary, R.N.P.; Mahapatra, P.K. Ferroelectric phase transitions in modified lead germanate. Ferroelectrics 1999, 227, 175–187. [Google Scholar] [CrossRef]
- Houlton, M.R.; Jons, G.R.; Robertson, D.S. A study of growth defects in lead germinate crystals. J. Phys. D. 1975, 8, 219–222. [Google Scholar] [CrossRef]
- Molak, A.; Koralewski, M.; Saunders, G.A.; Juszczyk, W. Effect of uniaxial pressure on the ferroelectric phase transition in Pb5Ge3O11: Ba crystals. Acta Phys. Pol. 2005, 108, 513–520. [Google Scholar] [CrossRef]
- Pecherskaya, E.A. The use of the Sawyer-Tower method and its modifications to measure the electrical parameters of ferroelectric materials. Meas. Tech. 2007, 50, 1101–1107. [Google Scholar] [CrossRef]
- Kutnjak, Z.; Rožič, B.; Pirc, R. Electrocaloric Effect: Theory, Measurements, and Applications. In Wiley Encyclopedia of Electrical and Electronics Engineering; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2015; pp. 1–19. [Google Scholar]
- Bush, A.; Kamentsev, K.E.; Siomko, V.O. Electret effect in Pb5Ge3O11 crystals. Inorg. Mater. 2011, 47, 983–989. [Google Scholar] [CrossRef]


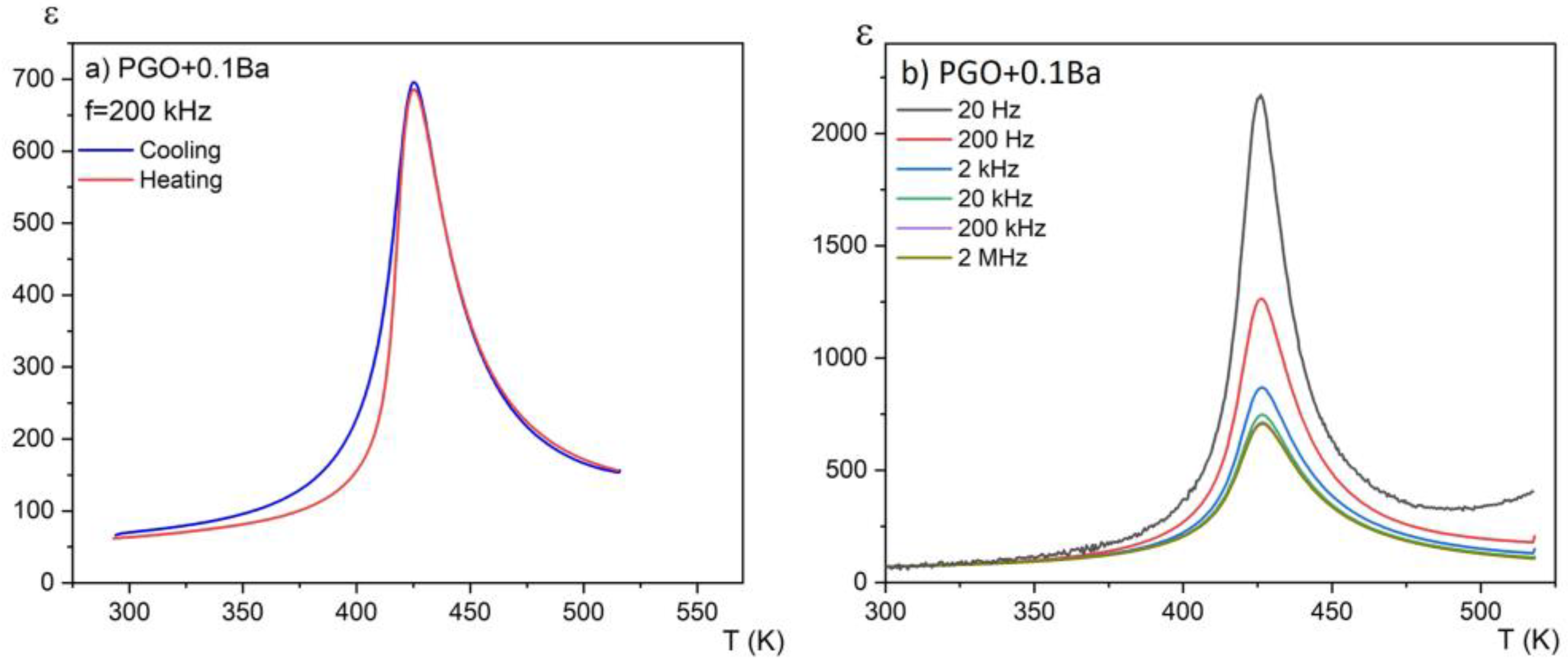
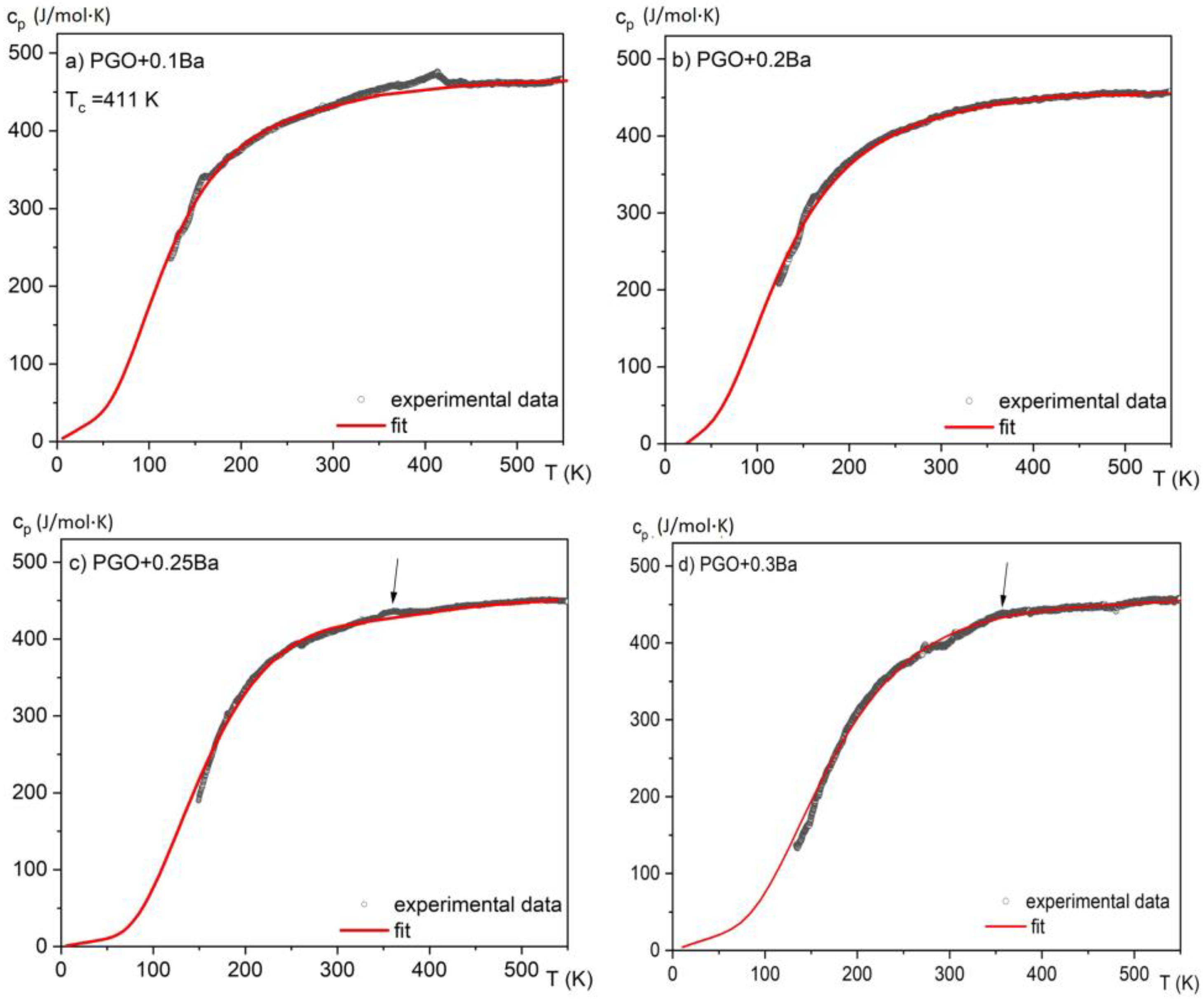
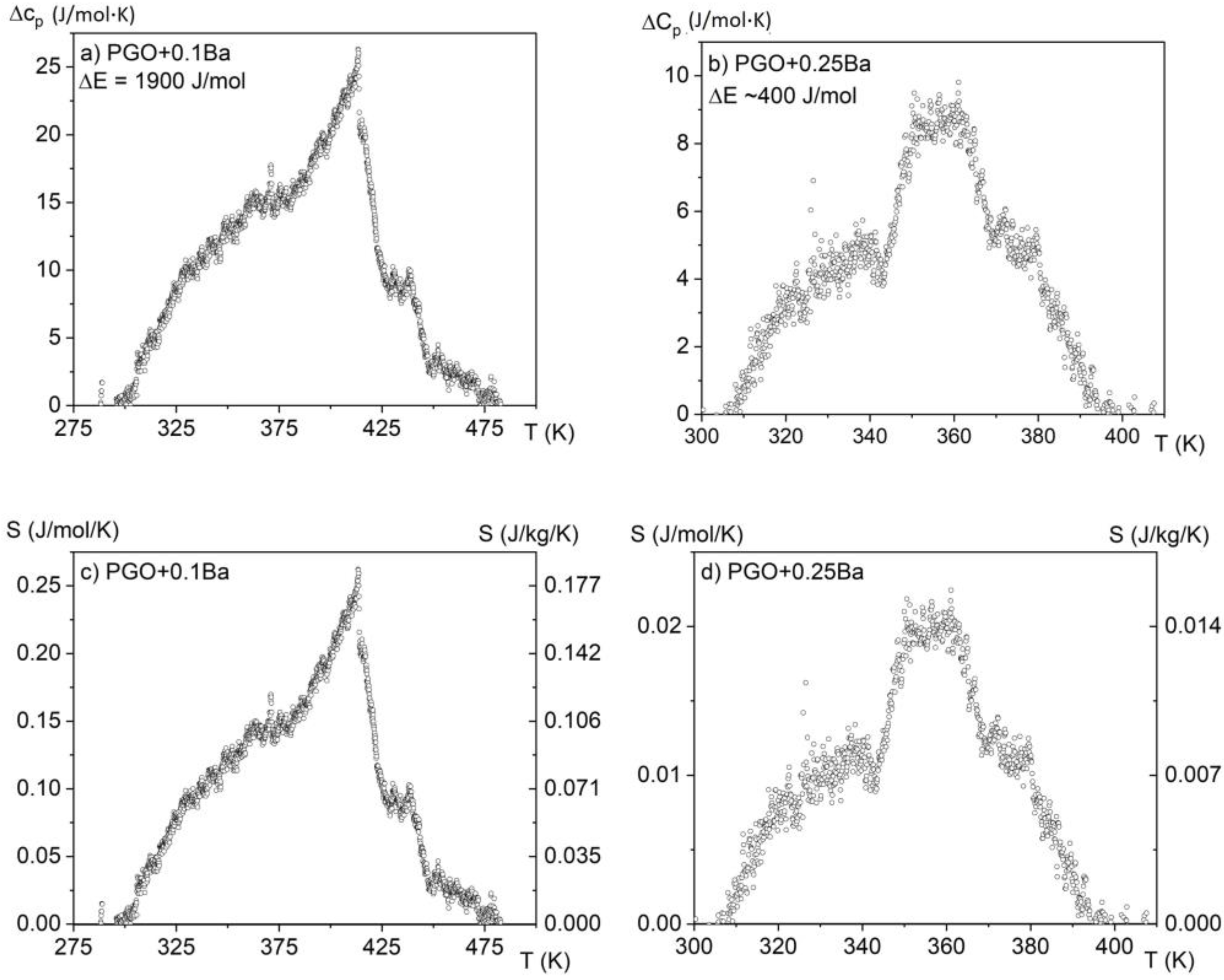
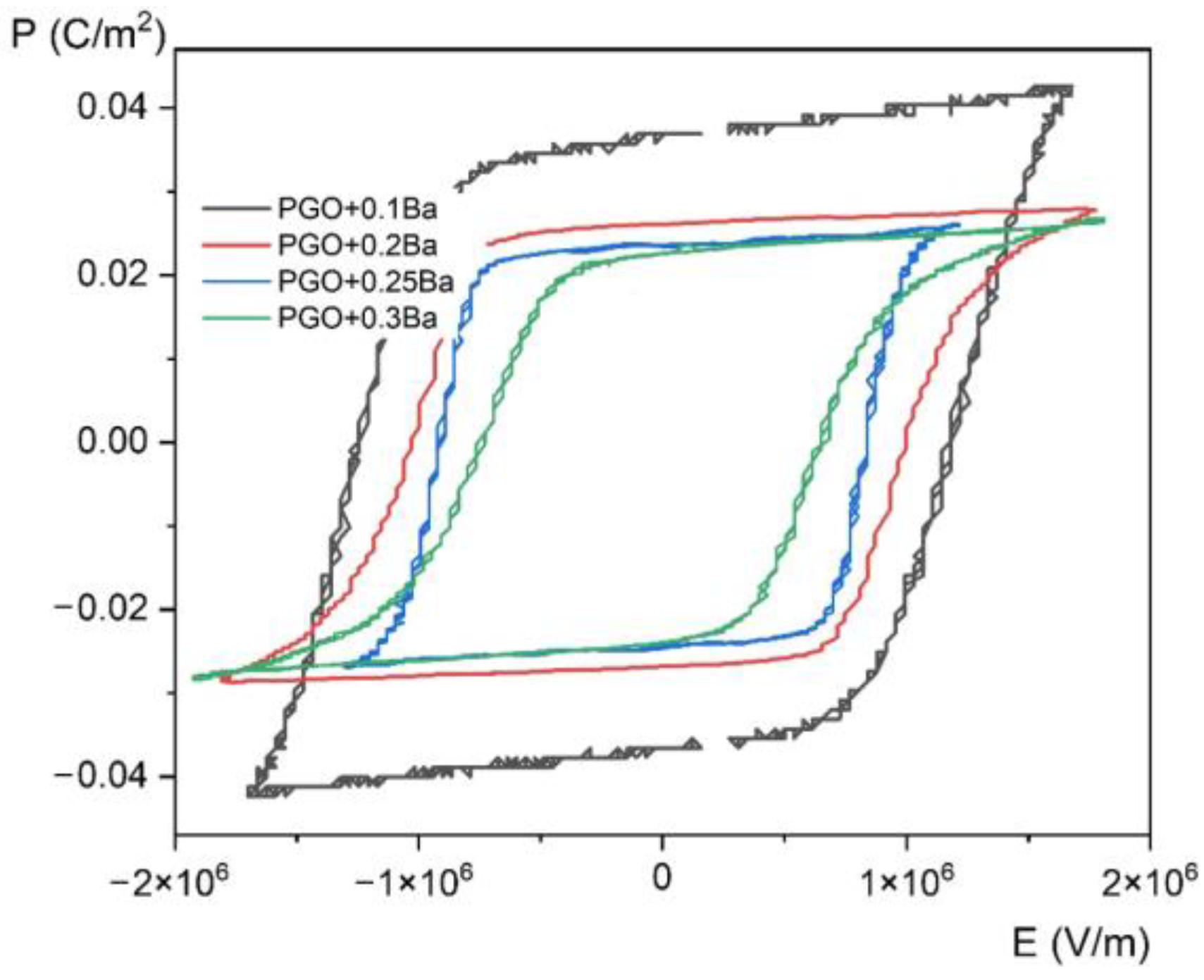



| Composition | TC [K] | TO [K] | C [K] | εmax (20 kHz) |
|---|---|---|---|---|
| PGO [10] | 453 | 453 | 9.8103 | 3600 |
| PGO + 0.1Ba | 425 | 420 | 1.00104 | 700 |
| PGO + 0.2Ba | 388 | 385 | 1.11104 | 570 |
| PGO + 0.25Ba | 370 | 371 | 9.73103 | 650 |
| PGO + 0.3Ba | 348 | 348 | 1.28104 | 600 |
| Composition | EC [V/m] | Pr [C/m2] for E = 0 V/m | Ps [C/m2] for E [V/m] |
|---|---|---|---|
| PGO [10] | 2.7 × 105 | 0.037 | 0.044 (E = 5.3 × 105 ) |
| PGO + 0.1Ba | 10.5 × 105 | 0.036 | 0.042 (E = 12.2 × 105 ) |
| PGO + 0.2Ba | 10 × 105 | 0.026 | 0.027 (E = 17.7 × 105 ) |
| PGO + 0.25Ba | 8.4 × 105 | 0.023 | 0.026 (E = 12.1 × 105 ) |
| PGO + 0.3Ba | 5 × 105 | 0.022 | 0.025 (E = 18 × 105 ) |
| Composition | ΔT [K] | E [kV/cm] |
|---|---|---|
| PGO + 0.1Ba | 0.18 | 12 |
| PGO + 0.2Ba | 0.09 | 12 |
| PGO + 0.25Ba | 0.12 | 12 |
| PGO + 0.3Ba | 0.09 | 12 |
| PGO [10] | 1 | 5.3 |
| PGO + 0.2Cr [10] | 1.5 | 6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krupska-Klimczak, M.; Jankowska-Sumara, I.; Gwizd, P.; Koralewski, M.; Soszyński, A. Composition-Related Dielectric, Ferroelectric and Electrocaloric Properties of Pb5Ge3O11 Single Crystals Modified by Ba Ions. Materials 2023, 16, 413. https://doi.org/10.3390/ma16010413
Krupska-Klimczak M, Jankowska-Sumara I, Gwizd P, Koralewski M, Soszyński A. Composition-Related Dielectric, Ferroelectric and Electrocaloric Properties of Pb5Ge3O11 Single Crystals Modified by Ba Ions. Materials. 2023; 16(1):413. https://doi.org/10.3390/ma16010413
Chicago/Turabian StyleKrupska-Klimczak, Magdalena, Irena Jankowska-Sumara, Przemysław Gwizd, Marceli Koralewski, and Andrzej Soszyński. 2023. "Composition-Related Dielectric, Ferroelectric and Electrocaloric Properties of Pb5Ge3O11 Single Crystals Modified by Ba Ions" Materials 16, no. 1: 413. https://doi.org/10.3390/ma16010413
APA StyleKrupska-Klimczak, M., Jankowska-Sumara, I., Gwizd, P., Koralewski, M., & Soszyński, A. (2023). Composition-Related Dielectric, Ferroelectric and Electrocaloric Properties of Pb5Ge3O11 Single Crystals Modified by Ba Ions. Materials, 16(1), 413. https://doi.org/10.3390/ma16010413







