Solid-State Dewetting as a Driving Force for Structural Transformation and Magnetization Reversal Mechanism in FePd Thin Films
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
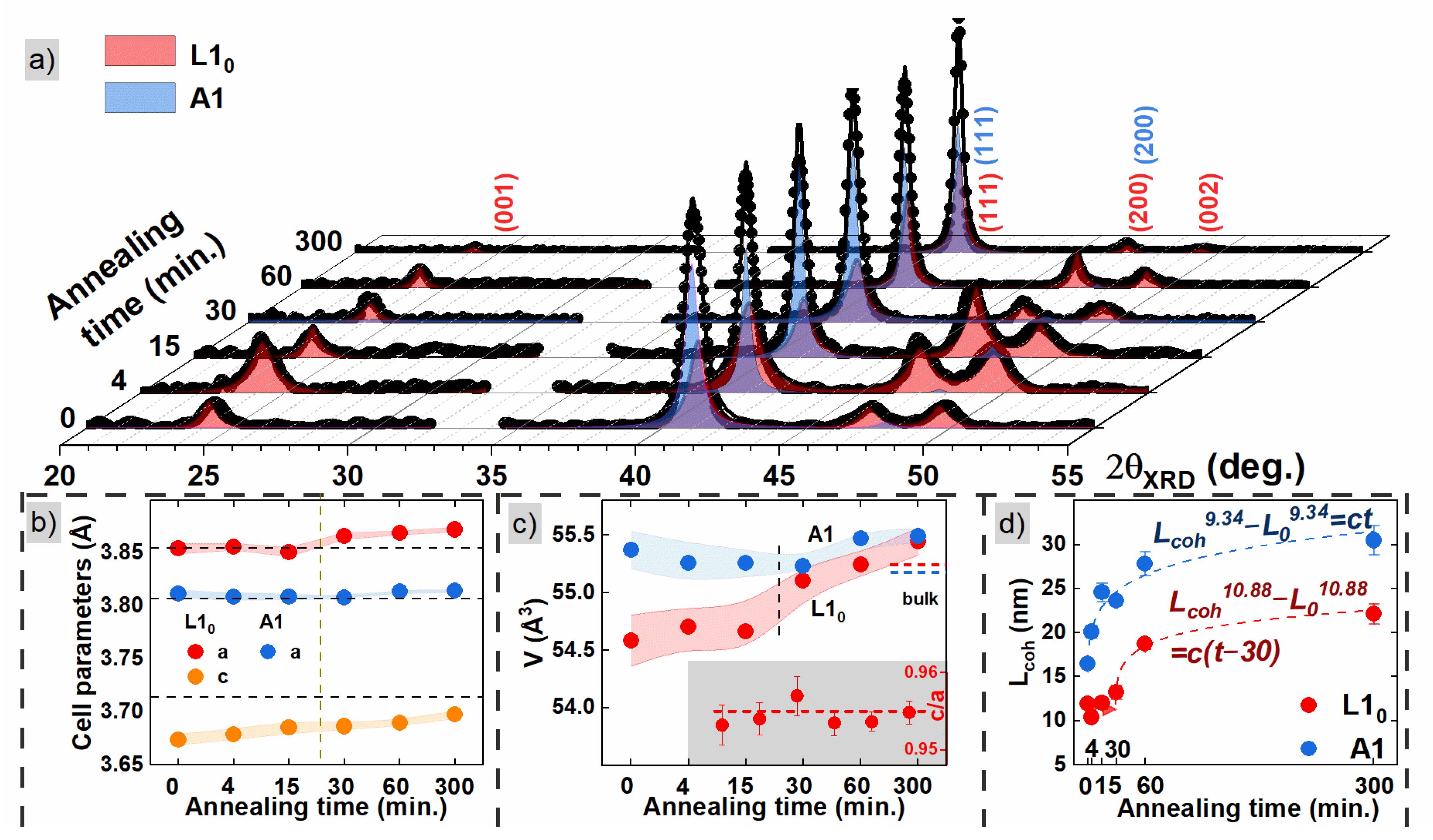
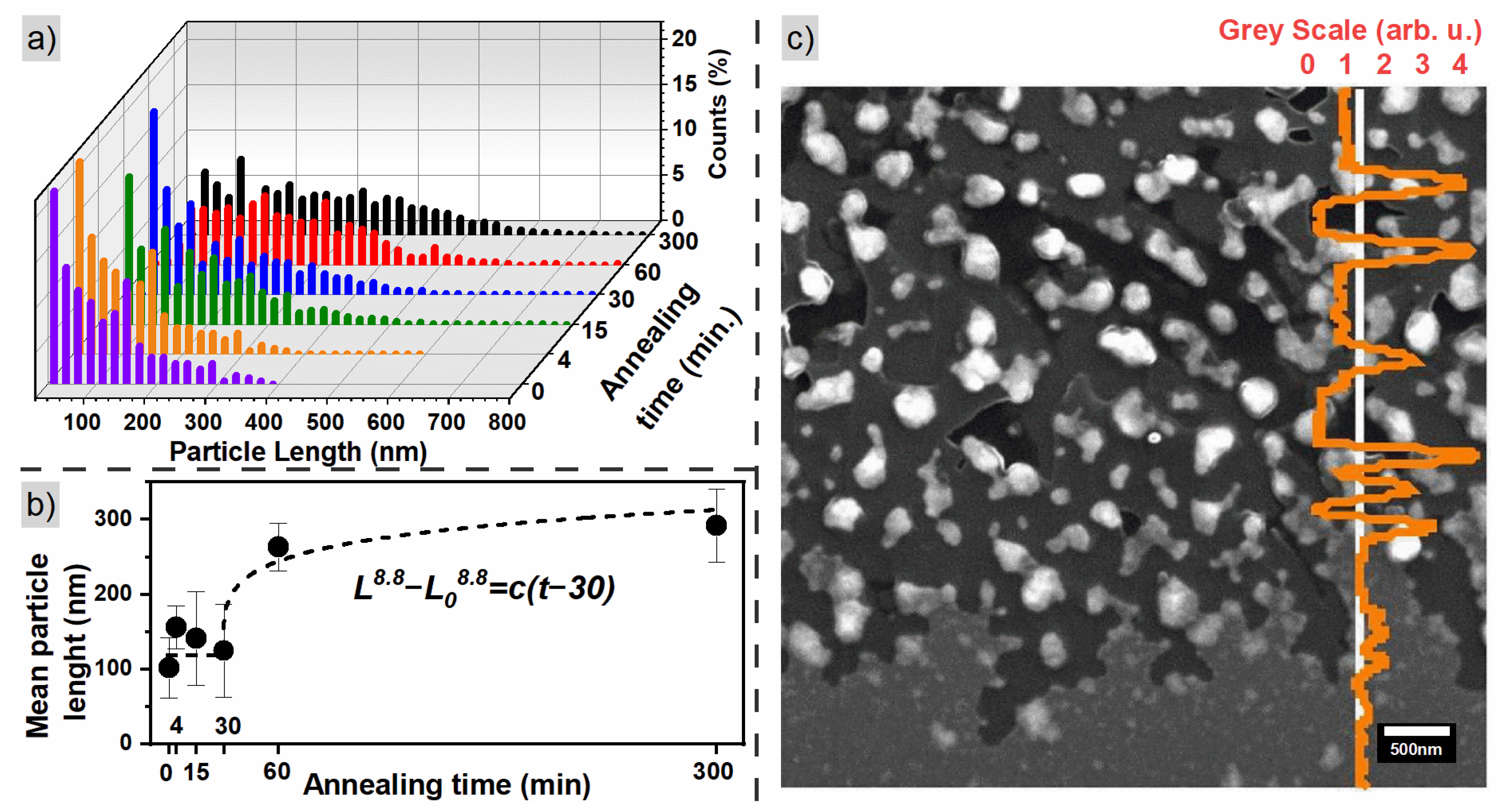
3.1. Crystallographic Structure and Morphology
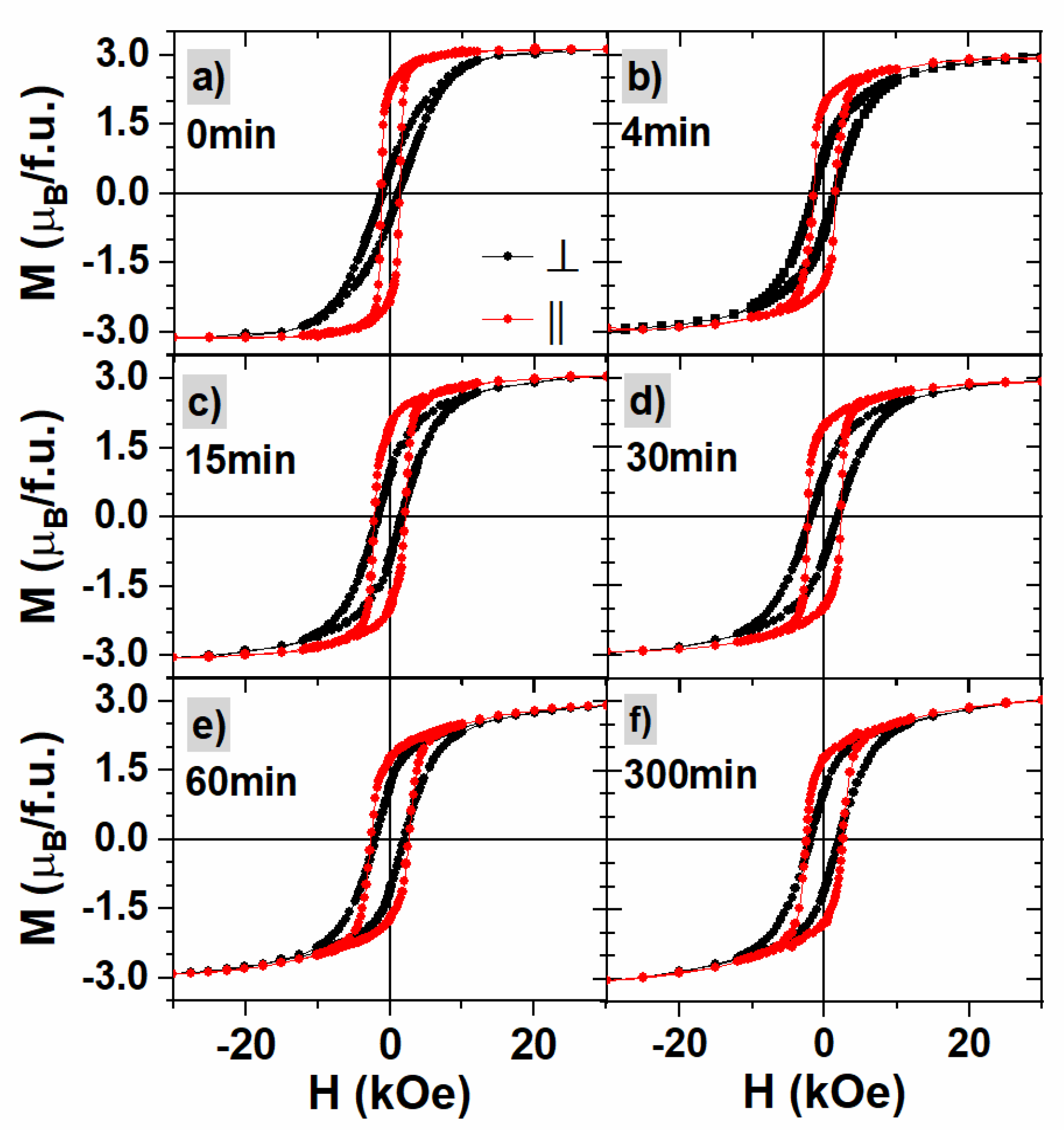
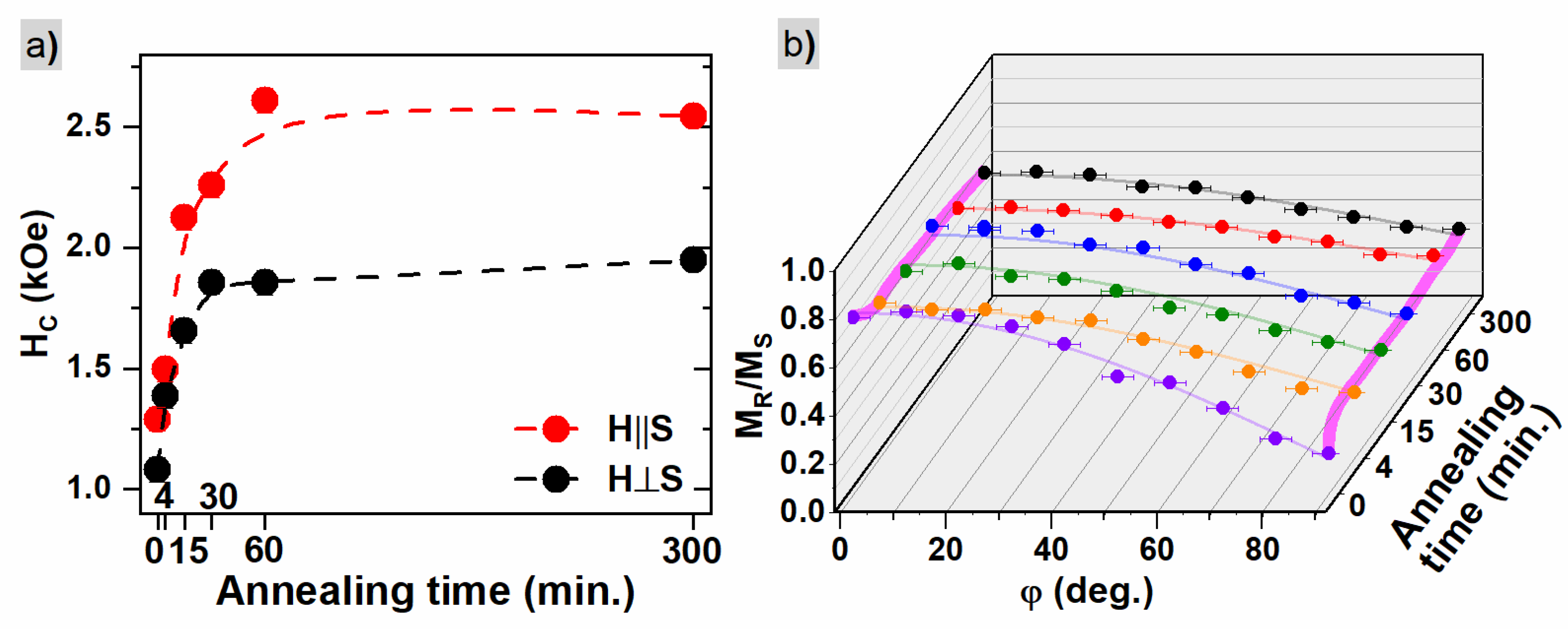
3.2. Macroscopic Magnetic Properties
- (the in-plane squareness value from Table 1);
- (the value of squareness for out-of-plane direction from Table 1).
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nguyen, D.C.; Chu, C.C.; Lee, C.H.; Lai, W.C.; Chang, C.-S.S. Coercivity enhancement of FePd thin films prepared by the post-annealing of off-stoichiometric magnetron-sputtered multilayers. J. Appl. Phys. 2018, 123, 073901. [Google Scholar] [CrossRef]
- Yu, G.-L.; Cheng, T.-M.; Cheng, Z.-R.; Zhang, X.-X. Exploration of new phase structure of FePd crystalline alloy with a stoichiometric of 1:1. Comput. Mater. Sci. 2021, 188, 110168. [Google Scholar] [CrossRef]
- Seiner, H.; Stoklasová, P.; Sedlák, P.; Ševčík, M.; Janovská, M.; Landa, M.; Fukuda, T.; Yamaguchi, T.; Kakeshita, T. Evolution of soft-phonon modes in Fe-Pd shape memory alloy under large elastic-like strains. Acta Mater. 2016, 105, 182–188. [Google Scholar] [CrossRef]
- Qin, H.J.; Zakeri, K.; Ernst, A.; Sandratskii, L.M.; Buczek, P.; Marmodoro, A.; Chuang, T.H.; Zhang, Y.; Kirschner, J. Long-living terahertz magnons in ultrathin metallic ferromagnets. Nat. Commun. 2015, 6, 6126. [Google Scholar] [CrossRef] [Green Version]
- Kumar, A.; Behera, N.; Gupta, R.; Husain, S.; Stopfel, H.; Kapaklis, V.; Brucas, R.; Svedlindh, P. Impact of the crystal orientation on spin-orbit torques in fe/pd bilayers. J. Phys. D. Appl. Phys. 2020, 53, 355003. [Google Scholar] [CrossRef]
- Mayr, S.; Ye, J.; Stahn, J.; Knoblich, B.; Klein, O.; Gilbert, D.A.; Albrecht, M.; Paul, A.; Böni, P.; Kreuzpaintner, W. Indications for Dzyaloshinskii-Moriya interaction at the Pd/Fe interface studied by in situ polarized neutron reflectometry. Phys. Rev. B 2020, 101, 24404. [Google Scholar] [CrossRef] [Green Version]
- Miranda, I.P.; Klautau, A.B.; Bergman, A.; Petrilli, H.M. Band filling effects on the emergence of magnetic skyrmions: Pd/Fe and Pd/Co bilayers on Ir(111). Phys. Rev. B 2022, 105, 224413. [Google Scholar] [CrossRef]
- Dupé, B.; Bihlmayer, G.; Böttcher, M.; Blügel, S.; Heinze, S. Engineering skyrmions in transition-metal multilayers for spintronics. Nat. Commun. 2016, 7, 11779. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Krylyuk, S.; Josell, D.; Zhang, D.; Wang, J.P.; Gopman, D.B. Effect of Oblique Versus Normal Deposition on the Properties of Perpendicularly Magnetized L10FePd Thin Films. IEEE Magn. Lett. 2020, 11, 2504105. [Google Scholar] [CrossRef]
- Iihama, S.; Sakuma, A.; Naganuma, H.; Oogane, M.; Mizukami, S.; Ando, Y. Influence of L10 order parameter on Gilbert damping constants for FePd thin films investigated by means of time-resolved magneto-optical Kerr effect. Phys. Rev. B 2016, 94, 174425. [Google Scholar] [CrossRef]
- Zhang, D.; Huang, D.; Wu, R.J.; Lattery, D.; Liu, J.; Wang, X.; Gopman, D.B.; Mkhoyan, K.A.; Wang, J.P.; Wang, X. Low Gilbert damping and high thermal stability of Ru-seeded L10-phase FePd perpendicular magnetic thin films at elevated temperatures. Appl. Phys. Lett. 2020, 117, 082405. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.L.; Sun, C.; Lv, Y.; Schliep, K.B.; Zhao, Z.; Chen, J.Y.; Voyles, P.M.; Wang, J.P. L10 Fe-Pd Synthetic Antiferromagnet through an fcc Ru Spacer Utilized for Perpendicular Magnetic Tunnel Junctions. Phys. Rev. Appl. 2018, 9, 44028. [Google Scholar] [CrossRef] [Green Version]
- Naganuma, H.; Kim, G.; Kawada, Y.; Inami, N.; Hatakeyama, K.; Iihama, S.; Nazrul Islam, K.M.; Oogane, M.; Mizukami, S.; Ando, Y. Electrical Detection of Millimeter-Waves by Magnetic Tunnel Junctions Using Perpendicular Magnetized L10 -FePd Free Layer. Nano Lett. 2015, 15, 623–628. [Google Scholar] [CrossRef]
- Zhang, D.-L.; Schliep, K.B.; Wu, R.J.; Quarterman, P.; Reifsnyder Hickey, D.; Lv, Y.; Chao, X.; Li, H.; Chen, J.-Y.; Zhao, Z.; et al. Enhancement of tunneling magnetoresistance by inserting a diffusion barrier in L1 0 -FePd perpendicular magnetic tunnel junctions. Appl. Phys. Lett. 2018, 112, 152401. [Google Scholar] [CrossRef] [Green Version]
- Bonell, F.; Murakami, S.; Shiota, Y.; Nozaki, T.; Shinjo, T.; Suzuki, Y. Large change in perpendicular magnetic anisotropy induced by an electric field in FePd ultrathin films. Appl. Phys. Lett. 2011, 98, 232510. [Google Scholar] [CrossRef]
- Seemann, K.M.; Hickey, M.C.; Baltz, V.; Hickey, B.J.; Marrows, C.H. Spin-dependent scattering and the spin polarization of a diffusive current in partly disordered L10 epitaxial FePd. New J. Phys. 2010, 12, 33033. [Google Scholar] [CrossRef] [Green Version]
- Wunderlich, W.; Takahashi, K.; Kubo, D.; Matsumura, Y.; Nishi, Y. Magnetostriction properties of FePd thin films: Dependence on microstructure. J. Alloys Compd. 2009, 475, 339–342. [Google Scholar] [CrossRef]
- Ma, Y.; Zink, M.; Mayr, S.G. Biocompatibility of single crystalline Fe70Pd30 ferromagnetic shape memory films. Appl. Phys. Lett. 2010, 96, 213703. [Google Scholar] [CrossRef]
- Rozman, K.Z.; Pecko, D.; Trafela, S.; Samardzija, Z.; Spreitzer, M.; Jaglicic, Z.; Nadrah, P.; Zorko, M.; Bele, M.; Tisler, T.; et al. Austenite-martensite transformation in electrodeposited Fe70Pd30 NWs: A step towards making bio-nano-actuators tested on in vivo systems. Smart Mater. Struct. 2018, 27, 35018. [Google Scholar] [CrossRef]
- Yang, Y.; Lyu, M.; Li, J.H.; Zhu, D.M.; Yuan, Y.F.; Liu, W. Ultra-small bimetallic iron-palladium (FePd) nanoparticle loaded macrophages for targeted tumor photothermal therapy in NIR-II biowindows and magnetic resonance imaging. RSC Adv. 2019, 9, 33378–33387. [Google Scholar] [CrossRef]
- Yang, Z.; Li, J.; Li, J.; Zhang, B.; Li, J.; Sheng, S.; Ding, P. Magnetic Properties and Biocompatibility of Different Thickness (Pd/Fe)n Coatings Deposited on Pure Ti Surface via Multi Arc Ion Plating. Materials 2022, 15, 1831. [Google Scholar] [CrossRef] [PubMed]
- Herrera, E.; Riva, J.; Aprea, S.; Silva, O.F.; Bercoff, P.G.; Granados, A.M. FePd nanowires modified with cyclodextrin as improved catalysts: Effect of the alloy composition on colloidal stability and catalytic capacity. Catal. Sci. Technol. 2022, 12, 2962–2971. [Google Scholar] [CrossRef]
- Zhang, N.; Qiu, Y.; Sun, H.; Hao, J.; Chen, J.; Xi, J.; Liu, J.; He, B.; Bai, Z.W. Substrate-Assisted Encapsulation of Pd-Fe Bimetal Nanoparticles on Functionalized Silica Nanotubes for Catalytic Hydrogenation of Nitroarenes and Azo Dyes. ACS Appl. Nano Mater. 2021, 4, 5854–5863. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Z.; Zhao, D.; Xu, C. Facile fabrication of nanoporous PdFe alloy for nonenzymatic electrochemical sensing of hydrogen peroxide and glucose. Anal. Chim. Acta 2014, 832, 34–43. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Feng, W.; Li, Y.; Tian, X.; Zhou, Z.; Lu, L.; Nie, Y. A promising method for diabetes early diagnosis via sensitive detection of urine glucose by Fe–Pd/rGO. Dye. Pigment. 2019, 164, 20–26. [Google Scholar] [CrossRef]
- Shao, Z.; An, L.; Li, Z.; Huang, Y.; Hu, Y.; Ren, S. Eutectic crystallized FePd nanoparticles for liquid metal magnet. Chem. Commun. 2020, 56, 6555–6558. [Google Scholar] [CrossRef] [PubMed]
- Chang, P.C.; Chuang, T.H.; Wei, D.H.; Lin, W.C. Thermally modulated hydrogenation in FexPd1-x alloy films: Temperature-driven peculiar variation of magnetism. Appl. Phys. Lett. 2020, 116, 102407. [Google Scholar] [CrossRef]
- Wang, W.H.; Cheng, Y.S.; Sheu, H.S.; Lin, W.C.; Jiang, P.H. Exchange-bias dependent diffusion rate of hydrogen discovered from evolution of hydrogen-induced noncollinear magnetic anisotropy in FePd thin films. Phys. Rev. B 2021, 104, 224420. [Google Scholar] [CrossRef]
- Vlasova, N.I.; Kandaurova, G.S.; Shchegoleva, N.N. Effect of the polytwinned microstructure parameters on magnetic domain structure and hysteresis properties of the CoPt-type alloys. J. Magn. Magn. Mater. 2000, 222, 138–158. [Google Scholar] [CrossRef]
- Steiner, M.A.; Comes, R.B.; Floro, J.A.; Soffa, W.A.; Fitz-Gerald, J.M. L1′ ordering: Evidence of L10–L12 hybridization in strained Fe38.5Pd61.5 epitaxial films. Acta Mater. 2015, 85, 261–269. [Google Scholar] [CrossRef]
- Vlasova, N.I.; Popov, A.G.; Shchegoleva, N.N.; Gaviko, V.S.; Stashkova, L.A.; Kandaurova, G.S.; Gunderov, D.V. Discovery of metastable tetragonal disordered phase upon phase transitions in the equiatomic nanostructured FePd alloy. Acta Mater. 2013, 61, 2560–2570. [Google Scholar] [CrossRef] [Green Version]
- Pathak, R.; Golovnia, O.A.; Gerasimov, E.G.; Popov, A.G.; Vlasova, N.I.; Skomski, R.; Kashyap, A. Ab initio study of the magnetic properties of possible phases in binary Fe-Pd alloys. J. Magn. Magn. Mater. 2020, 499, 166266. [Google Scholar] [CrossRef]
- Bahamida, S.; Fnidiki, A.; Coïsson, M.; Olivetti, E.S.; Barrera, G.; Celegato, F.; Tiberto, P.; Boudissa, M. Disordered to ordered phase transformation: Correlation between microstructure and magnetic properties in Fe-Pd thin films. J. Appl. Phys. 2022, 131, 123902. [Google Scholar] [CrossRef]
- Wang, X.; Krylyuk, S.; Josell, D.; Zhang, D.; Lyu, D.; Wang, J.P.; Gopman, D.B. Buffer layer engineering of L10FePd thin films with large perpendicular magnetic anisotropy. AIP Adv. 2021, 11, 25106. [Google Scholar] [CrossRef]
- Endo, Y.; Yamanaka, Y.; Kawamura, Y.; Yamamoto, M. Formation of L10-type ordered FePd phase in multilayers composed of Fe and Pd. Jpn. J. Appl. Phys. Part 1 Regul. Pap. Short Notes Rev. Pap. 2005, 44, 3009–3014. [Google Scholar] [CrossRef]
- Issro, C.; Püschl, W.; Pfeiler, W.; Rogl, P.F.; Soffa, W.A.; Acosta, M.; Schmerber, G.; Kozubski, R.; Pierron-Bohnes, V. Temperature-driven changes of order and magnetism in FePd thin films and thin foil. Scr. Mater. 2005, 53, 447–452. [Google Scholar] [CrossRef]
- Barrera, G.; Celegato, F.; Cialone, M.; Coïsson, M.; Rizzi, P.; Tiberto, P. Effect of the substrate crystallinity on morphological and magnetic properties of fe70pd30 nanoparticles obtained by the solid-state dewetting. Sensors 2021, 21, 7420. [Google Scholar] [CrossRef]
- Schuler, J.D.; Copeland, G.; Hattar, K.; Rupert, T.J.; Briggs, S.A. Solid-state dewetting instability in thermally-stable nanocrystalline binary alloys. Materialia 2020, 9, 100618. [Google Scholar] [CrossRef]
- Leroy, F.; Borowik, Ł.; Cheynis, F.; Almadori, Y.; Curiotto, S.; Trautmann, M.; Barbé, J.C.; Müller, P. How to control solid state dewetting: A short review. Surf. Sci. Rep. 2016, 71, 391–409. [Google Scholar] [CrossRef]
- Barrera, G.; Celegato, F.; Coïsson, M.; Cialone, M.; Rizzi, P.; Tiberto, P. Formation of free-standing magnetic particles by solid-state dewetting of Fe80Pd20 thin films. J. Alloys Compd. 2018, 742, 751–758. [Google Scholar] [CrossRef]
- Hsiao, S.N.; Liu, S.H.; Chen, C.C.; Chou, C.L.; Chen, S.K.; Su, S.H.; Chiu, K.F.; Sung, C.K. A comparison of rapid-annealed FePt and FePd thin films: Internal stress, L10 ordering, and texture. Vacuum 2016, 125, 1–5. [Google Scholar] [CrossRef]
- Perzanowski, M.; Zabila, Y.; Morgiel, J.; Polit, A.; Krupiński, M.; Dobrowolska, A.; Marszałek, M. AFM, XRD and HRTEM Studies οf Annealed FePd Thin Films. Acta Phys. Pol. A 2010, 117, 423–426. [Google Scholar] [CrossRef]
- Krupinski, M.; Perzanowski, M.; Zarzycki, A.; Zabila, Y.; Marszałek, M. Ordered FePdCu nanoisland arrays made by templated solid-state dewetting. Nanotechnology 2015, 26, 425301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Massalski, T.B.; Okamoto, H.; Subramanian, P.R.; Kacprzak, L. Alloy Phase Diagrams, 2nd ed.; Okamoto, H., Schlesinger, M.E., Mueller, E.M., Eds.; ASM International: Novelty, OH, USA, 2016; ISBN 978-1-62708-163-4. [Google Scholar]
- Perzanowski, M.; Krupinski, M.; Zarzycki, A.; Zabila, Y.; Marszalek, M. Determination of grain shape of laser-irradiated FePdCu thin alloy films. Appl. Surf. Sci. 2014, 302, 129–133. [Google Scholar] [CrossRef] [Green Version]
- Rodríguez-Carvajal, J. Recent developments of the program FULLPROF. Newsl. Comm. Powder Diffr. 2001, 26, 12–19. [Google Scholar]
- Ohtake, M.; Itabashi, A.; Futamoto, M.; Kirino, F.; Inaba, N. Crystal Orientation, Order Degree, and Surface Roughness of FePd-Alloy Film Formed on MgO(001) Substrate. IEEE Trans. Magn. 2015, 51, 2100904. [Google Scholar] [CrossRef]
- Vlasova, N.I.; Kleinerman, N.M.; Serikov, V.V.; Popov, A.G. Mössbauer study of fine structure features of equiatomic FePd alloy after severe plastic deformation and ordering annealing. J. Alloys Compd. 2014, 583, 191–197. [Google Scholar] [CrossRef]
- Futamoto, M.; Nakamura, M.; Ohtake, M.; Inaba, N.; Shimotsu, T. Growth of L10-ordered crystal in FePt and FePd thin films on MgO(001) substrate. AIP Adv. 2016, 6, 85302. [Google Scholar] [CrossRef] [Green Version]
- Shima, H.; Oikawa, K.; Fujita, A.; Fukamichi, K.; Ishida, K.; Sakuma, A. Lattice axial ratio and large uniaxial magnetocrystalline anisotropy in L10-type FePd single crystals prepared under compressive stress. Phys. Rev. B 2004, 70, 224408. [Google Scholar] [CrossRef]
- Krupinski, M.; Perzanowski, M.; Polit, A.; Zabila, Y.; Zarzycki, A.; Dobrowolska, A.; Marszalek, M. X-ray absorption fine structure and x-ray diffraction studies of crystallographic grains in nanocrystalline FePd:Cu thin films. J. Appl. Phys. 2011, 109, 64306. [Google Scholar] [CrossRef]
- Thompson, C. V Grain Growth in Thin Films. Annu. Rev. Mater. Sci. 1990, 20, 245–268. [Google Scholar] [CrossRef]
- Zotov, N.; Hiergeist, R.; Savan, A.; Ludwig, A. Effects of annealing time on the structural and magnetic properties of L10 FePt thin films. Thin Solid Films 2010, 518, 4977–4985. [Google Scholar] [CrossRef]
- Zaninetti, L. Poissonian and non-Poissonian Voronoi diagrams with application to the aggregation of molecules. Phys. Lett. Sect. A Gen. At. Solid State Phys. 2009, 373, 3223–3229. [Google Scholar] [CrossRef] [Green Version]
- Teran, A.V.; Bill, A.; Bergmann, R.B. Time-evolution of grain size distributions in random nucleation and growth crystallization processes. Phys. Rev. B 2010, 81, 75319. [Google Scholar] [CrossRef] [Green Version]
- Jacquet, P.; Podor, R.; Ravaux, J.; Teisseire, J.; Gozhyk, I.; Jupille, J.; Lazzari, R. Grain growth: The key to understand solid-state dewetting of silver thin films. Scr. Mater. 2016, 115, 128–132. [Google Scholar] [CrossRef] [Green Version]
- Sudheer; Mondal, P.; Rai, V.N.; Srivastava, A.K. A study of growth and thermal dewetting behavior of ultra-thin gold films using transmission electron microscopy. AIP Adv. 2017, 7, 75303. [Google Scholar] [CrossRef] [Green Version]
- Thompson, C.V. Solid-State Dewetting of Thin Films. Annu. Rev. Mater. Res. 2012, 42, 399–434. [Google Scholar] [CrossRef]
- Vlasova, N.I.; Popov, A.G.; Shchegoleva, N.N. Effect of the structural state of the FePd equiatomic alloy on the temperature dependence of the initial magnetic susceptibility and the Curie temperature. Phys. Met. Metallogr. 2009, 107, 359–369. [Google Scholar] [CrossRef]
- Cable, J.W.; Wollan, E.O.; Koehler, W.C. Distribution of magnetic moments in Pd-3d and Ni-3d alloys. Phys. Rev. 1965, 138, A755. [Google Scholar] [CrossRef]
- Galanakis, I.; Ostanin, S.; Alouani, M.; Dreyssé, H.; Wills, J.M. Theoretical study of magnetic properties and x-ray magnetic circular dichroism of the ordered Fe0.5Pd0.5 alloy. Phys. Rev. B 2000, 61, 599–608. [Google Scholar] [CrossRef]
- Liu, T.; Ma, L.; Zhao, S.Q.; Ma, D.D.; Li, L.; Cheng, G.; Rao, G.H. Crystal structure and magnetic properties of FexPd1−x thin films annealed at 550 °C. J. Mater. Sci. Mater. Electron. 2017, 28, 3616–3620. [Google Scholar] [CrossRef]
- O’Handley, R.C. Modern Magnetic Materials: Principles and Applications; Wiley-lnterscience Publicatio: New York, NY, USA, 2000; ISBN 978-0-471-15566-9. [Google Scholar]
- Yiping, L.; Hadjipanayis, G.C.; Sorensen, C.M.; Klabunde, K.J. Structural and magnetic properties of ultrafine Fe-Pd particles. J. Appl. Phys. 1994, 75, 5885–5887. [Google Scholar] [CrossRef]
- Idigoras, O.; Suszka, A.K.K.; Vavassori, P.; Obry, B.; Hillebrands, B.; Landeros, P.; Berger, A.; Vavasspri, P.; Obry, B.; Hillevrands, B.; et al. Magnetization reversal of in-plane uniaxial Co films and its dependence on epitaxial alignment. J. Appl. Phys. 2014, 115, 83912. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Z.; Ding, J.; Chen, J.; Wang, J. The effects of pinning layer on the magnetic properties of FePt perpendicular media. J. Magn. Magn. Mater. 2004, 272–276, 2186–2188. [Google Scholar] [CrossRef]
- Klemmer, T.; Hoydick, D.; Okumura, H.; Zhang, B.; Soffa, W.A. Magnetic hardening and coercivity mechanisms in L10ordered FePd ferromagnets. Scr. Metall. Mater. 1995, 33, 1793–1805. [Google Scholar] [CrossRef]
- Skomski, R.; Coey, J.M.D. Giant energy product in nanostructured two-phase magnets. Phys. Rev. B 1993, 48, 15812–15816. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baker, S.H.; Lees, M.; Roy, M.; Binns, C. Structure and magnetism in Fe/FexPd1-x core/shell nanoparticles formed by alloying in Pd-embedded Fe nanoparticles. J. Phys. Condens. Matter 2013, 25, 386004. [Google Scholar] [CrossRef]
- Tiberto, P.; Celegato, F.; Barrera, G.; Coisson, M.; Vinai, F.; Rizzi, P. Magnetization reversal and microstructure in polycrystalline Fe50Pd50 dot arrays by self-assembling of polystyrene nanospheres. Sci. Technol. Adv. Mater. 2016, 17, 462–472. [Google Scholar] [CrossRef] [Green Version]
- Stoner, E.C.; Wohlfarth, E.P. A mechanism of magnetic hysteresis in heterogeneous alloys. Philos. Trans. R. Soc. London. Ser. A Math. Phys. Sci. 1948, 240, 599–642. [Google Scholar] [CrossRef]
- Aharoni, A. Angular dependence of nucleation by curling in a prolate spheroid. J. Appl. Phys. 1997, 82, 1281–1287. [Google Scholar] [CrossRef]
- Kondorsky, E. On hysteresis in ferromagnetics. J. Phys. 1940, 2, 161. [Google Scholar]
- Ratnam, D.V.; Buessem, W.R. Angular Variation of Coercive Force in Barium Ferrite. J. Appl. Phys. 1972, 43, 1291–1293. [Google Scholar] [CrossRef]
- Suponev, N.P.; Grechishkin, R.M.; Lyakhova, M.B.; Pushkar, Y.E. Angular dependence of coercive field in (Sm,Zr) (Co,Cu,Fe) alloys. J. Magn. Magn. Mater. 1996, 157-158, 376–377. [Google Scholar] [CrossRef]
- Mathews, M.; Houwman, E.P.; Boschker, H.; Rijnders, G.; Blank, D.H.A. Magnetization reversal mechanism in La0.67Sr0.33MnO3thin films on NdGaO3substrates. J. Appl. Phys. 2010, 107, 013904. [Google Scholar] [CrossRef]
- Han, X.M.; Ma, J.H.; Wang, Z.; Yao, Y.L.; Zuo, Y.L.; Xi, L.; Xue, D.S. Tunable in-plane uniaxial anisotropy and the magnetization reversal mechanism of patterned high-frequency soft magnetic FeTa strips. J. Phys. D. Appl. Phys. 2013, 46, 485004. [Google Scholar] [CrossRef]
- Kronmüller, H.; Durst, K.-D.; Sagawa, M. Analysis of the magnetic hardening mechanism in RE-FeB permanent magnets. J. Magn. Magn. Mater. 1988, 74, 291–302. [Google Scholar] [CrossRef]
- Givord, D.; Rossignol, M.F.; Taylor, D.W. Coercivity mechanisms in hard magnetic materials. J. Phys. IV 1992, 02, C3-95–C3-104. [Google Scholar] [CrossRef]
- Viqueira, M.S.; Bajales, N.; Urreta, S.E.; Bercoff, P.G. Magnetization mechanisms in ordered arrays of polycrystalline Fe 100−x Co x nanowires. J. Appl. Phys. 2015, 117, 204302. [Google Scholar] [CrossRef] [Green Version]
- Komogortsev, S.V.; Fel’k, V.A.; Li, O.A. The magnetic dipole-dipole interaction effect on the magnetic hysteresis at zero temperature in nanoparticles randomly dispersed within a plane. J. Magn. Magn. Mater. 2019, 473, 410–415. [Google Scholar] [CrossRef]

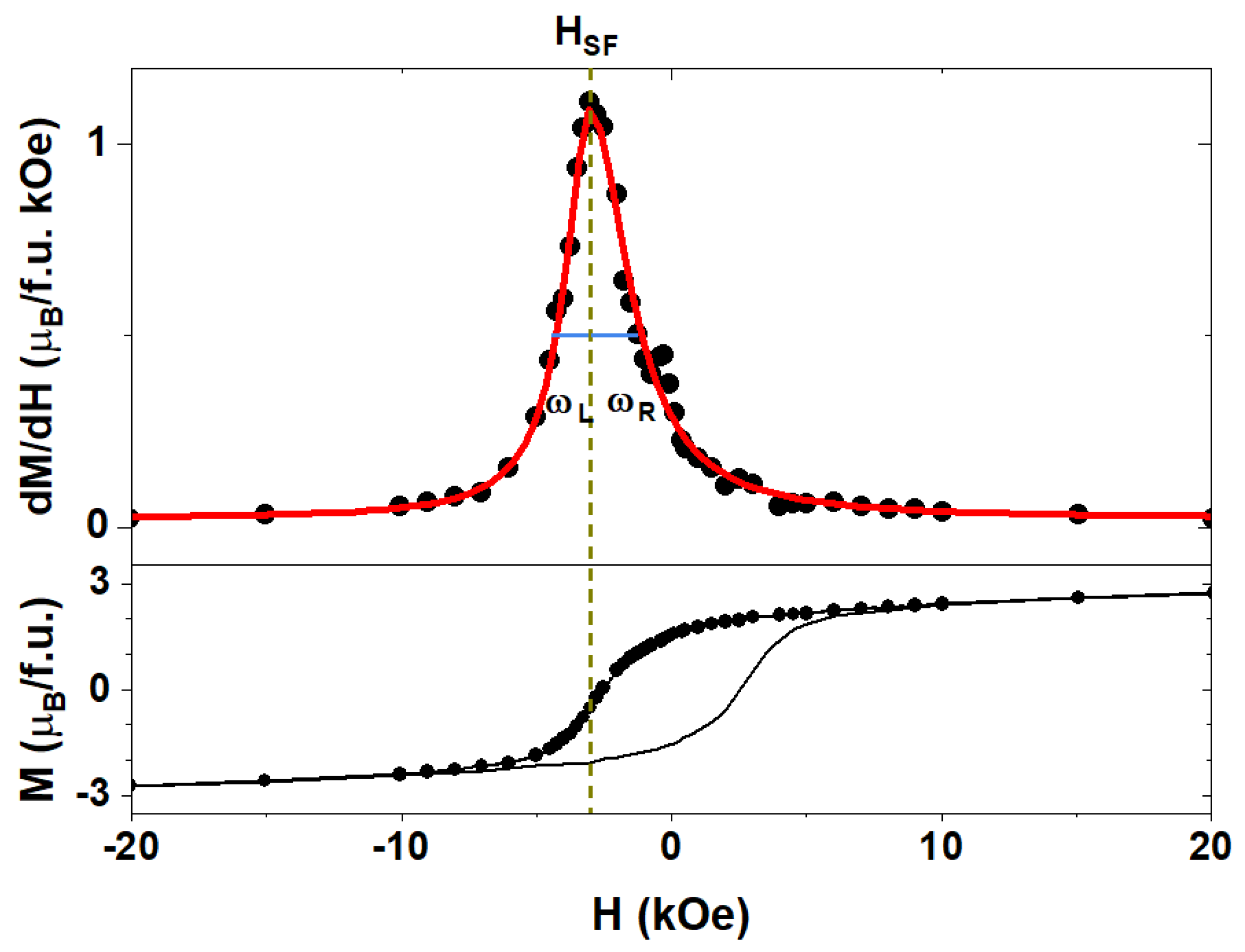
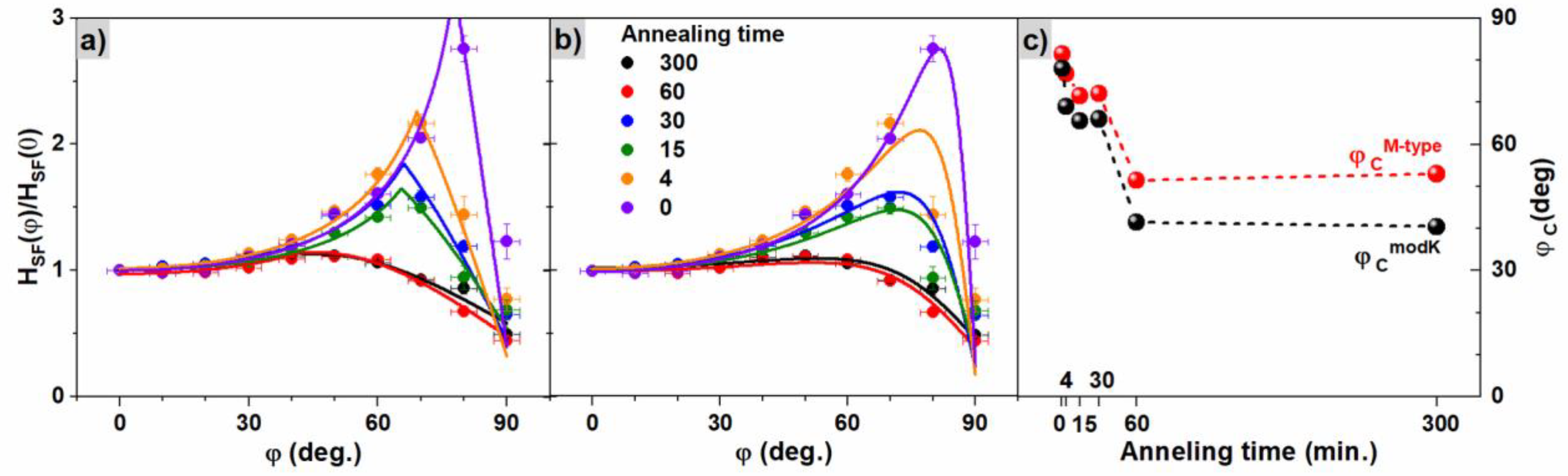
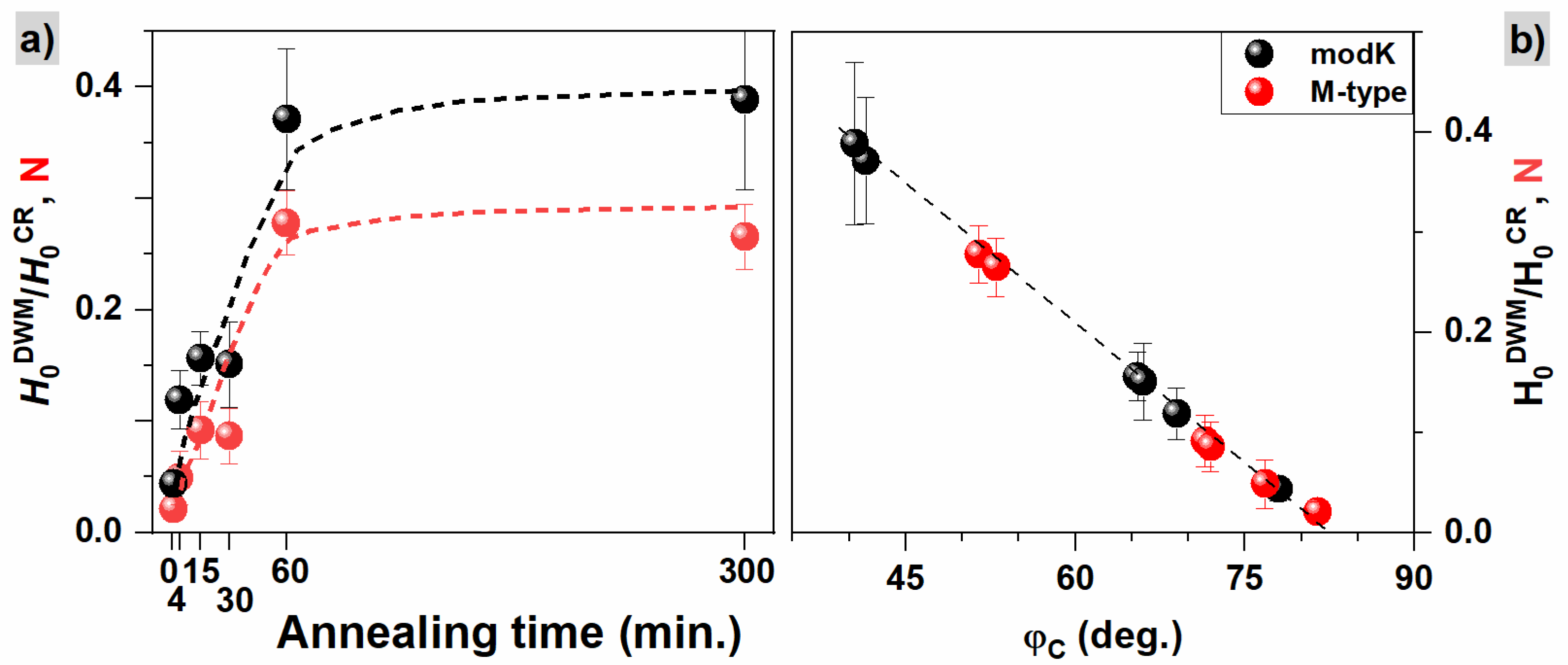
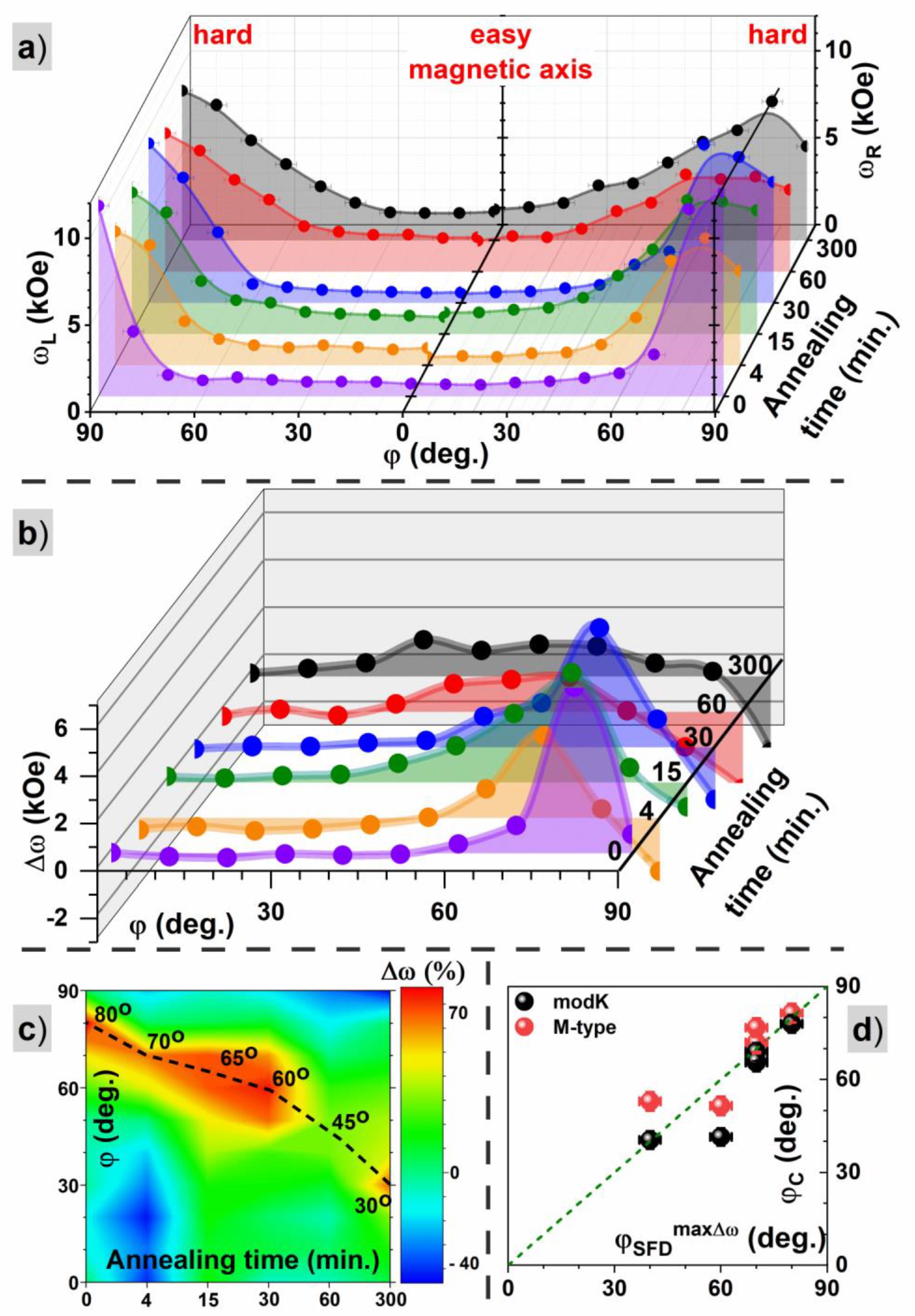
| Time of Annealing (min) | (kOe) ±0.05 | (f.u.) ±0.03 | (f.u.) ±0.03 | ±0.02 | (kOe) ±0.05 | (f.u.) ±0.03 | (f.u.) ±0.03 | ±0.01 | (MJ/m3) ±0.02 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1.29 | 2.28 | 3.11 | 0.73 | 1.08 | 0.53 | 3.12 | 0.17 | 0.41 |
| 4 | 1.49 | 1.91 | 2.97 | 0.64 | 1.38 | 0.81 | 2.96 | 0.27 | 0.26 |
| 15 | 2.12 | 1.92 | 3.06 | 0.63 | 1.66 | 0.91 | 3.04 | 0.30 | 0.26 |
| 30 | 2.26 | 1.94 | 2.94 | 0.66 | 1.86 | 0.89 | 2.96 | 0.30 | 0.26 |
| 60 | 2.61 | 1.69 | 2.88 | 0.60 | 1.85 | 1.15 | 2.94 | 0.39 | 0.16 |
| 300 | 2.55 | 1.79 | 3.08 | 0.61 | 1.95 | 1.08 | 3.09 | 0.35 | 0.16 |
| Time of Annealing (min) | (deg.) | ||||
|---|---|---|---|---|---|
| 0 | 0.613(22) | 0.151(14) | 0.764(36) | 1.7 | 0.80(4) |
| 4 | 0.399(14) | 0.249(9) | 0.648(24) | 3.0 | 0.62(4) |
| 15 | 0.361(14) | 0.279(9) | 0.641(23) | 3.2 | 0.56(5) |
| 30 | 0.379(12) | 0.283(8) | 0.662(20) | 2.8 | 0.57(4) |
| 60 | 0.216(5) | 0.377(4) | 0.593(9) | 3.5 | 0.36(3) |
| 300 | 0.256(9) | 0.331(6) | 0.588(14) | 4.4 | 0.44(4) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zarzycki, A.; Perzanowski, M.; Krupinski, M.; Marszalek, M. Solid-State Dewetting as a Driving Force for Structural Transformation and Magnetization Reversal Mechanism in FePd Thin Films. Materials 2023, 16, 92. https://doi.org/10.3390/ma16010092
Zarzycki A, Perzanowski M, Krupinski M, Marszalek M. Solid-State Dewetting as a Driving Force for Structural Transformation and Magnetization Reversal Mechanism in FePd Thin Films. Materials. 2023; 16(1):92. https://doi.org/10.3390/ma16010092
Chicago/Turabian StyleZarzycki, Arkadiusz, Marcin Perzanowski, Michal Krupinski, and Marta Marszalek. 2023. "Solid-State Dewetting as a Driving Force for Structural Transformation and Magnetization Reversal Mechanism in FePd Thin Films" Materials 16, no. 1: 92. https://doi.org/10.3390/ma16010092
APA StyleZarzycki, A., Perzanowski, M., Krupinski, M., & Marszalek, M. (2023). Solid-State Dewetting as a Driving Force for Structural Transformation and Magnetization Reversal Mechanism in FePd Thin Films. Materials, 16(1), 92. https://doi.org/10.3390/ma16010092






