A Numerical Investigation of Dimensionless Numbers Characterizing Meltpool Morphology of the Laser Powder Bed Fusion Process
Abstract
:1. Introduction
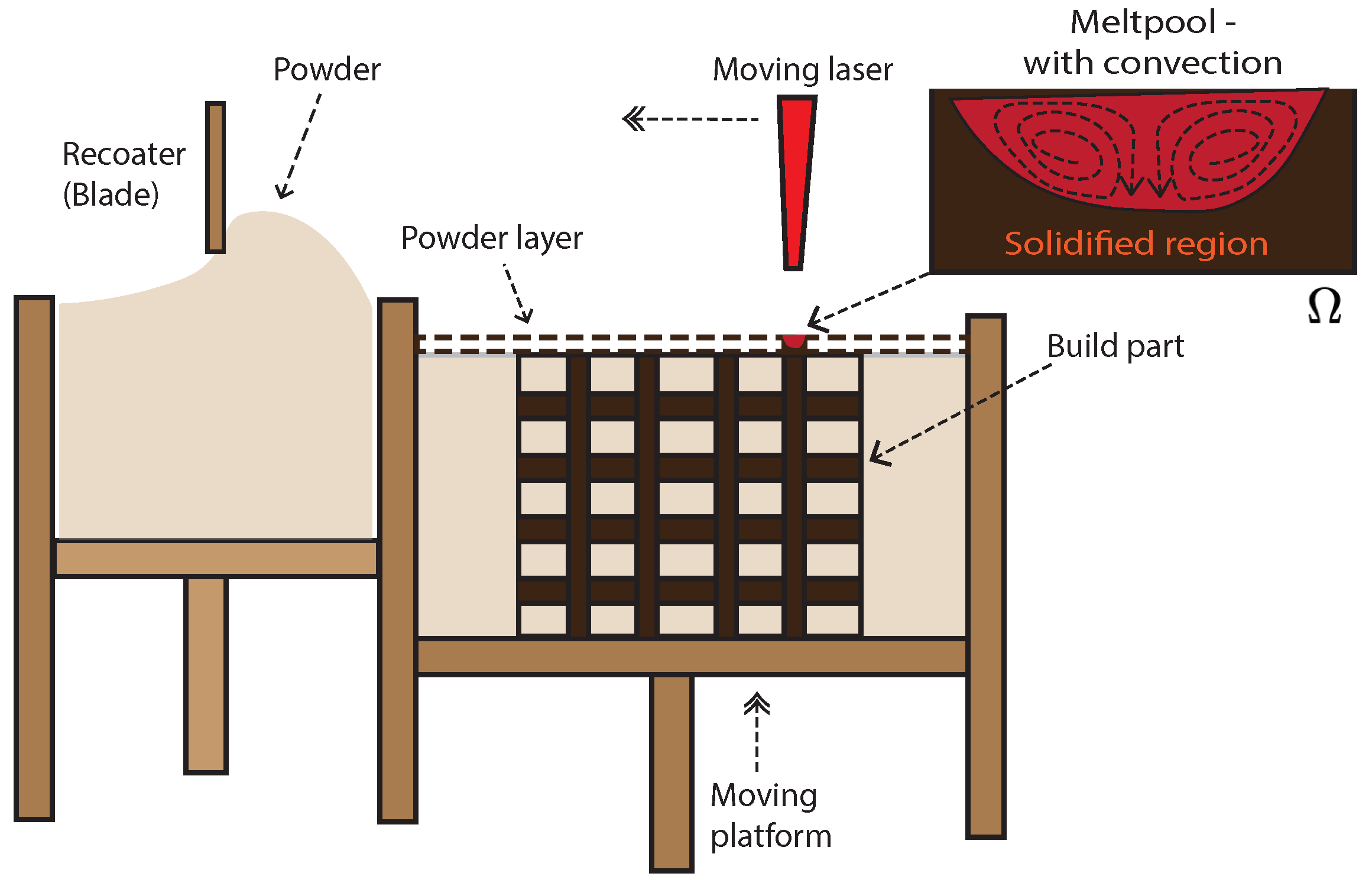
2. Governing Equations of the LPBF Process
2.1. Thermo-Fluidic Model of the LPBF Process
2.2. Non-Dimensional Formulation of the Governing Equations
Weak Formulation
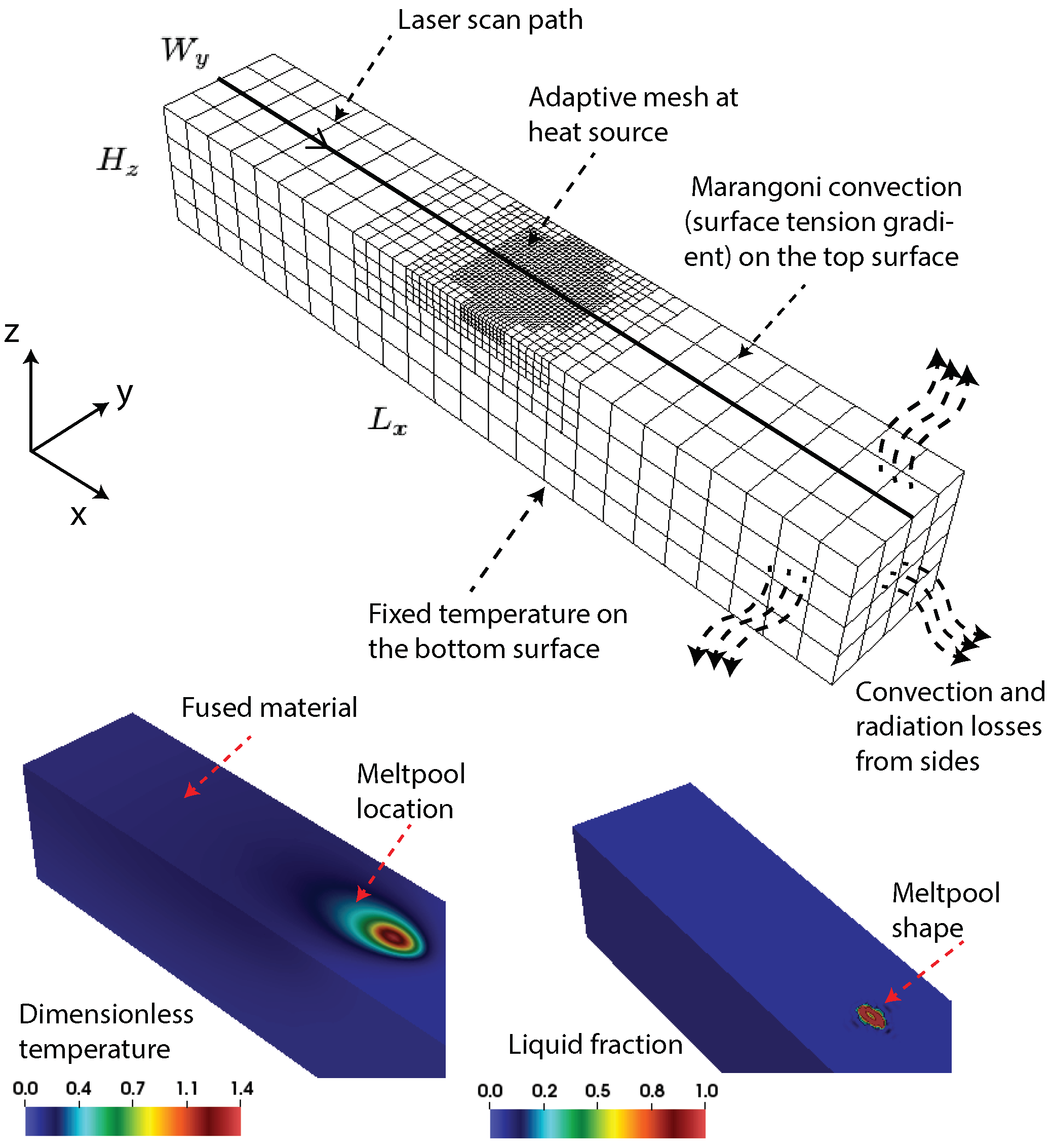
2.3. Computational Implementation
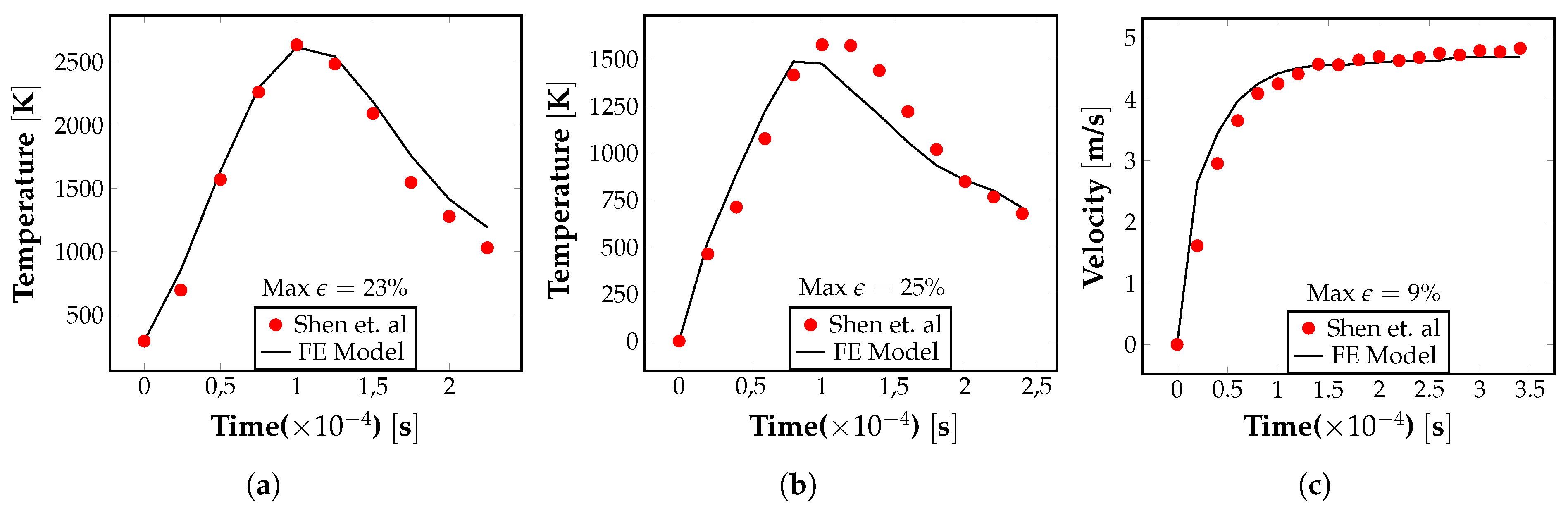
3. Experimental and Numerical Validation
4. Empirical Analysis of the Energy Absorbed by the Meltpool
4.1. Process Variables, Material Properties, and Output Variables
4.2. Parametrization in Terms of the Dimensionless Quantities
5. Results
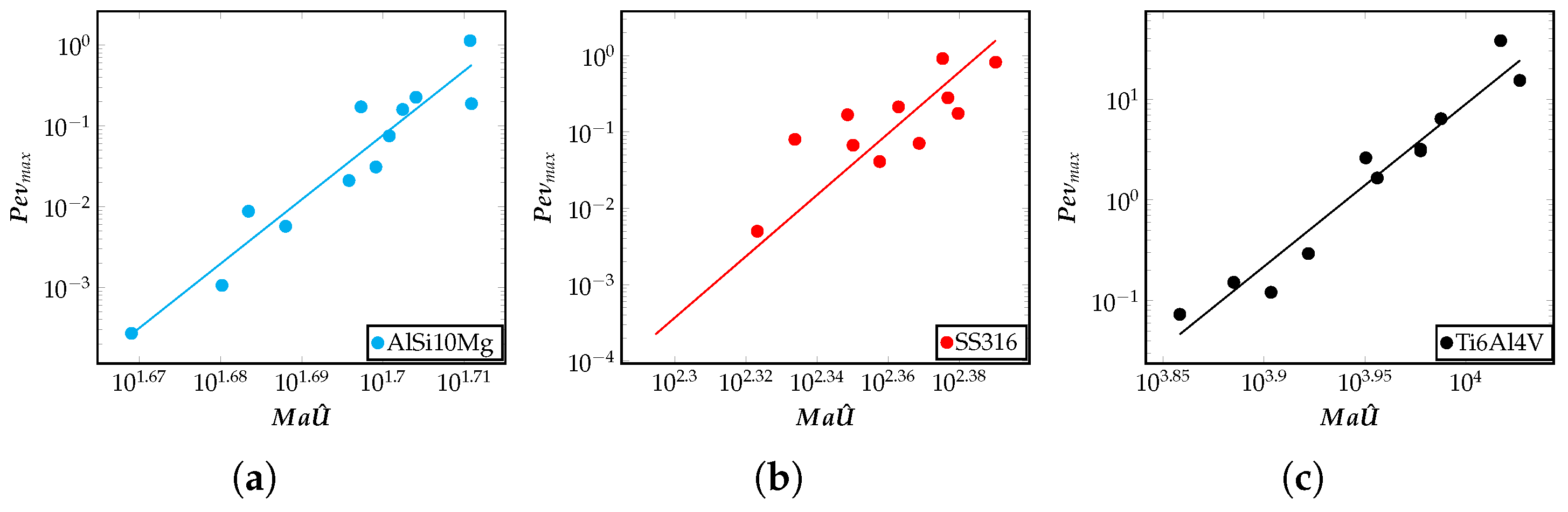
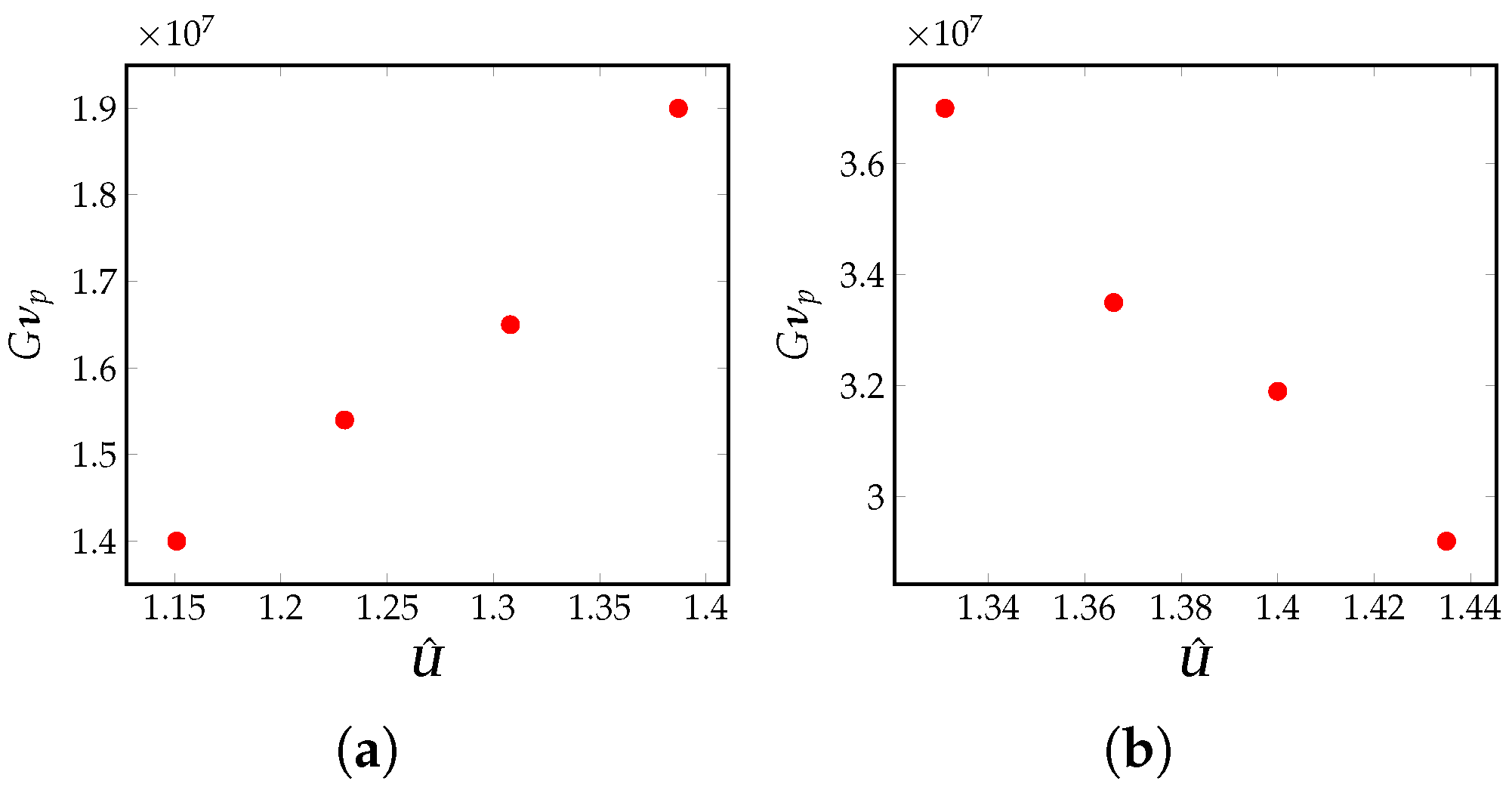
5.1. Influence of Péclet Number on Advection Transport in the Meltpool
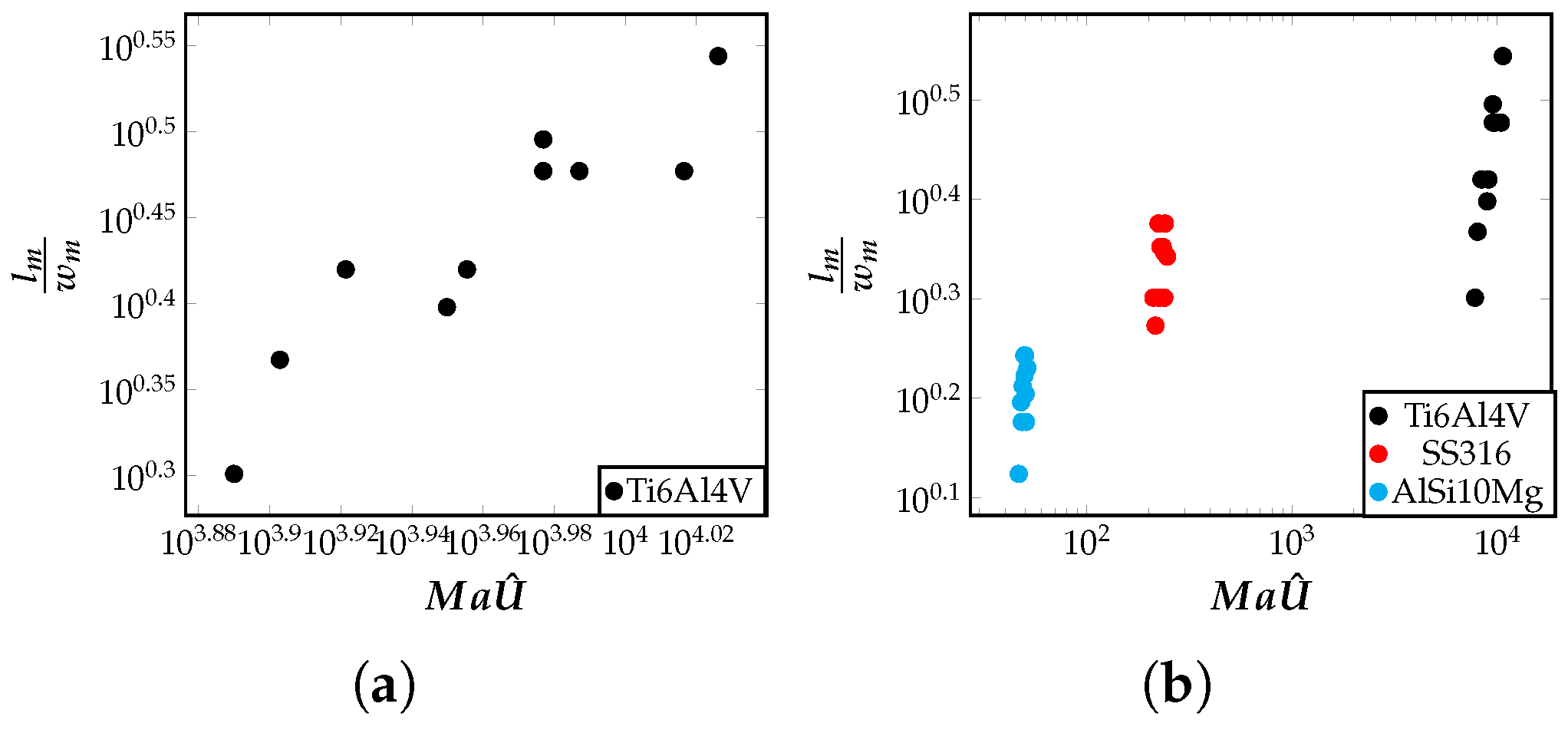
5.2. Influence of Marangoni Number on the Meltpool Aspect Ratio
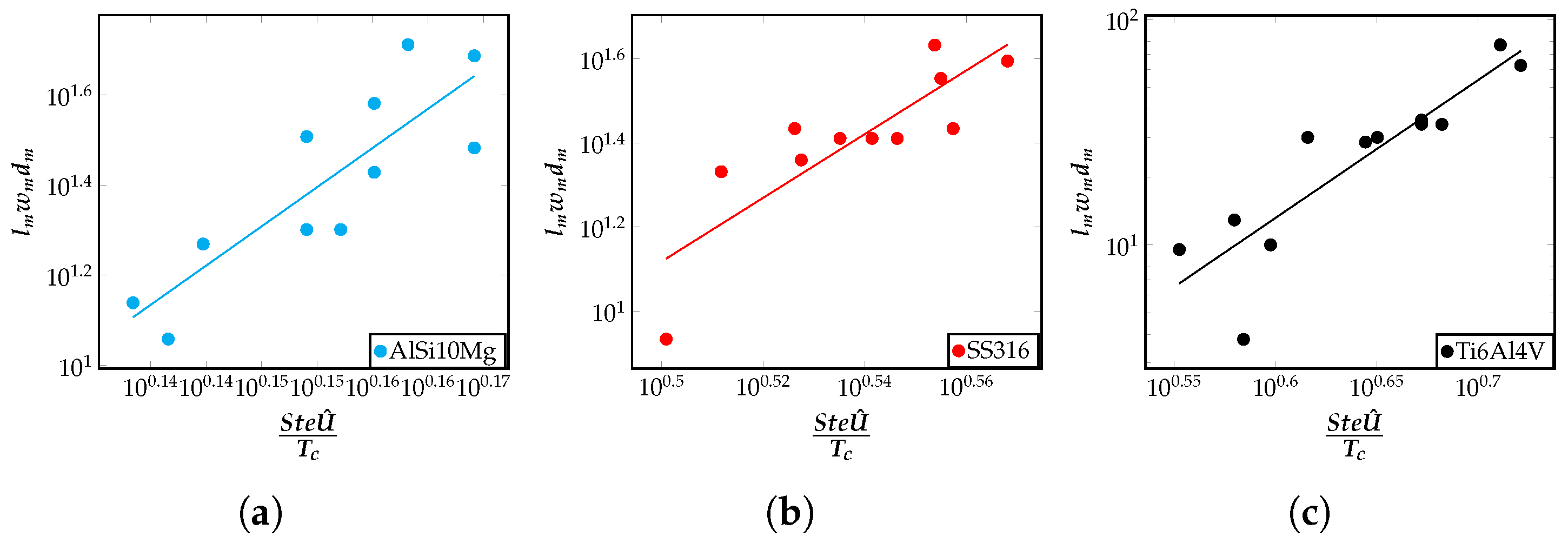
5.3. Influence of Stefan Number on Meltpool Volume
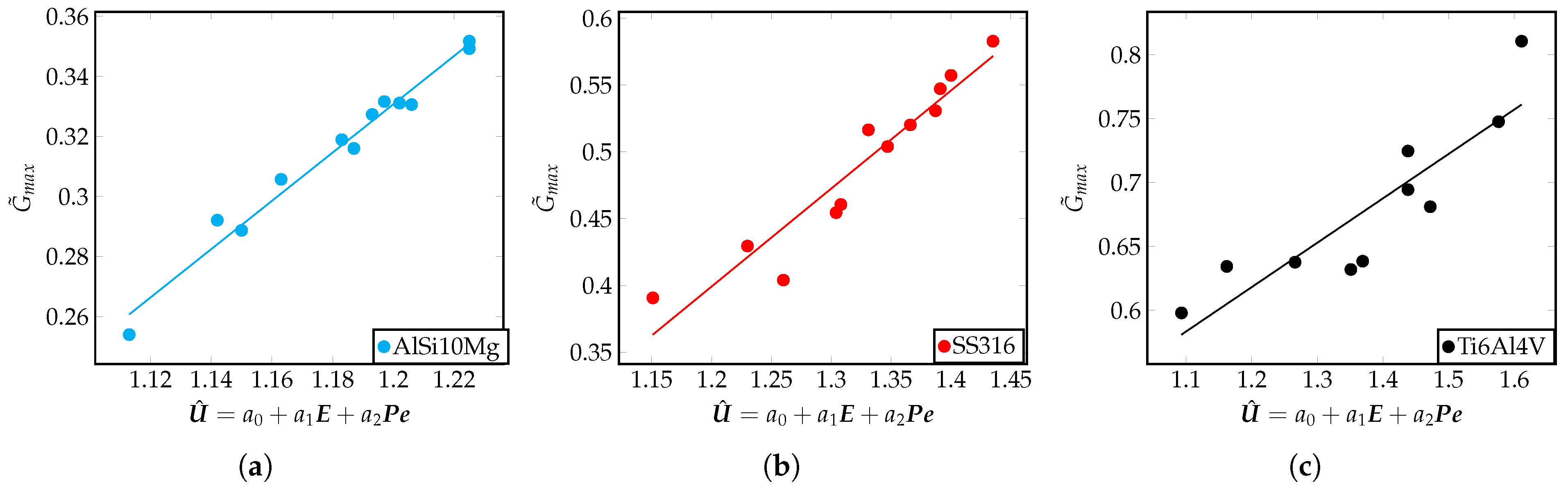
5.4. Influence of the Heat Absorbed on the Solidification Cooling Rates
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huang, Y.; Leu, M.C.; Mazumder, J.; Donmez, A. Additive manufacturing: Current state, future potential, gaps and needs, and recommendations. J. Manuf. Sci. Eng. 2015, 137, 014001. [Google Scholar] [CrossRef] [Green Version]
- Gibson, I.; Rosen, D.W.; Stucker, B.; Khorasani, M. Additive Manufacturing Technologies; Springer: Berlin/Heidelberg, Germany, 2021; Volume 17. [Google Scholar]
- Konda Gokuldoss, P.; Kolla, S.; Eckert, J. Additive manufacturing processes: Selective laser melting, electron beam melting and binder jetting—Selection guidelines. Materials 2017, 10, 672. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Y.M.; Voisin, T.; McKeown, J.T.; Ye, J.; Calta, N.P.; Li, Z.; Zeng, Z.; Zhang, Y.; Chen, W.; Roehling, T.T.; et al. Additively manufactured hierarchical stainless steels with high strength and ductility. Nat. Mater. 2018, 17, 63–71. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qian, M.; Xu, W.; Brandt, M.; Tang, H. Additive manufacturing and postprocessing of Ti-6Al-4V for superior mechanical properties. MRS Bull. 2016, 41, 775–784. [Google Scholar] [CrossRef] [Green Version]
- Rittinghaus, S.K.; Jägle, E.A.; Schmid, M.; Gökce, B. New Frontiers in Materials Design for Laser Additive Manufacturing. Materials 2022, 15, 6172. [Google Scholar] [CrossRef]
- King, W.E.; Anderson, A.T.; Ferencz, R.M.; Hodge, N.E.; Kamath, C.; Khairallah, S.A.; Rubenchik, A.M. Laser powder bed fusion additive manufacturing of metals; Physics, computational, and materials challenges. Appl. Phys. Rev. 2015, 2, 041304. [Google Scholar] [CrossRef]
- Fox, J.C.; Moylan, S.P.; Lane, B.M. Effect of process parameters on the surface roughness of overhanging structures in laser powder bed fusion additive manufacturing. Procedia Cirp 2016, 45, 131–134. [Google Scholar] [CrossRef] [Green Version]
- Dinovitzer, M.; Chen, X.; Laliberte, J.; Huang, X.; Frei, H. Effect of wire and arc additive manufacturing (WAAM) process parameters on bead geometry and microstructure. Addit. Manuf. 2019, 26, 138–146. [Google Scholar] [CrossRef]
- Ning, F.; Cong, W.; Hu, Y.; Wang, H. Additive manufacturing of carbon fiber-reinforced plastic composites using fused deposition modeling: Effects of process parameters on tensile properties. J. Compos. Mater. 2017, 51, 451–462. [Google Scholar] [CrossRef]
- Makoana, N.W.; Yadroitsava, I.; Möller, H.; Yadroitsev, I. Characterization of 17-4PH single tracks produced at different parametric conditions towards increased productivity of LPBF systems—The effect of laser power and spot size upscaling. Metals 2018, 8, 475. [Google Scholar] [CrossRef]
- Letenneur, M.; Kreitcberg, A.; Brailovski, V. Optimization of laser powder bed fusion processing using a combination of melt pool modeling and design of experiment approaches: Density control. J. Manuf. Mater. Process. 2019, 3, 21. [Google Scholar] [CrossRef] [Green Version]
- Mirkoohi, E.; Ning, J.; Bocchini, P.; Fergani, O.; Chiang, K.N.; Liang, S.Y. Thermal modeling of temperature distribution in metal additive manufacturing considering effects of build layers, latent heat, and temperature-sensitivity of material properties. J. Manuf. Mater. Process. 2018, 2, 63. [Google Scholar] [CrossRef] [Green Version]
- Mirkoohi, E.; Seivers, D.E.; Garmestani, H.; Liang, S.Y. Heat source modeling in selective laser melting. Materials 2019, 12, 2052. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mondal, S.; Gwynn, D.; Ray, A.; Basak, A. Investigation of melt pool geometry control in additive manufacturing using hybrid modeling. Metals 2020, 10, 683. [Google Scholar] [CrossRef]
- Abolhasani, D.; Seyedkashi, S.H.; Kang, N.; Kim, Y.J.; Woo, Y.Y.; Moon, Y.H. Analysis of melt-pool behaviors during selective laser melting of AISI 304 stainless-steel composites. Metals 2019, 9, 876. [Google Scholar] [CrossRef] [Green Version]
- Ansari, M.J.; Nguyen, D.S.; Park, H.S. Investigation of SLM process in terms of temperature distribution and melting pool size: Modeling and experimental approaches. Materials 2019, 12, 1272. [Google Scholar] [CrossRef] [Green Version]
- Dong, Z.; Liu, Y.; Wen, W.; Ge, J.; Liang, J. Effect of hatch spacing on melt pool and as-built quality during selective laser melting of stainless steel: Modeling and experimental approaches. Materials 2018, 12, 50. [Google Scholar] [CrossRef] [Green Version]
- Ansari, P.; Rehman, A.U.; Pitir, F.; Veziroglu, S.; Mishra, Y.K.; Aktas, O.C.; Salamci, M.U. Selective laser melting of 316l austenitic stainless steel: Detailed process understanding using multiphysics simulation and experimentation. Metals 2021, 11, 1076. [Google Scholar] [CrossRef]
- Gusarov, A.; Yadroitsev, I.; Bertrand, P.; Smurov, I. Heat transfer modelling and stability analysis of selective laser melting. Appl. Surf. Sci. 2007, 254, 975–979. [Google Scholar] [CrossRef]
- Mukherjee, T.; Wei, H.; De, A.; DebRoy, T. Heat and fluid flow in additive manufacturing—Part I: Modeling of powder bed fusion. Comput. Mater. Sci. 2018, 150, 304–313. [Google Scholar] [CrossRef]
- Khairallah, S.A.; Anderson, A. Mesoscopic simulation model of selective laser melting of stainless steel powder. J. Mater. Process. Technol. 2014, 214, 2627–2636. [Google Scholar] [CrossRef]
- Wang, Z.; Yan, W.; Liu, W.K.; Liu, M. Powder-scale multi-physics modeling of multi-layer multi-track selective laser melting with sharp interface capturing method. Comput. Mech. 2019, 63, 649–661. [Google Scholar] [CrossRef]
- Keshavarzkermani, A.; Marzbanrad, E.; Esmaeilizadeh, R.; Mahmoodkhani, Y.; Ali, U.; Enrique, P.D.; Zhou, N.Y.; Bonakdar, A.; Toyserkani, E. An investigation into the effect of process parameters on melt pool geometry, cell spacing, and grain refinement during laser powder bed fusion. Opt. Laser Technol. 2019, 116, 83–91. [Google Scholar] [CrossRef]
- Fayazfar, H.; Salarian, M.; Rogalsky, A.; Sarker, D.; Russo, P.; Paserin, V.; Toyserkani, E. A critical review of powder-based additive manufacturing of ferrous alloys: Process parameters, microstructure and mechanical properties. Mater. Des. 2018, 144, 98–128. [Google Scholar] [CrossRef]
- Ruzicka, M. On dimensionless numbers. Chem. Eng. Res. Des. 2008, 86, 835–868. [Google Scholar] [CrossRef]
- Van Elsen, M.; Al-Bender, F.; Kruth, J.P. Application of dimensional analysis to selective laser melting. Rapid Prototyp. J. 2008, 14, 15–22. [Google Scholar] [CrossRef]
- Islam, Z.; Agrawal, A.K.; Rankouhi, B.; Magnin, C.; Anderson, M.H.; Pfefferkorn, F.E.; Thoma, D.J. A high-throughput method to define additive manufacturing process parameters: Application to Haynes 282. Metall. Mater. Trans. A 2022, 53, 250–263. [Google Scholar] [CrossRef]
- Weaver, J.S.; Heigel, J.C.; Lane, B.M. Laser spot size and scaling laws for laser beam additive manufacturing. J. Manuf. Process. 2022, 73, 26–39. [Google Scholar] [CrossRef]
- Rankouhi, B.; Agrawal, A.K.; Pfefferkorn, F.E.; Thoma, D.J. A dimensionless number for predicting universal processing parameter boundaries in metal powder bed additive manufacturing. Manuf. Lett. 2021, 27, 13–17. [Google Scholar] [CrossRef]
- Gan, Z.; Kafka, O.L.; Parab, N.; Zhao, C.; Fang, L.; Heinonen, O.; Sun, T.; Liu, W.K. Universal scaling laws of keyhole stability and porosity in 3D printing of metals. Nat. Commun. 2021, 12, 2379. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, M. Dimensionless analysis on selective laser melting to predict porosity and track morphology. J. Mater. Process. Technol. 2019, 273, 116238. [Google Scholar] [CrossRef]
- Noh, J.; Lee, J.; Seo, Y.; Hong, S.; Kwon, Y.S.; Kim, D. Dimensionless parameters to define process windows of selective laser melting process to fabricate three-dimensional metal structures. Opt. Laser Technol. 2022, 149, 107880. [Google Scholar] [CrossRef]
- Ahsan, F.; Razmi, J.; Ladani, L. Global local modeling of melt pool dynamics and bead formation in laser bed powder fusion additive manufacturing using a multi-physics thermo-fluid simulation. Prog. Addit. Manuf. 2022, 7, 1275–1285. [Google Scholar] [CrossRef]
- Wu, J.; Zheng, X.; Zhang, Y.; Ren, S.; Yin, C.; Cao, Y.; Zhang, D. Modeling of whole-phase heat transport in laser-based directed energy deposition with multichannel coaxial powder feeding. Addit. Manuf. 2022, 59, 103161. [Google Scholar] [CrossRef]
- Cardaropoli, F.; Alfieri, V.; Caiazzo, F.; Sergi, V. Dimensional analysis for the definition of the influence of process parameters in selective laser melting of Ti–6Al–4V alloy. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2012, 226, 1136–1142. [Google Scholar] [CrossRef]
- Mukherjee, T.; Manvatkar, V.; De, A.; DebRoy, T. Dimensionless numbers in additive manufacturing. J. Appl. Phys. 2017, 121, 064904. [Google Scholar] [CrossRef] [Green Version]
- Robert, A.; Debroy, T. Geometry of laser spot welds from dimensionless numbers. Metall. Mater. Trans. B 2001, 32, 941–947. [Google Scholar] [CrossRef]
- Lu, S.; Fujii, H.; Nogi, K. Sensitivity of Marangoni convection and weld shape variations to welding parameters in O2–Ar shielded GTA welding. Scr. Mater. 2004, 51, 271–277. [Google Scholar] [CrossRef]
- Wei, P.; Ting, C.; Yeh, J.; DebRoy, T.; Chung, F.; Yan, G. Origin of wavy weld boundary. J. Appl. Phys. 2009, 105, 053508. [Google Scholar] [CrossRef]
- Asztalos, Z.; Száva, I.; Vlase, S.; Száva, R.I. Modern Dimensional Analysis Involved in Polymers Additive Manufacturing Optimization. Polymers 2022, 14, 3995. [Google Scholar] [CrossRef]
- Chia, H.Y.; Wu, J.; Wang, X.; Yan, W. Process parameter optimization of metal additive manufacturing: A review and outlook. J. Mater. Inform. 2022, 2, 16. [Google Scholar] [CrossRef]
- Bhagat, K.; Rudraraju, S. Modeling of dendritic solidification and numerical analysis of the phase-field approach to model complex morphologies in alloys. Eng. Comput. 2022, 1–19. [Google Scholar] [CrossRef]
- Brent, A.; Voller, V.R.; Reid, K. Enthalpy-porosity technique for modeling convection-diffusion phase change: Application to the melting of a pure metal. Numer. Heat Transf. Part A Appl. 1988, 13, 297–318. [Google Scholar]
- Kumar, A.; Roy, S. Effect of three-dimensional melt pool convection on process characteristics during laser cladding. Comput. Mater. Sci. 2009, 46, 495–506. [Google Scholar] [CrossRef]
- Yarin, L.P. The Pi-Theorem: Applications to Fluid Mechanics and Heat and Mass Transfer; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 1. [Google Scholar]
- Curtis, W.; Logan, J.D.; Parker, W. Dimensional analysis and the pi theorem. Linear Algebra Its Appl. 1982, 47, 117–126. [Google Scholar] [CrossRef] [Green Version]
- Bluman, G.W.; Kumei, S. Symmetries and Differential Equations; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 81. [Google Scholar]
- Hughes, T.J. The Finite Element Method: Linear Static and Dynamic Finite Element Analysis; Courier Corporation: Gloucester, MA, USA, 2012. [Google Scholar]
- Arndt, D.; Bangerth, W.; Blais, B.; Fehling, M.; Gassmöller, R.; Heister, T.; Heltai, L.; Köcher, U.; Kronbichler, M.; Maier, M.; et al. The deal.II Library, Version 9.3. J. Numer. Math. 2021, 29, 171–186. [Google Scholar] [CrossRef]
- Chorin, A.J. A numerical method for solving incompressible viscous flow problems. J. Comput. Phys. 1997, 135, 118–125. [Google Scholar] [CrossRef]
- Gulati, R.; Rudraraju, S. Spatio-temporal modeling of saltatory conduction in neurons using Poisson-Nernst–Planck treatment and estimation of conduction velocity. Brain Multiphys. 2022, 4, 100061. [Google Scholar] [CrossRef]
- Wang, Z.; Rudraraju, S.; Garikipati, K. A three dimensional field formulation, and isogeometric solutions to point and line defects using Toupin’s theory of gradient elasticity at finite strains. J. Mech. Phys. Solids 2016, 94, 336–361. [Google Scholar] [CrossRef] [Green Version]
- Jiang, T.; Rudraraju, S.; Roy, A.; Van der Ven, A.; Garikipati, K.; Falk, M.L. Multiphysics simulations of lithiation-induced stress in Li1+xTi2O4 electrode particles. J. Phys. Chem. C 2016, 120, 27871–27881. [Google Scholar] [CrossRef]
- Rudraraju, S.; Moulton, D.E.; Chirat, R.; Goriely, A.; Garikipati, K. A computational framework for the morpho-elastic development of molluskan shells by surface and volume growth. PLoS Comput. Biol. 2019, 15, e1007213. [Google Scholar] [CrossRef] [PubMed]
- Bhagat, K. Meltpool Thermo-Fluidics Simulation Framework for Metal Additive Manufacturing. 2022. Available online: https://github.com/cmmg/AMMeltpoolThermoFluidics (accessed on 19 December 2022).
- Bertsch, K.; De Bellefon, G.M.; Kuehl, B.; Thoma, D. Origin of dislocation structures in an additively manufactured austenitic stainless steel 316L. Acta Mater. 2020, 199, 19–33. [Google Scholar] [CrossRef]
- Shen, H.; Yan, J.; Niu, X. Thermo-fluid-dynamic modeling of the melt pool during selective laser melting for AZ91D magnesium alloy. Materials 2020, 13, 4157. [Google Scholar] [CrossRef] [PubMed]
- Rankouhi, B.; Bertsch, K.; de Bellefon, G.M.; Thevamaran, M.; Thoma, D.; Suresh, K. Experimental validation and microstructure characterization of topology optimized, additively manufactured SS316L components. Mater. Sci. Eng. A 2020, 776, 139050. [Google Scholar] [CrossRef]
- Thoma, D.; Charbon, C.; Lewis, G.; Nemec, R. Directed light fabrication of iron-based materials. MRS Online Proc. Libr. Arch. 1995, 397, 341–346. [Google Scholar] [CrossRef] [Green Version]
- Mohammadpour, P.; Plotkowski, A.; Phillion, A.B. Revisiting solidification microstructure selection maps in the frame of additive manufacturing. Addit. Manuf. 2020, 31, 100936. [Google Scholar] [CrossRef]
- Rappaz, M.; David, S.; Vitek, J.; Boatner, L. Analysis of solidification microstructures in Fe-Ni-Cr single-crystal welds. Metall. Trans. A 1990, 21, 1767–1782. [Google Scholar] [CrossRef]

| Parameter | Expression | Physical Interpretation |
|---|---|---|
| Dimensionless powder layer thickness | ||
| Dimensionless laser spot radius | ||
| Dimensionless time | ||
| Dimensionless temperature | ||
| Dimensionless velocity | ||
| Dimensionless pressure | ||
| Dimensionless gradient operator |
| Parameter | Expression | Physical Interpretation |
|---|---|---|
| Prandtl | Ratio of momentum to thermal diffusivity | |
| Grashof | Ratio of buoyancy force to viscous force | |
| Darcy | Ratio of permeability to the cross-sectional area | |
| Marangoni | Ratio of advection (surface tension) to diffusive transport | |
| Péclet | Ratio of advection transport to diffusive transport | |
| Stefan | Ratio of sensible heat to latent heat | |
| Power | Dimensionless power with velocity dependence | |
| Radiation measure | Measure of radiation contribution to the heat transfer | |
| Biot | Ratio of resistance to diffusion and convection heat transport |
| Parameter | Intercept | Q | ||||
|---|---|---|---|---|---|---|
| Parameter | Intercept | E | ||
|---|---|---|---|---|
| Parameter | Intercept | E | |
|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhagat, K.; Rudraraju, S. A Numerical Investigation of Dimensionless Numbers Characterizing Meltpool Morphology of the Laser Powder Bed Fusion Process. Materials 2023, 16, 94. https://doi.org/10.3390/ma16010094
Bhagat K, Rudraraju S. A Numerical Investigation of Dimensionless Numbers Characterizing Meltpool Morphology of the Laser Powder Bed Fusion Process. Materials. 2023; 16(1):94. https://doi.org/10.3390/ma16010094
Chicago/Turabian StyleBhagat, Kunal, and Shiva Rudraraju. 2023. "A Numerical Investigation of Dimensionless Numbers Characterizing Meltpool Morphology of the Laser Powder Bed Fusion Process" Materials 16, no. 1: 94. https://doi.org/10.3390/ma16010094





