Active Vibration Control of Composite Cantilever Beams
Abstract
1. Introduction
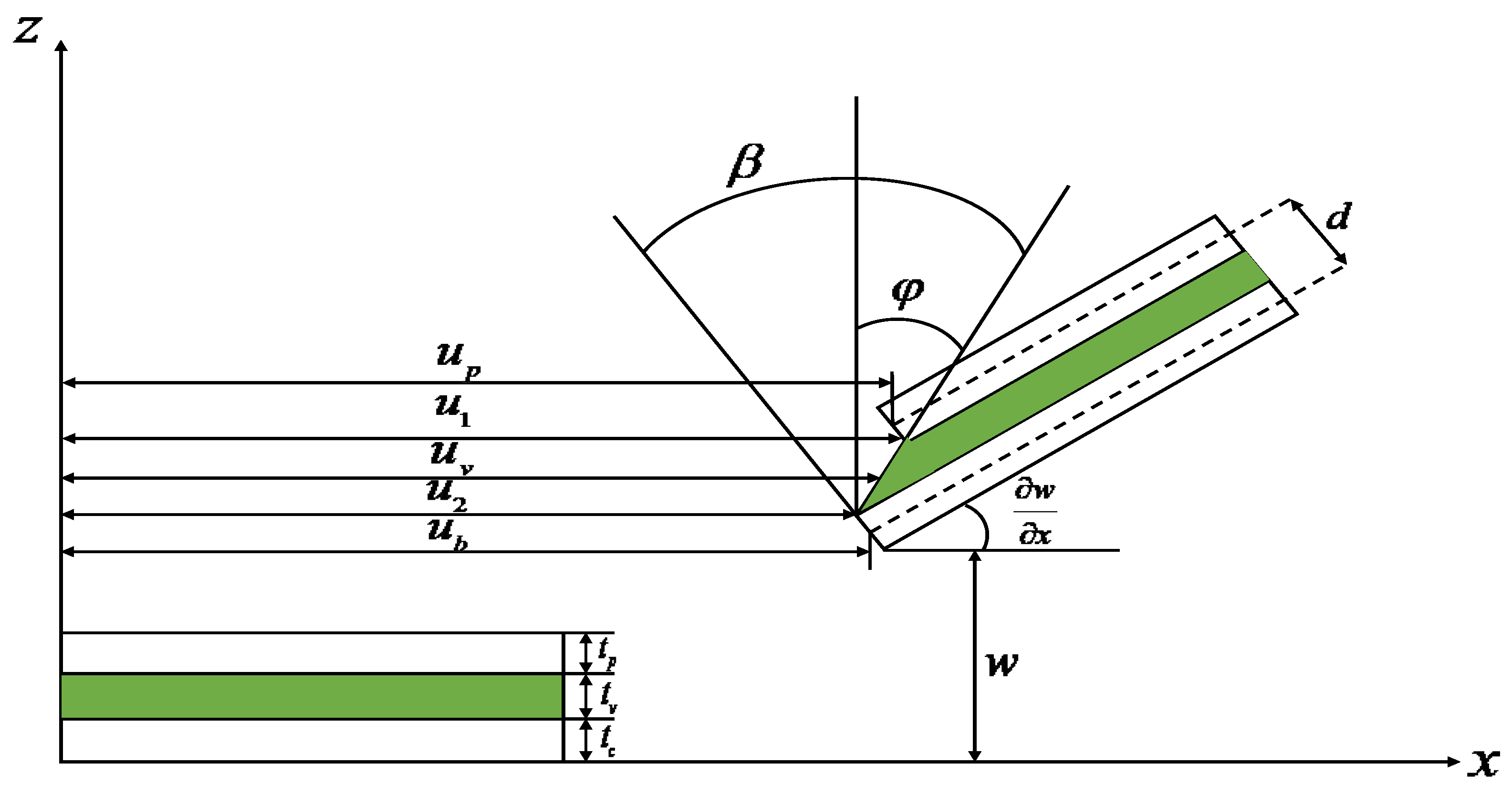
2. Finite Element Dynamic Modeling
2.1. Basic Assumptions
- ①
- The and piezoelectric layer satisfy the Euler-Bernoulli beam theory.
- ②
- The beam, viscoelastic layer and piezoelectric layer have the same lateral displacement (directional deformation).
- ③
- The effect of the moment of inertia of each layer is negligible.
- ④
- Only the structural damping provided by viscoelastic layer shear deformation is considered.
- ⑤
- Ideal paste between layers, no relative sliding between layers.
- ⑥
- Each layer conforms to linear theory.
2.2. Element Coupling Motion Relationships
2.3. ACLD Beam Element
2.4. Element Stiffness
2.5. Element Mass
2.6. Virtual Work
2.7. ACLD Beam Dynamics Model
2.8. GHM Model
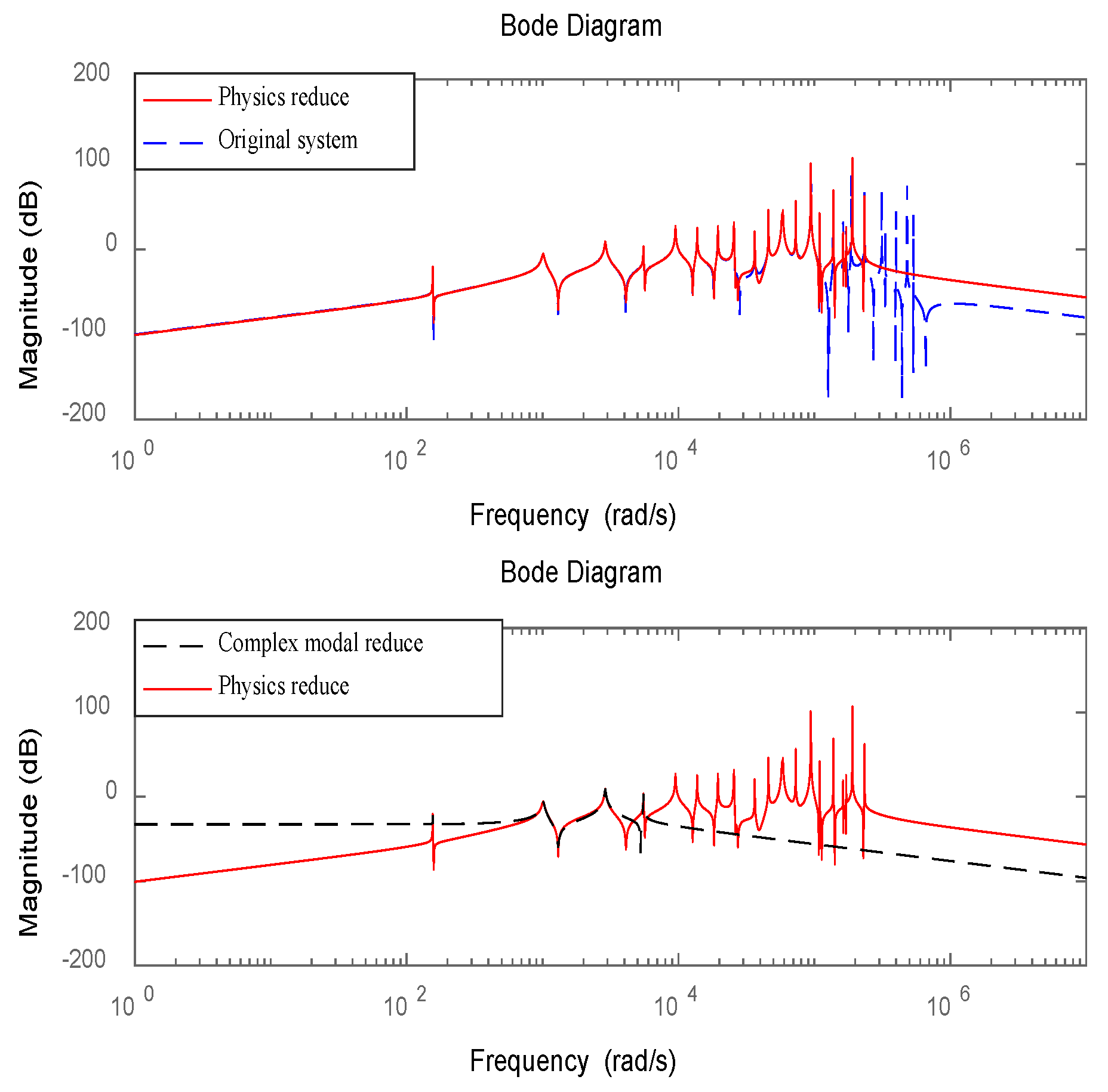
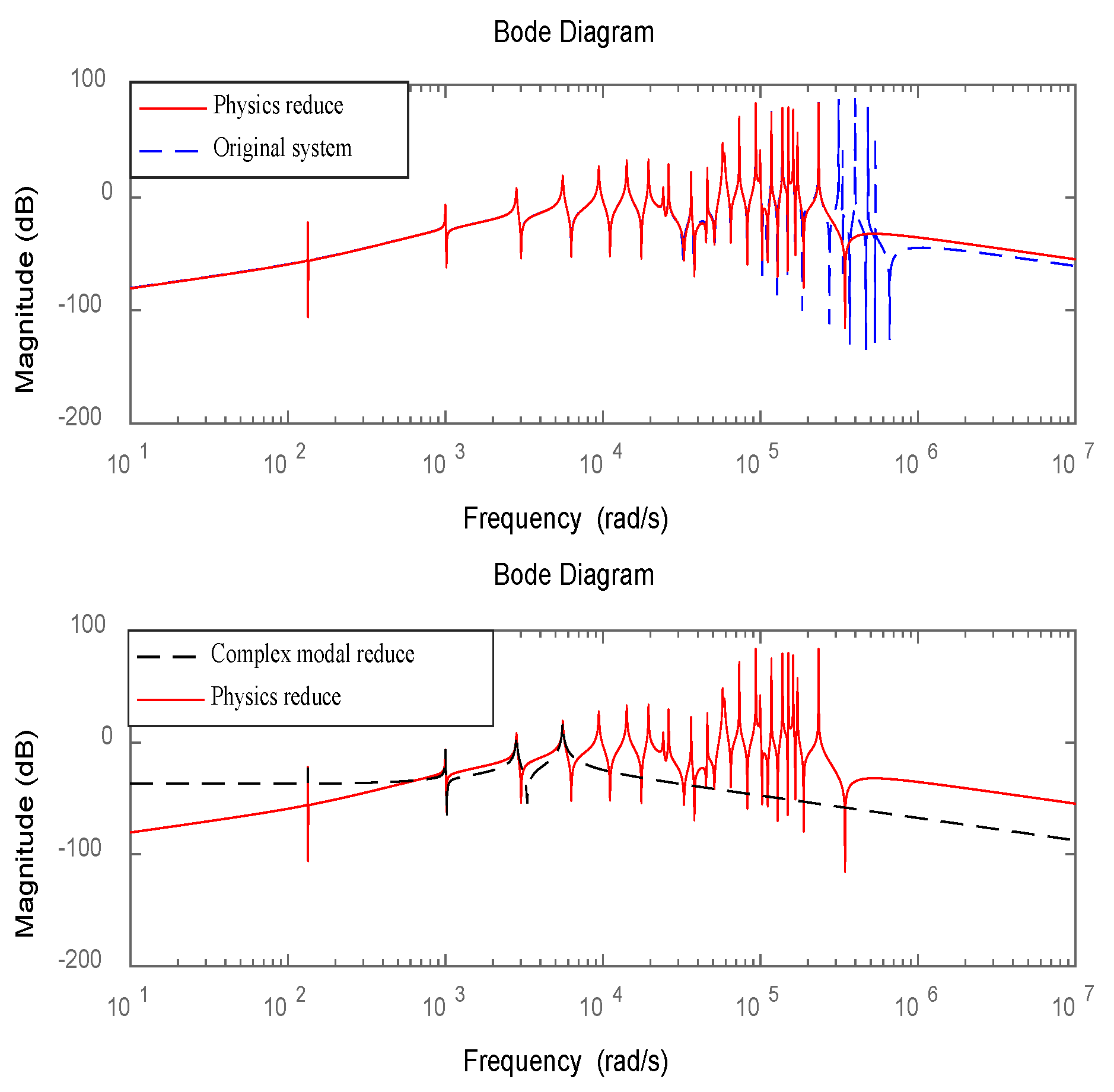
3. Model Reduction
3.1. High-Precision Degrees of Freedom Condensation in Physical Space
3.2. Complex-Modal Decoupling and Truncation in State Space
4. Control Law
4.1. LQR
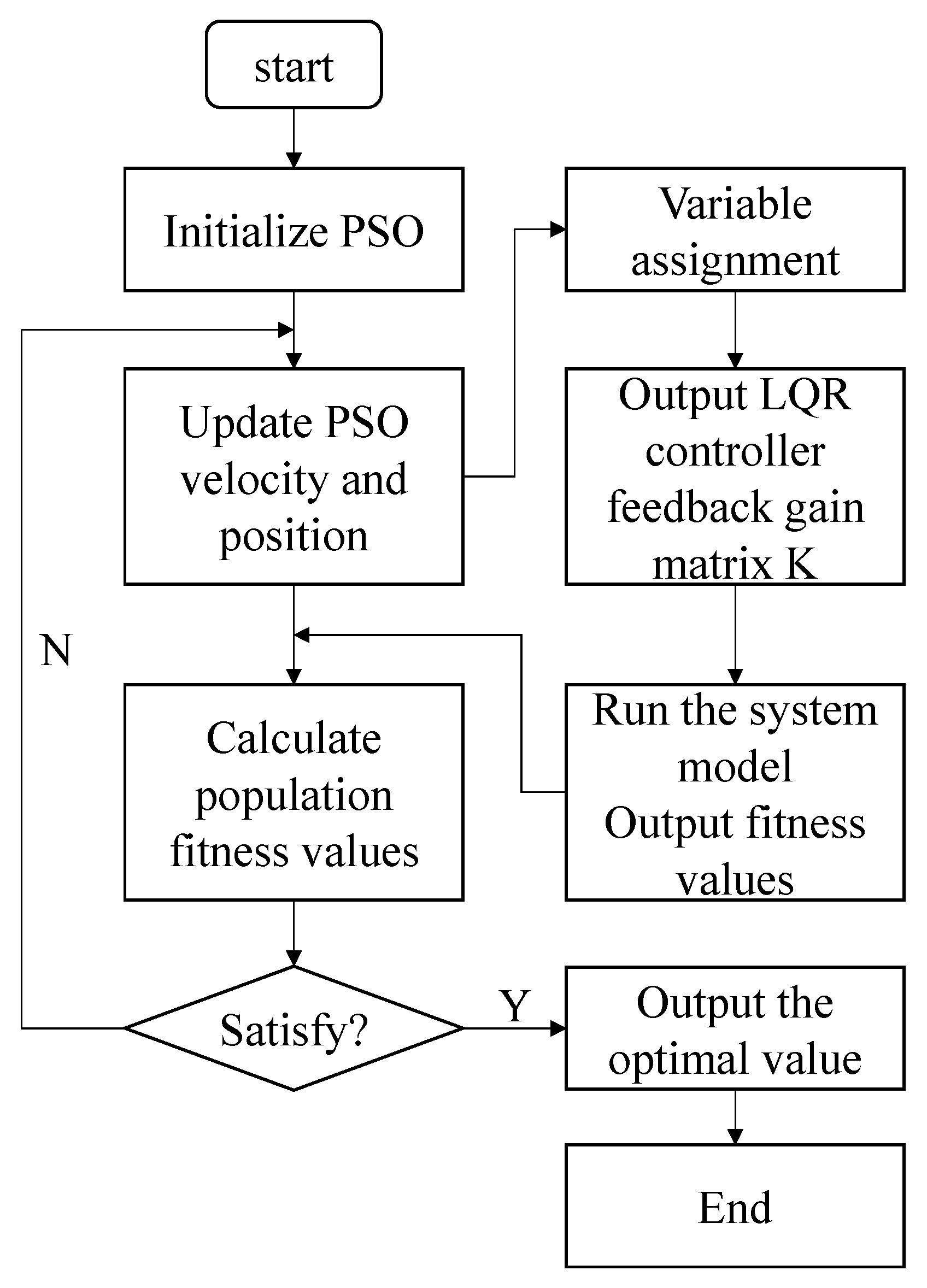
4.2. Particle Swarm Algorithm
4.3. Particle Swarm Optimization LQR-Weighted Parameters
- Step 1: Initialize the particle swarm scale and assign the individual particle swarms to the weighted matrix parameters.
- Step 2: Calculate the fitness value of the optimization parameters of this group according to the quadratic indicator.
- Step 3: Compare current particle fitness and historical fitness values for better individual and overall fitness.
- Step 4: Observe whether the fitness value of the quadratic index converges when the specified number of iterations is reached; If it has converged, the optimal solution of the weighted matrix is output.
5. Simulation and Verification
6. Conclusions
- The system dynamic equation is regarded as a whole and then introduced the GHM model to characterize the frequency characteristics of viscoelastic materials. This modeling method not only guarantees the correct results but also has clear physical meaning and low degrees of freedom.
- The dynamic polycondensation method can retain the low-frequency characteristics of the original system with high precision by constructing a suitable iterative matrix, and the physical significance is clear. The complex mode decoupling method realizes modal decoupling by constructing the modal space corresponding to the state space and independently controls the truncated mode.
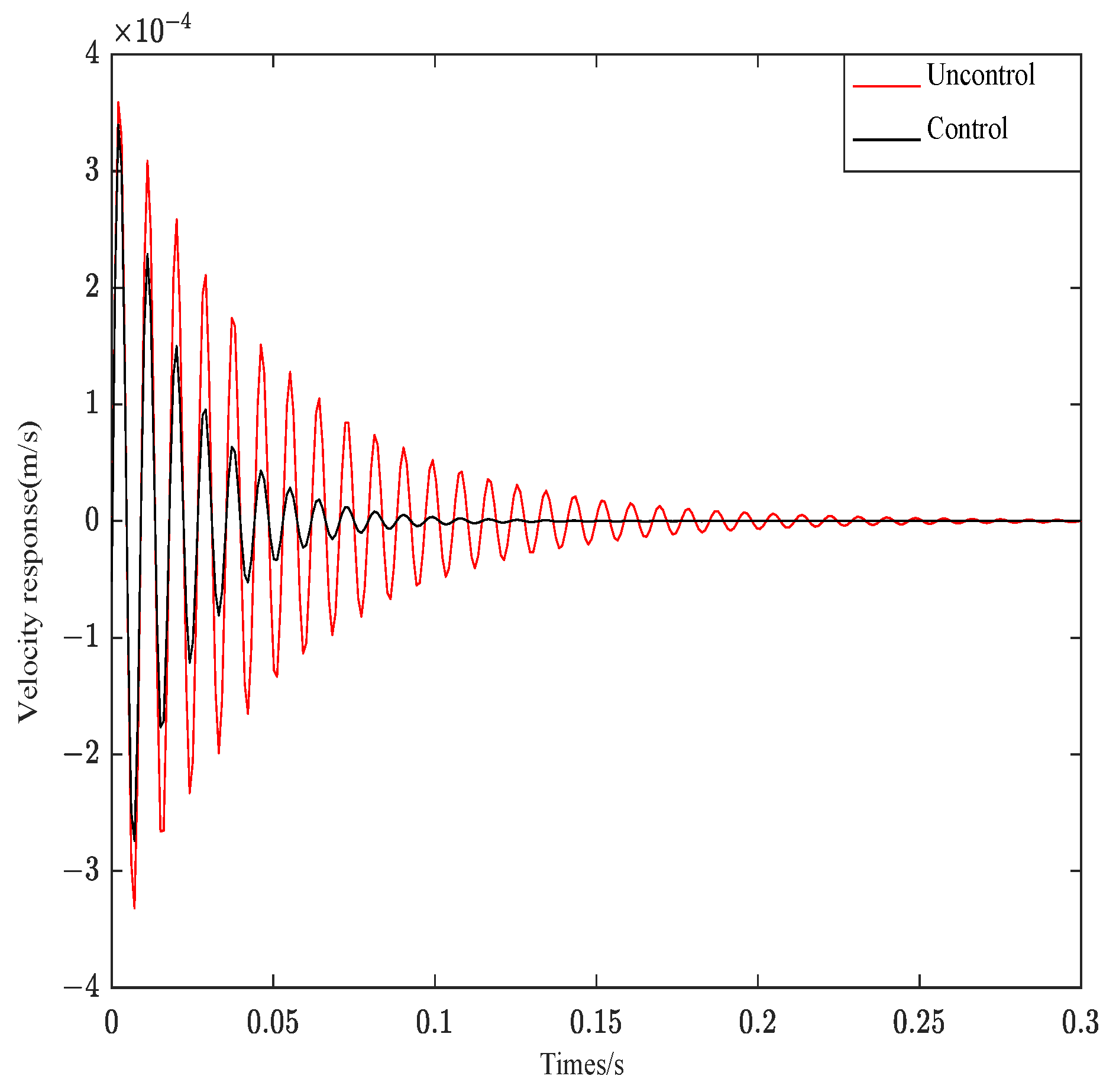
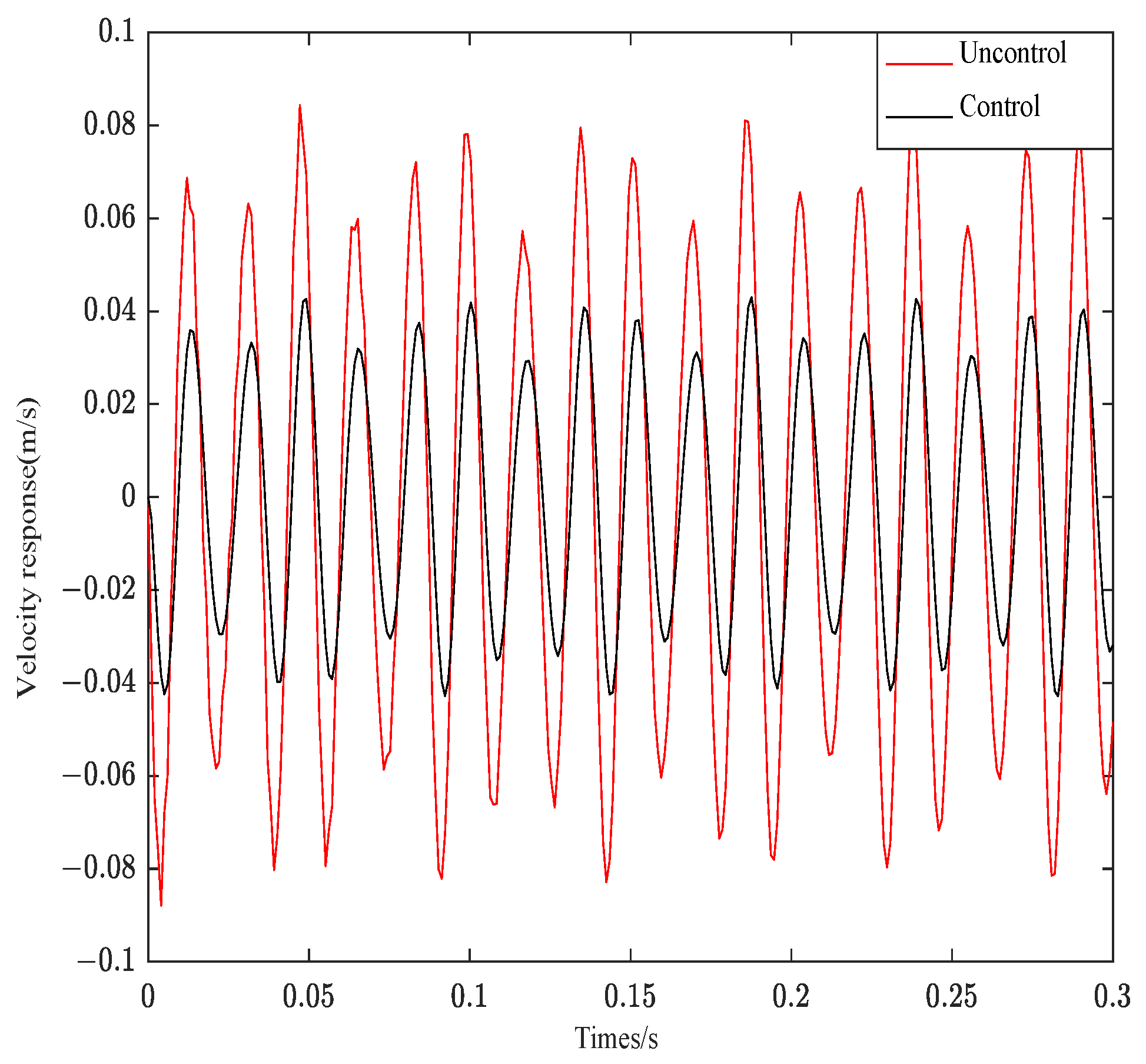
- The controller-weighted parameters optimized by the PSO algorithm not only balance the control effect and control cost but also effectively follow the system response. Different parameters influence the system control effect significantly, and the weighting coefficients Q and R control the amplitude and convergence rate of the system attenuation, respectively.
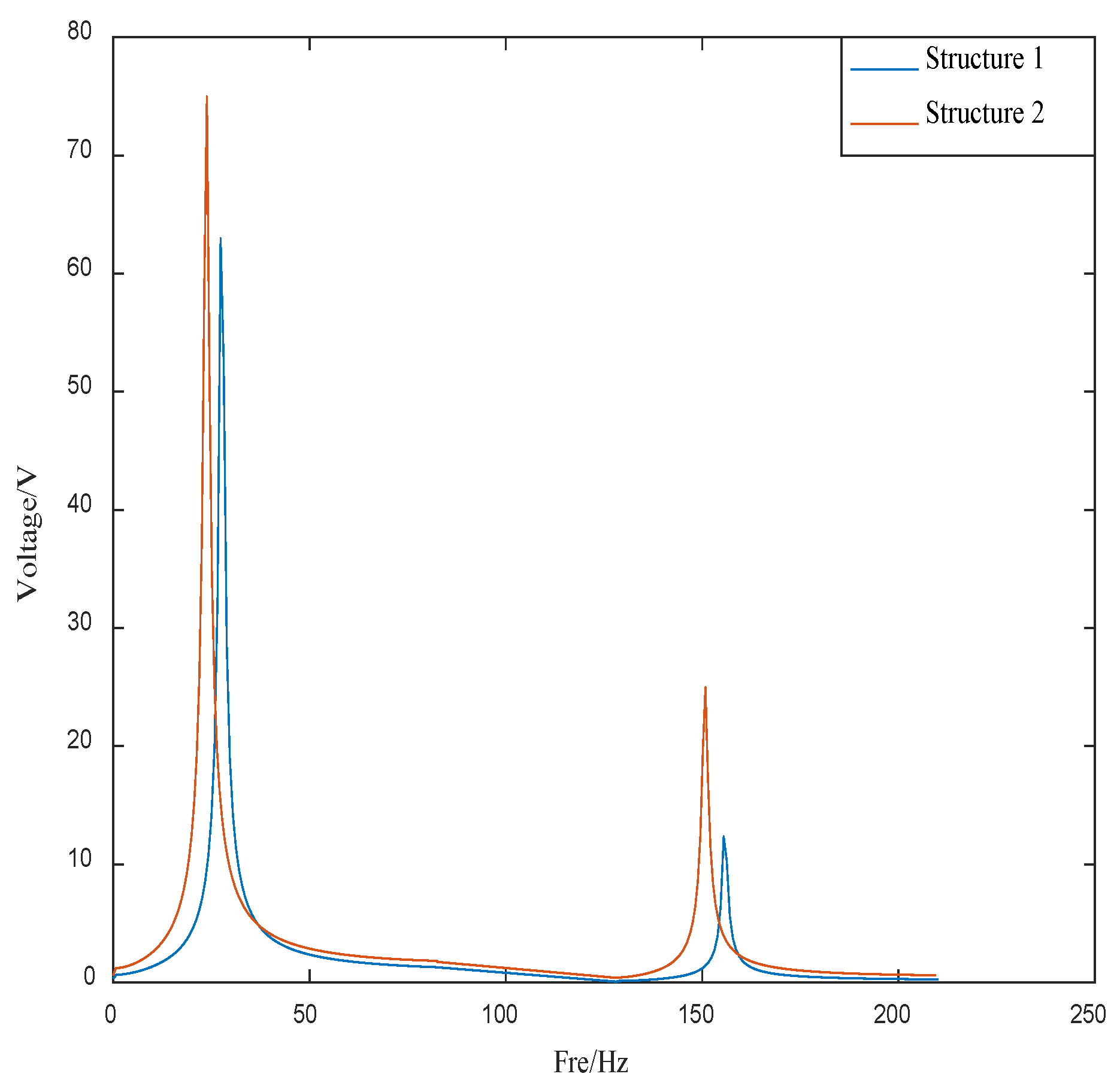
- The position of piezoelectric sheets and viscoelastic materials impacts vibration significantly. The closer the laying position is to the free end, the greater the additional effective mass of the free end, the smaller the natural frequency, and the greater the amplitude of the free vibration. Under the same control parameters, the control effect of the free-end is the worst. Conversely, the closer to the fixed end, the greater the natural frequency, the smaller the vibration amplitude, and the better the control effect.
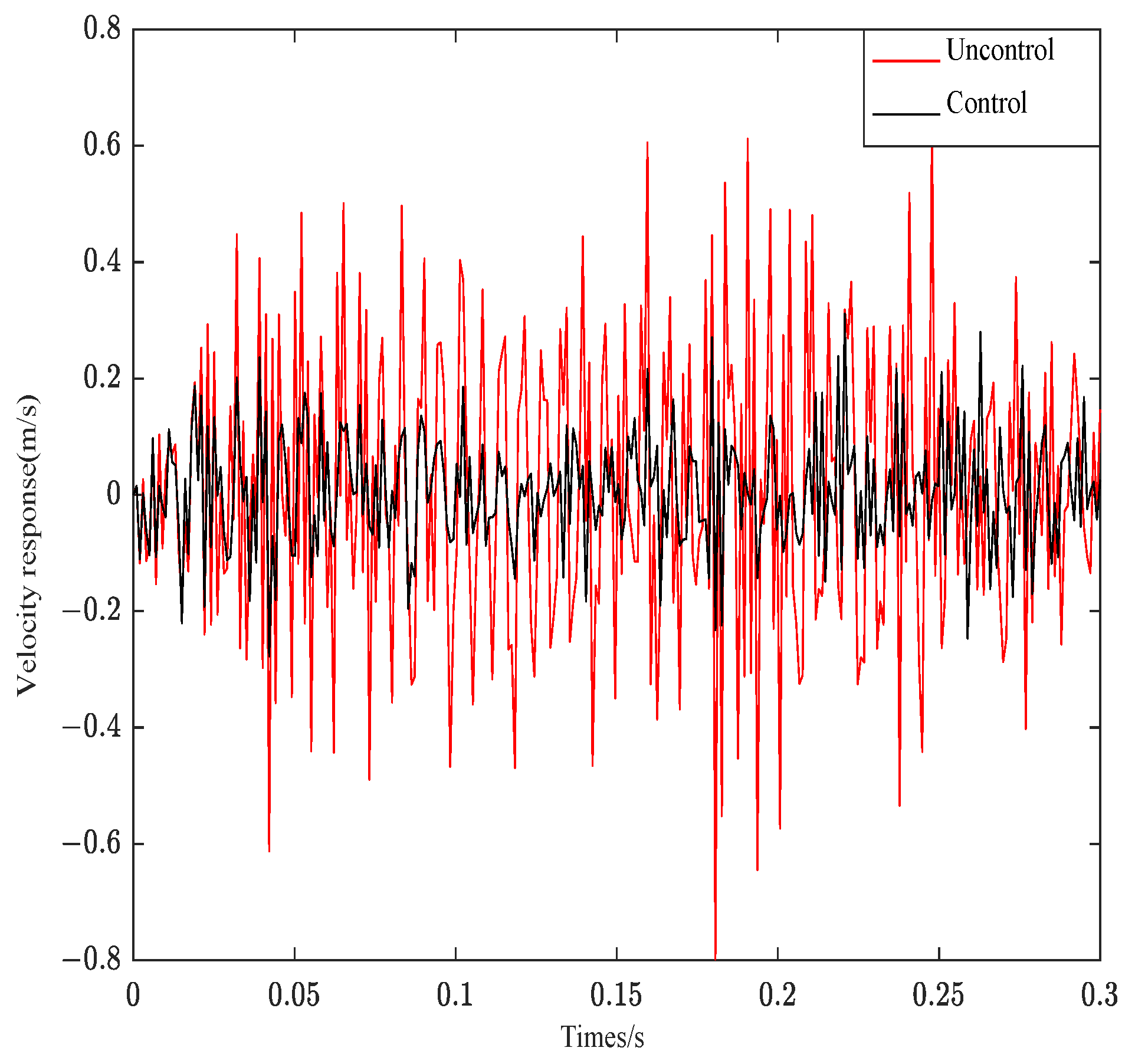
- The independent modes of the ACLD after decoupling can effectively track the response under different excitation signals. The system response to Gaussian white noise excitation is less effective than other excitation signals.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kumar, A.; Behera, R.K. Passive Constrained Layer Damping: A State of the Art Review. Mater. Sci. Eng. 2019, 653, 012036. [Google Scholar] [CrossRef]
- Hafidi, A.E.; Herrero, C.; Martin, B. Optimization of passive constrained layer damping (PCLD) treatments for vibration reduction. J. Vibroengineering 2015, 6, 3035–3045. [Google Scholar]
- Liu, Y.; Qin, Z.; Chu, F. Nonlinear forced vibrations of functionally graded piezoelectric cylindrical shells under electric-thermo-mechanical loads. Int. J. Mech. Sci. 2021, 201, 106474. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, F.; Qin, Z.; Han, Q.; Wang, T.; Chu, F. Piezoelectric energy harvester for rolling bearings with capability of self-powered condition monitoring. Energy 2022, 238, 121770. [Google Scholar] [CrossRef]
- Zhu, R.Z.; Zhang, X.N.; Zhang, S.G.; Dai, Q.Y.; Qin, Z.Y.; Chu, F.L. Modeling and topology optimization of cylindrical shells with partial CLD treatment. Int. J. Mech. Sci. 2022, 220, 107145. [Google Scholar] [CrossRef]
- Rezaiee-Pajand, M.; Masoodi, A.R. Hygro-thermo-elastic nonlinear analysis of functionally graded porous composite thin and moderately thick shallow panels. Mech. Adv. Mater. Struct. 2020, 29, 594–612. [Google Scholar] [CrossRef]
- Balamurugan, V.; Narayanan, S. Finite element formulation and active vibration control study on beams using smart constrained layer damping (SCLD) treatment. J. Sound Vib. 2002, 249, 227–250. [Google Scholar] [CrossRef]
- Baz, A.; Chen, T. Control of axi-symmetric vibrations of cylindrical shells using active constrained layer damping. Thin-Wall. Struct. 2000, 36, 1–20. [Google Scholar] [CrossRef]
- Lesieutre, G.A.; Bianchini, E. Time Domain Modeling of Linear Viscoelasticity Using Anelastic Displacement Fields. J. Vib. Acoust. 1995, 117, 424–430. [Google Scholar] [CrossRef]
- Shi, Y.M.; Li, Z.F.; Hua, H.X.; Fu, Z.F.; Liu, T.X. The modelling and vibration control of beams with active constrained layer damping. J. Sound Vib. 2001, 245, 785–800. [Google Scholar] [CrossRef]
- Adessina, A.; Hamdaoui, M.; Xu, C.; Daya, E.M. Damping properties of bi-dimensional sandwich structures with multi-layered frequency dependent viscoelastic cores. Compos. Struct. 2016, 154, 334–343. [Google Scholar] [CrossRef]
- Forward, R.L. Electronic Damping of Orthogonal Bending Modes in a Cylindrical Mast-Experiment. J. Spacecraft. Rockets. 1981, 18, 11–17. [Google Scholar] [CrossRef]
- Baz, A. Robust control of active constrained layer damping. J. Sound Vib. 1998, 211, 467–480. [Google Scholar] [CrossRef]
- Liu, T.X.; Hua, H.X.; Zhang, Z. Robust control of plate vibration via active constrained layer damping. Thin-Wall. Struct. 2004, 42, 427–448. [Google Scholar] [CrossRef]
- Gupta, A.; Panda, S. Hybrid damping treatment of a layered beam using a particle-filled viscoelastic composite layer. Compos. Struct. 2021, 262, 113623. [Google Scholar] [CrossRef]
- Mohammed, U.Q.; Wasmi, H.R. Active Vibration Control of Cantilever Beam by Using Optimal LQR Controller. J. Eng. 2018, 24, 1–17. [Google Scholar] [CrossRef]
- Boudaoud, H.; Belouettar, S.; Daya, E.M.; Potier-Ferry, M. A numerical method for nonlinear complex modes with application to passive-active damped sandwich structures. Eng. Struct. 2009, 31, 284–291. [Google Scholar] [CrossRef]
- Tian, J.; Guo, Q.; Shi, G. Laminated piezoelectric beam element for dynamic analysis of piezolaminated smart beams and GA-based LQR active vibration control. Compos. Struct. 2020, 252, 112480. [Google Scholar] [CrossRef]
- Oguntala, G.; Sobamowo, G. Vibration Analysis of Laminated Viscoelastic Beam: The Finite Difference Method Approach. Int. J. Eng. Tech. 2015, 5, 655. [Google Scholar]
- Huang, Z.C.; Pan, J.B.; Yang, Z.H.; Wang, X.G.; Chu, F.L. Transverse Vibration of Viscoelastic Sandwich Structures: Finite Element Modeling and Experimental Study. Materials 2021, 14, 7751. [Google Scholar] [CrossRef]
- Athans, M. The role and use of the stochastic linear-quadratic-Gaussian problem in control system design. IEEE Trans. Automat. Contr. 1971, 16, 529–552. [Google Scholar] [CrossRef]
- Davison, E. A method for simplifying linear dynamic systems. IEEE Trans. Automat. Contr. 1967, 11, 93–101. [Google Scholar] [CrossRef]
- Guyan, R. Reduction of stiffness and mass matrices. AIAA J. 1965, 3, 380. [Google Scholar] [CrossRef]
- Paz, M. Practical Reduction of Structural Eigenproblems. J. Struct. Eng. 1983, 109, 2591–2599. [Google Scholar] [CrossRef]
- Lu, J.; Wang, P. Active vibration control of thin-plate structures with partial SCLD treatment. Mech. Sys. Sig. Pro. 2017, 84, 531–550. [Google Scholar] [CrossRef]
- Miyamoto, K.; Sato, D.; She, J. A new performance index of LQR for combination of passive base isolation and active structural control. Eng. Struct. 2018, 157, 280–299. [Google Scholar] [CrossRef]
- Ezzraimi, M.; Tiberkak, R.; Melbous, A.; Rechak, S. LQR and PID Algorithms for Vibration Control of Piezoelectric Composite Plates. Mechanics 2018, 24, 20645. [Google Scholar] [CrossRef]
- Mastali, M.; Kheyroddin, A.; Samali, B.; Vahdani, R. Optimal placement of active braces by using PSO algorithm in near- and far-field earthquakes. Int. J. Adv. Struct. Eng. 2016, 8, 29–44. [Google Scholar] [CrossRef]
- Longman, R.W.; Alfriend, K.T. Actuator placement from degree of controllability criteria for regular slewing of flexible spacecraft. Acta Astronaut. 1981, 8, 703–718. [Google Scholar] [CrossRef]
- Johnson, C.D.; Kienholz, D.A. Finite Element Prediction of Damping in Structures with Constrained Viscoelastic Layers. AIAA J. 1982, 20, 1284–1290. [Google Scholar] [CrossRef]
- Britto, J.J.J.; Vasanthanathan, A.; Nagaraj, P. Finite Element Modeling and Simulation of Condition Monitoring on Composite Materials Using Piezoelectric Transducers—ANSYS. Mater. Today Proc. 2018, 5, 6684–6691. [Google Scholar] [CrossRef]
- Gozum, M.M.; Serhat, G.; Basdogan, I. A semi-analytical model for dynamic analysis of non-uniform plates. Appl. Math. Model. 2019, 76, 883–899. [Google Scholar] [CrossRef]
- Araújo, A.L.; Madeira, J. Multiobjective optimization solutions for noise reduction in composite sandwich panels using active control. Compos. Struct. 2020, 247, 112440. [Google Scholar] [CrossRef]
- Lu, P.; Wang, P.; Lu, J. Decentralized vibration control of smart constrained layer damping plate. J. Vib. Control 2020, 27, 529–542. [Google Scholar] [CrossRef]
- Huang, Z.C.; Mao, Y.H.; Dai, A.N. Active Vibration Control of Piezoelectric Sandwich Plates. Materials 2022, 15, 3907. [Google Scholar] [CrossRef]
- Baber, T.T.; Maddox, R.A.; Orozco, C.E. A finite element model for harmonically excited viscoelastic sandwich beams. Comput. Struct. 1998, 66, 105–113. [Google Scholar] [CrossRef]
- Felippe, W.N.; Barbosa, F.S. A nondeterministic GHM based model applied to sandwich beams. Procedia Eng. 2017, 199, 1098–1103. [Google Scholar] [CrossRef]
- Langote, P.K.; Seshu, P. Finite element analysis of a beam with active constrained layer damping (ACLD) treatment. J. Aerosp. Sci. Technol. 2004, 56, 240–253. [Google Scholar]
- Adhikari, S.; Friswell, M.I. Eigenderivative analysis of asymmetric non-conservative systems. Int. J. Num. Methods Eng. 2001, 51, 709–733. [Google Scholar] [CrossRef]
- Trindade, M.A. Reduced-Order Finite Element Models of Viscoelastically Damped Beams through Internal Variables Projection. J. Vib. Acoust. 2006, 128, 501–508. [Google Scholar] [CrossRef]
- Christensen, R. Theory of Viscoelasticity: An Introduction; Academic Press: New York, NY, USA, 1982. [Google Scholar]
- Skelton, R.E. Cost decomposition of linear systems with application to model reduction. Int. J. Control 1980, 32, 1031–1055. [Google Scholar] [CrossRef]



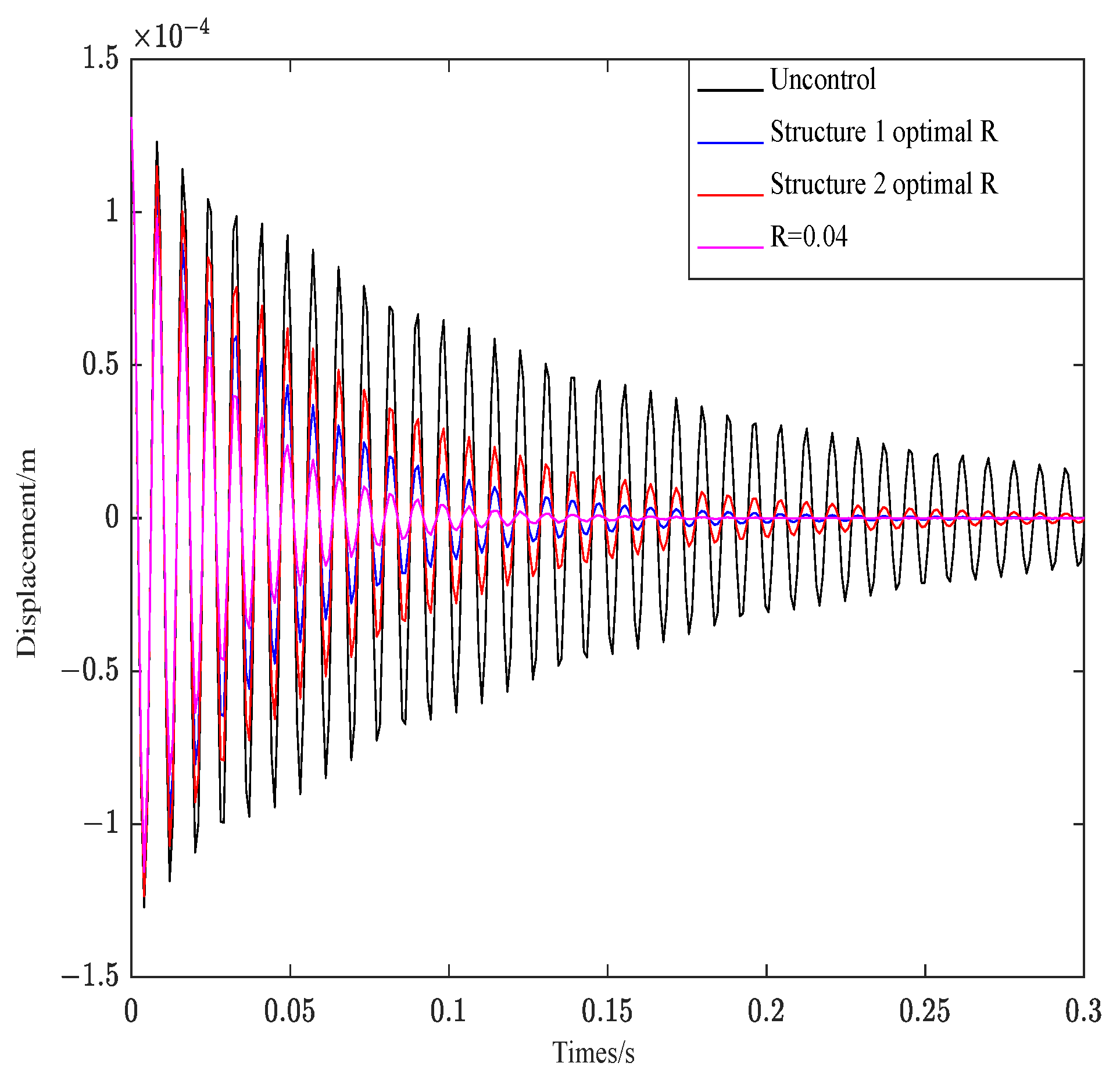
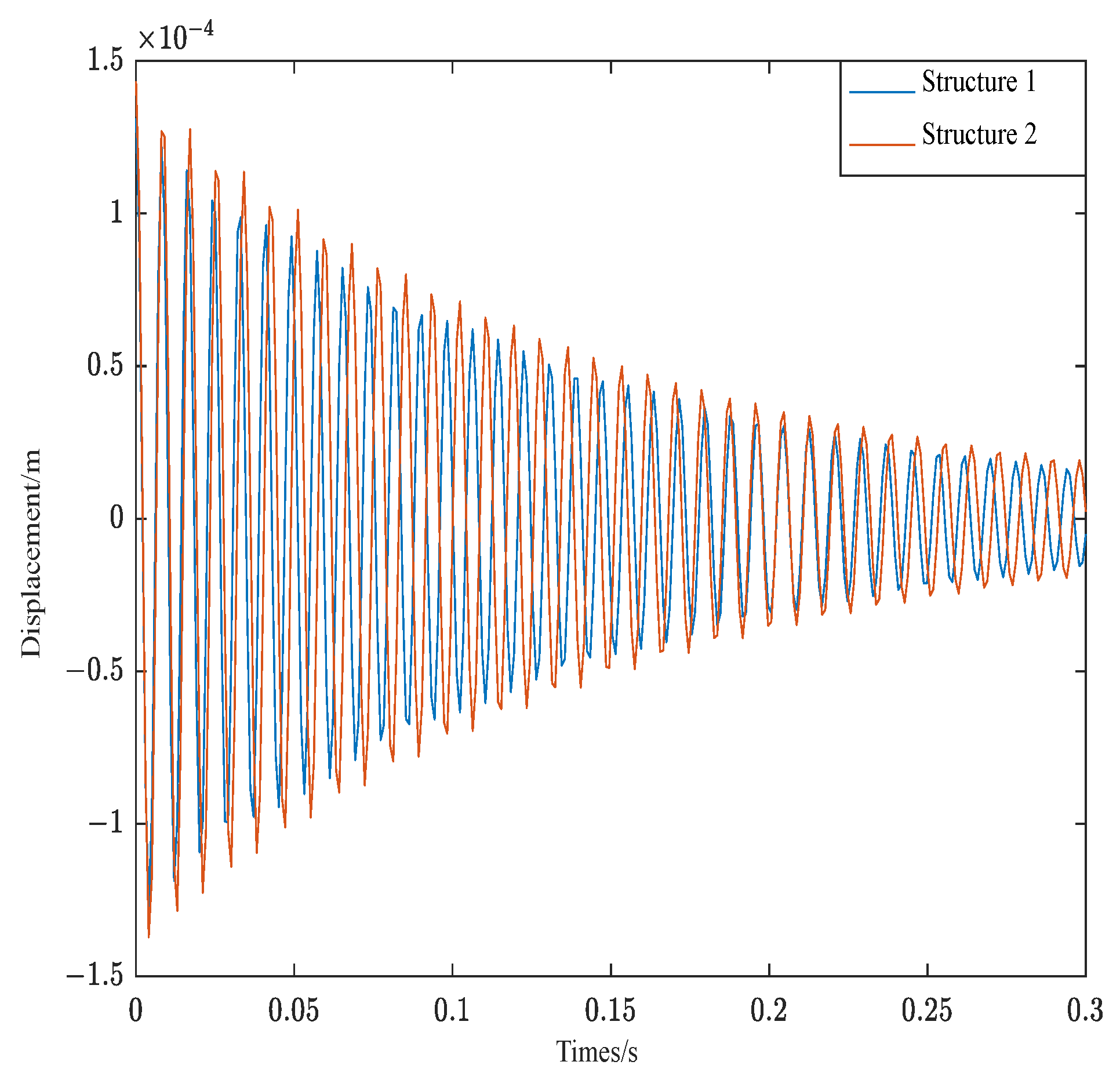
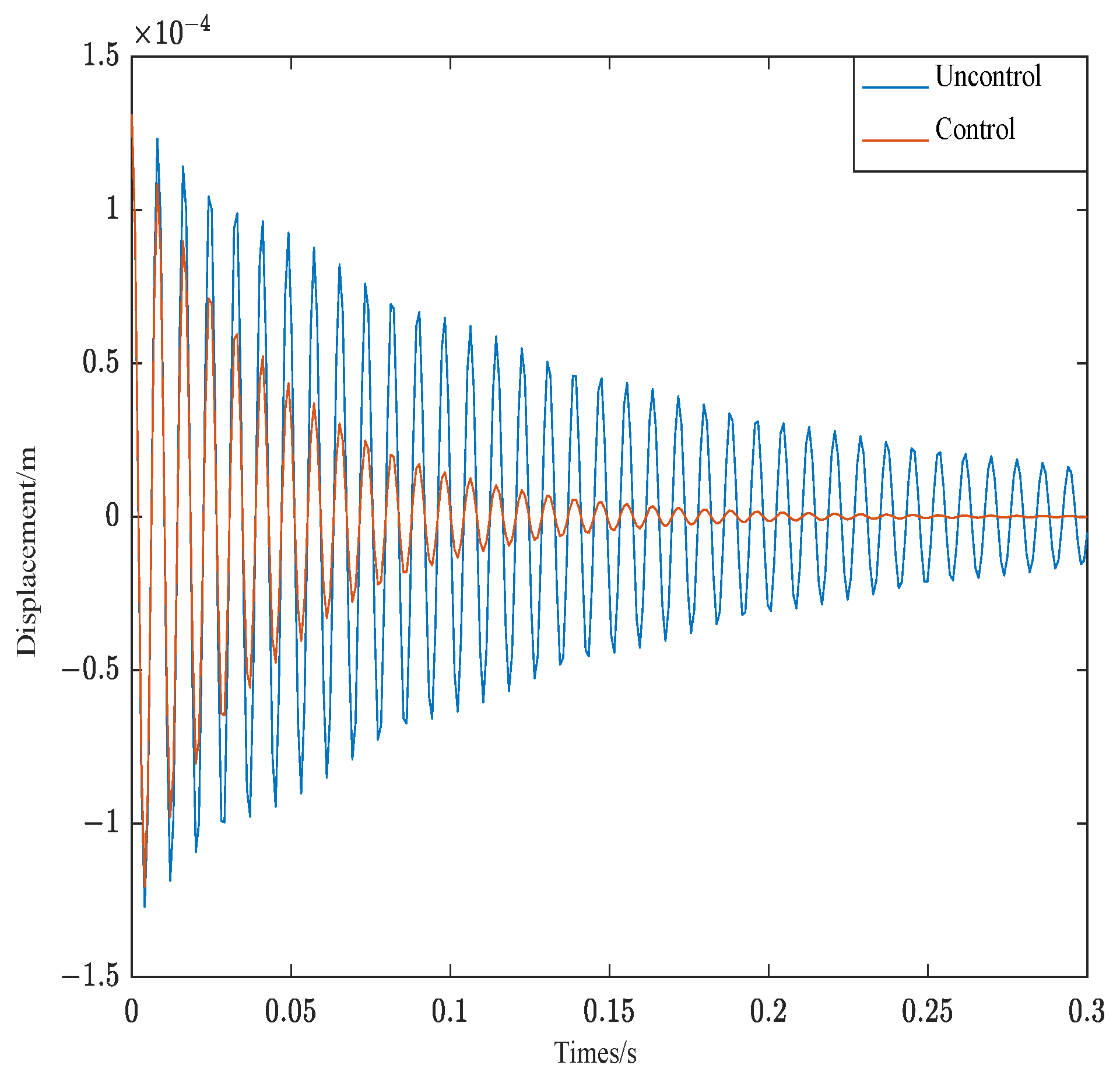
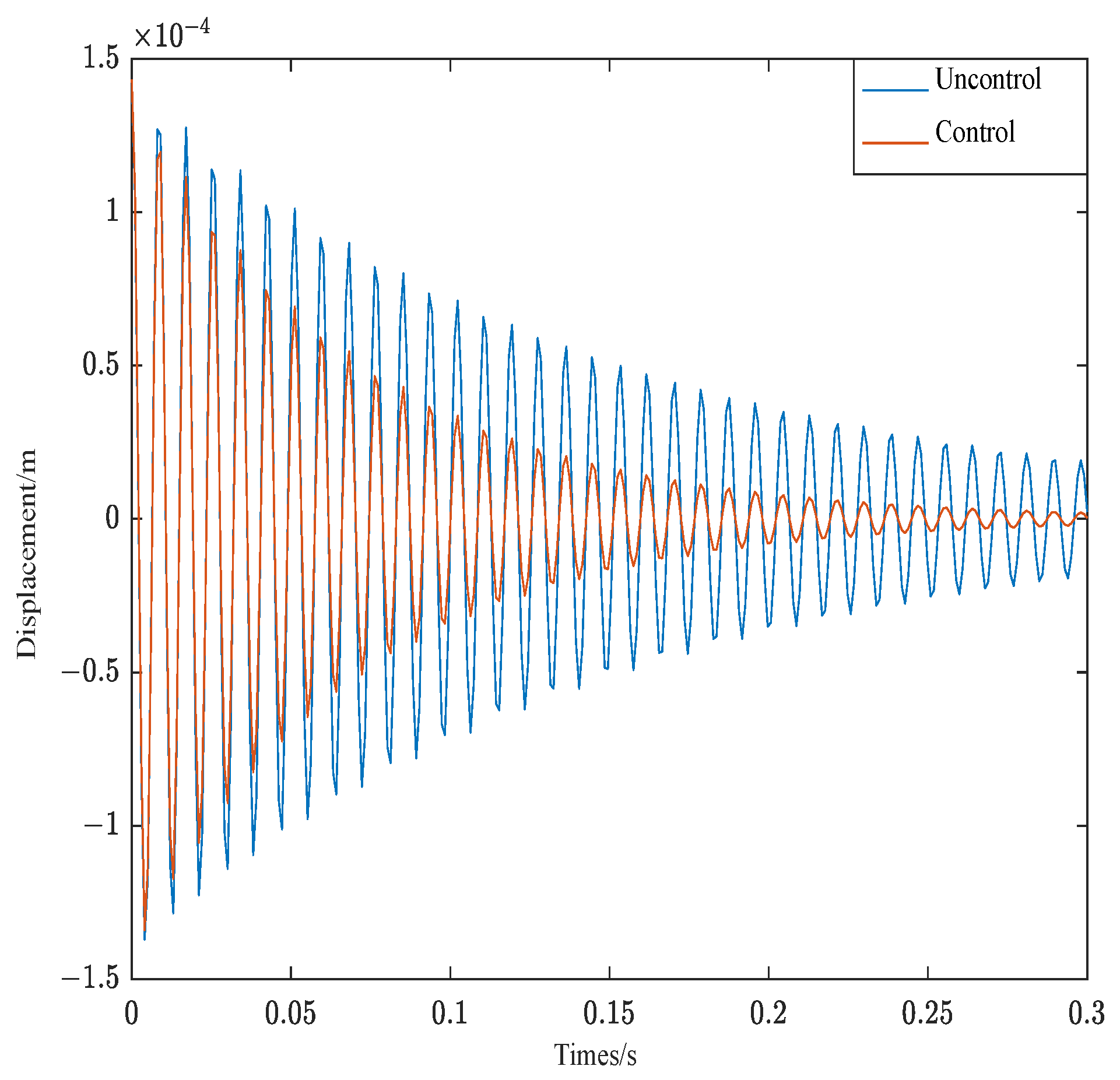

| Material Parameters | Base Beam | Viscoelastic Layer | Piezoelectric Layer |
|---|---|---|---|
| 0.2616 | |||
| 0.0127 | 0.0127 | 0.0127 | |
| 0.002286 | 0.00025 | 0.000762 | |
| GHM | |||
| 2700 | 1250 | 7600 | |
| GHM | |||
| Mode | Structure 1 | Structure 2 | Structure 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Shi 10 | Present | After | Before | After | Before | After | Before | After | |
| 1 | 27.9 | 27.89 | 27.89 | 27.24 | 27.24 | 24.76 | 24.76 | 21.28 | 21.28 |
| 2 | 150.12 | 150.12 | 150.12 | 150.54 | 150.54 | 160.84 | 160.83 | 158.79 | 158.78 |
| 3 | 442.97 | 443.65 | 443.65 | 444.06 | 444.05 | 460.35 | 460.35 | 448.75 | 448.74 |
| 4 | 831.76 | 832.14 | 832.14 | 874.34 | 874.34 | 879.23 | 879.23 | 883.02 | 883.01 |
| Q1 | Q2 | Q3 | Q4 | Q5 | Q6 | Q7 | Q8 | R | |
|---|---|---|---|---|---|---|---|---|---|
| Structure 1 | 50.52 | 24.36 | 51.97 | 0.01 | 41.46 | 67.71 | 76.01 | 69.91 | 0.01 |
| Structure 2 | 60.90 | 53.23 | 90.51 | 0.01 | 72.21 | 3.10 | 83.36 | 26.50 | 0.025 |
| Damping Ratio % | Structure 1 opt Q | Structure 2 opt Q | Q = 10*I |
|---|---|---|---|
| Structure 1 | 4.17 | 3.16 | 1.98 |
| Structure 2 | 2.37 | 3.19 | 1.80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Z.; Huang, F.; Wang, X.; Chu, F. Active Vibration Control of Composite Cantilever Beams. Materials 2023, 16, 95. https://doi.org/10.3390/ma16010095
Huang Z, Huang F, Wang X, Chu F. Active Vibration Control of Composite Cantilever Beams. Materials. 2023; 16(1):95. https://doi.org/10.3390/ma16010095
Chicago/Turabian StyleHuang, Zhicheng, Fan Huang, Xingguo Wang, and Fulei Chu. 2023. "Active Vibration Control of Composite Cantilever Beams" Materials 16, no. 1: 95. https://doi.org/10.3390/ma16010095
APA StyleHuang, Z., Huang, F., Wang, X., & Chu, F. (2023). Active Vibration Control of Composite Cantilever Beams. Materials, 16(1), 95. https://doi.org/10.3390/ma16010095






