Investigation on the Influence of Fiber Bundle Undulating Architecture on Tensile Behavior of Filament Wound Composite Laminates
Abstract
1. Introduction
2. Materials and Methods
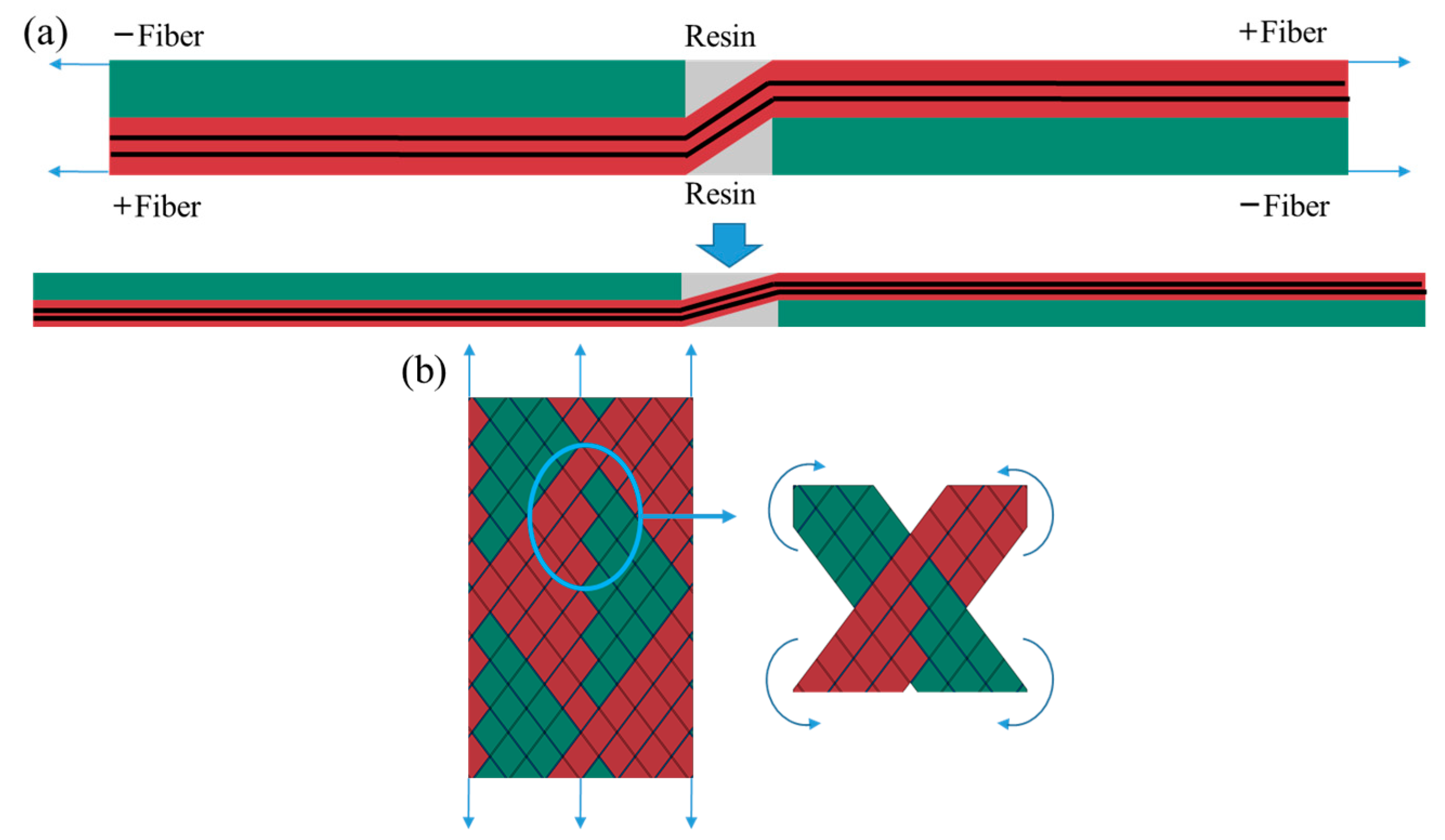
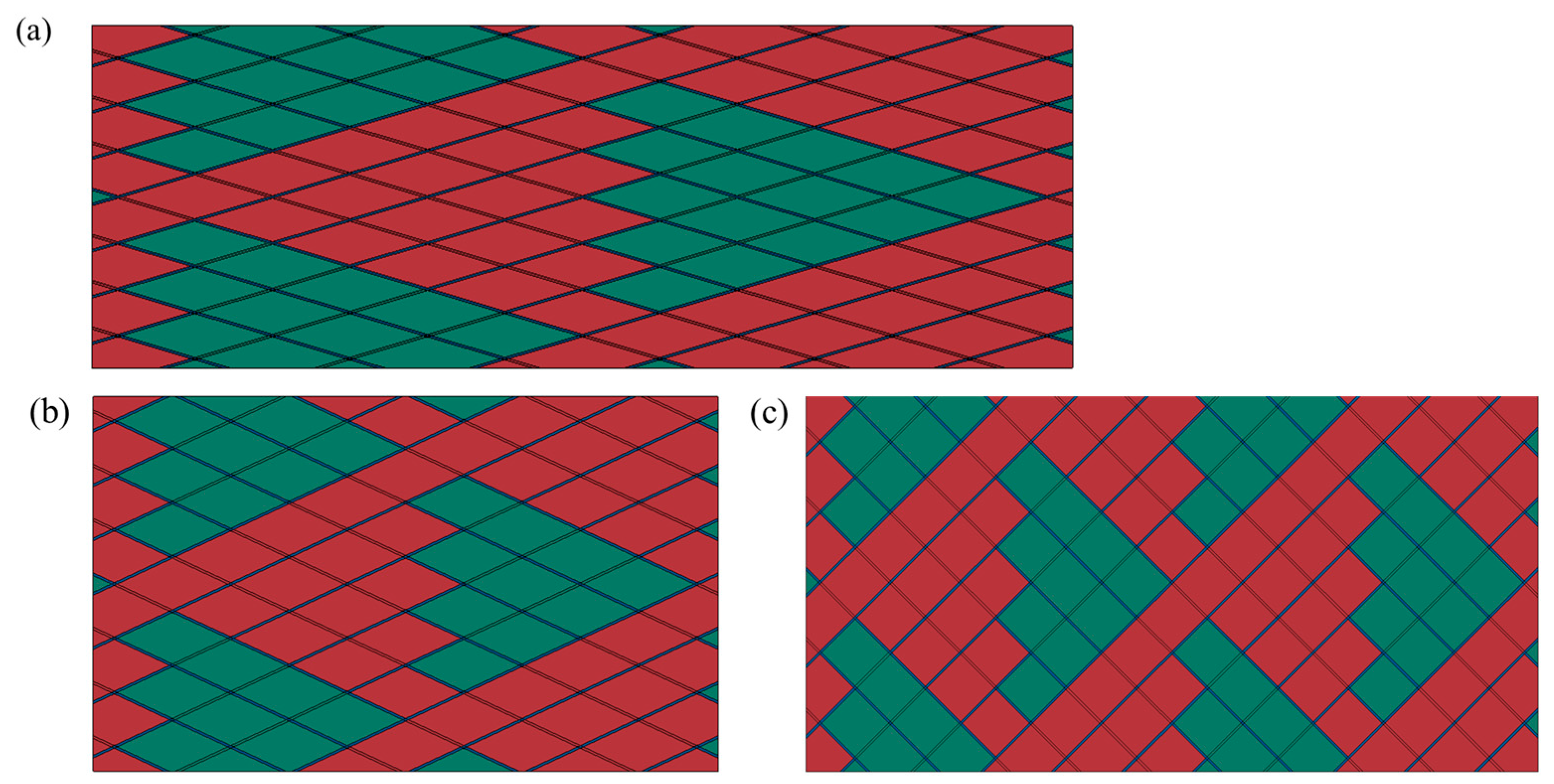
2.1. Materials and Sample Preparation
2.2. Testing and Characterization Methods
3. Experimental Results and Discussion
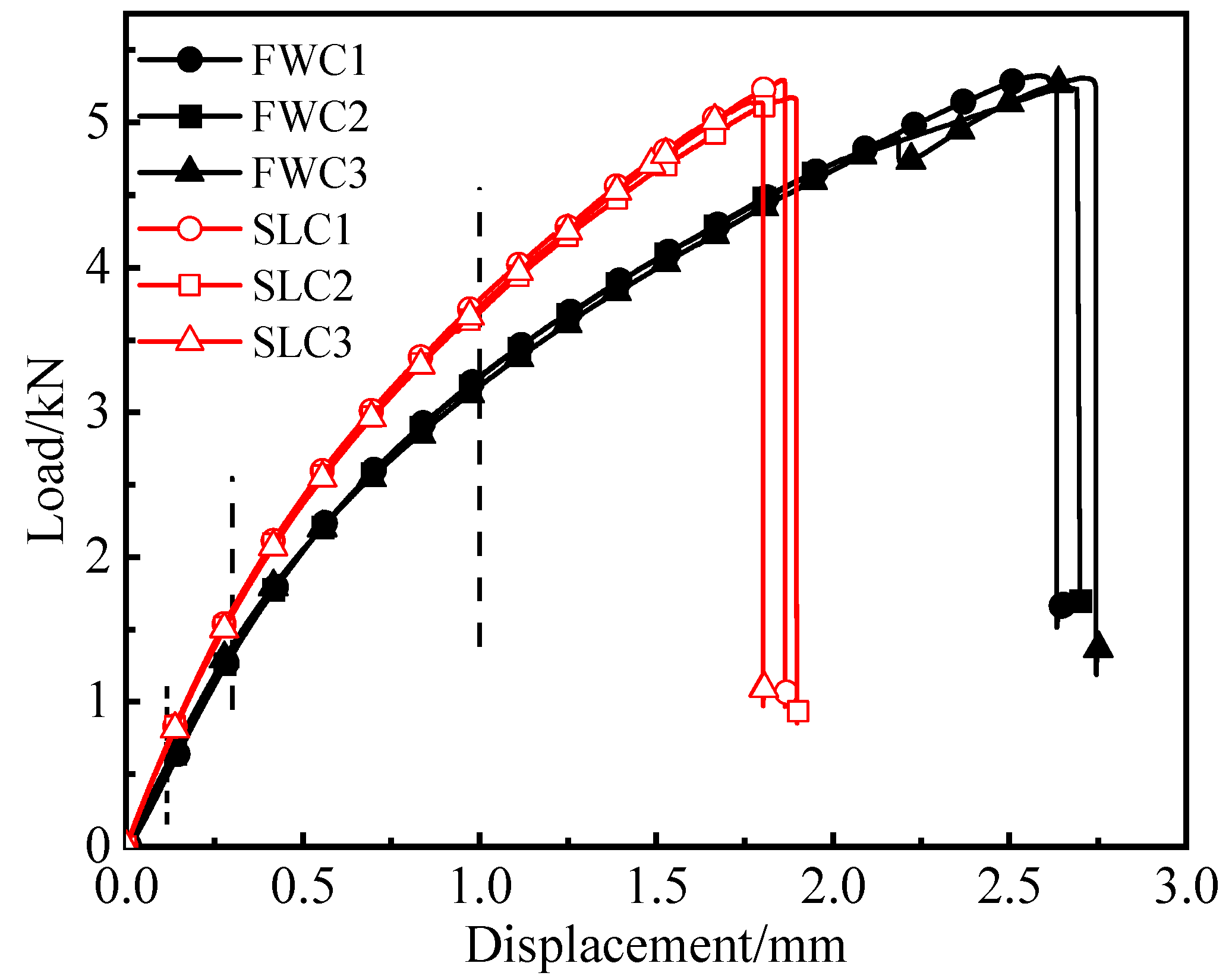
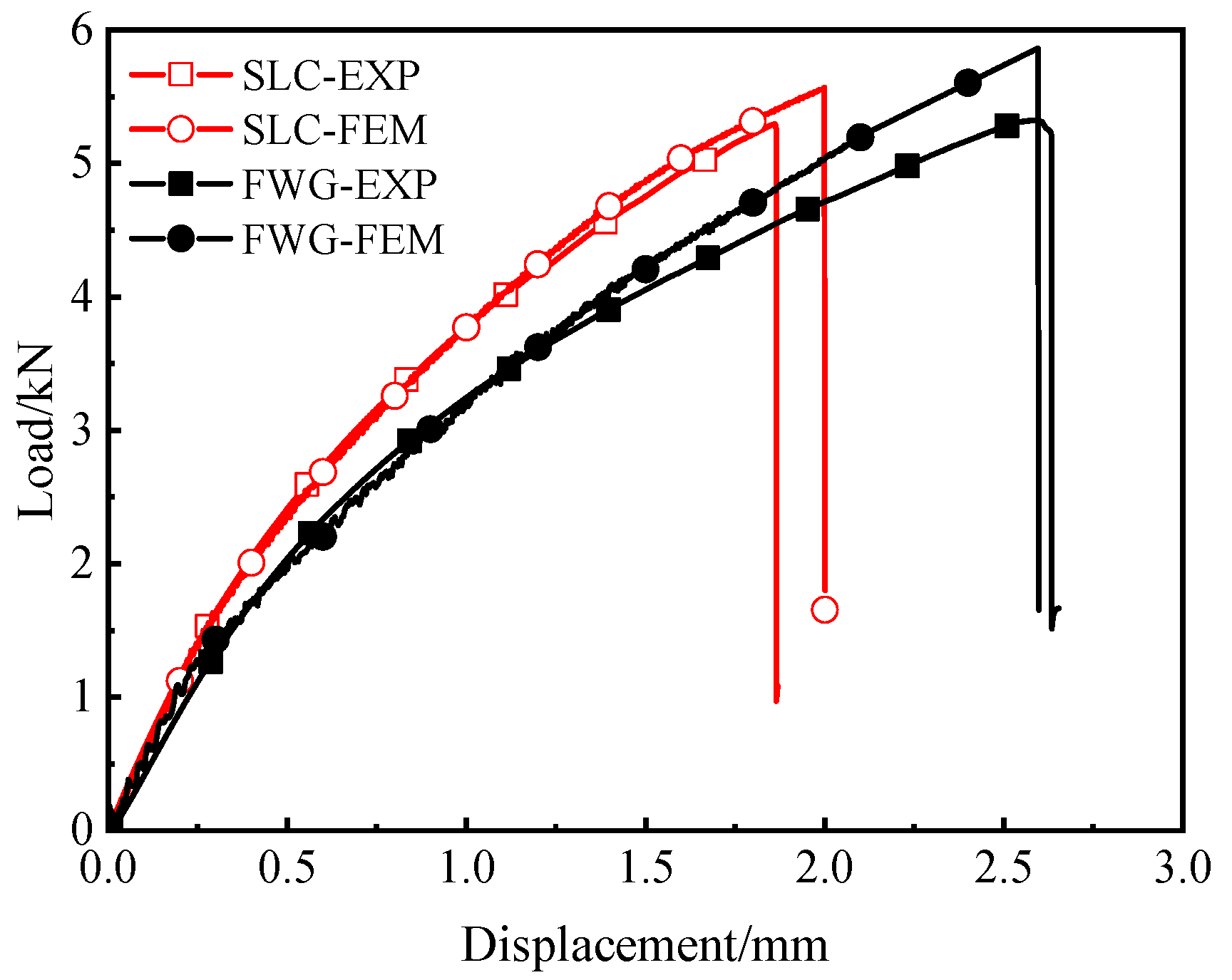
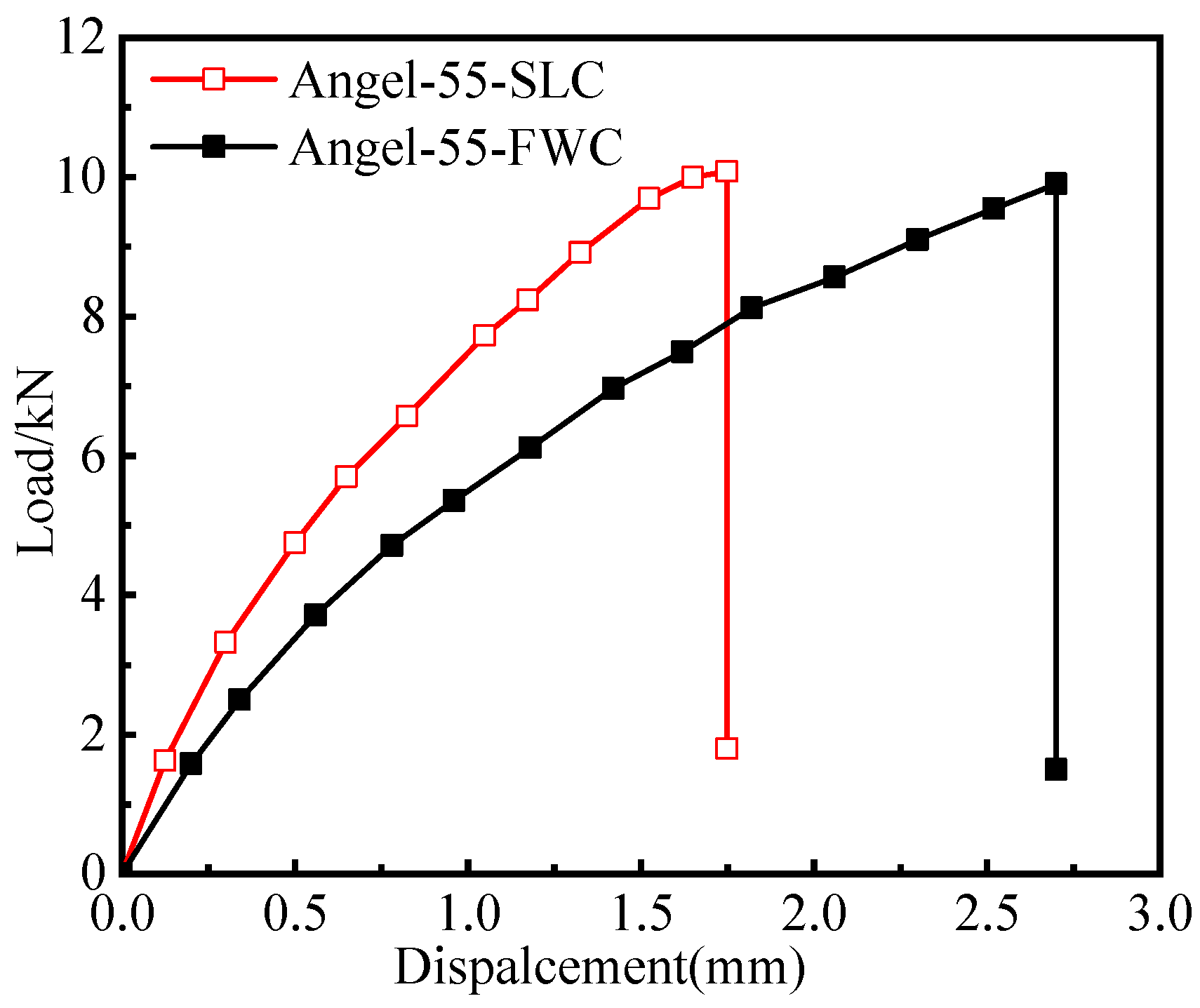
3.1. Test Results
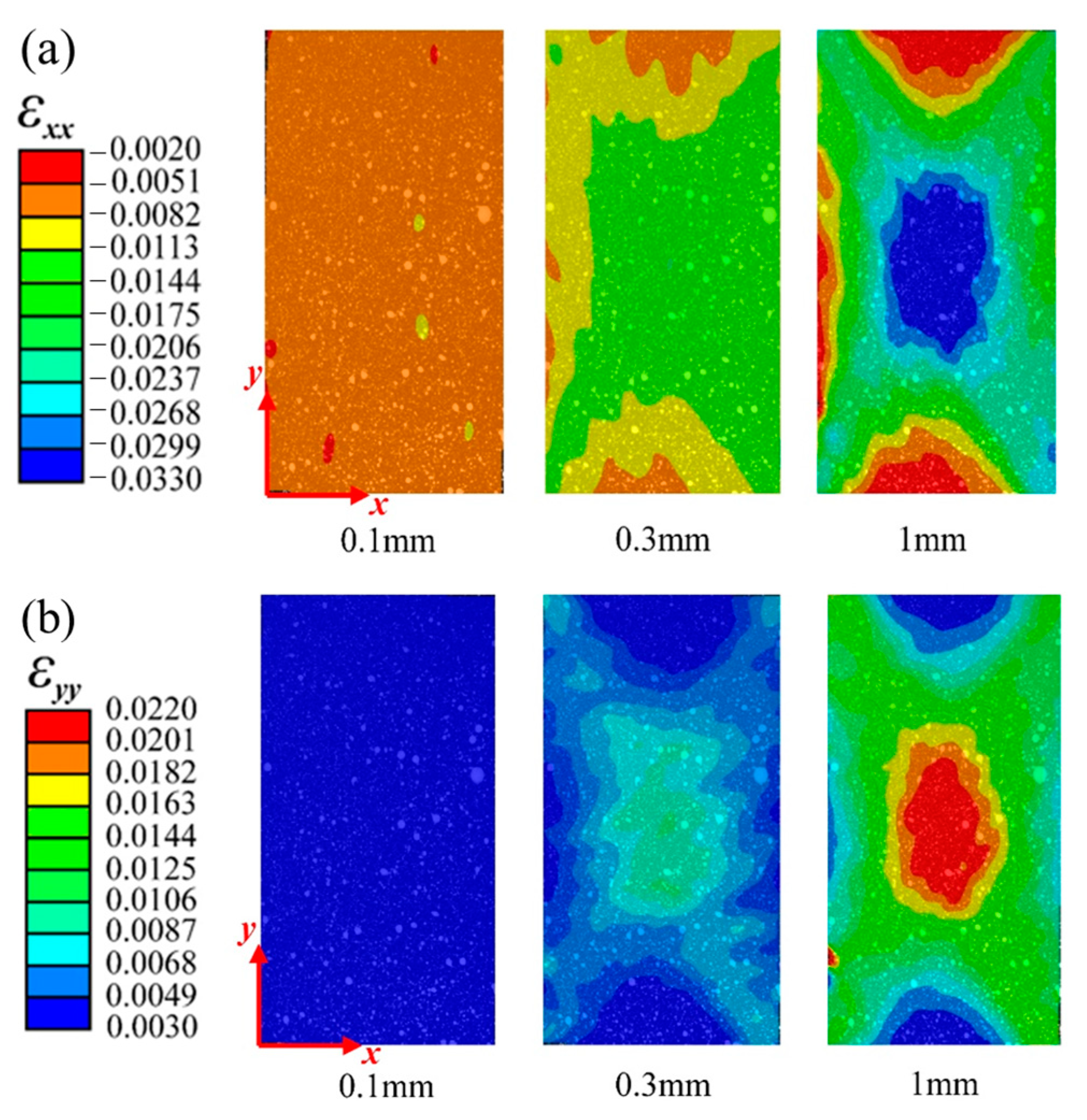
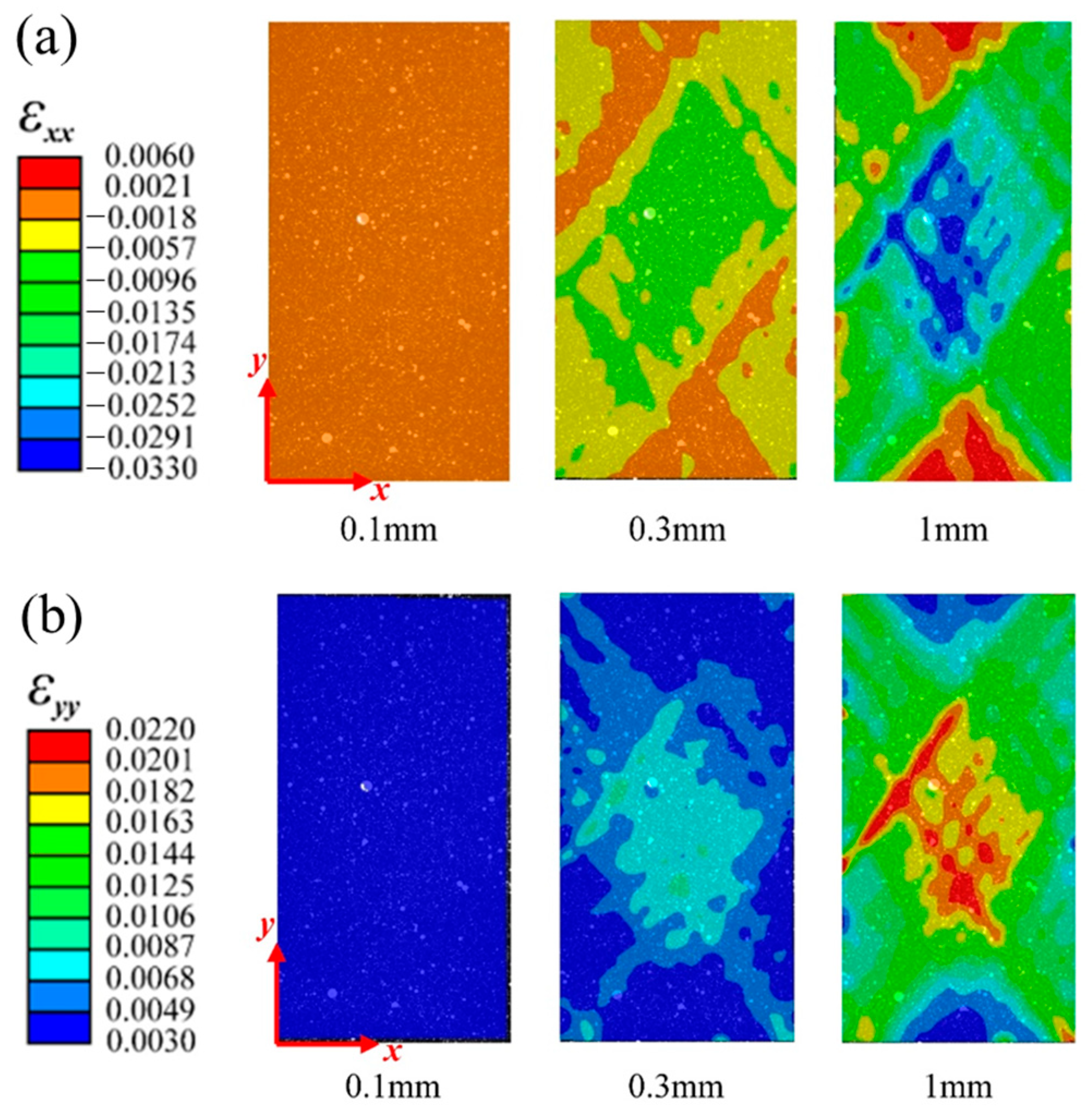
3.2. Analysis of Test Results
4. FEA Modeling
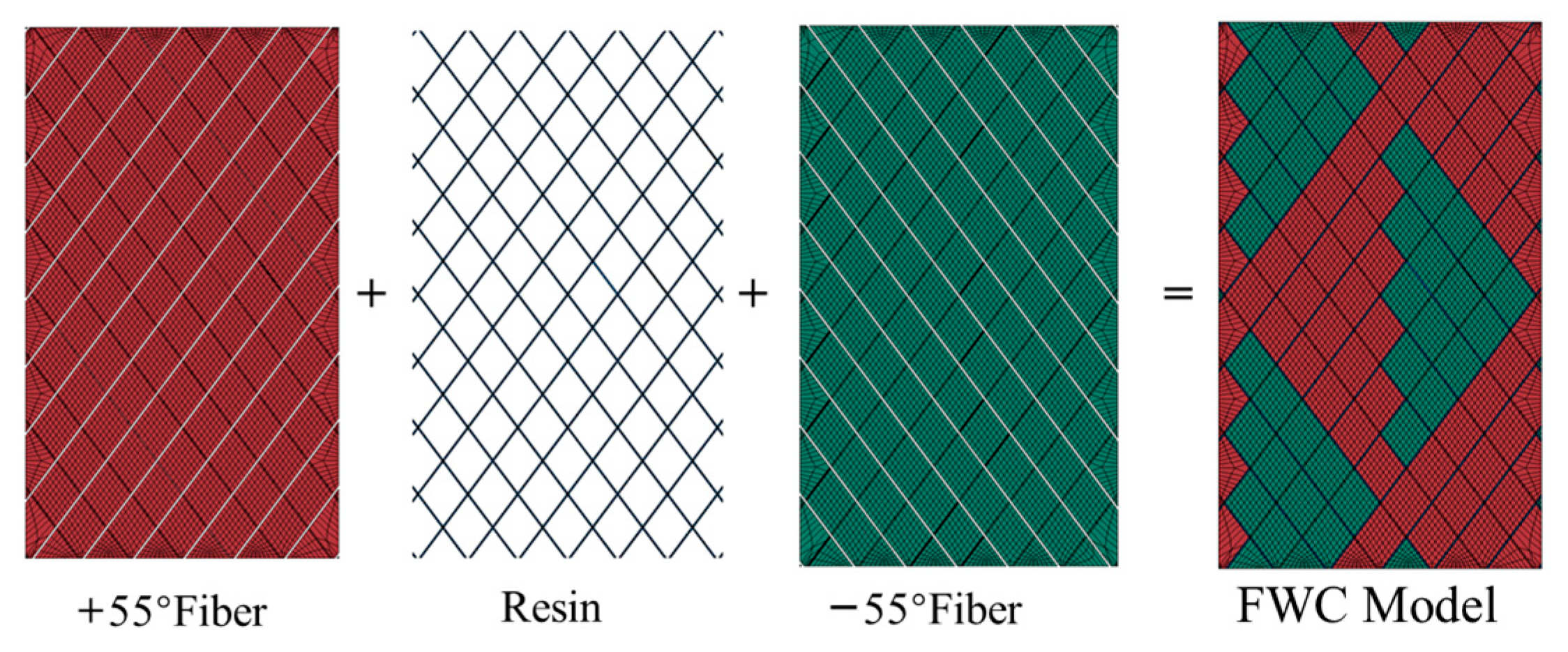
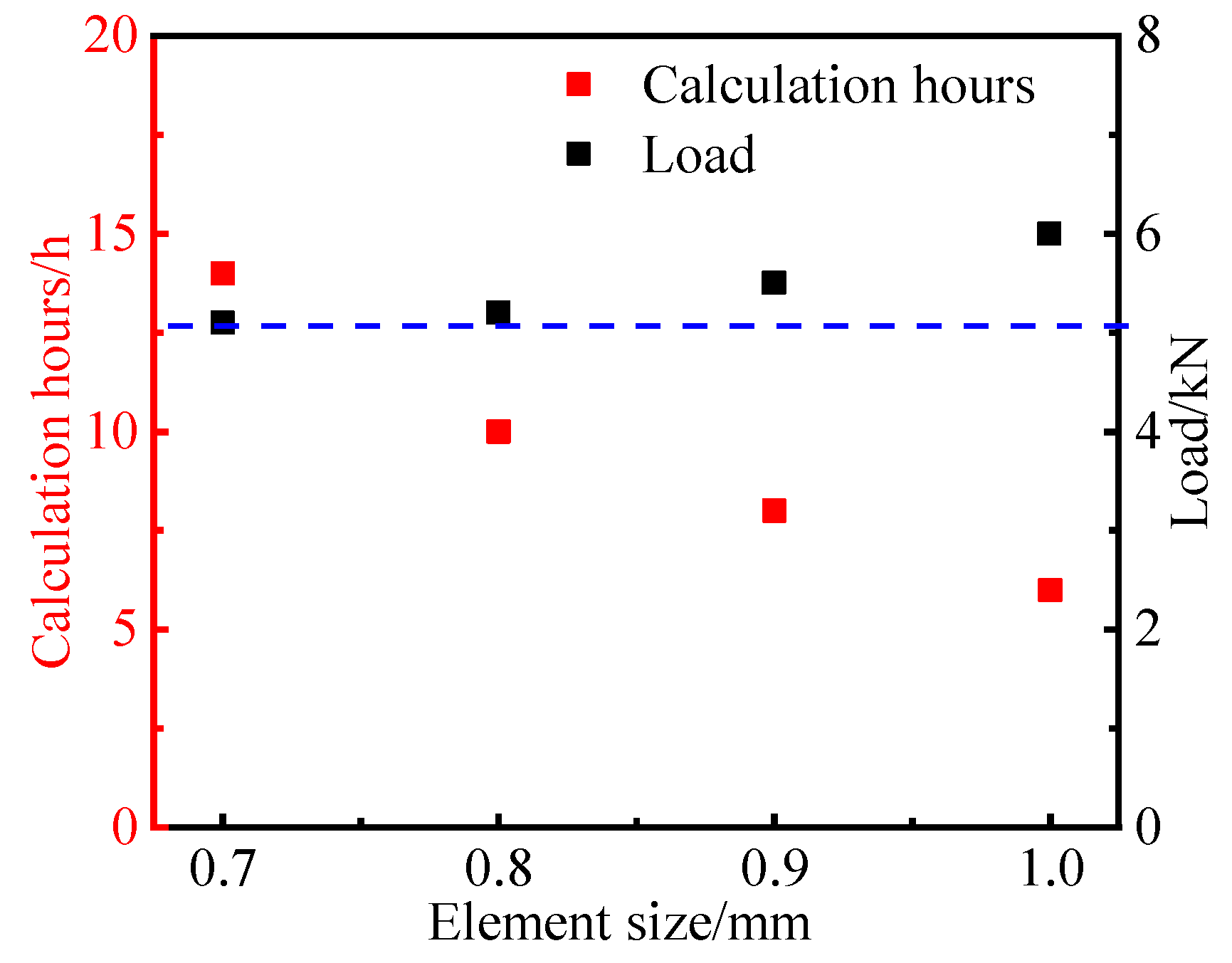
4.1. Finite Element Models
4.2. Nonlinear Shear Behavior and Progressive Failure Analysis Methods
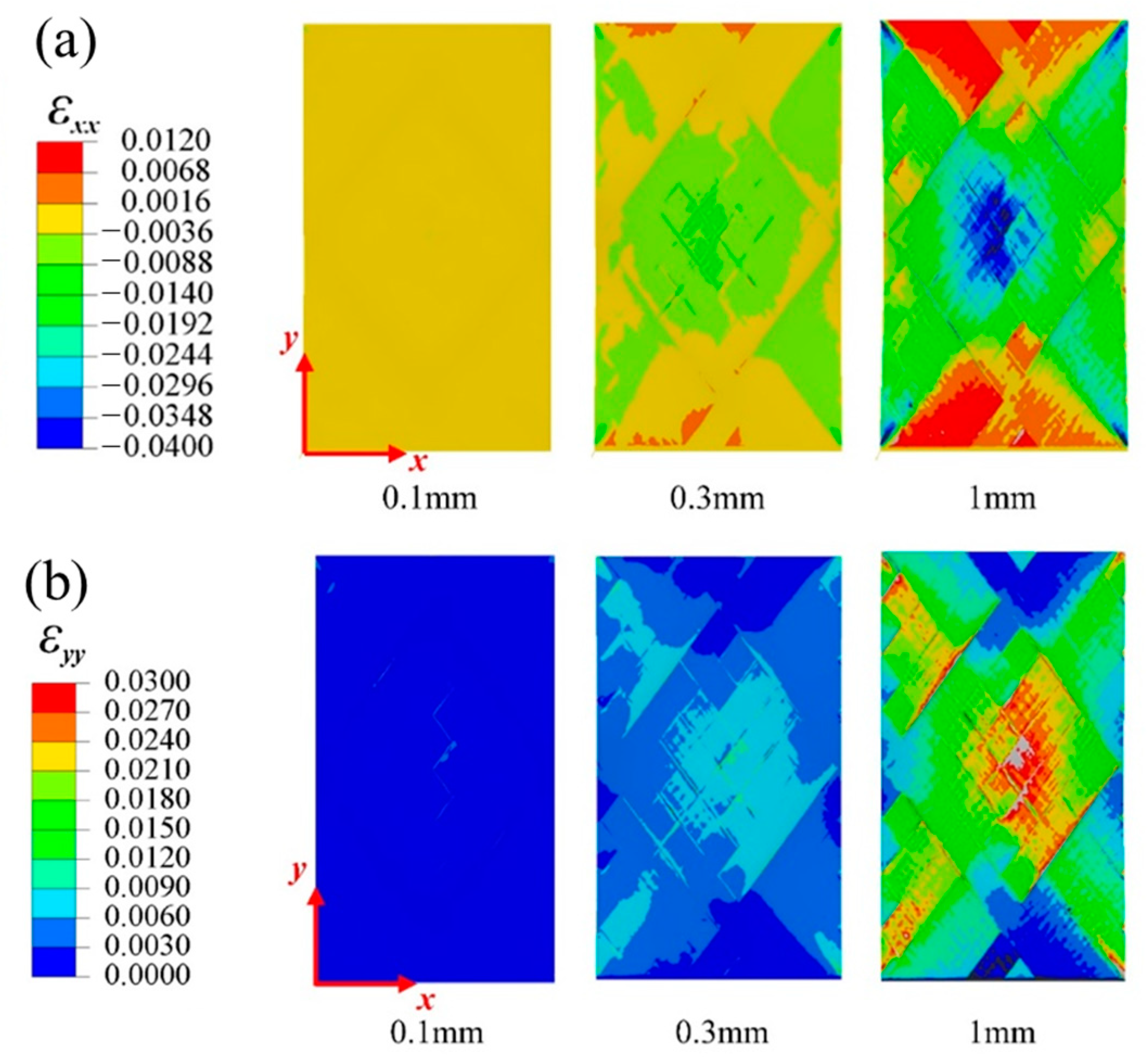
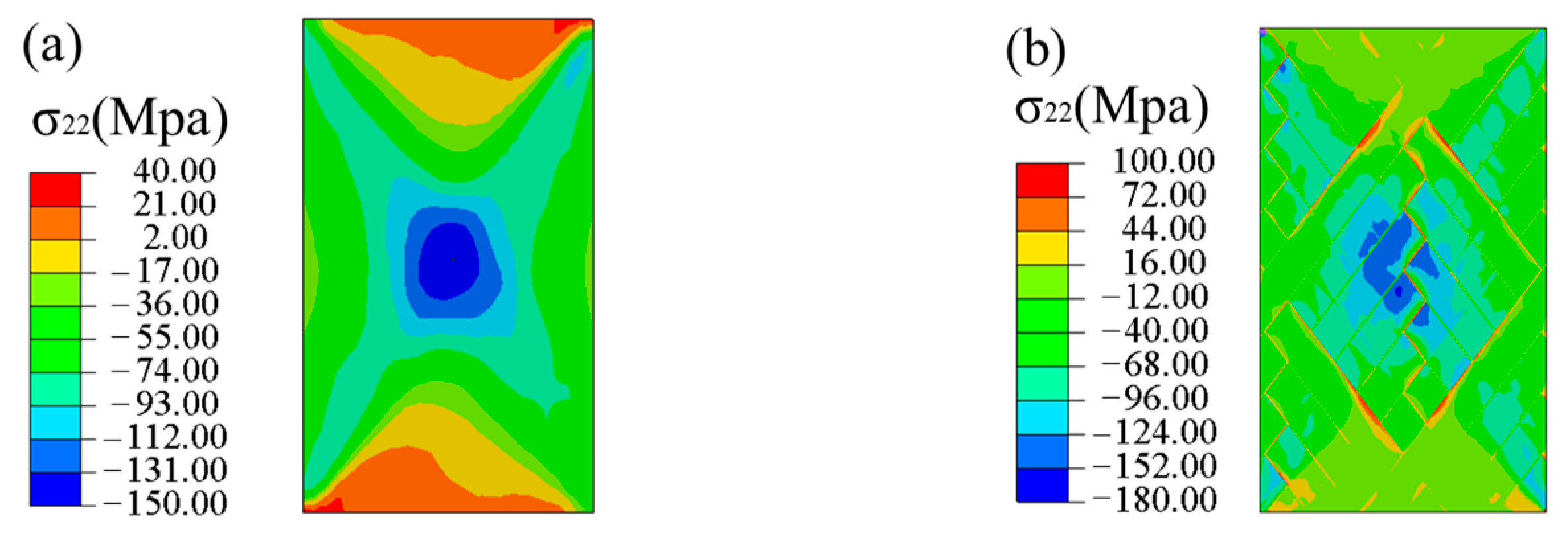
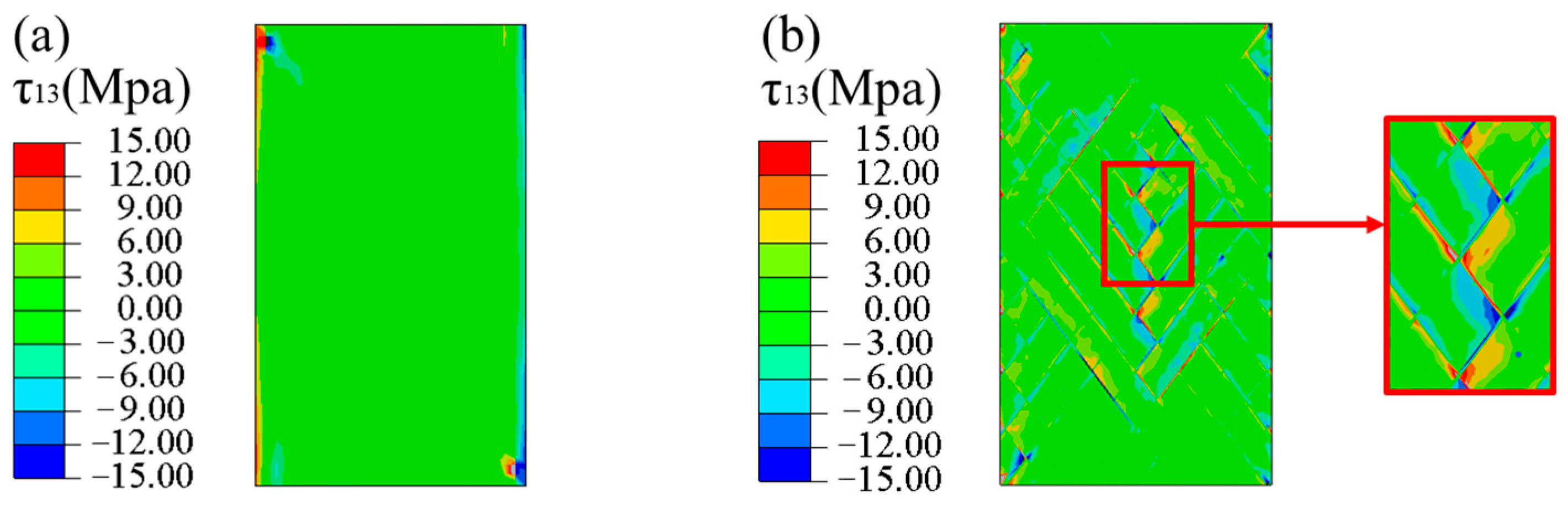
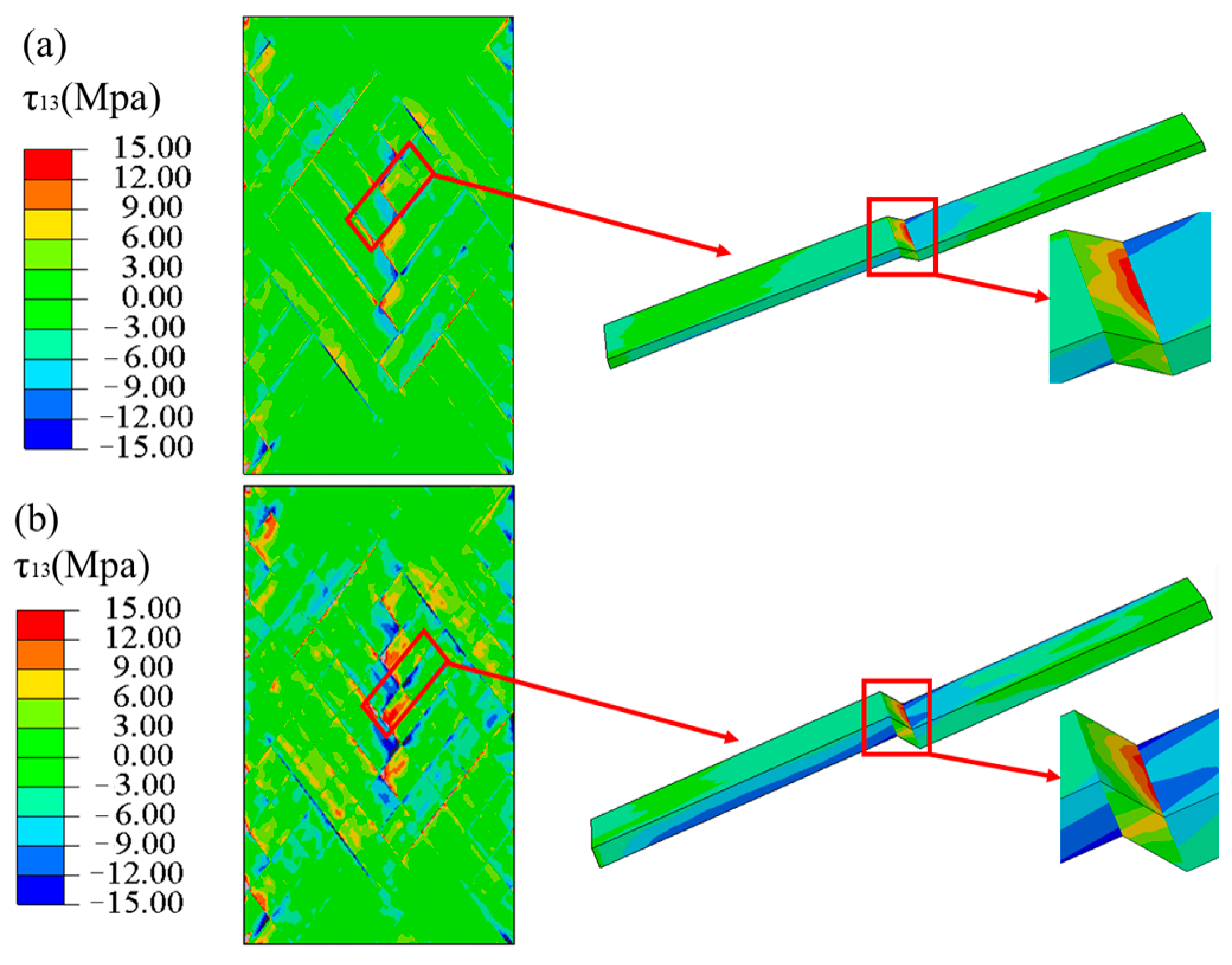
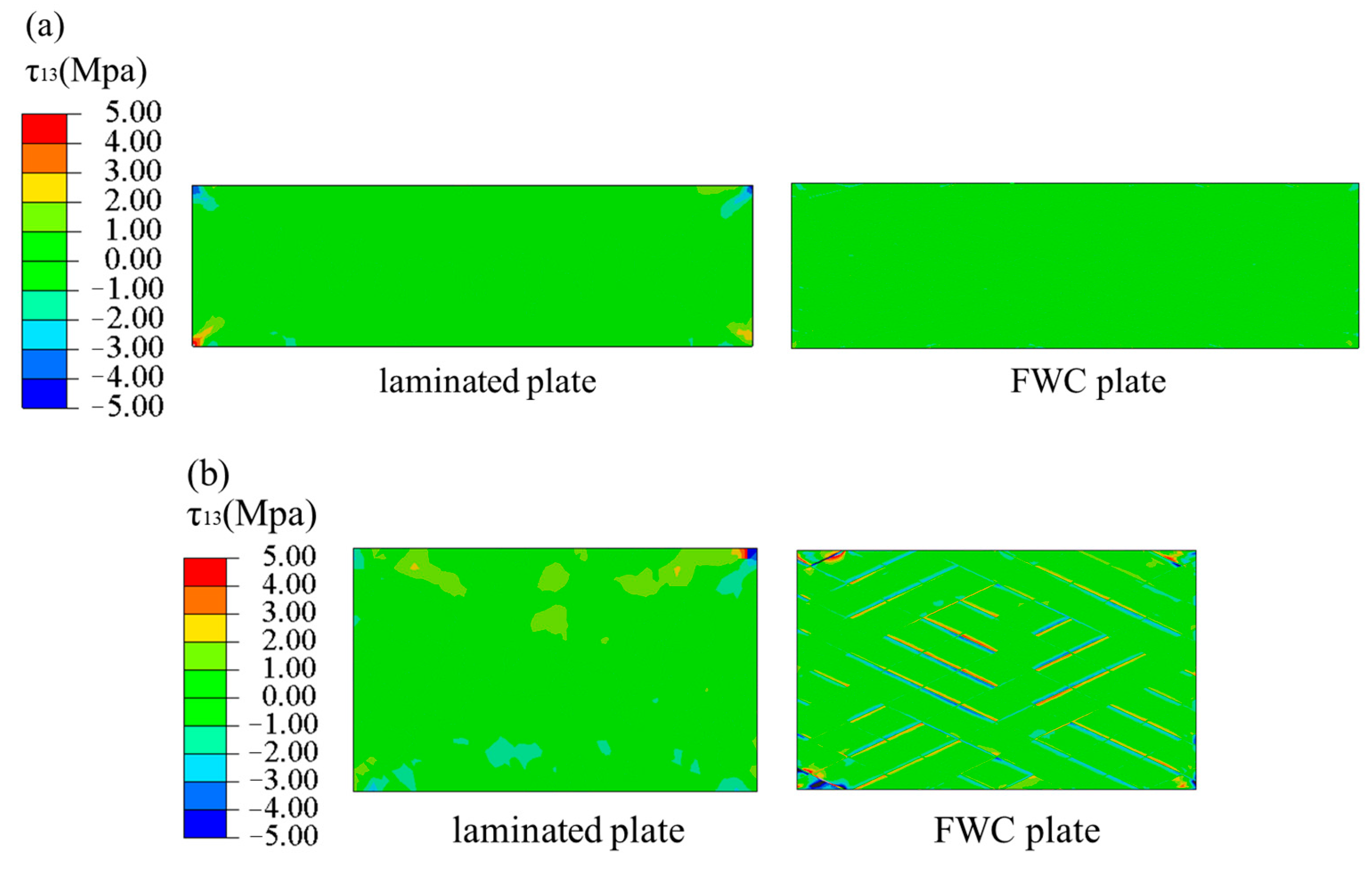
4.3. Numerical Results and Discussion
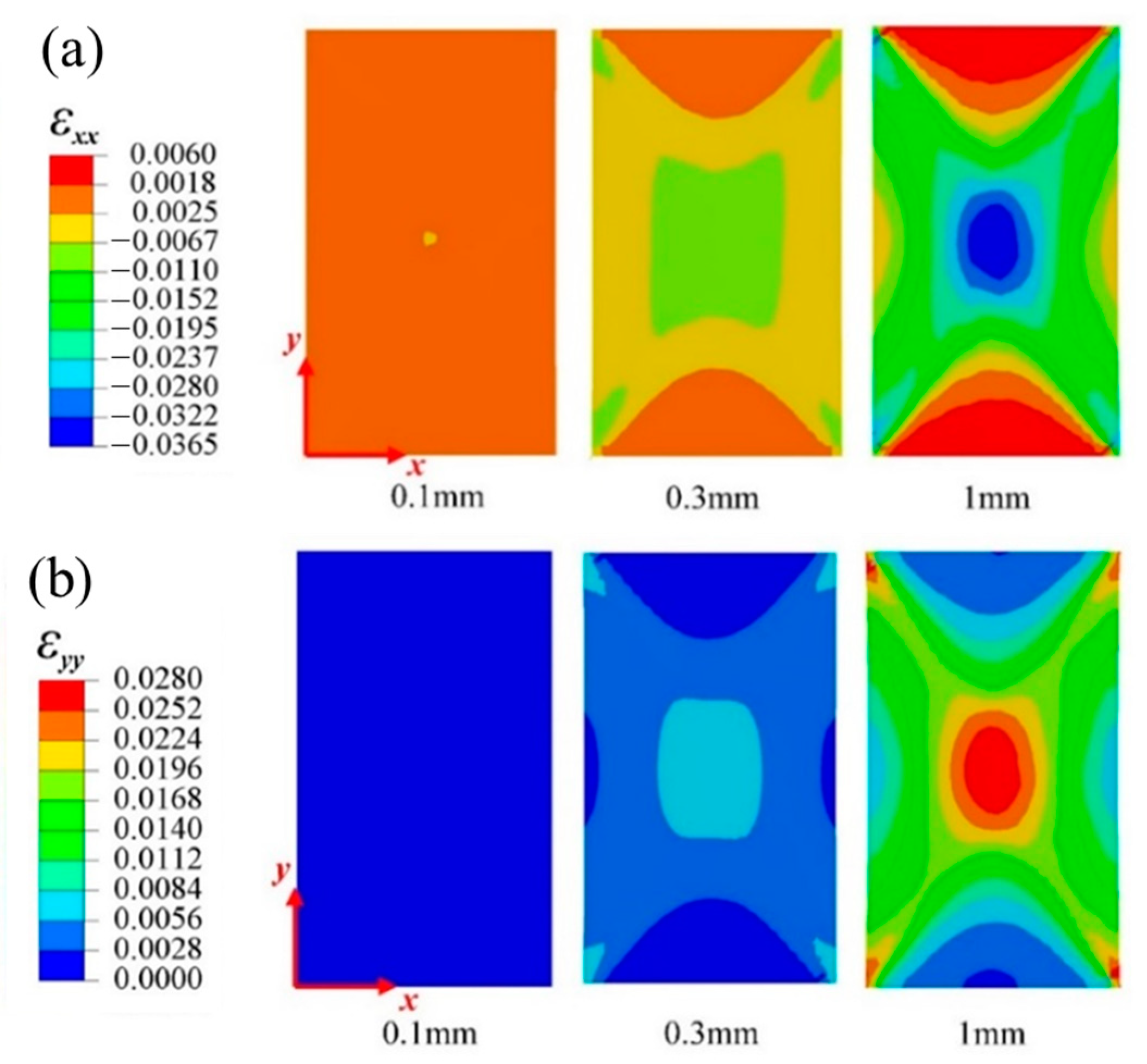
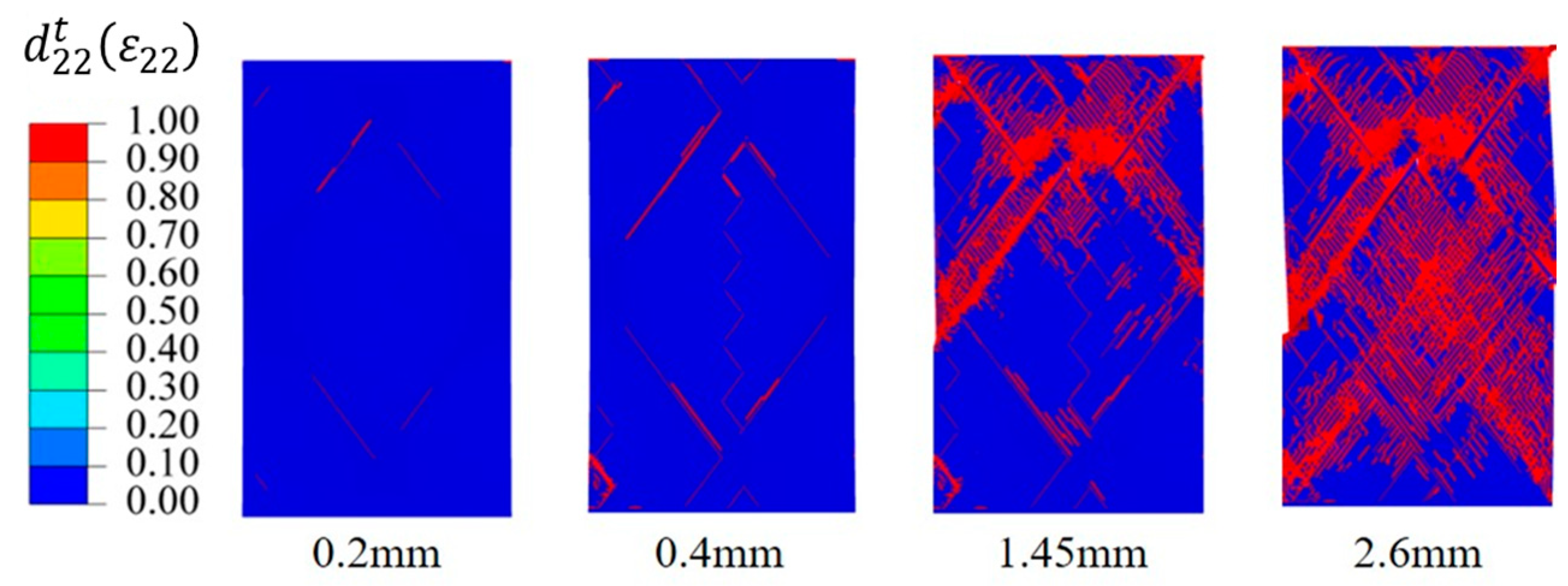
4.4. Progressive Damage Process
5. Numerical Exploration on the Influence of Bundle Thickness and Winding Angle
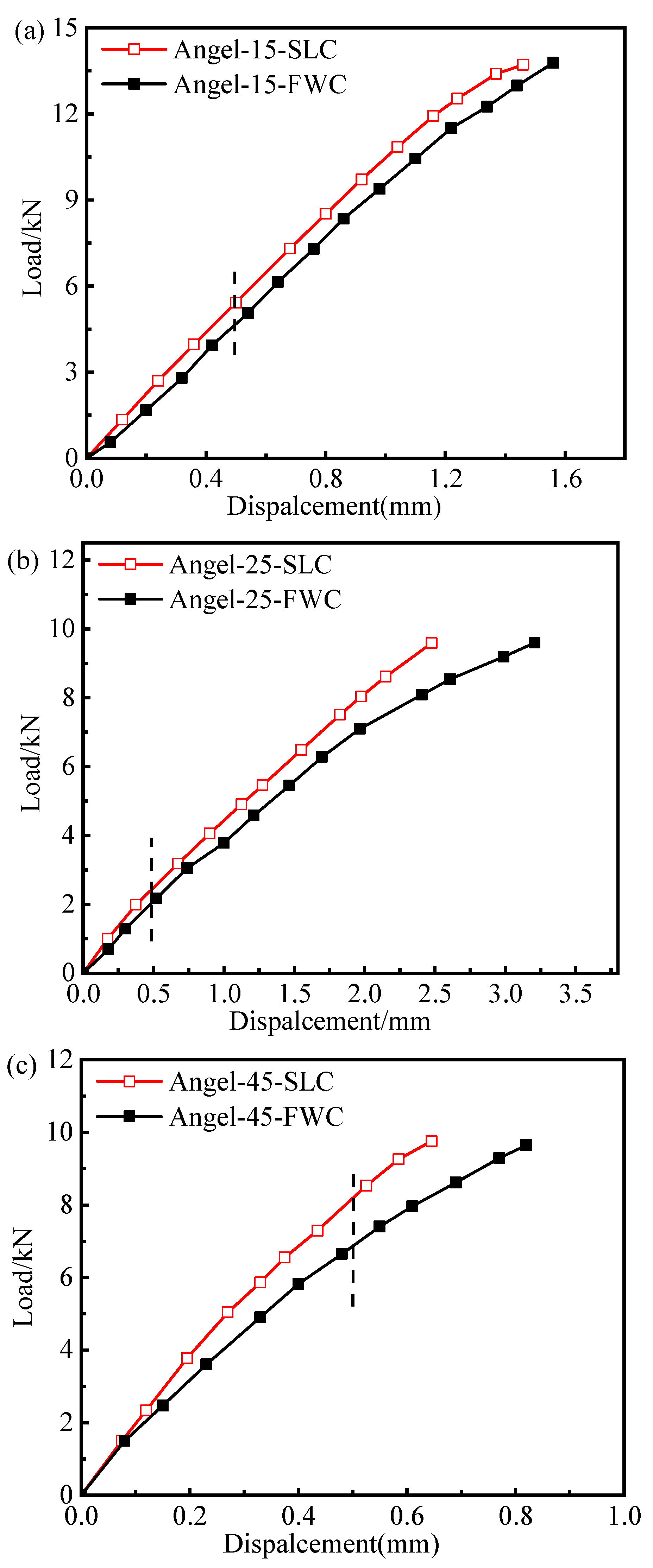
5.1. Influence of Bundle Thickness
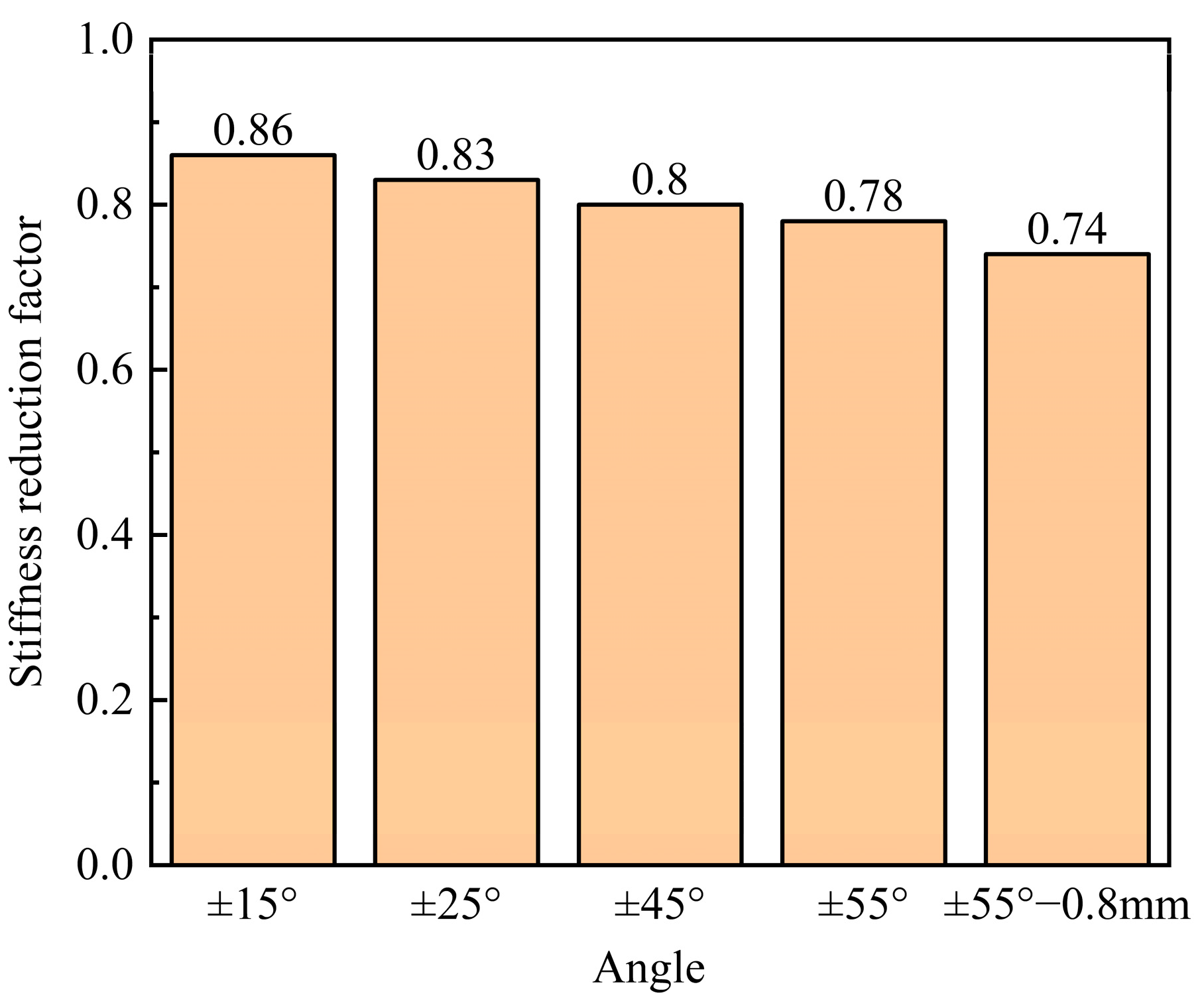
5.2. Influence of Winding Angle
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Martens, M.; Ellyin, F. Biaxial monotonic behavior of a multidirectional glass fiber epoxy pipe. Compos. Part A 2000, 31, 1001–1014. [Google Scholar] [CrossRef]
- Liu, P.; Zheng, J. Finite element analysis of al-carbon fiber/epoxy composite laminates. In Proceedings of the Asme Pressure Vessels & Piping Conference, Chicago, IL, USA, 27–31 July 2008; Volume 61435, pp. 581–589. [Google Scholar]
- Botelho, E.C.; Silva, R.A.; Pardini, L.C.; Rezende, M.C. Evaluation of adhesion of continuous fiber–epoxy composite/aluminum laminates. J. Adhes. Ence Technol. 2004, 18, 1799–1813. [Google Scholar] [CrossRef]
- Kucher, N.K.; Zarazovskii, M.N. Evaluation of the strength of unidirectional carbon-fiber-reinforced epoxy laminates. Strength Mater. 2006, 38, 637–650. [Google Scholar] [CrossRef]
- Guo, Z.; Li, Z.; Cui, J.; Li, Y.; Luan, Y. The effect of winding patterns on the mechanical behavior of filament-wound cylinder shells. Multidiscip. Model. Mater. Struct. 2019, 16, 508–518. [Google Scholar] [CrossRef]
- Morozov, E.V. The effect of filament-winding mosaic patterns on the strength of thin-walled composite shells. Compos. Struct. 2006, 76, 123–129. [Google Scholar] [CrossRef]
- Hernández-Moreno, H.; Douchin, B.; Collombet, F.; Choqueuse, D.; Davies, P. Influence of winding pattern on the mechanical behavior of filament wound composite cylinders under external pressure. Compos. Sci. Technol. 2008, 68, 1015–1024. [Google Scholar] [CrossRef]
- Xu, P.; Zheng, J.Y.; Liu, P.F. Finite element analysis of burst pressure of composite hydrogen storage vessels. Mater. Des. 2009, 30, 2295–2301. [Google Scholar] [CrossRef]
- Zu, L.; Koussios, S.; Beukers, A. Design of filament-wound isotensoid pressure vessels with unequal polar openings. Sci. Compos. Struct. 2010, 92, 2307–2313. [Google Scholar] [CrossRef]
- Guo, K.; Wen, L.; Xiao, J.; Lei, M.; Wang, S.; Zhang, C.; Hou, X. Design of winding pattern of filament-wound composite pressure vessel with unequal openings based on non-geodesics. J. Eng. Fibers Fabr. 2020, 15, 155892502093397. [Google Scholar] [CrossRef]
- Zheng, J.Y.; Liu, P.F. Elasto-plastic stress analysis and burst strength evaluation of Al-carbon fiber/epoxy composite cylindrical laminates. Comput. Mater. Sci. 2008, 42, 453–461. [Google Scholar] [CrossRef]
- Liu, P.F.; Zheng, J.Y. Recent developments on damage modeling and finite element analysis for composite laminates: A review. Mater. Des. 2010, 31, 3825–3834. [Google Scholar] [CrossRef]
- Liu, P.F.; Chu, J.K.; Hou, S.J.; Zheng, J.Y. Micromechanical damage modeling and multiscale progressive failure analysis of composite pressure vessel. Comput. Mater. Sci. 2012, 60, 137–148. [Google Scholar] [CrossRef]
- Lin, S.; Yang, L.; Xu, H.; Jia, X.; Yang, X.; Zu, L. Progressive damage analysis for multiscale modelling of composite pressure vessels based on Puck failure criterion. Compos. Struct. 2020, 255, 113046. [Google Scholar] [CrossRef]
- Liao, B.; Du, Y.; Zheng, J.; Wang, D.; Lin, Y.; Tao, R.; Zhou, C. Prediction of residual burst strength for composite pressure vessels after low velocity impact International. J. Hydrog. Energy 2020, 45, 10962–10976. [Google Scholar] [CrossRef]
- Alam, S.; Yandek, G.; Lee, R.C.; Mabry, J. A study of residual burst strength of composite over wrapped pressure vessel due to low velocity impact. Int. J. Press. Vessel. Pip. 2021, 194, 104511. [Google Scholar] [CrossRef]
- Zu, L.; Xu, H.; Wang, H.; Zhang, B.; Zi, B. Design and analysis of filament-wound composite pressure vessels based on non-geodesic winding. Compos. Struct. 2019, 207, 41–52. [Google Scholar] [CrossRef]
- Rousseau, J.; Perreux, D.; Verdière, N. The influence of winding patterns on the damage behaviour of filament-wound pipes Composites. Sci. Technol. 1999, 59, 1439–1449. [Google Scholar]
- Arellano, M.T.; Crouzeix, L.; Douchin, B.; Collombet, F.; Moreno, H.H.; Velázquez, J.G. Strain field measurement of filament-wound composites at ±55° using digital image correlation: An approach for unit cells employing flat specimens. Compos. Struct. 2010, 92, 2457–2464. [Google Scholar] [CrossRef]
- Henry, T.C.; Bakis, C.E. Compressive strength and stiffness of filament-wound cylinders. J. Reinf. Plast. Compos. 2016, 35, 1543–1553. [Google Scholar] [CrossRef]
- Mian, H.H.; Rahman, H. Influence of mosaic patterns on the structural integrity of filament wound composite pressure vessels International. J. Struct. Integr. 2011, 66, 185–188. [Google Scholar]
- Zhang, C.; Binienda, W.K.; Kohlman, L.W. Analytical model and numerical analysis of the elastic behavior of triaxial braided composites. J. Aerosp. Eng. 2014, 27, 473–483. [Google Scholar] [CrossRef]
- Shen, C.; Han, X. Meso-scale model for calculating the stiffness of filament wound composites considering fiber undulations. Struct. Eng. Mech. Int'l J. 2017, 62, 273–279. [Google Scholar] [CrossRef]
- Takahashi, T.; Ueda, M.; Miyoshi, K.; Todoroki, A. Initiation and propagation of fiber kinking from fiber undulation in a unidirectional carbon fiber reinforced plastic. Compos. Part C Open Access 2020, 3, 100056. [Google Scholar] [CrossRef]
- Pourahmadi, E.; Taheri-behrooz, F. The influence of fiber bundle width on the mechanical properties of filament-wound cylindrical structures. Int. J. Mech. Sci. 2020, 178, 105617. [Google Scholar] [CrossRef]
- Fuller, J.; Mitchell, S.; Pozegic, T.; Wu, X.; Longana, M.; Wisnom, M. Experimental evaluation of hygrothermal effects on pseudo-ductile thin ply angle-ply carbon/epoxy laminates. Compos. Part B Eng. 2021, 227, 109388. [Google Scholar] [CrossRef]
- Czel, G. Development of bi-directional pseudo-ductile glass/carbon-epoxy hybrid composites for improved safety in structural applications. Compos. Part B Eng. 2022, 231, 109546. [Google Scholar] [CrossRef]
- Conceptualisation, X.W.; Fuller, J.D.; Wisnom, M.R. An investigation into fatigue behaviour and damage progression in pseudo-ductile thin-ply angle-ply laminates. Compos. Part A Appl. Sci. Manuf. 2021, 149, 106518. [Google Scholar]
- Ead, A.B.Z. Crystal plasticity based modelling of shear response of carbon fibre reinforced composites. Procedia Struct. Integr. 2022, 35, 91–97. [Google Scholar]
- Kwon, J.; Choi, J.; Huh, H.; Lee, J. Evaluation of the effect of the strain rate on the tensile properties of carbon-epoxy composite laminates. J. Compos. Mater. 2017, 51, 0021998316683439. [Google Scholar] [CrossRef]
- Wan, L.; Ismail, Y.; Sheng, Y.; Wu, K.; Yang, D. Progressive Failure Analysis of CFRP Composite Laminates under Uniaxial Tension using a Discrete Element Method; SAGE Publications: London, UK, 2021; Volume 55, pp. 1091–1108. [Google Scholar]
- ASTMD6641/D6641M-16; Standard Test Method for Compressive Properties of Polymer Matrix Composite Materials Using a Combined Loading Compression (CLC) Test Fixture. ASTM International: West Conshohocken, PA, USA, 2016.
- ASTMD7905/D7905M; Standard Test Method for Determination of the Mode II Interlaminar Fracture Toughness of Unidirectional Fiber-Reinforced Polymer Matrix Composites Is a New Standard Now Available. ASTM International: West Conshohocken, PA, USA, 2020.
- ASTMD3518/D3518M-18; Standard Test Method for In-Plane Shear Response of Polymer Matrix Composite Materials by Tensile Test of a ±45◦ Laminate. ASTM International: West Conshohocken, PA, USA, 2018.
- ASTMD5528-13; Standard Test Method for Mode I Interlaminar Fracture Toughness of Unidirectional Fiber-Reinforced Polymer Matrix Composites. ASTM International: West Conshohocken, PA, USA, 2013.
- Zheng, K.; Hu, H.; Cao, D.; Zhong, Y.; Li, S. Experimental and numerical studies on the tensile behaviors of thin-ply and thick-ply open-hole laminates. Thin-Walled Struct. 2023, 186, 110649. [Google Scholar] [CrossRef]
- Din, I.U.; Hao, P.; Franz, G.; Panier, S. Elastoplastic CDM model based on Puck’s theory for the prediction of mechanical behavior of Fiber Reinforced Polymer (FRP) composites. Compos. Struct. 2018, 201, 291–302. [Google Scholar] [CrossRef]
- Din, I.U.; Tu, S.; Hao, P.; Panier, S.; Khan, K.A.; Umer, R.; Shah, S.Z.; Franz, G.; Aamir, M. Sequential damage study induced in fiber reinforced composites by shear and tensile stress using a newly developed Arcan fixture. J. Mater. Res. Technol. 2020, 9, 13352–13364. [Google Scholar] [CrossRef]
- Hashin, Z.; Bagchi, D.; Rosen, B.W. Non-Linear Behavior of Fiber Composite Laminate; NASA: Washington, DC, USA, 1974.
- Bogetti, T.A.; Hoppel, C.P.; Harik, V.M.; Newill, J.F.; Burns, B.P. Predicting the nonlinear response and progressive failure of composite laminates. In Failure Criteria in Fibre-Reinforced-Polymer Composites; Elsevier: Amsterdam, The Netherlands, 2004; pp. 402–428. [Google Scholar]
- Rose, C.A.; Dávila, C.; Leone, F.A. Analysis Methods for Progressive Damage of Composite Structures; NASA Center for AeroSpace Information: Hanover, MD, USA, 2013.
- Liu, B.; Zhao, L.; Hong-Lu, X.U. The research about damage of composite laminate in bolted joints based on the hashin failure criteria. Sci. Technol. Eng. 2012, 12, 1671–1815. [Google Scholar]
- Hashin, Z. Fatigue failure criteria for unidirectional fiber composites. J. Appl. Mech. 1981, 48, 846–852. [Google Scholar] [CrossRef]
- Duarte AP, C.; Diaz Saez, A.; Silvestre, N. Comparative study between XFEM and Hashin damage criterion applied to failure of composites. Thin-Walled Struct. 2017, 115, 277–288. [Google Scholar] [CrossRef]
- Simulia, D. Abaqus 6.11 Analysis User's Manual; Dassault Systèmes Simulia Corp.: Providence, RI, USA, 2011. [Google Scholar]





| Label | Number of Sample | Description |
|---|---|---|
| FWC | 3 | Filament wound plates |
| SLC | 3 | Laminated plates |
| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| E11 | 127 ± 3 GPa | E22 | 7.9 ± 0.3 GPa | E33 | 7.9 ± 0.3 GPa |
| v12 | 0.35 ± 0.01 | v13 | 0.35 ± 0.01 | v23 | 0.45 ± 0.01 |
| G12 | 2.1 ± 0.2 GPa | G13 | 2.1 ± 0.2 GPa | G23 | 4.8 GPa |
| XT | 2.0 ± 0.08 GPa | XC | 1.2 ± 0.02 GPa | YT | 38.5 ± 3 MPa |
| YC | 180.7 ± 5 MPa | S | 135.0 ± 3 MPa | Gft | 133 N/mm [36] |
| Gfc | 60 N/mm [36] | Gmt | 0.352 ± 0.03 N/mm | Gmt | 1.45 N/mm [36] |
| E | 3.0 GPa | μ | 0.37 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Hu, H.; Cao, D.; Ji, Y.; Wang, X.; Chen, H.; Li, S. Investigation on the Influence of Fiber Bundle Undulating Architecture on Tensile Behavior of Filament Wound Composite Laminates. Materials 2023, 16, 3697. https://doi.org/10.3390/ma16103697
Liu H, Hu H, Cao D, Ji Y, Wang X, Chen H, Li S. Investigation on the Influence of Fiber Bundle Undulating Architecture on Tensile Behavior of Filament Wound Composite Laminates. Materials. 2023; 16(10):3697. https://doi.org/10.3390/ma16103697
Chicago/Turabian StyleLiu, Hao, Haixiao Hu, Dongfeng Cao, Yundong Ji, Xiangjiang Wang, Hongda Chen, and Shuxin Li. 2023. "Investigation on the Influence of Fiber Bundle Undulating Architecture on Tensile Behavior of Filament Wound Composite Laminates" Materials 16, no. 10: 3697. https://doi.org/10.3390/ma16103697
APA StyleLiu, H., Hu, H., Cao, D., Ji, Y., Wang, X., Chen, H., & Li, S. (2023). Investigation on the Influence of Fiber Bundle Undulating Architecture on Tensile Behavior of Filament Wound Composite Laminates. Materials, 16(10), 3697. https://doi.org/10.3390/ma16103697





