Atomistic Study of the Effect of Hydrogen on the Tendency toward Slip Planarity in Bcc Iron
Abstract
:1. Introduction
2. Simulation Method
3. Results
3.1. H Binding Energy
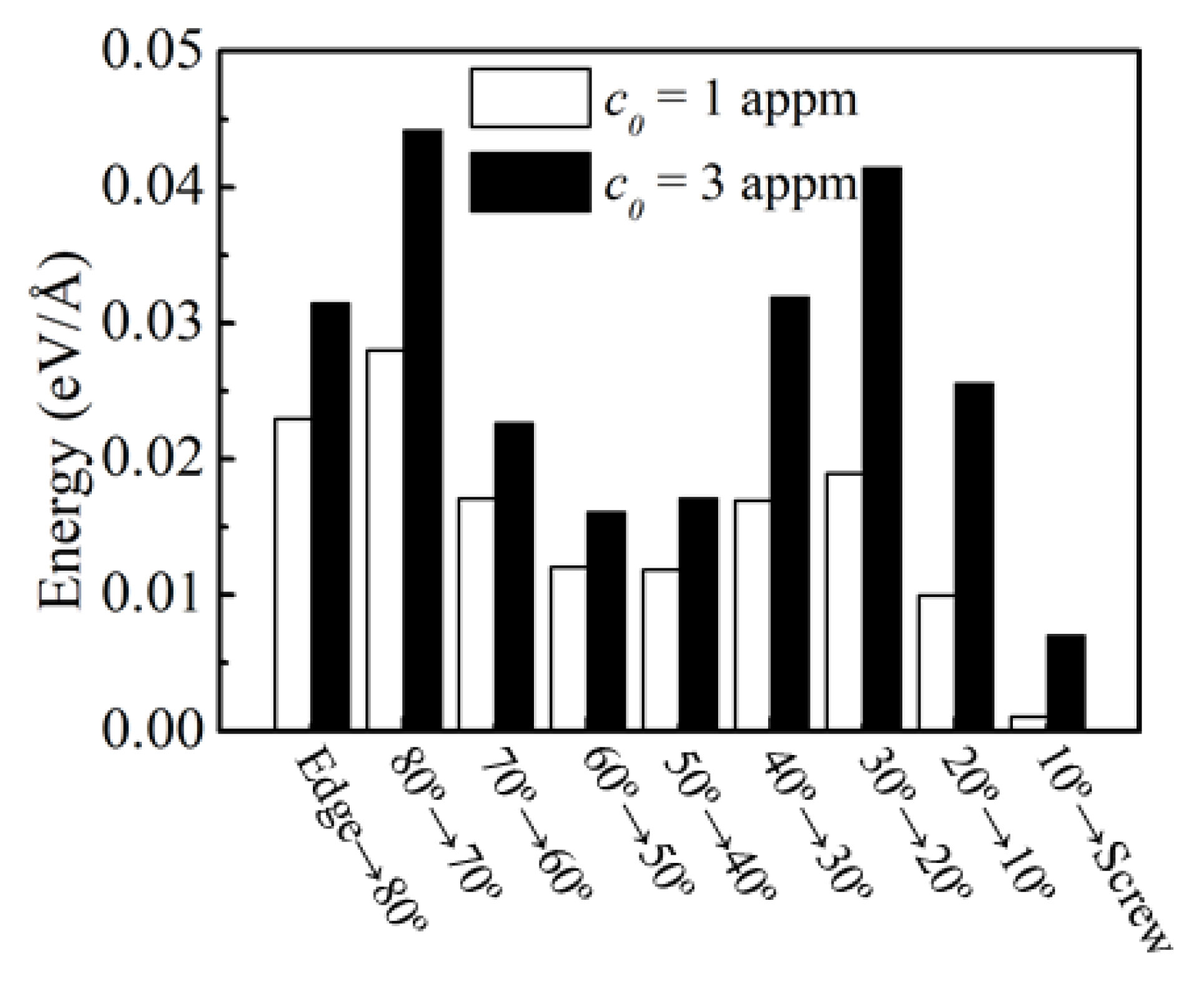
3.2. The Effect of H on the Dislocation Energies
3.3. H Atmosphere around the Dislocations
4. Discussions
4.1. The Interaction Energy of H
4.2. The Effect of H on Slip Planarity
5. Conclusions
- (1).
- The binding energies of H, the excess H in the atmosphere, and the decrements in the dislocation line energies were increasing with the edge components.
- (2).
- The interaction energy of H was slightly weaker than its binding energy because of the multiple H–H interactions.
- (3).
- H induced a significant increment in the energy change in the system, resulting in the inhibition of the reorientations towards the screw dislocations from the edge and mixed dislocations. The cross-slip in the bcc Fe was thus decreased, facilitating slip planarity.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Robertson, I.M.; Sofronis, P.; Nagao, A.; Martin, M.L.; Wang, S.; Gross, D.W.; Nygren, K.E. Hydrogen embrittlement understood. Metall. Mater. Trans. A 2015, 46, 2323–2341. [Google Scholar] [CrossRef] [Green Version]
- Khanchandani, H.; Rolli, R.; Schneider, H.C.; Kirchlechner, C.; Gault, B. Hydrogen embrittlement of twinning-induced plasticity steels: Contribution of segregation to twin boundaries. Scr. Mater. 2023, 60, 5160–5171. [Google Scholar] [CrossRef]
- Yang, X.; Sun, F.; Li, Q.; Zhu, R.; Liu, Z.; Du, C.; Li, X. Effect of Hydrogen Charging on the Stress Corrosion Cracking Behavior of X70 Steel in Simulated Deep Seawater Environment. Metals 2022, 12, 334. [Google Scholar] [CrossRef]
- Sun, Q.; He, J.; Nagao, A.; Ni, Y.; Wang, S. Hydrogen-prompted heterogeneous development of dislocation structure in Ni. Acta Mater. 2023, 118660, 1359–6454. [Google Scholar] [CrossRef]
- Stan, L. Discussion of some recent literature on hydrogen-embrittlement mechanisms: Addressing common misunderstandings. Corros. Rev. 2019, 37, 377–395. [Google Scholar]
- Bak, S.H.; Kim, S.S.; Lee, D.B. Effect of hydrogen on dislocation structure and strain-induced martensite transformation in 316L stainless steel. RSC Adv. 2017, 7, 27840–27845. [Google Scholar] [CrossRef] [Green Version]
- Kuhr, B.; Farkas, D.; Robertson, I.M. Atomistic studies of hydrogen effects on grain boundary structure and deformation response in FCC Ni. Comput. Mater. Sci. 2016, 122, 92–101. [Google Scholar] [CrossRef] [Green Version]
- Tehranchi, A.; Yin, B.; Curtin, W.A. Softening and hardening of yield stress by hydrogen–solute interactions. Philos. Mag. 2017, 97, 400–418. [Google Scholar] [CrossRef] [Green Version]
- Torres, E.; Pencer, J. Molecular dynamics study of the role of symmetric tilt grain boundaries on the helium distribution in nickel. J. Nucl. Mater. 2018, 502, 86–94. [Google Scholar] [CrossRef]
- Zheng, Y.; Yu, P.; Zhang, K.; Wen, M.; Zheng, J.; Zhou, C.; Zhang, L. Coupling effect of grain boundary and hydrogen segregation on dislocation nucleation in bi-crystal nickel. Int. J. Hydrog. Energy 2020, 45, 20021–20031. [Google Scholar] [CrossRef]
- Heuser, B.J.; Trinkle, D.R.; Yang, T.N.; He, L. Hydrogen trapping at dislocation cores at room temperature in deformed Pd. J. Alloys Compd. 2013, 577, 189–191. [Google Scholar] [CrossRef]
- Tang, Y.; El-Awady, J.A. Atomistic simulations of the interactions of hydrogen with dislocations in fcc metals. Phys. Rev. B 2012, 86, 174102. [Google Scholar] [CrossRef] [Green Version]
- Itakura, M.; Kaburaki, H.; Yamaguchi, M.; Okita, T. The effect of hydrogen atoms on the screw dislocation mobility in bcc iron: A first-principles study. Acta Mater. 2013, 61, 6857–6867. [Google Scholar] [CrossRef]
- Yu, P.; Cui, Y.; Zhu, G.Z.; Shen, Y.; Wen, M. The key role played by dislocation core radius and energy in hydrogen interaction with dislocations. Acta Mater. 2020, 185, 518–527. [Google Scholar] [CrossRef]
- Kholtobina, A.S.; Pippan, R.; Romaner, L.; Scheiber, D.; Ecker, W.; Razumovskiy, V.I. Hydrogen Trapping in bcc Iron. Materials 2020, 13, 2288. [Google Scholar] [CrossRef] [PubMed]
- Gesari, S.B.; Irigoyen, B.D.L.; Juan, A. Binding energy of hydrogen to mixed and screw dislocation. Surf. Rev. Lett. 2005, 12, 227–232. [Google Scholar] [CrossRef]
- Wen, M.; Fukuyama, S.; Yokogawa, K. Hydrogen-affected cross-slip process in fcc nickel. Phys. Rev. B 2004, 69, 174108. [Google Scholar] [CrossRef]
- Martin, M.L.; Somerday, B.P.; Ritchie, R.O.; Sofronis, P.; Robertson, I.M. Hydrogen-induced intergranular failure in nickel revisited. Acta Mater. 2012, 60, 2739–2745. [Google Scholar] [CrossRef]
- Krishnan, M.A.; Raja, V.S. Role of temper conditions on hydrogen embrittlement behavior of AA 7010. Corros. Sci. 2019, 152, 211–217. [Google Scholar] [CrossRef]
- Tondro, A.; Taherijam, M.; Abdolvand, H. Diffusion and redistribution of hydrogen atoms in the vicinity of localized deformation zones. Mech. Mater. 2023, 177, 104544. [Google Scholar] [CrossRef]
- Chateau, J.P.; Delafosse, D.; Magnin, T. Numerical simulations of hydrogen-dislocation interactions in fcc stainless steels. Part I: Hydrogen-dislocation interactions in bulk crystals. Acta Mater. 2020, 50, 1507–1522. [Google Scholar] [CrossRef]
- Barnoush, A.; Vehoff, H. Recent developments in the study of hydrogen embrittlement: Hydrogen. Acta Mater. 2010, 58, 5274–5285. [Google Scholar] [CrossRef]
- Kohnert, A.A.; Tummala, H.; Lebensohn, R.A.; Tomé, C.N.; Capolungo, L. On the use of transmission electron microscopy to quantify dislocation densities in bulk metals. Scr. Mater. 2020, 178, 161–165. [Google Scholar] [CrossRef]
- Song, J.; Curtin, W.A. Atomic mechanism and prediction of hydrogen embrittlement in iron. Nat. Mater. 2012, 12, 145–151. [Google Scholar] [CrossRef] [PubMed]
- Yu, P.; Zhu, G.Z.; Wen, M. Application of grand-canonical ensemble Monte Carlo simulation in metals using cavity-biased method. Mol. Simul. 2020, 46, 736–742. [Google Scholar] [CrossRef]
- Hagi, H.; Hayashi, Y. Effect of dislocation trapping on hydrogen and deuterium diffusion in iron. Trans. Jpn. Inst. Met. 1987, 38, 368–374. [Google Scholar] [CrossRef] [Green Version]
- Choo, W.Y.; Lee, J.Y. Effect of cold working on the hydrogen trapping phenomena in pure iron. Metall. Trans. A 1983, 14, 1299–1305. [Google Scholar] [CrossRef]
- Counts, W.A.; Wolverton, C.; Gibala, R. First-principles energetics of hydrogen traps in α-Fe: Point defects. Acta Mater. 2010, 58, 4730–4741. [Google Scholar] [CrossRef]
- Sills, R.B.; Cai, W. Free energy change of a dislocation due to a Cottrell atmosphere. Philos. Mag. 2018, 98, 1491–1510. [Google Scholar] [CrossRef]
- Kumar, P.; Adlakha, I. Effect of Interstitial Hydrogen on Elastic Behavior of Metals: An Ab-Initio Study. J. Eng. Mater. Tech. 2023, 145, 011003. [Google Scholar] [CrossRef]
- Jung, S.P.; Kwon, Y.; Lee, C.S.; Lee, B.J. Influence of hydrogen on the grain boundary crack propagation in bcc iron: A molecular dynamics simulation. Comput. Mater. Sci. 2018, 149, 424–434. [Google Scholar] [CrossRef]
- Simpson, E.L.; Paxton, A.T. Effect of applied strain on the interaction between hydrogen atoms and 1/2 <111> screw dislocations in α-iron. Int. J. Hydrog. Energy 2020, 45, 20069–20079. [Google Scholar]
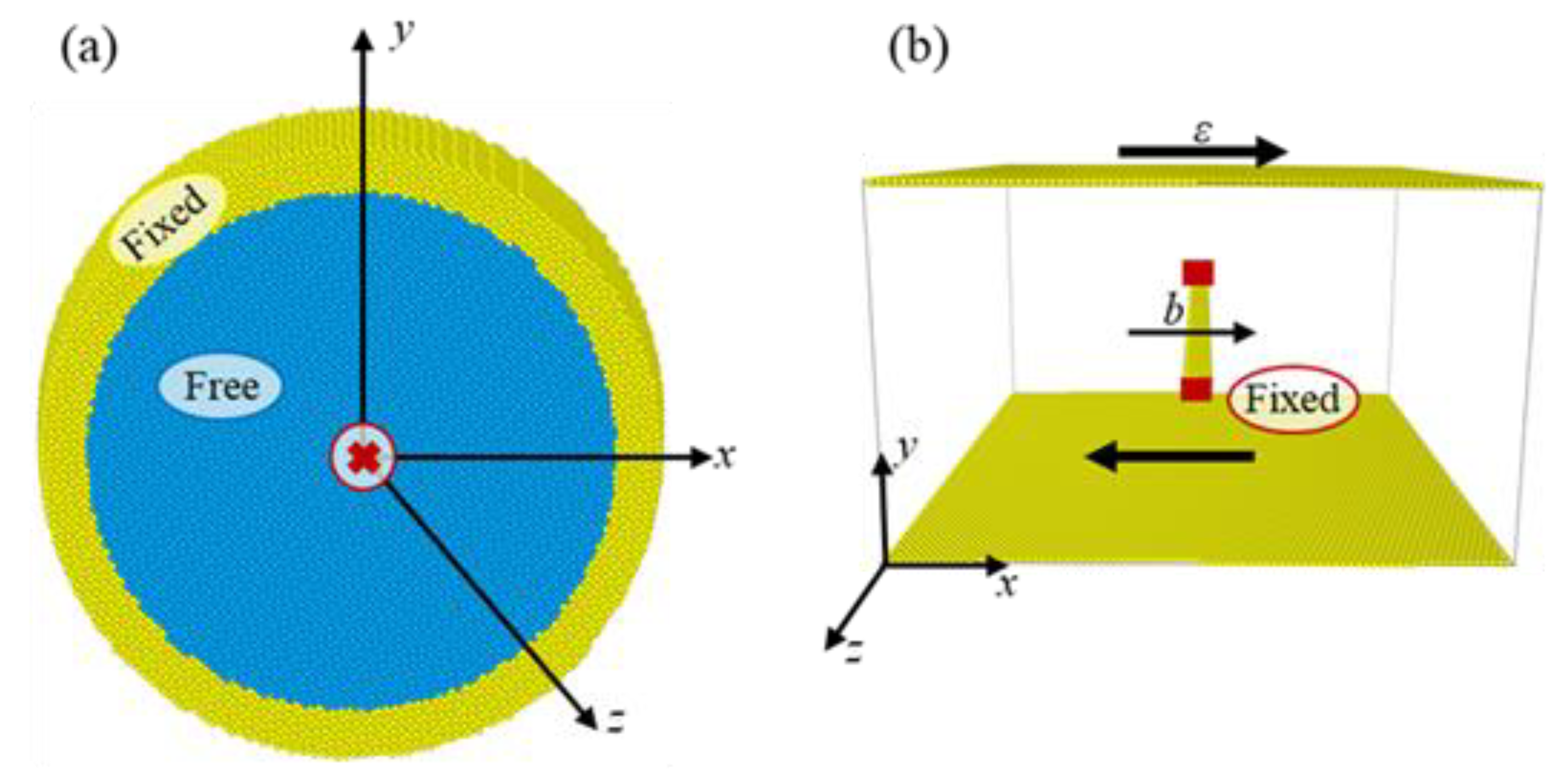
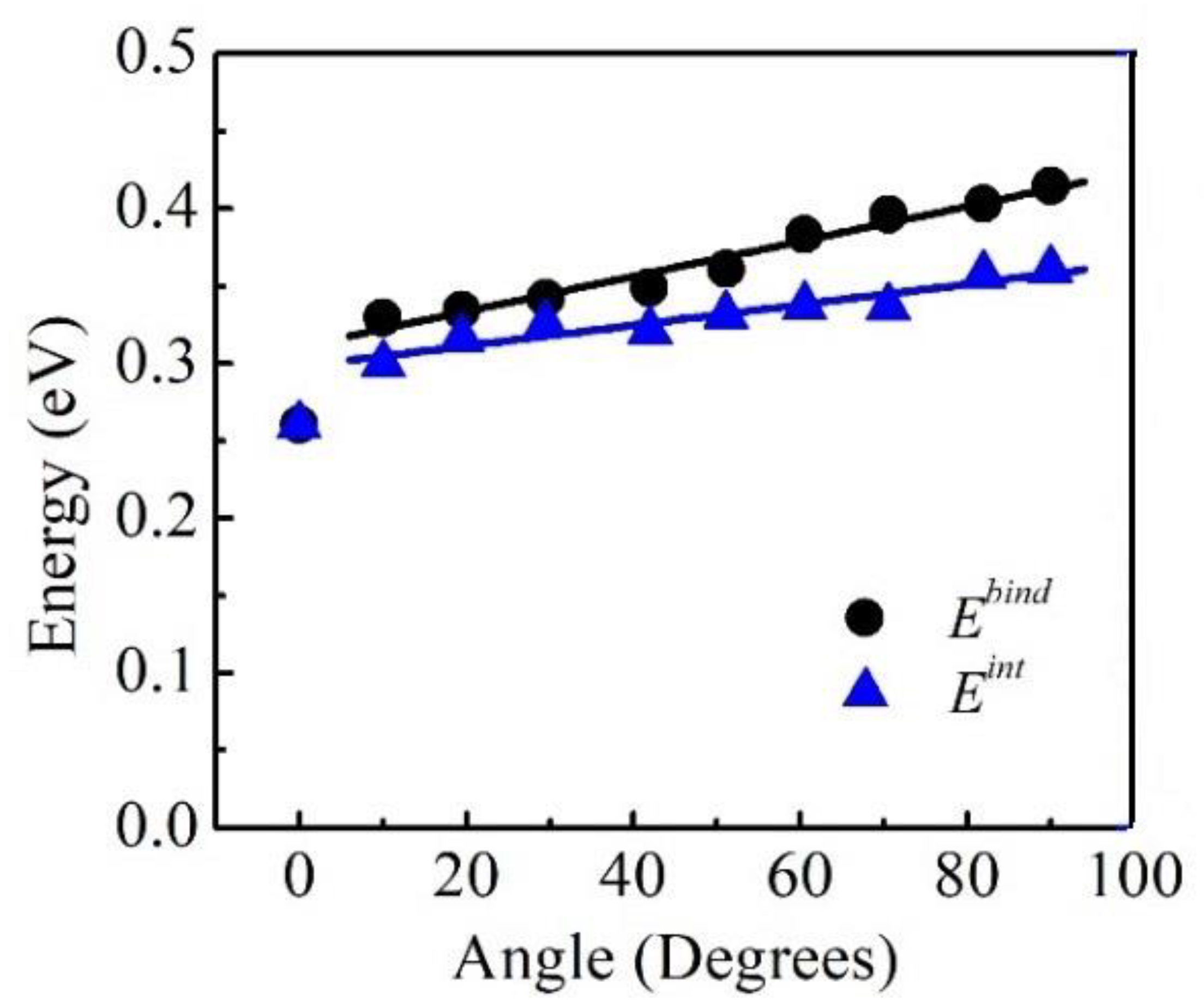
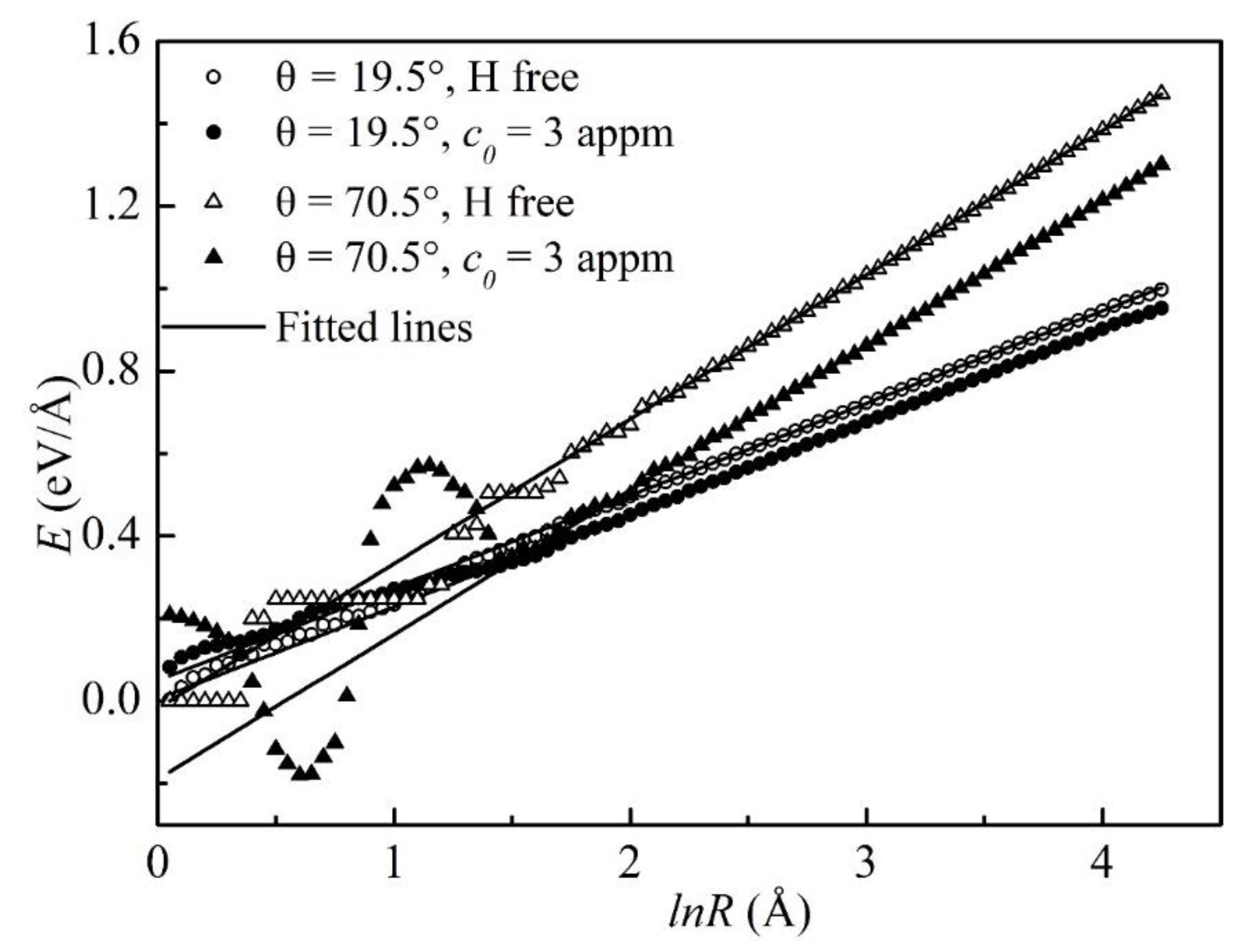
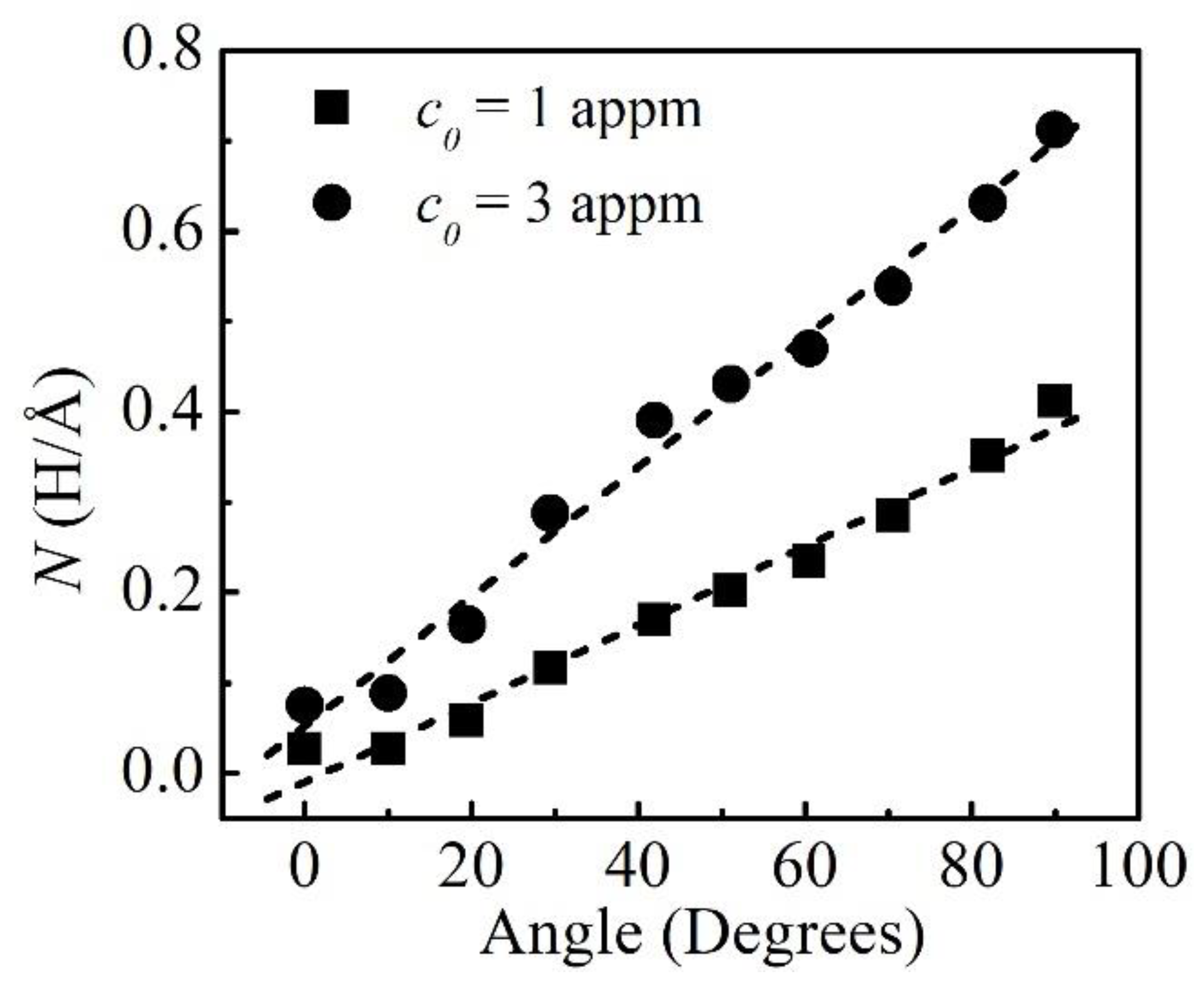

| θ (Degrees) | x | y | l//z |
|---|---|---|---|
| 90.0 | |||
| 82.0 | |||
| 70.5 | |||
| 60.5 | |||
| 51.1 | |||
| 42.0 | |||
| 29.5 | |||
| 19.5 | |||
| 10.0 | |||
| 0.0 |
| Ebind (eV/H) | Method |
|---|---|
| 0.27, 0.28 | Temperature dependence in H diffusivity |
| 0.28 | Thermal spectrum of H2 evolution |
| 0.50–0.60, 0.62 | Analysis of permeability |
| 0.21, 0.28 | Internal friction |
| θ (Degrees) | ΔE (eV/Å) | ||
|---|---|---|---|
| 1 appm | 3 appm | 5 appm | |
| 90.0 | 0.126 | 0.292 | 0.297 |
| 82.0 | 0.149 | 0.210 | 0.244 |
| 70.5 | 0.115 | 0.171 | 0.219 |
| 60.5 | 0.078 | 0.158 | 0.170 |
| 51.1 | 0.076 | 0.145 | 0.147 |
| 42.0 | 0.055 | 0.149 | 0.149 |
| 29.5 | 0.032 | 0.088 | 0.168 |
| 19.5 | 0.029 | 0.045 | 0.085 |
| 10.0 | 0.002 | 0.022 | 0.028 |
| 0.0 | 0.005 | 0.005 | 0.027 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Y.; Zheng, G.; Zhang, K.; Cao, L.; Yu, P.; Zhang, L. Atomistic Study of the Effect of Hydrogen on the Tendency toward Slip Planarity in Bcc Iron. Materials 2023, 16, 4991. https://doi.org/10.3390/ma16144991
Zheng Y, Zheng G, Zhang K, Cao L, Yu P, Zhang L. Atomistic Study of the Effect of Hydrogen on the Tendency toward Slip Planarity in Bcc Iron. Materials. 2023; 16(14):4991. https://doi.org/10.3390/ma16144991
Chicago/Turabian StyleZheng, Yuanyuan, Gang Zheng, Kaiyu Zhang, Lili Cao, Ping Yu, and Lin Zhang. 2023. "Atomistic Study of the Effect of Hydrogen on the Tendency toward Slip Planarity in Bcc Iron" Materials 16, no. 14: 4991. https://doi.org/10.3390/ma16144991
APA StyleZheng, Y., Zheng, G., Zhang, K., Cao, L., Yu, P., & Zhang, L. (2023). Atomistic Study of the Effect of Hydrogen on the Tendency toward Slip Planarity in Bcc Iron. Materials, 16(14), 4991. https://doi.org/10.3390/ma16144991




