Interaction of Nitrite Ions with Hydrated Portlandite Surfaces: Atomistic Computer Simulation Study
Abstract
:1. Introduction
2. Models and Methods
2.1. Structural Models
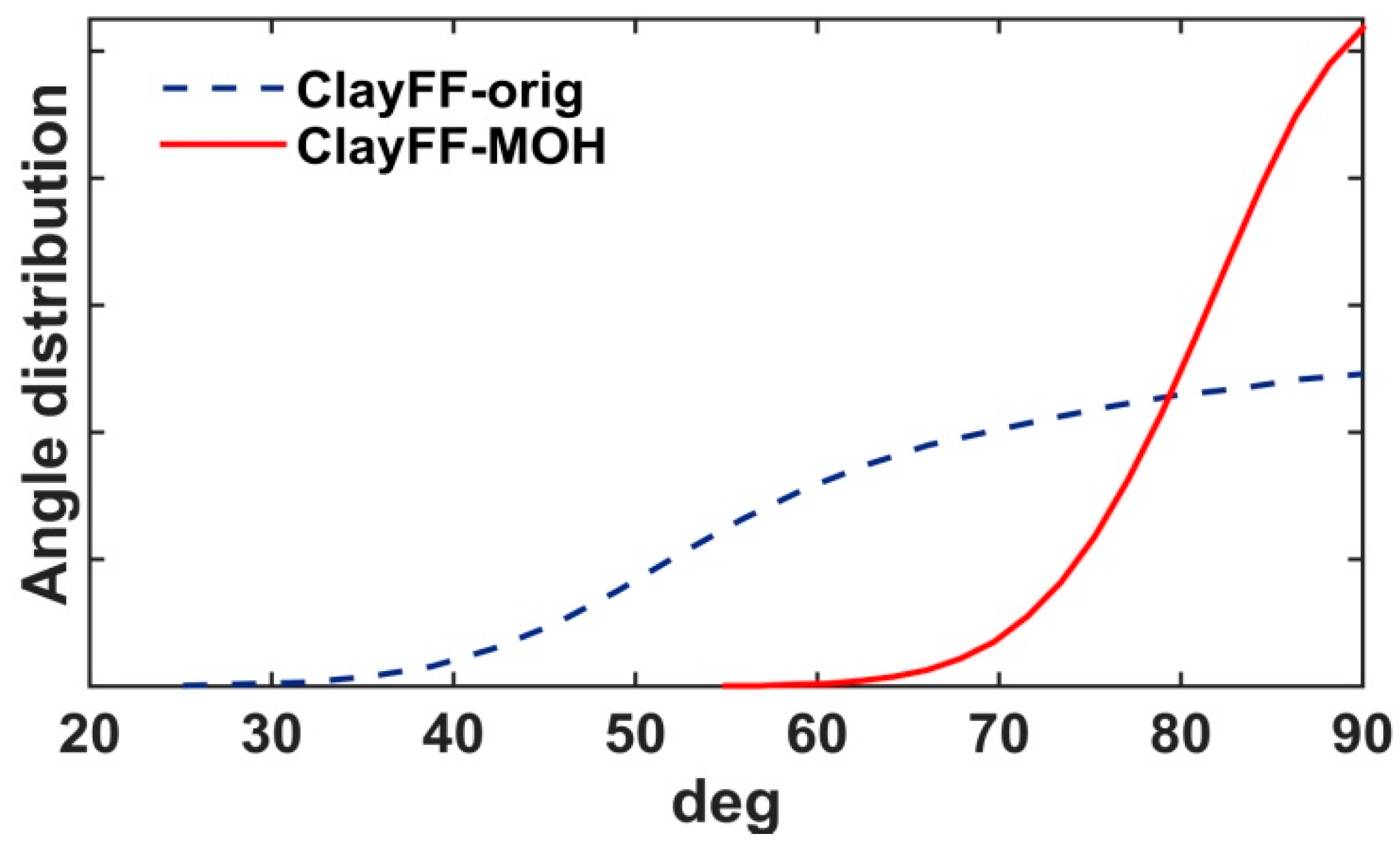
2.2. Force Field Parameters
2.3. Simulation Details
3. Results and Discussion
3.1. Bulk Portlandite Properties
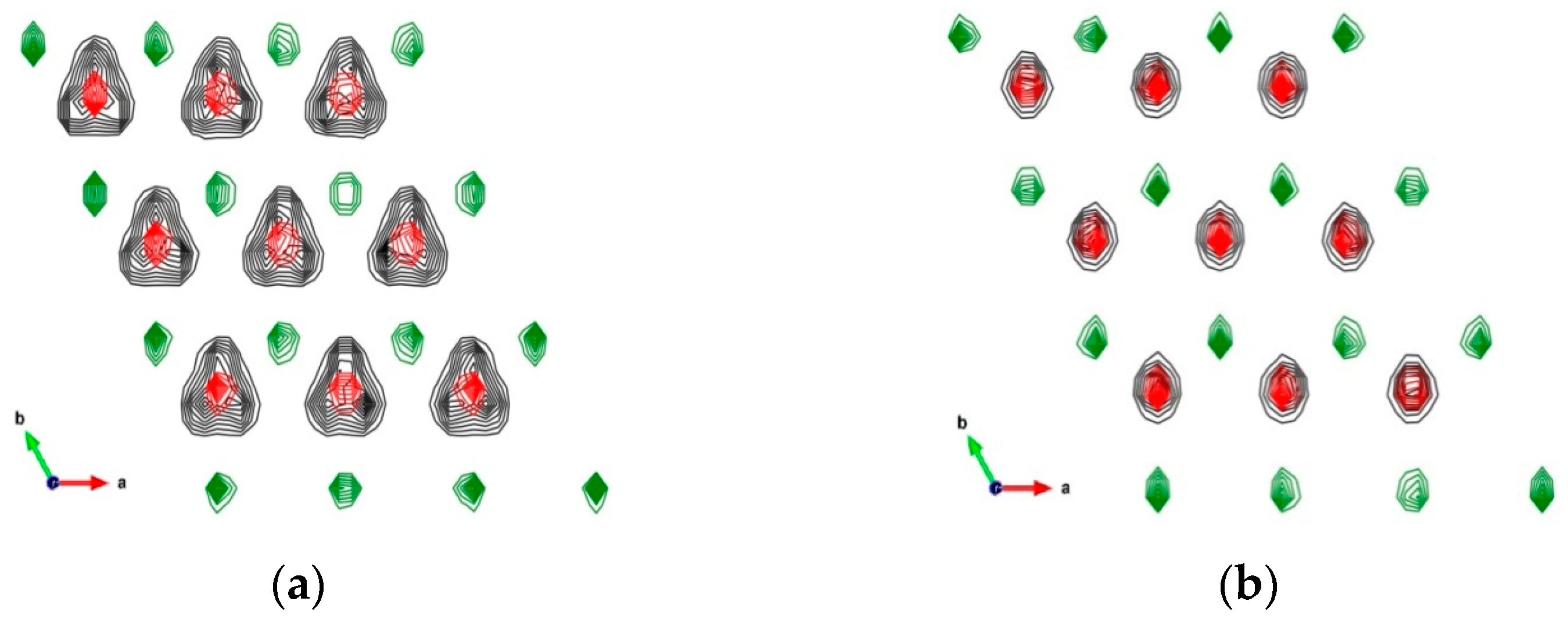
3.1.1. Crystallographic and Structural Parameters
3.1.2. Power Spectra of Atomic Vibrations in Portlandite Crystals
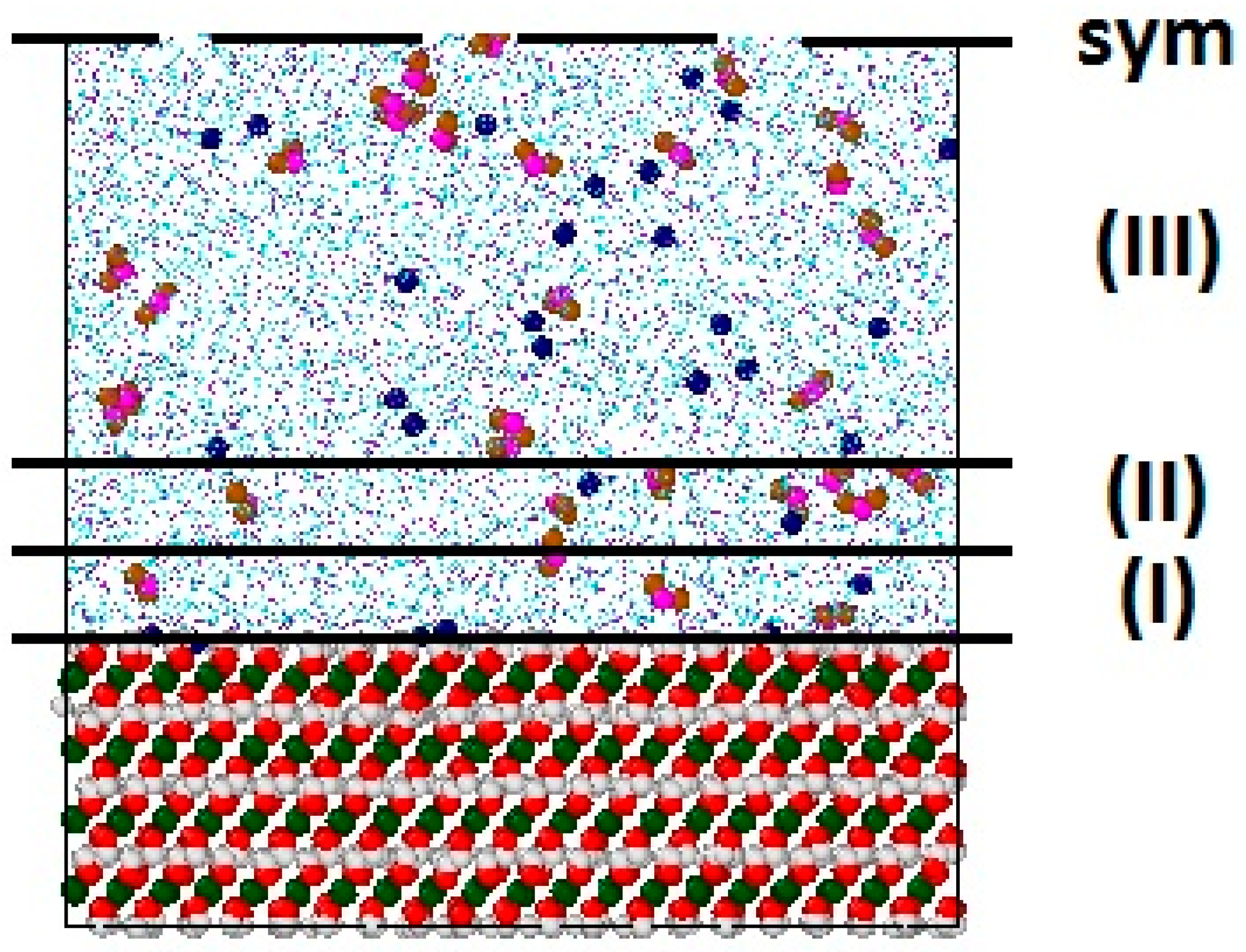
3.2. Properties of Portlandite-NaNO2 Aqueous Solution Interfaces
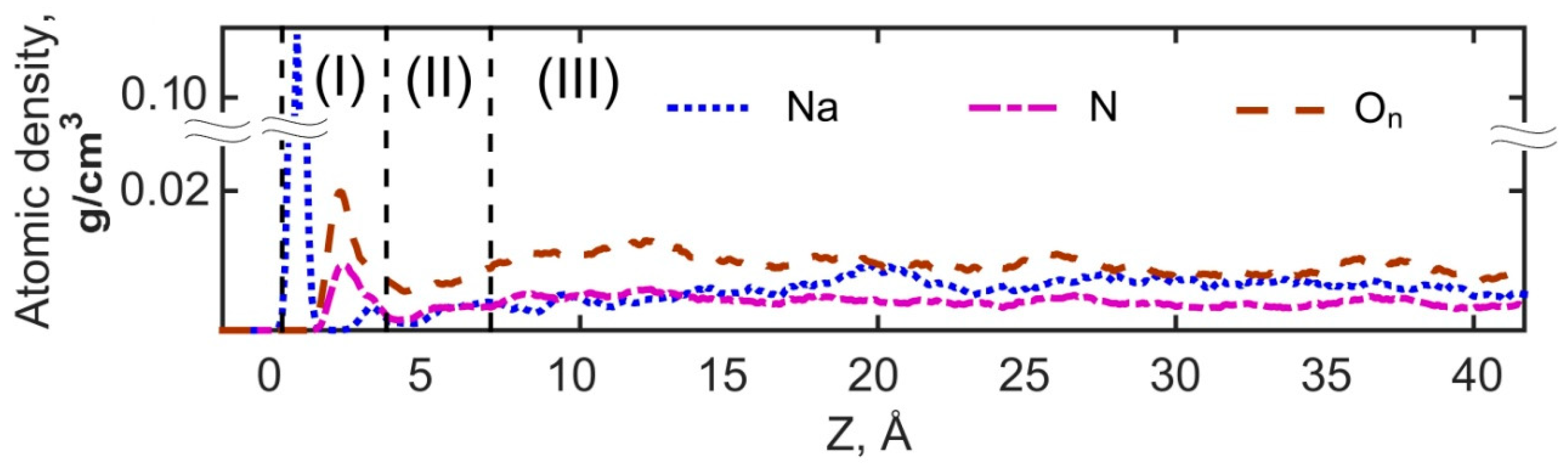
3.2.1. Structural Properties of Interfacial Solutions
3.2.2. Power Spectra of the Interfacial Dynamics
3.2.3. Structure and Dynamics of the Interfacial Hydrogen Bonding
3.2.4. Water Molecules and Nitrite Ions Orientational Relaxation
3.2.5. Diffusional Mobility of Water and Ions at the Portlandite Surface
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Phair, J.W. Green chemistry for sustainable cement production and use. Green Chem. 2006, 8, 763–780. [Google Scholar] [CrossRef]
- Rosemberg, A.M.; Gaidis, J.M. Mechanism of nitrite inhibition of chloride attack on reinforcing steel in alkaline aqueous environments. Mater. Perform. 2004, 18, 45–48. [Google Scholar]
- Schießl, P.; Moersch, J. Effectiveness and harmlessness of calcium nitrite as a corrosion inhibitor. In Proceedings of the International RILEM Conference on the Role of Admixtures in High Performance Concrete, Monterrey, Mexico, 21–26 March 1999; RILEM Publications SARL: Paris, France, 1999; pp. 169–182. [Google Scholar]
- Nmai, C.K. Cold weather concreting admixtures. Cem. Concr. Compos. 1998, 20, 121–128. [Google Scholar] [CrossRef]
- Yoneyama, A.; Choi, H.; Inoue, M.; Kim, J.; Lim, M.; Sudoh, Y. Effect of a nitrite/nitrate-based accelerator on the strength development and hydrate formation in cold-weather cementitious materials. Materials 2021, 14, 1006. [Google Scholar] [CrossRef]
- Tritthart, J.; Banfill, P.F.G. Nitrite binding in cement. Cem. Concr. Res. 2001, 31, 1093–1100. [Google Scholar] [CrossRef]
- Vollpracht, A.; Lothenbach, B.; Snellings, R.; Haufe, J. The pore solution of blended cements: A review. Mater. Struct. 2015, 49, 3341–3367. [Google Scholar] [CrossRef] [Green Version]
- Pu, Q.; Yao, Y.; Wang, L.; Shi, X.; Luo, J.; Xie, Y. The investigation of pH threshold value on the corrosion of steel reinforcement in concrete. Comp. Concr. 2017, 19, 257–262. [Google Scholar] [CrossRef]
- Scrivener, K.L.; Kirkpatrick, R.J. Innovation in use and research on cementitious material. Cem. Concr. Res. 2008, 38, 128–136. [Google Scholar] [CrossRef]
- Sanchez, F.; Sobolev, K. Nanotechnology in concrete—A review. Cons. Build. Mat. 2010, 24, 2060–2071. [Google Scholar] [CrossRef]
- Mishra, R.K.; Mohamed, A.K.; Geissbühler, D.; Manzano, H.; Jamil, T.; Shahsavari, R.; Kalinichev, A.G.; Galmarini, S.; Tao, L.; Heinz, H.; et al. CemFF: A force field database for cementitious materials including validations, applications and opportunities. Cem. Concr. Res. 2017, 102, 68–89. [Google Scholar] [CrossRef] [Green Version]
- Lasich, M. Sorption of natural gas in cement hydrate by Monte Carlo simulation. Eur. Phys. J. B 2018, 91, 299. [Google Scholar] [CrossRef]
- Pellenq, R.J.M.; Kushima, A.; Shahsavari, R.; Van Vliet, K.J.; Buehler, M.J.; Yip, S.; Ulm, F.J. A realistic molecular model of cement hydrates. Proc. Natl. Acad. Sci. USA 2009, 106, 16102–16107. [Google Scholar] [CrossRef]
- Tavakoli, D.; Tarighat, A. Molecular dynamics study on the mechanical properties of Portland cement clinker phases. Comput. Mater. Sci. 2016, 119, 65–73. [Google Scholar] [CrossRef]
- Bahraq, A.A.; Al-Osta, M.A.; Al-Amoudi, O.S.B.; Obot, I.B.; Maslehuddin, M.; Saleh, T.A. Molecular simulation of cement-based materials and their properties. Engineering 2022, 15, 165–178. [Google Scholar] [CrossRef]
- Cygan, R.T.; Greathouse, J.A.; Kalinichev, A.G. Advances in clayff molecular simulation of layered and nanoporous materials and their aqueous interfaces. J. Phys. Chem. C 2021, 125, 17573. [Google Scholar] [CrossRef]
- Pouvreau, M.; Greathouse, J.A.; Cygan, R.T.; Kalinichev, A.G. Structure of hydrated gibbsite and brucite edge surfaces: DFT results and further development of the ClayFF classical force field with metal-O-H angle bending terms. J. Phys. Chem. C 2017, 121, 14757–14771. [Google Scholar] [CrossRef] [Green Version]
- Tararushkin, E.V. Molecular dynamic modeling of the structural, dynamic, and vibrational properties of aqueous NaNO2. Russ. J. Phys. Chem. 2022, 96, 1439–1444. [Google Scholar] [CrossRef]
- Tararushkin, E.V.; Pisarev, V.V.; Kalinichev, A.G. Atomistic simulations of ettringite and its aqueous interfaces: Structure and properties revisited with the modified ClayFF force field. Cem. Concr. Res. 2022, 156, 106759. [Google Scholar] [CrossRef]
- Kalinichev, A.G.; Kirkpatrick, R.J. Molecular dynamics modeling of chloride binding to the surfaces of calcium hydroxide, hydrated calcium aluminate, and calcium silicate phases. Chem. Mater. 2002, 14, 3539–3549. [Google Scholar] [CrossRef]
- Cygan, R.T.; Liang, J.-J.; Kalinichev, A.G. Molecular models of hydroxide, oxyhydroxide, and clay phases and the development of a general force field. J. Phys. Chem. B 2004, 108, 1255–1266. [Google Scholar] [CrossRef]
- Desgranges, L.; Grebille, D.; Calvarin, G.; Chhor, K.; Pommier, C.; Floquet, N.; Niepce, J.C. Structural and thermodynamic evidence of a change in thermal motion of hydrogen atoms in Ca(OH)2 at low temperature. J. Phys. Chem. Sol. 1994, 55, 161–166. [Google Scholar] [CrossRef]
- Schaack, S.; Depondt, P.; Huppert, S.; Finocchi, F. Quantum driven proton diffusion in brucite-like minerals under high pressure. Sci. Rep. 2020, 10, 8123. [Google Scholar] [CrossRef] [PubMed]
- Busing, W.R.; Levy, H.A. Neutron diffraction study of calcium hydroxide. J. Chem. Phys. 1957, 26, 563–568. [Google Scholar] [CrossRef]
- Galmarini, S.; Aimable, A.; Ruffray, N.; Bowen, P. Changes in portlandite morphology with solvent composition: Atomistic simulations and experiment. Cem. Concr. Res. 2011, 41, 1330–1338. [Google Scholar] [CrossRef] [Green Version]
- Mutisya, S.M.; Kalinichev, A.G. Carbonation reaction mechanisms of portlandite predicted from enhanced Ab Initio molecular dynamics simulations. Minerals 2021, 11, 509. [Google Scholar] [CrossRef]
- Harutyunyan, V.S. Adsorption energy of stoichiometric molecules and surface energy at morphologically important facets of a Ca(OH)2 crystal. Mater. Chem. Phys. 2012, 134, 200–213. [Google Scholar] [CrossRef]
- Harutyunyan, V.S. Inhomogeneity, anisotropy, and size effect in the interfacial energy of Ca(OH)2 hexagonal-prism shaped nanocrystals in water. Mat. Chem. Phys. 2014, 147, 410–422. [Google Scholar] [CrossRef]
- Salah Uddin, K.M.; Izadifar, M.; Ukrainczyk, N.; Koenders, E.; Middendorf, B. Dissolution of portlandite in pure water: Part 1 molecular dynamics (MD) approach. Materials 2022, 15, 1404. [Google Scholar] [CrossRef] [PubMed]
- Izadifar, M.; Ukrainczyk, N.; Salah Uddin, K.M.; Middendorf, B.; Koenders, E. Dissolution of portlandite in pure water: Part 2 atomistic kinetic Monte Carlo (KMC) approach. Materials 2022, 15, 1442. [Google Scholar] [CrossRef]
- Gardeh, M.G.; Kistanov, A.A.; Nguyen, H.; Manzano, H.; Cao, W.; Kinnunen, P. Exploring mechanisms of hydration and carbonation of MgO and Mg(OH)2 in reactive magnesium oxide-based cements. J. Phys. Chem. C 2022, 126, 6196–6206. [Google Scholar] [CrossRef]
- Aili, A.; Maruyama, I. Review of several experimental methods for characterization of micro- and nano-scale pores in cement-based material. Int. J. Concr. Struct. Mater. 2020, 14, 55. [Google Scholar] [CrossRef]
- Berendsen, H.; Grigera, J.; Straatsma, T. The missing term in effective pair potentials. J. Phys. Chem. 1987, 91, 6269–6271. [Google Scholar] [CrossRef]
- Vchirawongkwin, S.; Kritayakornupong, C.; Tongraarc, A.; Vchirawongkwin, V. Hydration properties determining the reactivity of nitrite in aqueous solution. Dalton Trans. 2014, 43, 12164–12174. [Google Scholar] [CrossRef]
- Yadav, S.; Chandra, A. Solvation shell of the nitrite Ion in water: An ab initio molecular dynamics study. J. Phys. Chem. B 2020, 124, 7194–7204. [Google Scholar] [CrossRef]
- Liu, Y.; Shi, X. Molecular dynamics study of interaction between corrosion inhibitors, nanoparticles, and other minerals in hydrated cement. Trans. Res. Rec. J. Trans. Res. Board 2010, 2142, 58–66. [Google Scholar] [CrossRef]
- Richards, L.A.; Schäfer, A.I.; Richards, B.S.; Corry, B. The importance of dehydration in determining ion transport in narrow pores. Small 2012, 8, 1701–1709. [Google Scholar] [CrossRef] [Green Version]
- Ohkubo, T.; Ohnishi, R.; Sarou-Kanian, V.; Bessada, C.; Iwadate, Y. Molecular dynamics simulations of the thermal and transport properties of molten NaNO2–NaNO3 systems. Electrochemistry 2018, 86, 104–108. [Google Scholar] [CrossRef]
- Irish, D.E.; Thorpe, R.V. Raman spectral studies of cadmium–nitrite interactions in aqueous solutions and crystals. Can. J. Chem. 1975, 53, 1414–1423. [Google Scholar] [CrossRef]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; in’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS—A flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comp. Phys. Comm. 2022, 271, 108171. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids, 2nd ed.; Oxford University Press: New York, NY, USA, 2017. [Google Scholar] [CrossRef]
- Brown, W.M.; Kohlmeyer, A.; Plimpton, S.J.; Tharrington, A.N. Implementing molecular dynamics on hybrid high performance computers—Particle-particle particle-mesh. Comp. Phys. Comm. 2012, 183, 449–459. [Google Scholar] [CrossRef]
- Brown, W.M.; Wang, P.; Plimpton, S.J.; Tharrington, A.N. Implementing molecular dynamics on hybrid high performance computers—Short range forces. Comp. Phys. Comm. 2011, 182, 898–911. [Google Scholar] [CrossRef]
- Swope, W.C.; Andersen, H.C.; Berens, P.H.; Wilson, K.R. A computer simulation method for the calculation of equilibrium constants for the formation of physical clusters of molecules: Application to small water clusters. J. Chem. Phys. 1982, 76, 637–649. [Google Scholar] [CrossRef]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef] [Green Version]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kalinichev, A.G. Atomistic modeling of clays and related nanoporous materials with ClayFF force field. In Computational Modeling in Clay Mineralogy; Sainz-Díaz, C.I., Ed.; Association Internationale Pour l’Etude des Argiles (AIPEA): Bari, Italy, 2021; Volume 3, pp. 17–52. [Google Scholar]
- Henderson, D.M.; Gutowsky, H.S. A nuclear magnetic resonance determination of the hydrogen positions in Ca(OH)2. Amer. Miner. 1962, 47, 1231–1251. [Google Scholar]
- Laugesen, J.L. Density functional calculations of elastic properties of portlandite, Ca(OH)2. Cem. Concr. Res. 2005, 35, 199–202. [Google Scholar] [CrossRef]
- Ugliengo, P.; Zicovich-Wilson, C.M.; Tosoni, S.; Civalleri, B. Role of dispersive interactions in layered materials: A periodic B3LYP and B3LYP-D* study of Mg(OH)2, Ca(OH)2 and kaolinite. J. Mater. Chem. 2009, 19, 2564. [Google Scholar] [CrossRef]
- Hou, D.; Lu, Z.; Zhang, P.; Ding, Q. Molecular structure and dynamics of an aqueous sodium chloride solution in nano-pores between portlandite surfaces: A molecular dynamics study. Phys. Chem. Chem. Phys. 2016, 18, 2059–2069. [Google Scholar] [CrossRef]
- Hajilar, S.; Shafei, B. Assessment of structural, thermal, and mechanical properties of portlandite through molecular dynamics simulations. J. Solid State Chem. 2016, 244, 164–174. [Google Scholar] [CrossRef]
- Valavi, M.; Casar, Z.; Mohamed, A.K.; Bowen, P.; Galmarini, S. Molecular dynamic simulations of cementitious systems using a newly developed force field suite ERICA FF. Cem. Concr. Res. 2022, 154, 106712. [Google Scholar] [CrossRef]
- Sarkar, P.K.; Mitra, N. Molecular deformation response of portlandite under compressive loading. Constr. Build. Mater. 2021, 274, 122020. [Google Scholar] [CrossRef]
- Szczerba, M.; Kuligiewicz, A.; Derkowski, A.; Gionis, V.; Chryssikos, G.D.; Kalinichev, A.G. Structure and dynamics of watersmectite interfaces: Hydrogen bonding and the origin of the sharp O-DW/O-HW infrared band from molecular simulations. Clays Clay Min. 2016, 64, 452–471. [Google Scholar] [CrossRef] [Green Version]
- Lutz, H.D.; Möller, H.; Schmidt, M. Lattice vibration spectra. Part LXXXII. Brucite-type hydroxides M(OH)2 (M = Ca, Mn, Co, Fe, Cd)—IR and Raman spectra, neutron diffraction of Fe(OH)2. J. Molec. Struct. 1994, 328, 121–132. [Google Scholar] [CrossRef]
- Weckler, B.; Lutz, H.D. Near-infrared spectra of M(OH)Cl (M = Ca, Cd, Sr), Zn(OH)F, γ-Cd(OH)2, Sr(OH)2, and brucite-type hydroxides M(OH)2 (M = Mg, Ca, Mn, Fe, Co, Ni, Cd). Spectr. Acta Part A Molec. Biomolec. Spectrosc. 1996, 52, 1507–1513. [Google Scholar] [CrossRef]
- Tararushkin, E.V.; Shchelokova, T.N.; Kudryavtseva, V.D. A study of strength fluctuations of Portland cement by FTIR spectroscopy. IOP Conf. Ser. Mater. Sci. Eng. 2020, 919, 022017. [Google Scholar] [CrossRef]
- Zeitler, T.R.; Greathouse, J.A.; Gale, J.D.; Cygan, R.T. Vibrational analysis of brucite surfaces and the development of an improved force field for molecular simulation of interfaces. J. Phys. Chem. C 2014, 118, 7946–7953. [Google Scholar] [CrossRef]
- Dupuis, R.; Dolado, J.S.; Benoit, M.; Surga, J.; Ayuela, A. Quantum nuclear dynamics of protons within layered hydroxides at high pressure. Sci. Rep. 2017, 7, 4842. [Google Scholar] [CrossRef] [Green Version]
- Galmarini, S.; Bowen, P. Atomistic simulation of the adsorption of calcium and hydroxyl ions onto portlandite surfaces—Towards crystal growth mechanisms. Cem. Concr. Res. 2016, 81, 16–23. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2009, 18, 015012. [Google Scholar] [CrossRef]
- Hu, X.; Zheng, H.; Tao, R.; Wang, P. Migration of nitrite corrosion inhibitor in calcium silicate hydrate nanopore: A molecular dynamics simulation study. Front. Mater. 2022, 9, 965772. [Google Scholar] [CrossRef]
- Maréchal, Y. IR spectroscopy of an exceptional H-bonded liquid: Water. J. Molec. Struct. 1994, 322, 105–111. [Google Scholar] [CrossRef]
- Tominaga, Y.; Fujiwara, A.; Amo, Y. Dynamical structure of water by Raman spectroscopy. Fluid Phase Equilibria 1998, 144, 323–330. [Google Scholar] [CrossRef]
- Antipova, M.L.; Petrenko, V.E. Hydrogen bond lifetime for water in classic and quantum molecular dynamics. Russ. J. Phys. Chem. 2013, 87, 1170–1174. [Google Scholar] [CrossRef]
- Rapaport, D.C. Hydrogen bonds in water. Mol. Phys. 1983, 50, 1151–1162. [Google Scholar] [CrossRef]
- Chanda, J.; Bandyopadhyay, S. Hydrogen bond lifetime dynamics at the interface of a surfactant monolayer. J. Phys. Chem. B 2006, 110, 23443–23449. [Google Scholar] [CrossRef] [PubMed]
- Chowdhuri, S.; Chandra, A. Hydrogen bonds in aqueous electrolyte solutions: Statistics and dynamics based on both geometric and energetic criteria. Phys. Rev. E. 2002, 66, 041203. [Google Scholar] [CrossRef] [PubMed]
- Laage, D.; Hynes, J.T. A Molecular jump mechanism of water reorientation. Science 2006, 311, 832. [Google Scholar] [CrossRef]
- Laage, D.; Stirnemann, G.; Sterpone, F.; Rey, R.; Hynes, J.T. Reorientation and allied dynamics in water and aqueous solutions. Annu. Rev. Phys. Chem. 2011, 62, 395–416. [Google Scholar] [CrossRef]
- Mutisya, S.M.; Kirch, A.; de Almeida, J.M.; Sánchez, V.M.; Miranda, C.R. Molecular dynamics simulations of water confined in calcite slit pores: An NMR spin relaxation and hydrogen bond analysis. J. Phys. Chem. C 2017, 121, 6674–6684. [Google Scholar] [CrossRef]
- Kondratyuk, N.D.; Norman, G.E.; Stegailov, V.V. Self-consistent molecular dynamics calculation of diffusion in higher n-alkanes. J. Chem. Phys. 2016, 145, 204504. [Google Scholar] [CrossRef] [Green Version]
- Lide, D.R. CRC Handbook of Chemistry and Physics, 84th ed.; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Krynicki, K.; Green, C.D.; Sawyer, D.W. Pressure and temperature dependence of self-diffusion in water. Faraday Discuss. Chem. Soc. 1978, 66, 199–208. [Google Scholar] [CrossRef]
- Celebi, A.T.; Jamali, S.H.; Bardow, A.; Vlugt, T.J.H.; Moultos, O.A. Finite-size effects of diffusion coefficients computed from molecular dynamics: A review of what we have learned so far. Molec. Simul. 2020, 47, 831–845. [Google Scholar] [CrossRef]
- Kostenetskiy, P.S.; Chulkevich, R.A.; Kozyrev, V.I. HPC Resources of the Higher School of Economics. J. Phys. Conf. Ser. 2021, 1740, 012050. [Google Scholar] [CrossRef]
- Kostenetskiy, P.; Shamsutdinov, A.; Chulkevich, R.; Kozyrev, V.; Antonov, D. HPC TaskMaster—Task efficiency monitoring system for the supercomputer center. In Proceedings of the International Conference on Parallel Computational Technologies, Dubna, Russia, 29–31 March 2022; Volume 1618, pp. 17–29. [Google Scholar] [CrossRef]


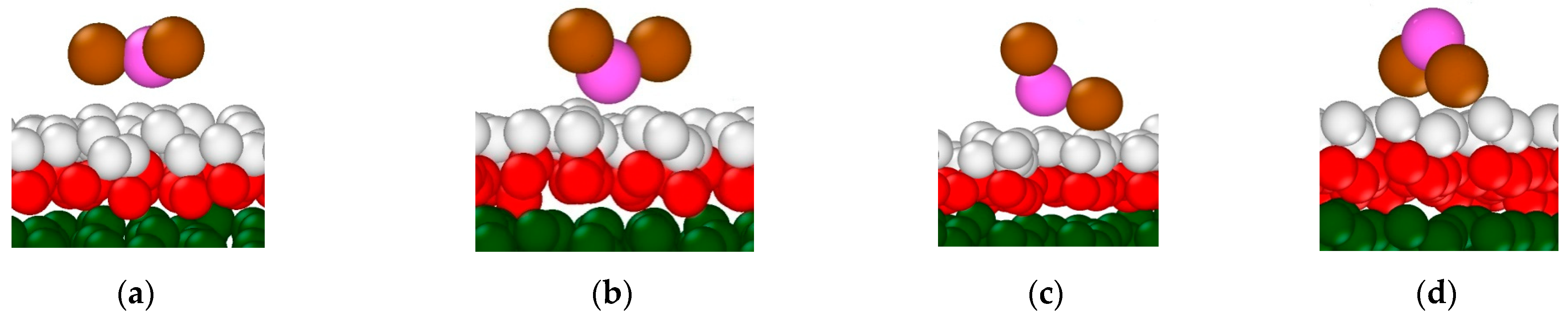

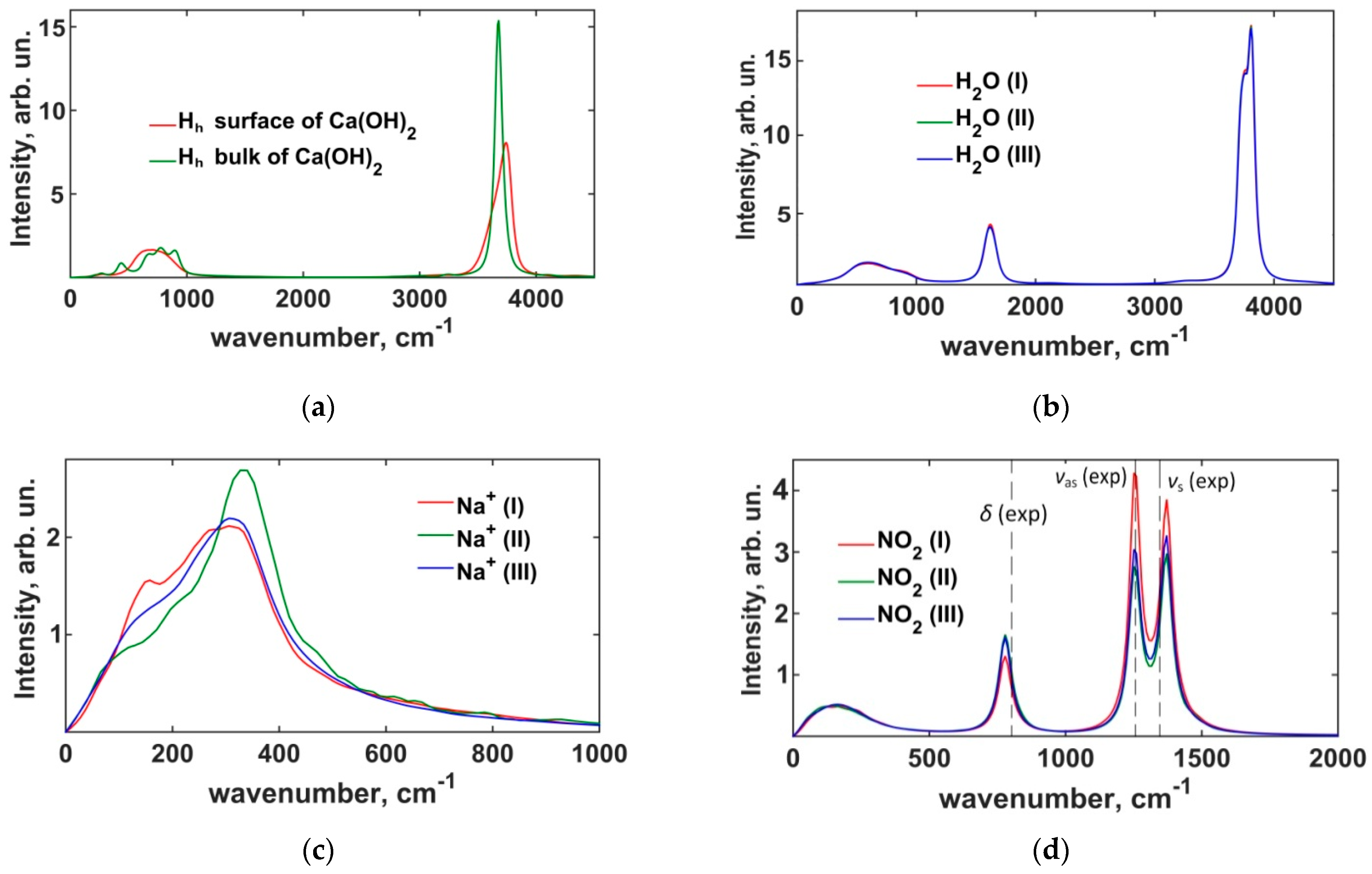

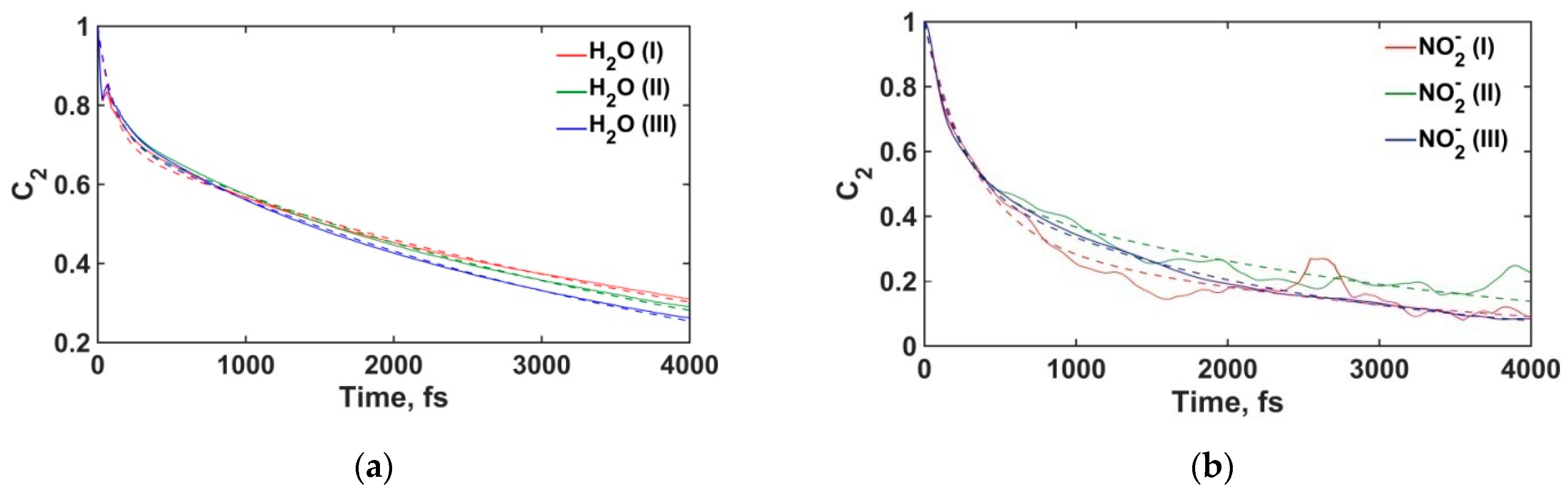
| Source | a, Å | b, Å | c, Å | α, ° | β, ° | γ, ° |
|---|---|---|---|---|---|---|
| ClayFF-orig (This work) | 3.6343 | 3.6357 | 4.8957 | 90.05 | 90.00 | 119.99 |
| ClayFF-MOH (This work) | 3.6779 | 3.6783 | 4.8767 | 90.03 | 89.98 | 119.99 |
| ClayFF [51] | 3.567 | 3.567 | 4.908 | 90 | 90 | 120 |
| IFF [11] | 3.75 | 3.75 | 4.38 | 90 | 90 | 120 |
| CementFF [11] | 3.68 | 3.67 | 4.81 | 90 | 90 | 120 |
| CSH-FF [52] | 3.5037 | 3.5037 | 4.8045 | 90 | 90 | 120 |
| ERICA FF [53] | 3.67 (2.2) | 3.67 (2.2) | 4.85 (0.4) | 89.7 | 89.9 | 120 |
| ReaxFF [54] | 3.63 | 3.63 | 5.10 | 89.67 | 90.05 | 120.11 |
| DFT [49] | 3.609 | 3.609 | 4.864 | 90 | 90 | 120 |
| DFT [26] | 3.696 | 3.696 | 5.147 | 90 | 90 | 120 |
| DFT [50] | 3.581–3.625 | 3.581–3.625 | 4.797–5.010 | 90 | 90 | 120 |
| Neutron diffraction [24] | 3.5918 | 3.5918 | 4.9063 | 90 | 90 | 120 |
| NMR [48] | 3.5925 | 3.5925 | 4.905 | 90 | 90 | 120 |
| Donor-Acceptor Pair | Layer | nHB | τHB, ps |
|---|---|---|---|
| Hw···Ow | (I) | 2.26 | 0.51 |
| (II) | 2.23 | 0.41 | |
| (III) | 3.53 | 0.54 | |
| Hw···On | (I) | 1.68 | 0.20 |
| (II) | 1.67 | 0.18 | |
| (III) | 2.69 | 0.21 | |
| Hw···N | (I) | 0.89 | 0.04 |
| (II) | 1.06 | 0.05 | |
| (III) | 1.64 | 0.05 | |
| Hw···Oh | (I) | 0.27 | 0.18 |
| Hh···Ow | (I) | 0.43 | 0.27 |
| Hh···On | (I) | 0.45 | 0.16 |
| Hh···N | (I) | 0.20 | 0.04 |
| Molecule/Ion | Layer | τ1, ps | τ2, ps |
|---|---|---|---|
| H2O | (I) | 0.11 | 4.76 |
| (II) | 0.11 | 4.21 | |
| (III) | 0.10 | 3.78 | |
| NO2− | (I) | 0.32 | 2.89 |
| (II) | 0.22 | 3.11 | |
| (III) | 0.20 | 2.08 |
| Molecule/Ion | Layer | 2d, 10−5 cm2/s | 3d, 10−5 cm2/s |
|---|---|---|---|
| H2O | (I) | 0.98 | 1.36 |
| (II) | 1.11 | 1.47 | |
| (III) | - | 1.81 | |
| Na+ | (III) | - | 0.84 |
| NO2− | (III) | - | 1.46 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tararushkin, E.V.; Pisarev, V.V.; Kalinichev, A.G. Interaction of Nitrite Ions with Hydrated Portlandite Surfaces: Atomistic Computer Simulation Study. Materials 2023, 16, 5026. https://doi.org/10.3390/ma16145026
Tararushkin EV, Pisarev VV, Kalinichev AG. Interaction of Nitrite Ions with Hydrated Portlandite Surfaces: Atomistic Computer Simulation Study. Materials. 2023; 16(14):5026. https://doi.org/10.3390/ma16145026
Chicago/Turabian StyleTararushkin, Evgeny V., Vasily V. Pisarev, and Andrey G. Kalinichev. 2023. "Interaction of Nitrite Ions with Hydrated Portlandite Surfaces: Atomistic Computer Simulation Study" Materials 16, no. 14: 5026. https://doi.org/10.3390/ma16145026
APA StyleTararushkin, E. V., Pisarev, V. V., & Kalinichev, A. G. (2023). Interaction of Nitrite Ions with Hydrated Portlandite Surfaces: Atomistic Computer Simulation Study. Materials, 16(14), 5026. https://doi.org/10.3390/ma16145026








