1. Introduction
Carbon-fiber-reinforced polymer (CFRP) composites have many attractive properties, such as high static and fatigue strength, high stiffness, low density and thermal expansion, and good corrosion resistance under various environmental conditions [
1,
2]. CFRP composites are particularly used in mechanical engineering due to their high strength-to-density ratio and are considered the standard construction material for new aerospace vehicles. These materials are also increasingly used in the automotive sector, and this use is expected to increase rapidly in the next two decades [
3]. The main reason for the growing interest in CFRP composites in the automotive sector is their ability to reduce vehicles’ weight and thus improve fuel efficiency and reduce carbon dioxide emissions, while maintaining or even improving safety and mechanical performance [
4,
5]. The parts of passenger cars made from CFRP composites can be divided into two categories: parts improving the aesthetics of vehicles and load-bearing parts. The first group includes interior parts and finishes, front dashboard trims, interior and external trim cover panels, door handles, and side mirror covers. Such parts have no significant effect on the weight of the car and do not carry the load. The major reason for using CFRP composites in these locations is the attractive appearance resulting from the weave pattern of the carbon rovings in fabrics. The use of CFRP composites for load-bearing parts is aimed at reducing the weight of the vehicle while maintaining the required strength and stiffness. Therefore, these materials are used for larger parts of the vehicle structure, such as the monocoque chassis, side frames, and internal doorsill stiffening parts [
6,
7], while other parts are currently in the testing phase—for example, B-pillars [
8]. It should be noted that in most cars, these parts are made of hot-formed (press hardening process) or cold-formed steels that ensure adequate stiffness and strength [
9]. To obtain a similar mechanical performance for parts made from CFRP composites, carbon fibers with a high mechanical performance must be used, which significantly increase the cost of these parts. There are also some difficulties associated with the application of the composite (particularly to items with large dimensions and irregular shapes), such as intricate design procedures, high cost, and complex manufacturing processes [
7]. All these reasons limit the use of CFRP composites in the construction of mass-produced passenger vehicles. The current use of parts made entirely of CFRP composites is restricted to niche segments of automobiles, such as luxury, premium, and sport cars [
10]. The design of automotive lightweight structures can also be achieved using steel/CFRP hybrid structures. The high weight-reduction potential of steel/CFRP hybrid structures is obtained by an effective thickness reduction in the steel part with the simultaneous use of high mechanical performance CFRP composites [
11]. Therefore, the application of steel/CFRP hybrid structures in the design and production of vehicle structures aims to increase the mass share of the lightweight and durable composite at the expense of the durable, but heavier, steel. Hybrid structures can also be used in another way, where the steel component of a vehicle body is locally reinforced with CFRP composite to improve its strength and stiffness with only a slight increase in weight.
The connection between the steel and composite is generally realized by adhesive bonding and mechanical fastening [
12]. Adhesive bonding is inherently preferable to mechanical fastening because of the continuous connection formed. Composite materials exhibit a major decrease in their mechanical properties due to holes for joining using rivets or bolts because of the high notch sensitivity of these materials [
13]. In addition, elements of mechanical fastenings, such as bolts or rivets, lead to a weight increase. Therefore, steel/CFRP hybrid structures, particularly when joined by an adhesive, have many advantages, and their use in automotive applications has great potential.
Despite their many advantages, steel/CFRP hybrid structures are currently only used to a limited extent in mass-produced passenger vehicles. According to the literature, there have not been many attempts to use steel/CFRP hybrid structures in the design of automotive parts, particularly those with large sizes and complicated shapes. An example is the research concerned with vehicle structural components, such as the center-pillar [
14,
15,
16,
17]. The limited use is due to the longer manufacturing lead-time compared with manufacturing steel components and difficulties in the measurement of the mechanical properties of these materials. The mechanical behavior of steel/CFRP hybrid structures depends not only on the properties of their components but also on the properties of the adhesive joint. As is well known, the mechanical behavior of fiber-reinforced polymers also depends on the manufacturing conditions, such as the manufacturing technique and curing cycle. For this reason, investigations on steel/CFRP hybrid structures are still at the basic experimental stage, and focus on their mechanical properties, adhesive joint strength, and formability [
17].
An additional difficulty in using steel/CFRP hybrid structures in engineering applications is the possibility of galvanic corrosion, which can occur due to steel and CFRP composites having very different electrical potentials [
18]. Extensive galvanic corrosion of steel in contact with carbon fibers particularly occurs in aggressive environments, such as aqueous solutions containing salts, acids, or fuel combustion products [
19]. Generally, corrosion propagation can lead to failure of the adhesively bonded joint in steel/CFRP hybrid structures. A basic method for suppressing galvanic corrosion is to have no contact between the carbon fibers and steel, so the adhesive layer alone can be effective in suppressing the potential galvanic corrosion of the steel/CFRP hybrid structure, and embedding glass fiber ply in the adhesive can additionally increase this effect [
18]. The application of additional glass fiber for increasing the protection against corrosion leads to a three-phase hybrid structure, which includes steel sheet, CFRP composite, and glass-fiber-reinforced polymer (GFRP) composite. This type of hybrid structure can be abbreviated as steel/GFRP(m)/CFRP(n), where the parameters m and n indicate the number of plies in the GFRP and CFRP composites, respectively.
To apply any material in engineering practice, it is necessary to study its key mechanical properties, such as strength and stiffness, under various load conditions. It is well known that steel and many types of polymer composites have sufficient tensile strength for most engineering applications. A particularly important mechanical property of steel/polymer composite hybrid structures intended for the automotive industry is the shear adhesive bond strength, because automotive components are generally thin-walled, and the dominant loading condition is bending. When a steel/polymer composite hybrid structure is subjected to bending, sliding shear and in-plane shear stresses are observed between the steel sheet and polymer composite, giving a risk of debonding formation and propagation, which may result in the complete destruction of the adhesive bond between the steel sheet and polymer composite.
Despite the considerable number of studies in the literature about the debonding failure of the steel/CFRP(n) adhesive joint [
20,
21,
22,
23,
24,
25,
26,
27], few systematic studies on the bond behavior between steel sheets and GFRP(m) polymer composites have been performed, and a very limited number of papers have been published that focus on this topic [
28,
29,
30,
31]. To the best knowledge of the authors, no research has been published on the mechanical behavior of the adhesive bonds between steel sheets and GFRP(m)/CFRP(n) hybrid composites under three-point bending. Therefore, the primary objective of this research was experimental examination of the bending response of steel/GFRP(m)/CFRP(n) hybrid structure specimens with a particular focus on the possibility of debonding between the steel sheet and the GFRP(m)/CFRP(n) hybrid composite. The purpose of this study was also to develop a numerical model of the steel/GFRP(m)/CFRP(n) hybrid structure. The simulation results were a valuable supplement to the experimental research. Experimental and numerical analysis of the mechanical properties of steel/GFRP(m)/CFRP(n) hybrid structures requires data on the mechanical properties of their individual components. Therefore, in the current study, additional tests and numerical simulations were carried out to determine the material properties of the individual components.
The remainder of this paper is organized as follows. In
Section 2, all the materials used in this study are characterized.
Section 3 presents the experimental procedures and details of the finite element (FE) models employed, while the experimental and numerical results are discussed in
Section 4. Finally, in
Section 5, conclusions are drawn, and a summary is presented.
2. Materials
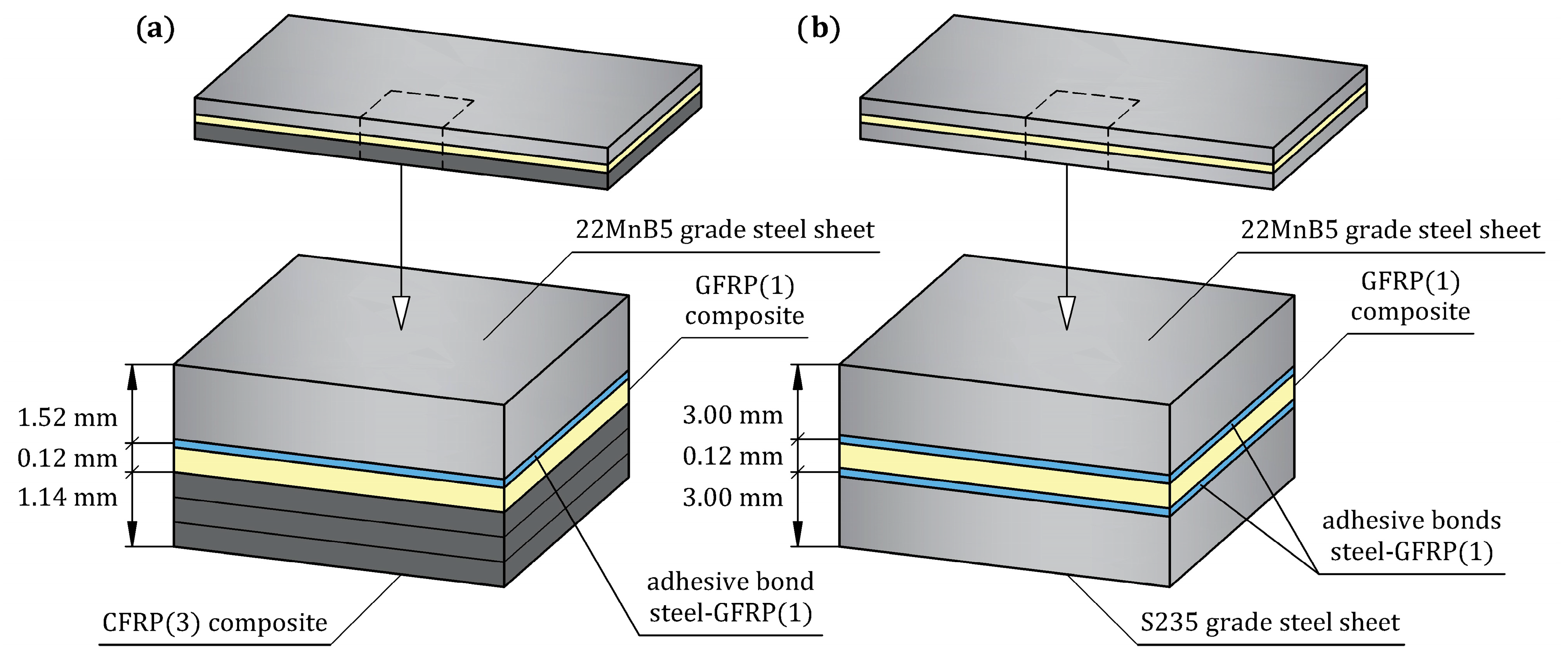
The experimental steel/GFRP(m)/CFRP(n) hybrid structure used in this research contained hot-formed 22MnB5 (1.5528) grade automotive steel, single-ply bidirectional GFRP composite (m = 1), and three-ply unidirectional CFRP composite (n = 3). The sequence of the individual materials of the steel/GFRP(1)/CFRP(3) hybrid structure with their average thickness are shown in
Figure 1a. Preliminary experimental studies showed that the application of a CFRP(n) composite with a greater number of plies (n > 3) just slightly increased the bending bearing capacity of the hybrid structure. This result is related to the greater thickness of the CFRP composite and the faster achievement of the breaking stress in the layers subjected to tension during the bending test. As mentioned, the basic adherents were a 22MnB5 grade steel sheet and CFRP(3) composite. In turn, the GFRP(1) composite was used as intermediate material between the steel sheet and CFRP(3) composite to increase protection against galvanic corrosion. As shown in
Figure 2, 22MnB5 grade steel sheets used to prepare steel/GFRP(1)/CFRP(3) hybrid structure specimens were cut off by a laser from flat surfaces of the hot-formed side door beam of a passenger car to take account of actual production conditions. The chemical composition of 22MnB5 grade steel in accordance with the DIN EN 10083-3 standard [
32] is given in
Table 1.
The unidirectional CFRP(3) and bidirectional GFRP(1) composites were made from three plies of a unidirectional (UD) non-crimp carbon fiber mat and bidirectional (BD) glass fiber fabric, respectively (
Figure 3). Details of the carbon fiber mat and glass fiber fabric selected for this study are listed in
Table 2. The principal coordinate system of the reinforcements was a coordinate system with the 1-axis aligned with the fibers in the UD carbon mat and aligned with the weft in the BD glass fabric and the 2-axis perpendicular to the fibers in the UD carbon mat and aligned with the warp in the BD glass fabric. The epoxy resin (Biresin
® CR122) and hardener (Biresin
® CH122-5), mixed at a weight ratio of 100:30, were used both as the matrix material in the CFRP(3) and GFRP(1) composites and as the adhesive bonding between the steel sheet and GFRP(1) composite. Selected properties of the epoxy matrix are given in
Table 3 according to the manufacturer’s datasheet. In this study, additional specimens of the hybrid structure, abbreviated as steel/GFRP(1)/steel, were used to investigate the mode II fracture toughness of the adhesive bond between the steel adherent and GFRP(1) composite. The adherents were made of S235 grade steel, the chemical composition of which is given in
Table 4. The sequence of the individual materials of the steel/GFRP(1)/steel hybrid structure with their average thickness are shown in
Figure 1b. All materials used in this study were supplied by local suppliers.