Experimental Research on the Energy Evolution of Concrete under Impact Loading
Abstract
:1. Introduction
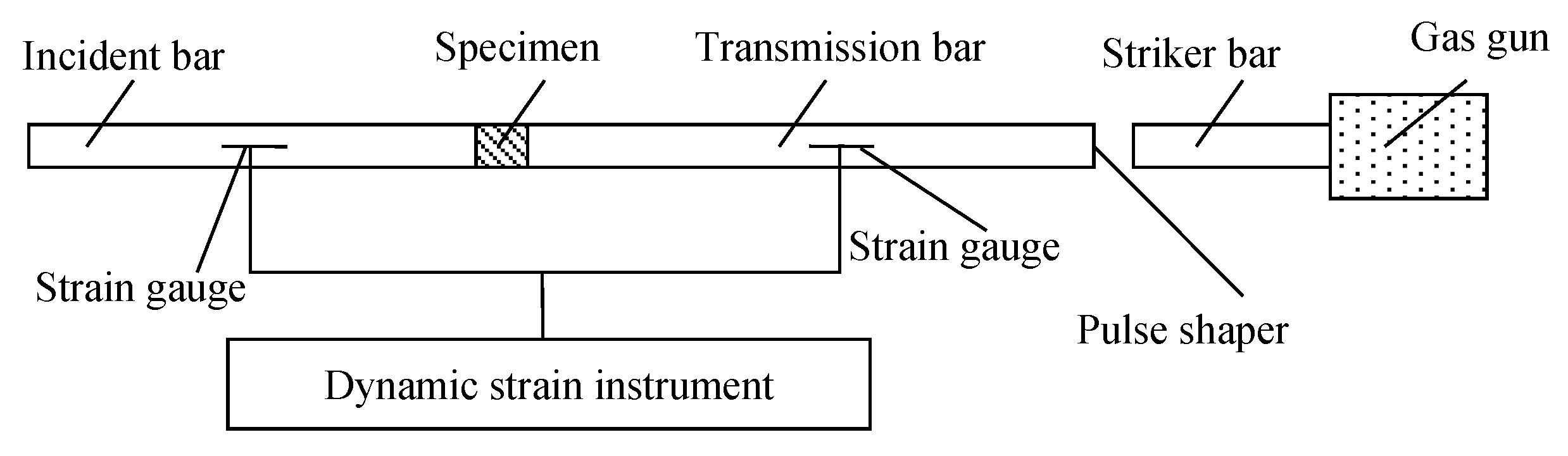
2. Tests on Concrete Using SHPB
2.1. Experimental Principle and Energy Analysis Method
2.2. Preparation for the Tests
3. Results and Discussion
3.1. Stress–Strain Curve
3.2. Analysis of Fragmentation
3.3. Process of Energy Evolution
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Khosravani, M.R.; Weinberg, K. A review on split Hopkinson bar experiments on the dynamic characterisation of concrete. Constr. Build. Mater. 2018, 190, 1264–1283. [Google Scholar]
- Lee, S.; Kim, K.-M.; Park, J.; Cho, J.-Y. Pure rate effect on the concrete compressive strength in the split Hopkinson pressure bar test. Int. J. Impact Eng. 2018, 113, 191–202. [Google Scholar] [CrossRef]
- Zielinski, A.J.; Reinhardt, H.W.; Koermeling, H.A. Experiments on concrete under repeated uniaxial impact tensile loading. Mater. Struct. 1981, 14, 103–112. [Google Scholar] [CrossRef]
- Liu, F.; Li, Q.M. Strain-rate effect on the compressive strength of brittle materials and its implementation into material strength model. Int. J. Impact Eng. 2019, 130, 113–123. [Google Scholar] [CrossRef]
- Hao, Y.F.; Hao, H.; Li, Z.X. Influence of end friction confinement on impact tests of concrete material at high strain rate. Int. J. Impact Eng. 2013, 60, 82–106. [Google Scholar] [CrossRef]
- Kim, K.-M.; Lee, S.; Cho, J.-Y. Effect of maximum coarse aggregate size on dynamic compressive strength of high-strength concrete. Int. J. Impact Eng. 2019, 125, 107–116. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, L.; Zheng, K.; Bakura, T.J.; Totakhil, P.G. Research on compressive impact dynamic behavior and constitutive model of polypropylene fiber reinforced concrete. Constr. Build. Mater. 2018, 187, 584–595. [Google Scholar] [CrossRef]
- Jin, L.; Zhang, R.; Tian, Y.; Dou, G.; Du, X. Experimental investigation on static and dynamic mechanical properties of steel fiber reinforced ultra-high-strength concretes. Constr. Build. Mater. 2018, 178, 102–111. [Google Scholar] [CrossRef]
- Wu, Z.; Shi, C.; He, W.; Wang, D. Static and dynamic compressive properties of ultra-high performance concrete (UHPC) with hybrid steel fiber reinforcements. Cem. Concr. Compos. 2017, 79, 148–157. [Google Scholar] [CrossRef]
- Chen, L.; Fang, Q.; Jiang, X.; Ruan, Z.; Hong, J. Combined effects of high temperature and high strain rate on normal weight concrete. Int. J. Impact Eng. 2015, 86, 40–56. [Google Scholar] [CrossRef]
- Qiao, Y.; Wang, H.; Cai, L.; Zhang, W.; Yang, B. Influence of low temperature on dynamic behavior of concrete. Constr. Build. Mater. 2016, 115, 214–220. [Google Scholar] [CrossRef]
- Cui, J.; Hao, H.; Shi, Y. Numerical study of the influences of pressure confinement on high-speed impact tests of dynamic material properties of concrete. Constr. Build. Mater. 2018, 171, 839–849. [Google Scholar] [CrossRef]
- Rossi, P. Influence of cracking in the presence of free water on the mechanical behavior of concrete. Mater. Struct. 1991, 24, 422–424. [Google Scholar] [CrossRef]
- Li, Q.M.; Meng, H. About the dynamic strength enhancement of concrete-like materials in a split Hopkinson pressure bar test. Int. J. Solids Struct. 2003, 40, 343–360. [Google Scholar] [CrossRef]
- Lu, Y.B.; Li, Q.M. About the dynamic uniaxial tensile strength of concrete-like materials. Int. J. Impact Eng. 2011, 38, 171–180. [Google Scholar]
- Zhang, M.; Wu, H.J.; Li, Q.M.; Huang, F.L. Further investigation on the dynamic compressive strength enhancement of concrete-like materials based on split Hopkinson pressure bar tests. Part I: Experiments. Int. J. Impact Eng. 2009, 36, 1327–1334. [Google Scholar]
- Hao, Y.; Hao, H.; Li, Z.X. Numerical analysis of lateral inertial confinement effects on impact test of concrete compressive material properties. Int. J. Prot. Struct. 2010, 1, 145–168. [Google Scholar] [CrossRef]
- Pan, F.; Dang, F.; Jiao, K.; Shi, J. Mechanism on enhancement of dynamic flexural tensile strength fornonuniform brittle materials under impact loading. Chin. J. Rock Mech. Eng. 2015, 34, 3948–3955. (In Chinese) [Google Scholar]
- Chen, T.; Li, Q.B.; Guan, J.F. Effect of Radial Inertia Confinement on Dynamic Compressive Strength of Concrete in SHPB Tests. Appl. Mech. Mater. 2013, 438–439, 215–219. [Google Scholar] [CrossRef]
- Xie, H.; Li, L.; Peng, R.; Ju, Y. Energy analysis and criteria for structural failure of rocks. J. Rock Mech. Geotech. Eng. 2009, 1, 11–20. [Google Scholar] [CrossRef] [Green Version]
- Feng, J.; Wang, E.; Chen, X.; Ding, H. Energy dissipation rate: An indicator of coal deformation and failure under static and dynamic compressive loads. Int. J. Min. Sci. Technol. 2018, 28, 397–406. [Google Scholar] [CrossRef]
- Khalilpour, S.; BaniAsad, E.; Dehestani, M. A review on concrete fracture energy and effective parameters. Cem. Concr. Res. 2019, 120, 294–321. [Google Scholar]
- Sim, J.-I.; Yang, K.-H.; Kim, H.-Y.; Choi, B.-J. Size and shape effects on compressive strength of lightweight concrete. Constr. Build. Mater. 2013, 38, 854–864. [Google Scholar]
- Morteza, H.A.; Beygi, M.T.K.; Iman, M.N.; Amiri, J.V.; Rabbanifar, S.; Rahmani, E. The influence of coarse aggregate size and volume on the fracture behavior and brittleness of self-compacting concrete. Cem. Concr. Res. 2014, 66, 75–90. [Google Scholar]
- Lu, S.; Xu, J.Y.; Bai, E.L.; Luo, X. Effect of particles with different mechanical properties on the energy dissipation properties of concrete. Constr. Build. Mater. 2017, 144, 502–515. [Google Scholar]
- Bai, Z.; Liu, Y.; Yang, J.; He, S. Exploring the dynamic response and energy dissipation capacity of functionally graded EPS concrete. Constr. Build. Mater. 2019, 227, 116574. [Google Scholar]







| Cement (kg/m3) | Water (kg/m3) | Sand (kg/m3) | Aggregates (kg/m3) | Water-to-Cement Ratio | Aggregates Size (mm) | Strength Grade |
|---|---|---|---|---|---|---|
| 383.88 | 153.55 | 782.3 | 1080.29 | 0.4 | 5-20 | C30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Dang, F.; Ren, J.; Li, Y.; Zhu, L. Experimental Research on the Energy Evolution of Concrete under Impact Loading. Materials 2023, 16, 5140. https://doi.org/10.3390/ma16145140
Wang H, Dang F, Ren J, Li Y, Zhu L. Experimental Research on the Energy Evolution of Concrete under Impact Loading. Materials. 2023; 16(14):5140. https://doi.org/10.3390/ma16145140
Chicago/Turabian StyleWang, Huan, Faning Dang, Jie Ren, Yanjun Li, and Lin Zhu. 2023. "Experimental Research on the Energy Evolution of Concrete under Impact Loading" Materials 16, no. 14: 5140. https://doi.org/10.3390/ma16145140




