Influence of Pre-Tension on Free-End Torsion Behavior and Mechanical Properties of an Extruded Magnesium Alloy
Abstract
:1. Introduction
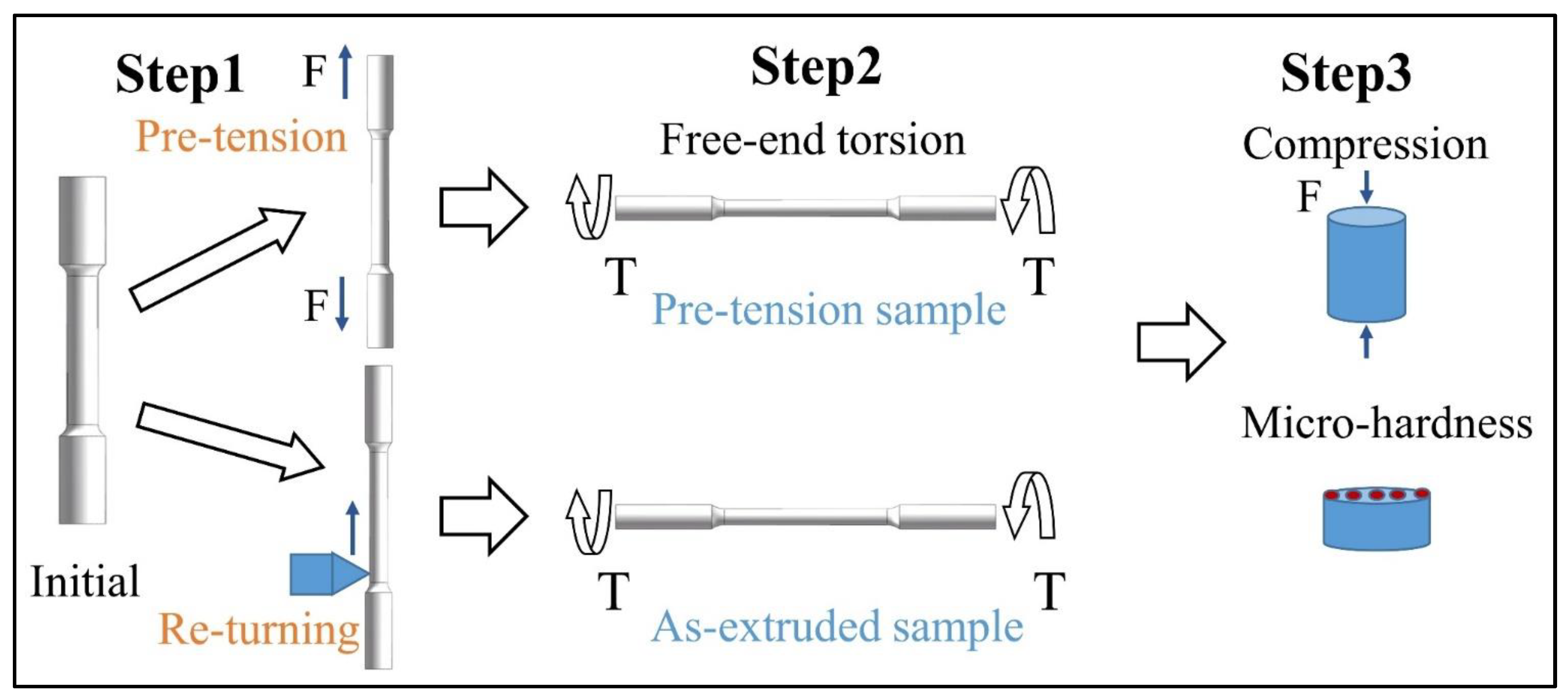
2. Materials and Methods
3. Results and Discussion
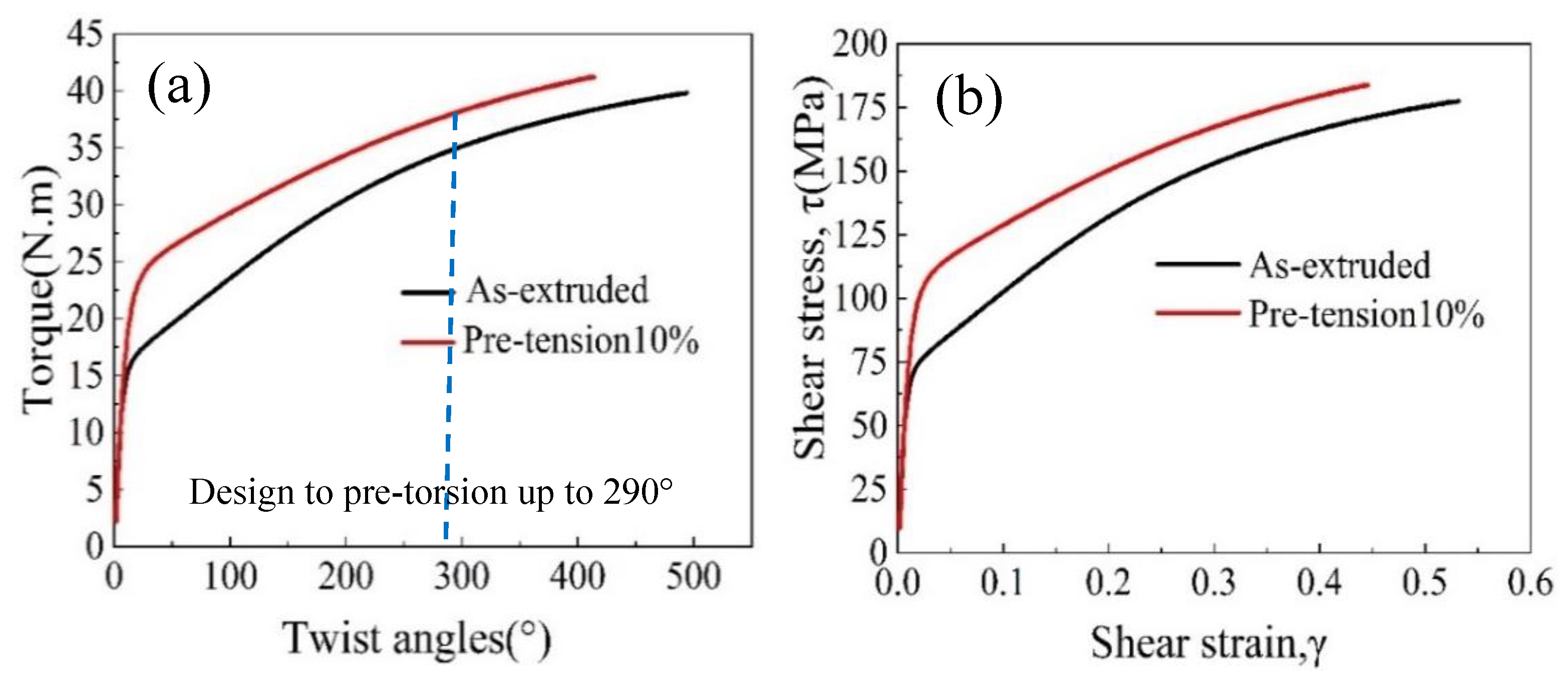
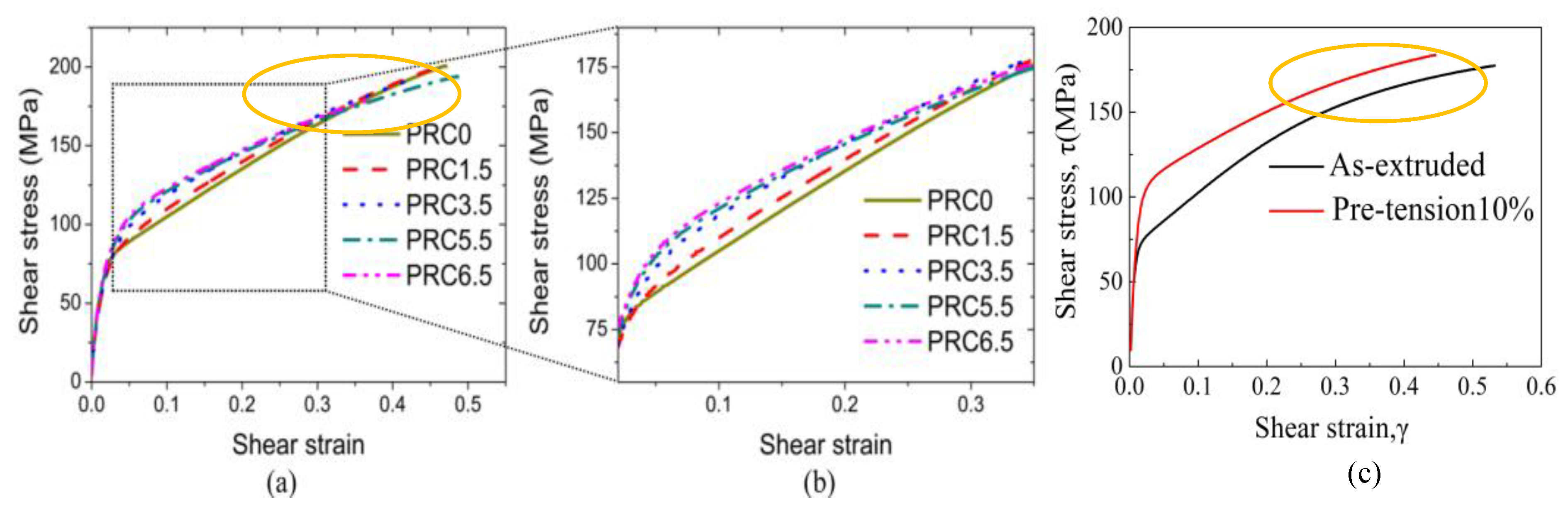
3.1. Shear Stress–Shear Strain Curves
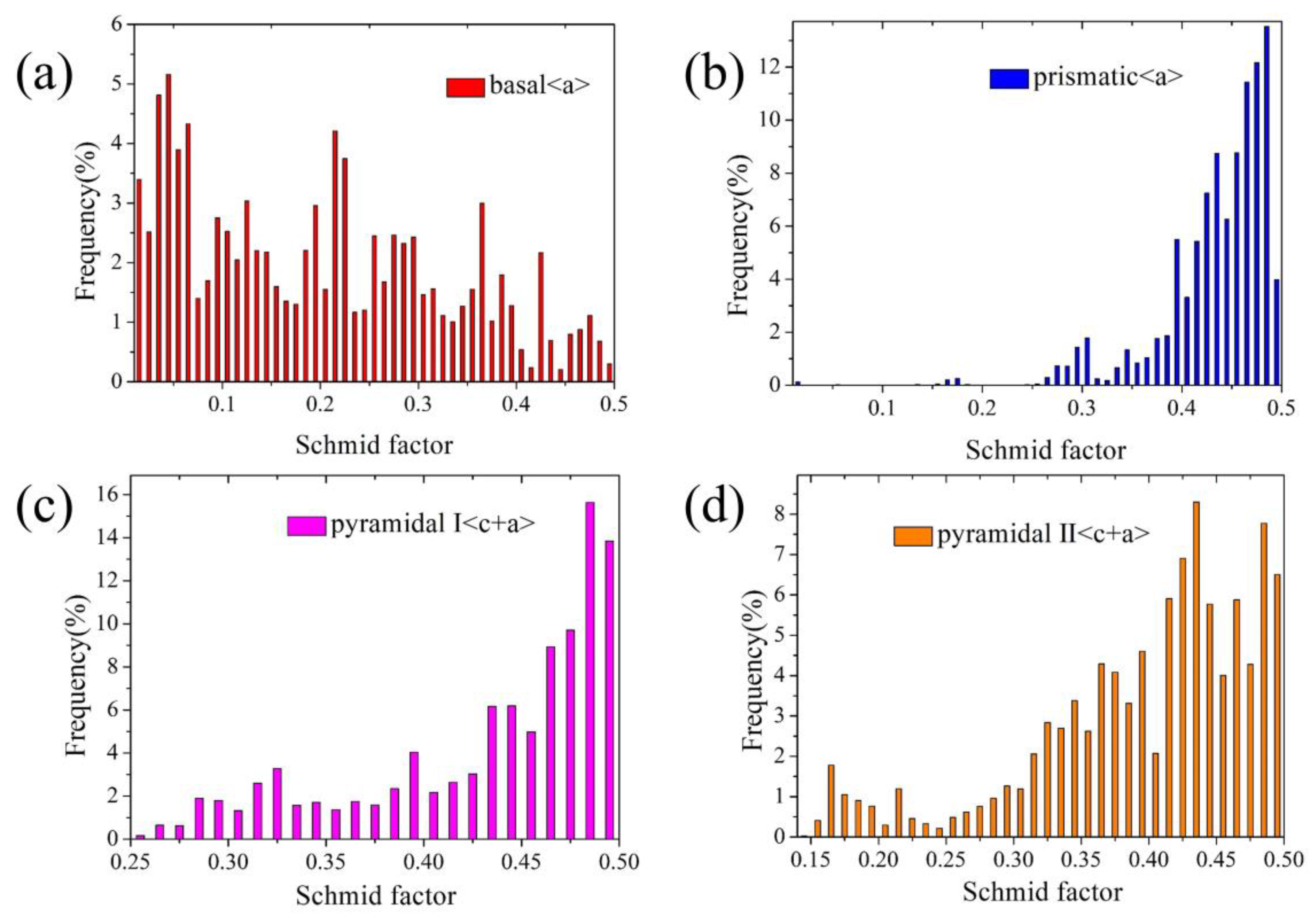
3.2. Microstructure Evolution during Pre-Tension and Free-End Torsion
3.2.1. Microstructure of the Initial Sample and Pre-Tension Sample
3.2.2. Microstructure of the Free-End Torsion Sample
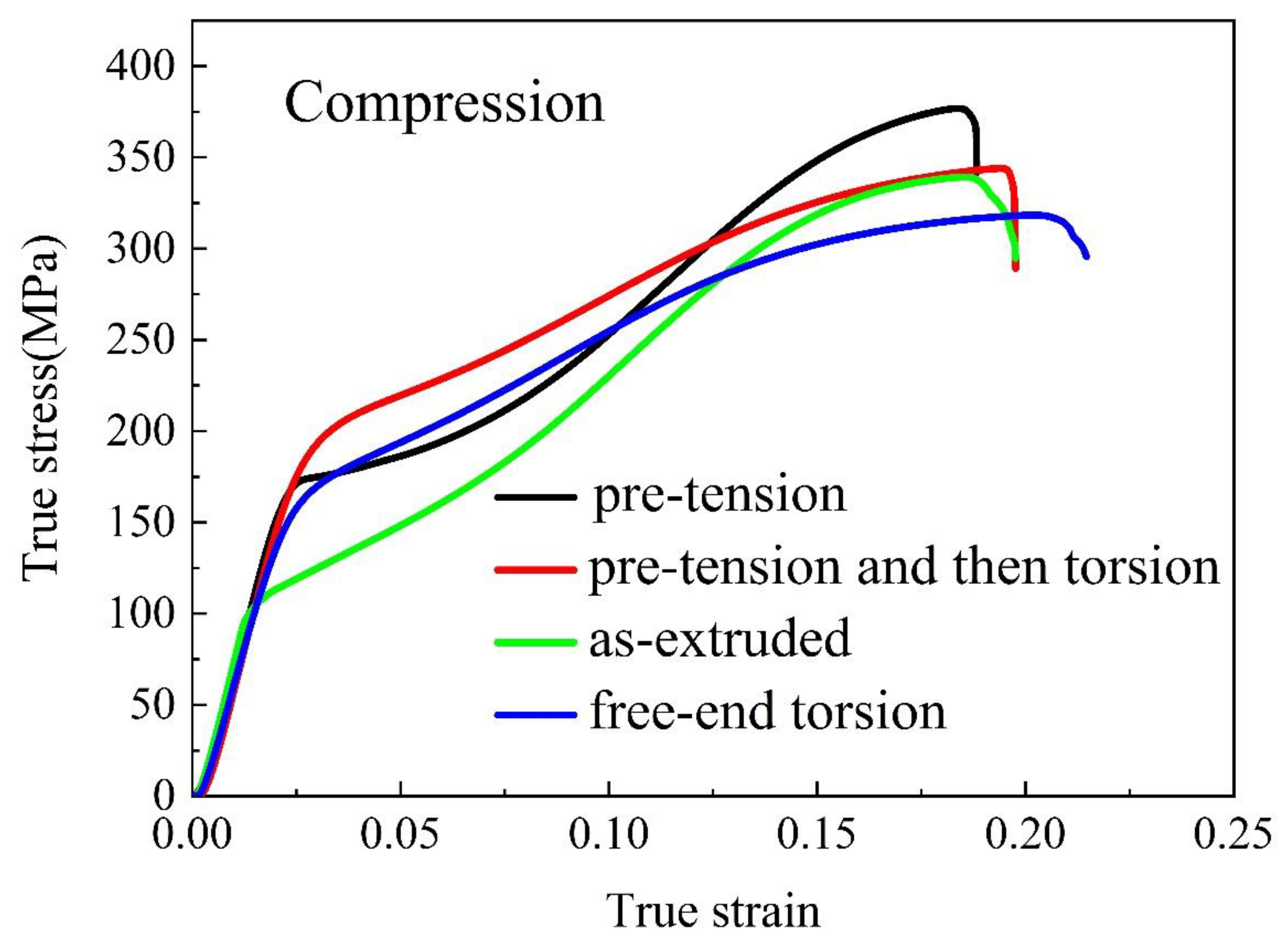
3.3. Compressive Mechanical Properties
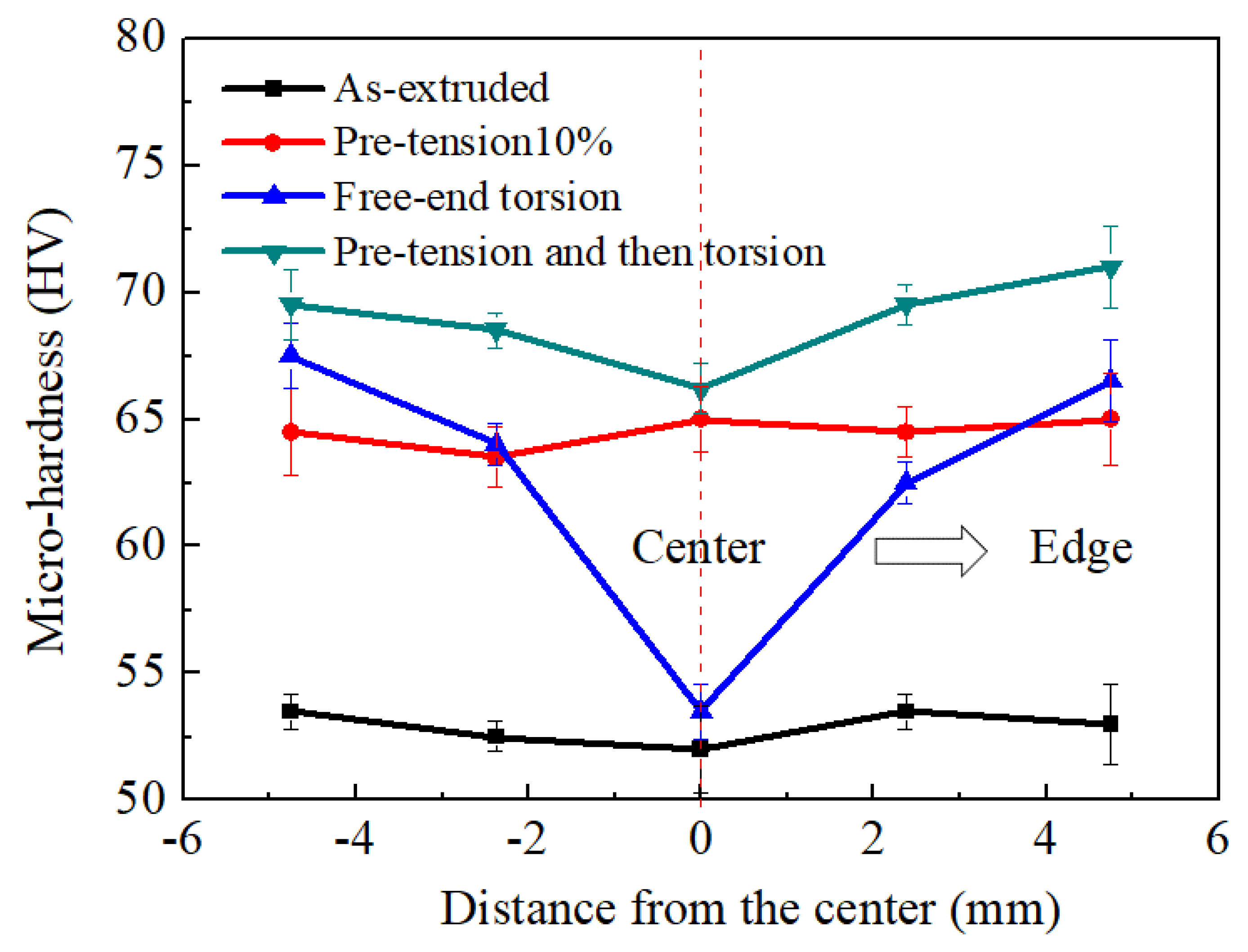
3.4. Micro-Hardness Variation during Pre-Tension and Free-End Torsion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Trang, T.T.T.; Zhang, J.H.; Kim, J.H.; Zargaran, A.; Hwang, J.H.; Suh, B.C.; Kim, N.J. Designing a magnesium alloy with high strength and high formability. Nat. Commun. 2018, 9, 2522. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, L.Y.; Xu, J.Q.; Choi, H.; Pozuelo, M.; Ma, X.; Bhowmick, S.; Yang, J.M.; Mathaudhu, S.; Li, X.C. Processing and properties of magnesium containing a dense uniform dispersion of nanoparticles. Nature 2015, 528, 539–543. [Google Scholar] [CrossRef] [PubMed]
- Yang, P.; Yang, Z.; Li, L.; Sun, Q.; Tan, L.; Ma, X.; Zhu, M. Towards understanding double extension twinning behaviors in magnesium alloy during uniaxial tension deformation. J. Alloys Compd. 2022, 894, 162491. [Google Scholar] [CrossRef]
- Zhu, Y.; Liu, F.; Xin, R.; Song, B.; Liu, Q. Improving mechanical properties of an AZ91 alloy by properly combining aging treatment and torsion deformation. Mater. Sci. Eng. A 2020, 779, 139156. [Google Scholar] [CrossRef]
- Zong, J.J.; Zhao, J.; Wang, X.D.; An, P.F.; Zhang, J.; Hu, T.D.; Cao, Q.P.; Zhang, D.X.; Jiang, B.; Jiang, J.Z. Local atomic structures of Gd and Zn atoms in extruded Mg-Gd-Zn alloys. Scr. Mater. 2021, 195, 113720. [Google Scholar] [CrossRef]
- Song, B.; Guo, N.; Xin, R.; Pan, H.; Guo, C. Strengthening and toughening of extruded magnesium alloy rods by combining pre-torsion deformation with subsequent annealing. Mater. Sci. Eng. A 2016, 650, 300–304. [Google Scholar] [CrossRef]
- Sofinowski, K.; Panzner, T.; Kubenova, M.; Čapek, J.; Van Petegem, S.; Van Swygenhoven, H. In situ tension-tension strain path changes of cold-rolled Mg AZ31B. Acta Mater. 2019, 164, 135–152. [Google Scholar] [CrossRef]
- Guo, F.; Luo, X.; Xin, Y.; Wu, G.; Liu, Q. Obtaining high strength and high plasticity in a Mg-3Al-1Zn plate using pre-tension and annealing treatments. J. Alloys Compd. 2017, 704, 406–412. [Google Scholar] [CrossRef]
- Zhong, L.P.; Wang, Y.; Luo, H.; Luo, C.; Peng, J. Evolution of the microstructure, texture and thermal conductivity of as-extruded ZM60 magnesium alloy in pre-compression. J. Alloys Compd. 2019, 775, 707–713. [Google Scholar] [CrossRef]
- Zhang, H.; Bai, X.; Hou, M.; Wang, L.; Zhang, Q.; Fan, J.; Wu, Y.; Dong, H.; Xu, B. Enhancing compressive mechanical properties of rolled AZ31 Mg alloy plates by pre-compression. Mater. Sci. Eng. A 2020, 772, 138686. [Google Scholar] [CrossRef]
- Yang, C.; Liu, H.; Yang, B.; Shi, B.; Peng, Y.; Pan, F.; Wu, L. The effect of pre-twinning on the mechanical behavior of free-end torsion for an extruded AZ31 magnesium alloy. Mater. Sci. Eng. A 2019, 743, 391–396. [Google Scholar] [CrossRef]
- Wang, C.; Li, F.; Li, J.; Dong, J.; Xue, F. Microstructure evolution, hardening and thermal behavior of commercially pure copper subjected to torsion deformation. Mater. Sci. Eng. A 2014, 598, 7–14. [Google Scholar] [CrossRef]
- Wang, C.; Li, F.; Wei, L.; Yang, Y.; Dong, J. Experimental microindentation of pure copper subjected to severe plastic deformation by combined tension–torsion. Mater. Sci. Eng. A 2013, 571, 95–102. [Google Scholar] [CrossRef]
- Chen, H.; Li, F.; Zhou, S.; Li, J.; Zhao, C.; Wan, Q. Experimental study on pure titanium subjected to different combined tension and torsion deformation processes. Mater. Sci. Eng. A 2017, 680, 278–290. [Google Scholar] [CrossRef]
- Chen, H.B.; Liu, T.M.; Zhang, Y.; Zhai, Y.B.; He, J.J. Reducing tension–compression yield asymmetry by free end torsion in extruded Mg alloy. Mater. Sci. Tech. 2016, 32, 111–118. [Google Scholar] [CrossRef]
- Guo, X.Q.; Wu, W.; Wu, P.D.; Qiao, H.; An, K.; Liaw, P.K. On the Swift effect and twinning in a rolled magnesium alloy under free-end torsion. Scr. Mater. 2013, 69, 319–322. [Google Scholar] [CrossRef]
- Song, B.; Du, Z.; Guo, N.; Yang, Q.; Wang, F.; Guo, S.; Xin, R. Effect of free-end torsion on microstructure and mechanical properties of AZ31 bars with square section. J. Mater. Sci. Technol. 2021, 69, 20–31. [Google Scholar] [CrossRef]
- Chen, Y.; Hu, L.; Shi, L.; Zhou, T.; Tu, J.; Chen, Q.; Yang, M. Effect of texture types on microstructure evolution and mechanical properties of AZ31 magnesium alloy undergoing uniaxial tension deformation at room temperature. Mater. Sci. Eng. A 2020, 769, 138497. [Google Scholar] [CrossRef]
- Hu, T.; Xiao, W.; Wang, F.; Li, Y.; Lyu, S.; Zheng, R.; Ma, C. Improving tensile properties of Mg-Sn-Zn magnesium alloy sheets using pre-tension and ageing treatment. J. Alloys Compd. 2018, 735, 1494–1504. [Google Scholar] [CrossRef]
- Carneiro, L.; Culbertson, D.; Yu, Q.; Jiang, Y. Twinning in rolled AZ31B magnesium alloy under free-end torsion. Mater. Sci. Eng. A 2021, 801, 140405. [Google Scholar] [CrossRef]
- Song, B.; Pan, H.; Chai, L.; Guo, N.; Zhao, H.; Xin, R. Evolution of gradient microstructure in an extruded AZ31 rod during torsion and annealing and its effects on mechanical properties. Mater. Sci. Eng. A 2017, 689, 78–88. [Google Scholar] [CrossRef]
- Zeng, Z.; Zhou, M.; Lynch, P.; Mompiou, F.; Gu, Q.; Esmaily, M.; Yan, Y.; Qiu, Y.; Xu, S.; Fujii, H.; et al. Deformation modes during room temperature tension of fine-grained pure magnesium. Acta Mater. 2021, 206, 116648. [Google Scholar] [CrossRef]
- Zhao, D.; Ma, X.; Srivastava, A.; Turner, G.; Karaman, I.; Xie, K.Y. Significant disparity of non-basal dislocation activities in hot-rolled highly-textured Mg and Mg-3Al-1Zn alloy under tension. Acta Mater. 2021, 207, 116691. [Google Scholar] [CrossRef]
- Malik, A.; Wang, Y.; Nazeer, F.; Khan, M.A.; Sajid, M.; Jamal, S.; Wang, M. Deformation behavior of Mg–Zn–Zr magnesium alloy on the basis of macro-texture and fine-grain size under tension and compression loading along various directions. J. Alloys Compd. 2021, 858, 157740. [Google Scholar] [CrossRef]
- Luo, X.; Feng, Z.; Yu, T.; Luo, J.; Huang, T.; Wu, G.; Hansen, N.; Huang, X. Transitions in mechanical behavior and in deformation mechanisms enhance the strength and ductility of Mg-3Gd. Acta Mater. 2020, 183, 398–407. [Google Scholar] [CrossRef]
- Park, S.H.; Hong, S.-G.; Lee, J.-H.; Kim, S.-H.; Cho, Y.-R.; Yoon, J.; Lee, C.S. Effects of pre-tension on fatigue behavior of rolled magnesium alloy. Mater. Sci. Eng. A 2017, 680, 351–358. [Google Scholar] [CrossRef]
- Mu, S.; Jonas, J.J.; Gottstein, G. Variant selection of primary, secondary and tertiary twins in a deformed Mg alloy. Acta Mater. 2012, 60, 2043–2053. [Google Scholar] [CrossRef]
- Chen, H.; Liu, T.; Yu, H.; Song, B.; Hou, D.; Guo, N.; He, J. Dependence of Microstructure and Hardening Behavior on Torsion Strain and Strain Rate in Extruded AZ31 Rods. Adv. Eng. Mater. 2016, 18, 1683–1689. [Google Scholar] [CrossRef]
- Beausir, B.T.; Tóth, L.S.S.; Qods, F.; Neale, K.W. Texture and Mechanical Behavior of Magnesium During Free-End Torsion. J. Eng. Mater. Technol. 2009, 131, 011108. [Google Scholar] [CrossRef] [Green Version]
- Hu, J.; Gao, H.; Meng, Y.; Zhang, Z.; Gao, L. Effects of free-end torsion on the microstructure evolution and fatigue properties in an extruded AZ31 rod. Mater. Sci. Eng. A 2018, 726, 215–222. [Google Scholar] [CrossRef]
- Cazacu, O.; Revil-Baudard, B.; Barlat, F. New interpretation of monotonic Swift effects: Role of tension–compression asymmetry. Mech. Mater. 2013, 57, 42–52. [Google Scholar] [CrossRef]
- Revil-Baudard, B.; Chandola, N.; Cazacu, O.; Barlat, F. Correlation between swift effects and tension–compression asymmetry in various polycrystalline materials. J. Mech. Phys. Solids 2014, 70, 104–115. [Google Scholar] [CrossRef]
- Guo, N.; Song, B.; Guo, C.; Xin, R.; Liu, Q. Improving tensile and compressive properties of magnesium alloy rods via a simple pre-torsion deformation. Mater. Des. 2015, 83, 270–275. [Google Scholar] [CrossRef]
- Guo, S.; He, Y.; Liu, D.; Li, Z.; Lei, J.; Han, S. Geometrically necessary dislocations induced size effect in the torsional stress relaxation behavior of thin metallic wires. Scr. Mater. 2019, 173, 129–133. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, B.; Wang, H. Geometrically necessary dislocations distribution in face-centred cubic alloy with varied grain size. Mater. Charact. 2020, 162, 110205. [Google Scholar] [CrossRef]
- Shi, D.F.; Cepeda-Jiménez, C.M.; Pérez-Prado, M.T. The relation between ductility at high temperature and solid solution in Mg alloys. J. Magn. Alloy. 2022, 10, 224–238. [Google Scholar] [CrossRef]
- Shi, R.; Song, B.; Xia, D.; Liu, T.; Yang, Q.; Guo, N.; Guo, S. Influence of initial {10–12} twins on twinning behavior of extruded AZ31 alloys during free-end torsion. Mater. Charact. 2023, 201, 112932. [Google Scholar] [CrossRef]


| Mechanical Properties | As-Extruded | Pre-Tension | Free-End Torsion | Pre-Tension and then Torsion |
|---|---|---|---|---|
| CYS (MPa) | 110.8 ± 3.5 | 174.9 ± 4.2 | 173.9 ± 2.7 | 206.8 ± 2.8 |
| PS (MPa) | 338.7 ± 1.3 | 377.8 ± 0.5 | 319.1 ± 2.1 | 342.3 ± 1.5 |
| Percentage increase in the CYS (%) | _ | 57.85 | 56.95 | 86.64 |
| Percentage increase in the PS (%) | _ | 11.54 | −5.79 | 1.06 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Shen, Z.; Song, B.; She, J. Influence of Pre-Tension on Free-End Torsion Behavior and Mechanical Properties of an Extruded Magnesium Alloy. Materials 2023, 16, 5343. https://doi.org/10.3390/ma16155343
Chen H, Shen Z, Song B, She J. Influence of Pre-Tension on Free-End Torsion Behavior and Mechanical Properties of an Extruded Magnesium Alloy. Materials. 2023; 16(15):5343. https://doi.org/10.3390/ma16155343
Chicago/Turabian StyleChen, Hongbing, Zhikang Shen, Bo Song, and Jia She. 2023. "Influence of Pre-Tension on Free-End Torsion Behavior and Mechanical Properties of an Extruded Magnesium Alloy" Materials 16, no. 15: 5343. https://doi.org/10.3390/ma16155343
APA StyleChen, H., Shen, Z., Song, B., & She, J. (2023). Influence of Pre-Tension on Free-End Torsion Behavior and Mechanical Properties of an Extruded Magnesium Alloy. Materials, 16(15), 5343. https://doi.org/10.3390/ma16155343






