Origin and Evolution of Cracks in the Glaze Surface of a Ceramic during the Cooling Process
Abstract
1. Introduction
2. Materials and Methods
2.1. Numerical Method
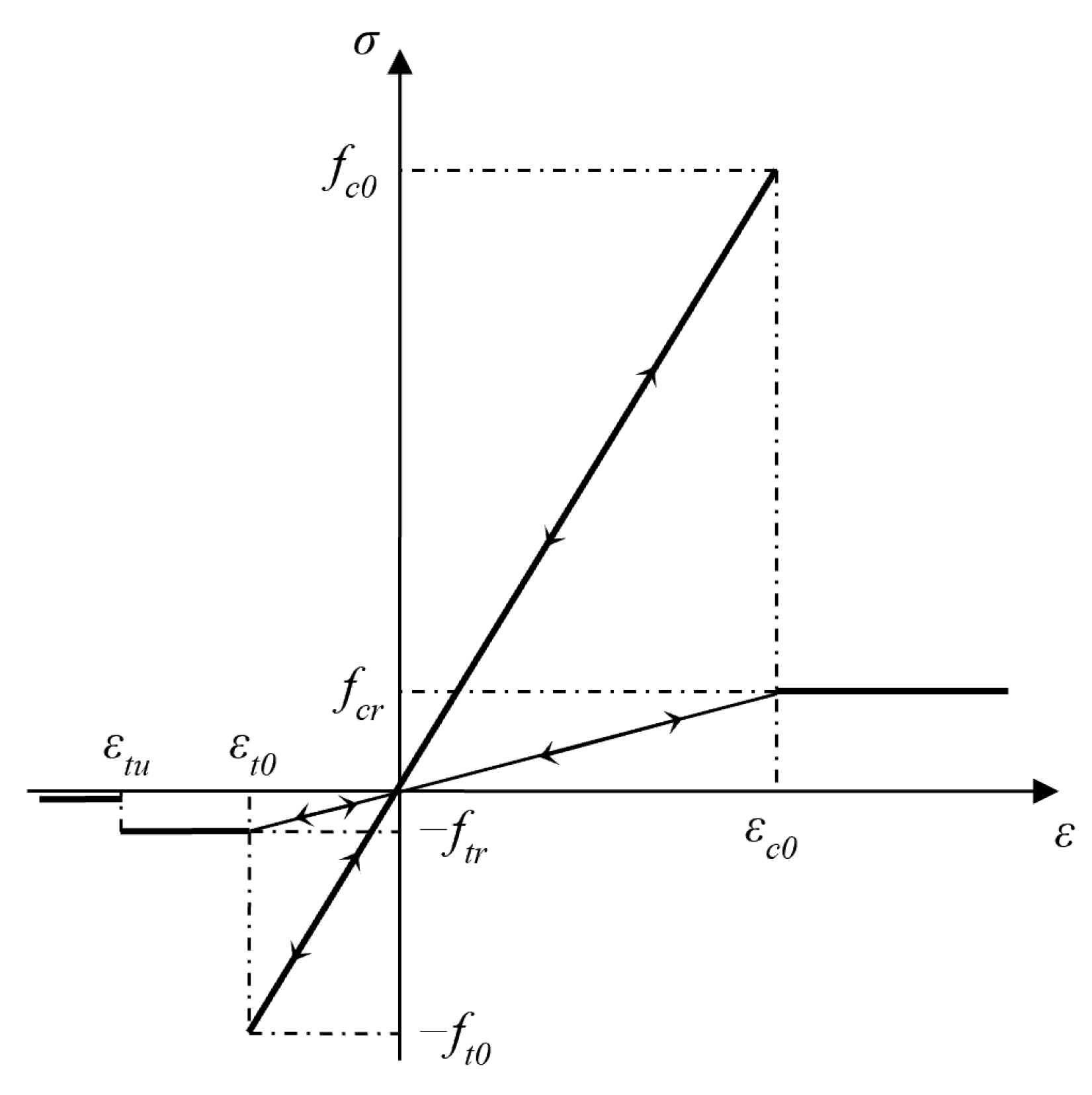
2.1.1. Constitutive Relation
2.1.2. Temperature Equation
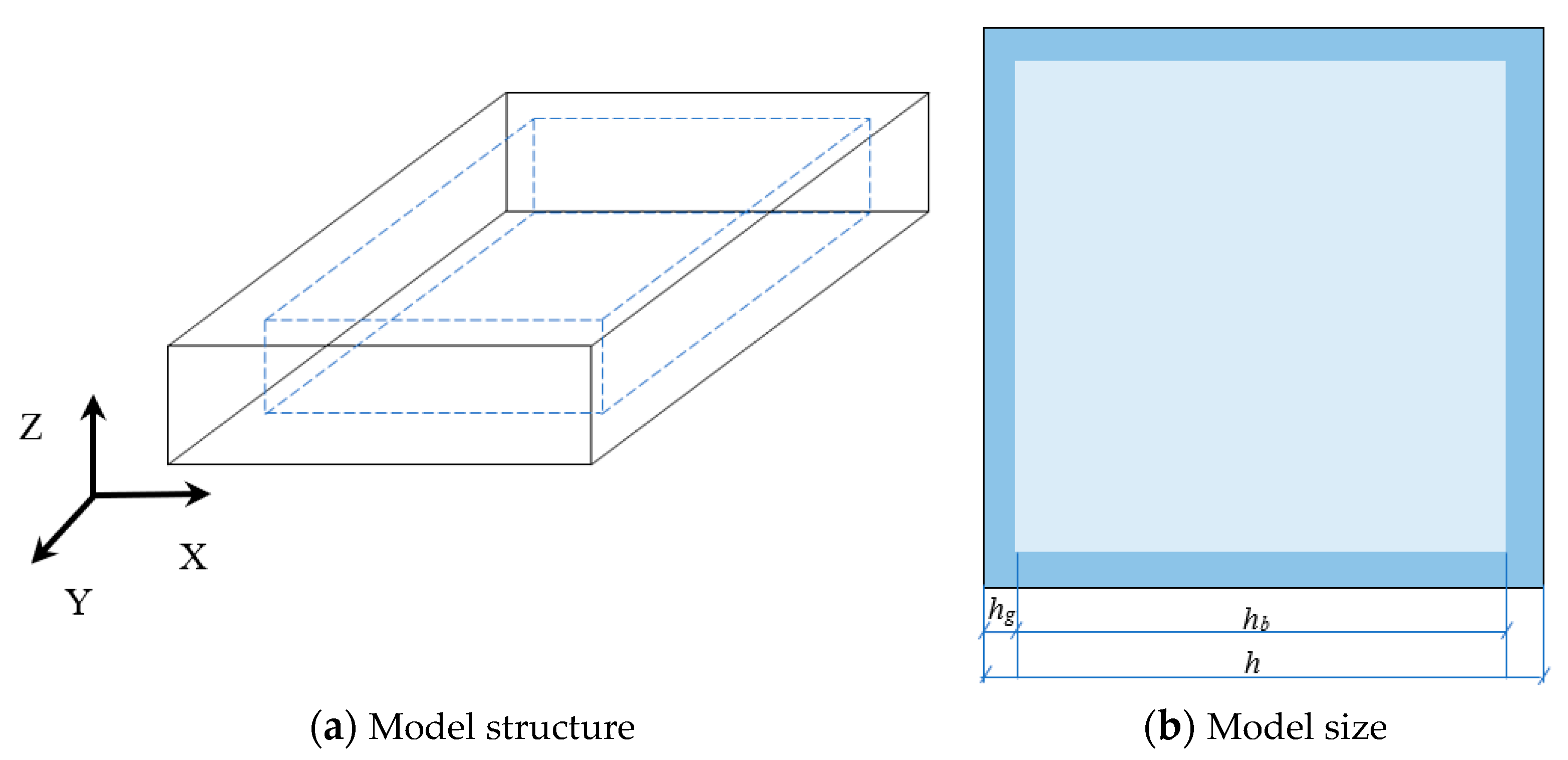
2.2. Model Configuration
3. Results
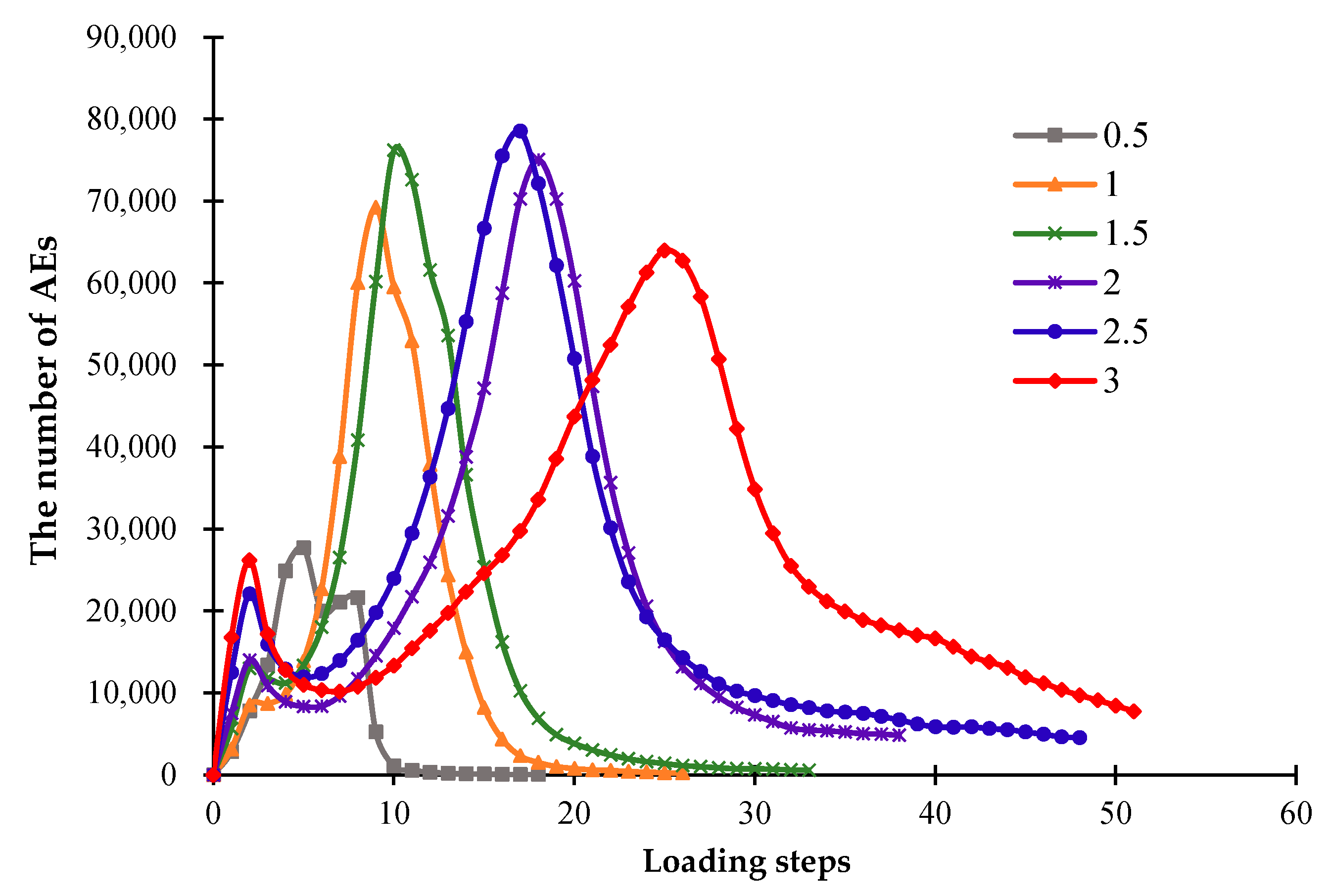
3.1. The Influence of Temperature Difference on the Fracture Process
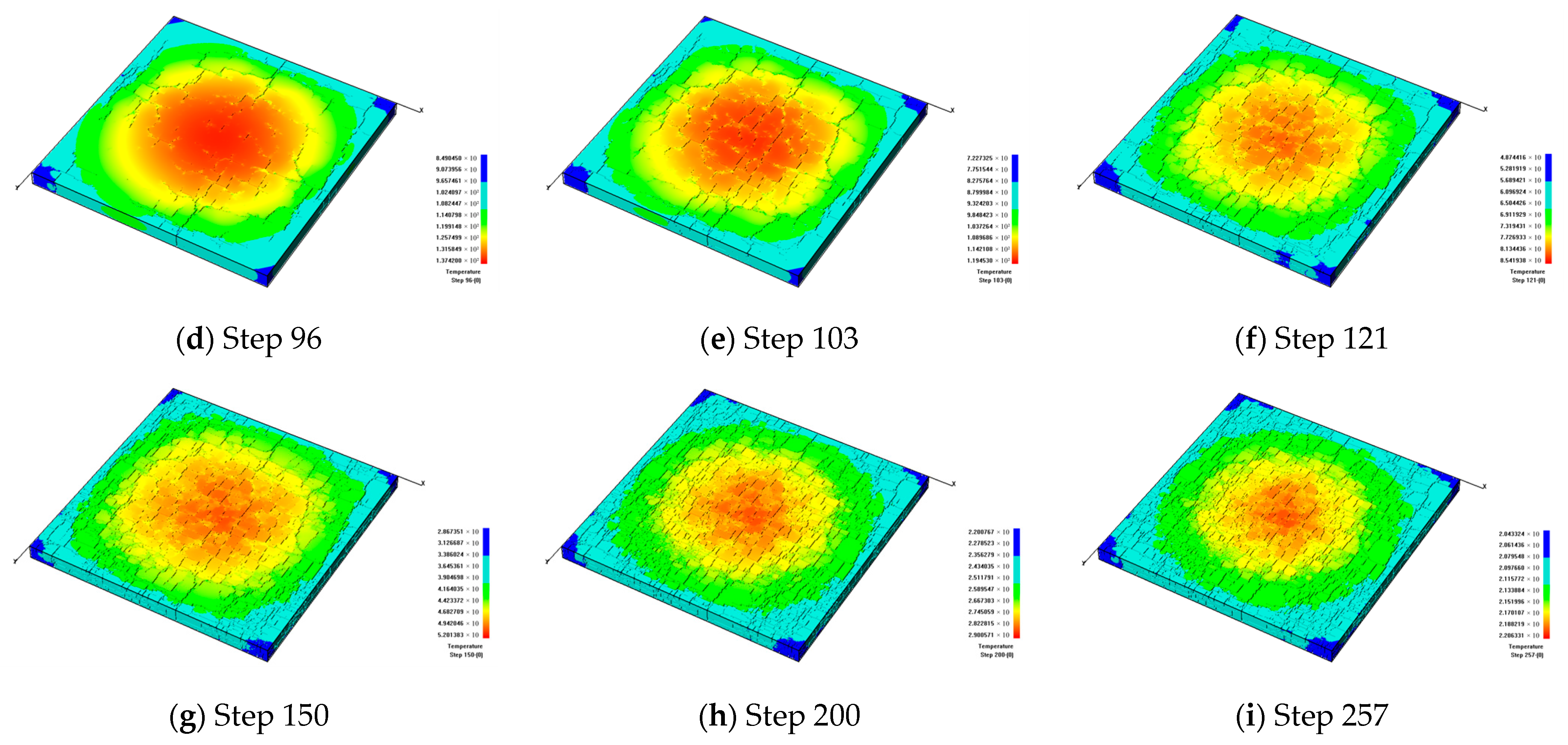
3.1.1. The Fracture Formation under Slow Cooling
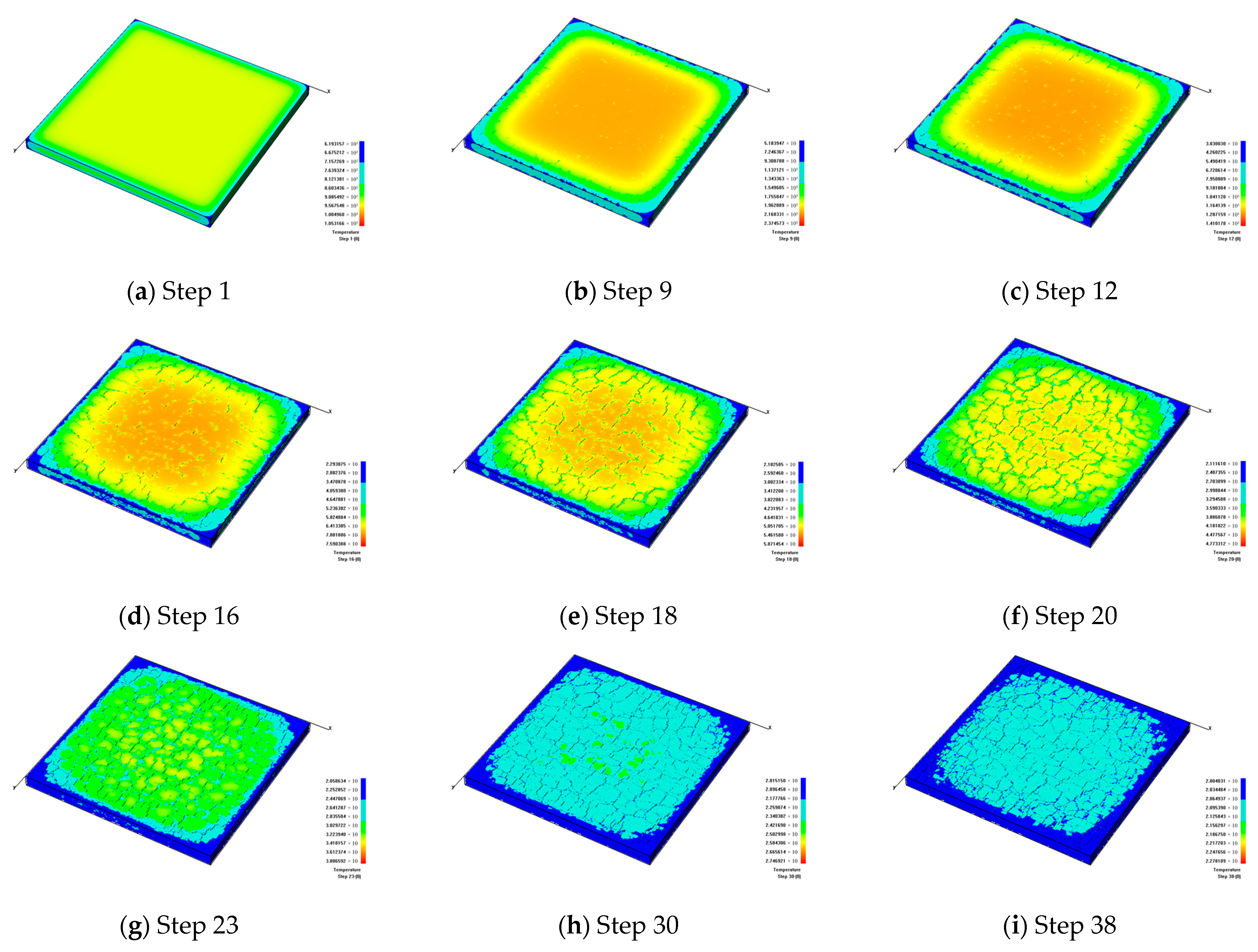
3.1.2. The Fracture Formation under Fast Cooling
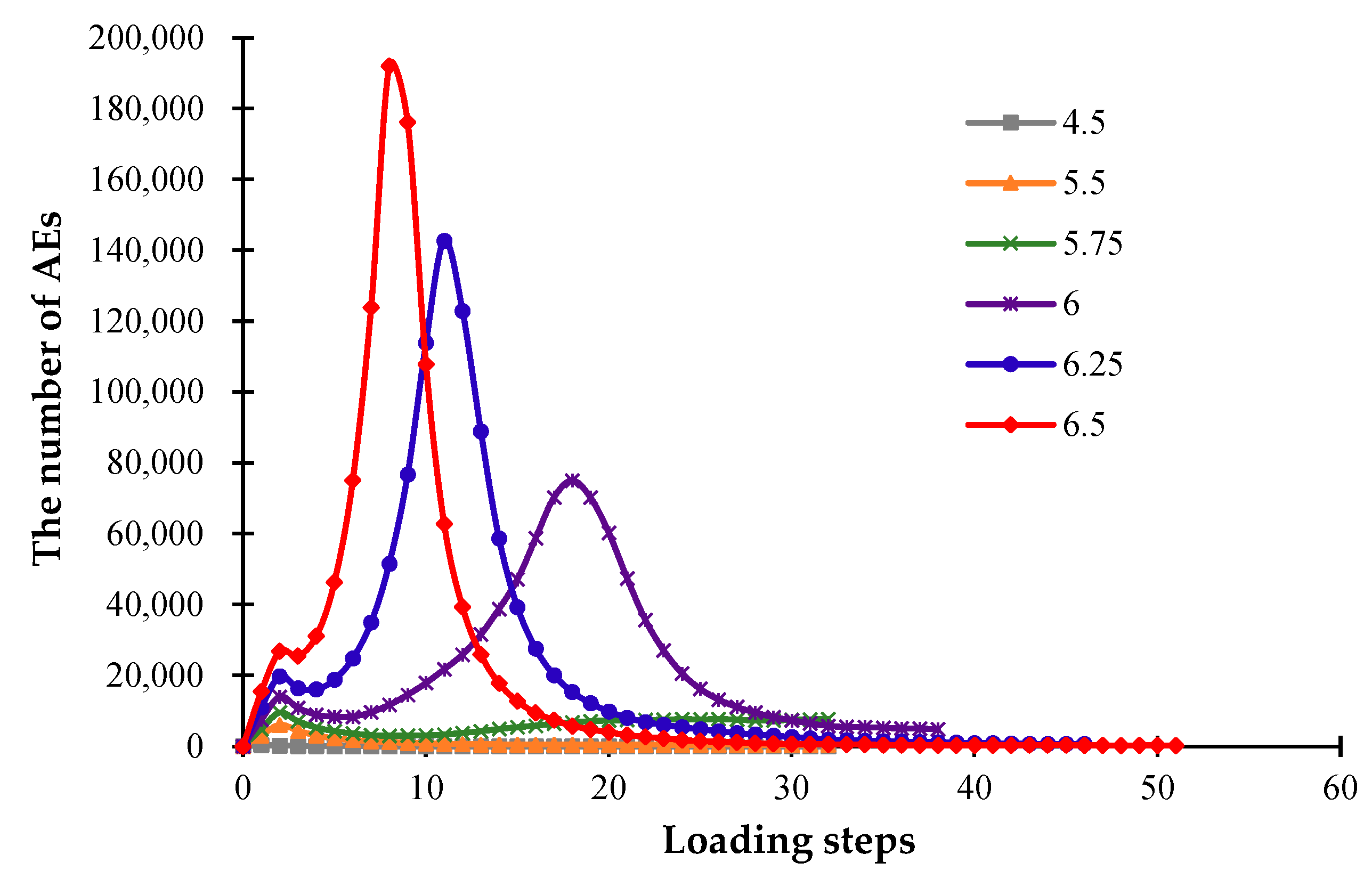
3.2. The Influence of the Glaze Heat Transfer Coefficient
3.3. The Influence of Glaze Thickness
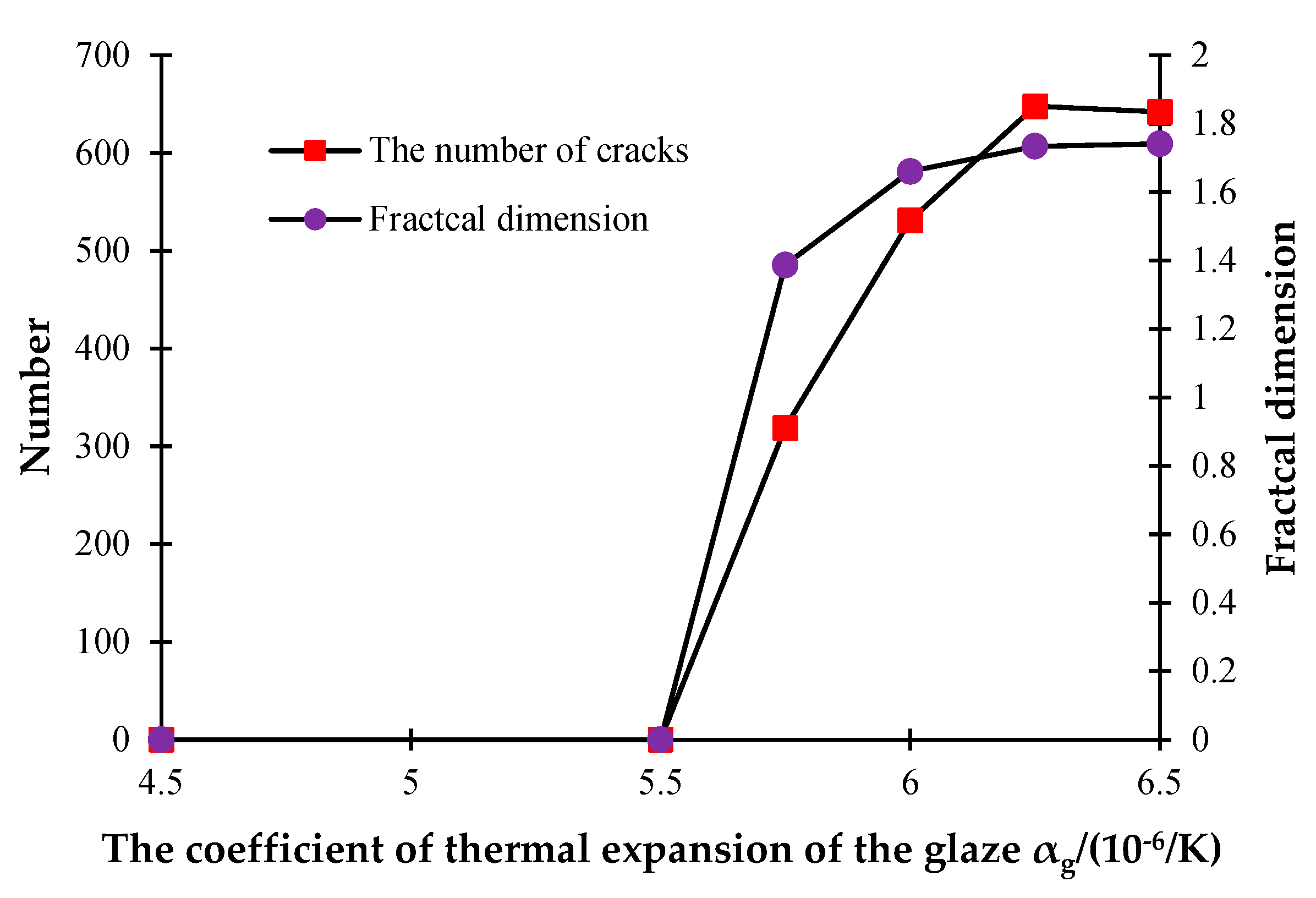
3.4. The Influence of Coefficient of Thermal Expansion (CTE) of Glaze
4. Conclusions
- (1)
- The cooling rate has a great influence on the formation of microcracks on a ceramic surface. Namely, a lower cooling rate will enhance the temperature difference in ceramics, leading to denser cracks. When the model temperature drops to essentially the temperature of surrounding environment, new cracks will not appear due to the small temperature difference, which means that the cracks on a ceramic surface become stable.
- (2)
- A higher heat transfer coefficient will lead to a faster cooling speed and a small temperature difference on the ceramic surface. When all the ceramic models are cooled to the same degree, a higher heat transfer coefficient will result in a more uniform surface temperature. Furthermore, a higher heat transfer coefficient will cause a faster drop in the ceramic temperature, resulting in a smaller temperature difference inside the model and a smaller number of microcracks. When the heat transfer coefficient increases to a certain level, the model can be cooled quickly, and many damage zones will occur inside the model at the beginning of cooling. As the cooling process continues, the model with a higher heat transfer coefficient will experience the second massive failure sooner, the failure process will end earlier.
- (3)
- As the thickness of the glaze layer increases, the distribution of cracks on a ceramic surface also changes. When the thickness of the glaze layer is much lower than that of the blank layer, only a few microcracks scatter on the surface of the glaze layer during the cooling process. As the thickness of the glaze layer increases, some through-cracks begin to appear. When the thicknesses of the glaze layer and the blank body becomes equal, cracks spread throughout the surface of ceramics. However, when the thickness of the glaze layer rises to a certain level, the number of cracks decreases and the growth of the cracks slows down, even showing a downward trend. Simultaneously, as the thickness of the glaze layer increases, the temperature stress required for producing cracks gradually rises, and the model becomes more difficult to destroy.
- (4)
- When the CTE of the glaze layer is smaller than that of the blank body, no cracks will occur during the cooling process. When the CTE of the glaze layer is greater than that of the blank body, with the growth of the CTE of glaze layer, the number of cracks on the ceramic surface will gradually increase. However, when the CTE of the glaze layer increases to a certain level, the number of cracks starts to decrease. This phenomenon occurs because with the increasing CTE, the heat will be lost more and more quickly, and it is difficult for the temperature stress to accumulate on the ceramic surface.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bai, T.; Plollard, D.D.; Gao, H. Explanation for fracture spacing in layered materials. Nature 2000, 403, 753–756. [Google Scholar] [CrossRef] [PubMed]
- Jitcharoen, J.; Padture, N.P.; Giannakopoulos, A.E.; Suresh, S. Hertzian-crack suppression in ceramics with elastic-modulus-graded surfaces. J. Am. Ceram. Soc. 2005, 81, 2301–2308. [Google Scholar] [CrossRef]
- Zok, F.W.; Spearing, S.M. Matrix crack spacing in brittle matrix composites. Acta Metall. Mater. 1992, 40, 2033–2043. [Google Scholar] [CrossRef]
- Vagaggini, E.; Domergue, J.M.; Evans, A.G. Relationships between hysteresis measurements and the constituent properties of ceramic matrix composites: I, Theory. J. Am. Ceram. Soc. 1995, 78, 2709–2720. [Google Scholar] [CrossRef]
- Daomergue, J.M.; Vagaggini, E.; Evans, A.G. Relationships between hysteresis measurements and the constituent properties of ceramic matrix composites: II, Experimental studies on unidirectional materials. J. Am. Ceram. Soc. 1995, 78, 2721–2731. [Google Scholar] [CrossRef]
- Li, L.B. Interface wear effects in ceramic composite crack opening. J. Compos Mater. 2022, 56, 3371–3384. [Google Scholar] [CrossRef]
- Sun, Y.J.; Singh, R.N. The generation of multiple matrix cracking and fiber-matrix interfacial debonding in a glass composite. Acta Mater. 1998, 46, 1657–1667. [Google Scholar] [CrossRef]
- Arslan, O. Hertzian crack propagation in graded glass/ceramic composites. J. Am. Ceram. 2003, 106, 4499–4514. [Google Scholar] [CrossRef]
- Weigel, N.; Dinkler, D.; Kroplin, B.H. Micromechanically based continuum damage mechanics material laws for fiber-reinforced ceramics. Comput. Struct. 2001, 79, 2277–2286. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, X.; Xiong, Y. Numerical simulation of zonal disintegration of surrounding rock in the deep-buried chamber. Deep Undergr. Sci. Eng. 2022, 1, 174–182. [Google Scholar] [CrossRef]
- Li, K.; Wang, D.L.; Chen, H.; Guo, L.C. Normalized evaluation of thermal shock resistance for ceramic materials. J. Adv. Ceram. 2014, 3, 250–258. [Google Scholar] [CrossRef]
- Wu, X.F.; Jiang, C.P.; Song, F.; Li, J.; Shao, Y.F.; Xu, X.H.; Yan, P. Size effect of thermal shock crack patterns in ceramics and numerical predictions. J. Eur. Ceram. Soc. 2015, 35, 1263–1271. [Google Scholar] [CrossRef]
- Jiang, C.P.; Wu, X.F.; Li, J.; Song, F.; Shao, Y.F.; Xu, X.H.; Yan, P. A study of the mechanism of formation and numerical simulations of crack patterns in ceramics subjected to thermal shock. Acta Mater. 2012, 60, 4540–4550. [Google Scholar] [CrossRef]
- Liu, Y.X.; Wu, X.F.; Guo, Q.K.; Jiang, C.P.; Song, F.; Li, J. Experiments and numerical simulations of thermal shock crack patterns in thin circular ceramic specimens. Ceram. Int. 2015, 41, 1107–1114. [Google Scholar] [CrossRef]
- Hong, C.; Shen, H.; Xu, Q.; Lu, X.L.; Cao, C. Factors influencing transparent crackle glaze. China Ceram. Ind. 2014, 21, 15–20. [Google Scholar]
- Dong, Y.L.; Wang, W.M. Progress of investigation on thermal shock resistance of ceramic materials. J. Adv. Ceram. 2004, 1, 37–41. [Google Scholar]
- Li, W.J.; Zhang, Y.; Zhang, X.H.; Hong, C.Q.; Han, W.B. Thermal shock behavior of ZrB2-SiC Ultra-high temperature ceramics with addition of zirconia. J. Alloys Compd. 2009, 478, 386–391. [Google Scholar] [CrossRef]
- Gyak, K.W.; Vishwakarma, N.K.; Hwang, Y.H.; Kim, J.; Yun, H.S.; Kim, D.P. 3D-printed monolithic SiCN ceramic microreactors from a photocurable preceramic resin for the high temperature ammonia cracking process. React. Chem. Eng. 2019, 4, 1393–1399. [Google Scholar] [CrossRef]
- Duan, W.J.; Jia, D.C.; Cai, D.L.; Niu, B.; Yang, H.L.; Yang, Z.H.; Zhou, Y. Thermal shock damage assessment of a BNW/SiO2 ceramic: Insight from temperature-dependent material properties. Ceram. Int. 2021, 47, 19737–19742. [Google Scholar] [CrossRef]
- Qi, F.; Meng, S.H.; Song, F.; Guo, H.; Xu, X.H.; Shao, Y.F.; Chen, Y. Fractal characterization of ceramic crack patterns after thermal shocks. J. Am. Ceram. Soc. 2019, 102, 3641–3652. [Google Scholar] [CrossRef]
- Zuo, C.; Li, Q.; Wang, Q.; Li, Y.; Li, L.; Wei, J.; Shao, Y.; Song, F. Effect of material parameters on thermal shock crack of ceramics calculated by phase-field method. J. Am. Ceram. Soc. 2022, 105, 7649–7657. [Google Scholar] [CrossRef]
- Osada, T.; Watabe, A.; Yamamoto, J.; Brouwer, J.C.; Kwakernaak, C.; Ozaki, S.; van der Zwaag, S.; Sloof, W.G. Full strength and toughness recovery after repeated cracking and healing in bone-like high temperature ceramics. Sci. Rep. 2020, 10, 18990. [Google Scholar] [CrossRef] [PubMed]
- Ma, T.C. Ceramic Technology, 2nd ed.; China Light Industry Press: Beijing, China, 2011. [Google Scholar]
- Zhou, J.E.; Liang, D.; Li, Q.J.; Zhang, M.L.; Wu, J.M. Study on the formation mechanism and preparation of ice crackle celadon. J. Synth. Cryst. 2011, 40, 1076–1082. [Google Scholar]
- Wei, A.; Liu, Z.; Zhang, F.; Ma, M.; Chen, G.; Li, Y. Thermal expansion coefficient tailoring of LAS glass-ceramic for anodic bondable low temperature co-fired ceramic application. Ceram. Int. 2020, 46, 4771–4777. [Google Scholar] [CrossRef]
- Roy, S.; Nagel, A.; Weidenmann, K.A. Anisotropic thermal expansion behavior of an interpenetrating metal/ceramic composite. Thermochim. Acta 2020, 684, 178488. [Google Scholar] [CrossRef]
- Wang, Q.; Li, F. Controllable thermal expansion in ferroelectric ceramics through two-dimensional periodically orthogonal poling. Scr. Mater. 2021, 191, 67–70. [Google Scholar] [CrossRef]
- Fan, X.; Ma, X.; Dang, X.; Xue, J.; Ye, F.; Zhao, D.; Cheng, L. In-plane thermal expansion behavior of dense ceramic matrix composites containing SiBC matrix. J. Eur. Ceram. Soc. 2020, 40, 3414–3422. [Google Scholar] [CrossRef]
- Tavangarian, F.; Hui, D.; Li, G. Crack-healing in ceramics. Compos. Part B Eng. 2018, 144, 56–87. [Google Scholar] [CrossRef]
- Junior, G.S.; Ferreira, J.; Millán-Arias, C.; Daniel, R.; Junior, A.C.; Fernandes, B.J.T. Ceramic cracks segmentation with deep learning. Appl. Sci. 2021, 11, 6017. [Google Scholar] [CrossRef]
- Shao, C.X.; Guo, H.; Meng, S.H.; Shao, Y.F.; Wang, S.X.; Xie, S.J.; Qi, F. Characterization of ceramic thermal shock cracks based on the multifractal spectrum. Fractal Fract. 2022, 6, 539. [Google Scholar] [CrossRef]
- Zhu, W.W.; Lei, G.; He, X.P.; Patzek, T.W.; Wang, M. Fractal and multifractal characterization of stochastic fracture networks and real outcrops. J. Struct. Geol. 2022, 155, 104508. [Google Scholar] [CrossRef]
- Wang, Y.; Gong, B.; Tang, C. Numerical investigation on anisotropy and shape effect of mechanical properties of columnar jointed basalts containing transverse joints. Rock Mech. Rock Eng. 2022, 55, 7191–7222. [Google Scholar] [CrossRef]
- Gong, B.; Liang, Z.Z.; Liu, X.X. Nonlinear deformation and failure characteristics of horseshoe-shaped tunnel under varying principal stress direction. Arab. J. Geosci. 2022, 15, 475. [Google Scholar] [CrossRef]
- Wang, Y.; Gong, B.; Zhang, Y.; Yang, X.; Tang, C. Progressive fracture behavior and acoustic emission release of CJBs affected by joint distance ratio. Mathematics 2022, 10, 4149. [Google Scholar] [CrossRef]
- Liang, Z.Z.; Xiao, D.K.; Li, C.C.; Wu, X.K.; Gong, B. Numerical study on strength and failure modes of rock mass with discontinuous joints. Chin. J. Geotech. Eng. 2014, 36, 2086–2095. [Google Scholar]
- Tang, S.B. Mesoscopic Numerical Model of Thermo-Hydro Cracking Process Concrete. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2009. [Google Scholar]
- Li, G.; Wang, K.; Gong, B.; Tao, Z.G.; Du, K. A multi-temporal series high-accuracy numerical manifold method for tran-sient thermoelastic fracture problems. Int. J. Solids Struct. 2021, 230–231, 111151. [Google Scholar] [CrossRef]
- Chen, T.T.; Foulger, G.R.; Tang, C.A.; Mathias, S.A.; Gong, B. Numerical investigation on origin and evolution of polygonal cracks on rock surfaces. Eng. Geol. 2022, 311, 106913. [Google Scholar] [CrossRef]
- Tang, C.S.; Cui, Y.J.; Tang, A.M.; Shi, B. Experiment evidence on the temperature dependence of desiccation cracking behavior of clayey soils. Eng. Geol. 2010, 114, 261–266. [Google Scholar] [CrossRef]
- Tang, C.S.; Shi, B.; Liu, C.; Zhao, L.; Wang, B. Influencing factors of geometrical structure of surface shrinkage cracks in clayey soils. Eng. Geol. 2008, 101, 204–219. [Google Scholar] [CrossRef]












| Material | Elastic Modulus (E)/MPa | Compressive Strength (σc)/MPa | Tensile Strength (σt) /MPa | Poisson’s Ratio (υ) | Heterogeneity (m) | Thermal Capacity J/(m3·k) | Thermal Conductivity W/(m·k) |
|---|---|---|---|---|---|---|---|
| Glaze | 61,240 | 450 | 90 | 0.24 | 8 | 2.1 | 1 |
| Blank | 100,000 | 800 | 160 | 0.3 | 5 | 2.1 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, T.; Gong, B.; Tang, C. Origin and Evolution of Cracks in the Glaze Surface of a Ceramic during the Cooling Process. Materials 2023, 16, 5508. https://doi.org/10.3390/ma16165508
Chen T, Gong B, Tang C. Origin and Evolution of Cracks in the Glaze Surface of a Ceramic during the Cooling Process. Materials. 2023; 16(16):5508. https://doi.org/10.3390/ma16165508
Chicago/Turabian StyleChen, Tiantian, Bin Gong, and Chun’an Tang. 2023. "Origin and Evolution of Cracks in the Glaze Surface of a Ceramic during the Cooling Process" Materials 16, no. 16: 5508. https://doi.org/10.3390/ma16165508
APA StyleChen, T., Gong, B., & Tang, C. (2023). Origin and Evolution of Cracks in the Glaze Surface of a Ceramic during the Cooling Process. Materials, 16(16), 5508. https://doi.org/10.3390/ma16165508







