Investigation of the Fracture and Fragmentation of Implosively Driven Thin-Walled Cylindrical Shell: From Thermodynamic Analysis to CDEM Simulation
Abstract
:1. Introduction
2. Thermodynamic State of Detonation Products
2.1. Calculation of Chemical Reaction Perspective
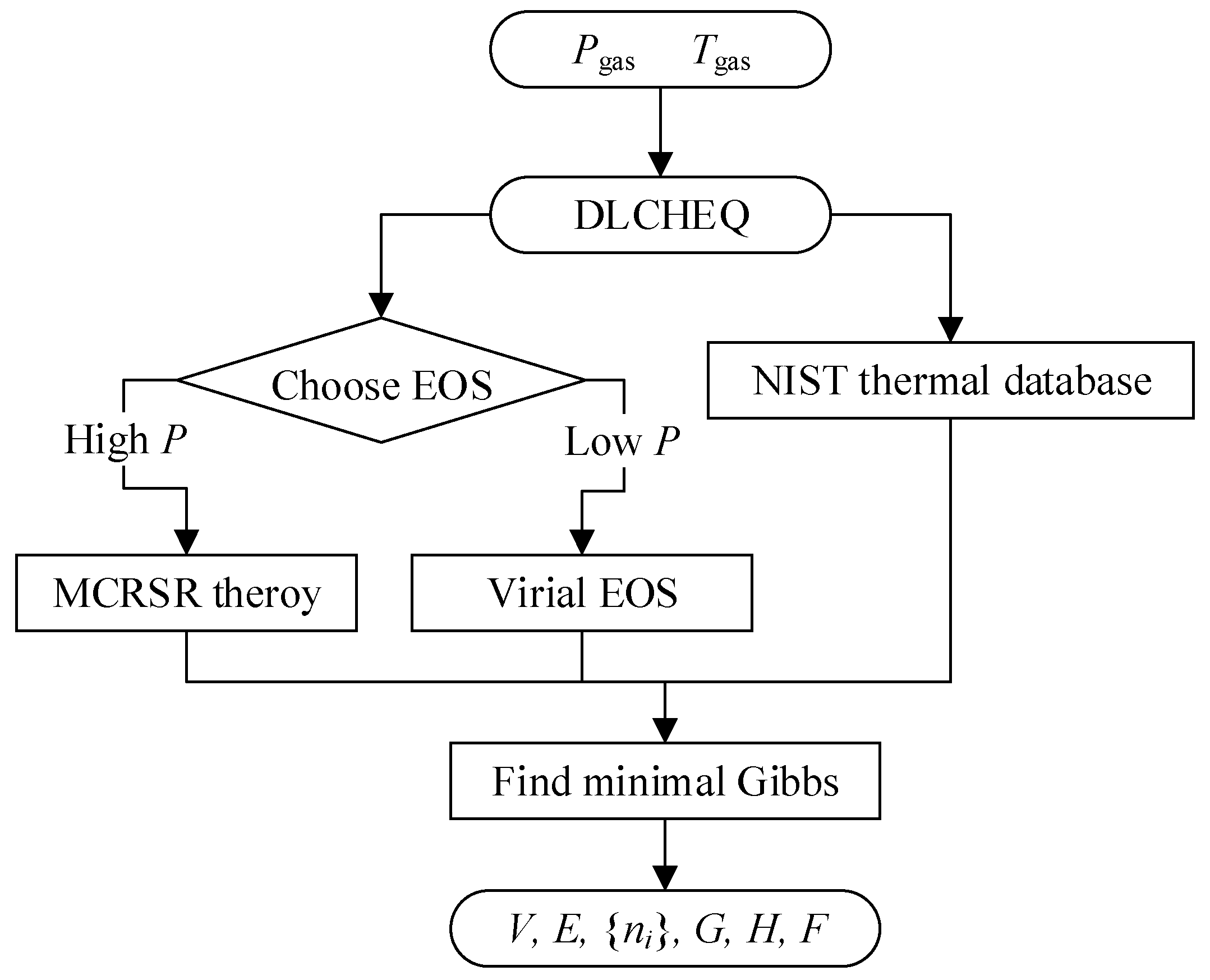
2.1.1. Thermochemical Code
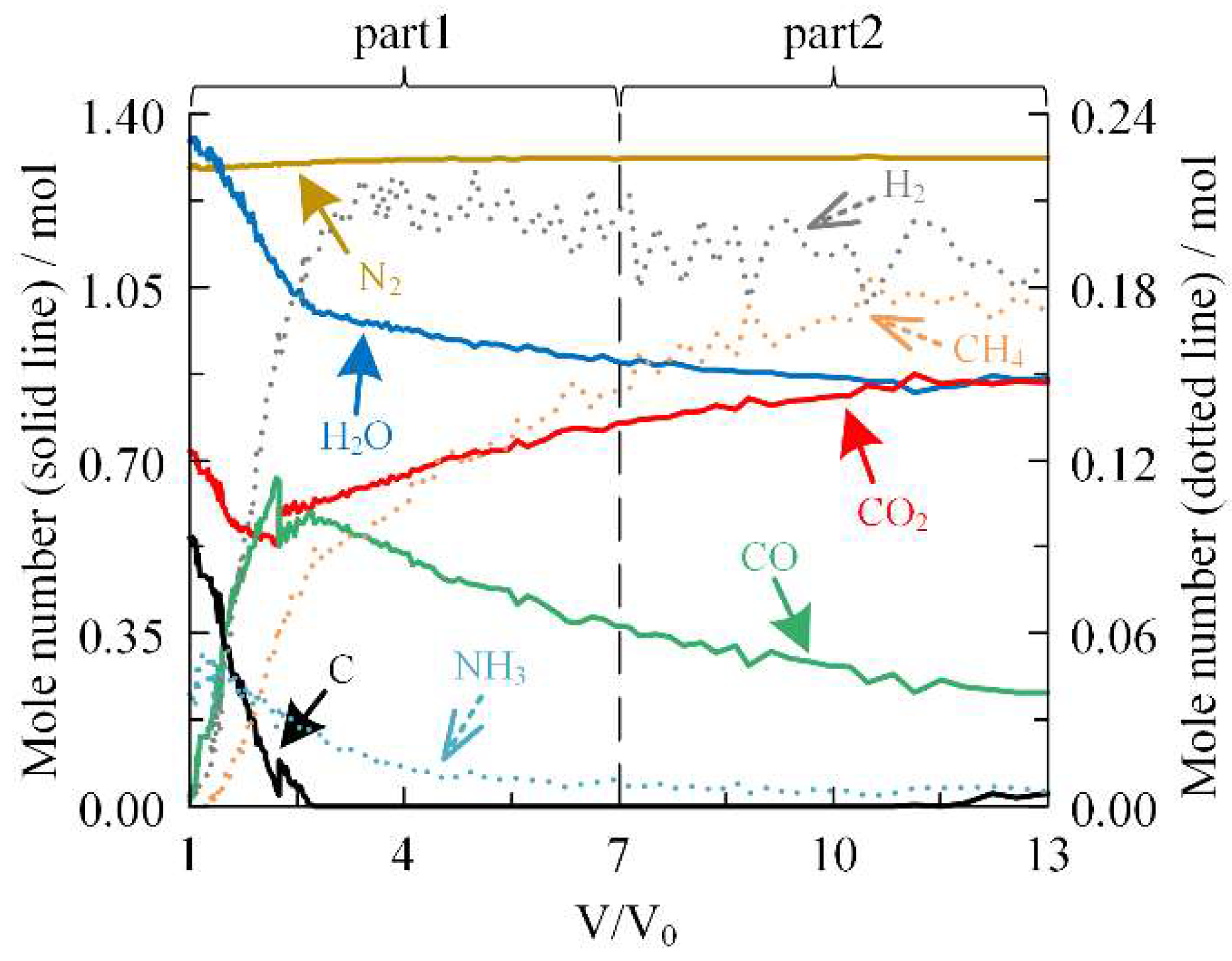
2.1.2. Compositional Evolution
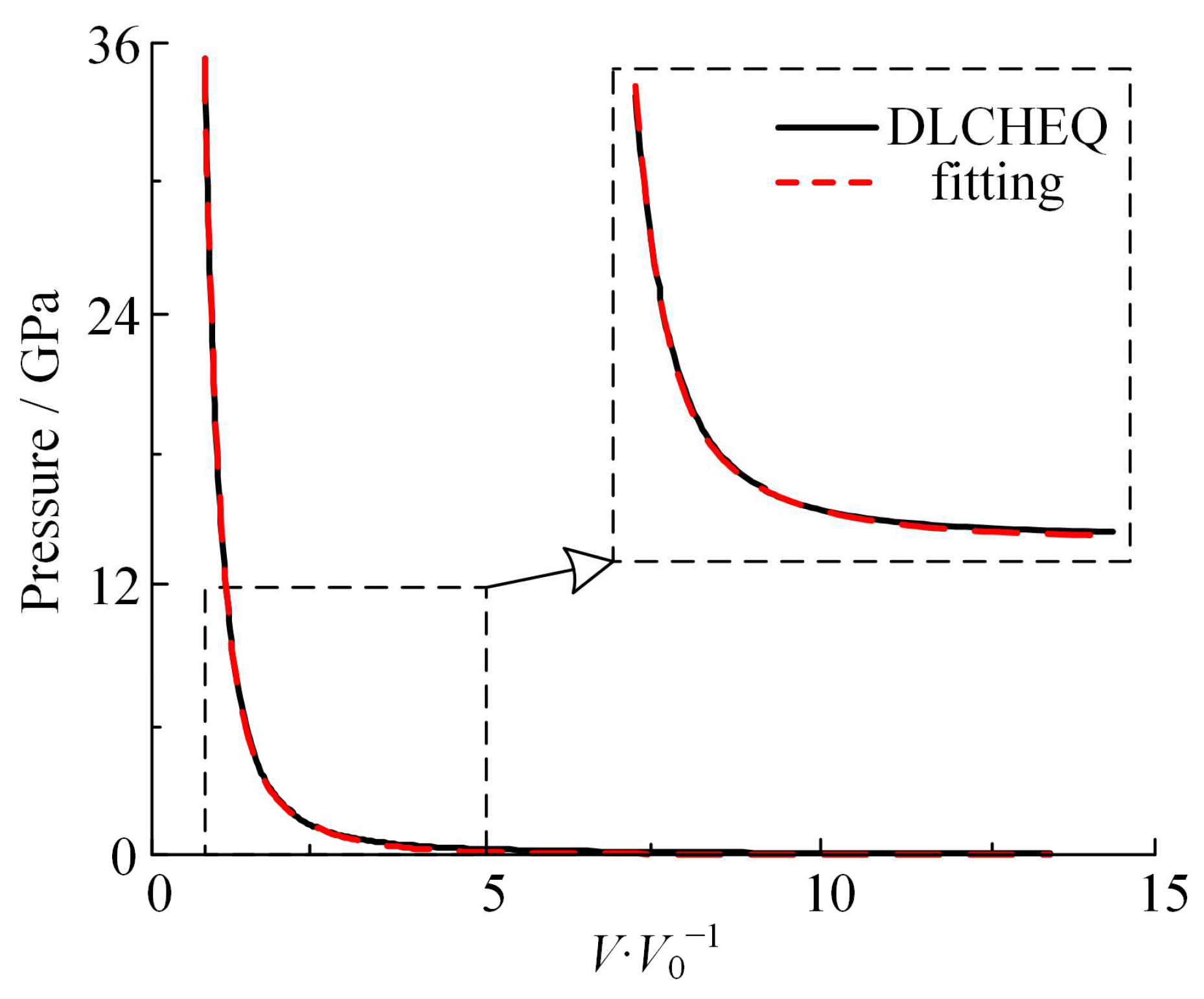
2.1.3. Isentropic Expansion Curve
2.2. Calibration of JWL Equation of State
2.2.1. Curve Fitting
2.2.2. Test Verification
3. Thin-Walled Cylindrical Shells Driven by Detonation Products
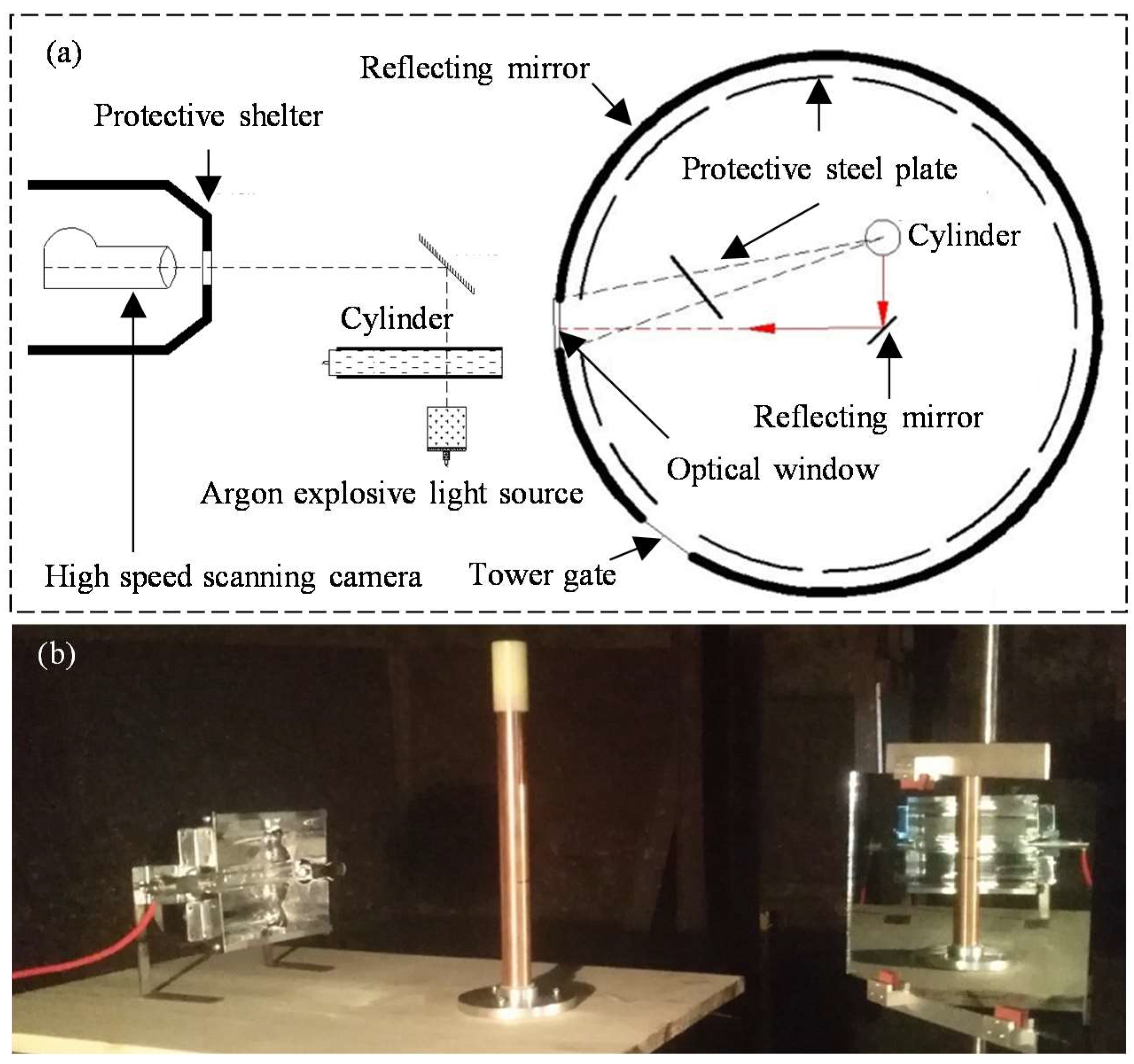
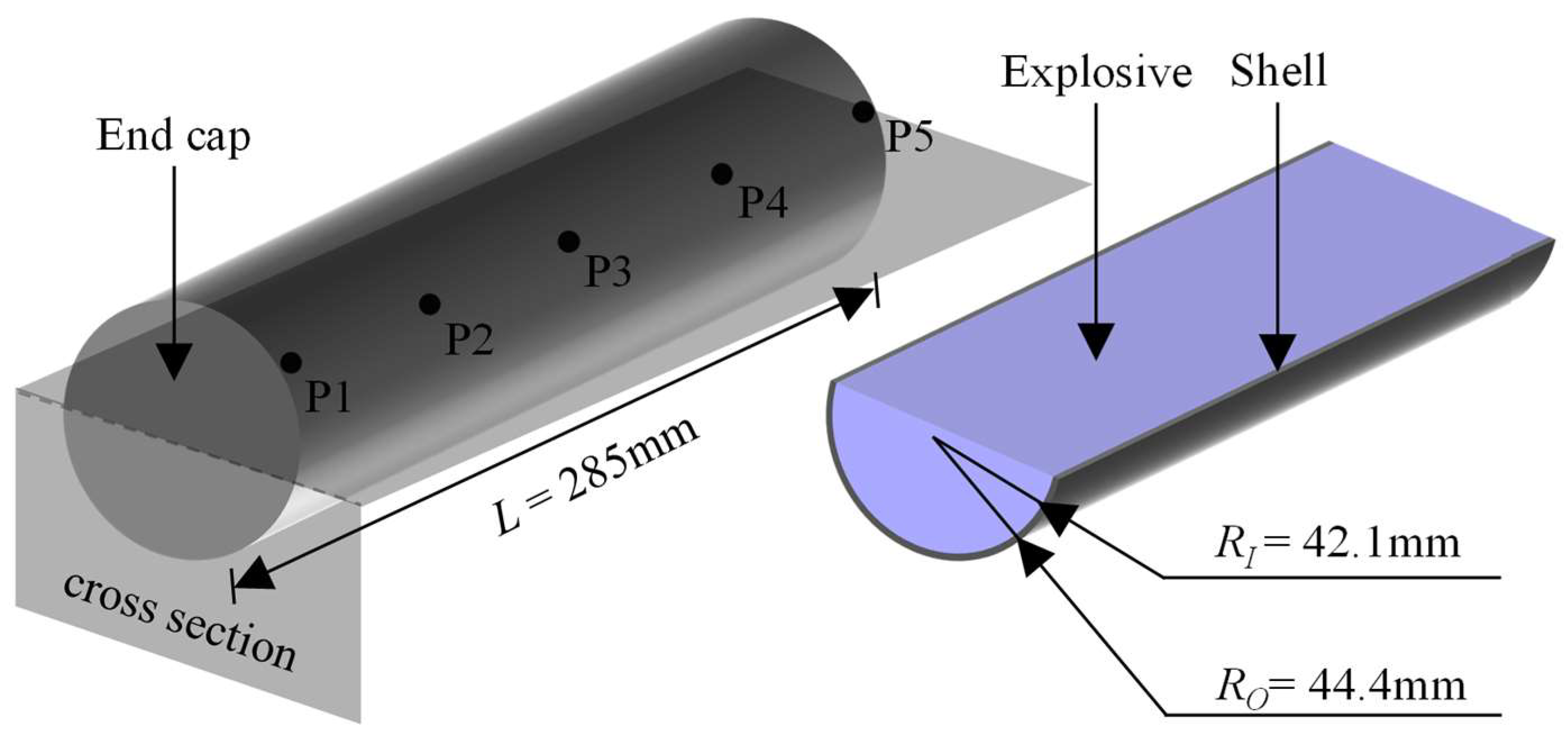
3.1. Experiment of Shelled Charge Explosion
3.2. Numerical Simulation Using Continuum–Discontinuum Element Method
3.2.1. Basic Concept
3.2.2. Explosion Model
3.2.3. Constitutive Model
3.3. Verification of Numerical Results
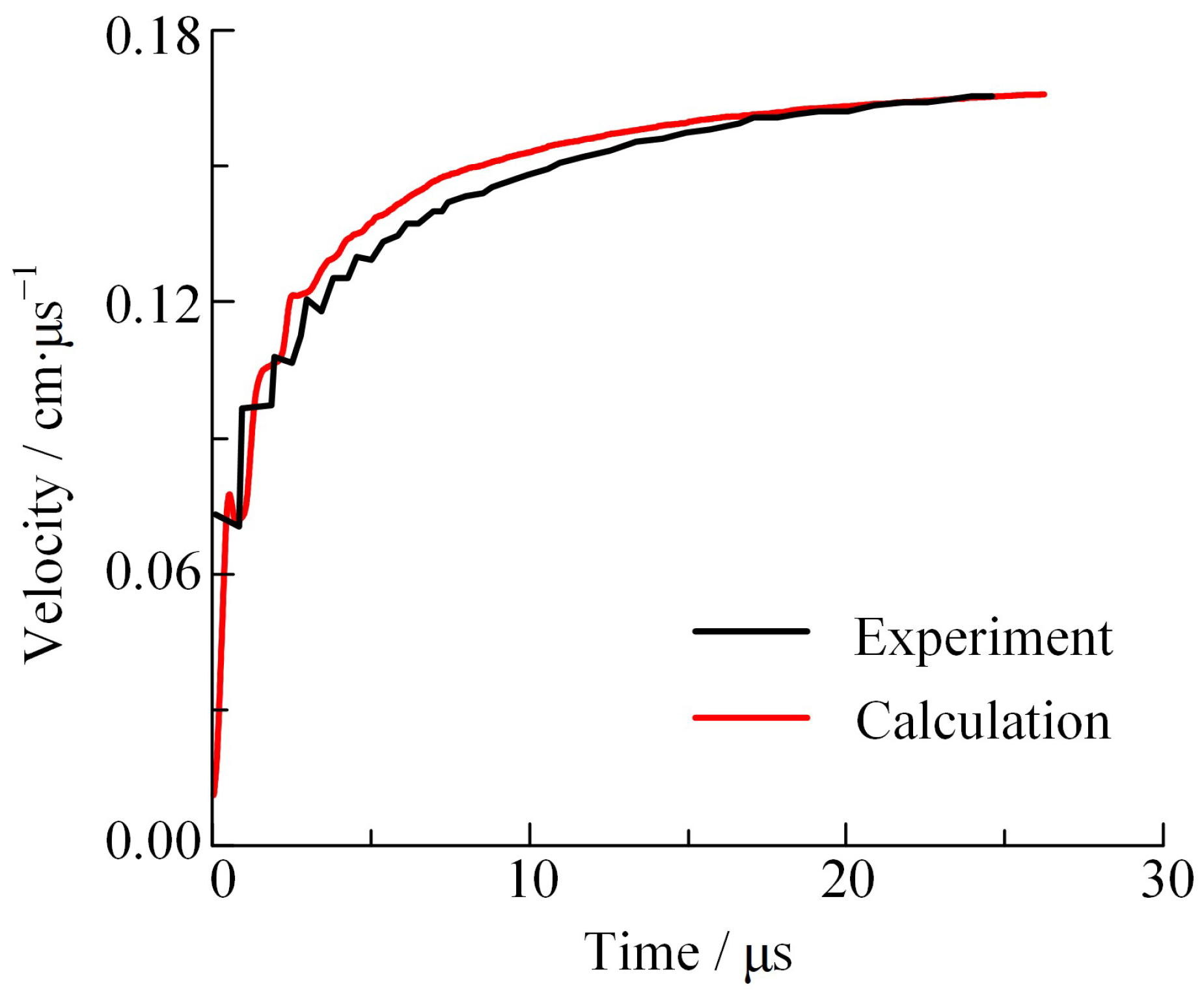
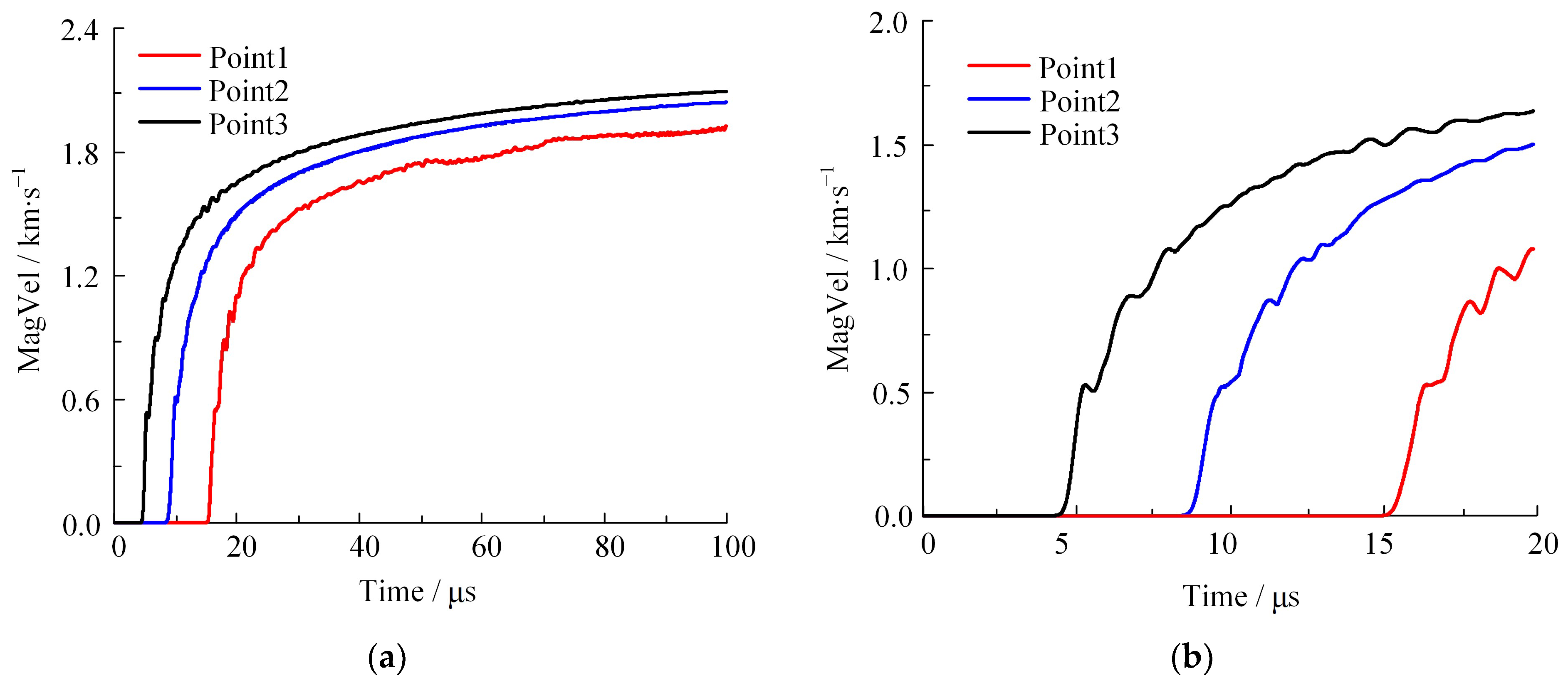
3.3.1. Initial Velocity of Fragments
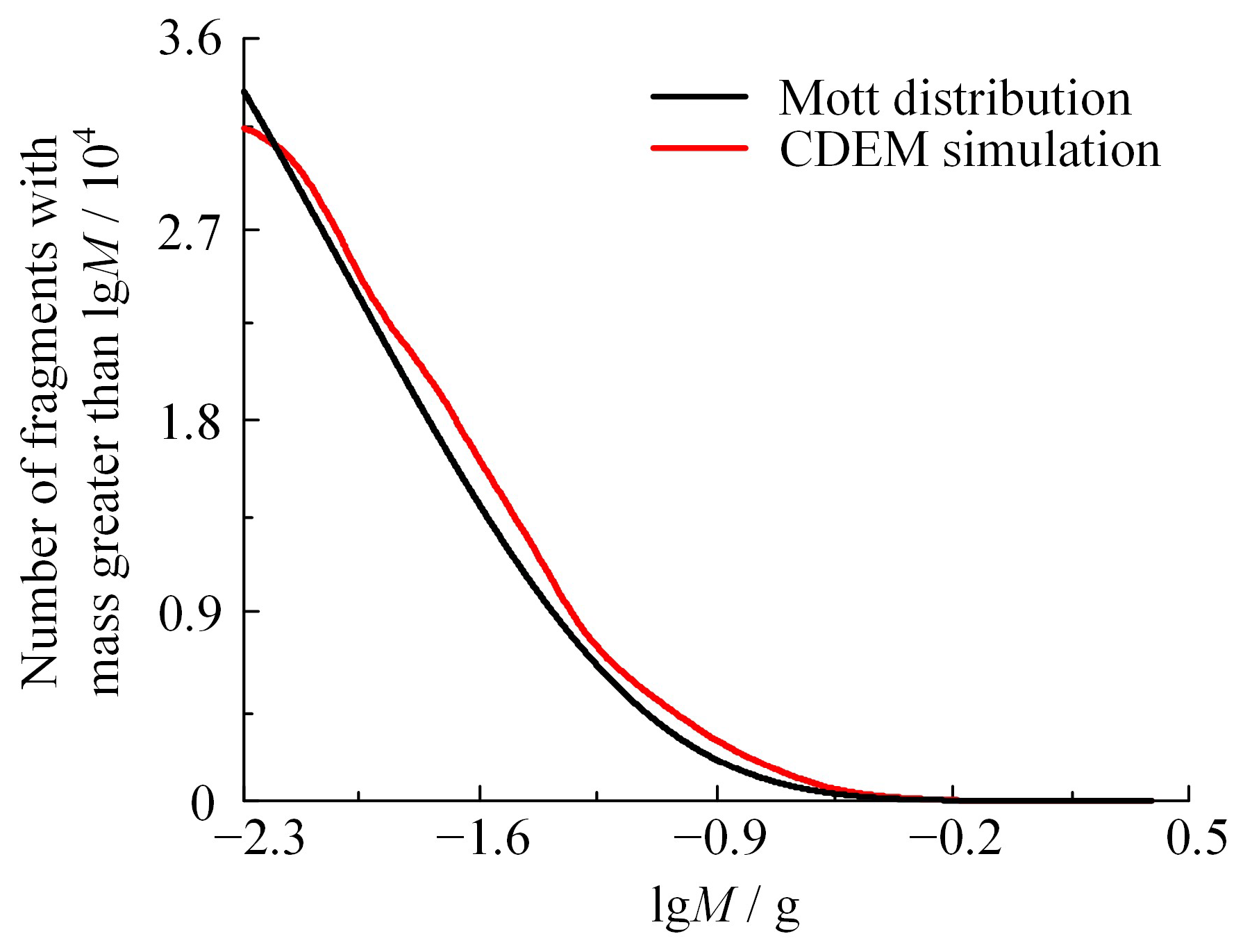
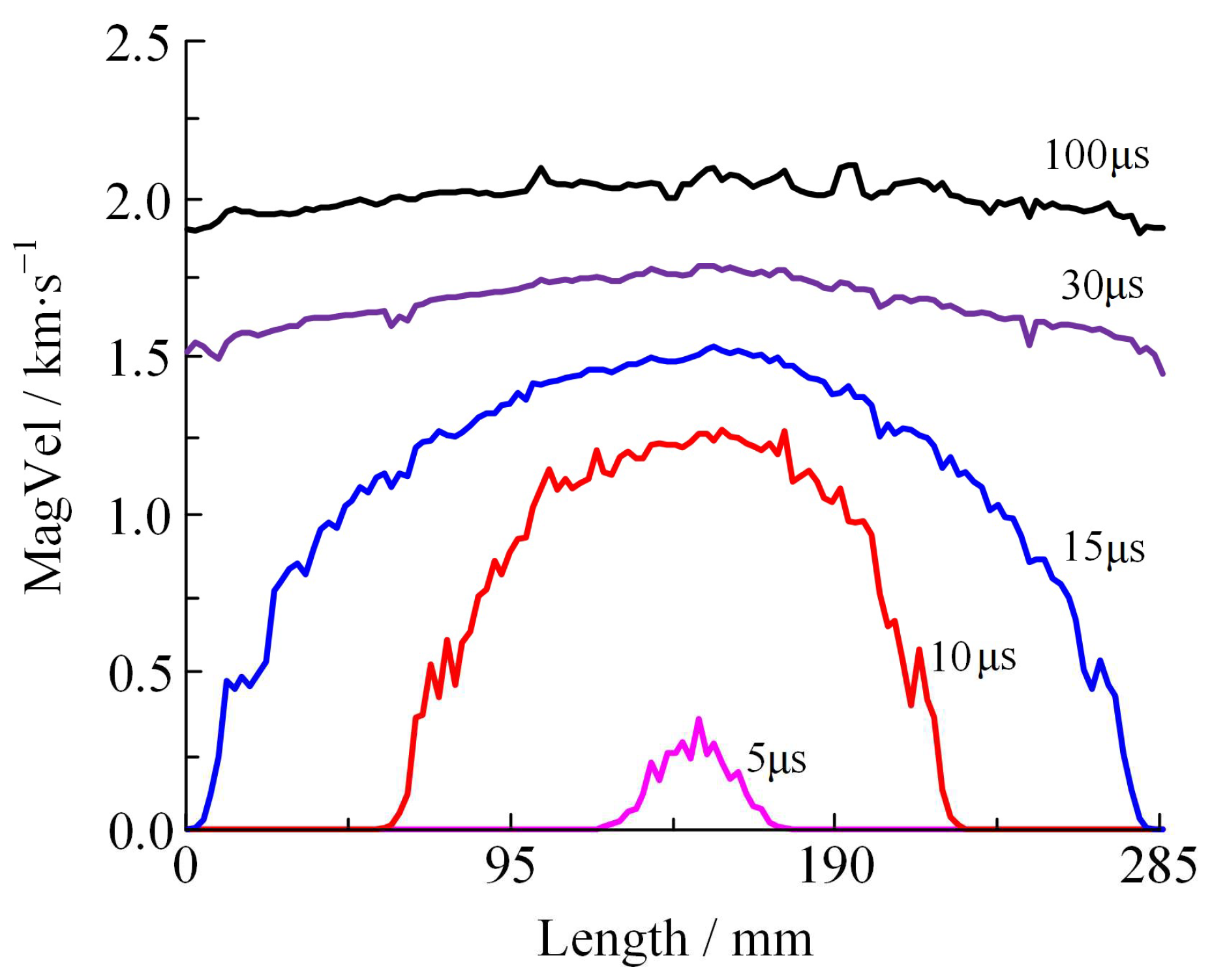
3.3.2. Mass–Quantity Distribution
4. Discussion
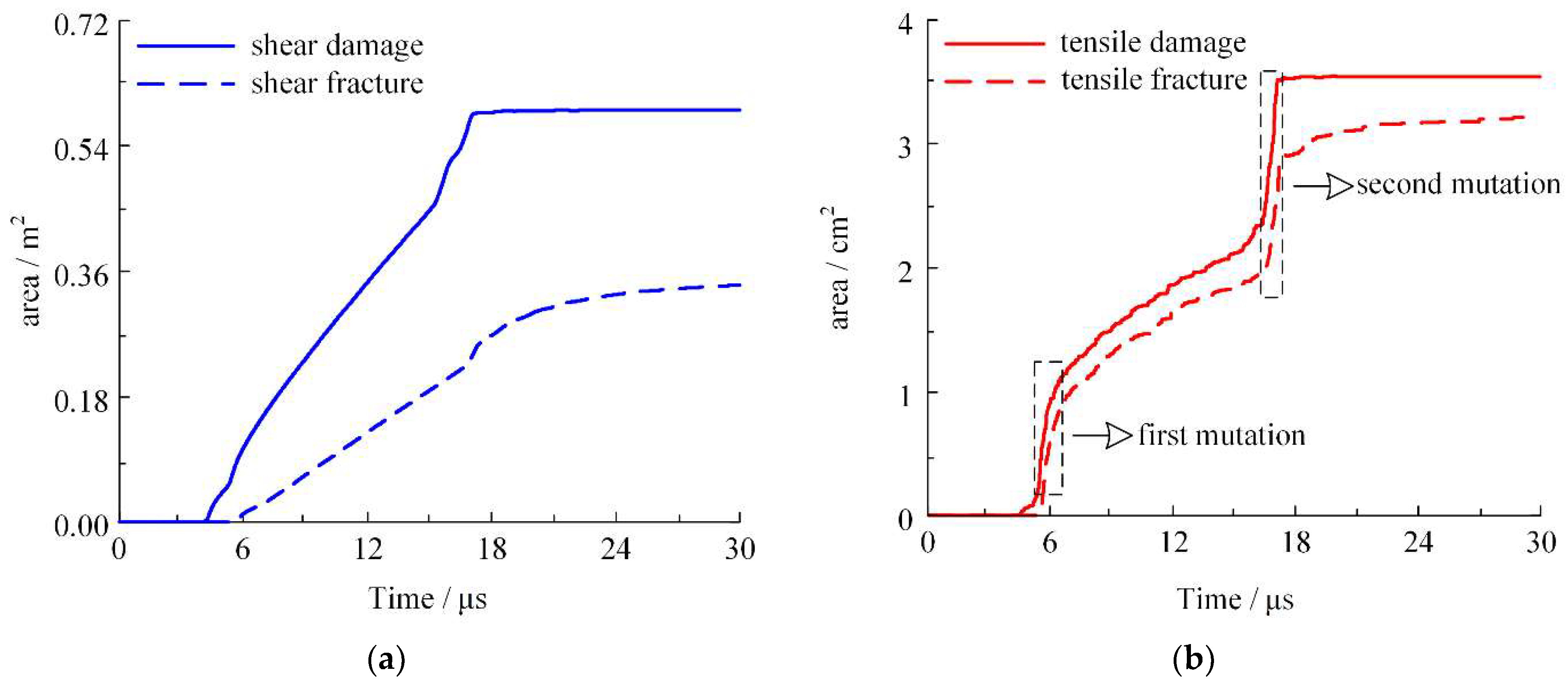
4.1. Fracture Mechanism of the Thin-Walled Cylindrical Shell
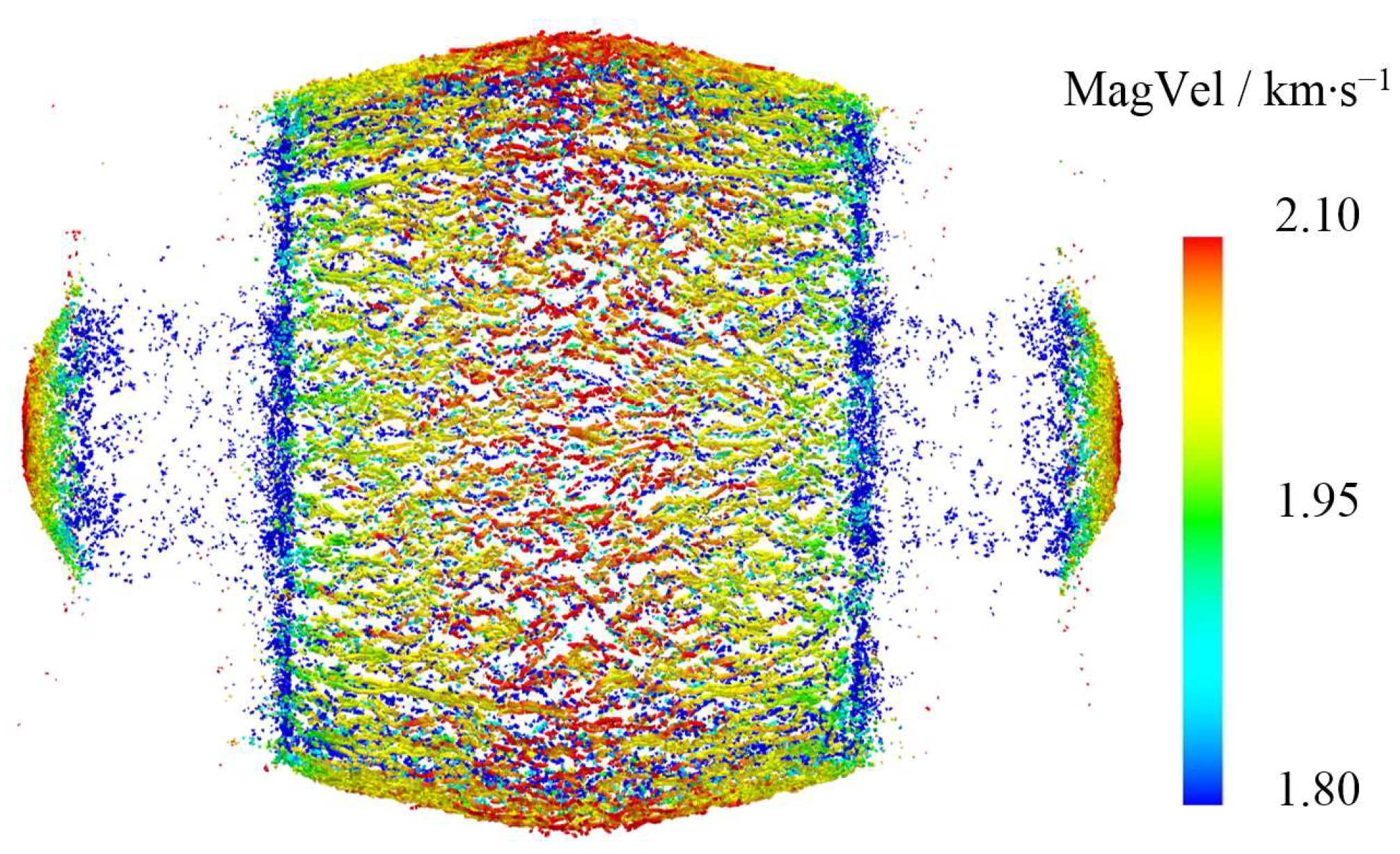
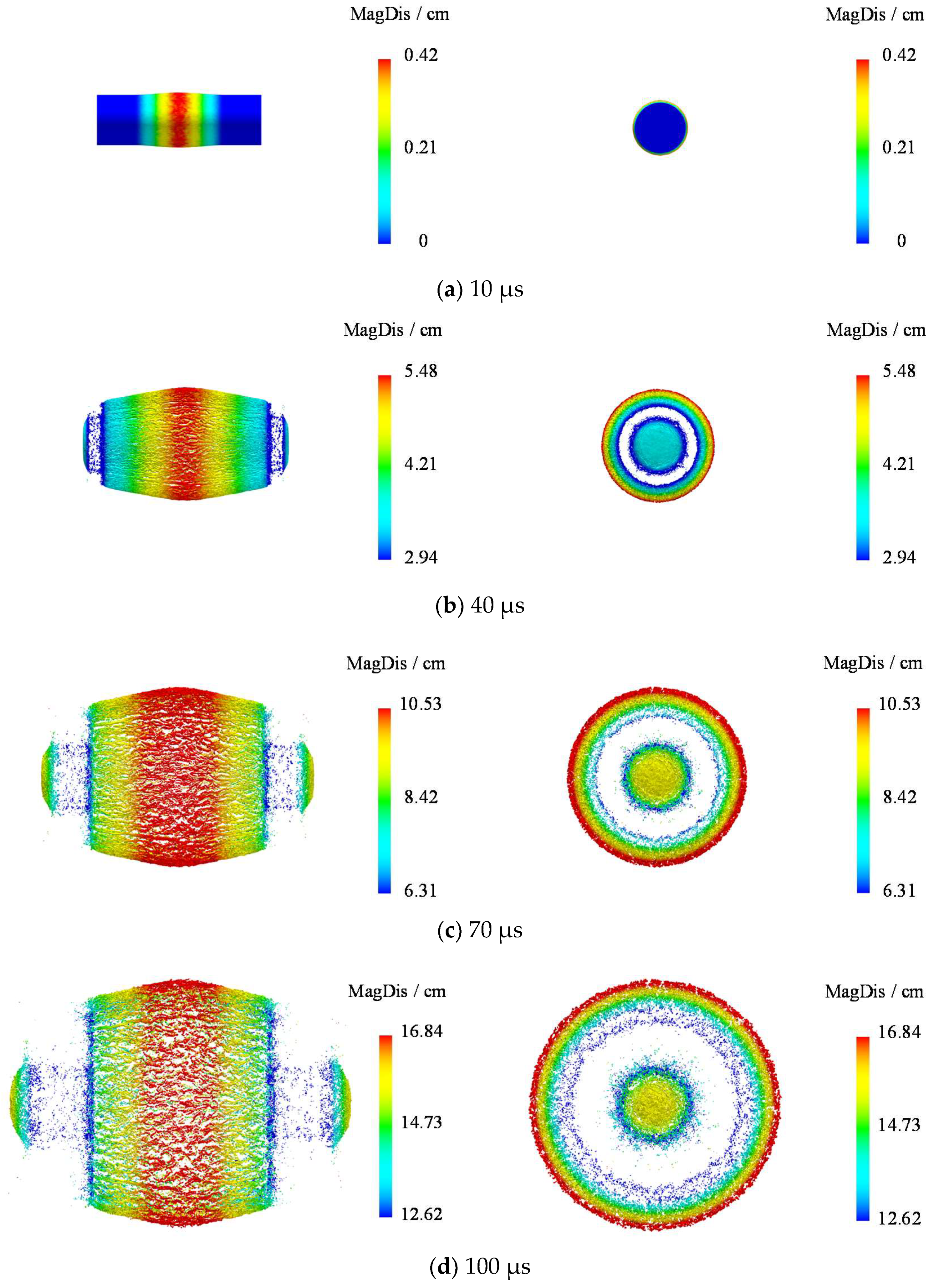
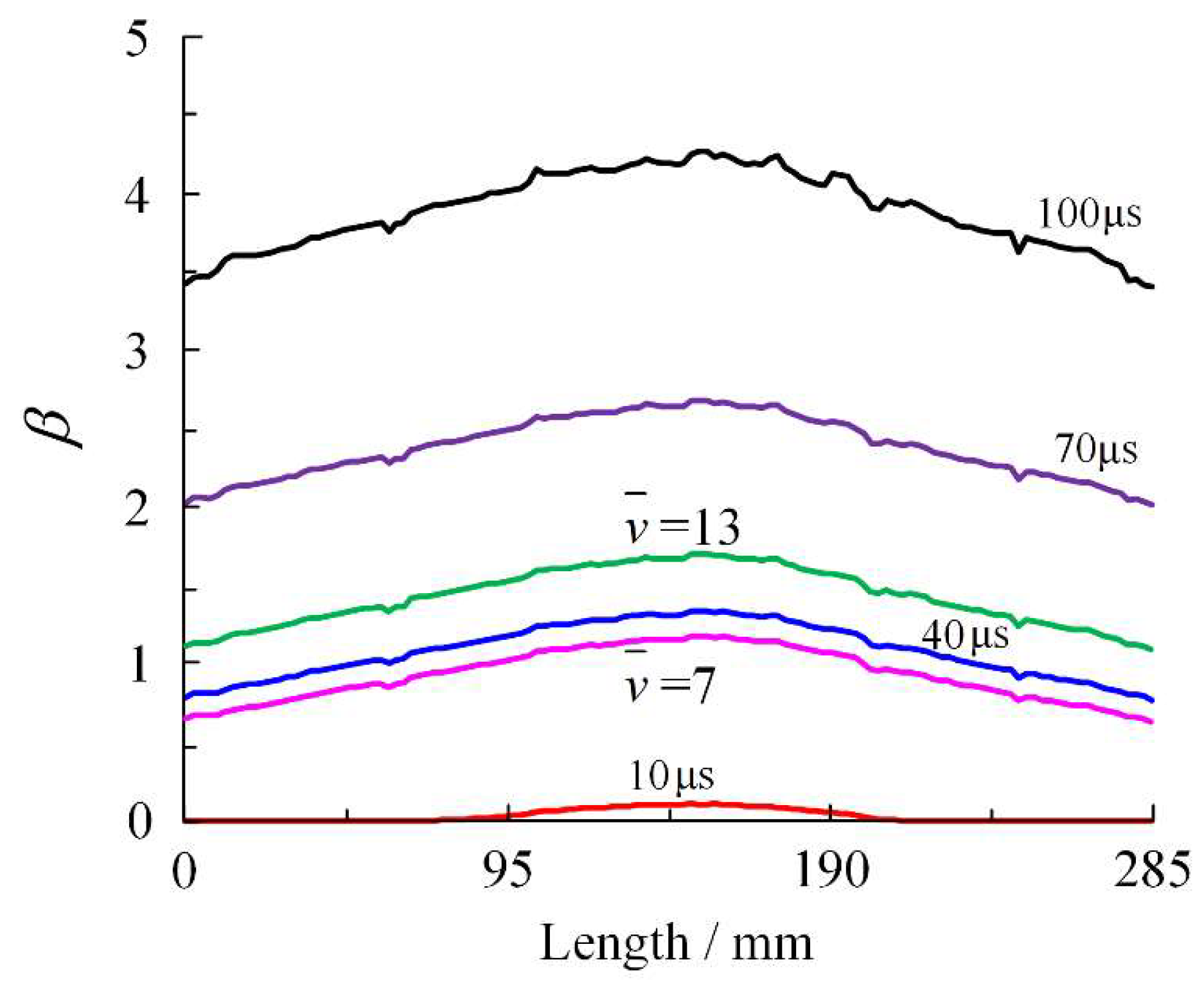
4.2. Scattering Characteristics of the Natural Fragments
5. Conclusions
- Using the thermochemical equation of state code DLCHEQ, the isentropic expansion curve of detonation products in the range of <13 was computed. Subsequently, the JWL EOS coefficients were calibrated across a wider range of temperature and pressure through curve fitting. This approach can successfully delineate an explosive’s work capacity, as the derived equation of state accurately reflects the cylinder test’s measurement results. Through this method, the fragmentation process of the shell can be described over a wider range.
- Simulation of dynamic fracture process of the shell was undertaken based on the continuum–discontinuum element method. The validity of the numerical simulation results was corroborated through the Mott mass–quantity distribution theory and shelled charge explosion test velocity measurement. The discrepancy between the average initial velocity of fragments and the experimental value was 9.04%. The mass–quantity distribution curve of the fragments aligned well with the theoretical curve, demonstrating a discrepancy of only 5.83% in the total fragment count when compared to Mott’s theoretical prediction. From these results, it can be seen that the scattering process of natural fragments generated by the thin-walled shell under implosion load is accurately described by the method.
- The thin-walled shell employed in this study primarily failed through shearing, generating strip fragments. In the evolution of tensile failure, two mutations generate local particle fragments, which constitute 1.8% of the total time and cover over 50% of the total failure area. Compared to shear failure, there is a “hysteresis effect” at the beginning of tensile failure and the hysteresis period is 0.5 μs. The shell’s failure process mainly lasts for 4–18 μs, after which the unit’s damage area stops growing and the fracture area begins to expand slowly. According to the processes of shell fracture and fragmentation, the acceleration process of natural fragments can be divided into three stages. The primary stages of fragment generation and acceleration are stages A and B, respectively. At 30 μs the shear/tensile damage/fracture area accounts for over 90% of the final value, and the average resultant velocity of fragments is 88.51% of the final value. The velocity and shear fracture area continue to gradually rise in stage C, indicating that fragments continue to be accelerated by detonation products outside the calibration range of the cylinder test. The final resultant velocity of fragments ranging from 1.8 to 2.1 km/s at 100 μs.
Author Contributions
Funding
Informed Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Baum, F.A.; Orlenko, L.P.; Stanyukovich, K.P.; Chelyshev, V.P.; Shekhter, B.I. Explosion Physics; Fizmatlit: Moscow, Russia, 1975. [Google Scholar]
- Zecevic, B.; Terzic, J.; Catovic, A. Influence of Warhead Case Material on Natural Fragmentation Performances. In Proceedings of the 15th International DAAAM Symposium, Vienna, Austria, 3–6 November 2004. [Google Scholar]
- Taylor, G.I. The Fragmentation of Tubular Bombs. Advis. Counc. Sci. Res. Tech. Dev. 1963, 5, 202–320. [Google Scholar]
- Gurney, R.W. The Initial Velocities of Fragments from Bombs, Shell, Grenades; Ballistic Research Laboratories Aberdeen Proving Ground: Aberdeen, MD, USA, 1943. [Google Scholar]
- Mott, N.F.; Linfoot, E.H. A Theory of Fragmentation. Minist. Supply AC 1943, 3348, 207–215. [Google Scholar]
- Gurney, R.W.; Sarmousakis, J.N. The Mass Distribution of Fragments from Bombs, Shell, and Grenades; Ballistic Research Laboratories: Aberdeen, MD, USA, 1944. [Google Scholar]
- Kury, J.W.; Hornig, H.C.; Lee, E.L.; McDonnel, J.L.; Ornellas, D.L.; Finger, M.; Strange, F.M.; Wilkins, M.L. Metal Acceleration by Chemical Explosives. In Proceedings: Fourth Symposium (International) on Detonation; US Government Printing Office: Washington, DC, USA, 1965; pp. 3–13. [Google Scholar]
- Bhatnagar, P.L.; Gross, E.P.; Krook, M. A Model for Collision Processes in Gases. I. Small Amplitude Processes in Charged and Neutral One-Component Systems. Phys. Rev. 1954, 94, 511. [Google Scholar]
- Weeks, J.D.; Chandler, D.; Andersen, H.C. Role of Repulsive Forces in Determining the Equilibrium Structure of Simple Liquids. J. Chem. Phys. 1971, 54, 5237–5247. [Google Scholar] [CrossRef]
- Wu, X. A Study on Thermodynamic Functions of Detonation Products. Propellants Explos. Pyrotech. 1985, 10, 47–52. [Google Scholar]
- Zhao, Y.; Liu, H.; Zhang, G.; Song, H.; Team, I. Equation of State of Detonation Products Based on Statistical Mechanical Theory. In Proceedings of the APS Shock Compression of Condensed Matter Meeting Abstracts, Washington, DC, USA, 7–12 July 2013; p. U3.002. [Google Scholar]
- Liu, Q.; Duan, Y.; Ma, H.; Long, X.; Han, Y. Review on the Exploration of Condensed Carbon Formation Mechanism in Detonation Products. AIP Adv. 2020, 10, 050701. [Google Scholar] [CrossRef]
- Li, X.; Yi, Z.; Liu, Q.; Liu, F.; Zhang, Z.; Hou, S.; Zheng, X.; Zhang, X.; Pei, H. Research of Detonation Products of RDX/Al from the Perspective of Composition. Def. Technol. 2022, 24, 31–45. [Google Scholar] [CrossRef]
- Zhao, Y.; Cao, W.; Huang, F.; Han, Y.; Long, X. Evaluation of Detonation Performance and Working Capacity of Explosives by Optimized VLW EOS. Combust. Flame 2022, 235, 111734. [Google Scholar] [CrossRef]
- Peng, Y.; Long, X.; Jiang, X.; Zhang, Z. A New High Order Virial Equation of State and Its Application in the Chapman-Jouguet Parameters Calculation of Explosives. Propellants Explos. Pyrotech. 2023, 48, e202100371. [Google Scholar] [CrossRef]
- Hoggatt, C.R.; Recht, R.F. Fracture Behavior of Tubular Bombs. J. Appl. Phys. 1968, 39, 1856–1862. [Google Scholar] [CrossRef]
- Martineau, R.L.; Anderson, C.A.; Smith, F.W. Expansion of Cylindrical Shells Subjected to Internal Explosive Detonations. Experimental Mechanics 2000, 40, 219–225. [Google Scholar] [CrossRef]
- Zhang, R.; Liu, J.; He, C.; Zhao, H.; Wang, Q. Test and Simulation Study of the Effect of Transverse Impact Stress on the Rosette 19-Hole Gun Propellant under Low Temperature. FirePhysChem 2022, 2, 147–153. [Google Scholar] [CrossRef]
- Cullis, I.G.; Dunsmore, P.; Harrison, A.; Lewtas, I.; Townsley, R. Numerical Simulation of the Natural Fragmentation of Explosively Loaded Thick Walled Cylinders. Def. Technol. 2014, 10, 198–210. [Google Scholar] [CrossRef] [Green Version]
- Felix, D.; Colwill, I.; Harris, P. A Fast and Accurate Model for the Creation of Explosion Fragments with Improved Fragment Shape and Dimensions. Def. Technol. 2022, 18, 159–169. [Google Scholar] [CrossRef]
- Wang, H.; Bai, C.; Feng, C.; Xue, K.; Zhu, X. An Efficient CDEM-Based Method to Calculate Full-Scale Fragment Field of Warhead. Int. J. Impact Eng. 2019, 133, 103331. [Google Scholar] [CrossRef]
- Zhu, X.; Feng, C.; Cheng, P.; Wang, X.; Li, S. A Novel Three-Dimensional Hydraulic Fracturing Model Based on Continuum–Discontinuum Element Method. Comput. Methods Appl. Mech. Eng. 2021, 383, 113887. [Google Scholar] [CrossRef]
- da Silva, L.A.; Johnson, S.; Critchley, R.; Clements, J.; Norris, K.; Stennett, C. Experimental Fragmentation of Pipe Bombs with Varying Case Thickness. Forensic Sci. Int. 2020, 306, 110034. [Google Scholar] [CrossRef]
- Shen, Z.-X.; Huang, H.-D.; Cen, Z.-B.; Chen, H.; Wang, D.; Zhu, G.-R.; Yuan, S.-Q. Natural Fragmentation Behavior of Steel Cylinders with Variable Charge Geometries under Detonation Loading. Combust. Explos. Shock Waves 2021, 57, 246–255. [Google Scholar] [CrossRef]
- Goto, D.M.; Becker, R.; Orzechowski, T.J.; Springer, H.K.; Sunwoo, A.J.; Syn, C.K. Investigation of the Fracture and Fragmentation of Explosively Driven Rings and Cylinders. Int. J. Impact Eng. 2008, 35, 1547–1556. [Google Scholar] [CrossRef]
- Tang, D.; Jia, X.; Huang, Z.; Chen, S.; Ma, B.; Xiao, Q.; Zu, X. Distribution of Shear Fragments Classified by Morphology. Int. J. Impact Eng. 2022, 165, 104217. [Google Scholar] [CrossRef]
- Gao, Y.; Feng, S.; Xiao, X.; Feng, Y.; Huang, Q. Fragment Characteristics from a Cylindrical Casing Constrained at One End. Int. J. Mech. Sci. 2023, 248, 108186. [Google Scholar] [CrossRef]
- Gao, Y.; Feng, S.; Xiao, X.; Zhang, B.; Huang, Q. Fragment Characteristics of Cylinder with Discontinuous Charge. Int. J. Impact Eng. 2023, 173, 104479. [Google Scholar] [CrossRef]
- Huang, G.; Li, W.; Feng, S. Axial Distribution of Fragment Velocities from Cylindrical Casing under Explosive Loading. Int. J. Impact Eng. 2015, 76, 20–27. [Google Scholar] [CrossRef]
- Li, W.; Huang, G.; Feng, S. Effect of Eccentric Edge Initiation on the Fragment Velocity Distribution of a Cylindrical Casing Filled with Charge. Int. J. Impact Eng. 2015, 80, 107–115. [Google Scholar] [CrossRef]
- Grisaro, H.; Dancygier, A.N. Numerical Study of Velocity Distribution of Fragments Caused by Explosion of a Cylindrical Cased Charge. Int. J. Impact Eng. 2015, 86, 1–12. [Google Scholar] [CrossRef]
- Zhu, J.; Zheng, Y.; Li, W.; Yang, Y.; Wang, X.; Qiao, X.; Li, R. Axial Distribution of Fragments from the Dynamic Explosion Fragmentation of Metal Shells. Int. J. Impact Eng. 2019, 123, 140–146. [Google Scholar] [CrossRef]
- Grady, D.E. Fragment Size Distributions from the Dynamic Fragmentation of Brittle Solids. Int. J. Impact Eng. 2008, 35, 1557–1562. [Google Scholar] [CrossRef]
- Guo, Z.; Huang, G.; Liu, C.; Feng, S. Velocity Axial Distribution of Fragments from Non-Cylindrical Symmetry Explosive-Filled Casing. Int. J. Impact Eng. 2018, 118, 1–10. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, B.; Yan, X.; Zhou, T.; Xiao, X.; Feng, S. Axial Distribution of Fragment Velocities from Cylindrical Casing with Air Parts at Two Ends. Int. J. Impact Eng. 2020, 140, 103535. [Google Scholar] [CrossRef]
- Liu, H.; Huang, G.; Guo, Z.; Feng, S. Fragments Velocity Distribution and Estimating Method of Thin-Walled Cylindrical Improvised Explosive Devices with Different Length-to-Diameter Ratios. Thin-Walled Struct. 2022, 175, 109212. [Google Scholar] [CrossRef]
- Li, X.-H.; Zhao, F.; Qin, J.-C.; Pei, H.-B. A New Method for Predicting the Detonation Velocity of Explosives with Micrometer Aluminum Powders. Propellants Explos. Pyrotech. 2018, 43, 333–341. [Google Scholar] [CrossRef]
- Li, X.; Li, G.; Wang, Z. A Self-Consistent Method to Research the Influence of Al Particle Temperature on Its Post-Detonation Reaction. AIP Adv. 2021, 11, 8. [Google Scholar] [CrossRef]
- Mao, X.; Zheng, Y.; Shen, F.; Wang, Y.; Wang, X.; Li, Y. A Method for Calculating the JWL Equation of State Parameters for the Detonation Products of CL-20-Based Aluminized Explosives. J. Energetic Mater. 2022, 40, 182–205. [Google Scholar] [CrossRef]


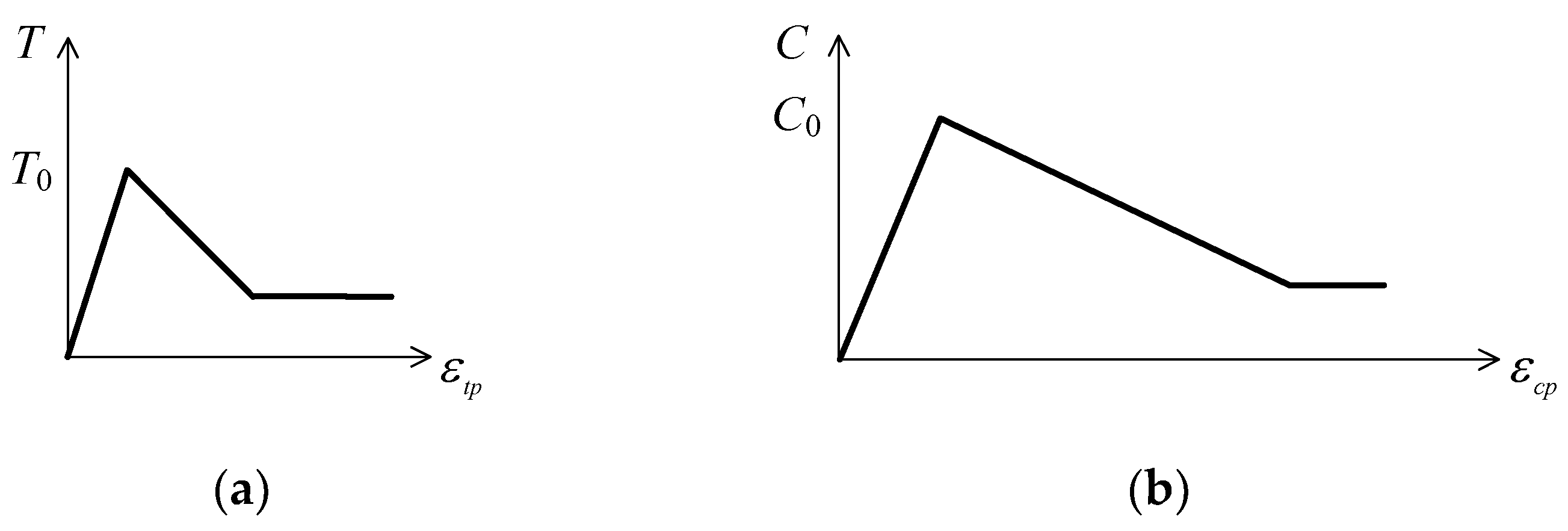


| A | B | C | R1 | R2 | ω |
|---|---|---|---|---|---|
| 8 | 0.16 | 0.004 | 4.3 | 1.1 | 0.36 |
| Velocity/km·s−1 | |||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | Average | ||
| Test distance/m | 4 | 1.49 | 2.00 | 1.92 | 1.80 |
| 5.2 | 2.03 | 1.60 | 1.43 | 1.69 | |
| Density ρ/g·cm−3 | Elastic Modulus E/GPa | Poisson Ratio | Cohesion Force C0/MPa | Tensile Strength T0/MPa | Internal Friction Angle f/° |
|---|---|---|---|---|---|
| 7.85 | 198 | 0.33 | 15 | 500 | 40 |
| Quality Interval/g | ||||||
|---|---|---|---|---|---|---|
| 0.01–0.0105 | 0.0105–0.0205 | 0.0205–0.0405 | 0.0405–0.0705 | >0.0705 | ||
| Mott theory | Number | 9188 | 8101 | 7157 | 4308 | 4779 |
| Proportion of total quantity | 27.4% | 24.16% | 21.34% | 12.85% | 14.25% | |
| Proportion of total mass | 1.23% | 19.81% | 24.23% | 19.81% | 34.92% | |
| CDEM | Number | 6353 | 6959 | 7852 | 4867 | 5732 |
| Proportion of total quantity | 20.00% | 21.91% | 24.72% | 15.32% | 18.05% | |
| Proportion of total mass | 3.31% | 6.59% | 14.75% | 16.20% | 59.15% | |
| Error of fragments quantity | 30.86% | 14.10% | 9.71% | 12.98% | 19.44% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ou, Y.; Yuan, J.; Lin, Q.; Jiao, W.; Yuan, J.; Su, J.; Feng, C.; Li, X.; Gan, Y. Investigation of the Fracture and Fragmentation of Implosively Driven Thin-Walled Cylindrical Shell: From Thermodynamic Analysis to CDEM Simulation. Materials 2023, 16, 5619. https://doi.org/10.3390/ma16165619
Ou Y, Yuan J, Lin Q, Jiao W, Yuan J, Su J, Feng C, Li X, Gan Y. Investigation of the Fracture and Fragmentation of Implosively Driven Thin-Walled Cylindrical Shell: From Thermodynamic Analysis to CDEM Simulation. Materials. 2023; 16(16):5619. https://doi.org/10.3390/ma16165619
Chicago/Turabian StyleOu, Yinzhe, Jianfei Yuan, Qindong Lin, Wenjun Jiao, Junming Yuan, Jianjun Su, Chun Feng, Xinghan Li, and Yundan Gan. 2023. "Investigation of the Fracture and Fragmentation of Implosively Driven Thin-Walled Cylindrical Shell: From Thermodynamic Analysis to CDEM Simulation" Materials 16, no. 16: 5619. https://doi.org/10.3390/ma16165619





